Addressing Due Date and Storage Restrictions in the S-Graph Scheduling Framework

Abstract

This paper addresses the Flexible Job Shop Scheduling Problem (FJSP) with the objective of minimizing both earliness/tardiness (E/T) and intermediate storage time (IST). An extended S-graph framework that incorporates E/T and IST minimization while maintaining the structural advantages of the original S-graph approach is presented. The framework is further enhanced by integrating linear programming (LP) techniques to adjust machine assignments and operation timings dynamically. The following four methodological approaches are systematically analyzed: a standalone S-graph for E/T minimization, an S-graph for combined E/T and IST minimization, a hybrid S-graph with LP for E/T minimization, and a comprehensive hybrid approach addressing both E/T and IST. Computational experiments on benchmark problems demonstrate the efficacy of the proposed methods, with the standalone S-graph showing efficiency for smaller instances and the hybrid approaches offering improved solution quality for more complex scenarios. The research provides insights into the trade-offs between computational time and solution quality across different problem configurations and storage policies. This work contributes to the field of production scheduling by offering a versatile framework capable of addressing the multi-objective nature of modern manufacturing environments.

1. Introduction

The Flexible Job Shop Problem (FJSP) represents a significant advancement over the classical Job Shop Scheduling Problem (JSP) by incorporating flexibility into machine assignments, thereby enhancing its applicability to complex real-world manufacturing scenarios. In the FJSP framework, each job comprises a series of operations, with each operation capable of being processed by multiple machines. This inherent flexibility is essential for accommodating variations in machine capabilities and availability, reflecting the dynamic nature of modern manufacturing environments [1]. The FJSP is characterized by several key features that contribute to its complexity as follows:

• Job-specific due dates: Each job has its own deadline, which introduces time-sensitive constraints that must be managed effectively [2].
• Machine-specific processing times: The time required to process an operation can vary significantly depending on the machine utilized, necessitating careful consideration of machine selection [3].
• Precedence constraints: Certain operations may need to be completed before others can commence, adding another layer of complexity to the scheduling process [4].

The initial research on the FJSP predominantly focused on single-objective optimization paradigms, with primary emphasis on minimizing key performance indicators such as makespan, economic costs, energy consumption, total tardiness, and total flow time. This approach laid the foundation for understanding the fundamental trade-offs inherent in complex manufacturing scheduling scenarios.

The complexity of the FJSP is further compounded by its multi-objective nature, which necessitates a delicate balance between maximizing machine utilization and adhering to scheduling constraints. This balance is crucial for minimizing overall production costs while ensuring timely delivery of products. The practical implications of the FJSP are particularly evident in various manufacturing sectors, including automotive assembly lines and semiconductor fabrication facilities. In these contexts, optimizing machine usage while meeting stringent deadlines is vital for sustaining operational efficiency and competitiveness [5].

Given its classification as an NP-hard problem, the FJSP poses significant challenges for traditional optimization techniques [6]. Consequently, researchers and practitioners have explored a range of advanced solution methodologies, including the following:

• Heuristic approaches: These methods provide quick, rule-based solutions that can yield satisfactory results within reasonable time frames [7,8].
• Metaheuristic techniques: Algorithms such as Genetic Algorithms (GAs), Simulated Annealing (SA), and Particle Swarm Optimization (PSO) have been employed to effectively explore large solution spaces and identify near-optimal schedules [9,10].
• Optimization-based approaches: Techniques such as Mixed Integer Linear Programming (MILP) are utilized to rigorously formulate the problem, although they may struggle with larger cases due to computational intensity [11].

This paper presents an extension of the S-graph framework [12] to address these complex scheduling challenges. The S-graph framework, originally developed for batch process scheduling, has proven effective in representing and solving various scheduling problems [13,14]. Our work enhances this framework to simultaneously minimize earliness/tardiness (E/T) penalties and intermediate storage time while accommodating different storage policies. The main contributions of this paper include the following:

• An extension of the S-graph framework to handle job-specific due dates and E/T minimization in FJSP.
• The integration of intermediate storage time considerations into the scheduling model.
• The development of a hybrid approach that combines the S-graph framework with Linear Programming (LP) to enhance solution quality.

We present a comprehensive methodology that includes problem formulation, algorithm development, and experimental results. Our approach is evaluated on a series of test instances, demonstrating its effectiveness in generating high-quality schedules that balance multiple objectives under various constraints.

This research contributes to the field of production scheduling by providing a robust framework for addressing complex, real-world scheduling scenarios in flexible job shop environments. The insights gained from this study have significant implications for improving operational efficiency in manufacturing systems, particularly in industries where due date adherence and storage management are critical factors.

1.1. Literature Review

The FJSP is a complex scheduling problem that extends the classical JSP by allowing operations to be processed on any machine from a given set of compatible machines. This flexibility adds a layer of complexity to the already challenging task of optimizing production schedules.

The FJSP is characterized by a set of jobs, each consisting of a sequence of operations, and a set of machines capable of performing these operations [11]. Unlike the traditional job shop problem, where each operation is assigned to a specific machine, FJSP allows for machine flexibility [15]. This means that an operation can be processed on any machine from a predefined set of compatible machines, with potentially different processing times. Key characteristics of the FJSP include the following:

• The system is initially empty, meaning no jobs are present at the start of the scheduling horizon.
• All machines are available at time zero.
• All jobs are available after the release dates.
• Operations can be assigned to multiple compatible machines.
• Each machine can only perform one operation at a time.
• The processing time of an operation may vary depending on the assigned machine.
• Operations within a job must be processed in a specific order.
• There are no precedence constraints among operations of different jobs.
• Preemption is not allowed; once an operation starts on a machine, it must be completed without interruption.
• Machines operate under deterministic conditions with no unplanned stoppages, breakdowns, or capacity reductions.
• All operations are assumed to be completed successfully on the first attempt, with a zero scrap rate.
• Buffers with infinite capacity are available for all machines, ensuring unrestricted intermediate storage for operations waiting to be processed.

The FJSP plays a crucial role in modern manufacturing and production environments, offering significant advantages in modeling flexible manufacturing systems where machines are multi-purpose and capable of handling various operations [16]. This approach enhances resource utilization by enabling better workload balancing and increased overall efficiency through the assignment of operations to multiple machines. The FJSP also improves production adaptability, allowing for quicker responses to changes in production requirements or machine availability. Furthermore, the additional degrees of freedom in scheduling decisions provided by the FJSP create opportunities for optimizing various performance metrics, ultimately leading to more efficient and cost-effective manufacturing processes.

Solving the FJSP is considerably more challenging than the classical job shop problem due to its increased complexity. Some of the main challenges include the following:

• The FJSP is an NP-hard combinatorial optimization problem, meaning that finding optimal solutions becomes computationally intractable as the problem size increases [17].
• The FJSP requires solving two interrelated subproblems simultaneously, as follows [1]:
  • Deciding which machine will process each operation.
  • Determining the processing order of operations on each machine.
• The flexibility in machine assignments significantly expands the solution space, making it more difficult to explore effectively.
• Real-world applications often require considering multiple, sometimes conflicting, objectives such as minimizing makespan, reducing tardiness, and balancing machine workloads.
• In practical settings, the FJSP often needs to account for dynamic factors such as machine breakdowns, rush orders, or changes in processing times, further complicating the scheduling process.

To address these challenges, researchers have developed various approaches, including metaheuristics, mathematical programming, and hybrid methods. These approaches aim to find high-quality solutions within reasonable computational times, often trading off optimality for practicality in large-scale problems [18].

One approach for handling these disruptions is the selection of the appropriate rescheduling schemes, which can significantly impact production efficiency. A decision-making framework utilizing the G1-improved entropy method and improved TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) has been proposed to evaluate and rank alternative rescheduling strategies. This model considers production loss cost, completion time, machine load balancing rate, and additional machine energy consumption, providing a structured approach to selecting the most effective rescheduling method in dynamic environments [19].

Scheduling objectives play a pivotal role in defining the performance metrics and goals for production scheduling problems, including the FJSP. Makespan, the time required to complete all jobs in a given schedule, is a fundamental objective in scheduling problems, particularly in manufacturing environments [20]. The importance of makespan minimization lies in its ability to increase overall production efficiency, reduce the idle time of machines and resources, and improve throughput and capacity utilization [21,22]. Minimizing makespan typically involves the efficient allocation of operations to machines, optimizing the sequence of operations on each machine, and balancing workload across available resources [23]. However, it is important to note that focusing solely on makespan can sometimes lead to suboptimal solutions in terms of other critical factors such as due dates or resource utilization [24].

E/T minimization aims to complete jobs as close as possible to their due dates [25]. This objective is particularly relevant in just-in-time production environments and industries where storage costs or penalties for late deliveries are significant [26]. Earliness is defined as the positive time difference between a job’s due date and its actual completion time when the job is finished early, while tardiness represents the positive time difference between the actual completion time and the due date when the job is completed late. These metrics quantify the deviation from the desired completion time in both directions.

Minimizing E/T involves balancing early completion (which may incur storage costs) with late completion (which may result in penalties or customer dissatisfaction), considering individual job priorities and due dates, and potentially allowing for idle time between operations to avoid early completion of certain jobs [27].

Real-world scheduling problems often require the consideration of multiple, sometimes conflicting, objectives. Balancing these objectives is a complex task that aims to find solutions that perform well across various performance metrics [28]. Common approaches to multi-objective scheduling include the following:

• Weighted sum method: Assigning weights to different objectives and optimizing their weighted sum [29].
• Pareto optimization: Finding a set of non-dominated solutions that represent different trade-offs between objectives [30].
• Lexicographic ordering: Prioritizing objectives and optimizing them in order of importance [31].
• Goal programming: Setting target levels for each objective and minimizing deviations from these targets [32].

Challenges in multi-objective scheduling include determining the appropriate weights or priorities for different objectives, handling conflicting objectives, increased computational complexity due to the need to evaluate multiple criteria, and presenting and interpreting results to decision-makers [33].

Overall, the choice and balancing of scheduling objectives should be tailored to the specific needs and constraints of the production environment, taking into account factors such as customer requirements, resource limitations, and the strategic goals of the organization [34].

The FJSP has garnered significant attention in the field of operations research due to its applicability to complex manufacturing systems [35]. Since its inception as an extension of the classical JSP, researchers have proposed a plethora of models and algorithms to address the increased complexity arising from machine flexibility and dynamic job constraints [1]. The methodologies for solving the FJSP can be categorized into three primary classifications as follows: exact methods, heuristics, and metaheuristics.

Initial research efforts focused on MILP models, which provided optimal solutions for small-scale FJSP instances [36]. However, the combinatorial explosion of variables as the problem size increases limits the scalability of exact methods. Branch-and-bound (B&B) and branch-and-cut techniques have been explored, but their computational complexity restricts their application to relatively small job sets [37].

To mitigate scalability issues, researchers have employed heuristic methods such as dispatching rules and greedy algorithms [38]. These approaches generate feasible schedules by prioritizing jobs based on criteria such as earliest due date or shortest processing time, while computationally efficient, heuristic methods often fail to guarantee optimality and may require significant parameter tuning to adapt to specific production environments [39].

Recent research has witnessed a paradigm shift towards metaheuristic algorithms, including GAs, SA, ant colony optimization (ACO), and PSO. These approaches have demonstrated efficacy in solving large-scale FJSPs due to their ability to explore the solution space more comprehensively and escape local optima [40]. For instance, hybrid algorithms combining GA with local search techniques have been utilized to balance the trade-off between solution quality and computational effort [41,42].

Beyond conventional techniques, reinforcement learning (RL) has gained prominence in scheduling research, offering adaptive decision-making capabilities that enhance scheduling flexibility and robustness. Methods such as Q-learning and deep Q-networks (DQN) enable real-time adaptation to dynamic production environments, allowing optimization strategies to effectively respond to uncertainties. Recent studies have explored hybrid optimization techniques that integrate RL into metaheuristics, known as Ensemble Meta-Heuristic and Reinforcement Learning (E-MHRL). A comprehensive review [43] highlights the growing application of RL in conjunction with metaheuristic algorithms such as GA, PSO, and SA. These hybrid models improve scheduling efficiency by dynamically adjusting search strategies and fine-tuning algorithmic parameters. The study emphasizes that E-MHRL approaches significantly outperform traditional scheduling methods by leveraging RL’s learning capabilities to optimize decision-making policies and enhance computational efficiency.

Expanding on this trend, a multi-objective flexible job shop scheduling framework has been proposed, leveraging Graph Attention Networks (GATs) and RL to optimize scheduling efficiency. The approach employs a dual GAT structure to capture machine and operation features, while an Actor-Critic RL model dynamically adjusts scheduling strategies to balance makespan, maximum machine load, and total machine load. Comparative experiments demonstrate that this hybrid method achieves superior Pareto front solutions, outperforming state-of-the-art multi-objective evolutionary algorithms in both solution quality and generalization to larger scheduling instances [44].

The literature also explores various FJSP extensions, such as the multi-objective FJSP, where factors like machine energy consumption, setup times, and workforce constraints are considered alongside E/T penalties [45,46]. Furthermore, the inclusion of dynamic FJSPs, where machine availability and job arrival times are stochastic, reflects more realistic production environments and introduces additional layers of complexity [47,48]. The development of efficient algorithms for the FJSP remains an active area of research, with metaheuristics playing a pivotal role in addressing the problem’s combinatorial complexity and multi-objective nature. These approaches not only improve machine utilization but also minimize penalties related to job E/T, contributing to significant gains in production efficiency [49].

The scheduling of jobs to minimize E/T penalties is a critical area of study in operations research, particularly within the domain of production scheduling [50]. The field of scheduling algorithms encompasses a variety of established techniques designed to effectively manage due date constraints, which are essential for optimizing operational efficiency and minimizing tardiness across various applications, particularly within complex manufacturing environments [51].

Priority rules involve assigning precedence values to tasks based on factors such as due date, processing time, and setup time. Tasks with higher priority values are scheduled before those with lower values, ensuring urgent tasks are addressed promptly. This method is particularly effective in task assignment problems where prioritization is based on due dates and processing times [52]. However, while effective for straightforward scenarios, priority rules can struggle with complex dependencies and dynamic environments [53].

Deadline adjustment algorithms dynamically modify task deadlines to ensure schedule feasibility while minimizing tardiness. These iterative techniques adjust deadlines based on task dependencies and execution risks [54]. While they enhance flexibility and adaptability in scheduling, they may require significant computational resources for real-time adjustments in large-scale systems [55].

Constraint programming (CP) offers a declarative approach that leverages constraint resolution algorithms to tackle scheduling challenges. By integrating domain-specific knowledge into the constraint set, such as precedence relations and heuristic rules, CP enhances problem-solving capabilities [56]. This method is particularly suited for complex scheduling problems where constraints are numerous and interdependent. However, the effectiveness of CP can be limited by the complexity of the constraint model and the computational effort required to solve it.

GAs utilize a population-based approach to optimize scheduling solutions iteratively. By simulating natural selection principles, GAs generate increasingly effective schedules over successive generations [57]. They are recognized for their robustness in handling complex scheduling problems but may require the careful tuning of parameters such as mutation rates and crossover strategies to avoid the premature convergence or excessive computation times.

Simulated annealing is a heuristic optimization technique inspired by the physical process of metal cooling. It explores potential solutions by gradually reducing the likelihood of accepting inferior solutions as the process progresses [58]. This method is effective in generating high-quality schedules under due date constraints by exploring various configurations and converging towards optimal solutions. Its main limitation is its sensitivity to the cooling schedule, which must be carefully designed to balance exploration and exploitation.

Backward scheduling starts from the due date and works in reverse to establish start times for each task. This method ensures alignment with deadlines and has been shown to enhance timeliness in task completion across various applications [59], while effective for ensuring deadline adherence, backward scheduling may not effectively account for resource availability or task dependencies without additional adjustments.

Improvement heuristics involve iterative techniques aimed at refining existing schedules. These heuristics facilitate adjustments in response to fluctuations in demand or changes in capacity while maintaining a focus on due date constraints [60,61]. They enhance responsiveness and adaptability but may require frequent recalibration to remain effective as conditions change.

B&B algorithms have been extensively studied and applied to solve single-machine scheduling problems with E/T penalties. These algorithms have proven to be effective in finding optimal solutions for various E/T scheduling problems. The validity of the B&B algorithm for single-machine problems with E/T penalties has been proven by utilizing lower bounds based on LP relaxation [62]. In the context of just-in-time manufacturing, B&B algorithms have been effectively applied to scheduling problems with quadratic E/T costs [63]. For problems involving job families, the sum of maximum earliness and maximum tardiness has been successfully minimized using B&B algorithms [64]. Additionally, B&B algorithms have demonstrated their versatility by being applied to related problems such as aircraft landing scheduling, which share similarities with E/T scheduling problems [65]. In the context of the FJSP with E/T penalties, B&B approaches have been enhanced to consider multiple time constraints, including setup times, transportation times, and delivery times [66]. Furthermore, B&B techniques have been integrated into other optimization methods to improve the solution quality and computational efficiency for FJSP problems with E/T considerations [67]. This integration has led to the development of hybrid approaches that can effectively handle the increased complexity of FJSP while still maintaining the ability to find optimal or near-optimal solutions for E/T objectives [68].

LP models play a crucial role in addressing E/T scheduling issues, particularly when integrated with frameworks like the S-graph. These models incorporate machine-to-operation assignments and sequencing constraints, allowing for dynamic adjustments as new constraints are introduced during the scheduling process [69]. The integration of LP models within a B&B framework facilitates real-time updates, ensuring that optimal solutions are maintained throughout the iterative process. The incorporation of these diverse techniques into scheduling algorithms enables organizations to effectively address due date constraints and minimize tardiness in complex manufacturing operations. The integration of these methodologies not only optimizes resource utilization but also enhances overall productivity and operational efficiency.

Recent studies have also extended FJSP models to incorporate energy efficiency as a key objective. In energy-intensive industries, scheduling optimization plays a crucial role in minimizing unnecessary energy consumption while balancing production constraints. Stochastic multi-objective models integrating energy and time-related criteria have been developed, using hybrid metaheuristics combined with simulation-based evaluation methods to optimize both total tardiness and energy usage [70]. Furthermore, distributed FJSP research has explored cooperative artificial bee colony algorithms with learning-driven mechanisms, addressing challenges such as preventive maintenance and transportation constraints. These approaches enhance scheduling robustness by integrating Q-learning-based strategies into multi-factory production environments [71].

In this direction, recent research has explored hybrid metaheuristic-based scheduling strategies aimed at optimizing both makespan and energy efficiency in smart manufacturing. A hybrid model integrating real-time adaptability mechanisms and predictive maintenance strategies has been developed to enhance scheduling robustness while minimizing energy costs. By dynamically adjusting schedules in response to machine failures and fluctuating energy demands, this approach improves energy efficiency without compromising production performance. Experimental evaluations confirm the effectiveness of this method in reducing energy waste while maintaining scheduling quality, making it a promising solution for modern smart factory environments [72].

These advancements highlight the ongoing shift towards intelligent, self-adaptive scheduling methods. Future research is expected to further develop deep reinforcement learning techniques, real-time scheduling adaptations, and multi-agent RL models to enhance performance in complex and dynamic manufacturing systems.

1.2. Problem Definition

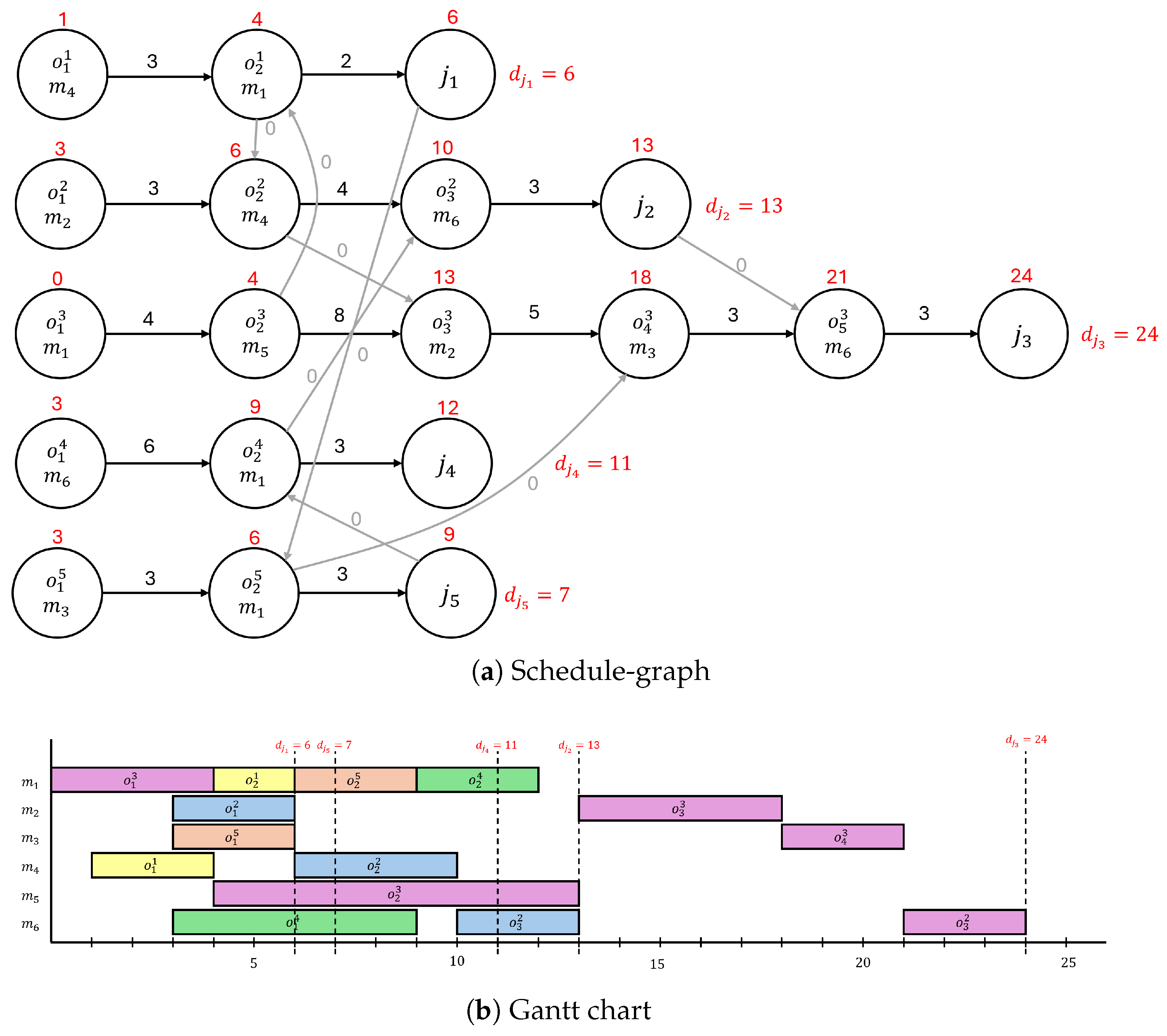
The FJSP addressed in this study focuses on scheduling a set of jobs, where each job consists of a sequence of operations. Each operation can be processed on one of several available machines, introducing flexibility in machine assignments. This flexibility, combined with job-specific due dates and precedence constraints between operations, makes the scheduling problem complex. The primary goal is to minimize both the earliness and tardiness of job completions, while optimizing machine assignments and operation sequencing.

To formally define the problem, let J represent the set of jobs, where $J=\{1,2,\cdots ,|J\left|\right\}$. Each job $j\in J$ is composed of a set of operations, denoted by $O_j$. The complete set of operations across all jobs is $O={\bigcup }_{j\in J}{O}_j$. Each operation $o\in O$ must be assigned to a machine from the set of available machines; $M=\{1,2,\cdots ,|M\left|\right\}$ and $M_o$ denotes the set of machines capable of performing operation $o\in O$. Each machine $m\in M$ can process specific operations, and the processing time of operation o on machine m is denoted by $p_{o,m}$. This processing time varies depending on the machine chosen, adding complexity to the scheduling process.

Precedence constraints exist within each job, meaning certain operations must be completed before others can begin. For each operation $o\in O_j$, let $O_o^{-}$ represent the set of prerequisite operations that must be finished before operation o can start.

Precedence constraints within jobs play a fundamental role in the scheduling process. Each operation follows a defined sequence, where an operation can only begin once its designated predecessor is completed. This establishes a structured progression, ensuring that each step follows a logical order without unnecessary dependencies.

A schedule can be represented as $S=\left\{(o,m,t^s,t^f)\right\}$, where o is assigned to machine m, with a start time $t^s$ and a finish time $t^f$. The problem is formally classified using the $\alpha \left|\beta \right|\gamma$ notation as $FJ\left|prec\right|\sum E_j+T_j$. In this notation, the following hold:

• $FJ$ represents the Flexible Job Shop structure, where each operation can be processed on a subset of eligible machines, with machine choice affecting the processing time.
• $prec$ refers to the precedence constraints between operations within a job, including AND-type constraints and potential parallel execution.
• The objective $\sum E_j+T_j$ represents minimizing both E/T across all jobs.

Each job has a distinct due date ($d_j$), specifying a target completion time that, if exceeded, incurs penalties. Additionally, processing times ($p_j$) vary based on machine selection, influencing scheduling decisions and overall efficiency.

Several key challenges arise when solving the FJSP. First, machine flexibility requires determining the optimal machine for each operation, as the processing time $p_{o,m}$ differs across machines, and not all machines can process every operation. This introduces complexity in balancing machine assignments to minimize both job completion times and penalties. Second, precedence constraints within jobs ensure that certain operations are completed before others can start. For example, if operation o precedes $o^{\prime }$, the start time of $o^{\prime }$, denoted by $t_{o^{\prime }}^s$, must satisfy $t_{o^{\prime }}^s\ge t_o^s+p_{o,m}$, where $t_o^s$ is the start time of o. Third, due date constraints enforce job-specific due dates, requiring the scheduler to minimize penalties for both early ($E_j$) and tardy ($T_j$) job completions.

Furthermore, the scheduling process is affected by two different storage policies. Under the No Intermediate Storage (NIS) policy, machines must wait for material transfers between operations, which can result in machine idle times. Conversely, the Unlimited Intermediate Storage (UIS) policy allows operations to proceed independently of material transfers, offering more flexibility and reducing potential delays due to machine idle times.

If the due date is not given for a job, then it is defined based on the total processing time of all its operations [73,74], scaled by a factor f [75]. The due date for job j is given by the following:

$$d_j=⌊f\sum _{o\in O_j}\underset{m\in M_o}{min}{p}_{o,m}⌋j\in J$$

(1)

This approach ensures that due dates are proportional to the expected processing times but does not directly account for system congestion. Congestion effects can be modeled by adjusting the factor f, depending on the system’s load ratio. The parameter f serves as a tightness factor, influencing the strictness of due dates. A value of $f=1.3$ was applied in this case, as an increase in f results in a relaxation in due dates, making the scheduling problem easier [76]. Setting $f=1$, however, is generally not advisable, as it assumes that jobs will not experience any waiting time, leading to overly strict due dates that may not be achievable in a congested system [75]. In addition, the framework allows for the specification of job-specific due dates as input parameters, thereby accommodating scheduling problems with heterogeneous temporal constraints. This functionality enhances the model’s versatility, enabling it to address a broader spectrum of real-world scheduling scenarios where individual job due dates are critical factors.

The goal of the FJSP is to minimize the total penalties for E/T across all jobs. Let $C_j$ denote the completion time of job j. The earliness $E_j$ is defined as $E_j=max(0,d_j-C_j)$, and it occurs when a job finishes before its due date. The tardiness $T_j$ is defined as $T_j=max(0,C_j-d_j)$, and it occurs when a job finishes after its due date. The total objective function can be written as follows:

$$min\sum _{j\in J}(w_j^E{E}_j+w_j^T{T}_j)$$

(2)

where $w_j^E$ and $w_j^T$ represent the job-specific penalty weights assigned to the E/T of job j, respectively. In many practical applications, tardiness is often penalized more heavily than earliness, as delays can result in missed deadlines, contract violations, or customer dissatisfaction. However, these penalty weights may vary for each job based on its priority, urgency, or contractual requirements. While these weights affect the evaluation of the schedule’s optimality, they do not alter the core functionality of the proposed methodology, which remains applicable regardless of the specific penalty structure.

This FJSP presents a significant scheduling challenge due to the flexibility in machine assignments, the need to respect precedence constraints, and the variability in processing times. The goal is to develop an efficient schedule that minimizes both E/T while adhering to the operational constraints of the production environment.

2. Methodology

2.1. S-Graph Framework

The S-graph framework [12] has emerged as a powerful approach for solving complex scheduling problems, particularly in batch process scheduling. This framework combines a directed graph-based model with specialized algorithms to efficiently generate optimal or near-optimal schedules [77]. At its core, the S-graph framework utilizes a directed acyclic graph to represent schedules, where nodes typically denote events and weighted arcs represent time differences between these events. This representation is complemented by specialized B&B algorithms and other combinatorial techniques that enable efficient exploration of the solution space [78].

Originally conceived for multipurpose batch process scheduling, the S-graph framework has since been extended to address a variety of production scheduling challenges [79]. Its versatility is evident in its successful application to resource-constrained project scheduling problems (RCPSP), both in single-mode and multi-mode variants. The framework has also been adapted to handle scenarios with limited waiting time constraints, where intermediate products have restricted storage times. Furthermore, its applicability has been demonstrated in various industrial contexts, including reactive scheduling scenarios where unexpected events, such as the arrival of new orders, need to be accommodated efficiently [14].

One of the key strengths of the S-graph framework lies in its efficient problem representation. The graph-based model offers a compact and intuitive way to represent scheduling problems, facilitating easier analysis and solution development. This efficiency extends to the algorithmic level, where specialized search strategies allow for faster exploration of the solution space compared to general-purpose optimization methods. The framework’s flexibility is another notable advantage, as it can be extended to accommodate various problem-specific constraints and objectives, making it adaptable to diverse scheduling scenarios. The S-graph approach has shown particular prowess in handling complex constraints, such as limited waiting times and time-varying resource capacities. Unlike some heuristic methods, it can provide optimality for many problem instances while maintaining the flexibility to quickly find near-optimal solutions for larger problems. This balance between optimality and computational efficiency makes the S-graph framework a valuable tool for both researchers and practitioners in the field of production scheduling. The framework’s ability to integrate different aspects of scheduling problems, including resource allocation, timing constraints, and multiple operational modes, further enhances its utility in real-world applications. Recent extensions have even allowed for the handling of resources with changing availability over time, broadening its applicability to more dynamic scheduling environments.

The S-graph consists of nodes N which are divided into two sets as follows: task nodes ($N^t\subset N$) and product nodes ($N^p\subset N$). Task nodes represent the start or execution of operations, while product nodes indicate the completion of jobs. These sets are disjoint, i.e., $N^t\cap N^p=\varnothing$, and together they form the node set N, with $N^t\cup N^p=N$.

Each operation is associated with a single task node, and each job is represented by a single product node. Thus, we have $\left|O\right|=|N^t|$ and $\left|J\right|=|N^p|$. The terms operation and task node can be used interchangeably since there is a one-to-one correspondence between them.

The S-graph utilizes two types of arcs to model the scheduling process: recipe arcs ($A_1$) and schedule arcs ($A_2$). Recipe arcs define the precedence constraints between operations, which are inherent in the production process. For instance, if operation o must be completed before operation $o^{\prime }$ can begin, a recipe arc $(o,o^{\prime })$ is created between the corresponding task nodes. The weight of a recipe arc $(o,o^{\prime })\in A_1$ represents the minimum processing time required for operation o on any available machine, denoted as follows:

$$c(o,o^{\prime })=\underset{m\in M_o}{min}{p}_{o,m}(o,o^{\prime })\in A_1$$

(3)

The weight can be adjusted during optimization once a specific machine is selected for operation o.

The structure containing all nodes and recipe arcs is referred as recipe-graph and it is denoted by $G(N,A_1,\varnothing )$. The recipe-graph serves as the input to the scheduling algorithm. The recipe-graph represents the set of operations to be executed and their dependencies. It defines the order of operations and specifies which machines can perform each operation.

Figure 1 illustrates a recipe-graph [12] for five jobs. The task nodes ($o_1^1,\dots ,o_2^5$) represent the operations, while product nodes ($j_1,\dots ,j_5$) indicate the completion of jobs. Arcs between task nodes show the sequence of operations, and arcs linking task nodes to product nodes denote the completion of the corresponding jobs. Each arc imposes a timing constraint, ensuring that the correct order of operations is maintained. Additionally, the set of machines capable of performing each operation is specified within the task node. The numbers above the arcs represent the minimum processing times, as described in Equation (3), ensuring that the scheduling constraints are properly accounted for.

A schedule-graph, in contrast, incorporates more detailed information about the sequencing of operations across specific machines. The key differences between recipe-graphs and schedule-graphs are:

• The machine sets are replaced by the specific machines selected by the scheduling algorithm.
• Additional arcs, called schedule arcs, are introduced to represent the exact sequence in which operations are performed on the machines.

The availability of intermediate storage in the manufacturing facility plays a significant role in how operations are scheduled [80]. In the case of NIS, machines cannot proceed to the next operation until the material from the previous operation has been transferred to the machine designated for the following operation. This is modeled using zero-weighted schedule arcs, as shown in Figure 2a. For example, unit $m_1$ performs operation $o_1^3$, transfers the processed material to unit $m_4$, and then begins operation $o_2^1$.

In contrast, under UIS, material can be stored between operations, providing more flexibility in sequencing. In this case, schedule arcs carry weights corresponding to the processing times of operations, as depicted in Figure 2b. For instance, machine $m_1$ first performs operation $o_1^3$, followed by operation $o_2^1$, with the processing time of operation $o_1^3$ represented by the weight on the arc between these two task nodes.

In both NIS and UIS scenarios, schedule arcs may also incorporate changeover times between operations if needed.

The complete schedule-graph, denoted by $G(N,A_1,A_2)$, includes both the original recipe arcs and the additional schedule arcs, thus reflecting the specific scheduling decisions made. Each feasible schedule, represented by a schedule-graph, must satisfy the timing constraints imposed by both the recipe arcs and the schedule arcs. The overall objective is to find the most efficient schedule-graph for the given production scenario.

To solve this scheduling problem, a B&B algorithm is employed. In this method, each node in the B&B tree corresponds to a subproblem, represented by a partially or fully scheduled S-graph. A solution is a schedule where all operations are assigned to machines and the activity orders of machines are determined. A feasible solution is a solution where the decisions are not contradictory, i.e., there is no cycle in its S-graph. Each feasible solution is represented by a schedule-graph. In a partial solution, only a subset of the operations has been assigned to machines.

In the proposed B&B procedure for generating all schedule-graphs, each node in the enumeration tree corresponds to a partial problem, which consists of an S-graph and a partial assignment of operations. The recipe-graph, with no assignments, acts as the root node of the tree.

The branching rule governs the expansion of the search tree by systematically exploring valid assignments. At each step, a machine is selected, and child nodes are generated by assigning this machine to all unscheduled operations compatible with the current subproblem’s constraints. Each child node represents a new partial solution, extending the current state of the schedule. This systematic approach ensures that all valid assignments are considered while effectively eliminating redundant or infeasible branches, optimizing the search process.

The algorithm iterates through all feasible assignments of the selected machine to the unscheduled operations in the current subproblem. For each assignment, the corresponding S-graph is updated to reflect the new state, including potential modifications to the operation processing times, which may depend on the selected machine.

To enhance computational efficiency, a bounding function is employed to compute a lower bound for each partial solution. The lower bound provides an estimate of the minimal possible makespan that can be achieved if the partial solution is extended to a complete solution. If the lower bound of a branch exceeds the objective value of the current best solution, the branch is pruned, as it cannot yield a better solution.

The algorithm evaluates the feasibility of each partial solution by applying the bounding function and eliminates branches that cannot improve upon the current best solution. When a partial solution leads to a state where no unscheduled operations remain, it is considered a complete solution. If this complete solution improves upon the current best solution, it is updated as the new optimal solution. Otherwise, the partial problems are retained in the search set for further exploration.

The original algorithm progressively assigns operations to machines with the objective of minimizing the makespan. If a partial solution is found to be infeasible, such as when cycles appear in the graph, the corresponding branch is pruned from the search.

2.2. Extension of the S-Graph Framework for Earliness/Tardiness Minimization

The original S-graph framework [12] has been extended with several enhancements to address the E/T minimization problem. These modifications primarily involve adjusting the objective function and incorporating additional technological considerations. By retaining the core strengths of the original S-graph framework, this extension introduces the E/T problem while maintaining structural integrity.

In the original B&B approach, one S-graph and its associated partial assignment corresponding to a specific subproblem are represented by a node within the enumeration tree. The root of the enumeration tree is represented by the recipe-graph, which initially contains no assignments. As the algorithm progresses, it selects a machine for each partial problem and generates child partial problems by assigning unscheduled operations to this machine. It is important to note that the processing time of an operation may be machine-dependent, potentially altering the weight of recipe arcs originating from the node representing the assigned operation.

The original S-graph framework has to be extended to handle due dates. While the recipe-graph still serves as the tree’s root, the derived subproblem has been expanded. This extension involves assigning estimated start and finish times to each operation and its corresponding task nodes. These assignments are determined based on the due dates associated with the jobs. Each branching step involves two key actions as follows:

• Assigning a machine to an operation.
• Determining the order of this operation.

When an assignment occurs and child partial problems are generated, the selected machine may modify the weight of the recipe arc, consequently affecting the operation’s finish time. Given that the finish time of a job’s final operation must coincide with the job’s due date, any modification to the recipe arc weight may necessitate an adjustment to the operation’s start time.

In the bounding procedure, the feasibility of each partial problem undergoes rigorous evaluation. The assessment of a partial problem’s feasibility is conducted through the implementation of a cycle detection algorithm within the graph structure. Upon positive verification of feasibility, the algorithm establishes a lower bound for the E/T metric encompassing all potential solutions derivable from the given partial problem.

In the initialization phase of the algorithm, the temporal parameters—specifically, the start and finish times—of each operation are ascertained through a systematic analysis of the recipe-graph. This process involves the traversal of the directed acyclic graph representing the recipe structure, enabling the establishment of preliminary temporal bounds for all operations based on their precedence relationships and processing requirements.

Each job $j\in J$ consists of a set of operations $O_j$ with precedence constraints. Let ${\widehat{o}}^j$ denote the final operation of job j. The completion time of operation ${\widehat{o}}^j$ determines whether the job meets its due date. The goal is to align the finish time $t_{{\widehat{o}}^j}^f$ of the last operation with the due date $d_j$, expressed as follows:

$$t_{{\widehat{o}}^j}^f=d_{j}j\in J$$

(4)

The start time of each operation o can be expressed as follows:

$$t_o^s=t_o^f-c(o,o^{\prime })o\in O,(o,o^{\prime })\in A_1$$

(5)

where $c(o,o^{\prime })$ is the weight of the arc between the task node representing operation o and its successor operation $o^{\prime }$. For the final operation of each job, this equation can be specialized as follows:

$$t_{{\widehat{o}}^j}^s=t_{{\widehat{o}}^j}^f-c({\widehat{o}}^j,j)j\in J,({\widehat{o}}^j,j)\in A_1$$

(6)

where $c({\widehat{o}}^j,j)$ is the weight of the arc between the task node representing the final operation of job j and the product node representing job j.

For preceding operations of a job, the finish time of each operation o must coincide with the start time of the subsequent operation $o^{\prime }$, as follows:

$$t_o^f=\underset{(o,o^{\prime })\in A_1,o^{\prime }\in O}{min}{t}_{o^{\prime }}^{s}o\in O$$

(7)

This set of constraints ensures that the start and finish times of all operations are calculated based on the job’s due date, thereby minimizing both E/T penalties. As a result, jobs are completed as close to their due dates as possible.

During each branching step, in addition to the original processes, an analysis of the modification’s impact on the recipe sequence is conducted. This examination is crucial for determining how changes in the weight of recipe arcs affect operations connected by edges to the modified operation. The following two scenarios may arise if the assignment increases the recipe arc weight:

• A reduction in the operation’s start time.
• An increase in the operation’s finish time.

Both scenarios require an investigation into how the start and finish times of preceding and subsequent operations are influenced.

If the weight increases, the start time of operation o will be earlier. Consequently, all operations ($O_o^{-}$) with arcs leading to operation o will have earlier finish times, which in turn necessitate earlier start times, while maintaining their original processing durations. This examination must be recursively applied to all elements of $O_o^{-}$ along the edges leading to their respective task nodes until no further prerequisite operations exist.

If all examination results show the modified start and finish times are still feasible, i.e., they are positive, the modification can be implemented and the child partial problem is finalized. However, if an operation’s start time is reduced below zero, it may result in an infeasible child partial problem. In such cases, the examination must be conducted in the opposite direction, necessitating an increase in the finish time of operation o.

A parallel examination is conducted for the machine sequence. This analysis involves examining the start and finish times of operations connected by schedule arcs leading to operation o. In each branching step, an operation is assigned to a machine which is put to the end of the activity list of the machine. Similarly to the recipe sequence analysis, the schedule sequence analysis must be conducted along the schedule arcs pointing to operation o, and then changes must be made depending on the results.

A special case may arise when the recipe sequence examination allows for a reduction in the start time of operation o, but the machine sequence examination does not permit this change. Suppose that operation o is assigned to machine m, at least one other operation has already been assigned to machine m and this operation is scheduled to execute before operation o. If the execution intervals of these operations overlap, an analysis for potential modifications must be conducted. This analysis investigates whether the start and finish times of the operation preceding o in the machine’s sequence can be reduced by at least the specified reduction factor. To achieve this, both recipe sequence analysis and schedule sequence analysis must be performed on the preceding operation. Depending on the outcomes of these analyses, the further examination of additional operations may be required. Since the number of analyses and the associated computational requirements can increase rapidly, the analyses are initially conducted to determine whether the specified reduction factor is available for all affected operations. If there are empty time gaps between operations in the existing sub-schedule, the number of required analyses may not be large. If the proposed modifications are deemed feasible based on the analysis, the start and finish times of all affected operations must be reconfigured. However, if the analyses indicate that the modifications are infeasible, the execution interval of operation o must be delayed, resulting in an increase in both the start time $t_o^s$ and finish time $t_o^f$ values.

Thus, the scheduler must simultaneously adhere to the following two types of sequences:

• The recipe sequence: Ensures that the operations within a job follow the predefined order enforced by recipe arcs.
• The machine sequence: Ensures the order of operations assigned to the same machine, as enforced by schedule arcs.

These constraints ensure that the schedule respects both the operational dependencies within each job and the specific machine sequences, resulting in a valid and efficient schedule.

Due to practical constraints, strictly adhering to all scheduling constraints may not always be feasible. Therefore, it is necessary to introduce a mechanism to relax some of these constraints. One such constraint is the timing constraint, as follows:

$$t_o^s=t_o^f-c(o,o^{\prime })o\in O,(o,o^{\prime })\in A_1$$

(8)

which may be relaxed based on whether a NIS or UIS policy is applied.

Under the NIS policy, a machine cannot start a new operation until the intermediate storage time for the previous operation is completed. Thus, the start time for an operation can be modified as follows:

$$t_o^s=t_o^f-(c(o,o^{\prime })+i{s}_o)o\in O,(o,o^{\prime })\in A_1$$

(9)

where $i{s}_o$ represents the intermediate storage time after completing operation o. Similarly, the start time of the next operation $o^{\prime }$ must respect both the finish time and the intermediate storage time of the previous operation o.

Under the NIS policy, a machine cannot start a new task until the intermediate storage process is completed. This means that the machine is occupied during the storage period, and no new operation can begin until the subsequent operation for the current job has started on the next machine. This constraint makes the NIS policy more restrictive.

The UIS policy is more flexible. In this case, the intermediate storage can be managed separately from the machine’s availability. After completing an operation, the machine can immediately begin a new operation, without waiting for the next operation to be scheduled. The storage of materials or products is handled externally, so there is no dependency on machine availability. Thus, the machine is not constrained by the intermediate storage process, and operations can more freely overlap in time as follows:

$$t_{o^{\prime }}^s\ge t_o^f=t_o^s+c(o,o^{\prime })(o,o^{\prime })\in A_1$$

(10)

In summary, under the NIS policy, the intermediate storage is handled by the machine itself, and the machine cannot start a new operation until the next operation has started on a different machine. Under the UIS policy, intermediate storage is managed separately, allowing for more flexible scheduling without machine downtime during the storage period. This approach allows the S-graph framework to handle E/T minimization while maintaining the integrity of the original scheduling structure.

2.3. Minimization of Intermediate Storage Time and Earliness/Tardiness

Minimizing E/T is a fundamental objective in job scheduling; however, an exclusive focus on this metric may result in suboptimal resource utilization. If the scheduling strategy only prioritizes E/T minimization, it could theoretically achieve favorable outcomes by scheduling the final operation of a job precisely at its due date, irrespective of the timing of the preceding operations. This approach permits gaps between successive operations, which can lead to idle periods as long as the final job completion coincides with its due date. While such a strategy may mitigate E/T penalties, it neglects other inefficiencies, including machine idle time, material handling costs, and overall resource under-utilization.

The presence of these gaps, stemming from uncoordinated operation timings, contributes to increased intermediate storage time (IST), where materials or partially completed jobs remain idle between operations. Excessive IST not only escalates storage costs but also diminishes overall production efficiency by prolonging periods of machine under-utilization.

To comprehensively address these challenges, it is essential to minimize both E/T and IST. Striking a balance between these objectives ensures that jobs are completed as close as possible to their due dates while avoiding unnecessary storage gaps between operations. This integrated approach enhances resource utilization, reduces handling costs, and improves the overall production flow, ultimately leading to a more efficient and cost-effective scheduling solution.

The extended S-graph framework aims to minimize both intermediate storage time and E/T in job completion, balancing these conflicting objectives through careful operation scheduling. This problem can be formally classified as $FJ\left|prec\text{IST-policy}\right|\sum E_j+T_j+IST$, where IST−policy refers to the intermediate storage policy, either NIS or UIS, and $IST$ denotes the intermediate storage time.

The multi-objective optimization problem can be formulated as follows:

$$min\left(\alpha ·I{S}_{\mathrm{total}}+\beta ·(E_{\mathrm{total}}+T_{\mathrm{total}})\right)$$

(11)

where $\alpha$ and $\beta$ are non-negative weighting coefficients that define the relative importance of minimizing intermediate storage time and reducing E/T penalties, respectively. The appropriate selection of these parameters is critical for balancing the trade-off between competing objectives. A widely adopted approach is to normalize the weights as follows:

$$\alpha +\beta =1$$

(12)

which ensures the consistent total weight allocation and simplifies comparisons across different configurations. In certain applications, independent weight scaling may instead be preferred to reflect domain-specific priorities or differences in unit magnitudes between objectives.

The intermediate storage time is calculated as follows:

$$I{S}_{\mathrm{total}}=\sum _{o\in O}i{s}_o$$

(13)

where $i{s}_o$ represents the storage time for operation o. Meanwhile, the total E/T penalties are expressed as follows:

$$E_{\mathrm{total}}=\sum _{j\in J}max(0,d_j-t_{{\widehat{o}}^j}^f)$$

(14)

$$T_{\mathrm{total}}=\sum _{j\in J}max(0,t_{{\widehat{o}}^j}^f-d_j)$$

(15)

where $t_{{\widehat{o}}^j}^f$ is the finish time of the last operation in job j, and $d_j$ is its due date.

During each branching step, an additional expansion beyond the augmentation described in Section 2.2 is required. The previously established examinations of recipe and machine sequences remain essential. Throughout these analyses, the execution interval of operation o has been treated as $[t_o^s,t_o^f]$, where $t_o^f=t_o^s+c(o,o^{\prime })+i{s}_o$. Given that this procedure also aims to minimize IST, the minimization of $i{s}_o$ for each operation becomes an additional objective. Consequently, the analyses now distinguish between the completion time ($c(o,o^{\prime })$) of operation o and its intermediate storage time ($i{s}_o$). The recipe sequence examination is extended to investigate whether intermediate storage occurs at operation o, i.e., $i{s}_o>0$. In the affirmative case, the examination proceeds under the hypothesis that $i{s}_o=0$ within the execution interval $[t_o^s,t_o^f]$.

If both the recipe sequence and the machine sequence examinations yield satisfactory results, the modification can be implemented. If, however, either test gives an infeasible result, a search procedure is initiated to determine the minimum value of $i{s}_o$ for the operation o that renders the partial problem feasible. Upon identifying this value, the modification for the child partial problem can be implemented.

An additional exceptional scenario may arise during the process when the recipe sequence examination permits a reduction in the start time of operation o, while the machine sequence examination precludes such an alteration. As described earlier, this analysis investigates whether there exists an operation assigned to the same machine with an overlapping execution interval for operation o, necessitating a search for an appropriate temporal gap on machine m. Should such a gap be identified, the start and finish times of operation o must be adjusted to match this interval.

In contrast to the previously described procedure, during the gap search process, this analytical procedure also considers whether the operations preceding and succeeding the examined time gap possess significant intermediate storage values. In the case that either condition is true, the analysis explores the scenario wherein the intermediate storage times of both the preceding and succeeding operations are set to zero, evaluating whether the identified time gap remains sufficiently large to accommodate the execution interval of operation o. If, under these conditions, the identified time gap proves adequately sized for operation o, the examination is reiterated for the operations bounding the investigated time gap, employing the minimized intermediate storage values. Should feasible results be obtained, the comprehensive modification is implemented for all affected operations.

Balancing the trade-offs between minimizing storage time and adhering to job due dates introduces inherent challenges. Reducing intermediate storage time enhances machine utilization but can limit flexibility in scheduling, potentially resulting in early or late job completions. Conversely, minimizing E/T improves schedule adherence but may require additional storage time as operations wait for machine availability. The NIS policy complicates these challenges by enforcing stricter material flow constraints, while the UIS policy offers more flexibility but increases storage costs.

By incorporating the minimization of both intermediate storage time and E/T, the extended S-graph framework provides a robust, adaptable solution to real-world production scheduling. The framework’s multi-objective nature allows for fine-tuning based on the specific priorities of the production environment, leading to schedules that efficiently balance machine utilization, storage management, and due-date compliance.

2.4. Integration of the S-Graph Framework and a LP Solver for Scheduling

This section presents a hybrid approach that enhances the scheduling process by integrating the S-graph framework with an LP solver. The S-graph framework effectively manages the sequencing of operations and job dependencies, while the LP solver dynamically adjusts machine assignments and operation timings in response to the current state of the scheduling problem. This combination utilizes both graph-based and optimization techniques, facilitating efficient solutions to complex job shop scheduling challenges.

The integration process begins with the transformation of the initial recipe-graph into a foundational LP model that accurately represents the system’s current state. The recipe-graph delineates the precedence relationships among operations within each job and outlines potential machine assignments, although it does not yet establish specific sequencing across machines. The LP model is designed to minimize total E/T penalties for each job, adhering to constraints related to operation start and finish times, processing durations, and precedence requirements. The general LP model for minimizing E/T penalties across all jobs is formulated as follows:

$$\mathrm{Minimize}\sum _{j\in J}\left(E_j+T_j\right)$$

(16)

Subject to the following:

$$\begin{array}{cccc}\hfill E_j+t_{{\widehat{o}}^j}^f& \ge d_j\hfill & \hfill & j\in J\hfill \end{array}$$

(17)

$$\begin{array}{cccc}\hfill -T_j+t_{{\widehat{o}}^j}^f& \le d_j\hfill & \hfill & j\in J\hfill \end{array}$$

(18)

$$\begin{array}{cccc}\hfill t_{o^{\prime }}^s-t_o^f& \ge 0\hfill & \hfill & (o,o^{\prime })\in A_1\cup A_2\hfill \end{array}$$

(19)

$$\begin{array}{cccc}\hfill t_o^f& =t_o^s+c(o,o^{\prime })\hfill & \hfill & (o,o^{\prime })\in A_1\hfill \end{array}$$

(20)

$$\begin{array}{cccc}\hfill t_{{\widehat{o}}^j}^f& =t_{{\widehat{o}}^j}^s+c({\widehat{o}}^j,j)\hfill & \hfill & j\in J,({\widehat{o}}^j,j)\in A_1\hfill \end{array}$$

(21)

$$\begin{array}{cccc}\hfill t_o^s& \ge 0\hfill & \hfill & o\in O\hfill \end{array}$$

(22)

In this formulation, the objective function minimizes the total earliness ($E_j$) and tardiness ($T_j$) penalties for each job j. The constraints governing E/T are defined in Equations (17) and (18).

The operation sequencing constraint, as defined in Equation (19), ensures that the start time of an operation cannot precede the finish times of its preceding operations. The finish time for each operation is calculated using Equation (20), which incorporates the weight of arc $c(o,o^{\prime })$ for operation o, which is determined by the dedicated machine. The overall completion time $C_j$ for each job is determined by the last operation in the sequence, as outlined in Equation (21).

The integration of this LP model with the S-graph framework takes place during the B&B process. Each node in the B&B tree corresponds to a subproblem representing a partially scheduled state. The S-graph framework manages machine assignments and introduces scheduling arcs that dynamically modify the LP model as follows:

• Machine-to-operation assignments: When an operation o is assigned to a specific machine m, its corresponding processing time $p_{o,m}$ is fixed in the LP model as $c(o,o^{\prime })=p_{o,m}$ for each $(o,o^{\prime })\in A_1$. This adjustment updates constraints on start and finish times, ensuring that the solver accurately reflects the processing time for the designated machine (see Equations (20) and (21)).
• Insertion of schedule-arcs: As sequencing constraints (schedule arcs) are introduced between operations within the S-graph framework, the LP model is updated accordingly. For example, if operations o and $o^{\prime }$ are scheduled on the same machine and o precedes $o^{\prime }$, the LP model ensures that $o^{\prime }$ ($t_{o^{\prime }}^s$) starts after o ($t_o^f$) finishes (see Equation (19)).

To further enhance this model, intermediate storage time (IST) can be integrated into the LP formulation, aimed at minimizing E/T penalties. This revised LP model is articulated as follows:

$$\mathrm{Minimize}\sum _{j=1}^n\left(E_j+T_j+I{S}_j\right)$$

(23)

Subject to the following:

$$\begin{array}{cccc}\hfill E_j+t_{{\widehat{o}}^j}^f& \ge d_j\hfill & \hfill & j\in J\hfill \end{array}$$

(24)

$$\begin{array}{cccc}\hfill -T_j+t_{{\widehat{o}}^j}^f& \le d_j\hfill & \hfill & j\in J\hfill \end{array}$$

(25)

$$\begin{array}{cccc}\hfill t_{o^{\prime }}^s-t_o^f& \ge 0\hfill & \hfill & (o,o^{\prime })\in A_1\cup A_2\hfill \end{array}$$

(26)

$$\begin{array}{cccc}\hfill t_o^f& =t_o^s+c(o,o^{\prime })+i{s}_o\hfill & \hfill & (o,o^{\prime })\in A_1\hfill \end{array}$$

(27)

$$\begin{array}{cccc}\hfill t_{{\widehat{o}}^j}^f& =t_{{\widehat{o}}^j}^s+c({\widehat{o}}^j,j)+i{s}_{{\widehat{o}}^j}\hfill & \hfill & j\in J,({\widehat{o}}^j,j)\in A_1\hfill \end{array}$$

(28)

$$\begin{array}{cccc}\hfill I{S}_j& =\sum _{o\in O_j}i{s}_o\hfill & \hfill & j\in J\hfill \end{array}$$

(29)

$$\begin{array}{cccc}\hfill t_o^s,i{s}_o& \ge 0\hfill & \hfill & o\in O\hfill \end{array}$$

(30)

In this updated formulation, $I{S}_j$ denotes the total intermediate storage time associated with each job, which is equal to the sum of the intermediate storage time of the operations belonging to job j, defined in Equation (29). This addition reflects a comprehensive approach to minimizing not only E/T but also the time associated with intermediate storage.

The equation governing the operations’ finish time (Equation (20)) has been modified to include $i{s}_o$ (Equation (27)), representing the intermediate storage time incurred between completing operation o and initiating operation $o^{\prime }$. Additionally, Equation (28) accounts for the total intermediate storage time related to the final operation of each job. This integration fosters a holistic optimization of the scheduling objectives, thereby enhancing overall production efficiency.

At each node of the B&B tree, the corresponding LP model is solved using a LP solver. The resulting solution provides the optimal start and finish times for operations based on the current machine assignments and sequencing constraints. These results inform subsequent branching decisions within the S-graph framework, such as identifying critical paths and potential scheduling conflicts, guiding additional machine assignments, and scheduling arcs in later branching steps.

This iterative process continues as the S-graph framework explores various branches of the tree. The LP model is updated at each step to reflect the state of the current subproblem, ensuring optimization at every stage. By solving the LP model for each subproblem, informed decisions are made that progressively refine schedules while minimizing both the intermediate storage and total E/T across all jobs.

3. Results

The aim of these experiments is to evaluate the proposed scheduling methodology by analyzing its performance across multiple problem instances. The study investigates how the method balances E/T minimization and IST minimization under different scheduling constraints. Through these experiments, we examine the scalability, efficiency, and trade-offs introduced by different storage policies and optimization approaches. The results provide insights into the method’s applicability to flexible job shop scheduling with due date constraints and intermediate storage considerations.

The results of our study on teh FJSP with E/T and IST minimization are presented in this section. All experiments were performed on a personal computer equipped with an Intel(R) Core(TM) i7-7820HQ CPU operating at 2.9 GHz and 16 GB memory. The S-graph framework and LP solver integration were implemented in C++ (MSVC 19.29), under Windows 11.

Table 1. Parameters of problem given in Figure 1.

Jobs (j)	Operation	Machine						${\mathit{d}}_{\mathit{j}}$
		${\mathit{m}}_{\mathbf{1}}$	${\mathit{m}}_{\mathbf{2}}$	${\mathit{m}}_{\mathbf{3}}$	${\mathit{m}}_{\mathbf{4}}$	${\mathit{m}}_{\mathbf{5}}$	${\mathit{m}}_{\mathbf{6}}$
Job 1	$o_1^1$	-	-	-	3	7	-	6
	$o_2^1$	2	-	-	-	-	-
Job 2	$o_1^2$	-	3	-	-	-	-	13
	$o_2^2$	-	-	-	4	8	-
	$o_3^2$	-	-	3	-	-	3
Job 3	$o_1^3$	4	-	-	-	-	-	24
	$o_2^3$	-	-	-	4	8	-
	$o_3^3$	-	5	-	-	-	-
	$o_4^3$	-	-	3	-	-	-
	$o_5^3$	-	-	-	-	-	3
Job 4	$o_1^4$	-	-	-	-	-	6	11
	$o_2^4$	3	-	-	-	-	-
Job 5	$o_1^5$	-	-	3	-	-	-	7
	$o_2^5$	3	-	-	-	-	-

presents the parameters of the example problem used to evaluate the proposed scheduling approach. It defines the job structures, including the number of operations per job, machine compatibility, and due dates. These parameters serve as the basis for the scheduling scenarios illustrated in the subsequent figures.

Figure 3 illustrates the optimal schedule resulting from E/T minimization, with the first part showing the schedule graph and the second part displaying the corresponding Gantt chart. Similarly, Figure 4 illustrates the solution obtained when considering both E/T and IST minimization, also divided into a schedule graph and a Gantt chart. In both figures, recipe and scheduling edges are distinctly represented in the schedule-graph, while the Gantt chart provides clear visualization of the operation start and finish times. Start times of nodes representing various operations are highlighted in red, and the due date values for each job are indicated.

A notable distinction between these two solutions is evident in the scheduling of operation $o_3^3$. In Figure 3, which represents the E/T minimization scenario, operation $o_3^3$ commences at time unit 13. This scheduling decision introduces a one-unit intermediate storage time on machine $m_5$ between the completion of $o_2^3$ and the initiation of $o_3^3$. The resultant objective function value for this solution is 3, comprising a tardiness of 1 for job $j_4$ and 2 for job $j_5$. Conversely, Figure 4, which incorporates IST minimization, demonstrates an earlier start time for operation $o_3^3$. This adjustment cascades through the schedule, causing earlier start times for subsequent operations within job $j_3$. Consequently, this solution eliminates intermediate storage on the machine. The objective function value for this solution totals 4, consisting of zero IST, an earliness of 1, and a cumulative tardiness of 3. The hybrid method described in Section 2.4, which integrates the S-graph framework into a LP solver, concluded with the same results for this specific task.

Table 2. The results of the problem given in Figure 1.

Objective	Method	Time (s)	Branches	$\sum {\mathit{E}}_{\mathit{j}}$	$\sum {\mathit{T}}_{\mathit{j}}$	$\sum \mathit{IST}$
E/T	S-graph	0.015	522	0	3	-
	S-graph + LP	0.069	679	0	3	-
E/T + IST	S-graph	0.017	735	1	3	0
	S-graph + LP	0.079	726	1	3	0

presents a comparative analysis of various solution methodologies applied to the problem illustrated in Figure 1. The table delineates four distinct approaches as follows: the S-graph framework with E/T optimization, its hybrid variant incorporating a LP, and corresponding versions that additionally consider IST.

To obtain a more comprehensive perspective on the efficacy of our methodologies, it is imperative to conduct a comparative analysis with extant research outcomes. However, it is noteworthy that publications presenting results under conditions precisely congruent with our problem definition are relatively scarce in the literature. The most comparable example with its initial parameters and results is delineated in

Table 3. Processing times of operations on different machines, job due dates ($d_j$), and job results ($E_j,T_j$) [81].

Jobs (j)	Operation	Machine			${\mathit{d}}_{\mathit{j}}$	${\mathit{E}}_{\mathit{j}}$	${\mathit{T}}_{\mathit{j}}$	${\mathit{w}}_{\mathit{j}}$
		${\mathit{m}}_{\mathbf{1}}$	${\mathit{m}}_{\mathbf{2}}$	${\mathit{m}}_{\mathbf{3}}$
Job 1	$o_1^1$	10	-	3	27	0	1	3
	$o_2^1$	4	-	11
	$o_3^1$	-	11	5
Job 2	$o_1^2$	7	10	13	36	0	19	1
	$o_2^2$	-	11	-
	$o_3^2$	13	6	13
	$o_4^2$	9	7	-
Job 3	$o_1^3$	14	3	-	29	0	3	4
	$o_2^3$	-	12	8
	$o_3^3$	-	-	12
	$o_4^3$	6	11	9
Job 4	$o_1^4$	11	-	15	31	0	9	7
	$o_2^4$	13	-	13
	$o_3^4$	-	7	7
	$o_4^4$	9	15	-

[81]. The authors present a MILP formulation for the FJSP incorporating sequencing flexibility. The model has been subsequently modified and augmented to integrate the just-in-time approach, thereby enhancing its applicability to contemporary manufacturing paradigms. An additional dimension to the problem as presented is the characterization of jobs by non-sequential precedence relationships. Specifically, the operation pairs $o_2^1,o_3^1$; $o_3^2,o_4^2$; $o_2^3,o_3^3$; and $o_2^4,o_3^4$ exhibit parallel relationships within their respective jobs. This parallelism allows these operations to be started at any time after the completion of the prerequisite operations without requiring the parallel operations to rely on each other.

Overall, the cumulative tardiness across all jobs, as quantified in the $T_j$ column of Table 3, totals 32 units, while the aggregate earliness is 0. Additionally, the $w_j$ values represent the weight assigned to each product’s E/T, which influences the total penalty when incorporated into the objective function. This outcome indicates that the prescribed due date values are incongruent with the actual job completion times. The computational experiment presented in the literature example was conducted on a personal computer equipped with an Intel(R) Core(TM) i7-10510U CPU operating at 1.80 GHz and 16 GB memory.

The results of the methodology described for this specific example are presented in

Table 4. Performance results for different objectives, methods, and IST policies, showing earliness ($\sum E_j$), tardiness ($\sum T_j$), intermediate storage time ($\sum \mathrm{IST}$), computation time, and number of branches.

Objective	Method	IST Policy	$\sum {\mathit{w}}_{\mathit{j}}{\mathit{E}}_{\mathit{j}}$	$\sum {\mathit{w}}_{\mathit{j}}{\mathit{T}}_{\mathit{j}}$	$\sum \mathbf{IST}$	Time (s)	Branches
E/T	S-graph	UIS	0	97	-	0.222	22,431
		NIS	0	144	-	1.112	107,178
	S-graph + LP	UIS	0	97	-	7.089	91,161
		NIS	0	144	-	36.234	258,679
E/T + IST	S-graph	UIS	0	97	17	0.683	54,034
		NIS	0	144	0	0.789	52,475
	S-graph + LP	UIS	0	97	17	12.301	142,589
		NIS	0	144	0	20.211	216,408

. The proposed S-graph method, incorporating E/T minimization, yielded superior results compared to the literature benchmark. Specifically, it achieved a total earliness of 0 and a total tardiness of 32 units, with a computational time of 0.222 s. This performance stands in contrast to the literature result, which reported a total tardiness of 32 units and required 1.6 s for computation. For proper comparison, the objective function was given the same weighting as the original problem. As a result, the same objective value as the original was achieved, i.e., $\sum w_j{T}_j=97$. These results highlight the improved efficacy and computational efficiency of the proposed methodology in solving this scheduling problem.

To ensure a thorough analysis, the problem was solved using both the standalone methods and their hybrid versions. Furthermore, the original problem applies the UIS policy, but the same problem was also solved in the case where the NIS policy was applid. The results indicate that the use of an UIS policy generally results in lower tardiness and improved performance for both objectives, at the cost of a higher IST in some cases. The NIS policy tends to increase E/T but can yield faster solution times for certain configurations. The inclusion of LP-based solutions improves the optimization process, but this is often at the cost of increased computational time and more extensive branching. The ‘Branch’ column quantifies the number of branches explored during the execution of the B&B algorithm, providing insight into the computational complexity of each approach. It should be noted that the incorporation of IST considerations leads to a marginal increase in the number of branches explored, reflecting the added complexity introduced by this additional constraint.

These results suggest that, while the S-graph methods are effective in minimizing E/T and IST, integrating LP methods can yield better results for certain problems, though at the cost of increased computation time. The choice between UIS and NIS policies should be aligned with specific operational constraints and performance trade-offs.

Table 5. Problem instance parameters.

Instance	njob	nmac	nop	nmo	proc	dd
dd_1	3	5	3–5	1–3	6–9	27–42
dd_2	3	5	4–5	2–4	6–9	32–43
dd_3	3	5	5–5	2–4	6–9	40–43
dd_4	4	5	5–5	1–3	6–9	40–46
dd_5	5	5	5–5	1–3	6–9	40–46

presents a comprehensive overview of the problem instances utilized in this study, delineating the key parameters that characterize each scenario. The table encapsulates five distinct problem configurations, labeled dd_1 through dd_5, each representing a unique set of scheduling constraints and complexities. Each instance is defined by the number of jobs (njob), number of machines (nmac), number of operations per job (nop), the minimum and maximum number of machines per operation (nmo), processing time range per operation (proc), and the minimum and maximum due dates of jobs (dd). Across the instances, we observe a systematic variation in problem complexity. The number of jobs (njob) increases monotonically from 3 to 5, while the number of machines (nmac) remains constant at 5 across all instances. The range of operations per job (nop) generally expands, culminating in a consistent 5–5 range for the more complex instances. The allocation of machines per operation (nmo) alternates between 1 and 3 and 2–4, introducing variability in resource flexibility. Processing times (proc) maintain a consistent range of 6–9 units across all instances, providing a controlled variable among other parameter variations. Due dates (dd) exhibit a general trend of increasing and widening ranges, reflecting the escalating complexity of temporal constraints as the problem size grows.

Table 6. Comparison of computation times and objective values for various scheduling methods and IST policies across different problem instances.

		S-Graph|ET		S-Graph + LP|ET		S-Graph|ET + IST		S-Graph + LP|ET + IST
		Time (s)	Obj.	Time (s)	Obj.	Time (s)	Obj.	Time (s)	Obj.
dd_1	UIS	0.008	12	0.062	12	0.01	21	0.088	21
	NIS	0.014	12	0.068	12	0.01	21	0.093	21
dd_2	UIS	0.016	2	1.043	2	0.07	6	0.542	4
	NIS	0.114	3	0.897	3	0.195	4	0.532	4
dd_3	UIS	0.014	0	0.107	0	0.181	3	0.952	3
	NIS	0.045	3	0.225	3	0.183	1	0.876	1
dd_4	UIS	0.25	4	2.795	4	0.321	11	1.624	11
	NIS	0.3	4	2.824	4	0.345	11	1.568	11
dd_5	UIS	3.684	19	133.662	19	7.953	45	54.215	44
	NIS	3.968	19	154.023	19	8.361	45	27.232	44

presents a comprehensive analysis of computational performance and solution quality across various scheduling methodologies and intermediate storage policies for a range of problem instances. The table interpret the efficacy of four distinct algorithmic approaches as follows: S-graph with E/T optimization, S-graph augmented with LP for E/T optimization, S-graph with combined E/T and IST optimization, and S-graph with LP for combined ET and IST optimization. For each problem case (dd_1 through dd_5), the table delineates the results under the following two storage policies: UIS and NIS. This divergence allows for a nuanced examination of the impact of storage constraints on scheduling outcomes. The performance metrics reported are computational time (in seconds) and objective function value. These dual criteria facilitate a multifaceted evaluation of algorithmic efficiency and solution quality.

Several notable trends emerge from the data as follows:

• As expected, computation times generally increase with problem size, with dd_5 instances requiring significantly more time across all methods.
• The incorporation of LP consistently increases computational time but does not always yield improved objective values, suggesting a trade-off between computational effort and solution quality.
• The choice between UIS and NIS policies exhibits varying impacts across instances, with some cases showing minimal differences (e.g., dd_1) and others demonstrating more pronounced effects (e.g., dd_3).
• The inclusion of IST in the optimization objective generally leads to higher objective values and increased computation times, reflecting the added complexity of considering storage time. However, when LP methods are applied, the computational time is often reduced for problems with IST compared to those solved without IST using LP methods, as demonstrated by the efficiency gains in these cases.
• The relative performance of the different methods appears to vary with problem size, indicating that the most suitable approach may depend on the specific case characteristics.

The results presented herein provide substantive evidence for the efficacy and robustness of the developed methodologies in addressing scheduling problems of small to medium scale and complexity. These findings demonstrate the viability and competitiveness of our proposed approaches within the specified problem domain, offering a significant contribution to the field of operational research and scheduling theory.

4. Discussion

This research presents a comprehensive analysis of four distinct methodological approaches to the FJSP, each representing a progressive enhancement in addressing complex scheduling scenarios. The study systematically explores the capabilities and limitations of these methods, offering a nuanced understanding of their applicability in modern manufacturing contexts.

Firstly, we examine the S-graph framework’s application to E/T minimization. This foundational approach leverages the S-graph’s inherent structural advantages in representing complex job dependencies and machine assignments. The framework’s efficacy in navigating the multidimensional solution space for E/T minimization in FJSP contexts is evaluated, providing insights into its performance characteristics and computational efficiency. Our results demonstrate that the S-graph framework for E/T minimization consistently produces high-quality solutions across various problem instances. For example, in the dd_1 to dd_3 instances, the method achieved optimal or near-optimal solutions with minimal computational time (0.008 to 0.045 s). This performance underscores the framework’s ability to efficiently handle small- to medium-sized scheduling problems.

Secondly, the research extends the S-graph framework to simultaneously address E/T and IST minimization. This extension represents a significant advancement, incorporating critical resource utilization concerns alongside traditional scheduling objectives. The adaptation of the S-graph to account for storage constraints is meticulously analyzed, highlighting the framework’s flexibility and its capacity to handle multi-objective optimization scenarios. The results indicate that this extended approach effectively balances the trade-off between E/T and IST minimization.

Thirdly, we introduce a novel hybrid approach that integrates the S-graph framework with a LP model for E/T minimization. This innovative methodology synergistically combines the S-graph’s efficient problem representation with LP’s optimization capabilities, particularly in fine-tuning operation timings. The hybrid model’s performance is critically assessed, focusing on its ability to enhance solution quality and computational efficiency in E/T minimization scenarios. Our experimental results reveal that while the hybrid approach often matches the solution quality of the standalone S-graph method, it generally requires more computational time. For example, in the dd_5 instance under the UIS policy, both methods achieved an objective value of 19, but the hybrid approach took 133.662 s compared to 3.684 s in the standalone method. This suggests that the additional complexity introduced by the LP component may not always justify the computational overhead for E/T minimization alone.

Finally, our research culminates in a comprehensive hybrid approach that utilizes the S-graph framework in conjunction with LP to simultaneously minimize E/T and IST. The integration of these techniques is thoroughly examined, with particular attention paid to the model’s ability to balance conflicting objectives and its applicability in complex manufacturing environments. The results demonstrate the potential of this comprehensive approach in finding high-quality solutions for complex scheduling scenarios. In the dd_5 instance under both UIS and NIS policies, the hybrid method achieved a slightly better objective value (44) compared to the standalone S-graph approach (45). However, this improvement comes at the cost of significantly increased computational time, particularly evident in the UIS case (54.215 s vs. 7.953 s).

Across all problem instances and methodologies, several key trends emerge. As problem complexity increases (from dd_1 to dd_5), computational times generally rise across all methods. This trend is particularly pronounced in the hybrid approaches, indicating potential scalability challenges for larger problem instances. The choice between UIS and NIS policies significantly influences both solution quality and computational time. NIS policies often lead to higher objective values and longer computation times, reflecting the additional constraints imposed by this storage policy. While the hybrid methods occasionally produce marginally better solutions, they consistently require substantially more computational resources. This trade-off becomes more pronounced as problem complexity increases. The inclusion of IST minimization alongside E/T generally leads to more balanced solutions but at the cost of increased computational complexity. This highlights the challenges inherent in addressing multiple, potentially conflicting objectives in scheduling problems.

The results demonstrate clear trade-offs between different optimization strategies. While UIS policies tend to minimize tardiness, they can lead to increased intermediate storage time, whereas NIS policies reduce IST but may result in higher E/T penalties. Similarly, integrating LP-based optimization consistently improves solution quality but comes at the cost of increased computation time. These findings provide insight into the practical considerations when selecting scheduling policies based on computational constraints and production priorities.

It is important to emphasize that the FJSP with due dates is NP-complete, meaning that its computational complexity increases exponentially with the number of jobs. The presented instances were selected to allow for a detailed and rigorous evaluation of the proposed method’s effectiveness while maintaining computational feasibility. These instances still encapsulate the core complexities of the FJSP, particularly the trade-offs between E/T penalties and intermediate storage time minimization, and they provide meaningful insights into the method’s decision-making process. Future research should focus on enhancing computational efficiency through heuristic-based approaches, metaheuristic techniques, or parallel computing implementations to extend applicability to larger-scale problems. However, the current study establishes a solid foundation for evaluating the methodology, demonstrating its ability to effectively handle due date constraints within the FJSP while maintaining high solution quality.

5. Conclusions

The results of this investigation contribute insights that may be valuable for both practitioners and researchers in the field of production scheduling, potentially offering perspectives that could inform theoretical frameworks and practical applications in this domain as follows:

• Method selection: The choice of scheduling method should be carefully considered based on the specific requirements of the manufacturing environment. For smaller problems or scenarios where rapid decision making is crucial, the standalone S-graph methods may be preferable. In contrast, for complex, multi-objective scenarios where solution quality is paramount, the hybrid approaches may be justified despite their higher computational demands.
• Storage policy considerations: The significant impact of storage policies on scheduling outcomes underscores the importance of carefully designing and implementing storage strategies in manufacturing environments. Future research could explore adaptive storage policies that dynamically adjust to current production conditions.
• Scalability challenges: As manufacturing systems grow in complexity, addressing the scalability limitations of current approaches becomes crucial. Future work could focus on developing more efficient algorithmic implementations or exploring parallel computing techniques to enhance the applicability of these methods to larger-scale problems.
• Multi-objective optimization: The integration of IST minimization with traditional E/T objectives opens up new avenues for production optimization. Further research could explore additional objectives, such as energy efficiency or workforce utilization, to develop even more comprehensive scheduling solutions.
• Real-world validation: While this study provides valuable insights based on benchmark problems, future research should focus on validating these approaches in real-world manufacturing settings. This could involve case studies in various industries to assess the practical applicability and benefits of these advanced scheduling techniques.

In conclusion, this research aimed to contribute to the fields of operations research and manufacturing systems by offering an analysis of advanced scheduling techniques and their potential practical implications for complex production environments. The progressive development from standalone S-graph methods to sophisticated hybrid approaches provides a valuable roadmap for addressing increasingly complex scheduling scenarios in modern manufacturing environments.