Dynamic Performance Analysis and Fault Ride-Through Enhancement by a Modified Fault Current Protection Scheme of a Grid-Connected Doubly Fed Induction Generator
Abstract
1. Introduction
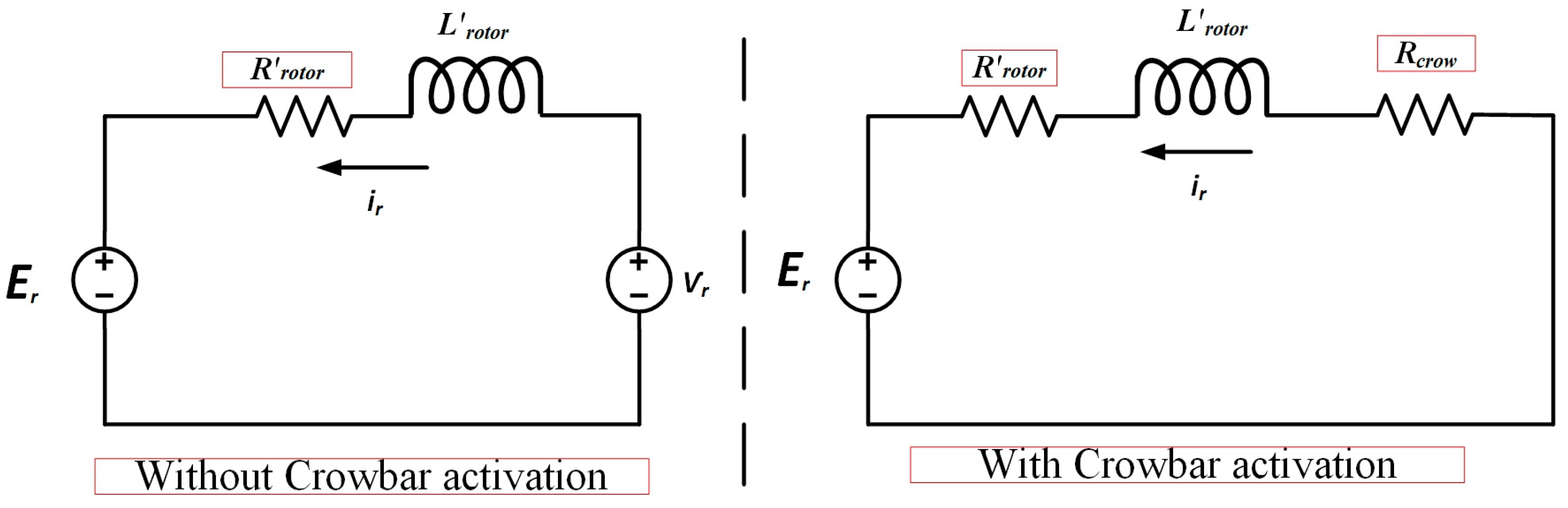
2. Proposed FRT-Based Modeling of Rotor and Stator
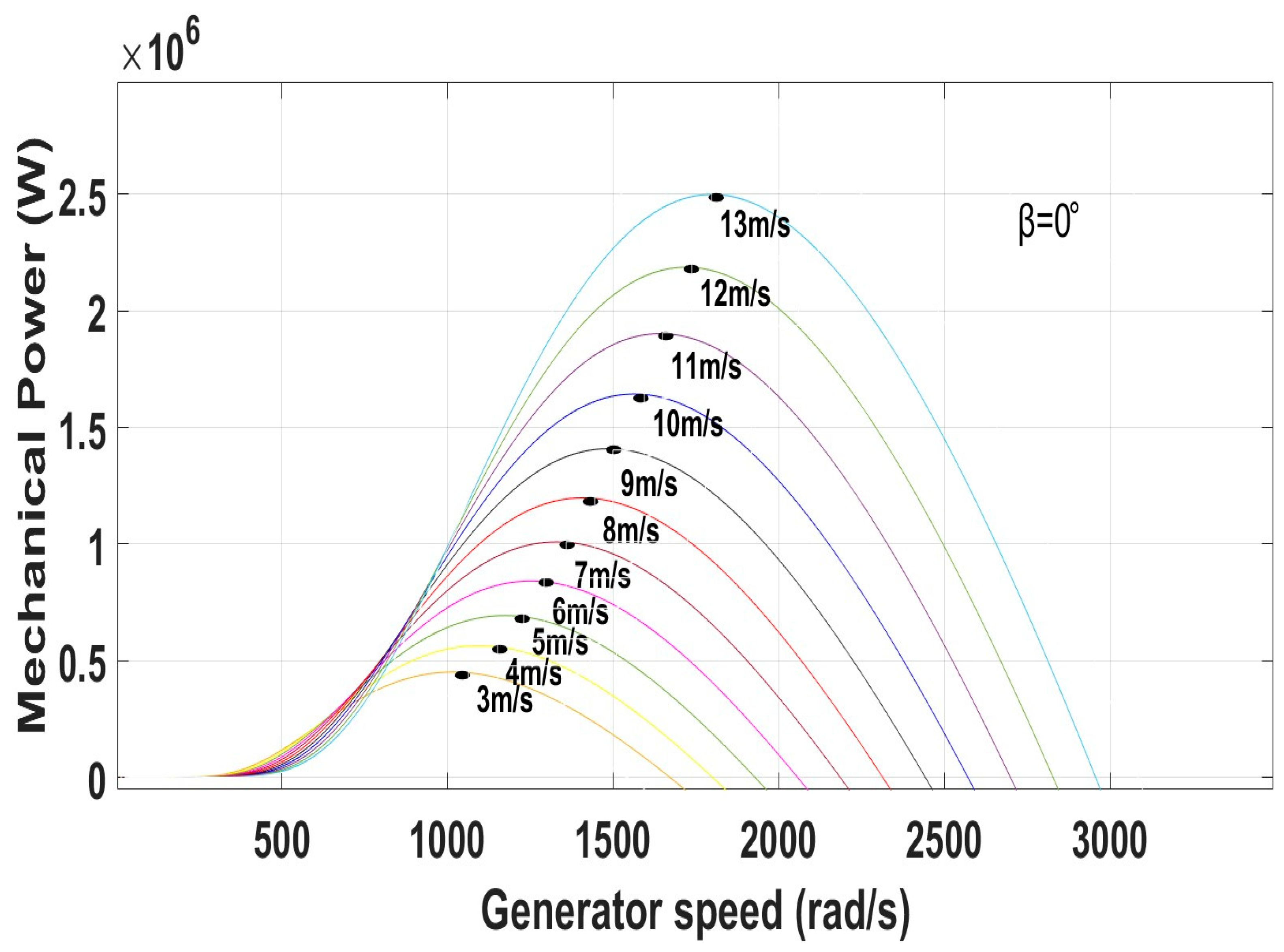
3. MPPT Modeling of Rotor Side Converter Control
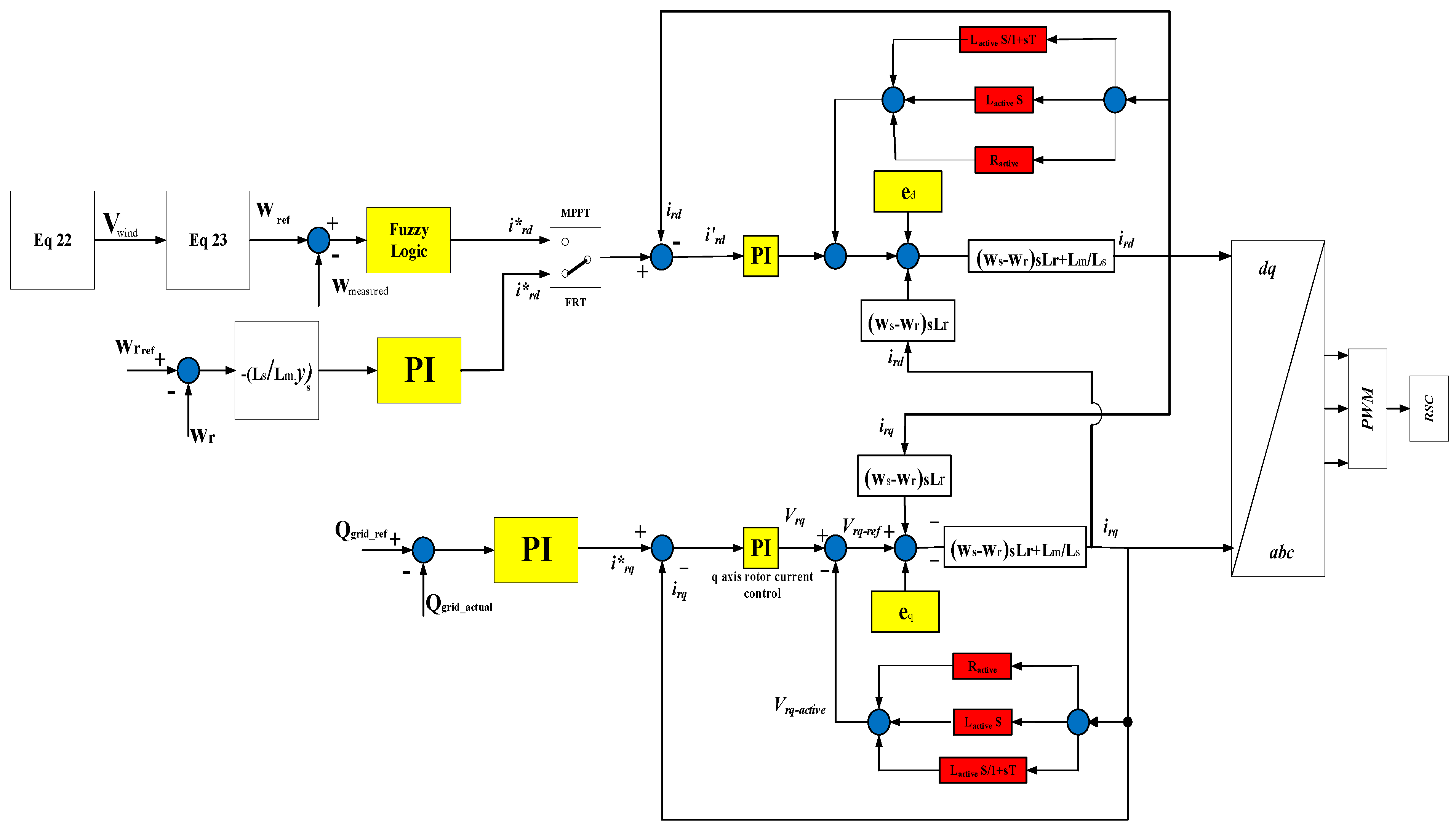
4. Proposed Control Scheme of the Rotor Side Converter
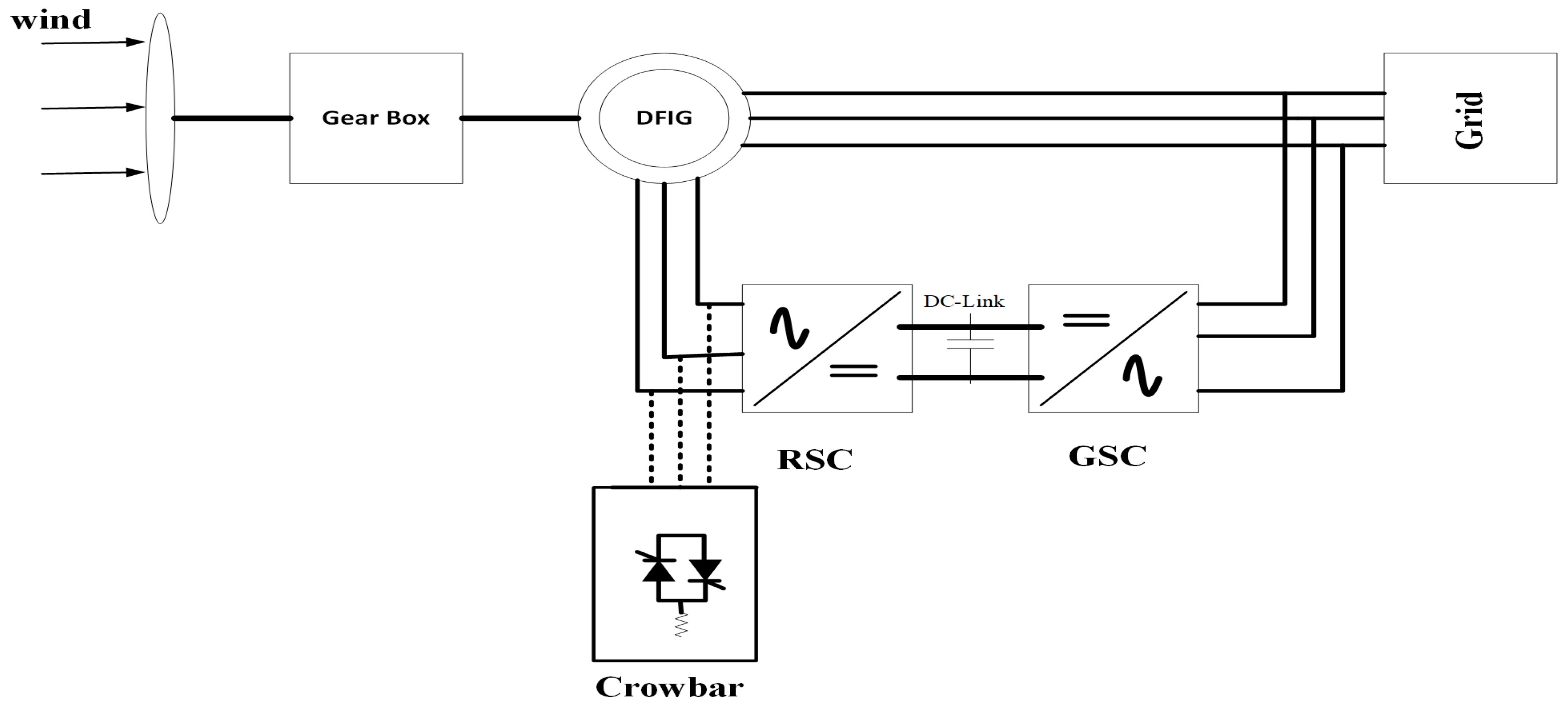
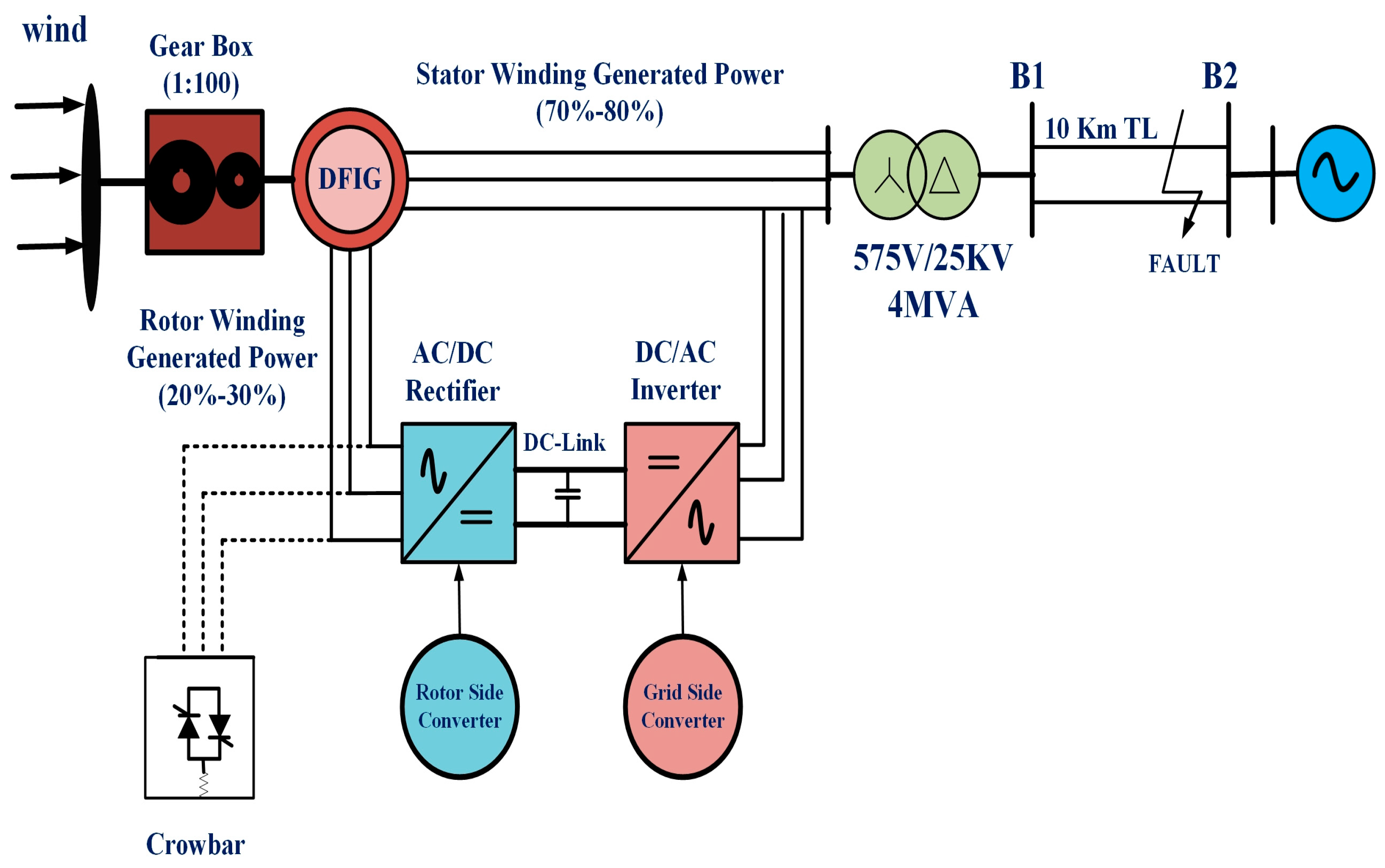
5. Test System Under Simulation Study with FRT Mode
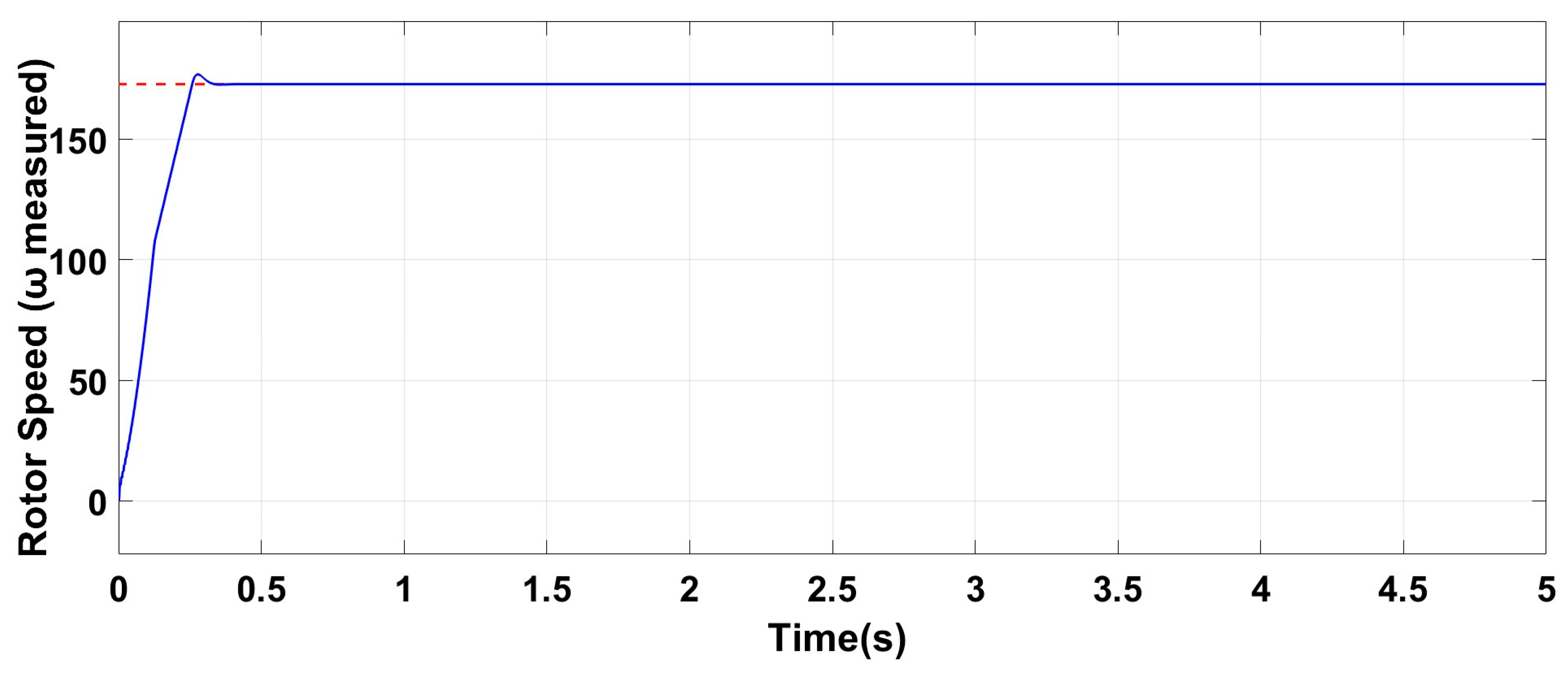
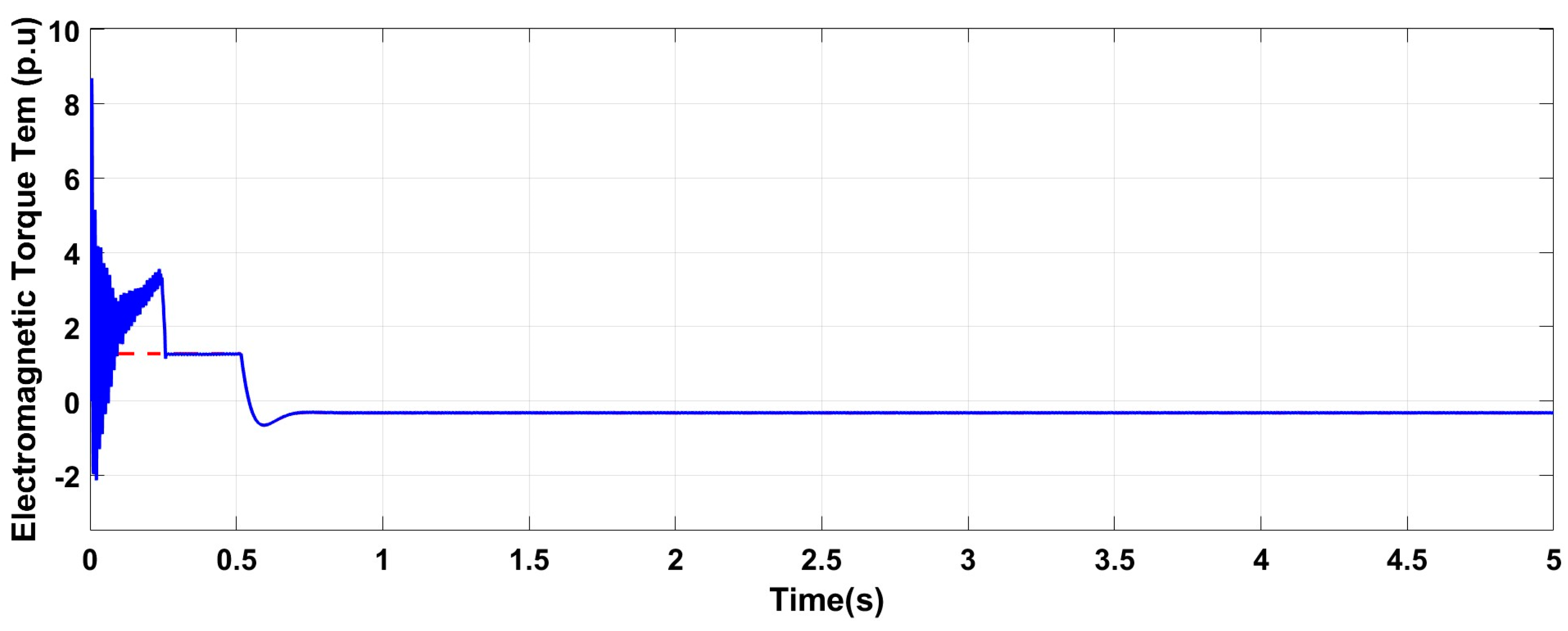
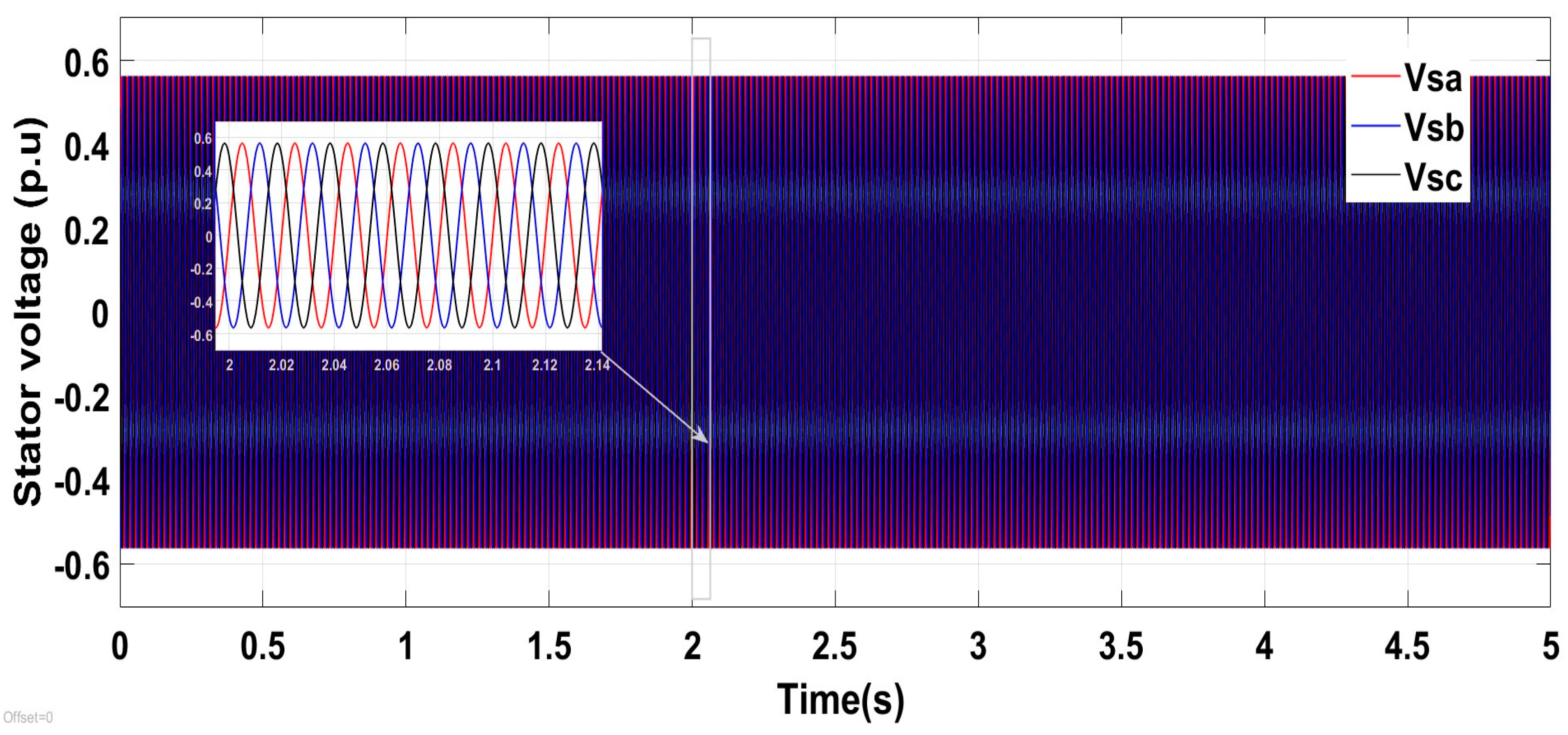
6. Results, Comparison, and Discussion
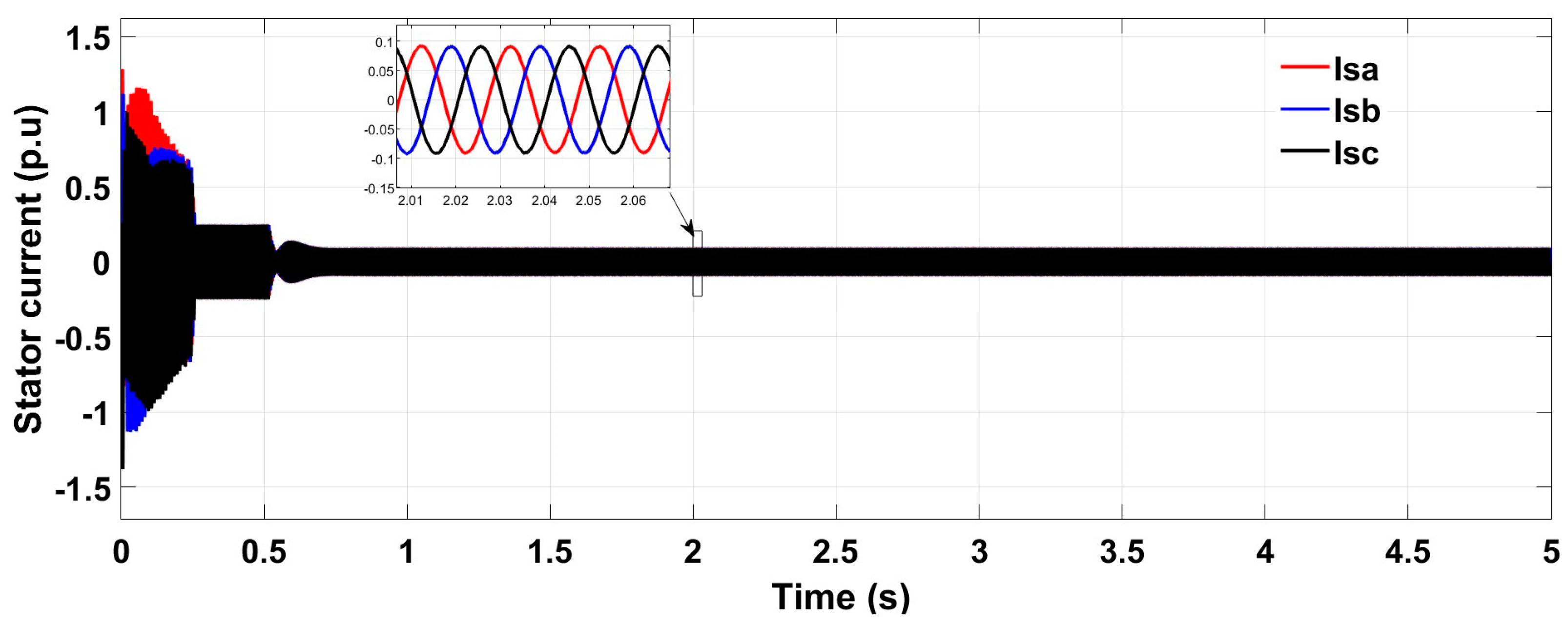
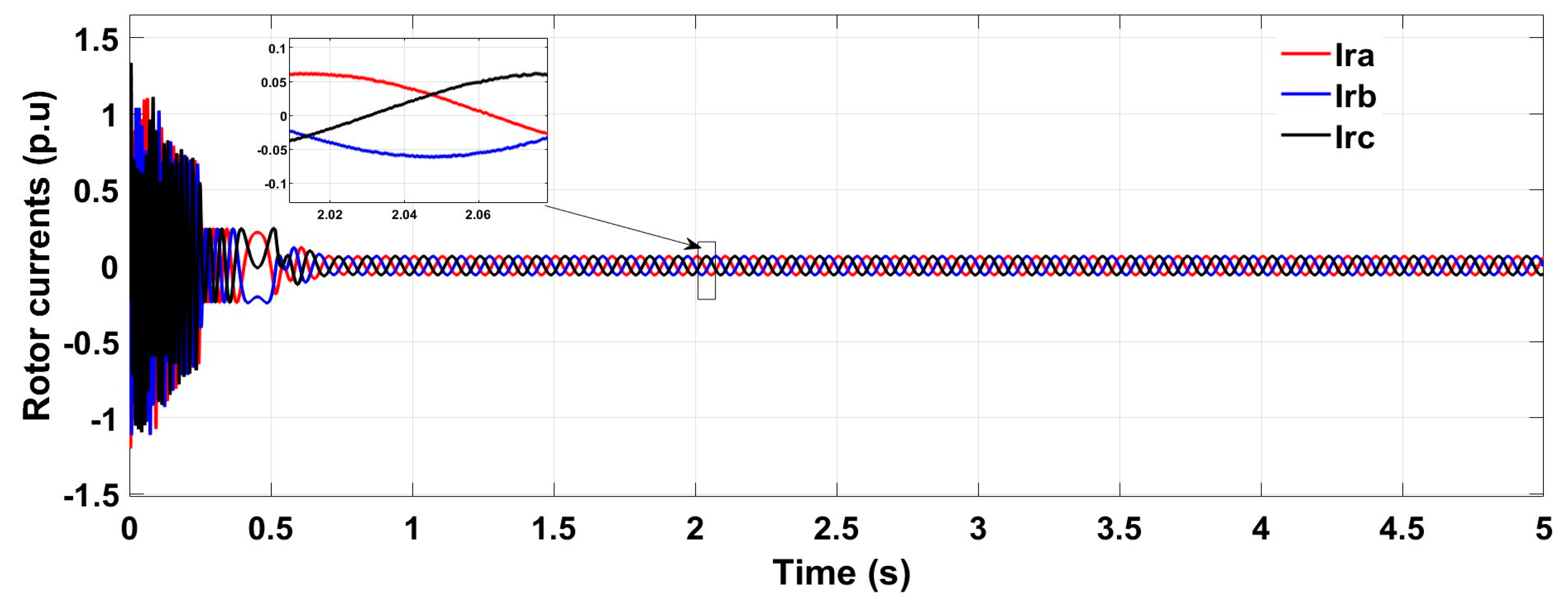
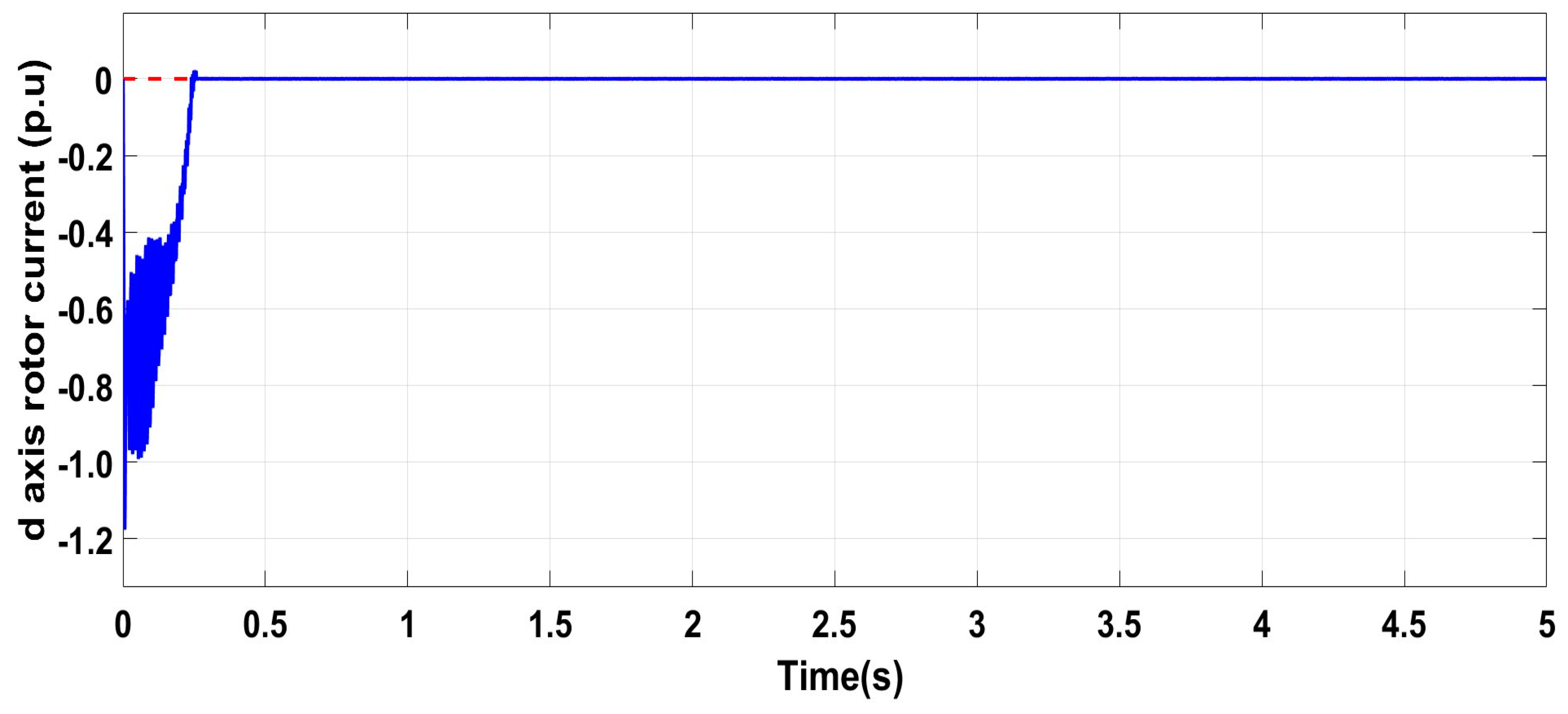
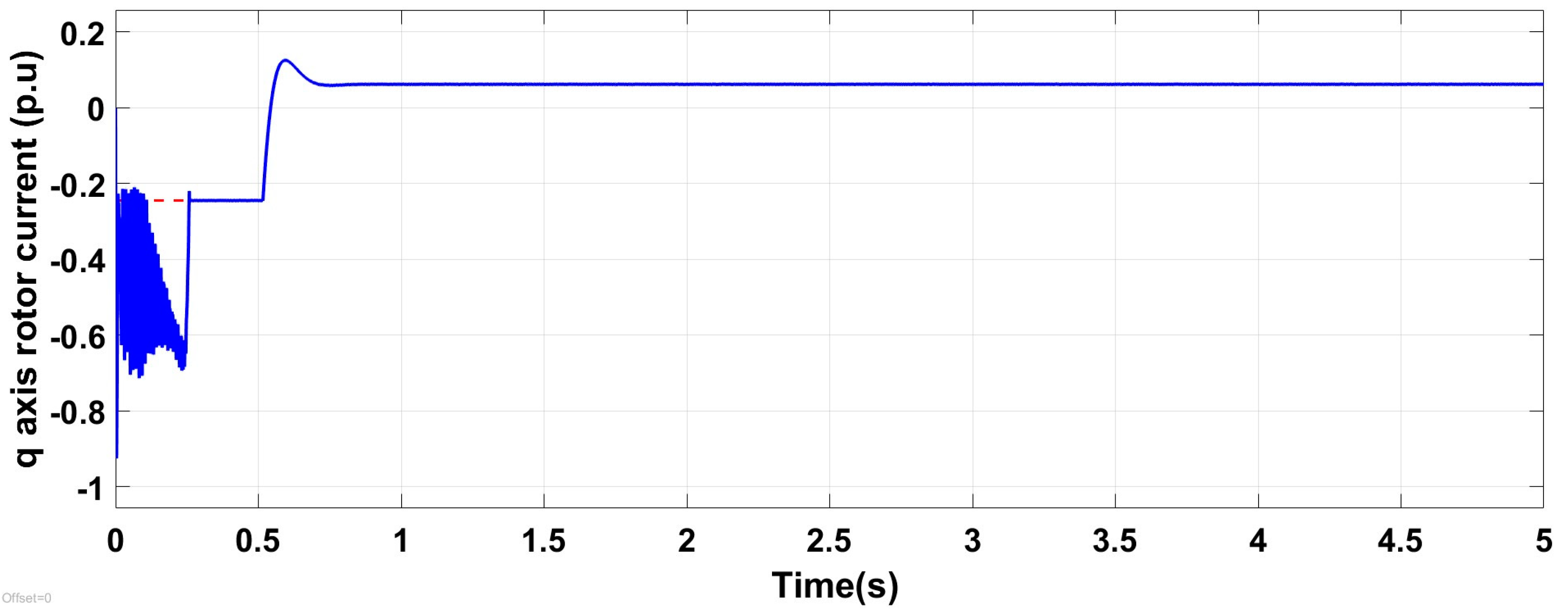
6.1. Test Response with Wind Speed Estimation-Based MPPT Under Normal Grid Conditions at Fixed Wind Speed
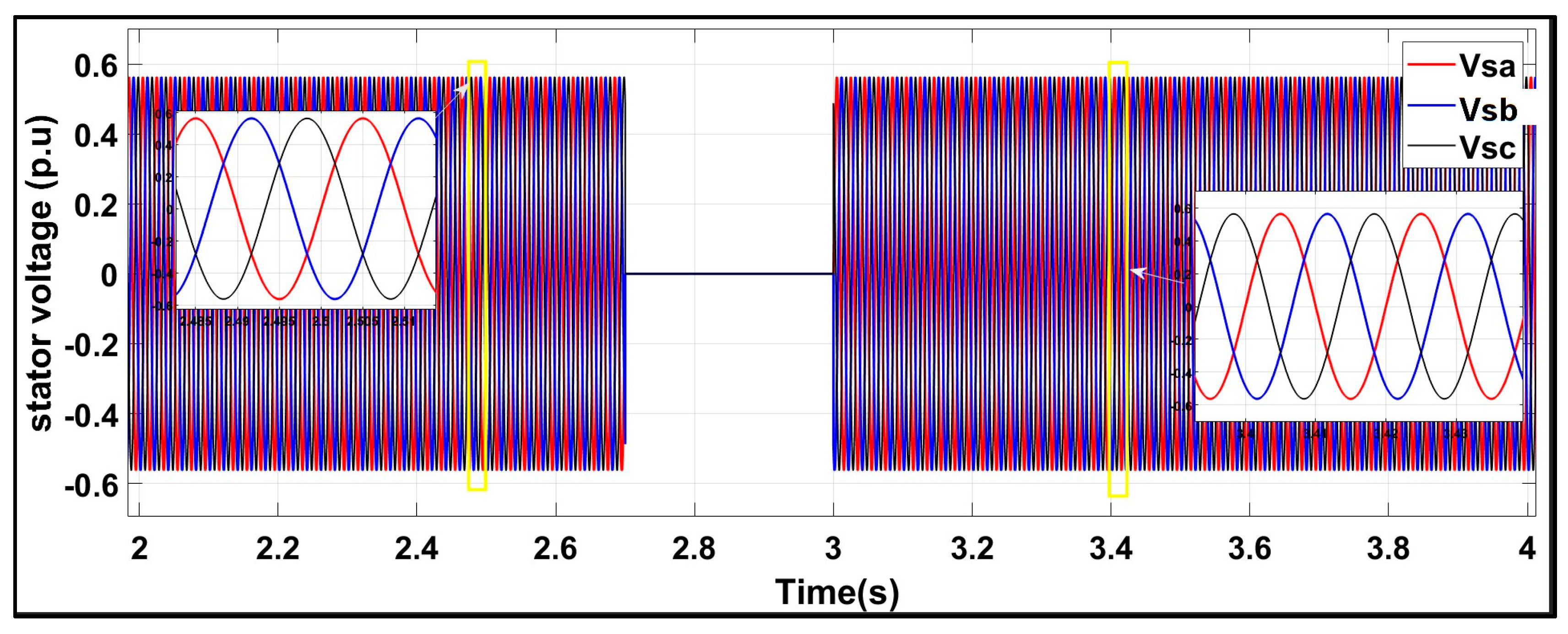
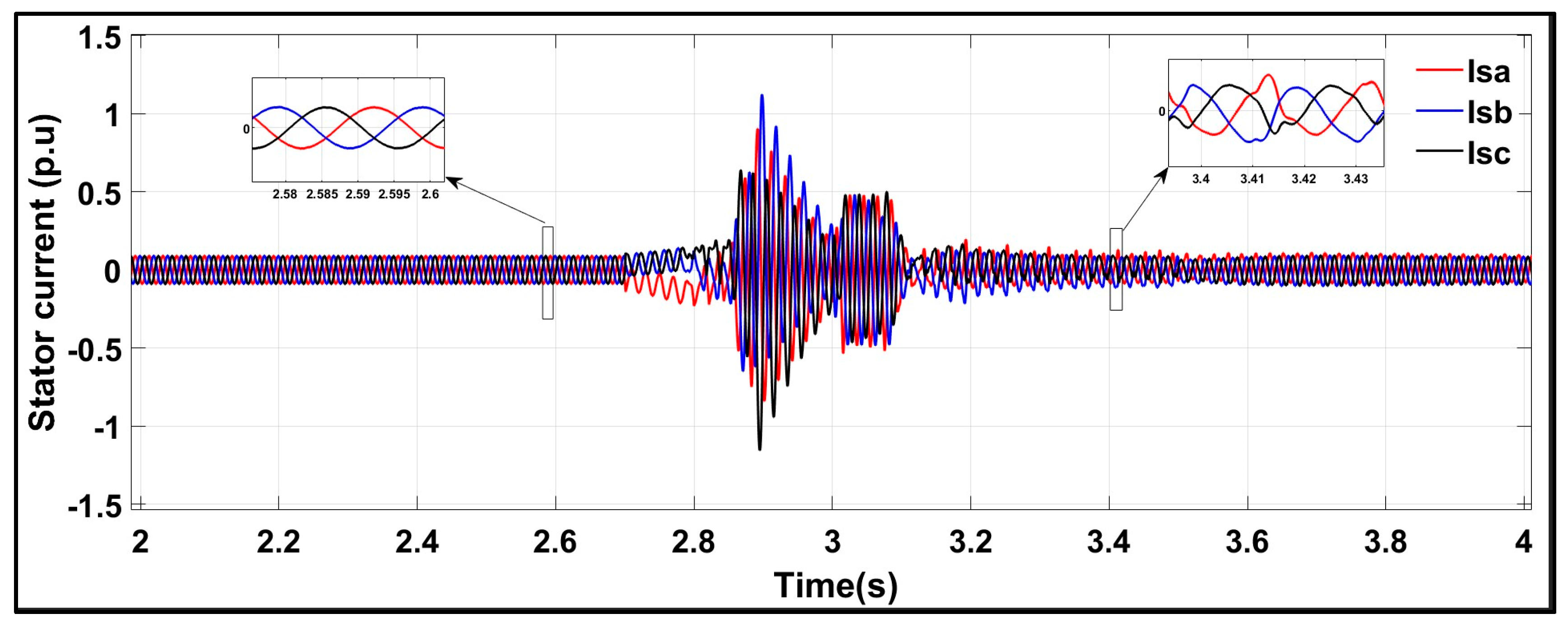
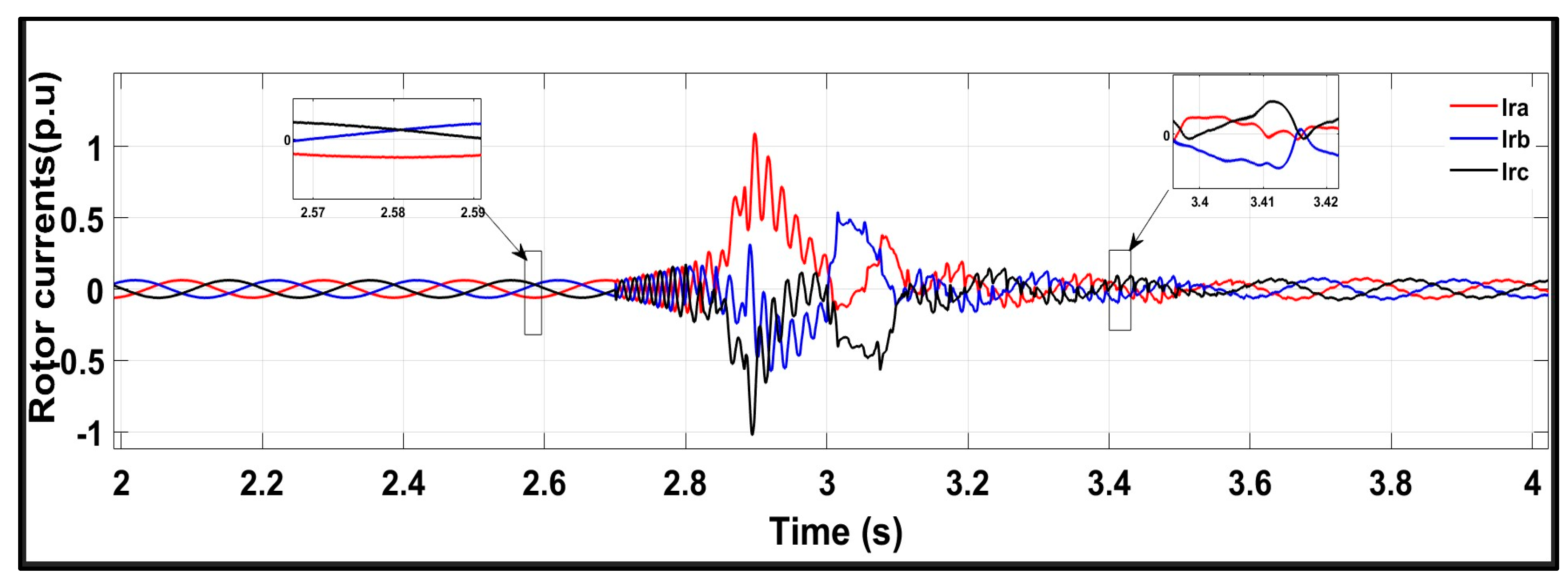
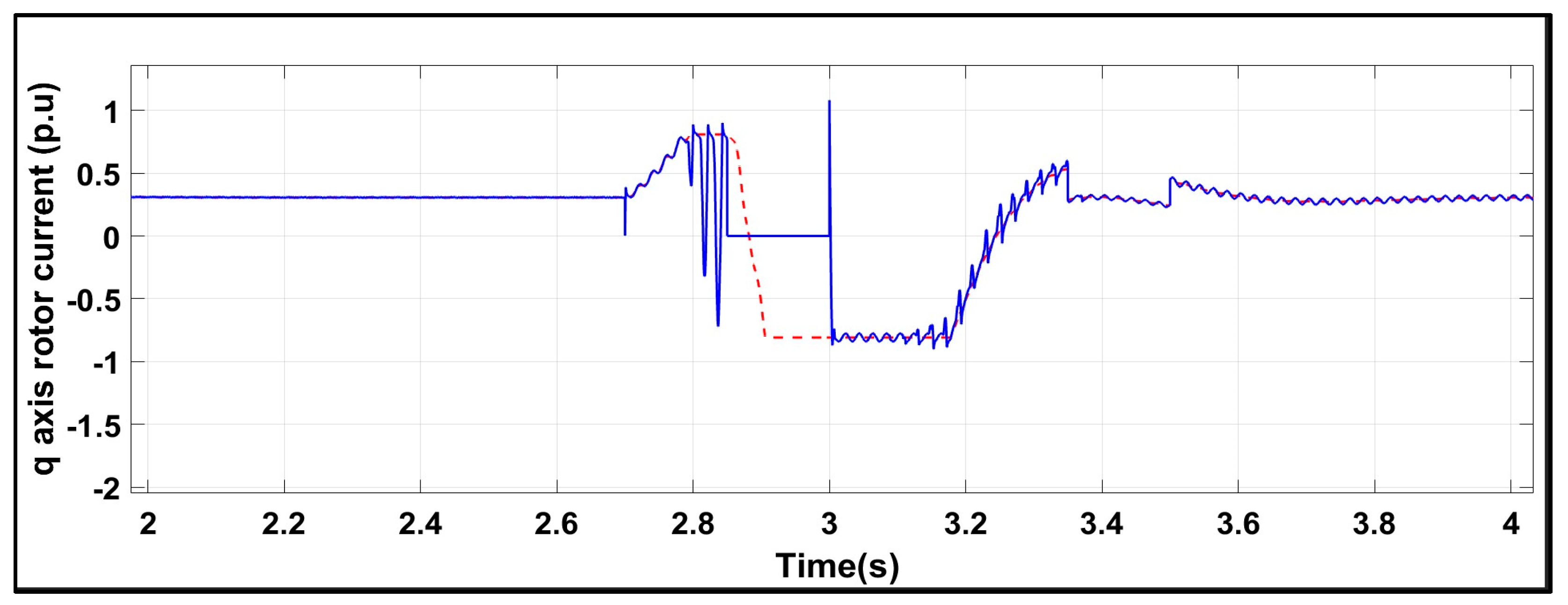
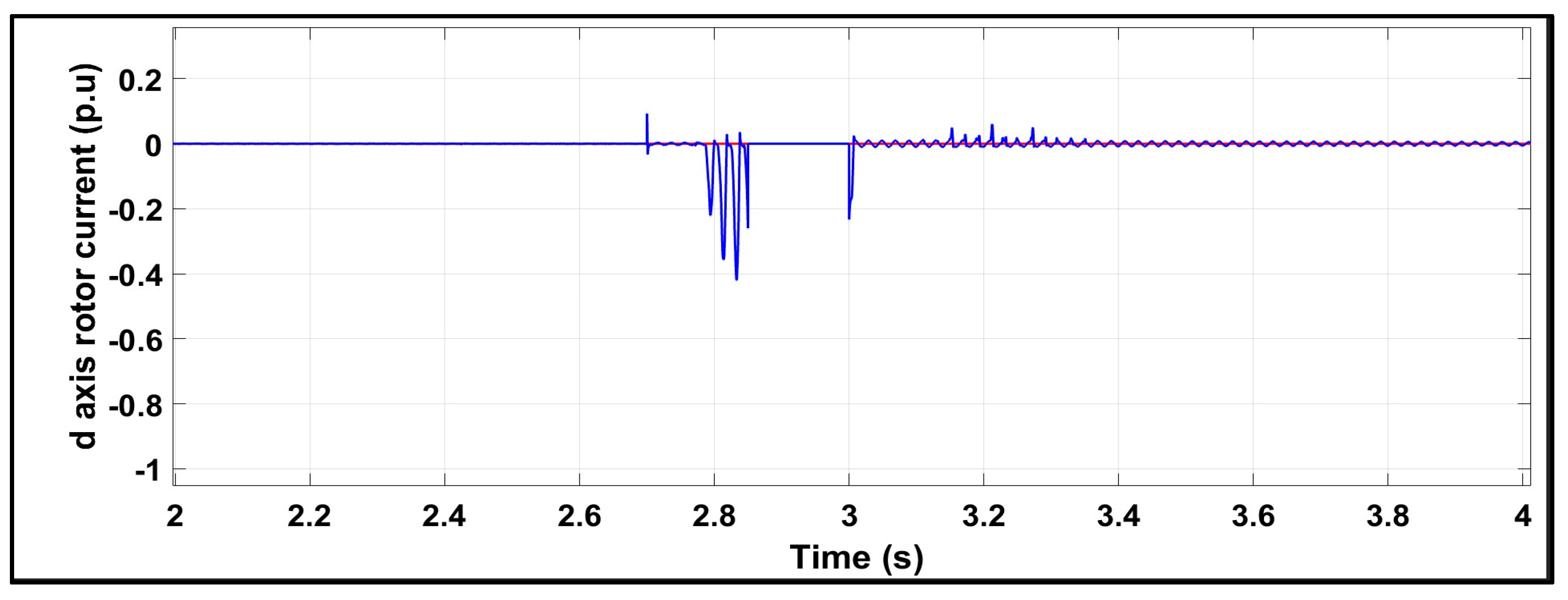
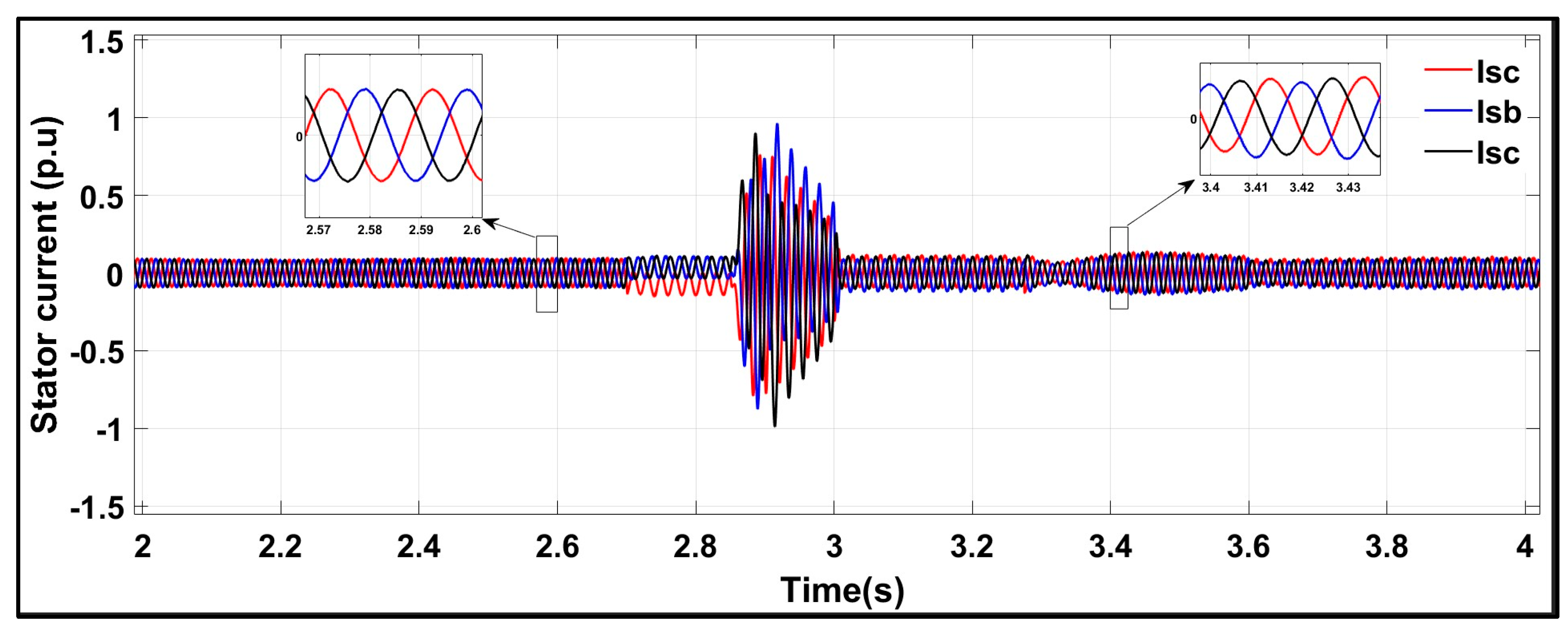
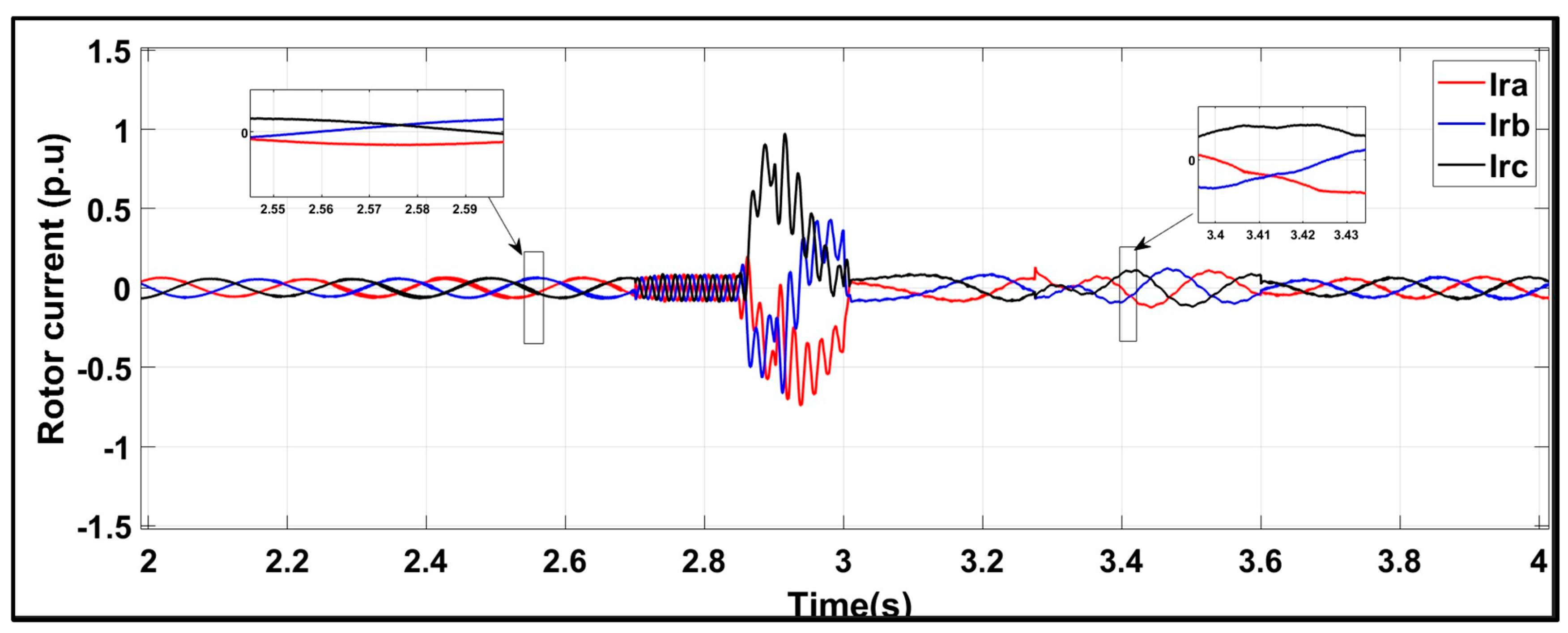
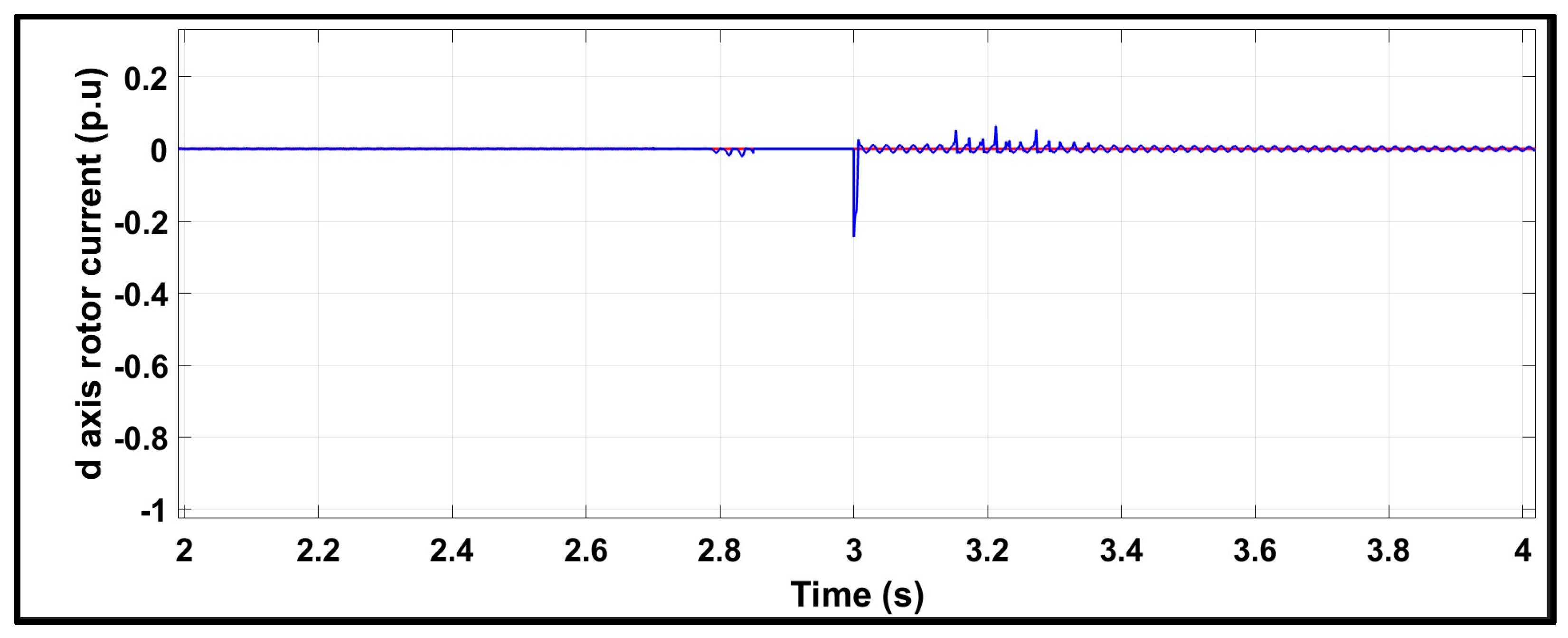
6.2. Test Response Under a Symmetrical Three-Phase Fault with the Conventional Scheme
6.3. Test Response Under a Symmetrical Three-Phase Fault with the Proposed Scheme
6.4. Comparing Various FRT Protection Schemes with the Proposed Approach
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gidwani, L. A comparative power quality study of DFIG and PMSG based wind Energ Conversion System. WSEAS Trans. Syst. Control. 2015, 10, 38–47. [Google Scholar]
- Beainy, A.; Maatouk, C.; Moubayed, N.; Kaddah, F. Comparison of different type of generator for wind energy conversion system topologies. In Proceedings of the 2016 3rd international conference on renewable energies for developing countries (REDEC-IEEE), Zouk Mosbeh, Lebanon, 13–15 July 2016; pp. 1–6. [Google Scholar]
- Dahiya, V.; Leena, G. Comparative study of DFIG and PMSG in wind energy conversion system. Int. J. Electr. Eng. Technol. (IJEET) 2019, 10, 73–79. [Google Scholar]
- Howlader, A.M.; Senjyu, T. A Comprehensive review of low voltage ride through capabiligy strategies for wind energy conversion system. Renew. Energy Sustain. Energy Rev. 2016, 56, 643–658. [Google Scholar] [CrossRef]
- Youssef, A.R.; Sayed, M.A.; Abdel-Wahab, M. MPPT control technique for direct drive five-phase PMSG wind turbines with wind speed estimation. Int. J. Sustain. Green Energy 2015, 4, 195–205. [Google Scholar]
- Mousa, H.H.; Youssef, A.R.; Mohamed, E.E. Variable step size P and O MPPT algorithm for optimal power extraction of multi-phase PMSG based wind generation system. Int. J. Electr. Power Energy Syst. 2019, 108, 218–231. [Google Scholar] [CrossRef]
- Jiao, X.; Sun, Y.; Ying, Y.; Yang, Q. Effective wind speed extimation based maximum power point tracking control for variable-speed wind turbine. In Proceedings of the Chinese Automation Congress, Jinan, China, 20–22 October 2017; pp. 6685–6690. [Google Scholar]
- Hossain, M.E. Performance of new solid-state fault current limiter for transient stability enhancement of DFIG based wind generator. In Proceedings of the North American Power Symposium Conference (NAPS), Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
- Lingling, F.; Zhixin, M. Modeling and Analysis of Doubly Fed Induction Generator Wind Energy Systems; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Kaloi, G.S.; Wang, J.; Baloch, M.H. Active and reactive power control of the doubly fed induction generator based on wind energy conversion system. Energy Rep. 2016, 2, 194200. [Google Scholar] [CrossRef]
- Ibrahim, A.O.; Nguyen, T.H.; Lee, D.-C.; Kim, S.-C. A fault ride- through technique of DFIG wind turbine systems using dynamic voltage restorers. IEEE Trans. Energy Convers. 2011, 26, 871–882. [Google Scholar] [CrossRef]
- Shen, Y.-W.; Ke, D.-P.; Sun, Y.-Z.; Kirschen, D.S.; Qiao, W.; Deng, X.-T. Advanced auxiliary control of an energy storage device for transient voltage support of a doubly fed induction generator. IEEE Trans. Sustain. Energy 2016, 7, 63–76. [Google Scholar] [CrossRef]
- de Souza, V.R.F.B.; Barros, L.S.; Costa, F.B. Modular multilevel converter for low-voltage ride-through support in AC networks. Energies 2021, 14, 5314. [Google Scholar] [CrossRef]
- Vinothkumar, K.; Selvan, M.P. Novel scheme for enhancement of fault ride- through capability of doubly fed induction generator based wind farms. Energy Convers Manag. 2011, 52, 2651–2658. [Google Scholar] [CrossRef]
- Rahimi, M.; Parniani, M. Grid-fault ride-through analysis and control of wind turbines with doubly fed induction generators. Electr. Power Syst. Res. 2010, 80, 184–196. [Google Scholar] [CrossRef]
- Dai, J.; Xu, D.; Wu, B.; Zargari, N.R. Unified DC-link current control for low-voltage ride-through in current-source-converter-based wind energy conversion systems. IEEE Trans Power Electron 2011, 26, 288–297. [Google Scholar]
- Yang, L.; Xu, Z.; Østergaard, J.; Dong, Z.Y.; Wong, K.P. Advanced Control Strategy of DFIG Wind Turbines for Power System Fault Ride Through. IEEE Trans. Power Syst. 2011, 27, 713–722. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Amin, S.U.; Al-Durra, A.; Ullah, N.; Ro, J.-S. Convergence enhancement of super twisting sliding mode control using artificial neural network for DFIG based wind energy conversion systems. IEEE Access 2022, 10, 97625–97641. [Google Scholar] [CrossRef]
- Haro-larrode, M.; Santos-Mugica, M.; Eguia, P.; Rodriguez-Sanchez, R.; Gil-de-Muro, A. Impact of propostional resonant controller parameters of VSC connected to AC grids with variable X/R characterics on the small signal stability. Int. J. Electr. Power Energy Syst. 2020, 118, 105746. [Google Scholar] [CrossRef]
- Rohten, J.A.; Silva, J.J.; Munoz, J.A.; Villarroel, F.A.; Dewar, D.N.; Rivera, M.E.; Espinoza, J.R. A simple self tunning resonan control approach for power electronics connected micro grids with distorted voltage conditions. IEEE Access 2020, 8, 216018–216028. [Google Scholar] [CrossRef]
- Damas, R.N.; Son, Y.; Yoon, M.; Kim, S.-Y.; Choi, S. Subsynchronous oscillation and advanced analysis: A review. IEEE Access 2020, 8, 224020–224032. [Google Scholar] [CrossRef]
- Yao, J.; Pei, J.; Xu, D.; Liu, R.; Wang, X.; Wang, C.; Li, Y. Coordinated control of a hybrid wind farm with DFIG-based and PMSG-based wind power generation systems under asymmetrical grid faults. Renew. Energy 2018, 127, 613–629. [Google Scholar] [CrossRef]
- Jin, J.; Yang, R.; Zhang, R.; Fan, Y.; Xie, Q.; Chen, X. Combined low voltage ride through and power smoothing control for DFIG/PMSG hybrid wind energy conversion system employing a SMES-based AC-DC unified power quality conditioner. Int. J. Electr. Power Energy Syst. 2021, 128, 106733. [Google Scholar] [CrossRef]
- Yesudhas, A.; Palanimuthu, K.; Lee, S.; Jeong, J.; Joo, Y. Performance enhancement of PMSG-based WECS using robust adaptive fuzzy sliding mode control. Control. Eng. Pract. J. 2025, 156, 106211. [Google Scholar] [CrossRef]
- Yang, L.; He, X.; Zhang, P.; Liu, S. Control scheme and performance analysis of dual-frequency single-phase grid-connected inverter interfaced with weak and distorted grids. IEEE Access 2020, 8, 178639–178650. [Google Scholar] [CrossRef]
- de Bosio, F.; Pastorelli, M.; Ribeiro, L.A.D.S.; Lima, M.S.; Freijedo, F.; Guerrero, J.M. Current control loop design and analysis based on resonant regulators for microgrid applications. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 5322–5327. [Google Scholar] [CrossRef]
- Haro-Larrode, M.; Bergna-Diaz, G.; Eguia, P.; Santos-Mugica, M. On the Tuning of Fractional Order Resonant Controllers for a Voltage Source Converter in a Weak AC Grid Context. IEEE Access 2021, 9, 52741–52758. [Google Scholar] [CrossRef]
- Chehaidia, S.E.; Abderezzak, A.; Kherfane, H.; Guersi, N.; Cherif, H.; Boukhezzar, B. Fuzzy gain scheduling of PI torque controller to capture the maximum power from variable speed wind turbines. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; pp. 1–6. [Google Scholar]
- Nouriani, A.; Moradi, H. Variable speed wind turbine power control: A comparison between multiple LVRT based methods. Int. J. Dyn. Control. 2022, 10, 654–667. [Google Scholar] [CrossRef]
- Kazemi Golkhandan, R.; Aghaebrahimi, M.R.; Farshad, M. Control strategies for enhancing frequency stability by DFIGs in a power system with high percentage of wind power penetration. Appl. Sci. 2017, 7, 1140. [Google Scholar] [CrossRef]
- Shahbazi, M.; Poure, P.; Saadate, S. Real-time power switch fault diagnosis and fault-tolerant operation in a DFIG-based wind energy system. Renew. Energy 2018, 116, 209–218. [Google Scholar] [CrossRef]
- Chojaa, H.; Derouich, A.; Taoussi, M.; Chehaidia, S.E.; Zamzoum, O.; Mosaad, M.I.; Alhejji, A.; Yessef, M. Nonlinear Control Strategies for Enhancing the Performance of DFIG-Based WECS under a Real Wind Profile. Energies 2022, 15, 6650. [Google Scholar] [CrossRef]
- Almozayen, M.A.; Knight, A.M. Modeling Grid-Connected DFIG under System Disturbances using Dynamic Phasor FEM. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5 September 2022; pp. 380–386. [Google Scholar] [CrossRef]
- Kang, Z.; Li, J. Zero-Voltage Ride-Through Scheme of PMSG Wind Power System Based on NLESO and GFTSMC. Electronics 2023, 12, 4348. [Google Scholar] [CrossRef]
- Bekiroglu, E.; Yazar, M.D. Fault-Ride through Improvement of DFIG under Symmetrical/Asymmetrical Voltage Dips. Electr. Power Compon. Syst. 2023, 51, 510–523. [Google Scholar] [CrossRef]
- Kaloi, G.S.; Baloch, M.H.; Kumar, M.; Soomro, D.M.; Chauhdary, S.T.; Memon, A.A.; Ishak, D. An LVRT Scheme for Grid Connected DFIG Based WECS Using State Feedback Linearization Control Technique. Electronics 2019, 8, 777. [Google Scholar] [CrossRef]
- Naderi, S.B.; Negnevitsky, M.; Muttaqi, K.M. A Modified DC Chopper for Limiting the Fault Current and Controlling the DC-Link Voltage to Enhance Fault Ride-Through Capability of Doubly-Fed Induction-Generator-Based Wind Turbine. IEEE Trans. Ind. Appl. 2019, 55, 2021–2032. [Google Scholar] [CrossRef]
- Ekanayake, J.B.; Holdsworth, L.; Jenkins, N. Comparison of 5th order and 3rd order machine models for double fed induction generators (DFIG) wind turbines. Electr. Power Syst. Res. 2003, 67, 207–215. [Google Scholar] [CrossRef]
- Krause, P.C. Analysis of Electric Machinery, 2nd ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Döşoğlu, M.K. Crowbar hardware design enhancement for fault ride through capability in doubly fed induction generator-based wind turbines. ISA Trans. 2020, 104, 321–328. [Google Scholar] [CrossRef]
- Lei, Y.; Mullane, A.; Lightbody, G.; Yacamini, R. Modeling of the wind turbine with a doubly fed induction generator for grid integration studies. IEEE Trans Energy Convers 2006, 21, 257–264. [Google Scholar] [CrossRef]
- Rahimi, M.; Azizi, A. Transient behavior representation, contribution to fault current assessment, and transient response improvement in DFIG-based wind turbines assisted with crowbar hardware. Int. Trans. Electr. Energy Syst. 2018, 29, e2698. [Google Scholar] [CrossRef]
- Raghavendran, C.R.; Roselyn, J.P.; Devaraj, D. Development and performance analysis of intelligent fault ride through control scheme in the dynamic behavior of grid connected DFIG based wind systems. Energy Rep. 2020, 6, 2560–2576. [Google Scholar] [CrossRef]
- Pannell, G.; Zahawi, B.; Atkinson, D.J.; Missailidis, P. Evaluation of the Performance of a DC-Link Brake Chopper as a DFIG Low-Voltage Fault-Ride-Through Device. IEEE Trans. Energy Convers. 2013, 28, 535–542. [Google Scholar] [CrossRef]
- Okedu, K.E.; Muyeen, S.M.; Takahashi, R.; Tamura, J. Wind Farms Fault Ride Through Using DFIG With New Protection Scheme. IEEE Trans. Sustain. Energy 2012, 3, 242–254. [Google Scholar] [CrossRef]
- Jabbour, N.; Tsioumas, E.; Medemlis, C.; Solomin, E. A highly effective Fault-Ride-Through Strategy for a wind Energy Conversion System with DFIG. IEEE Trans. Power Electron. 2020, 35, 8154–8164. [Google Scholar] [CrossRef]
- Mossa, M.A.; Do, T.D.; Al-Sumaiti, A.S.; Quynh, N.V.; Diab, A.A.Z. Effective Model Predictive Voltage Control for a Sensorless Doubly Fed Induction Generator. IEEE Can. J. Electr. Comput. Eng. 2021, 44, 50–64. [Google Scholar] [CrossRef]
- Zou, X.; Zhu, D.; Hu, J.; Zhou, S.; Kang, Y. Mechanism Analysis of the Required Rotor Current and Voltage for DFIG-Based WTs to Ride-Through Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2018, 33, 7300–7304. [Google Scholar] [CrossRef]
- Ali, M.A.S.; Mehmood, K.K.; Baloch, S.; Kim, C.-H. Modified rotor-side converter control design for improving the LVRT capability of a DFIG-based WECS. Electr. Power Syst. Res. 2020, 186, 106403. [Google Scholar] [CrossRef]
- Ansari, A.A.; Dyanamina, G. Fault Ride-Through Operation Analysis of Doubly Fed Induction Generator-Based Wind Energy Conversion Systems: A Comparative Review. Energies 2022, 15, 8026. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Rated power | 2 MW |
| Rated L-L stator voltage | 690 V |
| Rated stator current | 1760 A |
| Torque at generator mode | 12,732 N·m |
| L-L nominal rotor voltage | 2070 V |
| Number of pole pairs | 2 |
| Stator frequency | 50 Hz |
| Synchronous speed | 1500 rpm |
| Stator resistance | 0.0026 ohm |
| Rotor resistance | 0.0261 ohm |
| Stator leakage inductance | 0.87 mH |
| Magnetizing Inductance | 0.25 mH |
| Rotor leakage inductance | 0.783 mH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talani, R.A.; Kaloi, G.S.; Ali, A.; Bijarani, M.A.; Abbas, G.; Hatatah, M.; Mercorelli, P.; Touti, E. Dynamic Performance Analysis and Fault Ride-Through Enhancement by a Modified Fault Current Protection Scheme of a Grid-Connected Doubly Fed Induction Generator. Machines 2025, 13, 110. https://doi.org/10.3390/machines13020110
Talani RA, Kaloi GS, Ali A, Bijarani MA, Abbas G, Hatatah M, Mercorelli P, Touti E. Dynamic Performance Analysis and Fault Ride-Through Enhancement by a Modified Fault Current Protection Scheme of a Grid-Connected Doubly Fed Induction Generator. Machines. 2025; 13(2):110. https://doi.org/10.3390/machines13020110
Chicago/Turabian StyleTalani, Rameez Akbar, Ghulam Sarwar Kaloi, Aamir Ali, Muhammad Ali Bijarani, Ghulam Abbas, Mohammed Hatatah, Paolo Mercorelli, and Ezzeddine Touti. 2025. "Dynamic Performance Analysis and Fault Ride-Through Enhancement by a Modified Fault Current Protection Scheme of a Grid-Connected Doubly Fed Induction Generator" Machines 13, no. 2: 110. https://doi.org/10.3390/machines13020110
APA StyleTalani, R. A., Kaloi, G. S., Ali, A., Bijarani, M. A., Abbas, G., Hatatah, M., Mercorelli, P., & Touti, E. (2025). Dynamic Performance Analysis and Fault Ride-Through Enhancement by a Modified Fault Current Protection Scheme of a Grid-Connected Doubly Fed Induction Generator. Machines, 13(2), 110. https://doi.org/10.3390/machines13020110









