Six Sigma-Based Mathematical Optimization Framework for Flux-Switching Machines: A Roadmap for Quality, Performance, and Manufacturing Tolerances

Abstract

Flux-switching wound field machines (FSWFMs) offer high torque density and independence from rare-earth materials, making them promising candidates for sustainable electric vehicles and industrial applications. However, their adoption is limited by challenges such as high torque ripple, efficiency variations, and sensitivity to manufacturing tolerances. This study presents a Design for Six Sigma (DFSS) optimization framework that integrates sensitivity analysis, response surface modeling (RSM), and multi-objective genetic algorithms to address these challenges. The optimized solution reduces torque ripple by 7.69%, improves torque output, and enhances energy efficiency. By incorporating Six Sigma principles, the framework ensures robust performance under manufacturing variations, bridging the gap between theoretical optimization and practical implementation. This scalable and efficient methodology establishes FSWFMs as viable solutions for industrial applications, revolutionizing electric machine design.

1. Introduction

The design and optimization of electrical machines have undergone significant advancements in recent years, driven by the demand for high-performance, efficient, and reliable systems across various industries, including electric vehicles, renewable energy, and robotics [1]. Among these machines, the flux-switching wound field machine (FSWFM) stands out due to its inherent advantages, such as robust structural design, high torque density, and superior operational efficiency [2,3,4]. However, the performance of FSWFMs, like other electrical machines, is often affected by uncertainties arising from manufacturing tolerances. These tolerances, which stem from the limitations of manufacturing processes, result in dimensional deviations in critical components, including stators, rotors, and magnetic assemblies, leading to performance variability and degradation. Addressing these challenges necessitates the integration of advanced optimization methodologies during the design phase [5].

Motor optimization design is broadly categorized into two primary approaches: direct optimization using analytical models and indirect optimization based on prototypes. Direct optimization often employs equivalent magnetic circuit models or other analytical methods [6,7]. These methods provide a structured approach to the design process but are frequently challenged by the complexities involved in developing accurate models. Moreover, their reliance on idealized assumptions can result in outcomes that fall short of the desired accuracy, particularly in complex systems. Indirect optimization methods, on the other hand, include both local and global optimization strategies, each with distinct advantages and limitations. The Taguchi method, a widely recognized local optimization technique, is celebrated for its computational efficiency and rapid convergence. However, its constrained exploration of the design space often hampers its ability to identify globally optimal parameter combinations [8]. In contrast, global optimization methods such as genetic algorithms, particle swarm optimization, and evolutionary strategies are extensively utilized in machine design. These methods leverage surrogate models to capture the nonlinear relationships between motor structural parameters and optimization objectives, enabling a more comprehensive exploration of the design space. Common surrogate models include response surface models, Kriging models, and neural network models [9,10]. The accuracy of the optimization outcomes, however, is critically dependent on the fidelity of these surrogate models.

Despite significant advancements in precision and efficiency, machine optimization designs remain susceptible to uncertainties, such as parameter fluctuations arising from manufacturing tolerances. Even minor variations in parameters can significantly degrade performance [11]. This underscores the need to integrate manufacturing tolerances into the optimization design process. To address this, robust optimization methodologies have been developed to mitigate sensitivity to these uncertainties, ensuring enhanced product quality [12,13,14]. Manufacturing tolerances arise primarily from limitations in processing technologies and techniques, leading to dimensional deviations in components such as stators, rotors, and permanent magnets. These deviations may manifest as variations in pole widths, internal and external diameters, and the magnetic field properties of permanent magnets. To account for these tolerances, robust optimization techniques such as the Taguchi method, worst-case analysis (WCA), and Design for Six Sigma (DFSS) have been effectively applied [5]. The Taguchi method, grounded in statistical design principles, aims to minimize system sensitivity to noise factors, thereby achieving robust designs. However, its inability to consistently identify globally optimal solutions limits its broader applicability [15]. The WCA method, which evaluates system performance under worst-case parameter scenarios, is often overly conservative due to the assumptions made about these scenarios [16]. Meanwhile, DFSS, an approach rooted in Six Sigma quality management principles, employs sophisticated tools and methodologies to ensure high product performance across varying conditions [17]. This methodology combines statistical tools with advanced optimization techniques to ensure the design’s resilience to uncertainties. Unlike traditional deterministic optimization methods, which focus solely on ideal conditions, Six Sigma robust optimization incorporates real-world variabilities, including manufacturing tolerances, into the design process [18]. This ensures that the optimized machine not only meets performance targets under nominal conditions but also maintains high levels of performance consistency despite potential manufacturing deviations.

Several recent studies have explored the impact of manufacturing tolerances on machine performance and the efficacy of robust optimization methods. A sensitivity analysis on manufacturing tolerances in permanent magnet synchronous machines demonstrated how dimensional deviations influence machine performance [19]. A comparative study evaluated robust design optimization methods—including the Taguchi method, WCA, and DFSS—highlighting their strengths and limitations in addressing manufacturing tolerances [15]. The effect of eccentricities and dimensional deviations on electromotive force in permanent magnet synchronous motors emphasized the importance of considering these factors during the design stage [20]. A robust optimization framework for hybrid-excited generators was developed, utilizing enhanced surrogate modeling techniques and validating performance through simulations and prototypes [21]. Ref. [22] demonstrated the application of Six Sigma and Kriging frameworks in optimizing the design of plug-in hybrid electric buses, effectively reducing long-term operational costs. In [17], Six Sigma robust optimization was applied to optimize the design of outer rotor permanent magnet motors for hybrid vehicles, integrating response surface methodology with particle swarm optimization to achieve higher efficiency. A practical design and optimization method for a flux-switching permanent magnet (FSPM) drive system was implemented for a light-duty commercial electric vehicle (CEV) [23]. The optimization integrated response surface methodology (RSM) and genetic algorithms (GAs), achieving 84% high-efficiency running time during experimental testing on a prototype vehicle. A statistical analysis of ironless rotor axial flux permanent magnet (AFPM) manufacturing tolerances revealed substantial increases in cogging and ripple torque due to unavoidable combined tolerances [24]. A computationally efficient superposition method was used to identify parameters with the most significant impact on performance, providing a foundation for improving manufacturing processes. Ref. [25] explored the optimization of flux-switching permanent magnet machines using Six Sigma techniques to improve torque and reduce ripple and cogging. In [26], a multilevel genetic algorithm combined with Six Sigma robust optimization enhanced the performance of surface-mounted permanent magnet synchronous machines, validated through Monte Carlo simulations. Ref. [27] introduced a Six Sigma-based robust optimization for electrical drive systems, addressing uncertainties in materials and precision to improve reliability and quality. Recent advancements have also introduced innovative structures in flux-switching permanent magnet machines. A flux-switching permanent magnet linear machine with a partitioned stator (FSPMLM-PS) was optimized using a multi-objective genetic algorithm, achieving improvements in thrust ripple (22.03%), detent force (68.33%), and thrust force density (27.95%) compared to conventional designs [28]. These developments underscore the role of robust optimization frameworks, such as Six Sigma techniques and surrogate modeling, in addressing performance challenges like torque ripple and efficiency under practical constraints. Ref. [16] proposed a multi-objective sequential optimization method for robust electrical machine design, demonstrating enhanced performance and reduced computational costs compared to deterministic methods.

These studies highlight the necessity of incorporating manufacturing tolerances into the optimization design process to enhance both product quality and reliability. However, despite the progress made in robust optimization methodologies, no studies have specifically focused on the application of these techniques to FSWFMs. Addressing this gap represents a significant opportunity to advance the state of the art in robust machine optimization design. This paper introduces a novel DFSS-based optimization framework tailored to FSWFMs, combining sensitivity analysis, surrogate modeling with RSM, and multi-objective genetic algorithms to address the aforementioned gaps. The uniqueness of this study lies in integrating these established methodologies specifically for FSWFMs, ensuring robust performance under real-world manufacturing variabilities. By leveraging the Six Sigma principles, this approach bridges the gap between theoretical optimization and practical industrial implementation, making it suitable for addressing manufacturing tolerances. The primary objectives of this study are as follows:

• Improve critical parameters such as torque, torque ripple, power factor, and efficiency to meet industrial requirements for FSWFMs.
• Develop optimization strategies resilient to manufacturing variabilities, ensuring consistent performance across production batches.
• Leverage surrogate modeling to reduce computational overhead without compromising accuracy, facilitating rapid optimization cycles.

The remainder of this paper is organized as follows. Section 2 details the structural and operational characteristics of FSWFMs and introduces the optimization framework. Section 3 explains the implementation of the DFSS methodology, including surrogate modeling and sensitivity analysis. Section 4 presents the optimization results, compares various design models, and validates the findings through FEA simulations, and Section 5 concludes the study with potential avenues for future research.

2. Operational Characteristics and Optimization Framework of FSWFMs

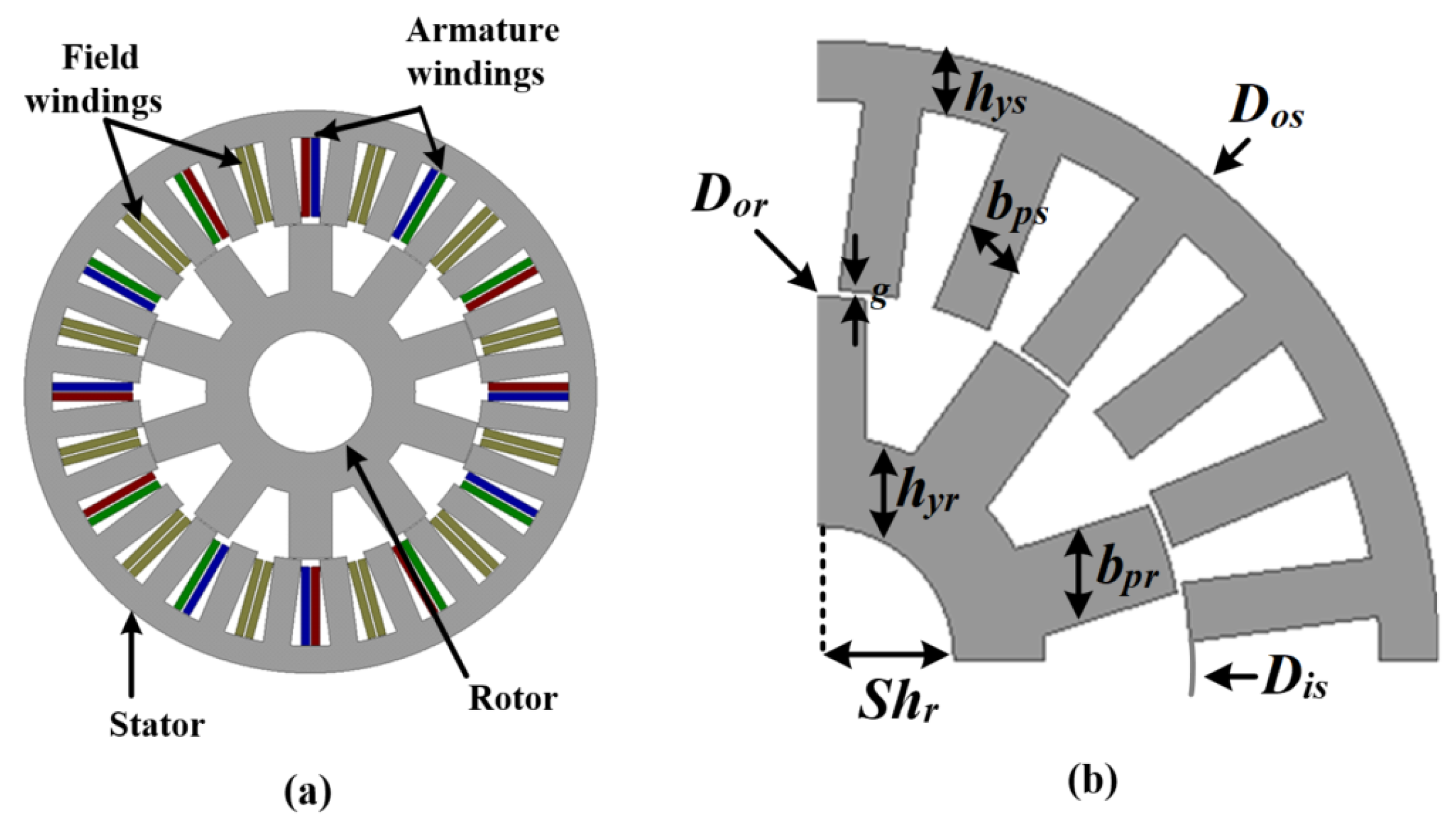
The operational principles and characteristics of FSWFMs stem from their unique design and topology, which enable efficient electromagnetic energy conversion. The model analyzed in this study features a radial flux configuration, employing a 24-slot/10-pole structure as presented in Figure 1a. This arrangement ensures effective torque production and highlights the advantages of eliminating permanent magnets, which are replaced by DC-fed field excitation coils (FECs). The stator, which contains the armature windings and the FECs, plays a dual role in generating AC voltage and establishing the magnetic flux required for torque production.

The FECs are arranged in a toroidal configuration within the stator slots. This toroidal arrangement contributes to a uniform magnetic flux distribution, which is essential for stable and efficient machine operation. When DC current flows through the FECs, the magnetic field generated interacts with the rotor, which consists of 10 laminated steel poles. The laminated construction reduces eddy current losses, while the pole design ensures optimized flux paths and mitigates torque ripple. The rotor’s interaction with the magnetic field induces alternating current (AC) in the armature windings, facilitating energy conversion.

Table 1. Design parameters of the FSWFM model [29].

Description	Parameter	Values	Unit
Rated speed	${\omega }_r$	1500	rpm
Number of stator slots	$P_s$	24	-
Airgap length	g	0.5	mm
Aspect ratio	k	0.7	-
Area of field coils	$A_c$	15	mm2
Split ratio	-	0.6	-
Number of rotor slots	$P_r$	10	-
Rotor outer diameter	$D_r$	152	mm
Stator inner diameter	$D_{in}$	152	mm
Stator outer diameter	$D_{os}$	254	mm
Stack length	$L_s$	107	mm
Stator tooth arc factor	$C_t$	0.25	-
Slot filling factor	$c_f$	0.45	-

provides an overview of the FSWFM design parameters, which include both electrical and mechanical features. The stator has 24 slots and operates at a rated speed of 1500 rpm. Key geometric parameters such as the airgap length ($g=0.5\mathrm{mm}$), rotor and stator diameters, and stack length ($L_s$) are precisely scaled to optimize the electromagnetic performance. The slot filling factor ($c_f=0.45$) ensures efficient use of the stator slot area, enhancing the overall performance.

The scaling of dimensions is governed by Equation (1), which relates the stator’s outer diameter ($D_{os}$) to key electromagnetic and mechanical parameters. This relationship accounts for variables such as the rated power output ($T_e$), the number of poles ($P_r$), and the airgap magnetic flux density ($B_g$):

$$D_{os}=\sqrt[5]{{\displaystyle \frac{4T_e}{{\pi }^2{P}_r{k}_e{k}_L{\Lambda }_0^3{A}_c^3{B}_g^2{c}_f}}},$$

(1)

where $k_e$ is the electrical loading factor, $k_L$ is the leakage coefficient, ${\Lambda }_0$ is the specific permeance coefficient, and $A_c$ is the total current density. After determining the $D_{os}$, the inner diameter ($D_{in}$) and stack length ($L_s$) are scaled proportionally to maintain balanced performance and structural integrity. Similarly, the rotor pole width ($b_p$), rotor yoke height ($h_r$), and stator yoke height ($h_s$) are defined as functions of the stator diameter, as expressed in Equation (2):

$$b_p=b_s=h_r=h_s={\displaystyle \frac{\pi D_{in}}{P_r}}.$$

(2)

Figure 1b shows the parametric model of the motor while

Table 2. Ranges of design variables.

Design Variable	Unit	Initialization	Range Min	Range Max
g	mm	0.50	0.450	0.550
$D_{os}$	mm	254.00	228.6	279.4
$D_{in}$	mm	152.00	136.8	167.2
$L_s$	mm	107.00	96.3	117.7
$h_r$	mm	19.98	19.082	20.878
$b_r$	mm	19.98	19.082	20.878
$h_y$	mm	12.14	10.926	13.354
$b_y$	mm	12.14	10.926	13.354
$S{h}_r$	mm	54.80	49.5	60.1
${\tau }_r$	mm	19.90	17.91	21.89
$r_f$	mm	47.44	42.696	52.184
$D_r$	mm	151.50	136.35	166.65

illustrates the range of critical design variables, such as the $h_r$ and $h_s$. The rotor outer diameter ($D_r$) varies between 136.8 mm and 167.2 mm, while the rotor yoke height ranges from 19.08 mm to 20.878 mm. These dimensions are selected to ensure proportionality and optimal flux linkage while maintaining manufacturability. The operational principles of the FSWFM ensure effective energy conversion by harnessing the interaction between the stator-generated magnetic flux and the rotor’s poles. This design achieves high torque density while reducing material dependence on rare earth elements. Furthermore, the proportional scaling of dimensions and the careful selection of design parameters enable efficient electromagnetic performance and reliable operation.

The output voltage of the inverter is directly applied to the motor terminals, initiating the flow of current through its phases. The relationship between the inverter’s output voltage and the motor input current is dictated by the RL circuit characteristics of the motor phases. These characteristics are critical in determining the interaction between the electrical and mechanical components of the machine. The inverter’s output voltage is regulated in the control loop, utilizing feedback from motor current sensors and the resistive and inductive properties of the motor phases.

In this study, uncertainties arising from sensors and the inverter, including variations in the DC link voltage, are considered. Furthermore, the resistance and inductance of the motor phases are incorporated as potential sources of variability in the input current to the motor. An additional uncertain parameter is the maximum amplitude of the motor input current ($I_{\max }$), which represents a significant factor influenced by external and internal disturbances in the inverter system. These uncertainties collectively affect the performance and operational stability of the machine.

The analysis incorporates ten critical design variables, including the air gap length (g), the stator’s outer and inner diameters ($D_{\mathrm{os}},D_{\mathrm{in}}$), the stack length ($L_{\mathrm{s}}$), the rotor yoke height ($h_{\mathrm{r}}$), and the stator yoke height ($h_{\mathrm{s}}$). Additional parameters include the slot height ($Sh$), rotor pole pitch (${\tau }_{\mathrm{r}}$), rotor radius ($r_{\mathrm{f}}$), and the rotor diameter ($D_{\mathrm{r}}$). Together with $I_{\max }$, these variables provide a comprehensive framework for evaluating the impact of uncertainties and ensuring optimal performance across a range of operating conditions. The inclusion of $I_{\max }$ as a key design variable inherently accounts for thermal considerations. Maximum current influences the heat generated within the windings through resistive losses ($I^{2}R$), which directly affects the thermal behavior and operating limits of the motor. By optimizing $I_{\max }$ variability, the proposed framework ensures that the motor operates within safe thermal limits, even under manufacturing tolerances. This indirect consideration of thermal effects highlights the coupling between electrical, mechanical, and thermal performance, reinforcing the robustness of the optimization framework.

The optimization process considers a weighted sum of the key objectives, targeting improvements in torque ripple, efficiency, and output performance while ensuring the design remains within manufacturable limits. The objective function is formulated as follows:

$$f{\left(x_i\right)}_{\min }={\lambda }_1{\displaystyle \frac{T_{\mathrm{avg}}^{\prime }}{T_{\mathrm{avg}}\left(x_i\right)}}+{\lambda }_2{\displaystyle \frac{T_{\mathrm{rip}}^{\prime }}{T_{\mathrm{rip}}\left(x_i\right)}}+{\lambda }_3{\displaystyle \frac{{\mathrm{PF}}^{\prime }}{\mathrm{PF}\left(x_i\right)}}+{\lambda }_4{\displaystyle \frac{{\eta }^{\prime }}{\eta \left(x_i\right)}}$$

(3)

Subject to:

$$g_1\left(\mathbf{x}\right)=D_{os}-D_{in}-2H_y\ge 0$$

(4)

$$g_2\left(\mathbf{x}\right)=D_{os}-S{h}_r-2H_y\ge 0$$

(5)

$$g_3\left(\mathbf{x}\right)=\pi (S_{h_r}+2H_y)-P_r{\tau }_r\ge 0$$

(6)

$$g_4\left(\mathbf{x}\right)=I_{\max }-I_{\mathrm{limit}}\ge 0$$

(7)

$$g_5\left(\mathbf{x}\right)=T_{\mathrm{avg}}-48.03\ge 0$$

(8)

$$g_6\left(\mathbf{x}\right)=14.32-T_{\mathrm{rip}}\ge 0$$

(9)

$$g_7\left(\mathbf{x}\right)=\mathrm{PF}-0.4752\ge 0$$

(10)

$$g_8\left(\mathbf{x}\right)=\eta -87.05\ge 0$$

(11)

$${\mathbf{x}}_i^L\le {\mathbf{x}}_i\le {\mathbf{x}}_i^U,\forall i$$

(12)

The terms $T_{\mathrm{avg}}^{\prime }$, $T_{\mathrm{rip}}^{\prime }$, ${\mathrm{PF}}^{\prime }$, and ${\eta }^{\prime }$ in the objective function denote the initial values of the average torque, torque ripple, power factor, and efficiency, respectively, which serve as benchmarks for evaluating the relative improvement achieved during optimization. The design variables $\mathbf{x}$ include geometric and operational parameters such as g, $D_{os}$, $D_{in}$, $L_s$, $h_r$, $b_r$, $h_y$, $b_y$, $S{h}_r$, $D_r$, and $I_{\max }$. Each variable is constrained to remain within its respective lower (${\mathbf{x}}_i^L$) and upper (${\mathbf{x}}_i^U$) bounds to ensure feasibility and adherence to physical and operational limits. The weight coefficients ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$ correspond to the mean torque, torque ripple, power factor, and efficiency, respectively. These coefficients are adjusted based on the priority of the objectives to ensure balanced performance across the various aspects of the machine. For this study, each weight coefficient is assigned a value of 0.25 to ensure that no single objective is prioritized at the expense of the others. This balanced distribution prevents bias and ensures the machine’s design achieves optimal trade-offs across all performance metrics.

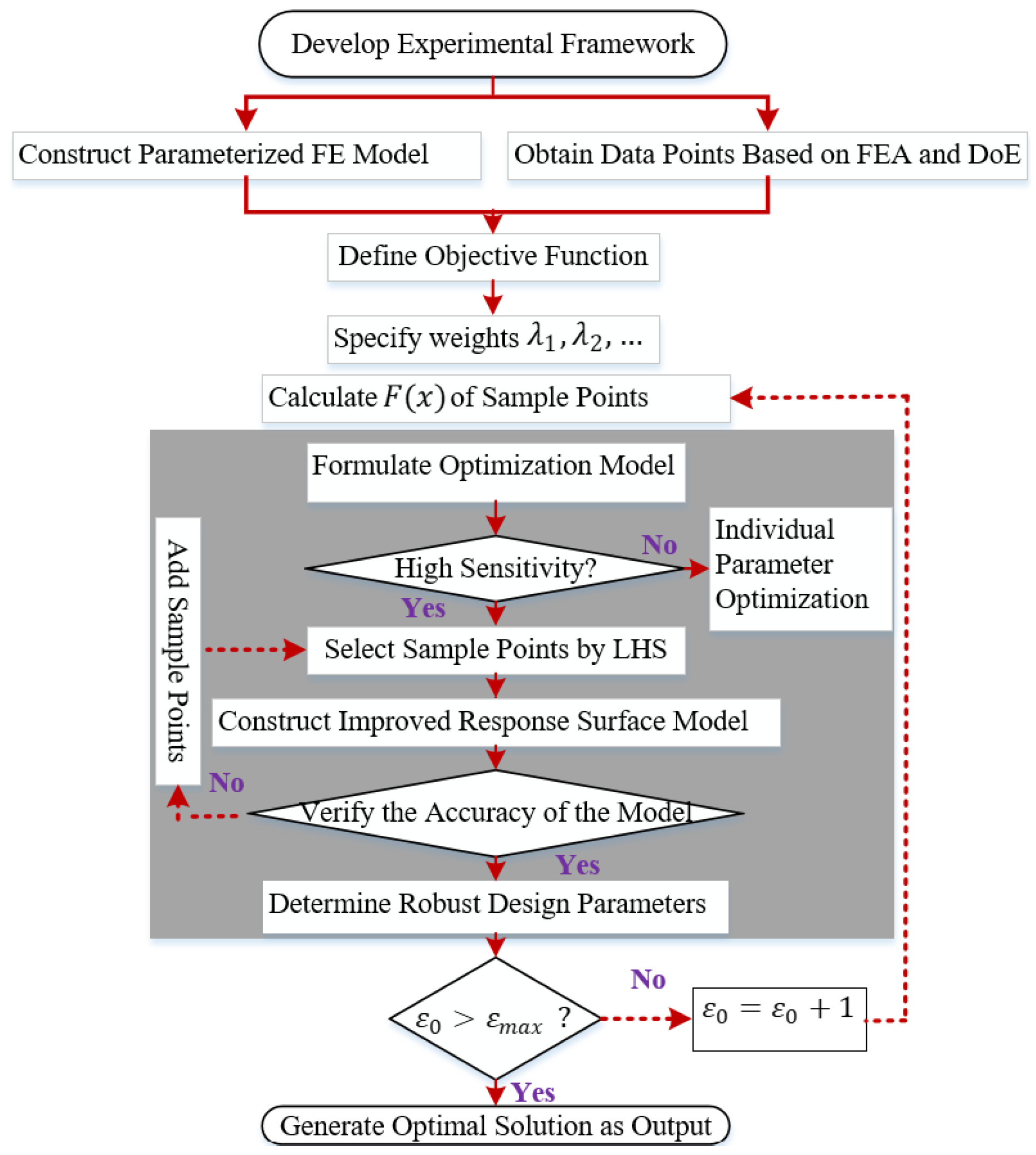
To solve the formulated optimization model efficiently, a robust optimization algorithm is proposed. This algorithm integrates parameterized finite element (FE) modeling, sensitivity analysis, and response surface modeling to iteratively refine the design parameters while ensuring high accuracy and robust performance. The NSGA-II algorithm was chosen for this study due to its well-documented effectiveness in solving multi-objective optimization problems. Its ability to maintain a diverse set of Pareto-optimal solutions, while converging efficiently towards trade-offs between conflicting objectives, makes it particularly suited for the high-dimensional design space of FSWFMs. In this work, NSGA-II facilitated the optimization of key parameters such as torque ripple and efficiency, ensuring robust and computationally efficient results.

Additionally, the algorithm incorporates Six Sigma analysis to address uncertainties and ensure that the optimized design meets performance requirements under varying conditions. The flowchart of the proposed algorithm is illustrated in Figure 2. While this section provides an overview of the optimization framework, the detailed application of Six Sigma methodology, including the statistical treatment of uncertainties, is discussed in Section 3.

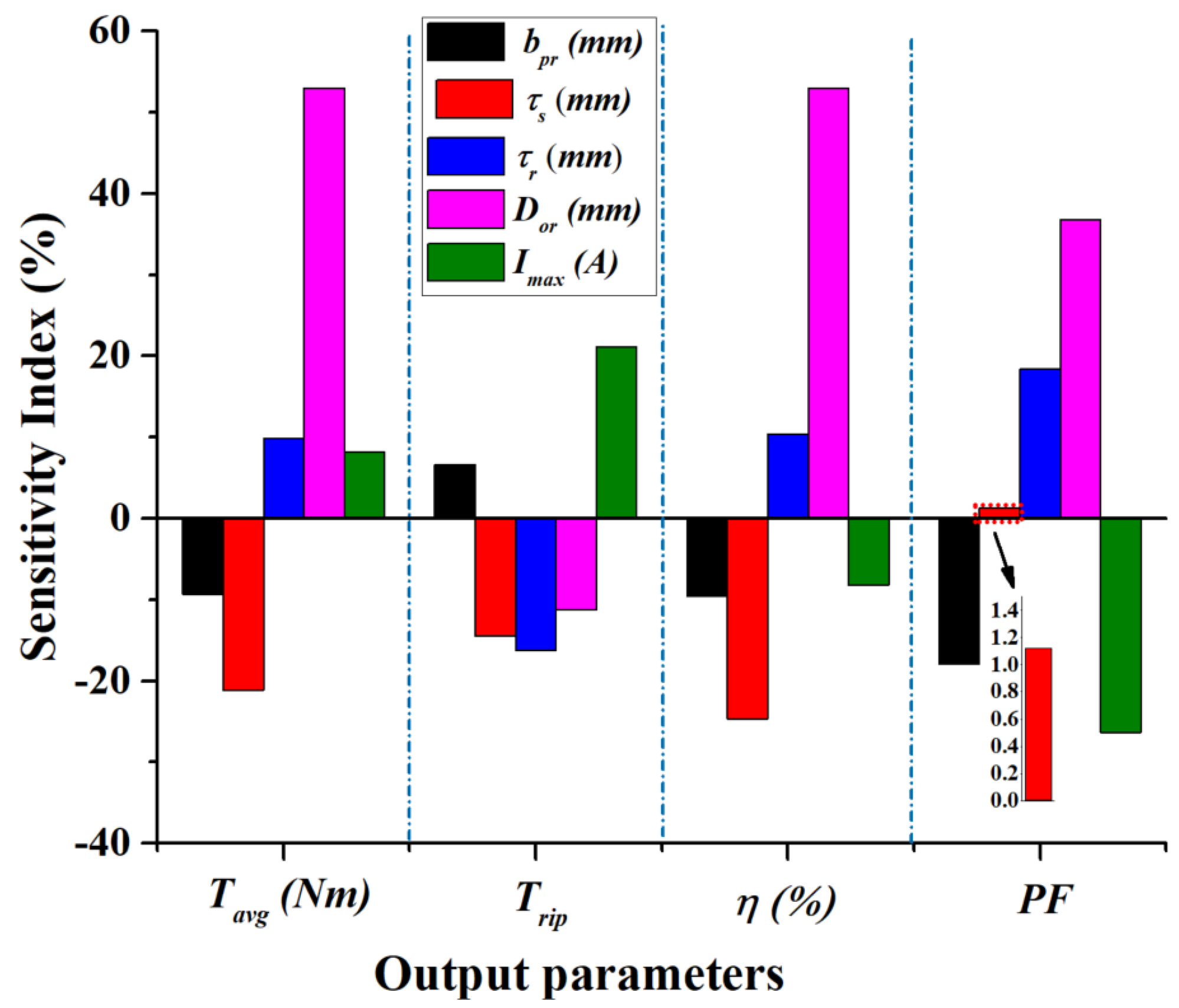
2.1. Sensitivity Analysis

Sensitivity analysis is a critical step in the optimization framework, aimed at prioritizing design variables based on their impact on the optimization objectives.

Table 3. Sensitivity indices of optimization objectives.

Parameters	${\mathit{Z}}_{{\mathit{T}}_{\mathbf{avg}}}$	${\mathit{Z}}_{{\mathit{T}}_{\mathbf{rip}}}$	${\mathit{Z}}_{\mathbf{PF}}$	${\mathit{Z}}_{\mathit{\eta }}$
g (mm)	−4.95	−11.22	−1.33	−4.56
$D_{os}$ (mm)	−4.29	−14.02	−2.95	−6.23
$D_{in}$ (mm)	−2.20	−0.40	−0.10	−0.10
$l_{st}$ (mm)	17.74	0.88	0.90	14.00
$h_{yr}$ (mm)	0.24	0.39	0.29	0.22
$b_{pr}$ (mm)	10.00	−20.00	−25.00	15.00
$h_{ys}$ (mm)	0.47	0.29	−0.62	0.50
$b_{ps}$ (mm)	14.41	18.10	15.01	15.27
$S{h}_d$ (mm)	−3.25	−1.98	0.19	0.27
${\tau }_s$ (mm)	20.00	−15.00	−10.00	10.00
${\tau }_r$ (mm)	−5.00	−30.00	−5.00	5.00
$D_{or}$ (mm)	50.00	−5.00	40.00	30.00
$I_{\max }$ (A)	25.00	−10.00	−15.00	20.00

summarizes the sensitivity indices for the key design variables, including the maximum current, $I_{\max }$. The sensitivity indices quantify how changes in a specific variable affect the $T_{\mathrm{avg}}$, $T_{\mathrm{rip}}$, PF, and $\eta$. By evaluating the sensitivity of these key objectives, this process ensures that the optimization focuses on the most impactful parameters. The sensitivity analysis in this study is conducted using a combination of FE simulations and statistical methods, providing a quantitative measure of the contribution of each variable to the overall performance. The sensitivity index of a design objective f with respect to a design variable $x_i$, assessed at the nominal operating point (NOP), can be quantified using the sensitivity index [30]:

$$s\left(x_i\right)={\displaystyle \frac{\partial f}{\partial x_i}}{|}_{\mathrm{NOP}}\approx {\displaystyle \frac{\Delta f/f}{\Delta x_i/x_i}}.$$

(13)

This index represents the percentage change in the objective f relative to the percentage change in the variable $x_i$. For this study, a comprehensive sensitivity function $s_{\mathrm{com}}\left(x\right)$, which combines the effects of all optimization objectives, is defined as follows:

$$s_{\mathrm{com}}\left(x\right)={\lambda }_1|s_{T_{\mathrm{avg}}}\left(x_i\right)|+{\lambda }_2|s_{T_{\mathrm{rip}}}\left(x_i\right)|+{\lambda }_3|s_{\mathrm{PF}}\left(x_i\right)|+{\lambda }_4\left|s_{\eta }\left(x_i\right)\right|.$$

(14)

where $s_{T_{\mathrm{avg}}}$, $s_{T_{\mathrm{rip}}}$, $s_{\mathrm{PF}}$, and $s_{\eta }$ are the sensitivity indices of average torque, torque ripple, power factor, and efficiency, respectively. The weights ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$ are set to 0.25 to ensure equal priority across all objectives.

From Table 3, it is evident that $b_{pr}$, ${\tau }_s$, ${\tau }_r$, $D_{or}$, and $I_{\max }$ significantly influence the optimization objectives compared to other variables. Additionally, $D_{or}$ exhibits notable sensitivity across all objectives, with a particularly high influence on $T_{\mathrm{avg}}$ and $\eta$, indicating its critical role in determining overall machine performance. Positive indices, such as those for $D_{or}$ on $T_{\mathrm{avg}}$ and $\eta$, suggest that increasing $D_{or}$ improves these objectives, while negative indices, such as those for $I_{\max }$ on PF and $\eta$, highlight potential trade-offs. Moreover, ${\tau }_r$ shows a high negative sensitivity for $T_{\mathrm{rip}}$, emphasizing its importance in reducing torque ripple. Similarly, the high sensitivity of $b_{pr}$ and ${\tau }_s$ underscores their dual role in influencing $T_{\mathrm{avg}}$ and PF, requiring careful optimization to balance their opposing effects.

The sensitivity chart of Figure 3 further illustrates the variability in design objectives with respect to high-sensitivity variables. In particular, $b_{pr}$ and ${\tau }_r$ show opposing effects on $T_{\mathrm{avg}}$ and $T_{\mathrm{rip}}$, highlighting the importance of balancing these parameters during optimization. Similarly, the high sensitivity of $D_{or}$ emphasizes its importance as a key variable in ensuring robust performance across varying operational conditions.

Overall, the sensitivity analysis informs the categorization of variables into high-sensitivity and low-sensitivity groups, streamlining the optimization process. High-sensitivity variables, such as $b_r$, ${\tau }_r$, $D_{or}$, and $I_{\max }$, are prioritized in optimization to achieve significant performance improvements, while low-sensitivity variables are constrained to reduce computational complexity while maintaining feasibility. This iterative approach not only enhances the accuracy of the optimization process but also ensures robust performance under varying operational conditions.

2.2. Response Surface Modeling

Response surface modeling serves as an essential tool in the optimization framework, enabling efficient approximation of the objective function across the design space. By constructing mathematical surrogates based on sampled data points derived from FE simulations, RSM significantly reduces computational complexity while maintaining high predictive accuracy [31]. RSM offers several advantages over Kriging as a surrogate modeling methodology. While Kriging provides highly accurate interpolations, it can become computationally intensive when scaling to larger datasets, making it less suitable for high-dimensional problems. In contrast, RSM uses polynomial regression, offering a simpler and more computationally efficient approach [32]. This simplicity allows RSM to maintain reasonable accuracy while significantly reducing computation time, making it better suited for iterative optimization processes. In this study, a second-order polynomial regression model is employed to approximate the nonlinear relationships between the design variables ($x_1,x_2,\dots ,x_n$) and the optimization objectives (f). The general form of the RSM is expressed as follows [33]:

$$f\left(x\right)\approx {\beta }_0+\sum _{i=1}^n{\beta }_i{x}_i+\sum _{i=1}^n{\beta }_{ii}{x}_i^2+\sum _{i=1}^n\sum _{j=i+1}^n{\beta }_{ij}{x}_i{x}_j.$$

(15)

where $f\left(x\right)$ represents the objective function, ${\beta }_0$ is the intercept term, ${\beta }_i$, ${\beta }_{ii}$, and ${\beta }_{ij}$ are the regression coefficients for the linear, quadratic, and interaction terms, respectively. $x_i$ and $x_j$ are the design variables. The coefficients are determined using least-squares fitting of the sampled data points, minimizing the prediction error. Statistical metrics, including the coefficient of determination ($R^2$) and root mean square error (RMSE), are used to evaluate the model’s accuracy [32]:

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^m{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^m{(y_i-\overline{y})}^2}},\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{m}}{\sum }_{i=1}^m{(y_i-{\widehat{y}}_i)}^2}.$$

(16)

where $y_i$ and ${\widehat{y}}_i$ are the observed and predicted values of the objective function, $\overline{y}$ is the mean of the observed values, m is the number of sampled data points. This approach enables accurate modeling of the relationships between key design variables—such as $b_r$, ${\tau }_s$, ${\tau }_r$, $D_{or}$, and $I_{\max }$—and the optimization objectives, including $T_{\mathrm{avg}}$, $T_{\mathrm{rip}}$, $\eta$, and PF. The response surface facilitates sensitivity analysis and optimization by identifying critical regions in the design space for refinement, ensuring computational efficiency without compromising precision.

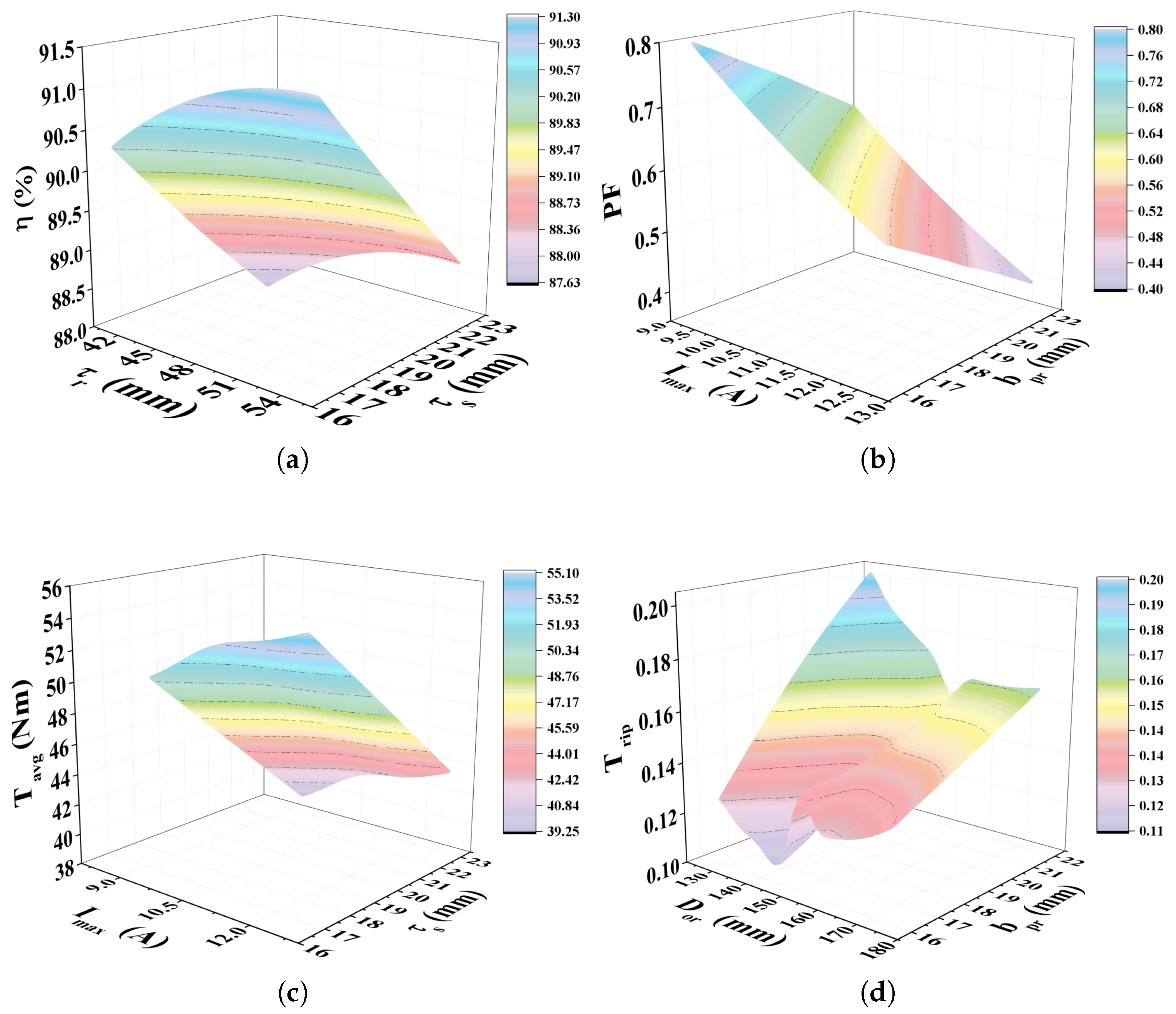
The results from the RSM demonstrate its capability to model and predict the optimization objectives effectively. The graphical representations of the objective functions, as shown in Figure 4, provide insights into the relationships between key design variables and performance metrics. The surface plot in Figure 4a shows the dependency of $\eta$ on the ${\tau }_s$ and ${\tau }_r$. It is evident that $\eta$ achieves higher values in regions where ${\tau }_s$ and ${\tau }_r$ are balanced, indicating a strong correlation between these variables. The power factor, as illustrated in Figure 4b, is influenced by the $I_{\max }$ and $b_{pr}$. A notable trade-off exists between these variables, where increasing $I_{\max }$ enhances $PF$ up to a certain limit, beyond which diminishing returns are observed. The RSM effectively maps this nonlinear relationship, aiding in the selection of optimal parameters to improve $PF$ without overloading the system. Meanwhile, Figure 4c reveals that $T_{\mathrm{avg}}$ is significantly affected by $I_{\max }$ and ${\tau }_r$. As $I_{\max }$ increases, $T_{\mathrm{avg}}$ rises, indicating a proportional relationship. Additionally, the impact of ${\tau }_r$ on $T_{\mathrm{avg}}$ emphasizes the need for precise parameter tuning to achieve desired torque values. The RSM model captures these variations effectively, demonstrating its ability to represent complex system dynamics. Additionally, the surface plot in Figure 4d illustrates the effects of $D_{or}$ and rotor pole width $b_{pr}$ on $T_{\mathrm{rip}}$. Lower values of $T_{\mathrm{rip}}$ are observed when $D_{or}$ and $b_{pr}$ are optimized simultaneously, minimizing mechanical vibrations and ensuring smooth operation. These results highlight the RSM’s robustness in optimizing torque, efficiency, and power factor, while reducing undesirable performance traits through accurate modeling. This balance ensures minimal energy loss and ripples, improving the overall system’s operational stability.

Incorporating RSM within the optimization framework drastically reduces computation time. Previous optimization studies [2,34,35,36] reported a computation time of 10–15 h for similar optimization tasks. However, in this study, the use of RSM shortened the computation time to 6.5 h. This efficiency enables quicker iterations, facilitating real-time adjustments and significantly enhancing the overall optimization workflow. Moreover, its simplicity compared to Kriging ensures scalability to high-dimensional problems, making RSM an indispensable tool in this study’s robust optimization approach.

3. Design for Six Sigma (DFSS) Methodology

The Design for Six Sigma (DFSS) methodology provides a systematic approach for achieving robust design optimization by identifying and mitigating uncertainties throughout the optimization process. DFSS emphasizes enhancing product performance and reliability while ensuring that critical quality metrics remain within specified limits [18]. The integration of DFSS in the optimization framework aligns the design variables, performance metrics, and constraints to achieve the desired system robustness and operational stability.

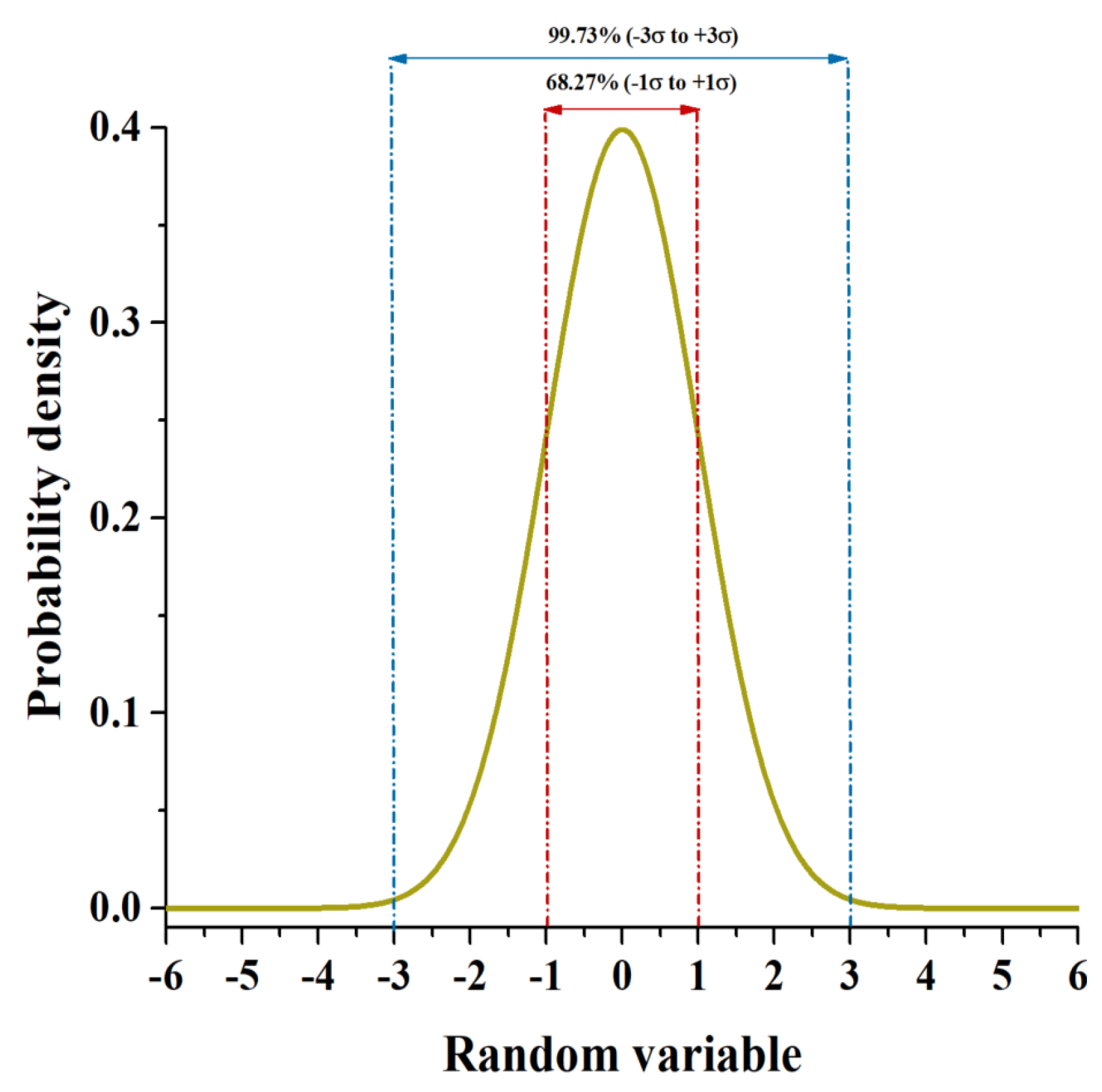
To model uncertainties in the optimization process, the design variables are assumed to follow a normal distribution, as depicted in Figure 5. The sigma level concept quantifies the probability of achieving optimal performance within a specified range [7].

The probability density function (PDF) of a normal distribution for a design variable x is given as

$$f\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}{e}^{-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}},$$

(17)

where $\mu$ is the mean value, and $\sigma$ is the standard deviation. The DFSS methodology integrates the uncertainty quantification within the optimization model to achieve robust performance. The optimization problem for the DFSS robust design approach is formulated as

$$\mathrm{minimize}:{\mu }_{f\left(\mathbf{x}\right)}\mathrm{subject}\mathrm{to}:{\sigma }_{f\left(\mathbf{x}\right)}\le \mathrm{USL},$$

(18)

where ${\mu }_{f\left(\mathbf{x}\right)}$ and ${\sigma }_{f\left(\mathbf{x}\right)}$ represent the mean and standard deviation of the objective function $f\left(\mathbf{x}\right)$, respectively. The upper specification limit (USL) defines the maximum allowable deviation to ensure robust performance. The variable $\mathbf{x}$ represents the set of design parameters, while $\mu$ and $\sigma$ are derived using statistical techniques, such as Monte Carlo analysis. Typically, the robust design ensures performance stability under uncertainties by satisfying the following condition:

$$x_L+n{\sigma }_x\le {\mu }_x\le x_U-n{\sigma }_x,\mathrm{LSL}\le {\mu }_f\pm n{\sigma }_f\le \mathrm{USL},$$

(19)

where $x_L$ and $x_U$ are the lower and upper bounds of the design parameters, and n is the sigma level, typically set to 6 for a Six Sigma framework. The value of $n=6$ corresponds to 3.4 defects per million opportunities or a 99.9999998% probability of success, ensuring high-quality robust performance under varying conditions [5,17].

3.1. Six Sigma-Based Robust Design Framework

The DFSS methodology incorporates statistical techniques to evaluate the impact of uncertainties in the design space. The process follows the Define, Measure, Analyze, Design, and Verify (DMADV) steps, ensuring a comprehensive exploration of the design space:

• Define: Identification of the critical objectives and design parameters, including $T_{\mathrm{avg}}$, $T_{\mathrm{rip}}$, PF, and $\eta$.
• Measure: Quantification of design variables’ sensitivity to uncertainties using sensitivity indices $s\left(x_i\right)$, as expressed in Equation (13). High-sensitivity variables are prioritized for optimization.
• Analyze: Statistical analysis is conducted to quantify the impact of variations in design variables. The process employs Six Sigma analysis to compute the process capability indices ($C_p,C_{pk}$) and ensure that performance remains within acceptable limits under uncertainties [5]:

  $$C_p={\displaystyle \frac{\mathrm{USL}-\mathrm{LSL}}{6\sigma }},C_{pk}=min\left({\displaystyle \frac{\mathrm{USL}-\mu }{3\sigma }},{\displaystyle \frac{\mu -\mathrm{LSL}}{3\sigma }}\right),$$

  (20)

  where USL and LSL denote the upper and lower specification limits, $\mu$ is the mean value, and $\sigma$ is the standard deviation.
• Design: A robust optimization process integrates the RSM to approximate performance metrics efficiently under varying conditions. The objective function incorporates uncertainties using Taguchi’s Loss Function [37]:

  $$L\left(x\right)=k{(y-T)}^2,$$

  (21)

  where y is the observed performance, T is the target value, and k is a proportionality constant.
• Verify: The optimized design is validated through Monte Carlo simulations, ensuring robustness against uncertainties. The system’s performance under varying operating conditions is compared against Six Sigma thresholds to confirm its reliability.

3.2. Application of DFSS in Robust Design Optimization

The DFSS methodology is applied to refine the optimization framework developed earlier. The response surface models constructed in Section 2 serve as surrogate models to evaluate the objective functions under multiple scenarios. By incorporating uncertainty quantification, the DFSS ensures that the system’s design objectives ($T_{\mathrm{avg}}$, $T_{\mathrm{rip}}$, $\eta$, PF) remain robust across varying operational and manufacturing conditions.

In this study, the uncertainty analysis focuses on the five most sensitive design variables, identified through the sensitivity analysis presented in Figure 3. These variables, namely $b_{\mathrm{pr}}$, ${\tau }_s$, ${\tau }_r$, $D_{\mathrm{or}}$, and $I_{\max }$, exhibited the most significant influence on the optimization objectives. To account for manufacturing and operational uncertainties, nominal values and their corresponding standard deviations are established. These uncertainties reflect the natural variability in material properties, machining tolerances, and electrical parameters. Proper characterization of these uncertainties is essential for ensuring robust and reliable machine performance under varying operational conditions.

Table 4. Uncertainty nominal values and standard deviations of selected design variables.

Symbol	Nominal Value	$\mathit{\sigma }$
$b_{\mathrm{pr}}$ (mm)	20.0	0.5
${\tau }_s$ (mm)	21.0	0.5
${\tau }_r$ (mm)	19.5	0.4
$D_{\mathrm{or}}$ (mm)	160.0	1.0
$I_{\max }$ (A)	10.5	0.5

presents the nominal values and standard deviations for the selected design variables:

$b_{\mathrm{pr}}$ significantly affects the machine’s average torque and torque ripple, as deviations in this parameter influence the magnetic flux density and rotor geometry. A standard deviation of $\sigma =0.5$ ensures manageable variability without compromising performance. The ${\tau }_s$ and ${\tau }_r$ are critical to achieving balanced magnetic flux distribution. These parameters play an essential role in minimizing torque ripple and improving efficiency. The standard deviations ($\sigma =0.5$ and $0.4$, respectively) are chosen to maintain geometric precision during the manufacturing process. The $D_{\mathrm{or}}$ influences both mechanical stability and magnetic coupling. A relatively larger standard deviation of $\sigma =1.0$ is acceptable due to its macroscopic nature, but strict control remains essential to minimize mechanical vibrations. The $I_{\max }$ is directly linked to the system’s electrical performance, impacting both efficiency and power factor. A standard deviation of $\sigma =0.5$ ensures efficient operation without excessive overheating under load conditions. This uncertainty analysis highlights the importance of precise parameter selection for ensuring the system’s optimal design. Integrating these uncertainties into the DFSS methodology ensures that the optimized machine maintains its performance stability under real-world operating conditions. The strong sensitivity indices (Figure 3) justify this approach, as small variations in critical parameters can significantly impact performance. Accounting for these ensures a resilient and reliable design.

The robust optimization framework integrates uncertainties in the design variables to ensure reliable system performance. This formulation builds upon the deterministic optimization model by accounting for variability in key design parameters, as previously defined in Equation (3). The robust optimization model can be expressed as follows:

$$\underset{\mathbf{x}}{min}{\mu }_f(\mathbf{x},\sigma )$$

(22)

$$\mathrm{s}.\mathrm{t}.\begin{array}{cc}\hfill & g_1\left(x\right)=D_{os}-D_{in}-2H_y\ge 0,\hfill \\ \hfill & g_2\left(x\right)=D_{os}-S{h}_r-2H_y\ge 0,\hfill \\ \hfill & g_3\left(x\right)=\pi (S_h+2H_y)-P_r{\tau }_s\ge 0,\hfill \\ \hfill & g_4\left(x\right)=I_{max}-\mathrm{limit}\ge 0,\hfill \\ \hfill & g_5\left(x\right)=T_{avg}-48.03\ge 0,\hfill \\ \hfill & g_6\left(x\right)=14.32-T_{rip}\ge 0,\hfill \\ \hfill & g_7\left(x\right)=\mathrm{PF}-0.4752\ge 0,\hfill \\ \hfill & g_8\left(x\right)=\eta -87.05\ge 0,\hfill \\ \hfill & x_i^L\le x_i\le x_i^U,\forall i,\hfill \\ \hfill & x_i^L\le x_i-{\mu }_i+6{\sigma }_i\le x_i^U,\hfill \\ \hfill & |SOC-SO{C}_f|\le 0.5\%,\hfill \\ \hfill & {\mu }_f(\mathbf{x},\sigma )\le \mathrm{USL},\hfill \end{array}$$

(23)

where:

• ${\mu }_f(\mathbf{x},\sigma )$: Mean value of the objective function considering uncertainties in design variables.
• $x_i$: Design variables $(b_{pr},{\tau }_s,{\tau }_r,D_{or},I_{max})$ selected based on sensitivity analysis.
• ${\sigma }_i$: Standard deviation of each design variable, capturing variability due to manufacturing and operational uncertainties.
• SOC: State of operation/control, ensuring constraints are within acceptable thresholds.
• USL: Upper specification limit for the objective function.

The probabilistic constraints ensure that the design remains feasible under uncertainty. The inclusion of standard deviations (${\sigma }_i$) mitigates deviations caused by variations in design variables, enabling robust performance of the machine under real-world conditions.

4. Results and Discussion

This section presents and discusses the results obtained through the optimization framework incorporating RSM and the DFSS methodology. The comparative analysis of the initial, NSGA-II optimized, and robust models demonstrates the effectiveness of the proposed approach in improving machine performance while accounting for uncertainties. Key performance metrics, including $T_{\mathrm{avg}}$, $T_{\mathrm{rip}}$, $\eta$, and PF, are analyzed for different models to highlight their improvements and trade-offs. 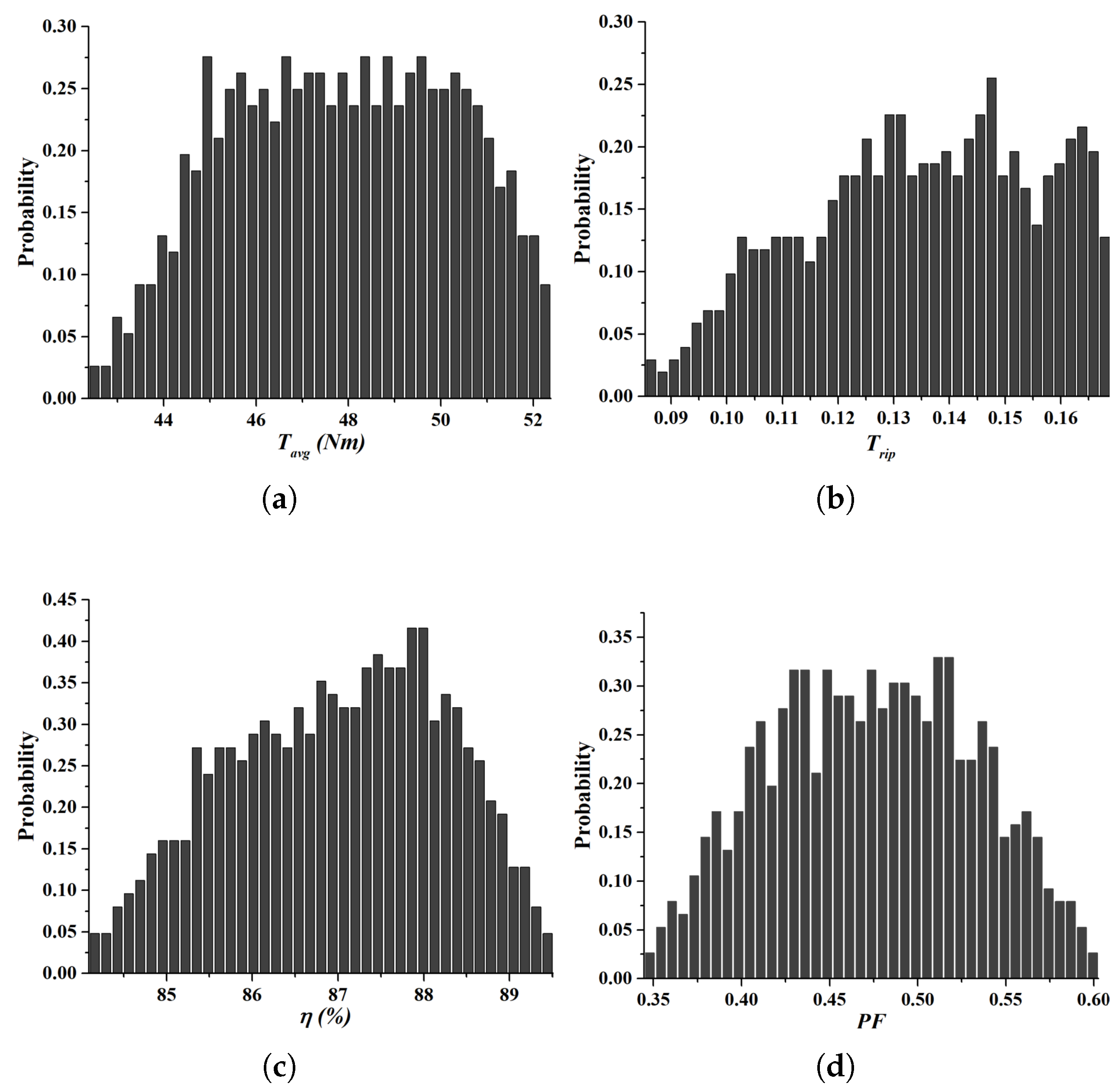Figure 6 shows the probability distributions of key performance metrics for the initial model.

Figure 6a depicts the distribution of $T_{\mathrm{avg}}$. The histogram demonstrates significant spread and variability, indicating the lack of precise parameter control, which results in inconsistent torque performance. Figure 6b presents the distribution of $T_{\mathrm{rip}}$. The observed high variability suggests irregular torque delivery, leading to mechanical vibrations. Figure 6c,d illustrate the distributions for $\eta$ and PF, respectively. Both metrics exhibit dispersed distributions with relatively lower values, highlighting inefficiencies in the initial machine design. These results underscore the need for optimization to achieve consistent and improved machine performance.

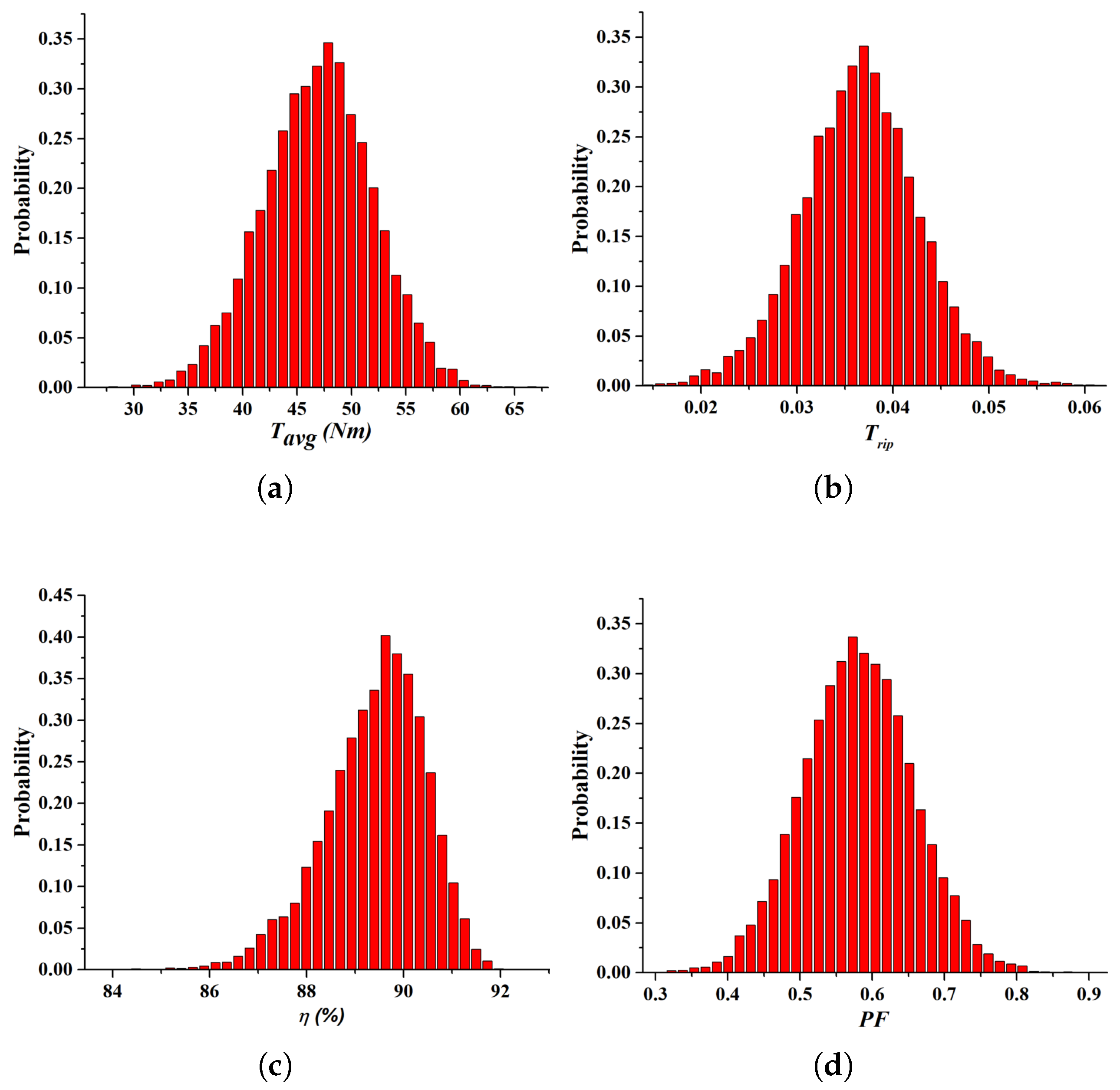
Figure 7 shows the results after applying the NSGA-II algorithm. Figure 7a demonstrates the distribution of $T_{\mathrm{avg}}$. The peak values are shifted towards higher torque, indicating performance improvement compared to the initial model. Figure 7b illustrates the reduction in $T_{\mathrm{rip}}$, reflecting improved torque consistency and reduced vibrations. Figure 7c shows significant enhancement in $\eta$, with the distribution becoming more concentrated and achieving higher values. Figure 7d presents the PF, which also shows a noticeable shift, emphasizing improved electrical performance. The results indicate that the NSGA-II optimization enhances machine performance significantly, yet uncertainties still impact the consistency of the design.

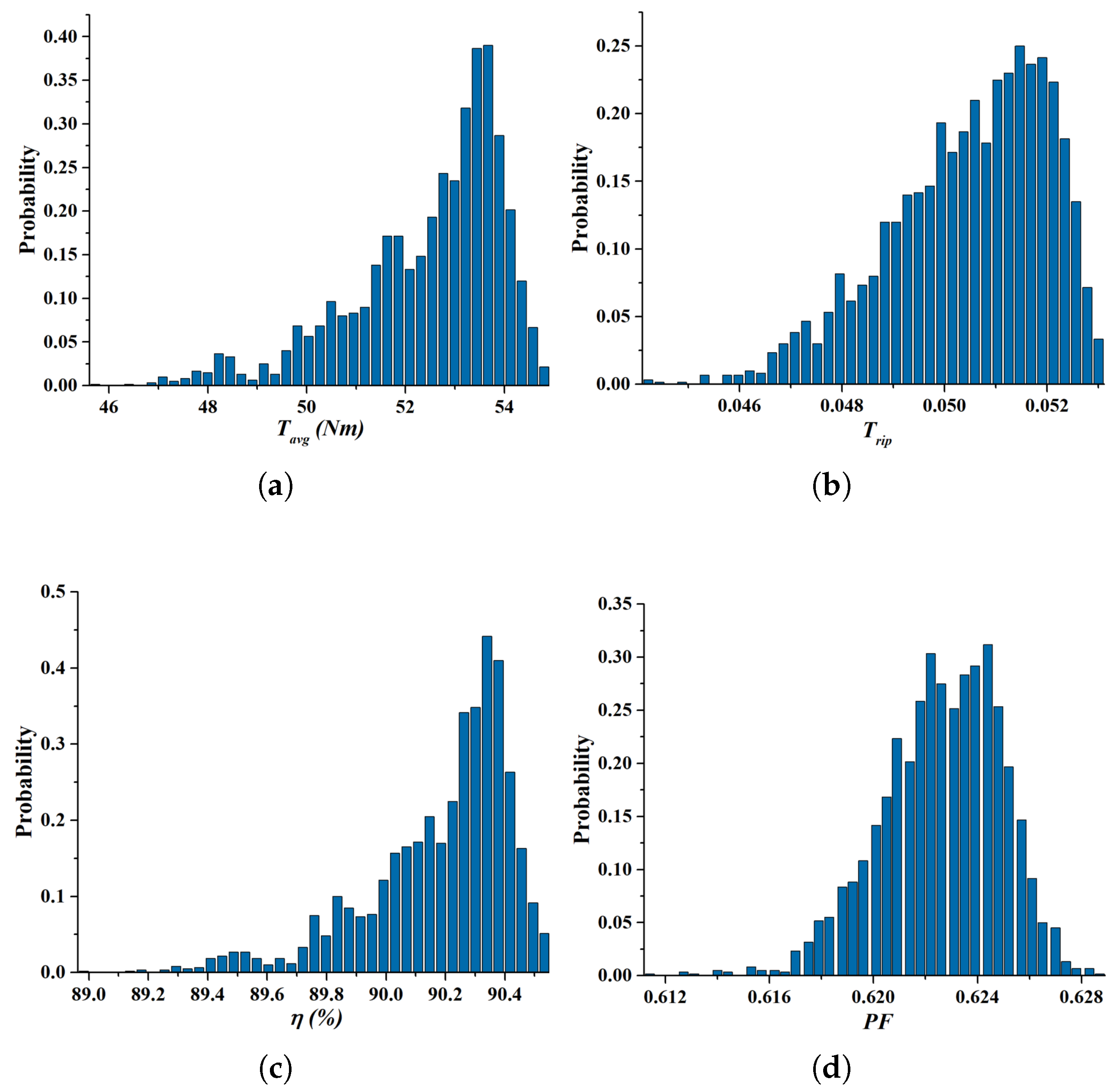
Figure 8 illustrates the results of the robust optimization model, where uncertainties are integrated into the DFSS framework. Figure 8a shows the distribution of $T_{\mathrm{avg}}$ becoming highly concentrated with a reduced spread, signifying precise control over the torque performance. Figure 8b highlights a significant reduction in $T_{\mathrm{rip}}$, with the histogram showcasing minimal variability. This outcome ensures smoother machine operation with reduced mechanical stress. Figure 8c demonstrates an enhanced and well-concentrated $\eta$, achieving values close to the ideal range. Figure 8d presents the power factor (PF), which achieves a more uniform and higher distribution, ensuring improved electrical performance. These results confirm that incorporating uncertainties within the robust optimization model leads to a highly reliable and consistent machine performance under real-world conditions.

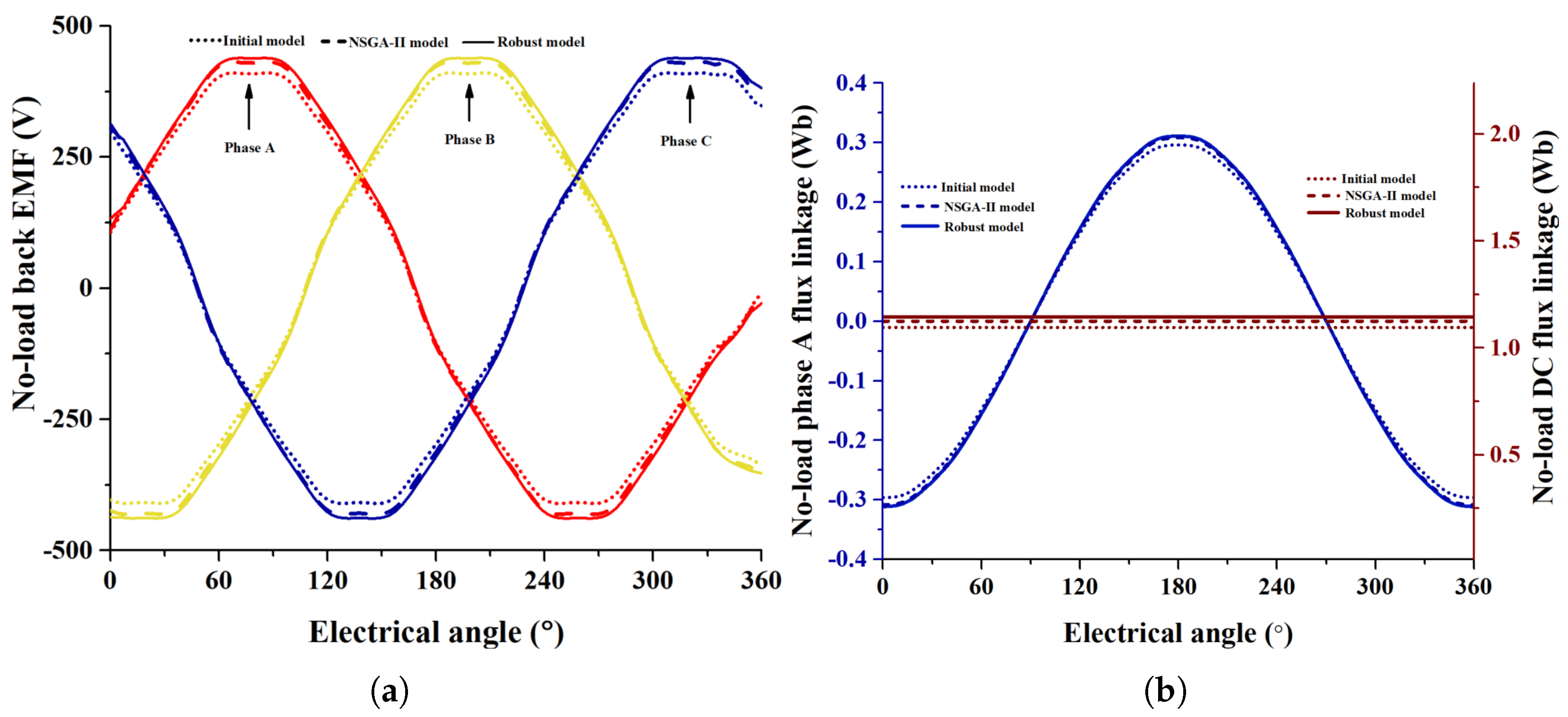
The robust model demonstrates smoother back EMF with reduced ripples compared to the other models, ensuring improved machine performance and minimal harmonics as presented in Figure 9a, while it achieves improved phase A flux symmetry with minimal DC flux offset, ensuring reduced saturation and enhanced operational stability in Figure 9b. These results emphasize the effectiveness of the robust optimization approach in minimizing fluctuations while maintaining system accuracy under real-world conditions.

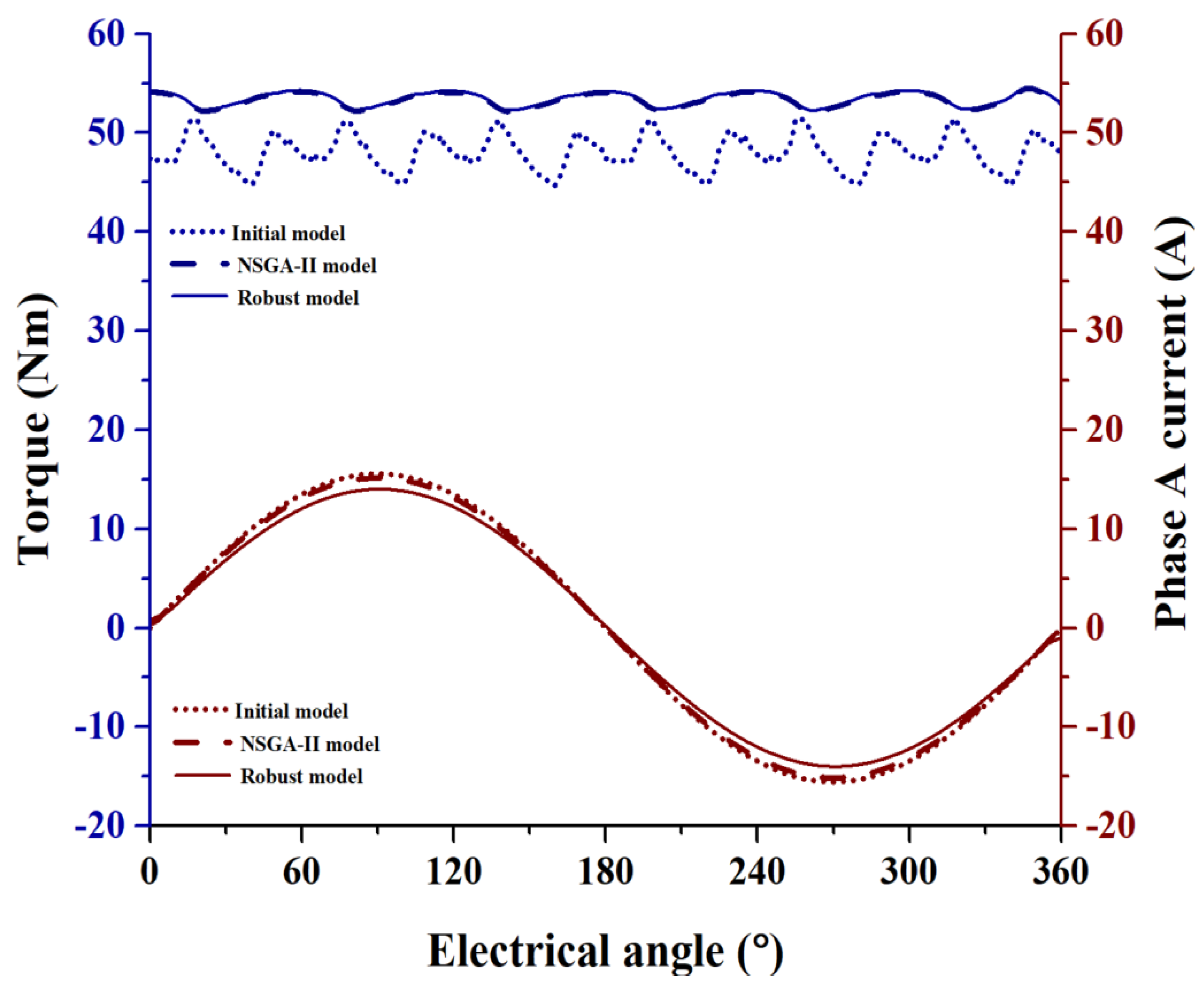
Figure 10 presents the torque and current waveforms. The robust model demonstrates smoother torque delivery with significantly reduced ripple, while the phase current waveform shows improved sinusoidal characteristics, ensuring reduced energy loss and operational stability. The results demonstrate that the proposed robust optimization framework effectively integrates RSM, sensitivity analysis, and DFSS methodology to optimize machine performance while managing uncertainties. The robust model achieves higher $T_{\mathrm{avg}}$ with minimal variations, reduced $T_{\mathrm{rip}}$ ensuring smoother mechanical operation, and enhanced $\eta$ and PF, ensuring superior electrical performance. The comparative analysis highlights the significant improvements over the initial and NSGA-II models, validating the robustness and reliability of the optimized machine under real-world operating conditions. This approach ensures that the machine design meets stringent performance and stability requirements, making it suitable for practical applications.

While Table 4 presents the initial nominal values and standard deviations of the selected design variables ($b_{pr},{\tau }_s,{\tau }_r,D_{or},I_{\max }$) used as a baseline for the optimization process,

Table 5. Numerical results for deterministic and robust optimization under uncertainty.

Parameter	Indicator	Robust Model	NSGA-II Model	% Change
$b_{pr}$	${\mu }_{b_{pr}}$	20.3	20.0	1.50%
	${\sigma }_{b_{pr}}$	0.48	0.55
${\tau }_s$	${\mu }_{{\tau }_s}$	21.2	21.0	0.95%
	${\sigma }_{{\tau }_s}$	0.45	0.50
${\tau }_r$	${\mu }_{{\tau }_r}$	19.6	19.5	0.51%
	${\sigma }_{{\tau }_r}$	0.38	0.44
$D_{or}$	${\mu }_{D_{or}}$	161.5	160.0	0.94%
	${\sigma }_{D_{or}}$	0.92	1.10
$I_{\max }$	${\mu }_{I_{\max }}$	10.5	10.3	1.94%
	${\sigma }_{I_{\max }}$	0.12	0.15
$T_{\mathrm{rip}}$	${\mu }_{T_{\mathrm{rip}}}$	0.048	0.052	−7.69%
	${\sigma }_{T_{\mathrm{rip}}}$	0.005	0.009
$T_{\mathrm{avg}}$	${\mu }_{T_{\mathrm{avg}}}$	50.2	49.8	0.80%
	${\sigma }_{T_{\mathrm{avg}}}$	0.18	0.25
$\eta$	${\mu }_{\eta }$	90.5	89.8	0.78%
	${\sigma }_{\eta }$	0.10	0.15
$PF$	${\mu }_{\mathrm{PF}}$	0.62	0.60	3.33%
	${\sigma }_{\mathrm{PF}}$	0.008	0.012

highlights the comparative results between the robust model and the NSGA-II model under uncertainty conditions. This comparison underscores the impact of the DFSS framework in improving machine performance and achieving robustness under varying levels of uncertainty.

For the design variables ($b_{pr},{\tau }_s,{\tau }_r,D_{or},I_{\max }$), the robust model outperforms the NSGA-II model in terms of improved mean values and reduced standard deviations as listed in Table 5:

• $b_{pr}$ improves by 1.50%, ensuring better flux density stability, compared to the NSGA-II model.
• ${\tau }_s$ and ${\tau }_r$ exhibit smaller deviations (0.45 and 0.38, respectively), contributing to a balanced magnetic flux distribution and torque ripple suppression.
• $D_{or}$ improves by 0.94%, enhancing mechanical stability while reducing variability.
• $I_{\max }$ achieves a 1.94% improvement, which positively influences electrical performance.

For performance metrics:

• $T_{\mathrm{rip}}$ is reduced by 7.69%, highlighting the robust model’s ability to suppress undesired ripples compared to the NSGA-II model.
• $T_{\mathrm{avg}}$ shows a notable 0.80% increase, ensuring more consistent torque output.
• $\eta$ improves by 0.78%, validating energy utilization enhancements under real-world disturbances.
• $PF$ sees a significant boost of 3.33%, ensuring better power quality.

While Table 4 establishes the baseline parameters and tolerances for optimization, the progression to the robust and NSGA-II models reveals the advancements achieved through the DFSS framework. For instance, the initial standard deviations in $b_{pr}$ and $D_{or}$ in Table 4 underscore the need for robust control, which is effectively addressed in the optimized models. Similarly, the initial mean values of $PF$ and $\eta$ highlight areas for improvement, which are realized through the robust optimization process.

The improvements in critical parameters highlight the effectiveness of the robust optimization framework and demonstrate the impact of incorporating manufacturing tolerances into the design process. Specifically, $T_{\mathrm{rip}}$ was reduced by 7.69%, ensuring smoother machine operation, while $\eta$ increased by 0.78%, improving energy utilization under varying conditions. Additionally, the PF saw a significant boost of 3.33%, further validating the robustness of the design. These performance enhancements are a direct result of optimizing manufacturing tolerances, which significantly impact the reliability of FSWFMs by minimizing deviations in key parameters. As shown in Table 5, the robust optimization process reduced the standard deviations of $b_{\mathrm{pr}}$, ${\tau }_{\mathrm{s}}$, and ${\tau }_{\mathrm{r}}$. These reductions improve flux density stability, ensure balanced magnetic flux distribution, and reduce torque ripple.

By minimizing manufacturing-induced variabilities, the proposed framework ensures consistent machine performance across production batches, enhancing scalability for industrial applications. These improvements collectively achieve this study’s objective of addressing uncertainties to deliver stable, reliable, and high-performing FSWFM designs, as validated by the results in Table 5.

5. Conclusions and Future Work

This study presented a robust Six Sigma-based optimization framework for flux-switching wound field machines, addressing uncertainties in performance metrics and manufacturing variations. By employing Design for Six Sigma (DFSS) principles and integrating response surface methodology with multi-objective optimization techniques, the proposed framework achieved significant improvements across key performance indicators.

This novel framework integrates established methodologies tailored specifically for FSWFMs, ensuring robust performance under real-world manufacturing variabilities. By leveraging Six Sigma principles, the approach bridges the gap between theoretical optimization and practical industrial implementation, addressing challenges such as torque ripple and efficiency in machine design.

Numerical results demonstrate the superiority of the robust optimization model compared to the deterministic NSGA-II model. Specifically, torque ripple was reduced by 7.69%, effectively suppressing unwanted ripples and ensuring smoother torque output. The variability in key design variables was minimized, further validating the robustness of the proposed approach. The rotor pole width showed a mean improvement of 1.50% with a 12.7% reduction in variability, ensuring better flux density stability. Slot pitch and rotor pitch exhibited smaller standard deviations of 0.45 and 0.38, respectively, achieving a balanced magnetic flux distribution and effective torque ripple suppression. The robust optimization framework also demonstrated computational efficiency, reducing the total optimization time to 6.5 h while achieving 12,500 evaluations. Compared to conventional methods that require 10–15 h, this marks a 56% improvement in computational efficiency, making it highly scalable for industrial applications. The Six Sigma validation confirmed that the optimized design met the required robustness thresholds. This ensures that the optimized system remains reliable under manufacturing tolerances and operational disturbances, maintaining stability and high performance.

In the future, further experimental validation of the optimized machine prototypes will be conducted to confirm the predicted improvements under real-world conditions. Additionally, the framework can be extended to explore other machine topologies, integrate advanced thermal management techniques, and incorporate material advancements to further enhance torque density and energy efficiency. By bridging the gap between theoretical optimization and industrial manufacturability, the DFSS-based framework provides a reliable solution for sustainable and high-performance electric machines, offering a roadmap for addressing challenges in modern industrial applications.