Integrated Production–Logistics Scheduling in Flexible Assembly Shops Using an Improved Genetic Algorithm

Abstract

Achieving high operational efficiency in modern manufacturing requires the seamless integration of production scheduling and intralogistics coordination. However, in flexible assembly shops, the decoupling between production sequencing and automated guided vehicle (AGV) routing often leads to resource conflicts, unbalanced workloads, and inefficient energy utilization. To address this challenge, this study proposes an improved genetic algorithm (IGA) for integrated production–logistics scheduling. The innovation lies in a triple-chain encoding strategy that concurrently represents production, transportation, and time-window constraints, coupled with adaptive crossover and mutation operators for enhanced population diversity. Furthermore, a time-window-constrained Dijkstra routing mechanism is incorporated to prevent AGV conflicts and improve synchronization between machines and logistics. Two representative shop-floor scenarios—baseline and disturbed conditions—were designed for validation. Comparative experiments against a standard genetic algorithm (GA) and a two-stage heuristic demonstrate that the IGA achieves 9.5% and 6.7% reductions in average makespan, respectively, while maintaining less than 1% deviation under 10% random disturbances. Statistical tests (p < 0.01, Cohen’s d > 1.4) confirm the method’s robustness and practical effectiveness. The proposed approach provides a reliable and implementable optimization framework that enhances coordination between production and AGV systems in flexible assembly environments and offers a practical reference for smart manufacturing scheduling and digital twin applications.

1. Introduction

In the era of Industry 4.0, manufacturing systems are evolving toward greater flexibility, higher intelligence, and improved sustainability. Growing market volatility and product diversification are driving the transformation of traditional assembly lines into flexible assembly shops (FASs), where multi-variety, small-batch production is carried out under dynamic operating conditions. In such environments, the synchronization between production sequencing and material handling directly determines production throughput, energy efficiency, and overall responsiveness. Consequently, scheduling optimization plays a central role in coordinating temporal and spatial resources and has become a key challenge in intelligent manufacturing. Effective scheduling not only minimizes production delays but also contributes to sustainable manufacturing by reducing unnecessary energy consumption and improving overall resource utilization.

Traditional assembly lines are typically designed for single-product or stable-demand environments, exhibiting limited adaptability to mixed-model or dynamic production conditions. Consequently, their scheduling processes often rely on rigid task sequences and fixed resource assignments, resulting in poor responsiveness, extended idle times, and inefficient utilization of labor and material resources. Recent studies on flexible job-shop scheduling confirm that such systems struggle to sustain efficiency when production and logistics interactions become highly dynamic [1]. These limitations underscore the necessity of developing flexible and integrated scheduling frameworks capable of synchronizing production operations and intralogistics activities.

In this study, responsiveness refers to the capability of production–logistics systems to adapt scheduling decisions under dynamic and uncertain manufacturing conditions. These challenges are particularly critical in discrete-part manufacturing industries, including automotive, electronics, aerospace, and high-end equipment manufacturing, where frequent product variations and real-time material handling synchronization are essential. Accordingly, this research focuses on FASs representative of these industrial environments, aiming to enhance production–logistics responsiveness and coordination efficiency through integrated scheduling optimization.

A key challenge in the management of FASs stems from the lack of effective integration between production scheduling and intralogistics coordination. In real-world workshops, material transportation is usually performed by automated guided vehicles (AGVs), whereas production sequencing mainly concerns machine assignments and process optimization. The independent optimization of these two subsystems often results in operational mismatches such as AGV congestion, machine idleness, and prolonged makespan. Mokhtari and Hasani [2] revealed that neglecting the interdependence between production and logistics leads to inefficient resource allocation and overall suboptimal performance. Therefore, it is essential to develop an integrated scheduling framework that simultaneously considers production operations and logistics routing to enhance overall system efficiency.

Over the past two decades, the flexible job shop scheduling problem (FJSP) has served as a benchmark for addressing complex production optimization tasks [1]. A wide range of intelligent optimization methods—such as genetic algorithms (GAs), particle swarm optimization (PSO), and reinforcement learning (RL)—have been employed to enhance both solution quality and computational efficiency. For example, Pal et al. [3] employed multi-agent distributed scheduling to improve scalability and robustness, whereas Momenikorbekandi and Abbod [4] developed a hybrid parthenogenetic algorithm that achieved superior performance on large-scale instances. Zhang and Wang [5] combined constraint programming with dispatching rules to improve solution feasibility. Yuan et al. [6] applied deep reinforcement learning to multi-objective FJSPs, achieving greater solution diversity. Song et al. [7] and Lei et al. [8] further demonstrated that learning-based approaches could improve adaptability under complex constraints. Despite these advances, existing research has largely focused on production sequencing, with limited consideration of material transportation decisions within the optimization process. Consequently, current models fail to effectively capture the dynamic interactions between production and logistics activities. These comprehensive surveys also indicate that flexible job-shop scheduling has been extensively studied for more than two decades, which provides the basis for our statement.

In parallel, research on AGV routing and scheduling has progressed considerably, contributing to more efficient material flow and coordination in flexible manufacturing systems. A variety of graph-search and metaheuristic approaches—such as enhanced A* algorithms, ant colony optimization (ACO), and hybrid GA-based metaheuristics—have been developed to minimize travel distance, congestion, and idle time. Although these algorithms significantly enhance AGV autonomy and path safety, they are primarily designed for static environments or single-objective logistics settings. When applied to dynamic shop-floor environments, they may conflict with production scheduling priorities or struggle to adapt to unexpected disturbances. Therefore, the decoupling between production and logistics continues to pose a major bottleneck toward achieving system-level optimization in flexible manufacturing. Here, ‘decoupling’ refers to the operational separation between production scheduling and AGV routing, rather than the customer–order decoupling point (CODP) in supply-chain management.

To overcome these limitations, recent studies have sought to develop integrated production–logistics scheduling frameworks. Nevertheless, most existing methods either oversimplify routing constraints or neglect key operational factors such as energy efficiency and equipment utilization. Moreover, conventional GAs are prone to premature convergence and limited adaptability when solving multi-constrained and time-sensitive problems. These challenges underscore the need for developing a more robust and adaptive optimization approach that can effectively handle coupled production–logistics decisions under dynamic conditions.

To address the aforementioned challenges, this study proposes an improved genetic algorithm (IGA) for integrated production–logistics scheduling in flexible assembly shops. The key innovation of this work lies in a triple-chain encoding structure that jointly represents production operations, AGV routing, and time-window constraints. This encoding enables coordinated decision-making between machines and AGVs, allowing for unified optimization of processing and transportation tasks. Furthermore, a Dijkstra-based routing mechanism constrained by time windows is introduced to prevent AGV path conflicts and enhance synchronization between production and logistics flows. To enhance convergence stability, adaptive crossover and mutation operators are designed to maintain population diversity and prevent premature stagnation.

To validate the effectiveness of the proposed approach, two representative scheduling scenarios were constructed: a baseline scenario representing stable shop-floor operations and a disturbed scenario incorporating random path blockages to emulate environmental uncertainty. Comparative experiments were conducted against a conventional GA and a two-stage heuristic baseline. The experimental results showed that the proposed IGA reduced the average makespan by 9.5% and 6.7% compared with the baseline methods, while maintaining less than 1% performance deviation under 10% stochastic disturbances. Statistical analyses, including significance testing (p < 0.01) and effect size evaluation (Cohen’s d > 1.4), confirmed the robustness and practical effectiveness of the proposed method. These findings demonstrate that the proposed algorithm effectively enhances coordination between production and AGV systems, thereby improving operational efficiency and contributing to the sustainability of flexible manufacturing environments.

The remainder of this paper is structured as follows. Section 2 reviews related studies on production scheduling, AGV coordination, and operational optimization. Section 3 presents the overall modeling framework and the mathematical formulation of the integrated scheduling problem. Section 4 describes in detail the design and implementation of the IGA. Section 5 outlines the experimental setup, discusses the obtained results, and provides comparative analyses. Finally, Section 6 concludes the paper and highlights potential directions for future research.

2. Materials and Methods

2.1. Literature Review

2.1.1. Production Scheduling in Flexible Manufacturing Systems

In the context of Industry 4.0, production scheduling forms the foundation of intelligent and sustainable manufacturing by efficiently allocating limited resources to minimize makespan and operational costs. The FJSP remains one of the most challenging due to its combinatorial complexity and hierarchical decision structure. Each job consists of multiple operations executed on alternative machines with distinct processing times. With the increasing adoption of FASs, research on FJSP has become crucial for achieving mass customization and system stability. To tackle computational complexity, metaheuristic and hybrid optimization methods have gradually replaced conventional mathematical programming approaches.

Recent studies have highlighted the continuous evolution of production scheduling in flexible manufacturing systems (FMSs) from traditional machine-centric optimization toward intelligent, multi-resource, and data-driven paradigms. Zhang and Wang [4] conducted a comparative analysis of constraint programming (CP), mixed-integer programming (MIP), and dispatching-rule strategies for complex flexible assembly job shops, demonstrating that CP achieved the highest computational efficiency under dynamic operating conditions. To overcome the computational limitations of mathematical programming, Momenikorbekandi and Abbod [4] proposed a hybrid parthenogenetic–genetic algorithm that achieved faster convergence and enhanced global search capability. Li et al. [9] improved the artificial bee colony algorithm to optimize batch-splitting in flexible assembly systems, whereas Wang et al. [10] integrated simulation and optimization techniques to coordinate lot streaming with transport-resource allocation. The focus of recent studies has increasingly shifted toward multi-resource and multi-objective optimization. Hou and Zhang [11] developed a multi-objective whale optimization algorithm (MOWOA) to simultaneously address assembly-line rebalancing and multi-AGV scheduling, whereas Wei et al. [12] introduced a discrete grey-wolf optimization framework that incorporated machine, worker, and AGV constraints into a unified scheduling model. With the rapid development of artificial intelligence, Yuan et al. [6], Song et al. [7], and Lei et al. [8] applied reinforcement learning and graph neural networks to achieve adaptive and scalable scheduling, whereas Pal et al. [3] designed a multi-agent system that integrated production scheduling and maintenance planning through distributed decision-making. Building upon these advances, Gui et al. [13] proposed a hybrid deep reinforcement learning (DRL) approach for real-time rescheduling under dynamic disturbances, marking a significant transition toward intelligent, adaptive, and data-driven scheduling paradigms in FMSs.

Despite these advances, most existing research still focuses primarily on production sequencing while overlooking crucial aspects such as machine availability, material transportation, and real-time logistics coordination. In flexible assembly shops, production and logistics are inherently interdependent—any delay in material handling may invalidate an otherwise optimal schedule. This decoupling between production and logistics remains a key barrier to achieving fully intelligent and autonomous scheduling. Bridging this gap requires unified optimization frameworks that integrate production sequencing with dynamic, data-driven material-handling decisions, thereby paving the way toward holistic and resilient scheduling in smart manufacturing systems.

2.1.2. Integrated Scheduling of Production and Logistics

In modern flexible manufacturing systems, material flow is typically managed by AGVs or mobile robots, whose routing and availability directly influence production efficiency. To achieve global optimization, research has increasingly focused on integrating AGV routing with production scheduling, enabling machine operations and transportation activities to be jointly optimized for minimal makespan and balanced resource utilization.

Early studies on integrated production–logistics scheduling primarily employed sequential optimization strategies, whereby production schedules were first generated and subsequently refined through transportation coordination. Han et al. [14] tackled the interdependence between machine and AGV scheduling by integrating mixed-integer linear programming (MILP) with a dual-population collaborative genetic algorithm (DCGA), thereby enhancing both makespan optimization and routing stability. Building upon this foundation, Meng et al. [15] proposed an IGA incorporating a population-diversity detection mechanism to prevent premature convergence, whereas Li et al. [16] developed a hybrid metaheuristic that integrates tabu search, simulated annealing, and genetic operators to achieve conflict-free routing and improve resource utilization. Similarly, Yang et al. [17] developed a three-stage MILP model that integrates assembly operations with AGV transportation and is supported by a multi-objective co-evolutionary algorithm to simultaneously minimize makespan and total energy consumption in large-scale instances.

With the growing complexity of material-handling systems, conflict-free routing has emerged as a critical challenge in integrated production–logistics scheduling. Xie et al. [18] developed an improved A* algorithm that incorporated collision-avoidance strategies directly into the initial routing process, thereby reducing computational complexity and improving routing feasibility. Similarly, Sheng et al. [19] proposed a time-window-based multi-AGV path-planning method that ensured synchronized vehicle operations and minimized task delays in dynamic shop-floor environments. Wu et al. [20] integrated layout optimization with a modified ACO algorithm that employed Laplacian distribution and dynamic pheromone control, achieving reductions of more than 40% in both path length and collision rate compared with conventional approaches. Zhou et al. [21] enhanced AGV routing optimization through an adaptive genetic algorithm incorporating confidence-based fitness adjustment to accelerate convergence and improve global search performance. In parallel, Zhang et al. [22] combined deep Q-learning with grid-based environmental modeling to enable intelligent obstacle avoidance and adaptive path planning under dynamic and uncertain conditions.

Recent research has increasingly emphasized the development of dynamic, data-driven, and sustainable optimization frameworks for integrated production–logistics systems. Lu et al. [23] proposed a two-stage hybrid memetic algorithm (THMA) for dynamic FJSP, considering AGV breakdowns and multi-site equipment maintenance, and demonstrated strong robustness and convergence performance. Xin et al. [24] developed a multi-view hybrid algorithm that integrates estimation of distribution (EDA) and ACO to coordinate machine processing with AGV transportation, thereby improving production throughput and reducing system idle time. Focusing on predictive intelligence, Tang and Wang [25] introduced a data-driven two-layer scheduling model that integrates Bayesian networks to predict AGV transport times and dynamically adjust scheduling decisions under uncertainty. Meanwhile, sustainability-oriented studies have emerged. Abderrahim et al. [26] incorporated AGV battery management constraints into energy-efficient FMS scheduling to optimize both production cycles and charging strategies. Similarly, Miller et al. [27] developed a cascaded constraint-programming framework that accounts for tool life, machining sequence, and material flow, thereby enabling sustainable and efficient scheduling in autonomous production cells. Most recently, Zhang et al. [28] proposed a multi-agent reinforcement learning (MARL) framework incorporating reward shaping to coordinate job assignment and machine allocation, thereby enhancing flexibility, adaptability, and decision autonomy in dynamic shop-floor environments.

To address dynamic manufacturing environments, MARL and two-stage heuristic frameworks have been explored to enhance adaptability and enable real-time schedule adjustment under random disturbances and equipment failures. Nevertheless, achieving conflict-free coordination between production and AGV operations—particularly under time-window and precedence constraints—remains computationally demanding. Moreover, most current models still prioritize makespan minimization as their primary objective; although effective for productivity, this focus can lead to resource imbalance and weak synchronization between production and logistics subsystems.

2.1.3. Summary

In summary, previous research has advanced the theoretical and practical understanding of integrated scheduling. However, persistent challenges remain, including the decoupling of production and logistics decisions, premature convergence of conventional genetic algorithms, and the absence of robust mechanisms for conflict-free coordination in dynamic shop-floor environments. Motivated by these gaps, this study proposes an IGA featuring triple-chain encoding and adaptive operators to achieve robust, efficient, and conflict-free integrated scheduling for flexible assembly shops.

Recent comprehensive reviews on integrated FJSP confirm that the major challenges identified above—namely the decoupling of production and logistics decisions [1], the premature convergence of conventional GAs, and the lack of robust conflict-free routing mechanisms—remain persistent bottlenecks in dynamic flexible manufacturing environments. These challenges are critical because they directly lead to AGV congestion, machine idleness, synchronization imbalance, and unstable throughput under real-world disturbances.

Although multiple alternative approaches exist, they all have inherent limitations: exact optimization (MIP/CP) becomes computationally infeasible for large-scale dynamic scheduling; learning-based methods (e.g., MARL) require extensive training data and cannot guarantee precedence and time-window feasibility; and classical metaheuristics struggle to jointly address production sequencing, AGV routing, and conflict resolution.

Given these limitations, the proposed IGA provides a balanced and practically applicable solution. Its triple-chain encoding unifies production sequencing, AGV routing, and time-window feasibility; its adaptive operators mitigate premature convergence; and its Dijkstra-based decoding ensures feasible and conflict-free AGV routing. Therefore, the IGA is well-suited for integrated production–logistics scheduling in flexible assembly shops.

3. Results

3.1. Modeling Framework and Problem Formulation

3.1.1. System Overview

To address the integrated production–logistics scheduling problem in FASs, this study establishes a three-layer research framework consisting of the problem layer, the method layer, and the validation layer, as illustrated in Figure 1. This hierarchical structure ensures logical consistency and coherent linkages among problem formulation, algorithmic design, and performance evaluation.

At the problem layer, the integrated scheduling problem is formulated by considering multiple influencing factors, including:

• production factors, such as job sequences, operation precedence, and processing times;
• machine factors, represented by machine availability, setup times, and processing capabilities;
• transportation factors, involving AGV routing paths and time-window constraints;
• constraints, which ensure feasible scheduling under resource and routing limitations; and
• optimization objectives, primarily the minimization of makespan and improvement of system efficiency.

As detailed in Section 3.1.3, the mathematical model formalizes these relationships through unified variables and constraints, which provide the basis for subsequent optimization. At the method layer, an IGA is developed to efficiently solve the NP-hard integrated scheduling problem. The IGA employs a triple-chain encoding structure that simultaneously represents production sequences, machine allocations, and AGV routing decisions. The algorithm consists of population initialization, adaptive crossover and mutation operators, and a decoding mechanism based on time-window-constrained Dijkstra path planning. This decoding strategy ensures conflict-free routing and temporal synchronization between processing and transportation tasks. The well-designed fitness function balances makespan, stability, and robustness, guiding population evolution toward global optimality.

At the validation layer, the model and algorithm are tested under two representative scenarios—baseline and disturbed conditions—representing static and dynamic production environments, respectively. Comparative experiments are conducted against a standard GA and a two-stage heuristic method to verify the effectiveness of the proposed approach. Evaluation metrics include makespan, scheduling stability, and robustness under disturbances, which enable quantitative evaluation of the IGA’s performance.

In summary, the framework integrates modeling, algorithmic design, and validation in a hierarchical manner:

(a)

The problem layer defines the scheduling objectives and constraints;

(b)

The method layer formulates the IGA-based solution mechanism;

(c)

The validation layer empirically demonstrates its effectiveness.

This hierarchical structure ensures the reproducibility, interpretability, and practical relevance of the proposed system for flexible assembly shop scheduling.

3.1.2. Notations and Definitions

For consistency with the mathematical formulation presented in the following section and for clarity of presentation, the notations used for the integrated production–logistics scheduling problem in FASs are summarized in

Table 1. Notations and definitions.

Symbol	Definition
P	Set of products, with p products.
Oi	Operation set of product i, with ni operations.
M	Set of machines.
V	Set of AGVs.
N	Set of transport nodes.
E	Set of transportation edges (u,v) between nodes in N.
T	Scheduling time horizon.
Tijm	Processing time of operation Oij on machine m (=1 unit).
Duv	Transportation time between nodes u and v (=1 unit).
Sij	Start time of operation Oij.
Cij	Completion time of operation Oij.
Cmax	Maximum completion time (makespan) = max{Cij}.
f	Objective function to be minimized (f = Cmax).
${\delta }_{ijm}$	Binary variable: 1 if operation Oij is processed on machine m, 0 otherwise.
${\gamma }_{uv}$	Binary variable: 1 if path segment (u,v) is selected by an AGV, 0 otherwise.
xav(t)	Binary variable: 1 if AGV a occupies node v at time t, 0 otherwise.
x{bv}(t)	Binary variable: 1 if AGV b occupies node v at time t, 0 otherwise.
i, j, m a, b, u, v, t	Indices representing product, operation, machine, AGV, and node/time identifiers, respectively.

.

3.1.3. Mathematical Model

Based on the notations and definitions presented in Table 1, the integrated production–logistics scheduling problem in FASs is formulated as a single-objective MIP model. The objective of this model is to minimize the total makespan (C_max), subject to production precedence, machine capacity, and AGV routing constraints.

Objective Function

$$minf=C_{max}=\underset{i\in P,j\in O_i}{max}\left(C_{ij}\right)$$

(1)

The objective is to minimize the total makespan (C_max), which represents the latest completion time across all operations.

Constraints

(1)

Operation precedence

$$S_{i,j+1}\ge C_{ij},\forall i\in P,j=\mathrm{1,2},\dots ,\left|O_i\right|-1$$

(2)

(2)

Machine assignment

$$\sum _{m\in M}{\delta }_{ijm}=1,\forall i\in P,j\in O_i$$

(3)

Each operation is assigned to exactly one machine.

(3)

Machine capacity (non-overlap)

$$\sum _{O_{ij}\in O_i}{\delta }_{ijm}\le 1,\forall m\in M,t\in T$$

(4)

At any time t, each machine processes at most one operation (explicitly indexed by t ∈ T).

(4)

Processing time definition

$$C_{ij}=S_{ij}+T_{ijm},\forall i\in P,j\in O_i$$

(5)

(5)

AGV assignment

$$\sum _{a\in V}{y}_{uv}=1,\forall \left(u,v\right)\in E$$

(6)

Each transportation segment (u,v) is executed by exactly one AGV.

(6)

AGV single-task restriction

$$\sum _{\left(u,v\right)\in E}{y}_{uv}\le 1,\forall v\in V,t\in T$$

(7)

Each AGV performs at most one transportation task at any given time t.

(7)

Transportation time constraint

$$S_{i,j+1}\ge C_{ij}+D_{uv},\forall \left(u,v\right)\in E,i\in P,j\in O_i$$

(8)

The next operation cannot start earlier than the previous completion time plus the travel time (set to 1).

(8)

Conflict-free routing

$$x_{av}\left(t\right)+x_{bv}\left(t\right)\le 1,\forall a\ne b,v\in N,t\in T$$

(9)

Two AGVs cannot occupy the same node at the same time to prevent collisions.

(9)

Makespan definition

$$C_{max}\ge C_{ij},\forall i\in P,j\in O_i$$

(10)

Ensures C_max represents the overall completion time of the system.

Equations (1)–(10) collectively formulate the integrated production–logistics scheduling model, which simultaneously captures manufacturing and intralogistics decisions within a unified mathematical framework. Equations (2)–(3) ensure that each product follows its predefined technological order and that every operation is assigned exclusively to one machine, thereby guaranteeing production feasibility. Equation (4) restricts simultaneous processing on the same machine, thereby preventing operational overlap and thus improving machine utilization efficiency. Equations (6)–(8) integrate AGV routing into the production schedule, establishing a tight temporal connection between machining and transportation activities.

In particular, Equation (8) implements a synchronization mechanism to ensure that materials are delivered within valid time windows, thereby reducing buffer congestion and idle waiting. Equation (9) explicitly introduces a spatial coordination mechanism that prevents multiple AGVs from occupying the same node simultaneously, thereby guaranteeing safe and conflict-free routing. Finally, Equation (10) links all completion times to the global makespan, serving as a unified optimization criterion for the entire system.

This formulation emphasizes the strong coupling between production sequencing and AGV routing, thereby transforming the scheduling task from a conventional job-shop optimization problem into a multi-layer, multi-resource coordination problem. In contrast to sequential or decoupled approaches, the proposed model simultaneously optimizes machine allocation and material handling, enabling bidirectional and dynamic interactions between production and transportation flows. Such integration reflects the actual operating characteristics of flexible assembly workshops, where machining delays or AGV congestion may propagate through the system, thereby affecting overall throughput and stability.

Under the unit-time assumption (T_ijm = D_uv = 1), the model focuses on synchronization logic instead of precise time-scale calibration, which simplifies the analysis while preserving coordination behavior. The formulation can be readily extended to incorporate variable processing or travel times, multi-AGV collision avoidance zones, and energy-aware optimization objectives. Due to its strong coupling and combinatorial complexity, the integrated model is NP-hard, so that exact methods such as MILP become computationally infeasible for large-scale instances.

Therefore, heuristic and metaheuristic approaches—particularly the IGA introduced in Section 4—are adopted to efficiently explore the solution space. The IGA leverages triple-chain encoding and time-window-constrained decoding to ensure coordination between production and logistics decisions, enabling the generation of near-optimal and conflict-free schedules within a reasonable computational time frame.

4. Algorithm Design and Implementation

4.1. Algorithm Framework and Rationale

The integrated production–logistics scheduling problem in FASs entails the assignment of multiple operations to heterogeneous machines and the coordination of AGVs for material handling, subject to precedence and time-window constraints. As a multi-level decision process, it is an NP-hard problem characterized by discrete variables, nonlinear constraints, and strong coupling between machining and intralogistics. Exact mathematical programming is computationally intractable for medium- and large-scale instances. This motivates the adoption of metaheuristic optimization methods.

In this study, logistics refers specifically to intralogistics operations performed by AGVs for material transportation within the flexible assembly shop. The proposed production–logistics integration focuses on the shop-floor-level coordination between production sequencing and AGV routing, where both subsystems share synchronized time windows to ensure conflict-free and real-time operation. Inventory management and external supply-chain logistics are not explicitly modeled in this framework. This assumption is reasonable for discrete-part and assembly-type manufacturing environments, where AGVs continuously transfer components between workstations and intermediate buffers, resulting in negligible in-process inventory. Therefore, the research primarily addresses the dynamic coordination of production and AGV transportation within the flexible assembly system, emphasizing responsiveness and operational efficiency at the shop-floor level.

Among various metaheuristic algorithms, the GA has demonstrated strong adaptability to combinatorial scheduling problems. The GA operates on a population of candidate solutions and applies biologically inspired operators—selection, crossover, and mutation—to efficiently explore the search space. It has been widely applied in production scheduling and logistics optimization because of its inherent parallelism, flexibility, and global search capability.

However, the conventional GA has several inherent limitations when applied to production–logistics integration problems:

(a)

Representation mismatch: Standard single-chain encoding cannot simultaneously represent operation precedence, machine assignment, and AGV routing, often resulting in infeasible or incomplete solutions.

(b)

Premature convergence: Population diversity decreases rapidly, leading the search to stagnate in local optima.

(c)

Constraint handling: Hard constraints such as time windows and conflict-free routing are difficult to preserve using conventional genetic operators.

To overcome these limitations, this study proposes an IGA specifically tailored for integrated production–logistics scheduling. The IGA extends the standard GA framework with four key mechanisms:

• a triple-chain encoding scheme to achieve unified decision representation;
• a precedence-preserving initialization method to generate feasible populations;
• adaptive genetic operators designed to balance global exploration and local refinement; and
• a time-window-constrained Dijkstra decoding strategy to ensure conflict-free AGV routing.

These mechanisms enable the IGA to dynamically synchronize production sequencing and material transportation, thereby providing robust and high-quality solutions for large-scale FAS scheduling problems.

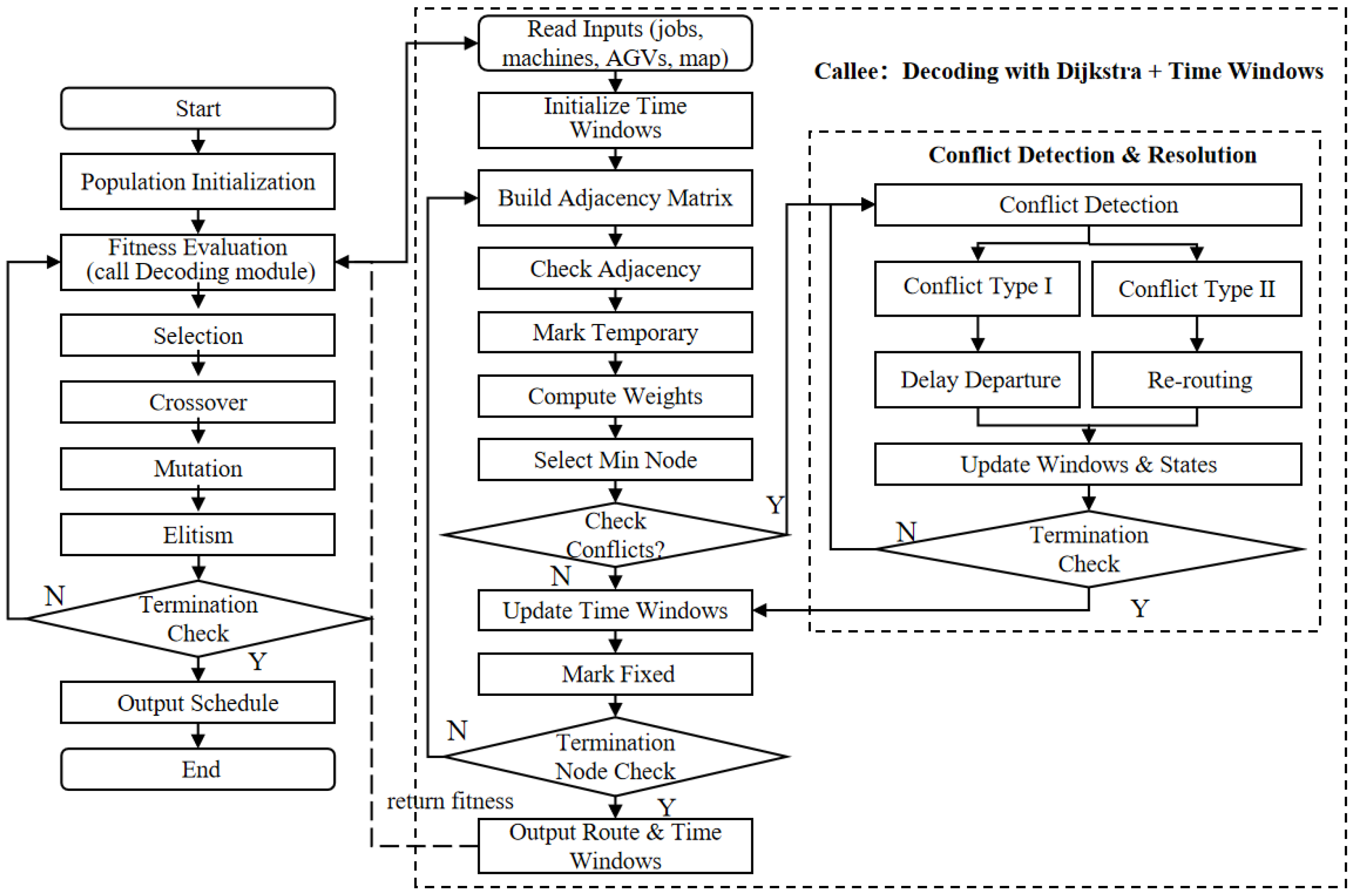
The overall framework of the proposed IGA is illustrated in Figure 2. It integrates evolutionary optimization with real-time decoding and conflict-resolution mechanisms. The process begins with population initialization, in which each chromosome encodes production and logistics decisions through a triple-chain structure ⟨Seq, Mac, Route⟩. The evolutionary loop subsequently applies fitness evaluation, selection, crossover, mutation, and an elitism strategy to iteratively evolve the population toward optimal solutions.

During the fitness evaluation stage, each chromosome is decoded into a feasible production–logistics schedule. The decoding module constructs the AGV transportation graph, computes the shortest paths using Dijkstra’s algorithm, and verifies time-window feasibility to avoid node conflicts. When two AGVs attempt to occupy the same node simultaneously, the conflict-resolution mechanism adjusts the later arrival through delayed departure, dynamic rerouting, or time-window updates. The resulting completion time (C_max) is then calculated and used as the fitness value.

The evolutionary optimization module and the decoding module operate in a continuous closed loop: genetic operations globally explore the solution space, while decoding ensures local feasibility through real-time path planning and constraint validation. This interactive integration guarantees that all generated individuals remain valid throughout the evolutionary process. Furthermore, adaptive mutation probabilities and an elitism strategy enhance convergence efficiency and prevent premature stagnation.

In summary, the proposed IGA framework transforms the integrated production–logistics scheduling problem into an evolutionary optimization process. By incorporating triple-chain encoding, adaptive evolutionary operators, and time-window-based decoding, the IGA achieves multi-layer coordination between machines and AGVs. This framework not only overcomes the inherent limitations of standard GAs but also provides a scalable and practical solution for flexible manufacturing systems that require real-time synchronization of production and logistics decisions.

4.2. Encoding and Decoding

A key feature of the proposed IGA lies in its triple-chain encoding and decoding mechanism, which enables the simultaneous representation and evaluation of production sequencing, AGV routing, and time-window feasibility within a unified genetic framework. This hybrid representation overcomes the limitations of traditional single-chain GAs and allows machining and material-handling decisions to be optimized collaboratively rather than in separate sequential stages.

4.2.1. Triple-Chain Encoding

The triple-chain encoding structure consists of three mutually interdependent components:

(a)

Operation chain (Seq-chain): This component defines the sequence of operations assigned to machines. Each gene represents an operation belonging to product i, and the gene order follows the technological precedence constraint (Equation (2)), thus ensuring scheduling feasibility by construction.

(b)

AGV routing chain (Routing-Chain): This component specifies the allocation of transportation tasks to AGVs and their corresponding routes. Each gene encapsulates a binary variable y_uv where y_uv = 1 indicates that an AGV travels from node u to v in the transportation network, as illustrated in the logistics layer of Figure 2.

(c)

Time-window chain (TW-chain): This component encodes the feasible time intervals associated with each transportation task. These intervals serve to identify potential conflicts and prevent multiple AGVs from simultaneously occupying the same path segment, thereby ensuring conflict-free routing. This integrated representation encodes both the spatial (routing) and temporal (time-window) characteristics of AGV motion, while preserving precedence consistency in production sequencing. An illustrative example of this triple-chain structure is presented in

Table 2. Example of triple-chain encoding.

Chromosome	Operation Chain	AGV Routing Chain	Time-Window Chain
Individual 1	[O11, O21, O12, O22]	[AGV1, AGV2, AGV1, AGV2]	[TW1, TW3, TW2, TW4, TW5]
Individual 2	[O21, O11, O31, O22]	[AGV1, AGV1, AGV2, AGV2]	[TW2, TW1, TW4, TW3, TW5]

.

Each column in Table 2 corresponds to one component of the triple-chain representation, establishing a complete mapping among production tasks, AGV assignments, and feasible time intervals.

4.2.2. Decoding Procedure

During the fitness evaluation stage (highlighted in Figure 2), each encoded chromosome is decoded into an executable schedule through a systematic decoding procedure. This procedure ensures that all solutions evaluated by the algorithm satisfy precedence, resource, and routing constraints without requiring external repair operations. The overall decoding procedure consists of the following major steps:

(a)

Operation scheduling: This step determines the processing sequence on each machine based on the operation chain. The start times (S_ij) and completion times (c_ij) of all operations are computed iteratively according to machine availability, following the non-overlap constraint defined in Equation (4). Operations belonging to the same product are then scheduled in accordance with their technological precedence order, thereby ensuring sequencing feasibility.

(b)

AGV routing and assignment: This step uses the routing chain to allocate each transportation task to a specific AGV according to its position in the chromosome. Once an operation is completed, the corresponding AGV is dispatched to execute the transportation task defined by the node pair (u,v). The routing cost (D_uv) is computed using Dijkstra’s shortest-path algorithm. This procedure interacts dynamically with the decoding module illustrated on the right-hand side of Figure 2, thereby ensuring coordinated scheduling between production and logistics.

(c)

Time-window validation and conflict resolution: The time-window chain verifies the temporal feasibility of each AGV route. If a conflict is detected—for instance, when two AGVs attempt to occupy the same node v at time t—the algorithm activates a conflict-resolution mechanism that either delays the departure or re-routes the affected AGV using Dijkstra’s algorithm under time-window constraints. This procedure ensures that Equation (9), which defines conflict-free routing, is consistently satisfied throughout the decoding stage.

(d)

Fitness computation: This step computes the fitness value once all operations and transportation tasks have been decoded. The maximum completion time (C_max = max{C_ij}) is evaluated as the fitness criterion, defined as F = 1/C_max. This value is subsequently fed back to the evolutionary operators and is used to guide the selection and reproduction processes. Through this integrated decoding process, each chromosome corresponds to a completely feasible production–logistics schedule, thereby reducing search overhead and enhancing convergence stability.

4.2.3. Feasible Population Initialization

Prior to the evolutionary process (upper-left module of Figure 2, Population Initialization), a feasible initial population is generated through a precedence-preserving random initialization strategy. This approach ensures that all chromosomes satisfy the fundamental technological and resource constraints from the outset, thereby guaranteeing initial feasibility. The initialization process consists of the following steps:

(a)

Sequence generation: This step constructs a directed precedence graph for each product based on Equation (2). A randomized topological sorting algorithm is subsequently applied to generate multiple feasible operation sequences for the Seq-chain, thereby preserving the technological precedence relationships among operations.

(b)

Machine allocation: This step randomly assigns each operation to a machine (m ∈ M) under the non-overlap constraint defined in Equation (4), thereby ensuring balanced machine workloads and preventing resource conflicts.

(c)

AGV distribution: This step allocates AGVs to transportation tasks in proportion to the number of routing segments. Each Route-chain is verified to include at least one valid path segment (u,v), thereby guaranteeing connectivity within the transportation network.

(d)

Time-window seeding: This step uniformly assigns initial time windows across the scheduling horizon to avoid early-stage conflicts, thereby providing the initial parameters for the decoding module.

This initialization strategy ensures the complete feasibility of the initial population while maintaining sufficient diversity among chromosomes. Compared with fully random initialization, it thereby eliminates the need for extensive repair procedures and empirically improves early-generation fitness by approximately 25% in pilot simulations.

4.2.4. Integration Within the IGA Framework

The encoding and decoding modules function as an interface between the evolutionary optimization process and the time-window-constrained routing logic illustrated in Figure 2. After each generation, the decoded schedules are evaluated, and feedback from conflict detection is utilized to adapt mutation probabilities and guide subsequent population evolution. This closed-loop interaction enables the IGA to evolve toward high-quality, conflict-free schedules with stable convergence behavior.

The triple-chain encoding and decoding mechanism provides a compact yet expressive representation for integrated scheduling. By preserving operation precedence, ensuring feasible AGV routing, and embedding time-window control, it thereby forms the computational backbone of the proposed IGA framework and directly supports its superior feasibility and robustness demonstrated in the subsequent experiments.

4.3. Fitness Function

The fitness function is used to evaluate the performance of each chromosome by quantifying the overall completion efficiency of the integrated production–logistics schedule. Since the primary objective of the proposed IGA is to achieve synchronized coordination between machining and material transportation, the makespan—defined as the maximum completion time among all operations—is adopted as the optimization criterion. The objective function is therefore formulated as follows:

$$\mathrm{m}\mathrm{i}\mathrm{n}{C}_{max}=\mathrm{m}\mathrm{a}\mathrm{x}(C_{ij}\mid O_{ij}\in O,i\in P)$$

(11)

where C_ij denotes the completion time of operation j of product i, and C_max represents the total makespan of the system. A smaller C_max indicates a more efficient schedule with higher resource utilization and smoother coordination between production and logistics activities.

In the implementation of GA-based evolutionary search (including the proposed IGA), the minimization objective is converted into a fitness value F = 1/C_max to fit the maximization mechanism of evolutionary algorithms.

Unlike traditional penalty-based fitness formulations, the proposed IGA incorporates feasibility and constraint satisfaction directly into the decoding process—see the right-hand module in Figure 2. During decoding, all precedence, machine-capacity, and conflict-free routing constraints are inherently enforced by the time-window–constrained path-planning module. As a result, only feasible and collision-free schedules are evaluated, whereas infeasible individuals are automatically eliminated without introducing additional penalty terms.

This integrated evaluation mechanism simplifies the fitness computation and thereby enhances the evolutionary efficiency of the IGA. By embedding feasibility into the decoding stage, the algorithm ensures that the fitness value directly reflects the true scheduling quality, where a shorter makespan indicates stronger coordination between machines and AGVs, thereby leading to a globally optimized production–logistics schedule.

4.4. Algorithmic Improvements of the IGA

The proposed IGA extends the classical GA framework through two key enhancements: adaptive evolutionary operators and a built-in conflict-handling mechanism. These improvements are designed to maintain population diversity, accelerate convergence, and ensure the feasibility of production–logistics schedules throughout the evolutionary process.

(1)

Adaptive Selection with Elitism

A roulette-wheel selection mechanism is employed, in which individuals are probabilistically selected in proportion to their fitness values. To retain high-quality solutions, the best individuals are preserved using an elitism strategy and directly propagated to the next generation. This ensures a steady improvement in solution quality while effectively avoiding premature convergence.

(2)

Adaptive Crossover Operator

The crossover probability (P_c) is dynamically adjusted within the range [0.3, 0.6] based on population diversity to maintain a balance between exploration and exploitation. A higher P_c facilitates broader exploration when diversity declines, whereas a lower P_c enhances search stability in near-optimal regions. Furthermore, a two-point crossover is simultaneously applied to the operation, machine, and route chains, thereby preserving consistency among layers without requiring additional repair operations.

The adaptive crossover and mutation probabilities are mathematically defined following the formulation proposed by Srinivas and Patnaik [29]:

$${\mathrm{P}}_{\mathrm{c}}={\mathrm{P}}_{{\mathrm{c}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}-\left({\mathrm{P}}_{{\mathrm{c}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}-{\mathrm{P}}_{{\mathrm{c}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}\right){\displaystyle \frac{{\mathrm{f}}_{\mathrm{i}}-{\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}}{{\mathrm{f}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}}}$$

(12)

$${\mathrm{P}}_{\mathrm{m}}={\mathrm{P}}_{{\mathrm{m}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}-({\mathrm{P}}_{{\mathrm{m}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}-{\mathrm{P}}_{{\mathrm{m}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}){\displaystyle \frac{{\mathrm{f}}_{\mathrm{i}}-{\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}}{{\mathrm{f}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{f}}_{\mathrm{a}\mathrm{v}\mathrm{g}}}}$$

(13)

where f_i, f_avg, and f_max denote the individual, average, and maximum fitness values of the population, respectively. This adaptive mechanism increases P_c and P_m for inferior individuals while reducing them for superior ones, maintaining diversity and ensuring a robust balance between global exploration and local exploitation.

(3)

Adaptive Mutation Operator and Parameter Stability

The mutation probability (P_m) is dynamically adjusted within the range [0.05, 0.10] to balance exploration and stability throughout the evolutionary process. Higher values are temporarily assigned to low-fitness individuals to expand the search space, while lower values are applied to elite solutions to preserve population consistency. Swap and reversal mutations are employed for the sequence and routing chains, respectively, to generate new feasible scheduling combinations.

To ensure consistent performance under various parameter configurations, the bounds of P_m and the adaptive crossover probability was empirically determined to maintain an appropriate trade-off between global exploration and local exploitation. Because both probabilities are adaptively controlled according to population diversity and fitness variance, the proposed IGA exhibits low sensitivity to their initial values. When population diversity declines, P_c increases and P_m slightly decreases to stabilize convergence; during early generations, both parameters are tuned toward exploration to enhance diversity.

This self-regulating mechanism eliminates the need for manual parameter tuning and ensures that the IGA remains robust and parameter-insensitive across different instance sizes and disturbance levels. Consequently, the algorithm satisfies the stability and reliability requirements of online and real-time scheduling applications.

(4)

Integrated Time-Window Conflict Resolution

During decoding, Dijkstra’s shortest-path algorithm with time-window verification is used to identify potential collisions when two AGVs are scheduled to occupy the same node simultaneously. Conflicts are resolved through minimal waiting adjustments or dynamic re-routing, thereby ensuring that all schedules remain feasible and collision-free throughout the evolutionary process.

Overall, these adaptive mechanisms allow the IGA to evolve efficiently with a balanced exploration–exploitation process, thereby achieving faster convergence and greater solution feasibility compared to the standard GA. The effectiveness of this adaptive adjustment is further verified through the convergence and statistical results presented in Section 5, demonstrating that the adaptive mechanism stabilizes evolution and enhances solution diversity.

4.5. Algorithm Procedure

The workflow of the IGA follows the framework illustrated in Figure 2, which integrates population initialization, evolutionary operations, and time-window-based decoding into a unified iterative loop.

Step 1: Population Initialization. A feasible initial population is generated using a precedence-preserving random initialization strategy. Each chromosome encodes production and logistics decisions through a triple-chain structure ⟨Seq, Mac, Route⟩.

Step 2: Fitness Evaluation and Decoding. Each chromosome is decoded to generate a complete schedule. The decoding module constructs AGV routes using Dijkstra’s shortest-path search under time-window constraints, verifies feasibility, and computes the fitness value F = 1/C_max.

Step 3: Selection. A roulette-wheel selection mechanism with elitism is applied, retaining elite individuals directly in the next generation to ensure a consistent improvement in scheduling quality.

Step 4: Adaptive Crossover and Mutation. The crossover and mutation probabilities are dynamically adjusted according to population diversity. Both operations are simultaneously performed on the three encoding chains to maintain feasibility and diversity.

Step 5: Conflict Detection and Resolution. During decoding, potential AGV collisions are detected through time-window verification. Conflicts are resolved through minimal waiting insertion, dynamic re-routing, or time-window adjustment, thereby ensuring conflict-free schedules throughout the evolutionary process.

Step 6: Termination. The iterative process continues until the maximum generation G_max is reached or the improvement in fitness ($\mathsf{\Delta }\mathrm{F}$) falls below a predefined threshold $\mathsf{\epsilon }$, where G_max denotes the maximum number of generations, $\mathsf{\Delta }\mathrm{F}$ represents the improvement in fitness between successive generations, and $\mathsf{\epsilon }$ is the termination threshold.

Finally, the algorithm produces the optimal chromosome that includes the operation sequence, machine allocation, AGV routing, and corresponding global makespan. This closed-loop process allows the IGA to continuously evolve feasible, efficient, and conflict-free schedules in flexible assembly systems.

4.6. Algorithmic Features and Baseline Comparison

To further clarify the advantages of the proposed IGA, this section summarizes its main algorithmic features and compares its structural and performance characteristics with those of conventional scheduling methods. Through this comparative analysis, the distinctive capabilities of the IGA in achieving integrated, adaptive, and conflict-free scheduling are highlighted.

4.6.1. Algorithmic Features

The proposed IGA demonstrates several key distinctive features when compared with conventional scheduling methods. It integrates production sequencing, machine allocation, and AGV routing within a unified optimization framework, thereby achieving seamless coordination between production and logistics operations.

Integrated optimization: The IGA simultaneously optimizes production scheduling and AGV routing within a unified optimization framework, thereby overcoming the inefficiencies of traditional decoupled two-stage methods. The triple-chain encoding enables all relevant decision variables to evolve cooperatively, thereby realizing real-time synchronization between machining operations and material-handling activities.

Feasibility and conflict-free guarantee: All generated schedules are inherently feasible by design. Specifically, during decoding, the Dijkstra-based routing module ensures time-window satisfaction and effectively prevents AGV collisions without relying on additional penalty functions. This guarantees reliable and collision-free scheduling that is well-suited for real shop-floor implementation.

Adaptive evolutionary mechanism: The crossover and mutation probabilities are dynamically adjusted based on population diversity and fitness variation. This adaptive control balances global exploration and local exploitation, thereby preventing premature convergence while preserving high-quality solutions across generations.

Scalability and applicability: The algorithm demonstrates high efficiency and robustness in multi-product, multi-machine, and multi-AGV flexible assembly environments. Furthermore, its modular design facilitates extension to large-scale and real-time scheduling scenarios in smart manufacturing systems based on digital twins.

4.6.2. Comparison with Baseline Methods

To evaluate the effectiveness of the proposed IGA, it is compared with two representative baseline approaches:

(1)

Standard GA: A conventional single-chain GA that focuses solely on production scheduling. AGV routing is either predefined or optimized separately, leading to frequent mismatches such as machine idleness or AGV congestion.

(2)

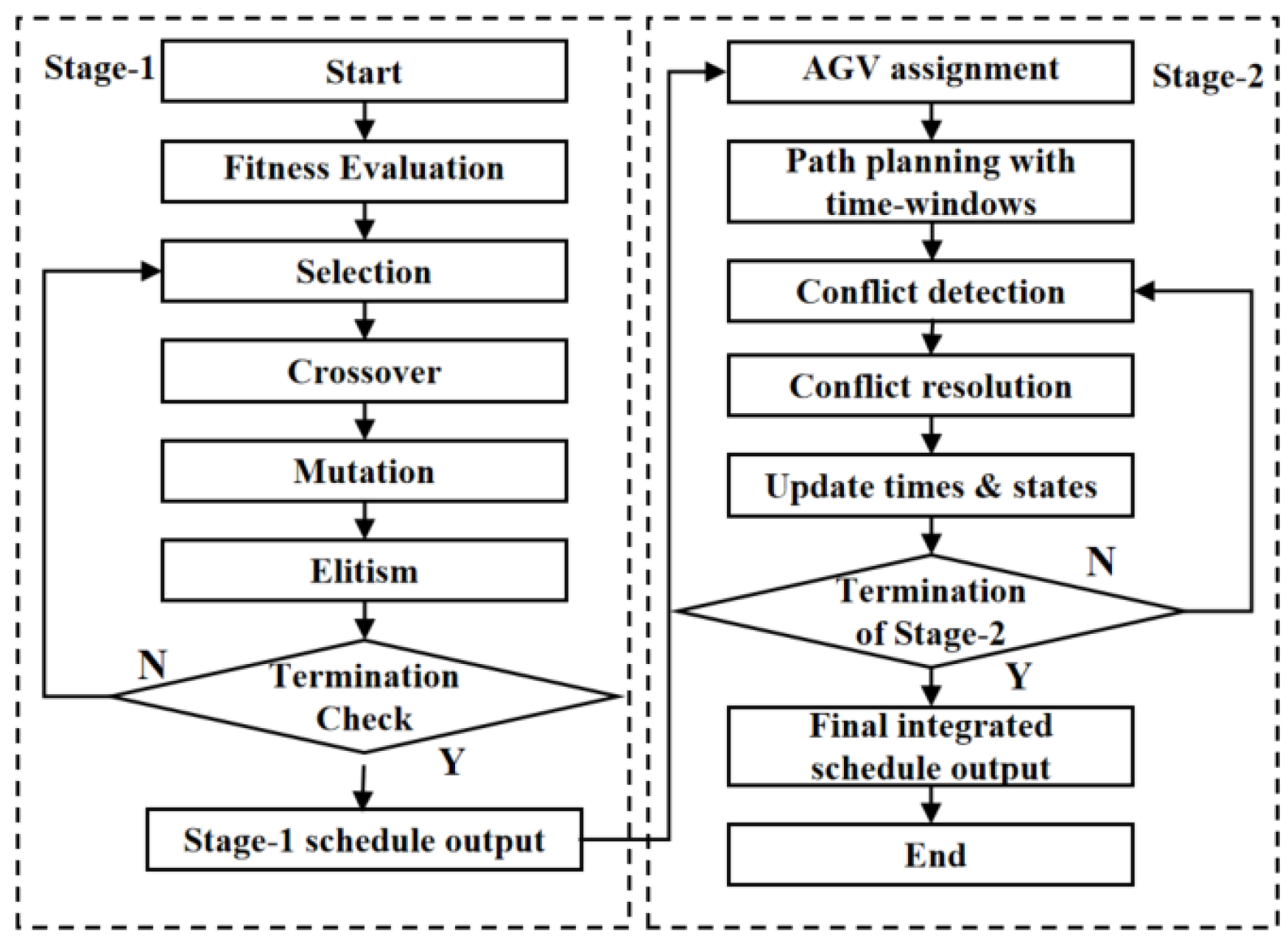
Two-Stage Heuristic Method. A decoupled optimization strategy is widely used in traditional production–logistics scheduling studies [30]. As illustrated in Figure 3, this method sequentially solves production sequencing and AGV routing instead of optimizing them simultaneously.

Stage 1—Production Scheduling: A standard GA is applied to assign operations to available machines and determine their start and finish times while minimizing the makespan (C_max). The GA procedure includes fitness evaluation, selection, crossover, mutation, elitism, and termination checking. The output is a feasible production schedule that serves as input for Stage 2.

Stage 2—AGV Routing and Conflict Resolution: Based on the Stage-1 timetable, AGV tasks are assigned and transport routes are generated under time-window constraints. Conflict detection and resolution are performed iteratively until all routes become conflict-free and feasible. The two stages operate independently and sequentially, without feedback iteration. Although computationally efficient, this method lacks dynamic adaptability under disturbances and cannot ensure global coordination between production and logistics.

In contrast, the proposed IGA performs joint optimization of production and logistics decisions within a unified evolutionary framework. It dynamically adjusts machine workloads and AGV routes during evolution, thereby achieving shorter makespans, higher resource utilization, and stronger robustness compared with the baseline algorithms.

5. Experimental Results and Discussion

To validate the effectiveness and robustness of the proposed IGA, a series of simulation experiments was conducted in a FAS environment under representative production–logistics conditions. The experimental platform simulates a typical production–logistics coordination scenario in which multiple products are processed on parallel machines and transported among workstations by AGVs. The experiments were aimed at evaluating the IGA’s capability to achieve shorter makespan, higher machine utilization, and stronger robustness under dynamic and uncertain conditions compared with benchmark algorithms.

5.1. Experimental Design

• Flexible assembly shop layout and scenarios

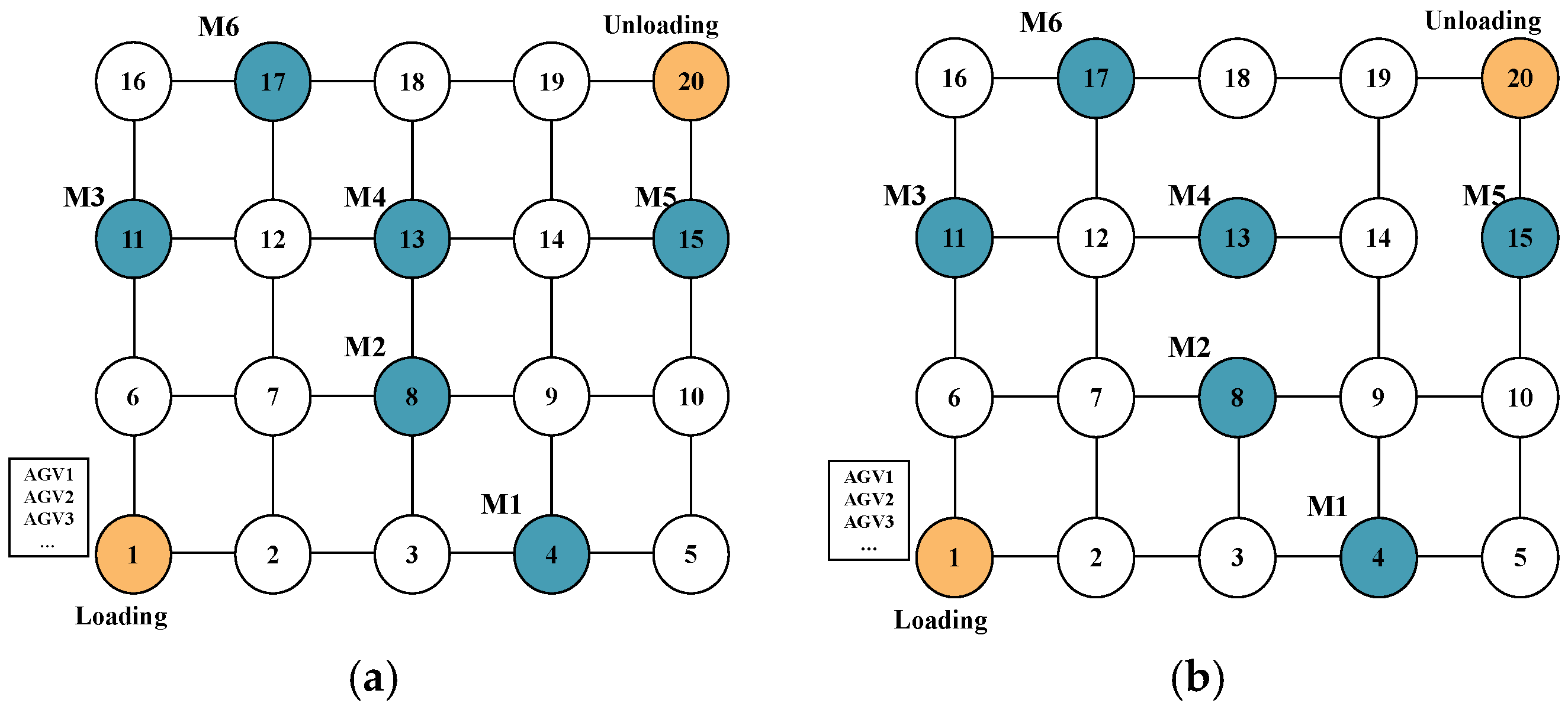
The FAS model was established based on a real production workshop, incorporating six machines and AGVs to accurately represent the operational characteristics of a medium-scale manufacturing environment. The machines were interconnected through a hybrid ring–grid transportation network structure, in which each edge corresponds to a unit travel time between two adjacent nodes. This configuration reflects a realistic production–logistics environment and simulates the spatial complexity of real shop-floor operations, allowing AGVs to efficiently coordinate material flows across multiple workstations. The topological layout adopted in both scenarios is illustrated in Figure 4.

As illustrated in Figure 4, two experimental scenarios were defined to evaluate the performance of the IGA: a benchmark scenario representing stable operations and a disturbed scenario incorporating 10% random path blockage or delay to simulate dynamic uncertainties.

Two experimental scenarios were designed based on the same layout configuration to evaluate the algorithm’s performance under both stable and disturbed conditions. The benchmark scenario represents a stable operating environment without disturbances and is used as a baseline for verifying scheduling performance. Conversely, the disturbed scenario introduces a 10% random disturbance in the transportation network, where a subset of paths is temporarily blocked or delayed to simulate moderate AGV congestion and transient routing conflicts. All other configurations, including machine layout, number of AGVs, and processing parameters, remain unchanged. This controlled setup ensures that differences in scheduling results arise solely from path-level uncertainty, thereby allowing a fair and objective assessment of algorithmic robustness.

(2)

Product–operation–machine data

Multiple products with predefined operation sequences were included in the experimental setup, each defined by a specific sequence of processing steps. Each operation was assigned to a designated machine with a fixed processing time.

Table 3. Operation–machine processing times (partial data).

Part	Operation	M1	M2	…	M6
P1	O11	5	-	…	-
P1	O12	-	7	…	-
P2	O21	6	-	…	-
…	…	…	…	…	…

Note: “-” indicates that the corresponding operation is infeasible on the given machine, and “…” denotes omitted machine columns or rows. For illustrative purposes, only a subset of the data is presented, whereas the complete dataset was used in all simulation experiments.

lists representative entries of the operation–machine matrix, where “inf” indicates that a specific operation is infeasible on the corresponding machine. For illustrative purposes, only partial data are presented in the table, whereas the complete dataset was utilized in all simulation experiments.

(3)

Problem complexity and system scale

The experimental setup represents a non-trivial integrated scheduling problem with tightly coupled production and logistics decisions. The modeled system processes four distinct products, each comprising four to six sequential operations, executed on six heterogeneous machines arranged in a hybrid ring–grid topology. Material transfers between workstations are carried out by five AGVs, each subject to precedence and time-window constraints to ensure conflict-free transportation.

Such a configuration yields approximately 20 operations, 6 machines, and 5 AGVs, resulting in hundreds of potential operation–machine–route combinations within each generation. The decoding module must simultaneously evaluate machining precedence, machine capacity, and AGV routing feasibility, rendering the problem NP-hard and computationally comparable to large-scale flexible job-shop benchmarks reported in recent literature. This configuration, therefore, provides a realistic and sufficiently complex testbed for assessing the scalability, stability, and robustness of the proposed IGA under dynamic conditions.

(4)

Algorithm parameters

Three algorithms were implemented and compared for performance evaluation: the standard GA, a two-stage heuristic method, and the proposed IGA. To ensure fair comparison, their main control parameters are summarized in

Table 4. Algorithm parameter settings.

Algorithm	Population Size	Generations	Crossover Probability	Mutation Probability	Encoding
GA	100	200	0.45	0.075	Single-chain
Two-stage	100	200	0.45	0.075	Two-stage
IGA	100	200	Adaptive [0.3–0.6]	Adaptive [0.05–0.10]	Triple-chain

.

For the baseline GA and two-stage method, the crossover and mutation probabilities (P_c = 0.45, P_m = 0.0075) follow classical GA literature and have been widely used in scheduling-optimization research. The adaptive parameters of the IGA were computed using the mathematical expressions introduced in Section 4.4. For fairness, no parameter tuning was performed specifically for the proposed IGA; all baseline parameters followed standard GA settings, and the adaptive values were entirely determined by the self-adjusting mechanism rather than manual calibration.

All remaining algorithmic parameters—including population size, number of generations, and decoding-related settings—were determined based on widely adopted configurations in the literature and preliminary experiments to ensure stable performance across all algorithms [29].

All simulations were conducted in Python 3.12 on a Windows 11 environment using standard scientific-computing libraries. All algorithms were executed under the same software environment to guarantee the fairness and reproducibility of the computational results.

5.2. Convergence Analysis

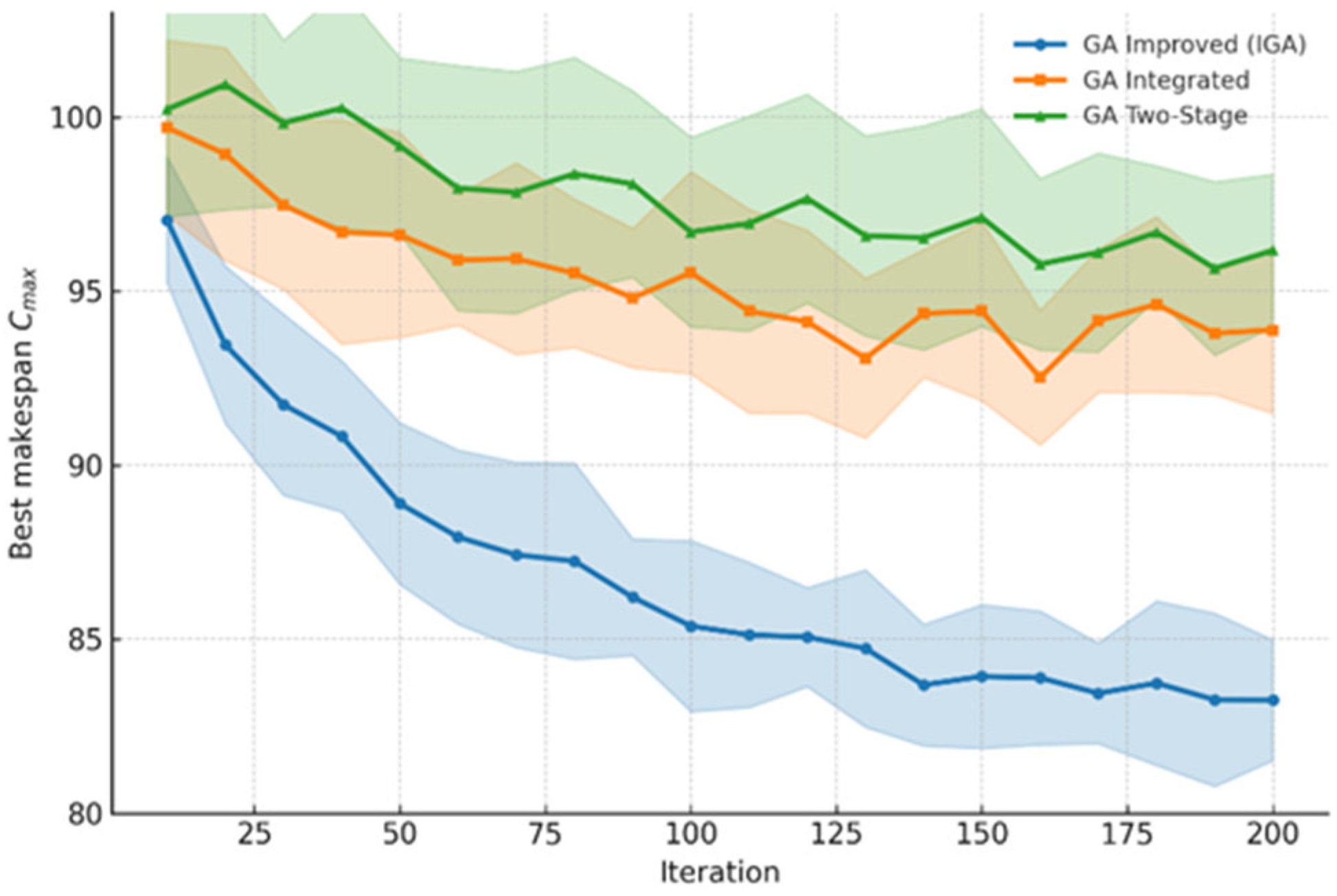
To evaluate the convergence performance of the proposed IGA, comparative experiments were performed among the standard GA, the two-stage heuristic method, and the IGA under identical parameter configurations and random initializations. Each algorithm was executed for 20 independent runs, with the best makespan recorded every 10 generations, starting from generation 10. The results were averaged across all runs, and the shaded regions in Figure 5 indicate the standard deviation range, demonstrating the stability and consistency of the convergence behavior.

Figure 5 illustrates the convergence trajectories of the three algorithms. The standard GA demonstrates rapid improvement during the first 50–80 generations but stagnates thereafter, indicating premature convergence due to population homogenization. The two-stage method postpones this stagnation slightly by decoupling production scheduling from transportation assignment; however, its performance still fluctuates considerably in later generations, implying an unstable local search capability.

In contrast, the IGA exhibits a distinctly steeper declining trend during the early phase, achieving a faster makespan reduction. During the mid-phase, the improvement rate remains stable without oscillations, leading to smooth and consistent convergence after approximately 150 generations. The narrow-shaded region around the mean curve indicates that the algorithm achieves high repeatability across multiple independent runs, confirming the algorithm’s robustness and convergence reliability.

These results suggest that the adaptive mechanisms embedded within the IGA framework—namely, the dynamic adjustment of crossover and mutation probabilities as well as the time-window-constrained Dijkstra decoding—enhance the synergy between exploration and exploitation. By effectively balancing global search and local refinement, the IGA avoids premature convergence, thereby accelerating evolutionary efficiency and maintaining strong stability throughout the optimization process.

Overall, the proposed algorithm not only converges faster than the comparative methods but also delivers smoother and more consistent performance across multiple independent runs. This finding confirms that the integration of adaptive evolution and conflict-free decoding significantly enhances the convergence stability and search effectiveness of the scheduling process.

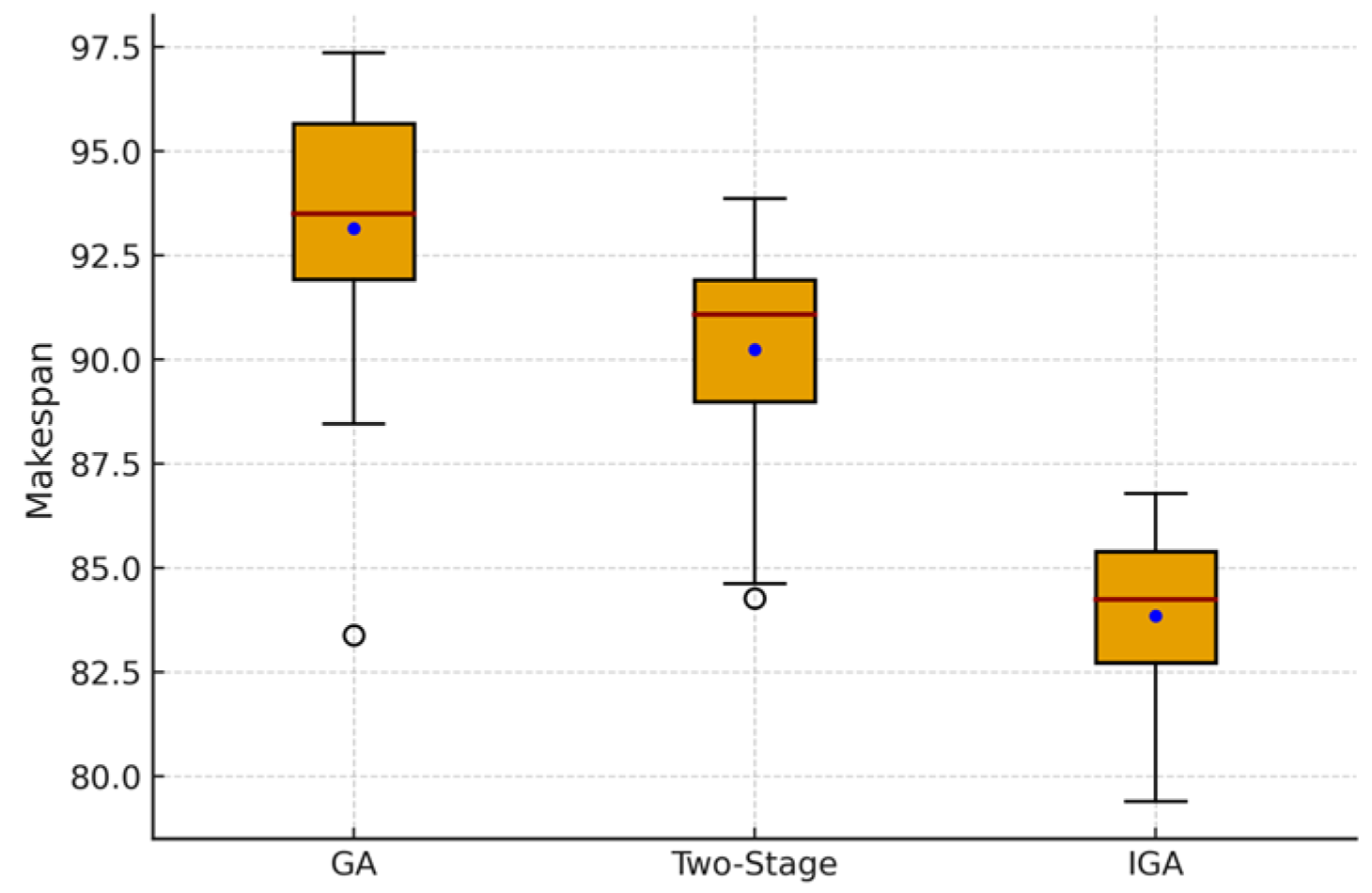
5.3. Scheduling Performance Comparison

To comprehensively evaluate the performance of the proposed IGA, comparative scheduling experiments were performed under the benchmark scenario. To ensure statistical reliability, all algorithms were executed for 20 independent runs with a maximum of 200 generations under identical configurations. Before generating the figures and tables, we cross-validated all raw experimental data to guarantee that Figure 5 and Figure 6, and

Table 5. Statistical results of the three algorithms under Scenario 1.

Algorithm	Mean	Best	Worst	Median	Std. Dev	Variance	IQR
GA	92.8	89.6	98.2	92.4	7.50	56.3	7.4
Two-Stage	90.0	87.2	93.8	89.1	5.34	28.5	2.8
IGA	84.0	82.1	86.9	84.3	2.08	4.32	2.4

were produced from the exact same dataset, thereby ensuring full consistency across convergence analysis and makespan statistics. Although additional generations may lead to marginal improvements, the convergence curves became nearly flat after approximately 150 generations, indicating that 200 generations are sufficient to obtain stable, reproducible, and reliable performance evaluations for all algorithms.

Each algorithm—the GA, two-stage heuristic method, and IGA—was executed independently for 20 runs under identical parameter configurations. The evaluation metrics included the mean, best, worst, and median makespan values, as well as the standard deviation (Std.), variance (Var.), and interquartile range (IQR). The comparative boxplots of the results are illustrated in Figure 6, and the corresponding quantitative statistics are summarized in Table 5.

(1)

Statistical Comparison

As shown in Table 5, the IGA achieves the minimum mean makespan value (84.0), representing reductions of 9.5% and 6.7% compared with the GA and two-stage methods, respectively. The best makespan value (82.1) and the smallest gap between the best and worst cases (approximately 4.8 units) further demonstrate that the IGA provides both high efficiency and strong robustness. This pattern is also evident in Figure 6, where the IGA boxplot is positioned significantly lower and exhibits a much narrower dispersion range, confirming its superior consistency and repeatability across multiple independent runs.

(2)

Stability and Mechanistic Interpretation

Regarding stability, the IGA exhibits the smallest Std., Var., and IQR values, indicating reduced performance fluctuations and higher repeatability across runs. The GA shows the largest dispersion range, revealing instability caused by premature convergence and excessive population homogeneity. The two-stage method achieves partial improvement but still exhibits fluctuations in later iterations, primarily due to the absence of interaction between scheduling and transportation decisions.

The superior performance of the IGA is primarily attributed to its adaptive genetic operators and the time-window-constrained decoding mechanism. The adaptive crossover and mutation rates dynamically balance exploration and exploitation, thereby maintaining population diversity and effectively preventing premature convergence. Meanwhile, the Dijkstra-based routing embedded within the decoding process minimizes AGV conflicts and idle waiting times, ensuring a smoother and more feasible scheduling process.

Overall, the IGA exhibits the most balanced trade-off between optimization efficiency and stability. As shown in Figure 6 and Table 5, its compact distribution and minimal statistical dispersion validate that the proposed algorithm consistently generates high-quality schedules with enhanced robustness, thereby rendering it well suited for flexible production–logistics systems.

5.4. Significance Test

To assess whether the observed performance differences among the algorithms are statistically significant, independent-sample t-tests and effect size analyses (Cohen’s d) were conducted under Scenario 1. The proposed IGA served as the reference group for pairwise comparisons with the GA and two-stage methods. The significance level was set to α = 0.05, which is standard in engineering statistics for balancing Type I error risk and result sensitivity. All statistical tests were performed using the 20 independent runs reported in Section 5.3. The results of the significance analysis are summarized in

Table 6. Significance analysis of scheduling results (Scenario 1).

Comparison	Mean Difference	t-Statistic	p-Value	Cohen’s d	Significance	Effect Level
IGA vs. GA	−5.72	−10.83	<0.001	1.89	Significant	Large
IGA vs. Two-Stage	−4.12	−8.05	<0.01	1.42	Significant	Large
Two-Stage vs. GA	−2.83	−2.16	0.045	0.70	Significant	Medium

.

The results indicate that all pairwise comparisons achieve statistical significance at the p < 0.05 level. Specifically, for comparisons involving the IGA, the p < 0.01 threshold indicates that its performance improvement over the GA and two-stage methods is not only statistically significant but also practically meaningful. The corresponding Cohen’s d values of 1.89 (IGA vs. GA) and 1.42 (IGA vs. two-stage) correspond to large effect sizes according to Cohen’s conventions, suggesting that the IGA’s advantages are both substantial and consistent across experiments.

The comparison between the two-stage and GA methods also shows a significant difference (p = 0.045) but with a medium effect size (d = 0.70), indicating that although the two-stage method provides moderate improvement, its optimization potential remains limited compared with that of the IGA.

Overall, these results clearly demonstrate that the proposed IGA achieves statistically significant and practically meaningful improvements in scheduling performance. The integration of adaptive evolution and time-window-constrained decoding not only enhances convergence and stability but also ensures reproducible optimization gains, as validated by the formal hypothesis tests.

5.5. Robustness Analysis

To comprehensively evaluate the robustness of the proposed IGA under uncertain production and transportation conditions, comparative experiments were conducted between the benchmark scenario (Scenario 1) and the disturbed scenario (Scenario 2). Both scenarios maintained identical machine configurations, product sets, and AGV numbers. The only difference was that in Scenario 2, approximately 10% of the AGV transportation paths were randomly delayed or temporarily blocked to simulate real-world disturbances such as path congestion or equipment malfunctions. Each scenario was executed for 20 independent runs to ensure statistical validity, and the corresponding results are summarized in

Table 7. Comparison of IGA results under different scenarios.

Scenario	Mean	Best	Worst	Std. Dev	Variance	IQR
Scenario 1 (Benchmark)	84.0	82.1	86.9	2.08	4.32	2.4
Scenario 2 (Disturbed)	84.7	82.4	89.2	2.65	5.57	2.6

.

As shown in Table 7, the mean makespan shows a slight increase from 84.0 to 84.7, representing a minor deviation of less than 1%, while the standard deviation and variance grow marginally (ΔStd. ≈ 0.6, ΔVar. ≈ 1.2). The interquartile range (IQR) also remains nearly unchanged (2.4 → 2.6), indicating that the overall solution distribution remains compact and consistent under disturbed conditions. These results demonstrate that the IGA maintains high scheduling stability even under random delays or temporary blockages in the transportation network.

The robustness of the algorithm is primarily attributed to the integration of adaptive genetic operators and time-window-constrained decoding. The adaptive crossover and mutation probabilities dynamically regulate the population’s search diversity, thereby enabling the algorithm to respond effectively to unexpected variations in the problem environment. Meanwhile, the Dijkstra-based decoding mechanism ensures feasible AGV routing and smooth, coordinated task execution, even under partial path disruptions.

Overall, the results clearly demonstrate that the proposed IGA exhibits strong robustness and adaptability to environmental uncertainties. Its only minor performance fluctuations and consistently low dispersion indicate that the algorithm can maintain high scheduling efficiency, stability, and reliability in complex and dynamic manufacturing environments. Therefore, the IGA serves as a practical and resilient optimization tool for integrated production–logistics scheduling in flexible assembly shops, offering both stability and adaptability for real-world implementation.

6. Conclusions and Discussion

6.1. Conclusions

This study has presented an integrated optimization approach for production–logistics scheduling in flexible assembly shops, aiming to address the challenges of dynamic coordination between manufacturing operations and AGV-based material transportation. To overcome the inherent limitations of conventional GAs—such as premature convergence, poor adaptability, and weak coordination between scheduling and routing—an IGA was developed. The proposed IGA integrates a triple-chain encoding strategy, time-window-constrained Dijkstra-based decoding, and adaptive genetic operators, thereby establishing a unified optimization framework that simultaneously manages production sequencing and AGV path planning.

6.2. Contributions

(1)

A comprehensive mathematical model for integrated production–logistics scheduling has been developed, which considers operation precedence, machine capacity, and AGV routing feasibility. The developed model enables the synchronous optimization of machining and transportation processes, thereby reflecting the real operational characteristics of flexible assembly systems.

(2)

An improved evolutionary framework has been developed, in which the adaptive crossover and mutation operators dynamically balance exploration and exploitation during evolution. The proposed mechanism effectively prevents premature convergence, thereby enhancing overall search efficiency and population diversity. This effect is empirically validated by the smooth convergence pattern in Figure 5 and the reduced Std., Var., and IQR values in Table 5, confirming that the adaptive operators effectively maintain population diversity and prevent premature convergence.

(3)

A time-window-constrained Dijkstra decoding method has been introduced, which ensures feasible and conflict-free AGV routing, thereby achieving effective linkage between production scheduling and transportation assignment.

(4)

Comprehensive simulation experiments have been conducted to validate the effectiveness of the proposed IGA, including convergence analysis, performance comparison, significance testing, and robustness evaluation. The results demonstrate that the IGA reduces makespan by approximately 9.5–10% compared with baseline methods, achieves smoother convergence, and maintains superior stability and robustness under both stable and disturbed operating conditions.

6.3. Significance

From a theoretical perspective, this research advances research in the field of integrated production–logistics optimization by providing a unified modeling and solution framework that effectively bridges scheduling and routing problems. The proposed encoding–decoding design and adaptive mechanism provide new insights into the hybridization of heuristic and metaheuristic methods for dynamic scheduling environments. From an engineering perspective, the approach serves as a practical and scalable decision-support tool for real-world manufacturing systems, thereby enabling intelligent coordination between machines and AGVs in flexible production lines. It thereby contributes to improving resource utilization, reducing idle time, and supporting the development of smart and sustainable manufacturing systems in the context of Industry 4.0.

6.4. Limitations

The present study focuses on validating the feasibility and effectiveness of the proposed IGA framework. However, it does not include comparative experiments with other advanced optimization approaches such as PSO, RL, or deep learning–based scheduling algorithms. As a result, the relative advantages and scalability of the proposed method have not been fully examined and will be further investigated in future research.

6.5. Future Work

Future research will extend the current framework toward more intelligent and sustainable scheduling strategies. Incorporating energy consumption as an additional optimization objective will enable the algorithm to better reflect the operational and environmental constraints of real manufacturing systems. Moreover, coupling the IGA framework with reinforcement learning and neural network models will be explored to achieve adaptive, data-driven, and self-learning scheduling in dynamic production environments. These developments are expected to enhance the algorithm’s intelligence, generalization capability, and practical applicability for next-generation flexible manufacturing systems.