Research on Dual-Actuator Shift Control of Dual-Mode Coupling Drive Electric Vehicles

Abstract

Dual-mode coupling drive system can improve the dynamic performance of electric vehicles through mode switching, and the quality of mode switching directly affects the comfort of drivers and passengers. Mechanical coupling on the left and right sides of the single actuator causes mutual interference during shifting, resulting in prolonged power interruption time and shifting shock. Therefore, this paper analyzes the mutual interference mechanism of single-actuator shifting, designs a new dual actuator, and proposes a staged fuzzy PID controller. Finally, the effectiveness of dual-actuator shifting is proven through simulations and real vehicle testing. Compared with conventional PID control and BP neural network PID control, the shock degree is reduced by 64% and 50%, which improves the mode-switching quality of the dual-mode coupling drive system.

1. Introduction

Pure electric vehicles can be classified as possessing either centralized drive or distributed drive systems according to the layout of their drive motor. Centralized drive technology is mature and safe, but the drive system itself does not have dynamic control performance [1]. The torque of each wheel of a distributed drive system is independently controllable, which can realize various dynamic control functions such as anti-skid driving and differential steering [2,3,4]. However, when the drive motor fails [5,6], complex dynamic control is required to maintain safe driving of the vehicle, which increases the complexity of the control system. By combining the advantages of the above centralized drive and distributed drive systems and avoiding their disadvantages, our research group has invented a dual-mode coupling drive system as shown in Figure 1, which can use both centralized drive and distributed drive and has a two-speed transmission capacity [7]. The system can also use a single-motor centralized drive mode in the case of unilateral drive motor failure, and improve the safety of the distributed drive. 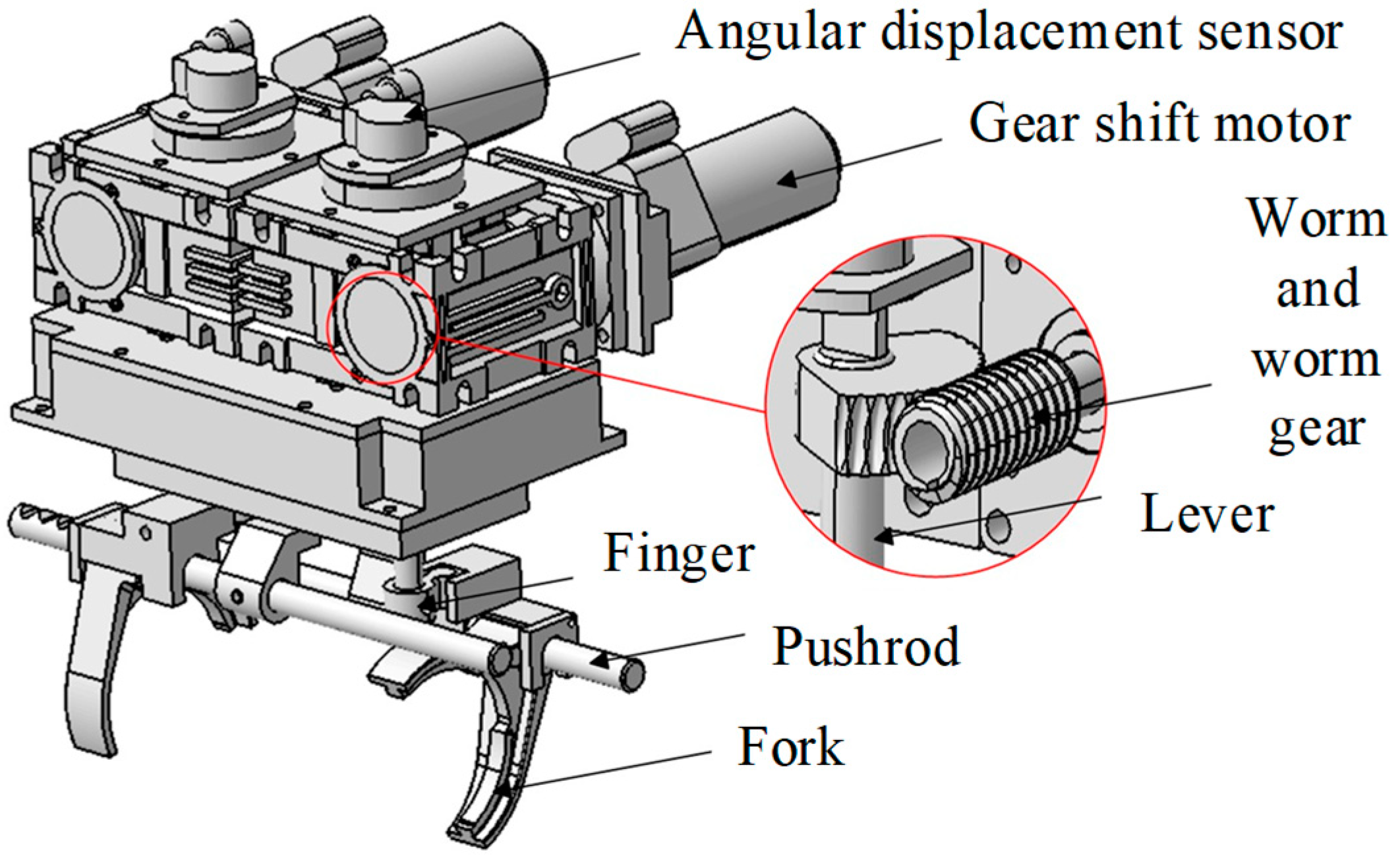The drive system achieves different driving modes by controlling the position of the joint sleeve in the synchronizer through the shift actuator [8,9]. An existing single actuator is shown in Figure 2. It includes a selector motor and a shift motor, which are decelerated by a worm gear. The selector motor controls the up and down movement of the lever to achieve simultaneous or independent fork control. The shift motor controls the rotation of the lever and plays a role in mode switching. In order to ensure the safety of shifting, the left and right shift forks are moved by a single lever. If one side fails to engage, the other side cannot engage. However, due to the mechanical coupling between the left and right sides, there is a mutual interference problem between the synchronizers on both sides, that is, at any stage of the shift process, one side must wait for the other side to complete the corresponding stage before entering the next stage. This will extend the power interruption time. Moreover, there are gaps in the real system, and it is impossible to ensure that the synchronizers on both sides are in the same stage when shifting, thus causing shifting shock. Therefore, in view of this mutual interference problem existing in single actuators, a new design and control method of shift actuators is required.

Domestic and foreign scholars have performed a lot of research on the structural design of shift actuators. Hu et al. added grooves to the camshaft [10]. The rotation of the camshaft drives the shift fork to move to achieve gear shifting. However, wear will occur at the contact between the shift fork and the camshaft, which will lead to a decrease in gear shifting accuracy after long-term use. Lin et al. used electromagnetic linear actuators to achieve precise shift displacement control, but the actuator itself was large and occupied cabin space [11]. Petrov et al. designed a self-holding three-position electric tubular actuator that could achieve a shifting function and had a holding force of 50 N [12]. Its disadvantages are that it had a complex structure and occupied a large space. Szabó Á et al. designed a floating piston pneumatic actuator, which consisted of a double-acting floating cylinder, a shift finger and other components [13]. It had a large shift force, but the pneumatic device was large in size, which affected the layout of the transmission. The above-mentioned shifting actuator can achieve a shifting function. However, considering the compact structure and manufacturing cost of a dual-mode coupling drive system, the above-mentioned shifting actuator is not suitable for use in dual-mode coupling drive electric vehicles.

The mode-switching principle of a dual-mode coupling drive system is similar to the AMT (automated manual transmission) shifting principle, and the related research content can be used as a reference for this study. Zhong et al. used the LQR algorithm to control the shift actuator and improved shift quality [14], but the shift time still needed to be further optimized. Gao et al. used the fast motor response method to reduce the shift time for their invented I-AMT [15], but the sliding friction was considerable, and the problem of overheating causing damage to the friction surface still needs to be considered. Wang et al. designed a double-loop self-learning fuzzy control framework [16]. The outer loop adjusts the expected trajectory of the actuator motor through fuzzy logic, and the inner loop controls the trajectory of the actuator motor through the model reference self-learning method. This method can control AMT without accurate system parameters. Montazeri-Gh et al. designed an AMT control strategy for parallel hybrid vehicles [17]. According to the local traffic conditions, the genetic algorithm was used to optimize the shift control, which improved the economy of the vehicle, but did not consider the shift quality problem. Roozegar et al. used a discrete PID controller for shift control, and used a trial-and-error method and genetic algorithm to optimize PID, which achieved the initial requirements of fast shifting, and still needed to be optimized in the later stage to achieve better results [18].

In order to solve the problem of mutual interference during the mode switching of single actuators and improve the compactness of shift actuators, a new dual actuator is designed based on the original shift actuator. The mode switching process is theoretically analyzed, and a staged control method is designed to improve the quality of mode switching. In this paper, a dual actuator is designed and the dynamic model of a shift actuator is established. Secondly, a theoretical analysis of the dual-mode coupling drive system’s shift process is carried out. Next, the mutual interference mechanism of the single actuator is analyzed. Then, the dual-actuator shift control method is studied. Finally, the effectiveness of the dual-actuator shift control is verified by real vehicle tests.

2. Dual-Actuator Design and System Modeling

A worm gear has the advantages of a large transmission ratio, compact structure and self-locking ability. The dual actuator still adopts this design scheme. The specific structure is shown in Figure 3, including the shift motor, worm gear reducer, shift lever, shift finger, pushrod, shift fork and angular displacement sensor. The shift motor drives the lever to rotate after the worm gear is decelerated, the lever makes the pushrod move horizontally through the finger and the shift fork drives the sleeve to move left and right to realize the mode-switching function. The synchronizers on both sides are decoupled and do not affect each other during gear shifting. The key differences between the dual actuator and single actuator are shown in

Table 1. The key differences between the dual actuator and single actuator.

	Single Actuator	Dual Actuator
Gear ratio	99	50
Coupling relationship	Yes	No
Reducer	Secondary deceleration	Single-stage deceleration

.

2.1. Synchronizer Model

The synchronizer is a key component of gear shifting. The dual-mode coupling drive system uses a lock ring inertia synchronizer. The complete gear shifting process includes five stages: torque reduction, gear disengagement, speed regulation, gear engagement and torque recovery [19,20]. Of the above five stages, the gear engagement stage is the most complicated. If no active control is performed, a large gear shifting shock will occur [7,11]. This paper studies the control problem of the gear engagement stage, so it is subdivided into the following six stages: the first sliding stage, the synchronization stage, the ring-shifting stage, the second sliding stage, the tooth-shifting stage and the third sliding stage. The purpose of the three sliding stages is to eliminate the gap between the components. The function of the synchronization stage is to eliminate the speed difference between the sleeve and the target gear. According to the empirical formula, the synchronization time of the synchronizer can be expressed as:

$$t={\displaystyle \frac{\mathsf{\Delta }\omega J_{in}}{M_t}}$$

(1)

where Δω is the speed difference (r/min), J_in is the total rotational inertia of the input end (kg∙m²) and M_t is the average synchronous torque (Nm).

The calculation formula of the synchronous torque of the ring-locking inertial synchronizer is [21]:

$$T_c=\left\{\begin{array}{cc}4\pi \mu R_c^3\rho {\displaystyle \frac{\mathsf{\Delta }\omega }{h}}& x<x_1\\ T_s& x\ge x_1,\mathsf{\Delta }\omega =0\\ {\displaystyle \frac{f_c{F}_s{R}_c}{\mathit{sin}\alpha }}& x\ge x_1,\mathsf{\Delta }\omega \ne 0\end{array}\right.$$

(2)

where T_c is the synchronous torque (Nm), μ is the motion friction coefficient of the synchronous ring, R_c is the average radius of the synchronous ring (m), ρ is the half-cone angle (°), h is the height of the friction cone angle (m), x₁ is the joint lock position (m), f_c is the cone surface friction coefficient, F_s is the shift force (N), α is the friction cone angle (°) and T_s is the torque of the average static friction of the cone surface (Nm).

The force between the sleeve and the tooth surface of the synchronous ring in the ring-shifting stage is shown in Figure 4.

The torque of the ring can be expressed as:

$$T_b=\left(F_d-F_c\right){\displaystyle \frac{d_s}{2}}={\displaystyle \frac{F_e{d}_s\left(\mathit{cos}\beta -{\mu }_s\mathit{sin}\beta \right)}{2\left(\mathit{sin}\beta +{\mu }_s\mathit{cos}\beta \right)}}$$

(3)

where F_e is the axial force at the engagement tooth surface (N), F_e = F_a + F_b, F_a and F_b are the axial component force of the positive pressure F_N and the friction force F_R of the meshing cone (N), F_c and F_d are the radial component force of the friction force F_R between the cones and the positive pressure F_N of the meshing cone (N), T_b is the ring-shifting torque (Nm), β is the friction cone half-cone angle (°), μ_s is the friction coefficient between the engaging teeth and d_s is the average diameter of the engaging teeth (m).

The tooth-shifting stage is divided into a collision stage and a stable tooth-shifting stage. The collision stage is random and it is impossible to establish an accurate mathematical model, while the stable tooth-shifting stage is similar to the ring-shifting stage. When analyzing the entire shifting process, the shifting resistance of the clutch sleeve can be expressed as:

$$m_{s}x=F_s+f_s+f_m+f_k+f_t+f_d$$

(4)

where m_s is the mass of the sleeve (kg), f_d is the contact resistance between the sleeve and the gear to be engaged after speed synchronization (N), f_t is the axial synchronization force required to eliminate the speed difference (N), f_k is the self-locking resistance between the sleeve and the slider (N), f_m is the total friction resistance encountered by the sleeve during the gear-shifting process (N) and f_s is the self-locking force of the shift fork shaft (N).

2.2. Single-Actuator Dynamics Model

In order to analyze the mutual interference problem of the single actuator, a mathematical model of the actuator is established. The two pushrods are pushed by the shifting finger to move horizontally, achieving simultaneous gear shifting on both sides. The mathematical model can be expressed as:

$$\left\{\begin{array}{l}{T}_L={\displaystyle \frac{\left(\left(F_{s1}+F_{s2}\right)h+o\right)}{i}}\\ {\theta }_m={\theta }_{out}i\\ {\theta }_{out}={\displaystyle \frac{x_d}{h}}\\ a_1={\displaystyle \frac{\frac{T_L}{i}-F_{s1}h}{m_s}}\\ a_2={\displaystyle \frac{\frac{T_L}{i}-F_{s2}h}{m_s}}\\ x_1={\displaystyle \iint a_{1}dt}={\displaystyle \iint \frac{\frac{T_L}{i}-F_{s1}h}{m_s}dt}\\ x_2={\displaystyle \iint a_{2}dt}={\displaystyle \iint \frac{\frac{T_L}{i}-F_{s2}h}{m_s}dt}\\ t={\displaystyle \frac{\mathsf{\Delta }\omega J_{in}}{M_t}}\end{array}\right.$$

(5)

where F_s1 and F_s2 are the shift resistance of the left and right sleeves (N), h is the effective length of the shift finger (m), o is the uncertain interference factor in the system, i is the worm gear ratio, θ_m is the angular displacement of the motor (rad), θ_out is the angular displacement of the lever (rad), x_d is the displacement of the sleeve (m), a₁ and a₂ are the axial accelerations of the left and right sleeves (m/s²) and x₁ and x₂ are the axial displacements of the left and right sleeves (m).

2.3. Dual-Actuator Dynamics Model

The left and right sides of the dual actuator are symmetrically designed, so the unilateral shift actuator model can be established. The mathematical model can be expressed as:

$$\left\{\begin{array}{l}{T}_L={\displaystyle \frac{F_{S}h+o}{i}}\\ {\theta }_m={\theta }_{out}i\\ {\theta }_{out}={\displaystyle \frac{x_d}{h}}\\ a={\displaystyle \frac{\frac{T_L}{i}-F_{s}h}{m_s}}\\ x={\displaystyle \iint adt}={\displaystyle \iint \frac{\frac{T_L}{i}-F_{s}h}{m_s}dt}\\ t={\displaystyle \frac{\mathsf{\Delta }\omega J_{in}}{M_t}}\end{array}\right.$$

(6)

2.4. The Shift Motor Model

The shift motor adopts a DC brush motor, and its model can be expressed as [22,23]:

$$\left\{\begin{array}{l}u{V}_{DC}=L_a{i^{\prime }}_a+R_a{i}_a+K_e{\omega }_m\\ J_m{\dot{\omega }}_m=K_T{i}_a-T_L\end{array}\right.$$

(7)

where V_DC is the power supply voltage (V), L_a is the armature inductance (H), R_a is the armature resistance (Ω), i_a is the armature current (A), K_e is the back electromotive force coefficient (V/rad/s), K_T is the torque coefficient (Nm/A), J_m is the moment of inertia of the motor rotor (kg·m²), ω_m is the motor angular velocity (rad/s), T_L is the load torque (Nm) and u is the duty cycle.

2.5. Mode Switching Evaluation Index

Commonly used AMT shift evaluation indicators include shift time, shift shock and slipping friction work. Since the mode-switching principle of the dual-mode coupling drive system is similar to that of AMT, this paper adopts the same evaluation indicators. It is stipulated that the gear shift time should not exceed 200 ms and the shock degree should not exceed 10 m/s³ to meet the gear shift requirements [7].

3. Analysis of Mutual Interference Mechanism of Single Actuator

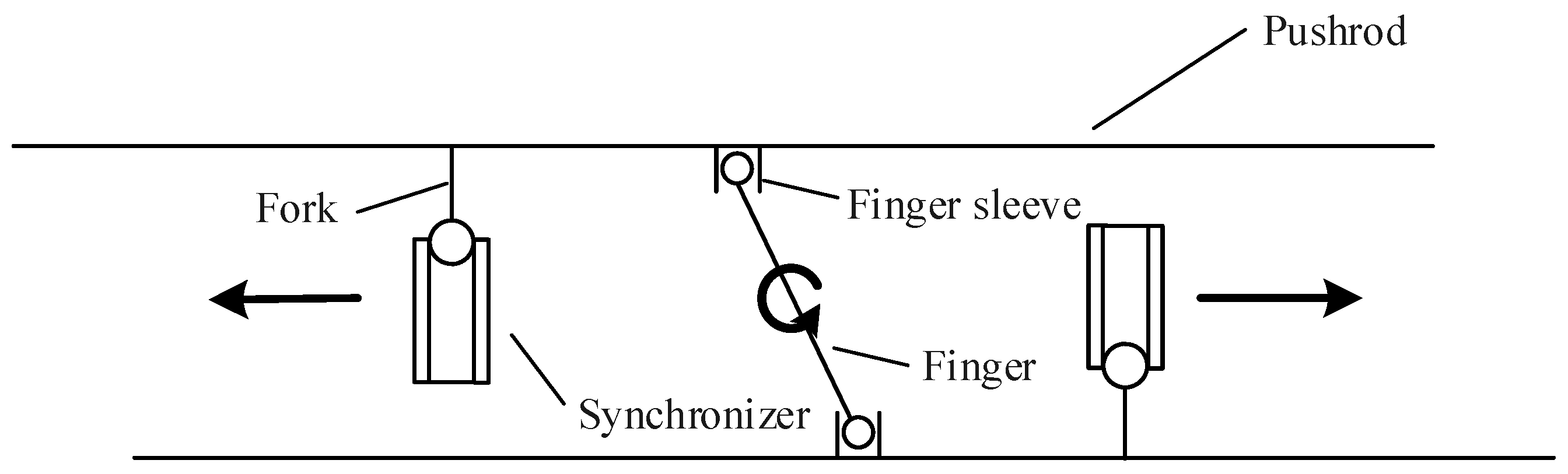
The motion plane diagram of single-actuator gear shifting is shown in Figure 5. When the single-actuator gear shift is used, the left and right sleeves are controlled by one finger, which may cause the following problems. There must be gaps between parts due to wear or assembly, so the stage on both sides may be different when shifting. The synchronous torques during the synchronization process are inconsistent, and the completion time is different. The side with a smaller speed difference can enter the next stage in advance under the drive of the shift motor while the side with a larger speed difference has not yet completed synchronization. Due to the mechanical coupling relationship on both sides, this will prevent the side with a smaller speed difference from entering the next stage. It may also cause shocks due to forced gear shifting. The target gear speeds will be inconsistent when the wheels on both sides are turning or sliding, and the speed regulation performance of the drive motors on both sides cannot be guaranteed to be exactly the same, which leads to the side that has completed speed regulation having to wait for the other side to complete speed regulation before it can shift gears. During the important stage of tooth shifting, if there is a collision on one side, this will directly affect the tooth shifting state on the other side. Due to the above reasons, there is mutual interference between the two sides of the single actuator, which will cause the power interruption time to be prolonged and the shift shock to seriously affect shift quality.

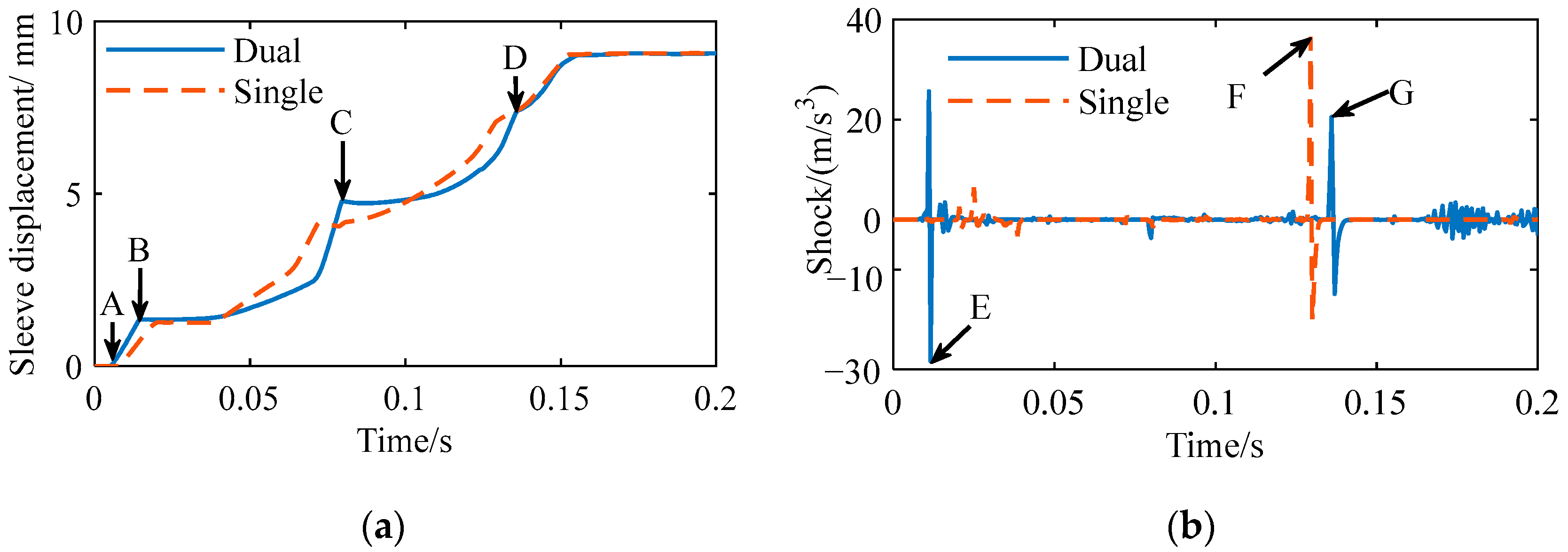
The interference caused by the shift speed regulation stage is mainly reflected in the extension of the power interruption time. The existence of a gap mainly affects the gear shift shock, and due to the difficulty in installing the sensor, it cannot be verified through using a real vehicle. Therefore, this paper uses Adams (2019) to establish a shift actuator model to simulate and analyze the mutual interference problem of single actuators. The simulation results are shown in Figure 6; the displacement of the left and right sleeves of the single actuator at point A is inconsistent. The stage indicated by arrows A and B, i.e., 0.04–0.065 s, is the ring-shifting stage. In this stage, the displacement curves of the left and right coupling sleeves of the single actuator are different, i.e., the synchronization time required for the above two sides is different. One side completes synchronization first, but the other side does not, so the coupling sleeve on the completed side tends to enter the ring-shifting stage in advance. The axial resistance of the synchronizer that enters the ring-shifting stage in advance will disappear, and when the other side enters the ring-shifting stage, mutual interference will occur, resulting in obvious shock in the later stages. The shock on the left side is greater because the right side enters the ring-shifting stage early, causing interference on the left side. The time of shock on the left and right sides is not consistent, but relatively close. The shock is random. The simulation shows that the single-actuator shift will produce mutual interference and lead to a higher shock when the gap between the left and right sides is inconsistent.

4. Design of Fuzzy PID Controller Stage

According to the analysis of the shifting process in Section 2.1, the forces in each stage are not the same, so using different controllers for different stages can achieve better control effects. 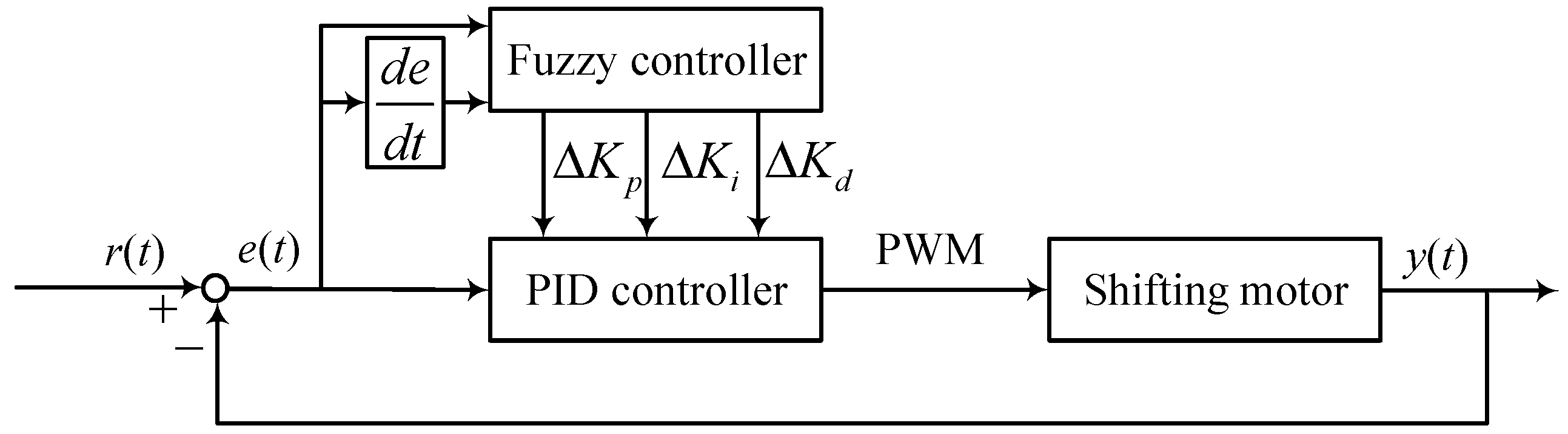Fuzzy PID is based on PID, according to the relationship between the error change rate and the error correction PID control parameters in real time; the modified parameters are input into the PID controller through continuous feedback regulation so that the controlled object has good dynamic performance [24]. The structure of the fuzzy PID control system is shown in Figure 7.

According to the error e and the error change rate e_c, the control system uses the fuzzy controller to obtain the correction of the three parameters K_p, K_i and K_d. The adjustment mechanism can be expressed as follows:

$$\left\{\begin{array}{l}{K}_p=K_{p-1}+\mathsf{\Delta }{K}_p\\ K_i=K_{i-1}+\mathsf{\Delta }{K}_i\\ K_d=K_{d-1}+\mathsf{\Delta }{K}_d\end{array}\right.$$

(8)

where K_p−1 is the proportional constant of the previous period, ΔK_p is the proportional constant correction, K_i−1 is the integral constant of the previous period, ΔK_i is the correction of integral constant, K_d−1 is the differential constant of the previous period and ΔK_d is the correction of differential constant.

4.1. Design and Implementation of Fuzzy Controller

The fuzzy controller must first fuzzify the input and output quantities and formulate fuzzy rules, then defuzzify the output and finally obtain the output quantity. The fuzzy control process is shown in Figure 8, including fuzzification, fuzzy reasoning and defuzzification.

(1)

Input and output fuzzification

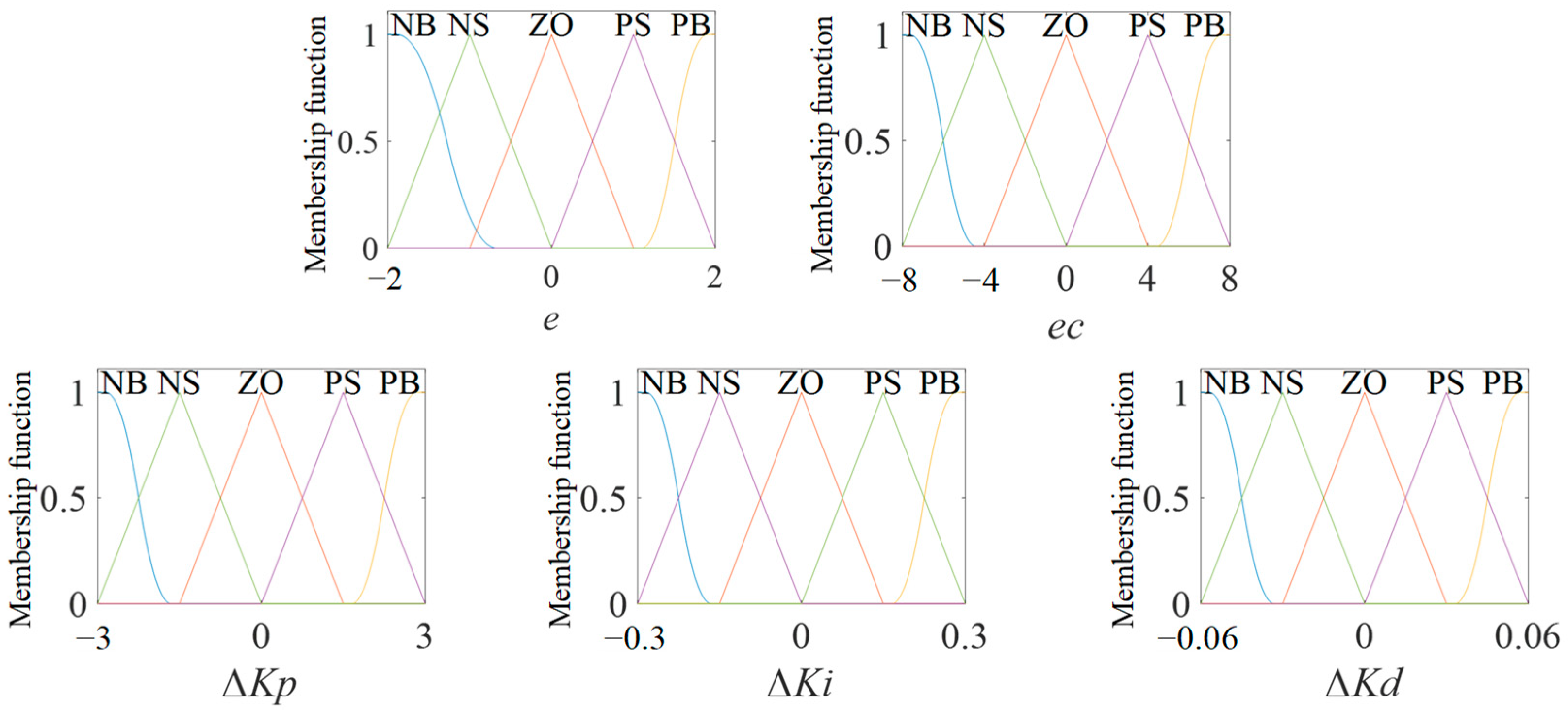
Firstly, the input quantity was fuzzified, and the fuzzy domains of the error e and error change rate ec were defined as [−2,2] and [−8,8], respectively. The fuzzy domains of ΔK_p, ΔK_i and ΔK_d were defined as [−3,3], [−0.3,0.3] and [−0.06,0.06], respectively. The fuzzy domain represents the value range of the variable. Each variable was divided into intervals and NB, NM, ZO, PS and PB were used to represent each fuzzy subset. The definition of the membership function in this paper is shown in Figure 9. The role of the membership function is to find the membership of the variable and perform fuzzy reasoning based on the membership.

(2)

Fuzzy rule making

Fuzzy rules mainly determine the corresponding relationship between input and output, which is determined by operating experience and expert knowledge. The fuzzy control rules used in this paper are shown in

Table 2. Fuzzy control rules of ∆K_p.

	NB	NS	ZO	PS	PB
NB	NB	NS	NS	NS	ZO
NS	NS	NS	NS	ZO	PS
ZO	NS	NS	ZO	PS	PS
PS	NS	ZO	PS	PS	PS
PB	ZO	PS	PS	PS	PB

,

Table 3. Fuzzy control rules of ∆K_i.

	NB	NS	ZO	PS	PB
NB	PB	PS	PS	PS	ZO
NS	PB	PS	PS	ZO	NS
ZO	PS	PS	ZO	NS	NS
PS	PS	ZO	NS	NS	NB
PB	ZO	PS	PS	NB	NB

and

Table 4. Fuzzy control rules of ∆K_d.

	NB	NS	ZO	PS	PB
NB	PS	NB	NB	NB	PS
NS	ZO	NB	NB	NS	ZO
ZO	ZO	NS	NS	NS	ZO
PS	PB	PS	PS	PS	PB
PB	ZO	ZO	ZO	ZO	ZO

.

(3)

Defuzzification

The data calculated by fuzzy rules need to be defuzzied. The common methods of defuzzification are the weighted average method, centroid method and maximum membership method [25]. In this study, the centroid method was used for defuzzification. The formula can be expressed as:

$$x_0={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{x}_i\mu \left(i\right)}}{{\displaystyle \sum _{i=1}^n\mu \left(i\right)}}}$$

(9)

where x_i is the element in the domain and μ(i) is the membership weighting coefficient of fuzzy set.

4.2. Simulation Result Analysis

In this study, the controller was established in MATLAB/Simulink (R2019b) and co-simulated with the shift model established in Adams. The key simulation parameters are shown in

Table 5. The key simulation parameters.

Symbol	Value	Symbol	Value
Rc	0.028	VDC	12
μs	0.1	La	0.0005
h	0.02	Ra	0.3067
α	7	Ke	0.0209
β	53	KT	0.0379
ms	0.3	Jm	0.000017

.

In the case of position control, the target positions at each stage are shown in

Table 6. The target position of each stage.

Stage	Target Position (mm)
The first sliding stage	1.6
The synchronization stage	1.8
The ring-shifting stage	2.8
The second sliding stage	4.2
The tooth-shifting stage	6.4
The third sliding stage	9

. The single-actuator shift and the dual-actuator shift were compared. The same control method, control parameters and control strategy were used in the shift process, and the simulation results are shown in Figure 10. The single-actuator shift showed a 36 m/s³ shock at F, the shock degree of the dual-actuator shift at E was 28 m/s³, and the shock degree at G was 20 m/s³. Under the same control method, the shock degree of the dual-actuator shift was 28.57% lower than that of the single-actuator shift. Because the velocity of the sleeve of the dual-actuator shift at A to B was faster than that of the single-actuator shift due to the absence of mutual interference, the dual-actuator shift at E had a greater shock than the single-actuator shift, which could be avoided by control in the later stage. Points F and G are at the beginning of the tooth-shifting stage and have higher shocks, but since there is no interference between the left and right sides of the dual actuator, the shock at point G is lower than that at point F. On the whole, the dual-actuator shift eliminates the mutual interference problem of the single-actuator shift, and the shock of the dual-actuator shift is smaller under the same control method.

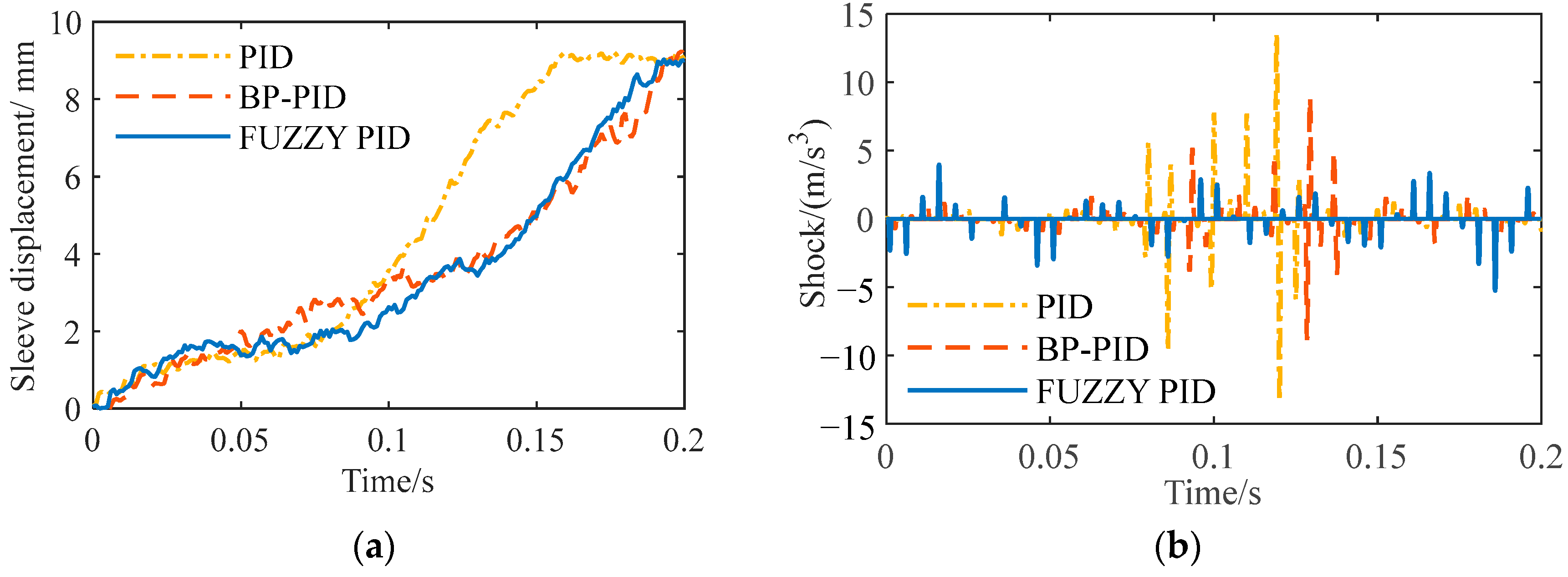
In order to verify the effectiveness of the staged fuzzy PID controller proposed in this paper, it was compared with the staged PID control [26,27] and the staged BP neural network PID control [28,29]. The simulation results are shown in Figure 11. From Figure 11a, it can be seen that the three control methods all completed the shift within 200 ms, meeting the shift requirements [30]. The shift time of the staged PID control was 115 ms, the shift time of the staged BP neural network PID control was 135 ms and the shift time of the staged fuzzy PID control was 175 ms. The maximum shock generated by the staged PID control was about 13 m/s³, the maximum shock generated by the staged BP neural network PID control was about 10 m/s³ and the maximum shock generated by the staged fuzzy PID control was about 5 m/s³. Compared with the other two methods, it was reduced by 61.54% and 50%. The staged PID generated 0.84 J of the slipping friction work, the staged BP neural network PID control generated 0.39 J and the staged fuzzy PID control generated 0.58 J. The shifting time of the staged fuzzy PID control is longer, mainly because the shifting ring and gear stages take up a longer time. These two stages affect the shock degree and slipping friction work. Therefore, the shock degree generated was greatly reduced compared with the other two methods, and the slipping friction work was also significantly reduced compared with the staged PID control. The original intention of the dual-actuator shifting design is to reduce shifting shock. Therefore, the staged fuzzy PID control is more suitable for dual-actuator shifting, which produces the smallest shock and has moderate slipping friction work, which can extend the service life of the synchronizer.

5. Actual Vehicle Test and Result Analysis

In this paper, the control effect of the dual-actuator shift was verified by a real vehicle test. The test equipment included a host computer, dSPACE controller, dual-mode coupling drive electric vehicle and high-precision integrated positioning system. The test equipment diagram is shown in Figure 12.

This paper verified the effectiveness of the dual actuator combined with the staged fuzzy PID control compared with the other two control methods. The test vehicle ran on a straight road, and adopted a centralized drive in the initial stage. When the speed reached 30 km/h, the drive mode was switched to a distributed drive. The test results are shown in Figure 13.

It can be seen that the staged PID control has a short shift time, but the maximum shock is 14 m/s³. The shift time of the staged BP neural network PID control is basically the same as that of the staged fuzzy PID control, but the shock is reduced by 64% and 50%, respectively, by using the staged fuzzy PID control, and the shift quality is obviously improved. The comparison of different control methods is shown in

Table 7. The comparison of different control methods.

Control Method	Peak Shock (m/s3)	Recommended Shock (m/s3)	Time (s)	Recommended Time (s)
Staged PID	14	10	0.16	0.2
Staged BP neural network PID	10		0.193
Staged fuzzy PID	5		0.19

. The test results are basically consistent with the simulation results, which proves the effectiveness of the staged fuzzy PID control.

6. Conclusions

Dual-mode coupling drive systems can significantly improve the dynamic performance of vehicles, and their mode switching quality directly affects the comfort of drivers and passengers. Aiming at the problem of mutual interference caused by the mechanical coupling of a single actuator, a simulation analysis was carried out, and the mutual interference mechanism of single-actuator shift is obtained. A new dual actuator was obtained by decoupling the shift actuator. According to the mode-switching characteristics of the dual-mode coupling drive system, a staged fuzzy PID shift controller was designed. In a real vehicle test, compared with a traditional staged PID controller and a staged BP-PID controller, the shift shock was reduced by 64% and 50%, and the shift quality was obviously improved.