Weak Signal Extraction in Noise Using Variable-Step Gaussian-Sinusiodal Filter
Abstract
1. Introduction
2. Mathematical Characteristic Analysis
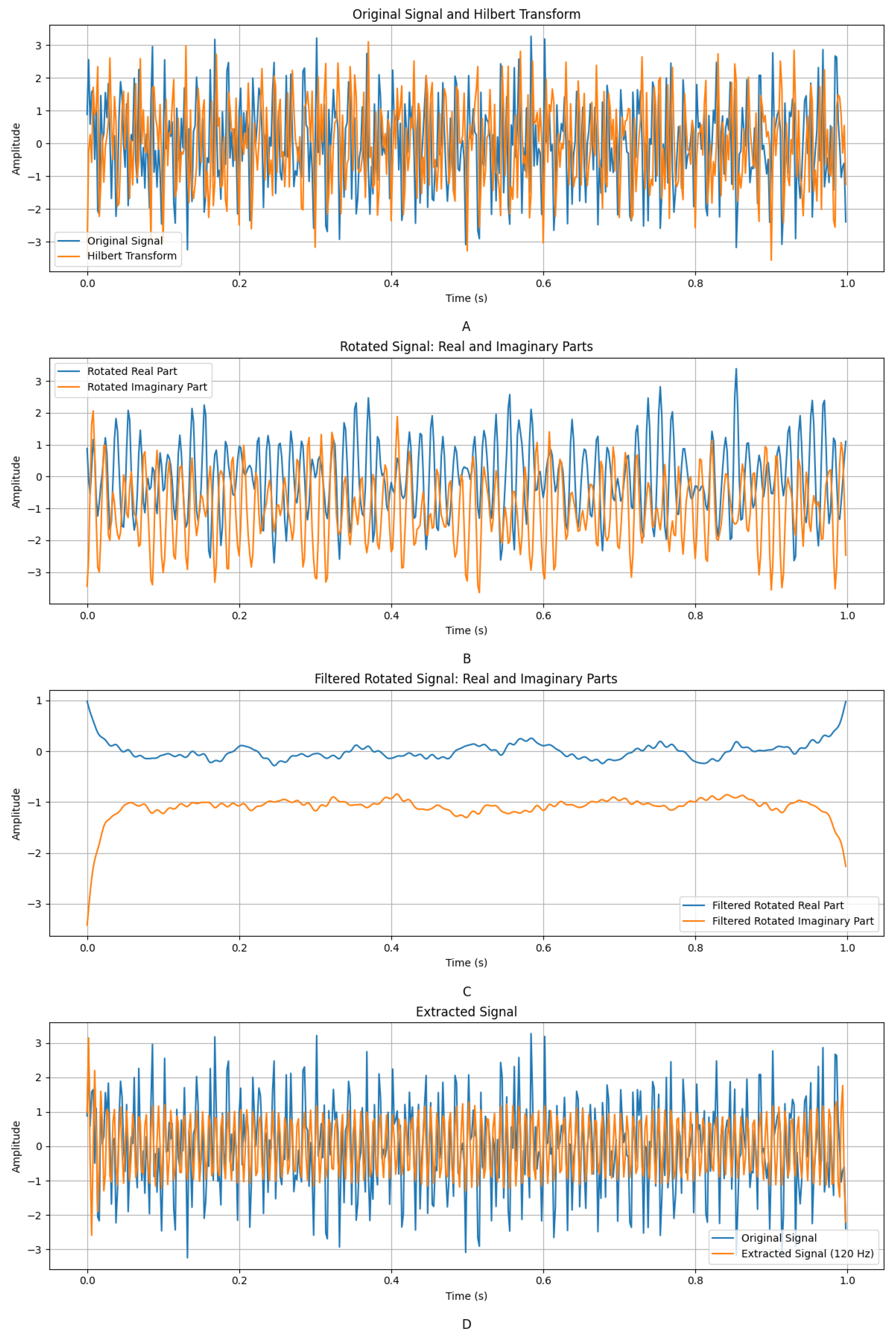
2.1. Rotating Coordinate Transformation
2.2. Gaussian-Sinusoidal Filter Fundamentals
- The standard Gaussian filter has a fixed bandwidth determined by its standard deviation (). This limitation restricts its flexibility in handling signals with different noise profiles or varying frequency components.
- Although Gaussian filters are effective at reducing noise, they can also cause signal distortion, particularly at the edges of the signal.
- The Gaussian filter is not inherently selective to specific frequency components.
- In environments with strong background noise, the standard Gaussian filter’s performance degrades.
2.3. Mathematical Characteristic Comparative Analysis
2.3.1. Time Domain Analysis
2.3.2. Frequency Domain Analysis
- The Gaussian filter has a frequency response that is also Gaussian-shaped, centered at zero frequency.
- The width of the Gaussian function in the frequency domain is inversely proportional to the standard deviation in the time domain.
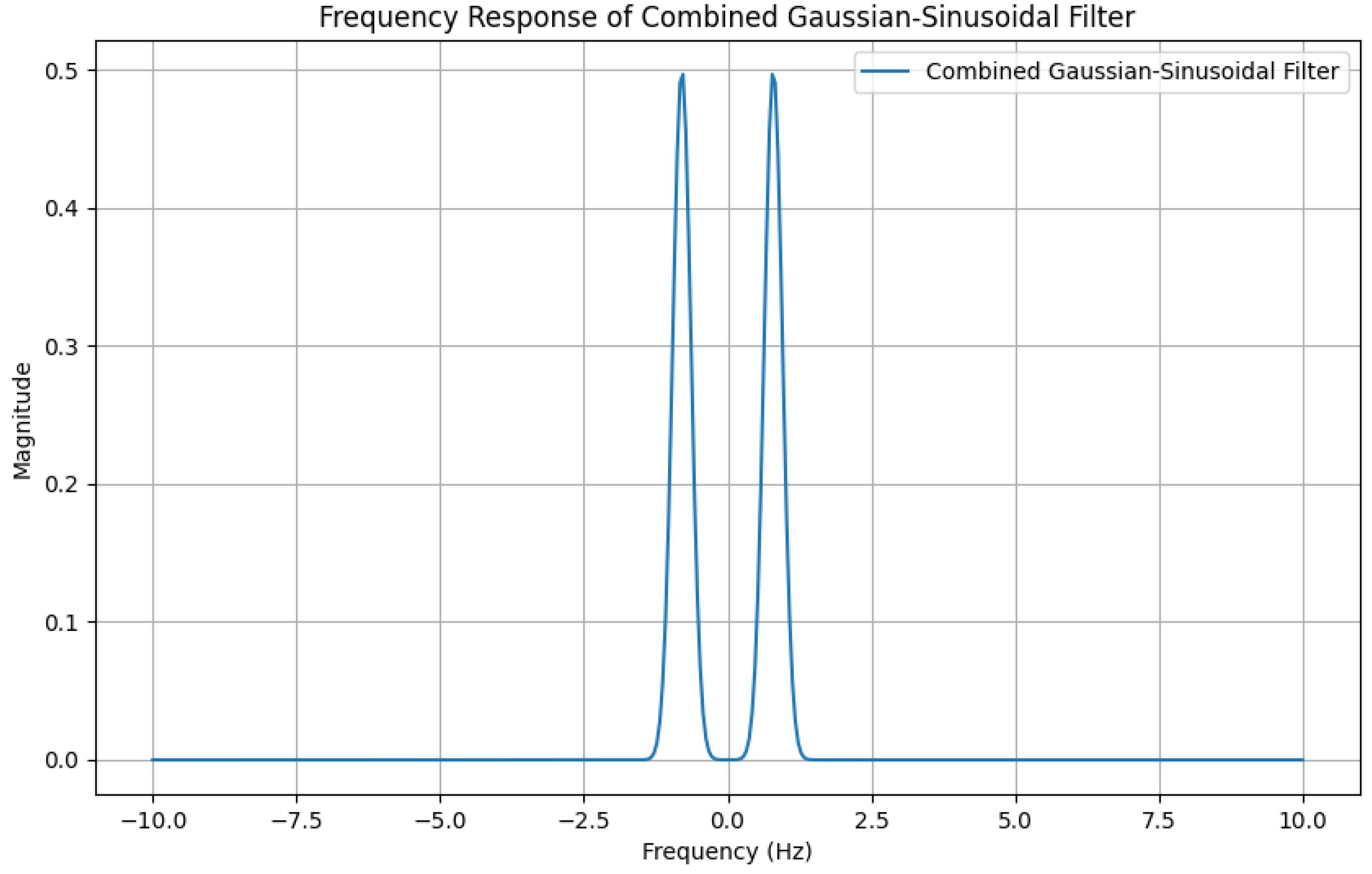
- The frequency response of the Gaussian-Sinusoidal filter exhibits two peaks, corresponding to the sinusoidal modulation.
- The Gaussian envelope in the frequency domain is shifted to due to the sinusoidal component, resulting in two peaks.
- The width of each peak is still influenced by the standard deviation of the Gaussian function in the time domain.
2.4. Normalization of the Sinusoidal-Gaussian Filter
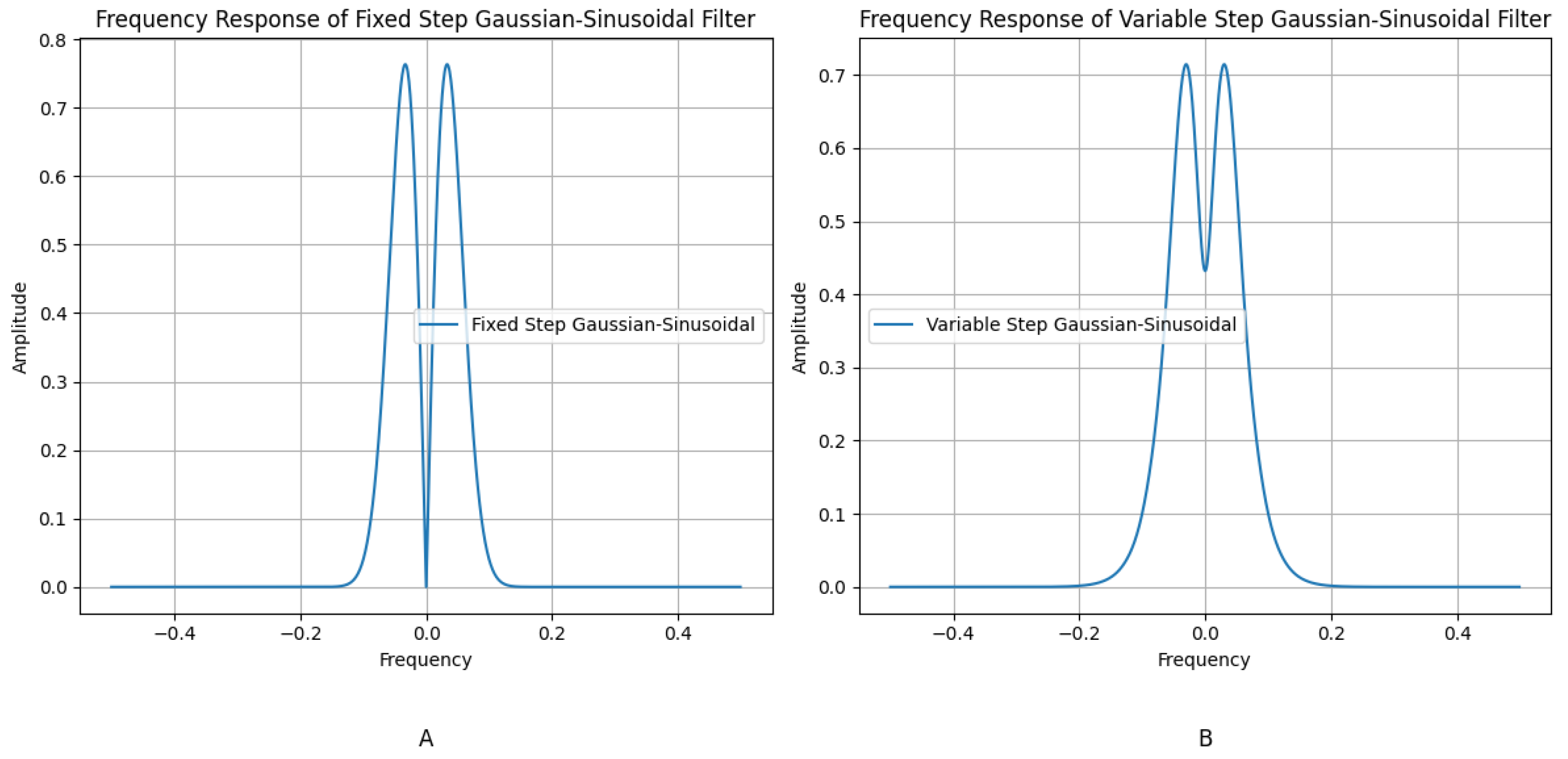
2.5. Variable-Step Algorithm
- is the time-varying standard deviation, with being the initial standard deviation and k the tuning parameter.
- is the time-varying frequency, with being the initial frequency and m the tuning parameter.
- The VSGF uses a smaller standard deviation in regions with high change rates to better preserve signal details, while a larger is used in regions with low change rates to more effectively smooth noise. This adaptive characteristic enables more effective noise suppression while preserving signal details.
- The VSGF can adaptively adjust its frequency response based on the local characteristics of the signal, thereby better selecting and preserving specific frequency components. This is particularly effective for processing multi-frequency signals, enhancing the representation of specific frequency components.
- The VSGF can adaptively adjust filtering parameters according to the local characteristics of the signal, improving the flexibility and adaptability of signal processing. This adaptability provides a significant advantage when dealing with non-stationary signals.
3. VSGF Simulation Experiment
3.1. The Application of Neural Networks in Parameter Selection
- represents the predicted value.
- represents the true value.
- N is the number of samples.
3.2. Simulation Analysis
- VSGF should show superior performance in noise reduction due to its dynamic adaptation and combination with rotating coordinate transformation.
- Stochastic resonance relies on tuning the noise level and might not be as effective for very low SNRs.
- Modal decomposition effectively isolates modes but can struggle with non-stationary noise.
- Chaotic algorithms can be highly effective in nonlinear and chaotic environments but may require careful parameter tuning.
- VSGF provides precise frequency selection, improving the extraction of specific signal components.
- Stochastic resonance enhances weak signals but may not isolate them as effectively as VSGF.
- Modal decomposition decomposes the signal into intrinsic modes, aiding in feature extraction but potentially missing weak components.
- Chaotic algorithms are effective in complex signals but can be computationally intensive.
4. Experimental Validation
4.1. Experimental Setup
4.2. Filtering Methods
4.2.1. Gaussian Filter
4.2.2. Stochastic Resonance
4.2.3. VSGF + Rotating
4.3. Results and Discussion
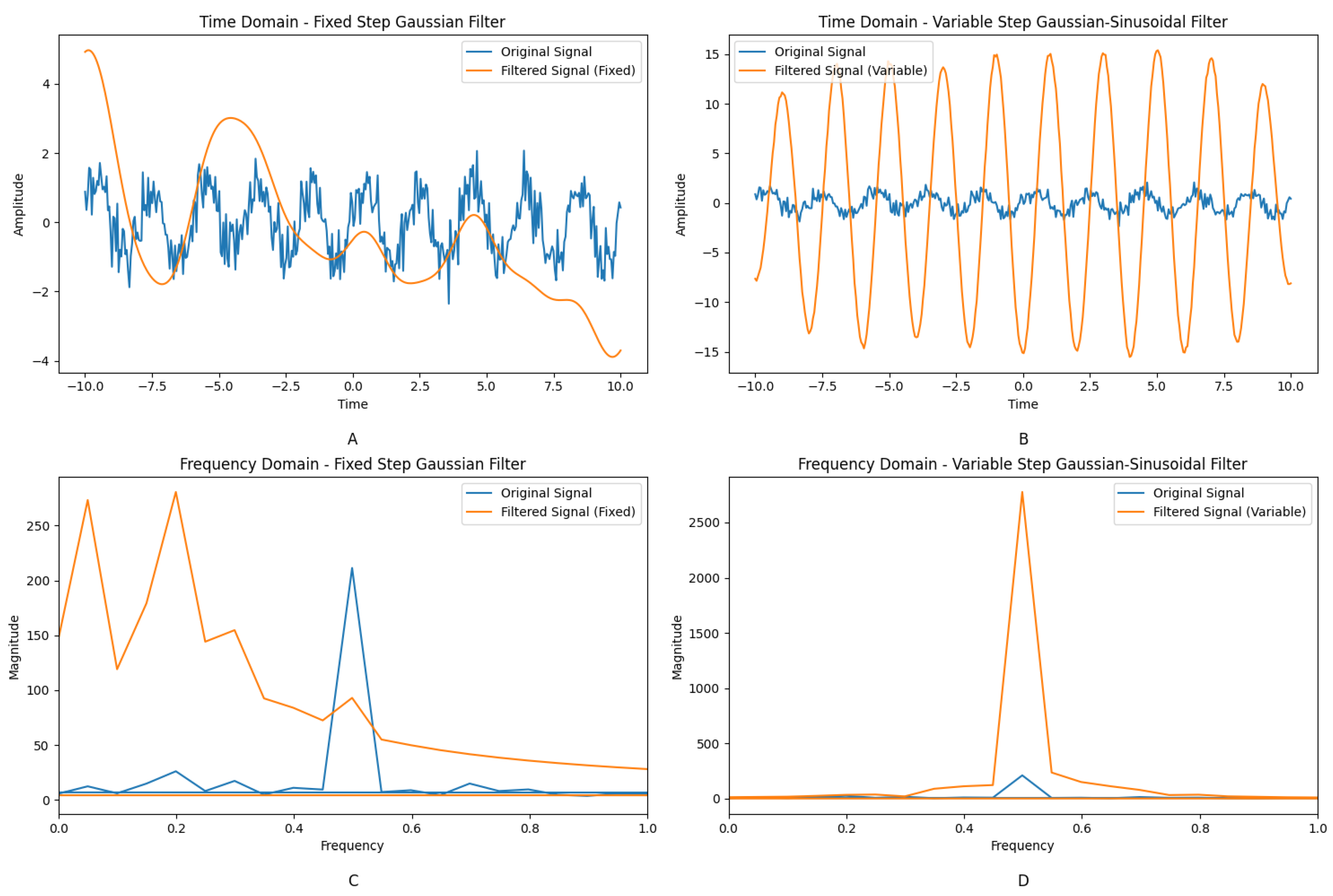
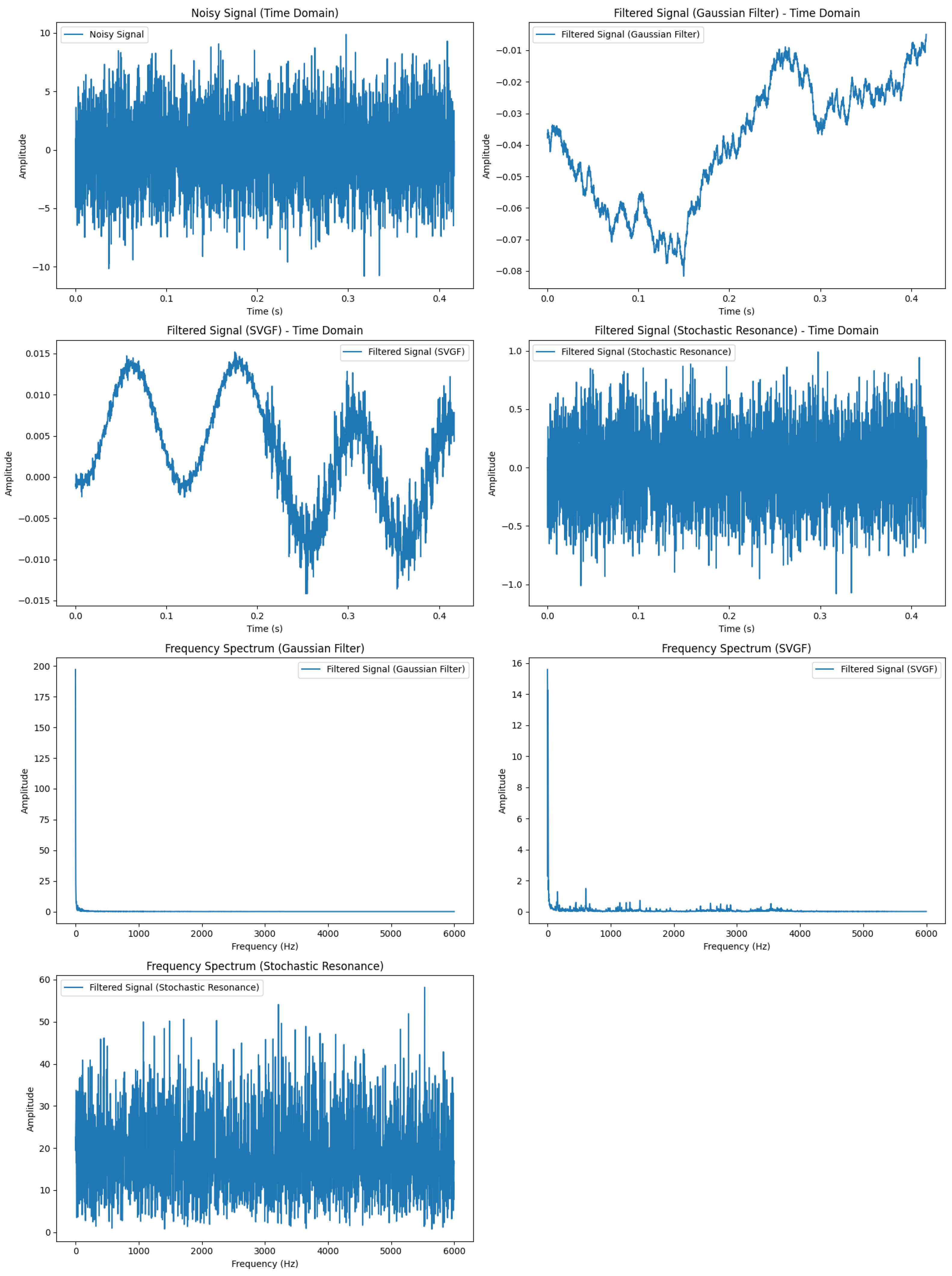
4.3.1. Time Domain Analysis
- The Gaussian filter reduces noise, but the signal remains unclear, indicating its limitations in high-noise environments.
- The SVGF method shows a significant noise reduction effect, with signal features clearly visible, preserving the original signal better than the Gaussian filter
- Stochastic resonance reduces noise, but signal features are still not distinct, demonstrating its limited performance in high-noise environments.
4.3.2. Frequency Domain Analysis
- Stochastic resonance reduces noise, but signal features are still not distinct, demonstrating its limited performance in high-noise environments.
- The SVGF method shows significant noise reduction, making target signal frequencies more prominent, with better frequency selectivity through its adaptive and combined filtering approach.
- Stochastic resonance reduces noise, but target signal frequencies are still partially covered, showing its limitations compared to SVGF
5. Conclusions
- 1.
- Adaptive Filtering: The variable-step size allows for adaptive adjustments to filter parameters, ensuring optimal performance across different noise levels and signal conditions.
- 2.
- Enhanced Frequency Selection: The rotating coordinate transformation enables precise frequency selection, isolating desired signal components from noise.
- 3.
- Improved Signal Integrity: The combination of Gaussian and sinusoidal filtering mechanisms ensures that essential signal characteristics are preserved, even in high-noise environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martínez, J.P.; Almeida, R.; Olmos, S.; Rocha, A.P.; Laguna, P. A Wavelet-Based ECG Delineator: Evaluation on Standard Databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.D.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Self-Adaptive Noise Cancellation Technique. Mech. Syst. Signal Process. 2005, 19, 897–913. [Google Scholar]
- Antoni, J. The Spectral Kurtosis: A Useful Tool for Characterizing Non-Stationary Signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Z.; Zhong, S. A New Chaotic System and Its Application to Signal De-Noising. Chaos, Solitons Fractals 2017, 105, 143–152. [Google Scholar]
- Zhang, Z.; Yang, X. Adaptive Gaussian Filtering for Signal Denoising. IEEE Trans. Signal Process. 2019, 67, 1231–1243. [Google Scholar]
- Mäkitalo, M.; Foi, A. Optimal Inversion of the Generalized Anscombe Transformation for Poisson-Gaussian Noise. IEEE Trans. Image Process. 2013, 22, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, W.Z. Adaptive Filtering Techniques for Weak Signal Detection in High Noise Environments. IEEE Trans. Signal Process. 1997, 45, 2468–2477. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Bellanger, M.G. Digital Signal Processing: Principles and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Li, X.M.; Zhou, J.F.; Chen, W.J. Detection of Bearing Faults Using the Ensemble Empirical Mode Decomposition Method. Mech. Syst. Signal Process. 2011, 25, 2573–2587. [Google Scholar]
- Benzi, R.; Parisi, G.; Vulpiani, A. Stochastic Resonance in Climatic Change. Tellus 1982, 34, 10–16. [Google Scholar] [CrossRef]
- Hou, X.; Huang, W.; Jing, Z. Stochastic Resonance for Signal Detection in the Presence of Colored Noise. IEEE Trans. Instrum. Meas. 2007, 56, 1458–1466. [Google Scholar]
- McNamara, B.; Wiesenfeld, K. Theory of Stochastic Resonance. Phys. Rev. A 1989, 39, 4854–4869. [Google Scholar] [CrossRef] [PubMed]
- Barbini, L.; Cole, M.O.T.; Hillis, A.J.; du Bois, J.L. Weak Signal Detection Based on Two Dimensional Stochastic Resonance. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 2147–2151. [Google Scholar]
- Liu, C.; Xie, L.; Wang, D.; Zhou, G.; Zhou, Q.; Miao, Q. Application of Stochastic Resonance in Bearing Fault Diagnosis. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangjiajie, China, 24–27 August 2014; pp. 223–228. [Google Scholar]
- Jiang, S.Y.; Yu, F.; Chen, K.Y.; Chen, E. Application of Stochastic Resonance Technology in Underwater Acoustic Weak Signal Detection. In Proceedings of the OCEANS 2016—Shanghai Conference, Shanghai, China, 10–13 April 2016; pp. 1–5. [Google Scholar]
- Liu, X.; Wang, Y.; Li, J. Enhancement of Weak Signals Using Combined Stochastic Resonance and Chaotic Systems. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3881–3889. [Google Scholar]
- Ribeiro, M.I.; de Freitas, M.V.; Marques de Sá, J.P. Detection of Weak Signals in Chaotic Environments Using Wavelets. IEEE Trans. Signal Process. 2005, 53, 2950–2961. [Google Scholar]
- Gruber, F.K.; Ziegler, J.F. Noise Reduction in Nonlinear Systems: A Chaotic Approach. Chaos 2007, 17, 023109. [Google Scholar]
- Parisi, G.; Vulpiani, A. Stochastic Resonance: Theory and Experiments. J. Stat. Phys. 1991, 63, 907–915. [Google Scholar]
- Chen, L.Y.; Liu, P.S. Wavelet-Based Techniques for Fault Detection in Mechanical Systems. Mech. Syst. Signal Process. 2001, 15, 1191–1211. [Google Scholar]
- Bai, E.W.; Douglas, S.C. A Chaotic-Based Filter for Weak Signal Detection. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 997–1005. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Brown, R.H.; Strand, J.A. Noise Reduction and Signal Detection Using a Neural Network Approach. IEEE Trans. Neural Netw. 2002, 13, 216–224. [Google Scholar]
- Benedetto, J.J.; Pfander, G. Wavelet Transform and Time-Frequency Analysis for Signal Detection. IEEE Trans. Signal Process. 1994, 42, 1349–1361. [Google Scholar]
- Reed, G.T.; Liu, A.P. Stochastic Resonance in Fiber Optic Systems. IEEE Photonics Technol. Lett. 2002, 14, 1422–1424. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]





| Bearing Condition | Load (HP) | Samples | Fault Diameter (Inches) | Data Length (Samples) |
|---|---|---|---|---|
| Normal | 0, 1, 2, 3 | 4 sets | N/A | 120,000 |
| Inner Race Fault | 0, 1, 2, 3 | 4 sets | 0.007 | 120,000 |
| Outer Race Fault | 0, 1, 2, 3 | 4 sets | 0.007 | 120,000 |
| Ball Fault | 0, 1, 2, 3 | 4 sets | 0.007 | 120,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, H.; Hao, R.; Zhang, J. Weak Signal Extraction in Noise Using Variable-Step Gaussian-Sinusiodal Filter. Machines 2024, 12, 601. https://doi.org/10.3390/machines12090601
Lou H, Hao R, Zhang J. Weak Signal Extraction in Noise Using Variable-Step Gaussian-Sinusiodal Filter. Machines. 2024; 12(9):601. https://doi.org/10.3390/machines12090601
Chicago/Turabian StyleLou, Haiyang, Rujiang Hao, and Jianchao Zhang. 2024. "Weak Signal Extraction in Noise Using Variable-Step Gaussian-Sinusiodal Filter" Machines 12, no. 9: 601. https://doi.org/10.3390/machines12090601
APA StyleLou, H., Hao, R., & Zhang, J. (2024). Weak Signal Extraction in Noise Using Variable-Step Gaussian-Sinusiodal Filter. Machines, 12(9), 601. https://doi.org/10.3390/machines12090601






