Comparison of Electromagnetic Performance in Interior Permanent Magnet Motors with Different Central and Bilateral Bridges
Abstract
1. Introduction
2. Motor Specification and Mechanical Stress Analysis
2.1. Motor Specification
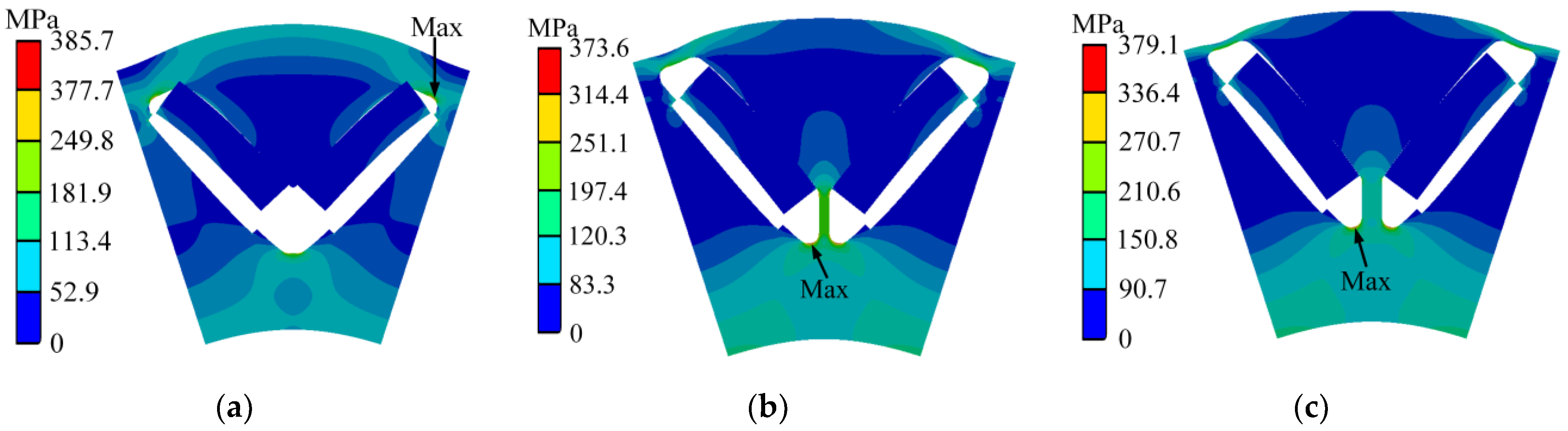
2.2. Mechanical Stress Analysis
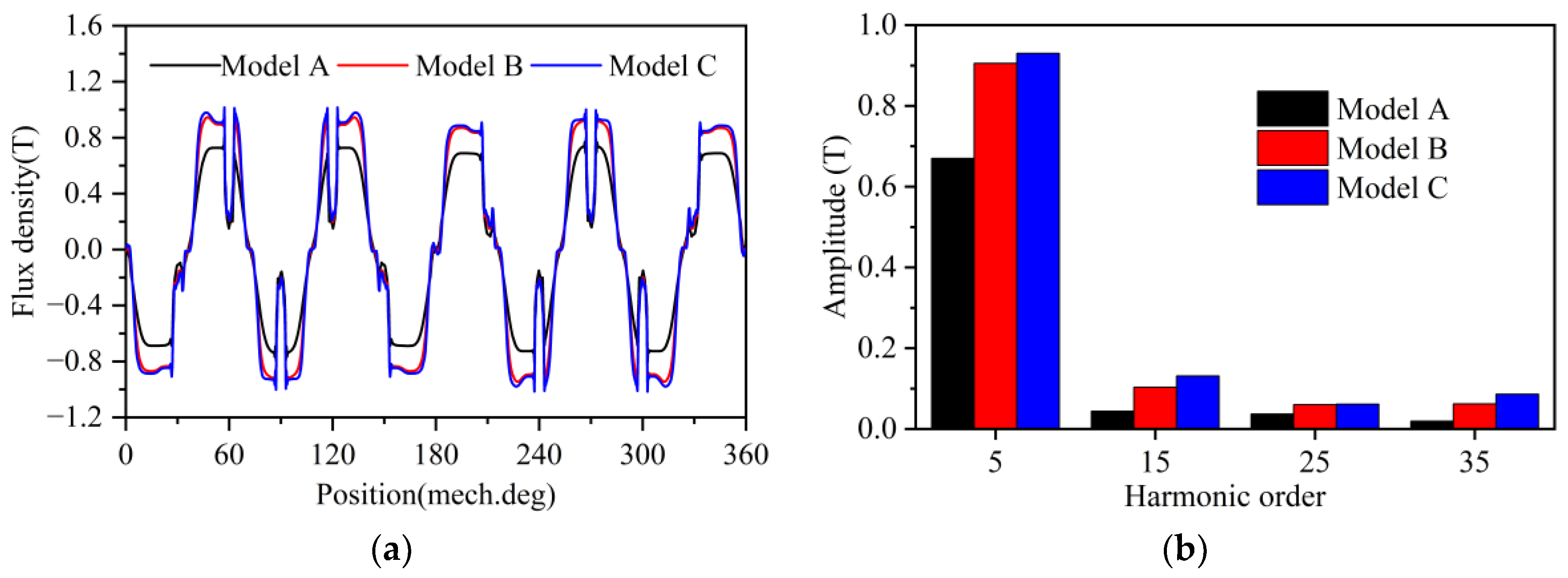
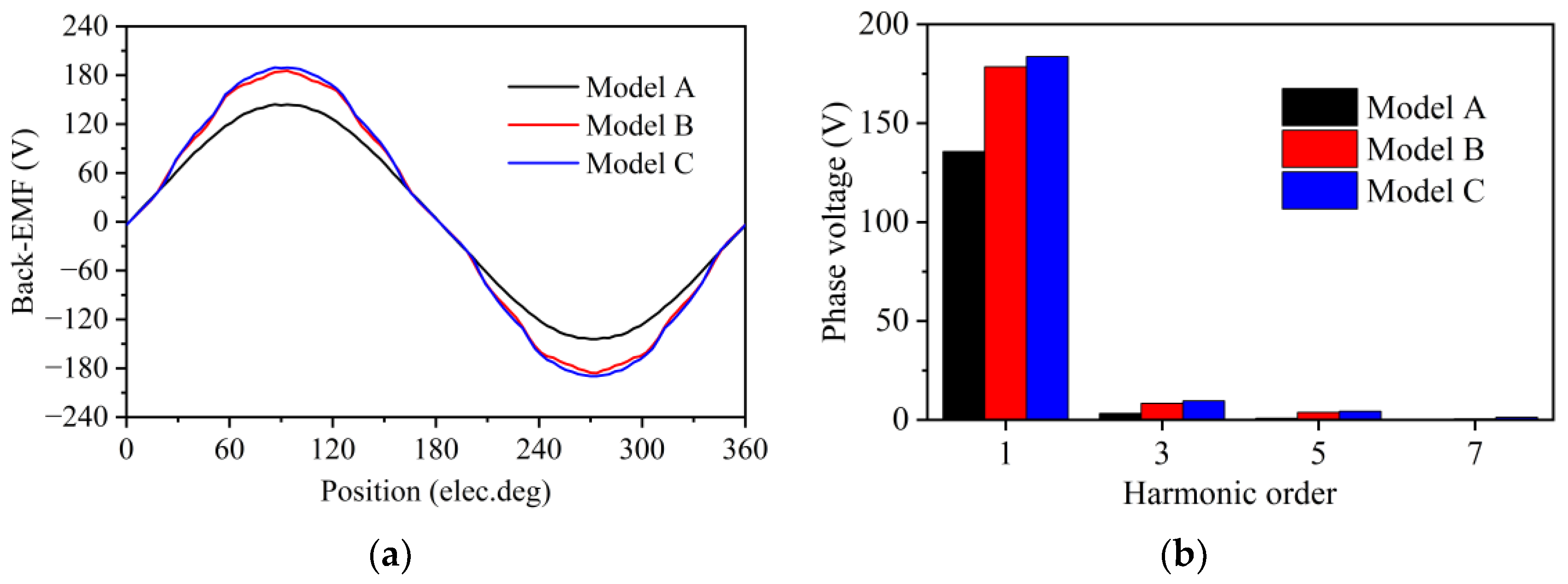
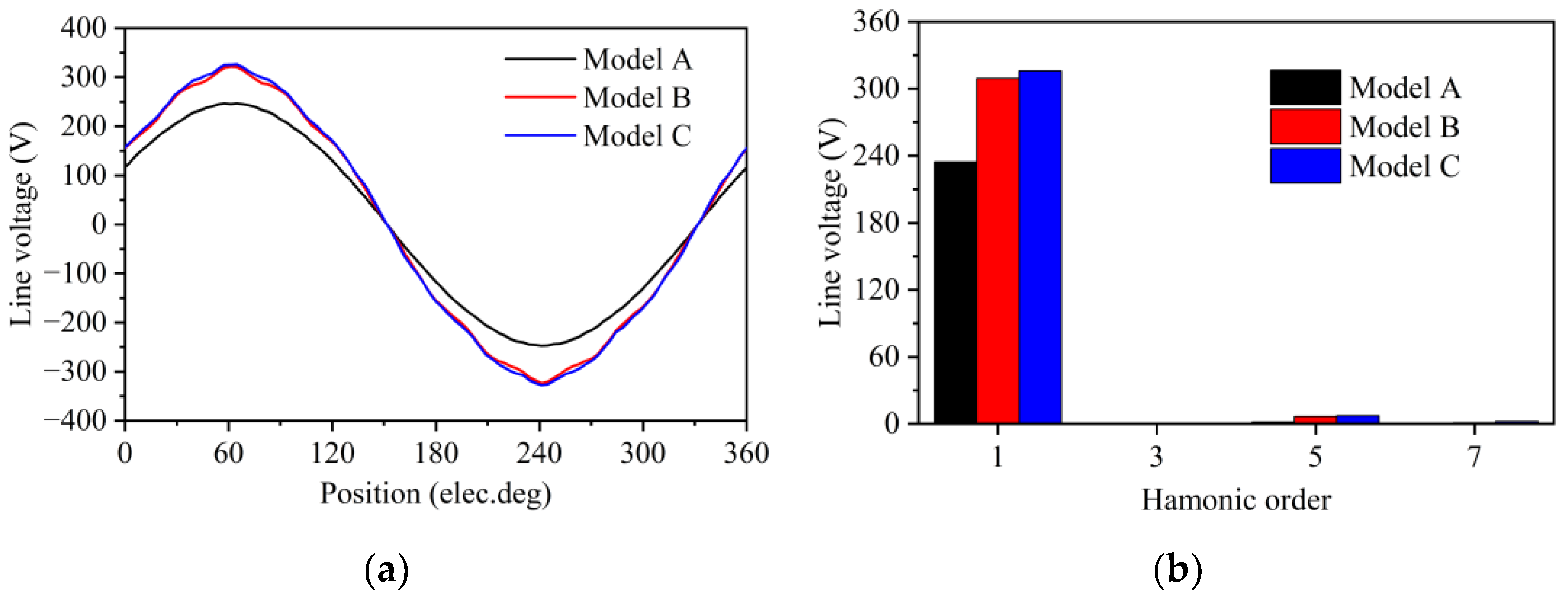
3. Comparison of No-Load Performance
4. Comparison of Load Performance
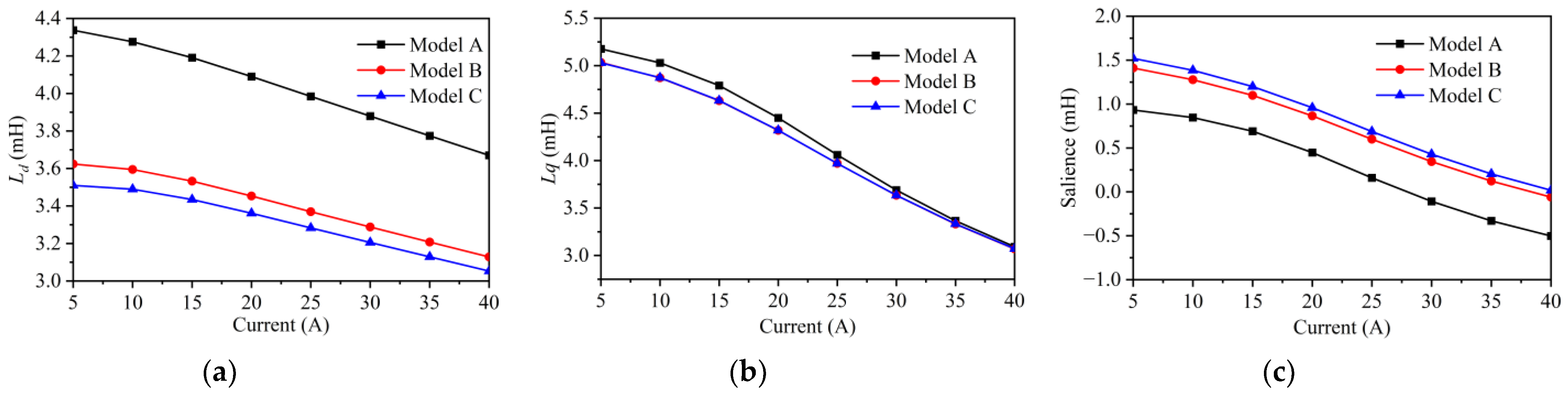
4.1. Inductance and Salience
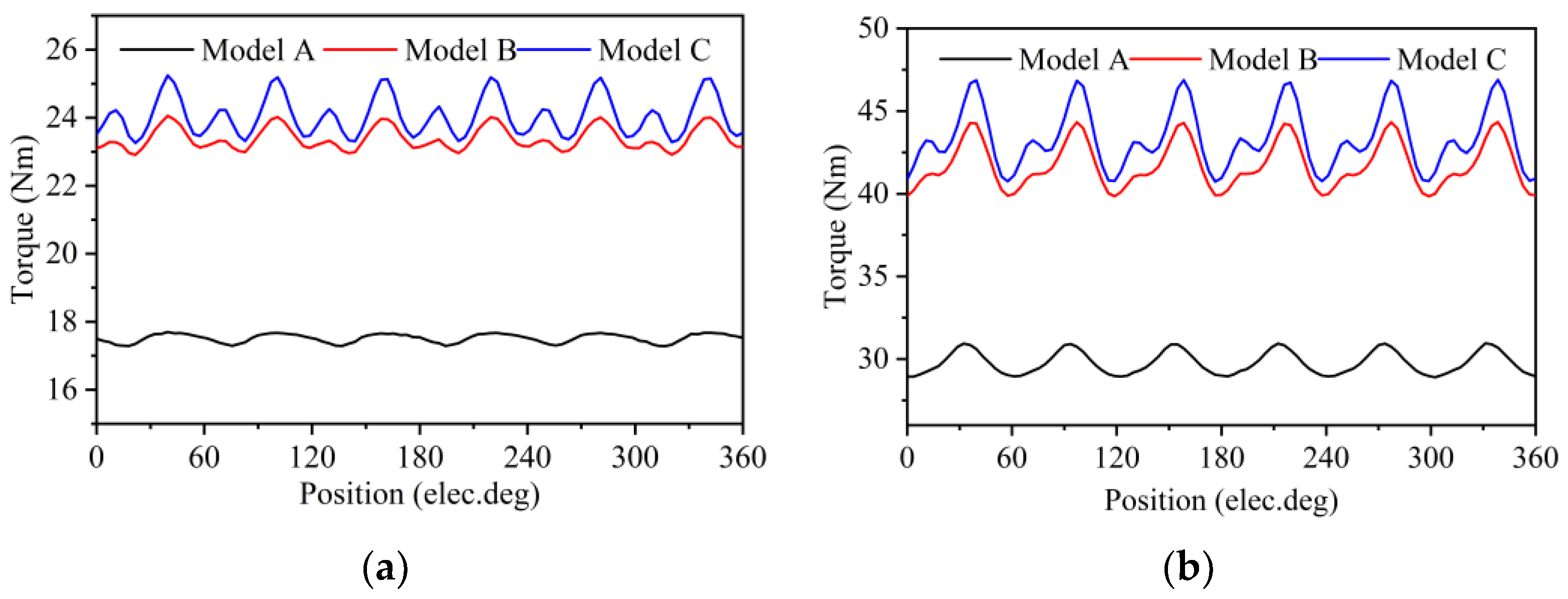
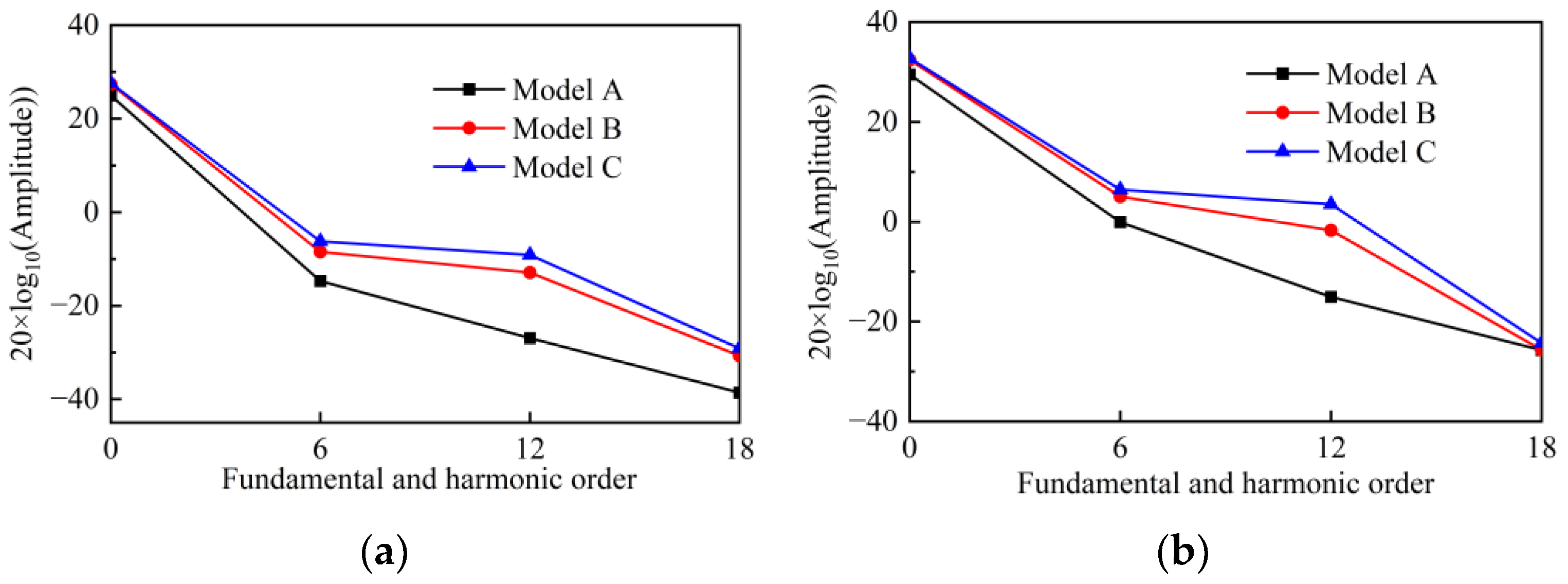
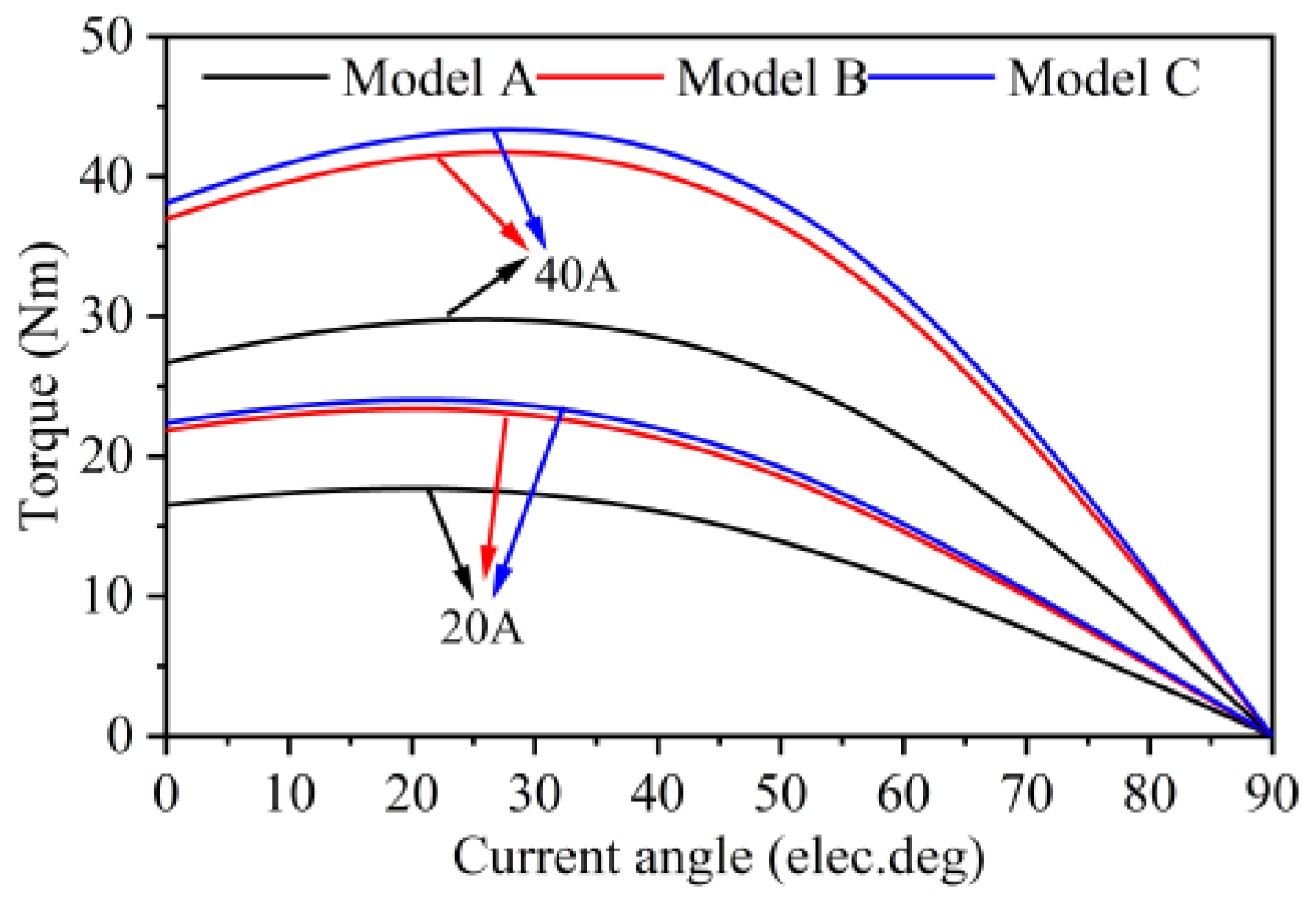
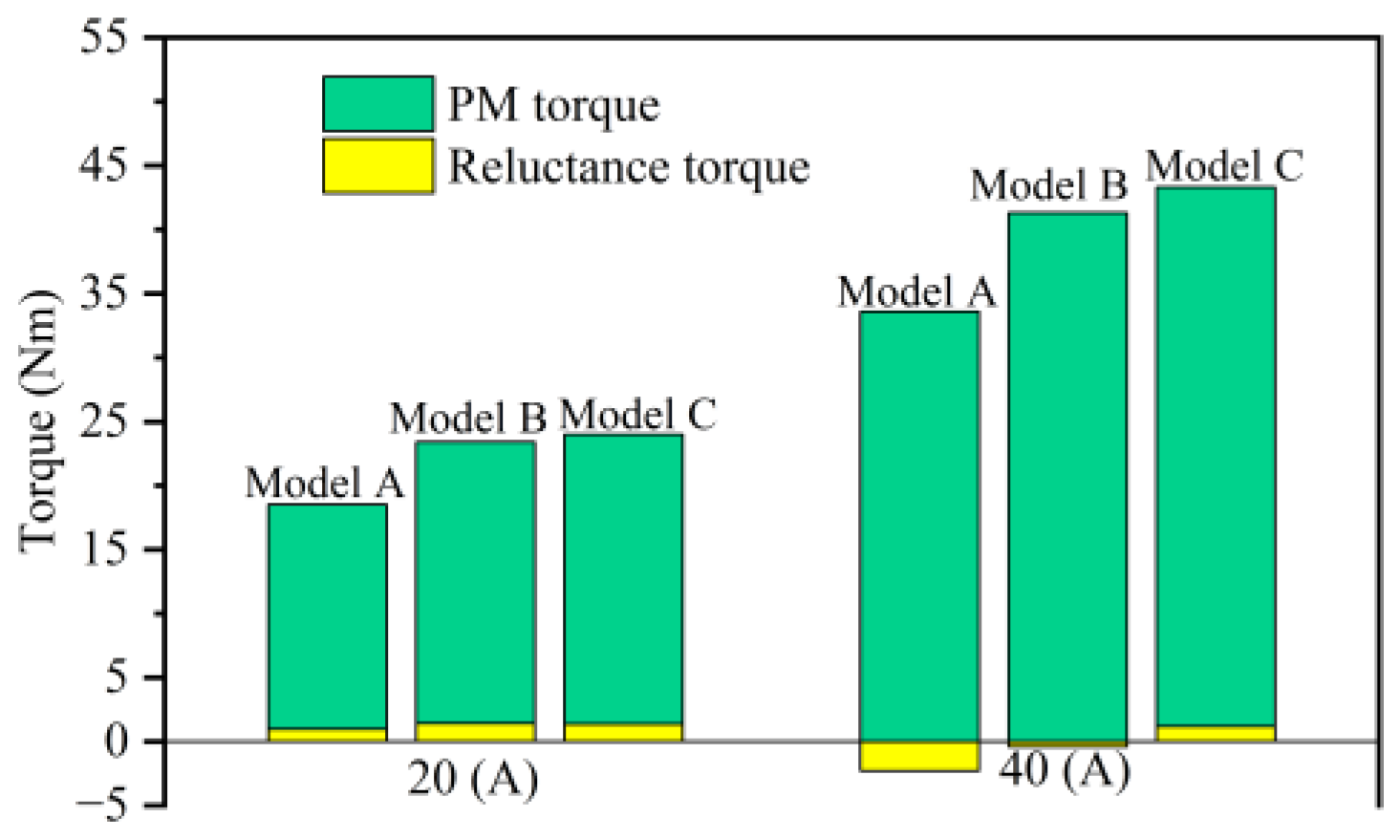
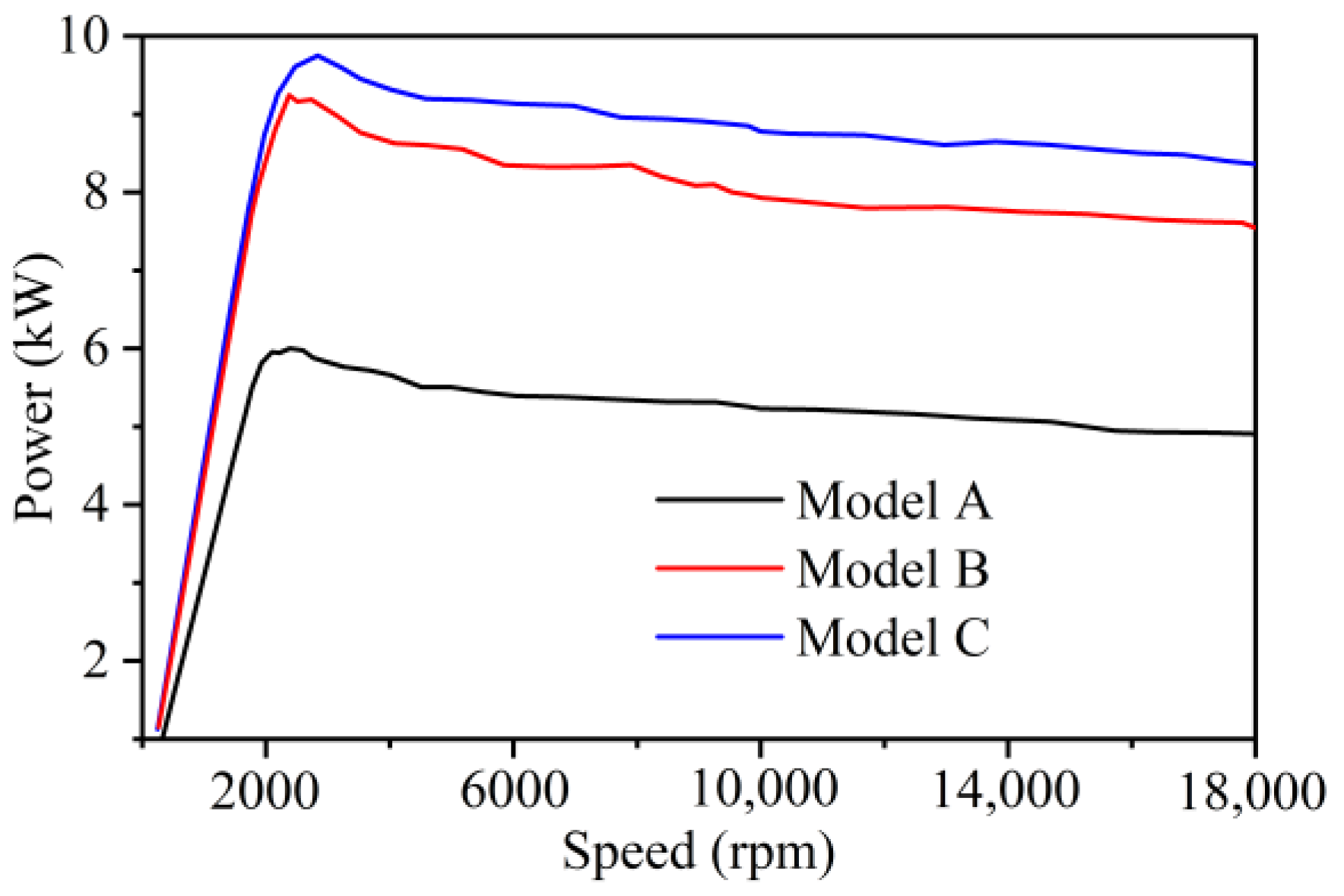
4.2. Torque and Power
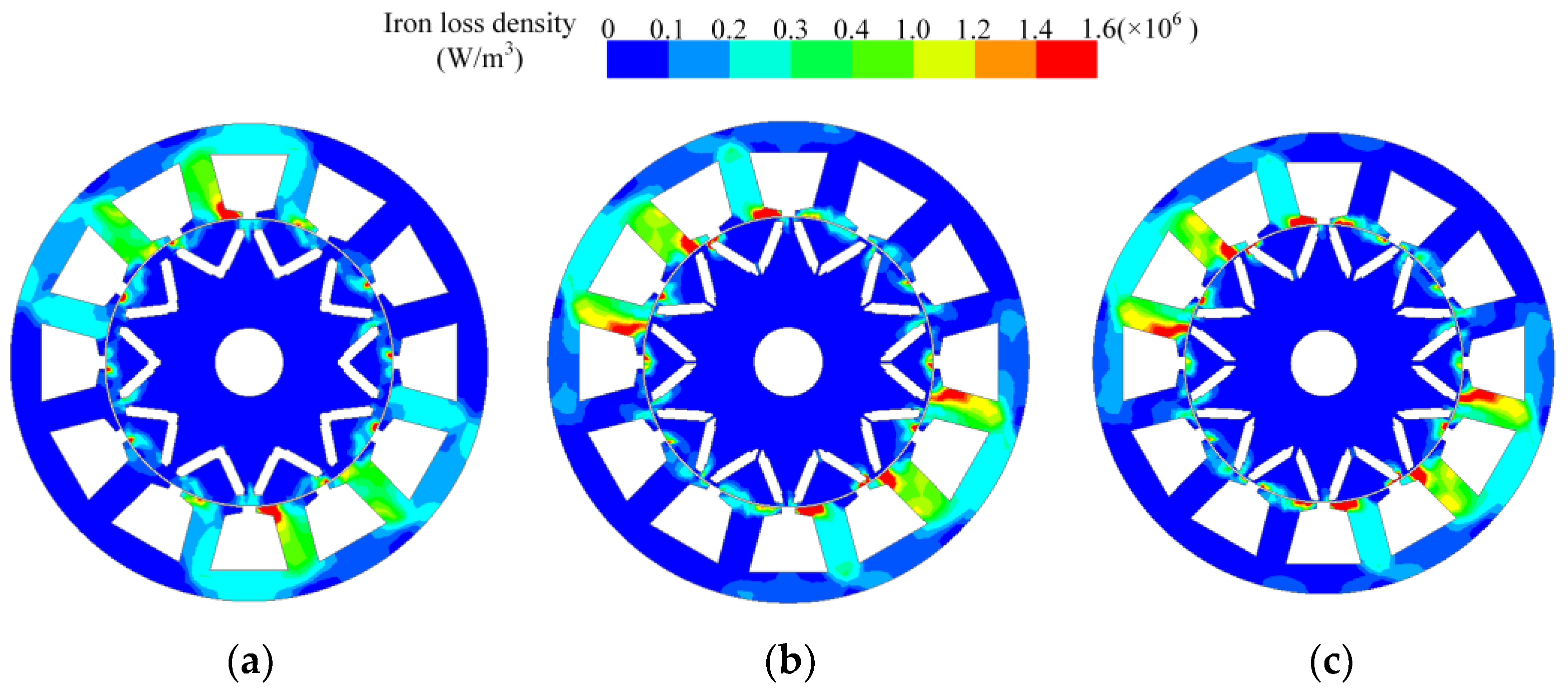
4.3. Loss and Efficiency
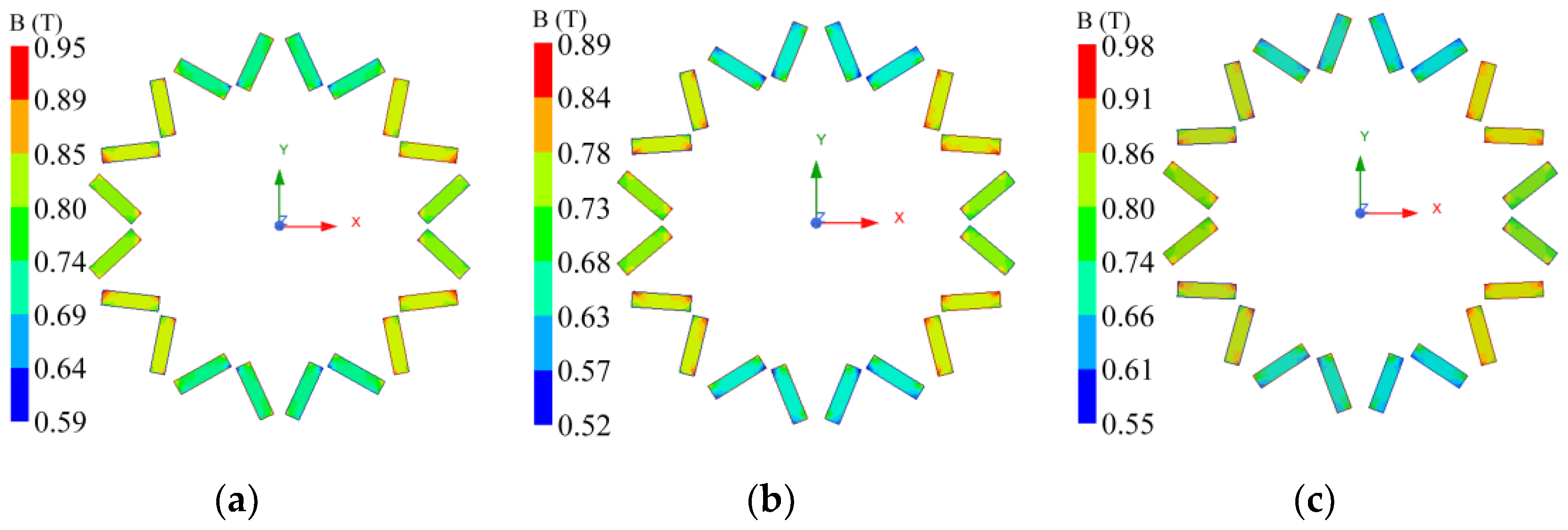
4.4. Demagnetization Analysis
4.4.1. Demagnetization Analysis
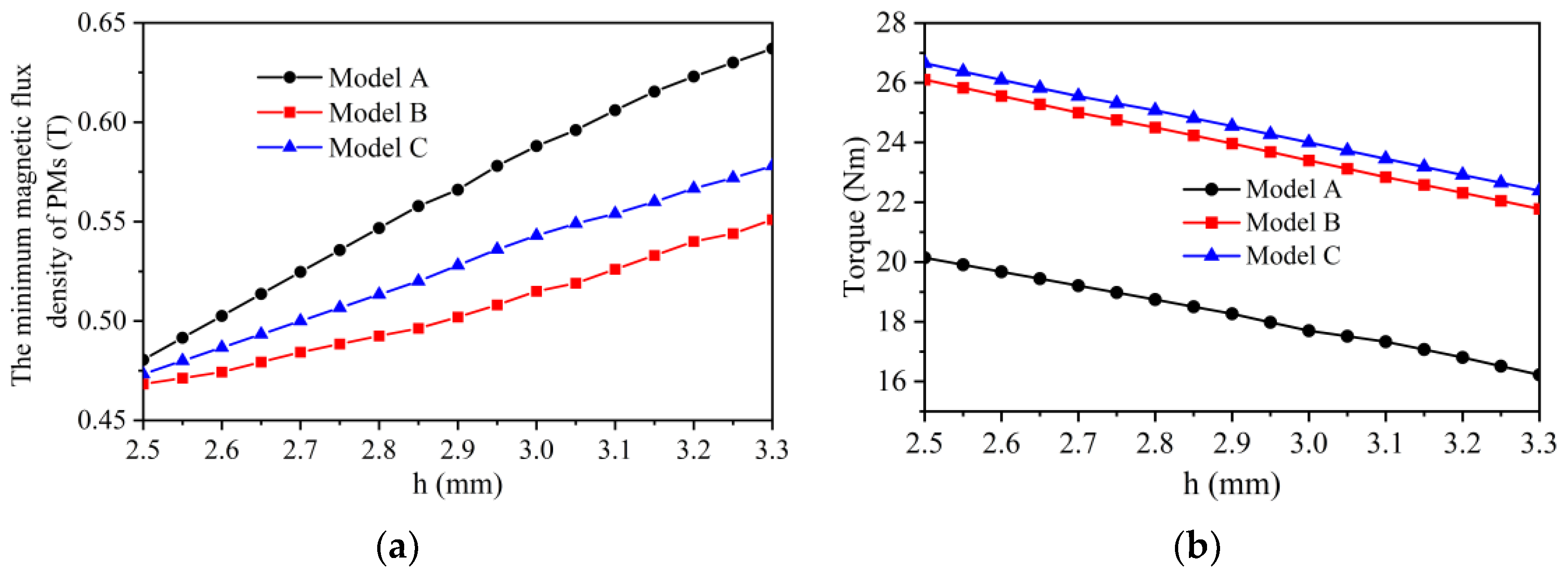
4.4.2. Analysis of the Impact of PM Dimensions on Demagnetization and Torque
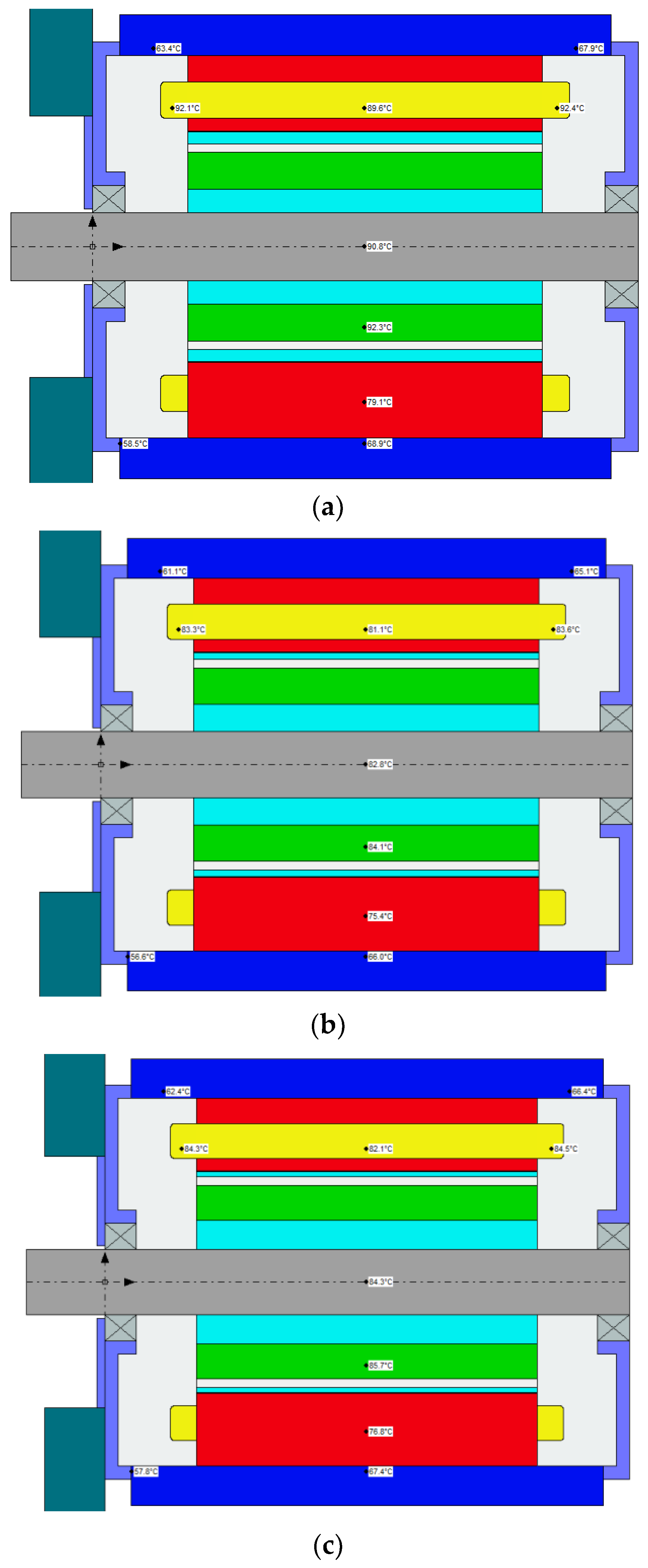
4.5. Thermal Analysis
5. Conclusions
- (1)
- Due to the absence of a central bridge, Model A requires a very thick bilateral bridge to ensure rotor operation, resulting in a significant increase in magnetic flux leakage and causing Model A to not meet torque requirements.
- (2)
- The total bridge width of Model B and Model C is significantly smaller than that of Model A, resulting in a reduction in inductance for both Model B and Model C. However, the decrease in the Ld compared to Lq is more significant for Model B and Model C, leading to an increased salience for both. Among them, Model C has the smallest Ld, maximizing its salience, which results in Model C having the highest reluctance torque.
- (3)
- Model B and Model C, both equipped with a central bridge configuration, meet the torque design requirements. However, the narrow bilateral bridge design of Model C results in the maximum air-gap flux density, leading to Model C exhibiting the highest torque. Nonetheless, due to the higher THD of Model C, torque ripple also increases.
- (4)
- At rated current, the losses of the three models follow the order Model C > Model B > Model A. However, due to the lower losses of Model B, it has the highest efficiency.
- (5)
- By adjusting the thickness of the PMs to ensure uniform demagnetization conditions across all three models, Model C maintains the highest torque, while Model A continues to exhibit the lowest torque.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kubik, A.; Turoń, K.; Folęga, P.; Chen, F. CO2 Emissions—Evidence from internal combustion and electric engine vehicles from car-sharing systems. Energies 2023, 16, 2185. [Google Scholar] [CrossRef]
- Husain, I.; Ozpineci, B.; Islam, M.S.; Gurpinar, E.; Su, G.-J.; Yu, W.; Chowdhury, S.; Xue, L.; Rahman, D.; Sahu, R. Electric drive technology trends, challenges, and opportunities for future electric vehicles. Proc. IEEE 2021, 109, 1039–1059. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T.; Lee, C.H.T.; Song, Z. A critical review of advanced electric machines and control strategies for electric vehicles. Proc. IEEE 2020, 109, 1004–1028. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Yang, Z.; Li, G. Coordinating flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: A bi-level approach. IEEE Trans. Sustain. Energy 2021, 12, 2321–2331. [Google Scholar] [CrossRef]
- Palangar, M.F.; Soong, W.L.; Bianchi, N.; Wang, R.-J. Design and optimization techniques in performance improvement of line-start permanent magnet synchronous motors: A review. IEEE Trans. Magn. 2021, 57, 900214. [Google Scholar] [CrossRef]
- Dambrauskas, K.; Vanagas, J.; Zimnickas, T.; Kalvaitis, A.; Ažubalis, M. A method for efficiency determination of permanent magnet synchronous motor. Energies 2020, 13, 1004. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.; Liu, H.; Ning, F.; Hong, X.; Du, J.; Yu, M. Modal analysis and structure optimization of permanent magnet synchronous motor. IEEE Access 2020, 8, 151856–151865. [Google Scholar] [CrossRef]
- Deng, W.; Zuo, S.; Chen, W.; Qian, Z.; Qian, C.; Cao, W. Comparison of eccentricity impact on electromagnetic forces in internal-and external-rotor permanent magnet synchronous motors. IEEE Trans. Transp. Electrif. 2021, 8, 1242–1254. [Google Scholar] [CrossRef]
- Yoon, K.Y.; Baek, S.W. Performance improvement of concentrated-flux type IPM PMSM motor with flared-shape magnet arrangement. Appl. Sci. 2020, 10, 6061. [Google Scholar] [CrossRef]
- Du, G.; Li, N.; Zhou, Q.; Gao, W.; Wang, L.; Pu, T. Multi-Physics Comparison of surface-mounted and interior permanent magnet synchronous motor for high-speed applications. Machines 2022, 10, 700. [Google Scholar] [CrossRef]
- Kamiev, K.; Montonen, J.; Ragavendra, M.P.; Pyrhonen, J.; Tapia, J.A.; Niemela, M. Design principles of permanent magnet synchronous machines for parallel hybrid or traction applications. IEEE Trans. Ind. Electron. 2012, 60, 4881–4890. [Google Scholar] [CrossRef]
- El-Refaie, A.M. Fractional-slot concentrated-windings synchronous permanent magnet machines: Opportunities and challenges. IEEE Trans. Ind. Electron. 2009, 57, 107–121. [Google Scholar] [CrossRef]
- Sarlioglu, B.; Morris, C.T.; Han, D.; Li, S. Driving toward accessibility: A review of technological improvements for electric ma-chines, power electronics, and batteries for electric and hybrid vehicles. IEEE Ind. Appl. Mag. 2016, 23, 14–25. [Google Scholar] [CrossRef]
- Binder, J.; Silvagni, M.; Ferrari, S.; Deusinger, B.; Tonoli, A.; Pellegrino, G. High-speed IPM motors with rotor sleeve: Structural design and performance evaluation. In Proceedings of the 2023 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Newcastle upon Tyne, UK, 13–14 April 2023; pp. 1–6. [Google Scholar]
- Cao, R.; Mi, C.; Cheng, M. Quantitative comparison of flux-switching permanent-magnet motors with interior permanent magnet motor for EV, HEV, and PHEV applications. IEEE Trans. Magn. 2012, 48, 2374–2384. [Google Scholar] [CrossRef]
- Goss, J.; Popescu, M.; Staton, D. A comparison of an interior permanent magnet and copper rotor induction motor in a hybrid electric vehicle application. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 220–225. [Google Scholar]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Analysis and design optimization of a permanent magnet synchronous motor for a campus patrol electric vehicle. IEEE Trans. Veh. Technol. 2019, 68, 10535–10544. [Google Scholar] [CrossRef]
- Varaticeanu, B.; Minciunescu, P.; Matei, S. Performance evaluation of permanent magnet assisted synchronous reluctance motor for micro electric vehicle. In Advanced Microsystems for Automotive Applications 2015: Smart Systems for Green and Automated Driving; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 173–186. [Google Scholar]
- Agamloh, E.; Von Jouanne, A.; Yokochi, A. An overview of electric machine trends in modern electric vehicles. Machines 2020, 8, 20. [Google Scholar] [CrossRef]
- Shao, B.; Cai, W.; Xie, Y.; Yang, C.; Guo, G.; Tang, Y. Design of a novel rib for improving the mechanical and electromagnetic performance of IPMSMs. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 464–467. [Google Scholar]
- Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the performances and parameters of interior PMSM used for electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
- Song, C.H.; Kim, D.H.; Kim, K.C. Design of a novel IPMSM bridge for torque ripple reduction. IEEE Trans. Magn. 2020, 57, 8201004. [Google Scholar] [CrossRef]
- Jin, C.S.; Jung, D.S.; Kim, K.C.; Chun, Y.-D.; Lee, H.-W.; Lee, J. A study on improvement magnetic torque characteristics of IPMSM for direct drive washing machine. IEEE Trans. Magn. 2009, 45, 2811–2814. [Google Scholar]
- Chen, H.; Lee, C.H.T. Parametric sensitivity analysis and design optimization of an interior permanent magnet synchronous motor. IEEE Access 2019, 7, 159918–159929. [Google Scholar] [CrossRef]
- Binder, A.; Schneider, T.; Klohr, M. Fixation of buried and surface-mounted magnets in high-speed permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2006, 42, 1031–1037. [Google Scholar] [CrossRef]
- Chai, F.; Li, Y.; Liang, P.; Pei, Y. Calculation of the maximum mechanical stress on the rotor of interior permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2016, 63, 3420–3432. [Google Scholar] [CrossRef]
- Chu, G.; Dutta, R.; Rahman, M.F.; Lovatt, H.; Sarlioglu, B. Analytical calculation of maximum mechanical stress on the rotor of interior permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2019, 56, 1321–1331. [Google Scholar] [CrossRef]
- Barcaro, M.; Meneghetti, G.; Bianchi, N. Structural analysis of the interior PM rotor considering both static and fatigue loading. IEEE Trans. Ind. Appl. 2013, 50, 253–260. [Google Scholar] [CrossRef]
- Monissen, C.; Arslan, M.E.; Krings, A.; Andert, J. Mechanical stress in rotors of permanent magnet machines—Comparison of different determination methods. Energies 2022, 15, 9169. [Google Scholar] [CrossRef]
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance comparison between surface-mounted and interior PM motor drives for electric vehicle application. IEEE Trans. Ind. Electron. 2011, 59, 803–811. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kumagai, M. Torque analysis of interior permanent-magnet synchronous motors by considering cross-magnetization: Variation in torque components with permanent-magnet configurations. IEEE Trans. Ind. Electron. 2013, 61, 3192–3201. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
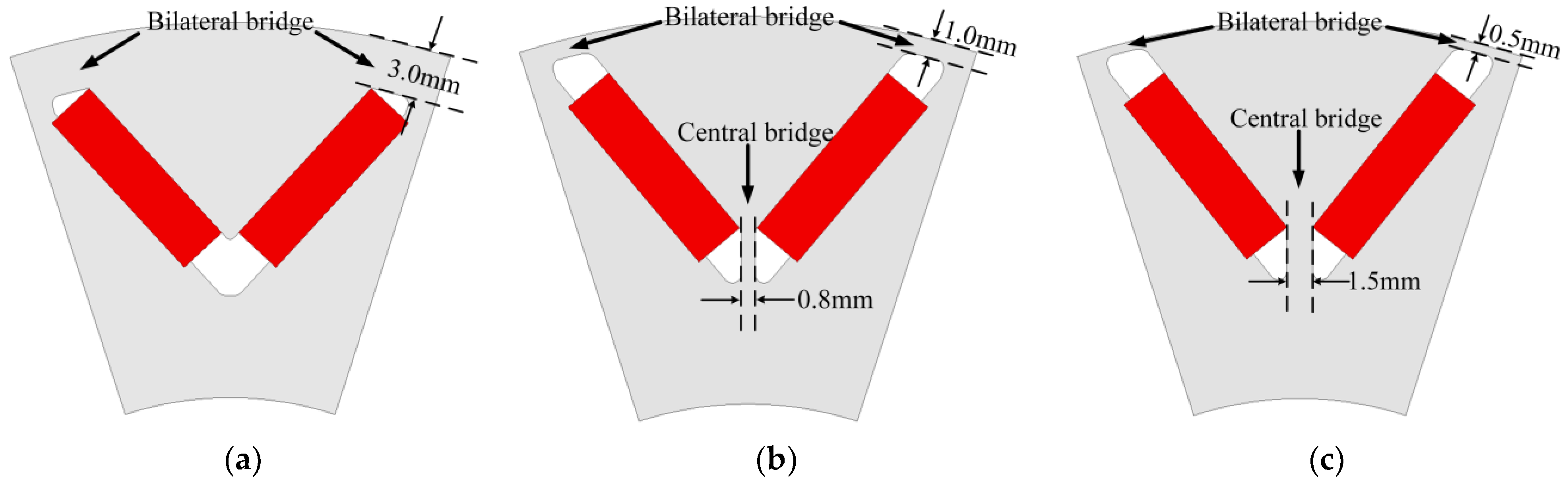

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Slot number | 12 | pole number | 10 |
| Turns per coil | 60 | Outer stator diameter (mm) | 140 |
| Rated speed (rpm) | 3000 | Axial length (mm) | 130 |
| Rated torque (Nm) | 20 | Air gap (mm) | 0.5 |
| Max speed (rpm) | 18,000 | DC voltage (V) | 350 |
| PM remanence (T) | 1.28 | PM coercivity (kA/m) | 1023 |
| Parameters | Steel | Magnet |
|---|---|---|
| Young’s modulus (GPa) | 210 | 200 |
| Density (kg/m3) | 7600 | 8200 |
| Poisson’s ratio | 0.27 | 0.3 |
| Yield strength (MPa) | 390 | - |
| Parameters | Model A | Model B | Model C |
|---|---|---|---|
| 6th (Nm) | 0.184 | 0.377 | 0.488 |
| 12th (Nm) | 0.0451 | 0.226 | 0.641 |
| 18th (Nm) | 0.012 | 0.029 | 0.035 |
| Tave (Nm) | 17.7 | 23.4 | 24.0 |
| ΔTp-p (Nm) | 0.430 | 1.15 | 1.99 |
| Tripple (%) | 2.43 | 4.91 | 8.29 |
| Parameters | Model A | Model B | Model C |
|---|---|---|---|
| 6th (Nm) | 0.993 | 1.79 | 2.10 |
| 12th (Nm) | 0.18 | 0.82 | 1.49 |
| 18th (Nm) | 0.051 | 0.052 | 0.061 |
| Tave (Nm) | 29.8 | 41.8 | 43.4 |
| ΔTp-p (Nm) | 2.03 | 4.49 | 6.17 |
| Tripple (%) | 6.81 | 10.74 | 14.21 |
| Parameters | Model A | Model B | Model C |
|---|---|---|---|
| Stator current (A) | 23.0 | 17.0 | 16.5 |
| Stator iron loss (W) | 220.0 | 243.6 | 250.1 |
| Rotor iron loss (W) | 44.6 | 38.0 | 37.6 |
| PM loss (W) | 6.7 | 4.0 | 3.3 |
| Mechanical loss (W) | 27.5 | 27.5 | 27.5 |
| Copper loss (W) | 187.7 | 137.4 | 133.1 |
| Efficiency (%) | 92.81 | 93.33 | 93.29 |
| Reluctance torque (Nm) | 0.66 | 1.25 | 1.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, B.; Cai, W.; Yang, C. Comparison of Electromagnetic Performance in Interior Permanent Magnet Motors with Different Central and Bilateral Bridges. Machines 2024, 12, 423. https://doi.org/10.3390/machines12060423
Shao B, Cai W, Yang C. Comparison of Electromagnetic Performance in Interior Permanent Magnet Motors with Different Central and Bilateral Bridges. Machines. 2024; 12(6):423. https://doi.org/10.3390/machines12060423
Chicago/Turabian StyleShao, Baicheng, Wei Cai, and Chen Yang. 2024. "Comparison of Electromagnetic Performance in Interior Permanent Magnet Motors with Different Central and Bilateral Bridges" Machines 12, no. 6: 423. https://doi.org/10.3390/machines12060423
APA StyleShao, B., Cai, W., & Yang, C. (2024). Comparison of Electromagnetic Performance in Interior Permanent Magnet Motors with Different Central and Bilateral Bridges. Machines, 12(6), 423. https://doi.org/10.3390/machines12060423






