Application of an Improved Laplacian-of-Gaussian Filter for Bearing Fault Signal Enhancement of Motors
Abstract
1. Introduction
2. Theoretical Basis
LoG Filter Coefficient
3. Simulation
4. Experimental Results
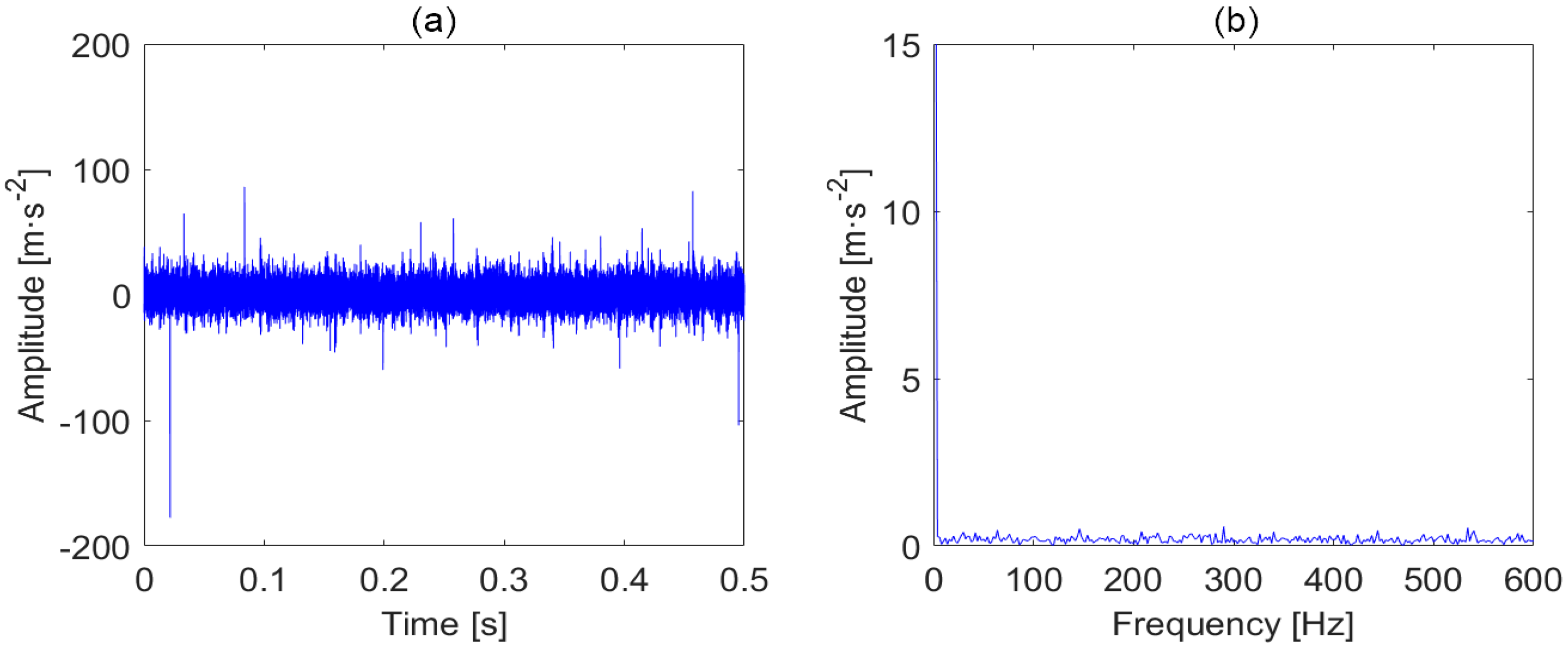
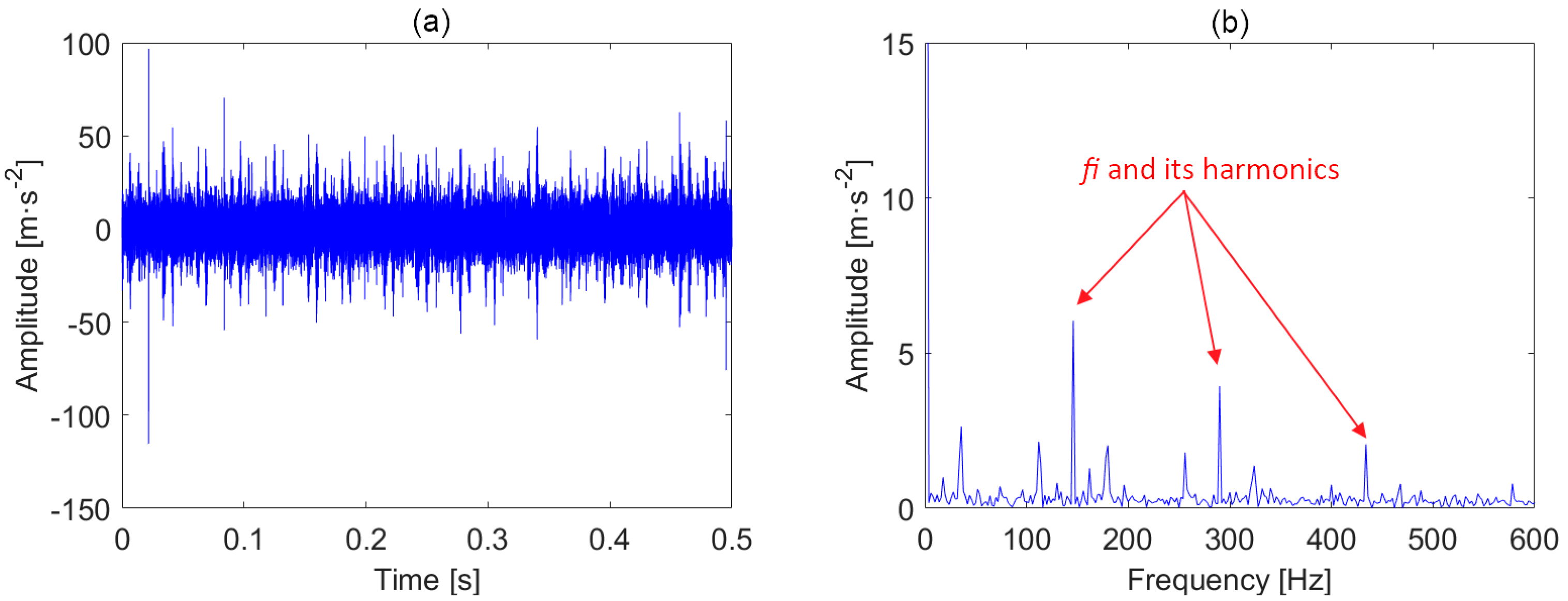
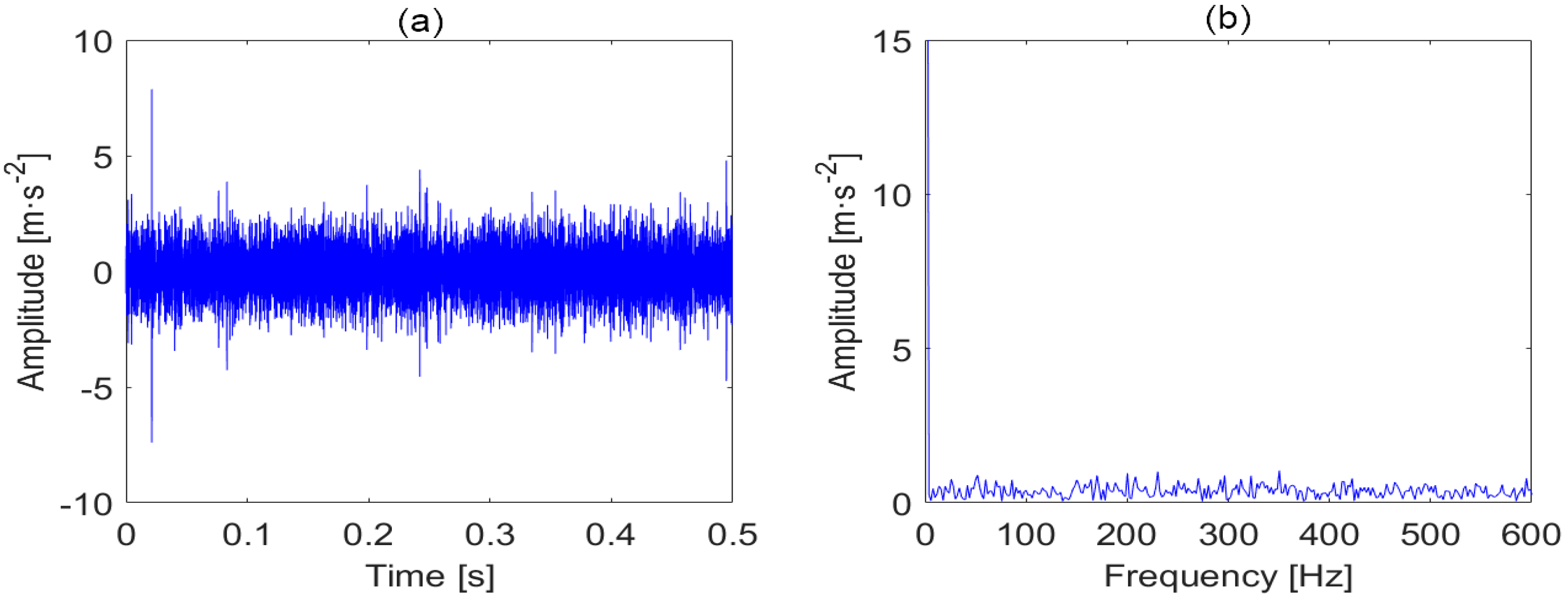
4.1. Case 1: Inner Race Fault Signal Measured from Spectra Quest Motor Fault Simulator
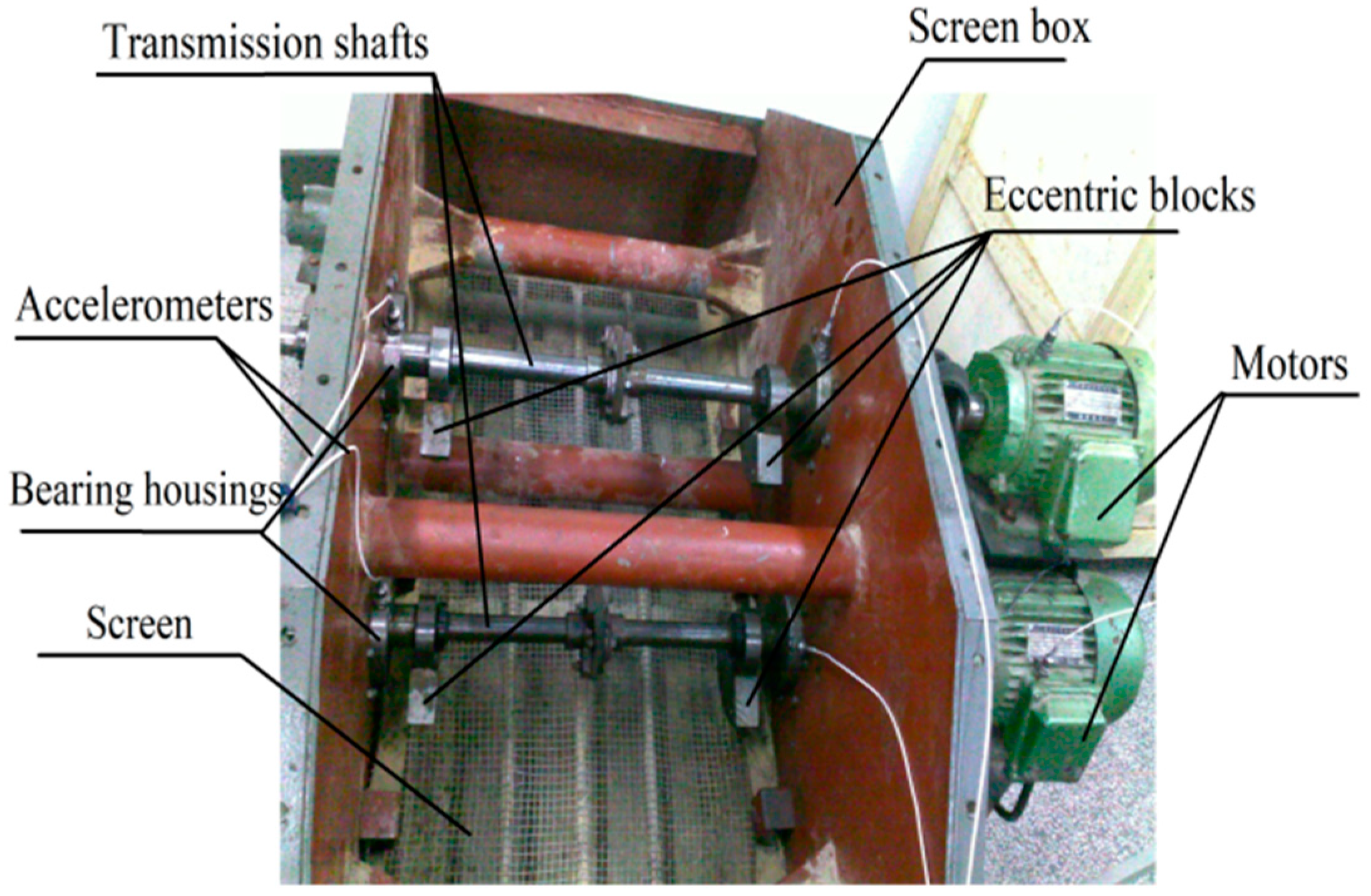
4.2. Case 2: Outer Race Fault Signal Measured from the Motor of a Vibrating Screen
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, C.; Li, J.; Cheng, X. Comprehensive Learning Particle Swarm Optimized Fuzzy Petri Net for Motor-Bearing Fault Diagnosis. Machines 2022, 10, 1022. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Puche-Panadero, R.; Riera-Guasp, M.; Perez-Cruz, J.; Roger-Folch, J.; Pons-Llinares, J.; Climente-Alarcon, V.; Antonino-Daviu, J.A. Application of the Teager-Kaiser Energy Operator to the Fault Diagnosis of Induction Motors. IEEE Trans. Energy Convers. 2013, 28, 1036–1044. [Google Scholar] [CrossRef]
- Liang, T.; Lu, H.; Sun, H. Application of Parameter Optimized Variational Mode Decomposition Method in Fault Feature Extraction of Rolling Bearing. Entropy 2021, 23, 520. [Google Scholar] [CrossRef]
- Zhang, Y.; Shang, L.; Gao, H.; He, Y.; Xu, X.; Chen, Y. A New Method for Diagnosing Motor Bearing Faults Based on Gramian Angular Field Image Coding and Improved CNN-ELM. IEEE Access 2023, 11, 11337–11349. [Google Scholar] [CrossRef]
- Gong, X.; Zhi, Z.; Feng, K.; Du, W.; Wang, T. Improved DCNN Based on Multi-Source Signals for Motor Compound Fault Diagnosis. Machines 2022, 10, 277. [Google Scholar] [CrossRef]
- Zhou, W.; Lu, B.; Habetler, T.G.; Harley, R.G. Incipient Bearing Fault Detection via Motor Stator Current Noise Cancellation Using Wiener Filter. IEEE Trans. Ind. Appl. 2009, 45, 1309–1317. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, M.; Deng, W.; Yang, X. A New Feature Extraction Method Based on EEMD and Multi-Scale Fuzzy Entropy for Motor Bearing. Entropy 2016, 19, 14. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.; Zhao, H.; Yang, X. A Novel Fault Diagnosis Method Based on Integrating Empirical Wavelet Transform and Fuzzy Entropy for Motor Bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Tang, H.; Lu, S.; Qian, G.; Ding, J.; Liu, Y.; Wang, Q. IoT-Based Signal Enhancement and Compression Method for Efficient Motor Bearing Fault Diagnosis. IEEE Sens. J. 2021, 21, 1820–1828. [Google Scholar] [CrossRef]
- Kumar, K.; Shukla, S.; Singh, S.K. Early Detection of Bearing Faults Using Minimum Entropy Deconvolution Adjusted and Zero Frequency Filter. JVC/J. Vib. Control 2022, 28, 1011–1024. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Zheng, J.; Feng, K.; Ji, J.C. Based Weak Feature Extraction for a Rotor-Bearing System. Meas. Sci. Technol. 2023, 34, 065011. [Google Scholar] [CrossRef]
- Hao, Z.; Jian, Y.; Hua, X. An adaptive morphological filtering and feature enhancement method for spindle motor bearing fault diagnosis. Appl. Acoust. 2023, 209, 109400. [Google Scholar]
- Feng, K.; Yang, R.; Wei, Z. An optimized Laplacian of Gaussian filter using improved sparrow search algorithm for bearing fault extraction. Meas. Sci. Technol. 2023, 35, 036105. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Z.; Huang, H.; Xiang, J. A TEO-Based Modified Laplacian of Gaussian Filter to Detect Faults in Rolling Element Bearing for Variable Rotational Speed Machine. IET Sci. Meas. Technol. 2021, 15, 193–203. [Google Scholar] [CrossRef]
- Barszcz, T.; Jabłoński, A. A Novel Method for the Optimal Band Selection for Vibration Signal Demodulation and Comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An Effective Approach for Selecting the Optimal Demodulation Band in Rolling Element Bearings Diagnosis. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Liang, K.; Lin, J. Application of an Improved MCKDA for Fault Detection of Wind Turbine Gear Based on Encoder Signal. Renew. Energy 2020, 151, 192–203. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum Correlated Kurtosis Deconvolution and Application on Gear Tooth Chip Fault Detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Wang, G.; Lopez-Molina, C.; De Baets, B. Automated Blob Detection Using Iterative Laplacian of Gaussian Filtering and Unilateral Second-Order Gaussian Kernels. Digit. Signal Process. 2020, 96, 102592. [Google Scholar] [CrossRef]
- Saad, O.M.; Shalaby, A.; Samy, L.; Sayed, M.S. Automatic Arrival Time Detection for Earthquakes Based on Modified Laplacian of Gaussian Filter. Comput. Geosci. 2018, 113, 43–53. [Google Scholar] [CrossRef]
- Jiang, R.; Chen, J.; Dong, G.; Liu, T.; Xiao, W. The Weak Fault Diagnosis and Condition Monitoring of Rolling Element Bearing Using Minimum Entropy Deconvolution and Envelop Spectrum. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 1116–1129. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B.; Endo, H. The Enhancement of Fault Detection and Diagnosis in Rolling Element Bearings Using Minimum Entropy Deconvolution Combined with Spectral Kurtosis. Mech. Syst. Signal Process. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- Buzzoni, M.; Antoni, J.; D’Elia, G. Blind Deconvolution Based on Cyclostationarity Maximization and Its Application to Fault Identification. J. Sound Vib. 2018, 432, 569–601. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, Y.; Nolan, J.P. An alternative bearing fault detection strategy for vibrating screen bearings. JVC/J. Vib. Control 2023, 10775463231208818. [Google Scholar]
- Cicone, A.; Zhou, H. Numerical Analysis for Iterative Filtering with New Efficient Implementations Based on FFT. Numer. Math. 2021, 147, 1–17. [Google Scholar] [CrossRef]
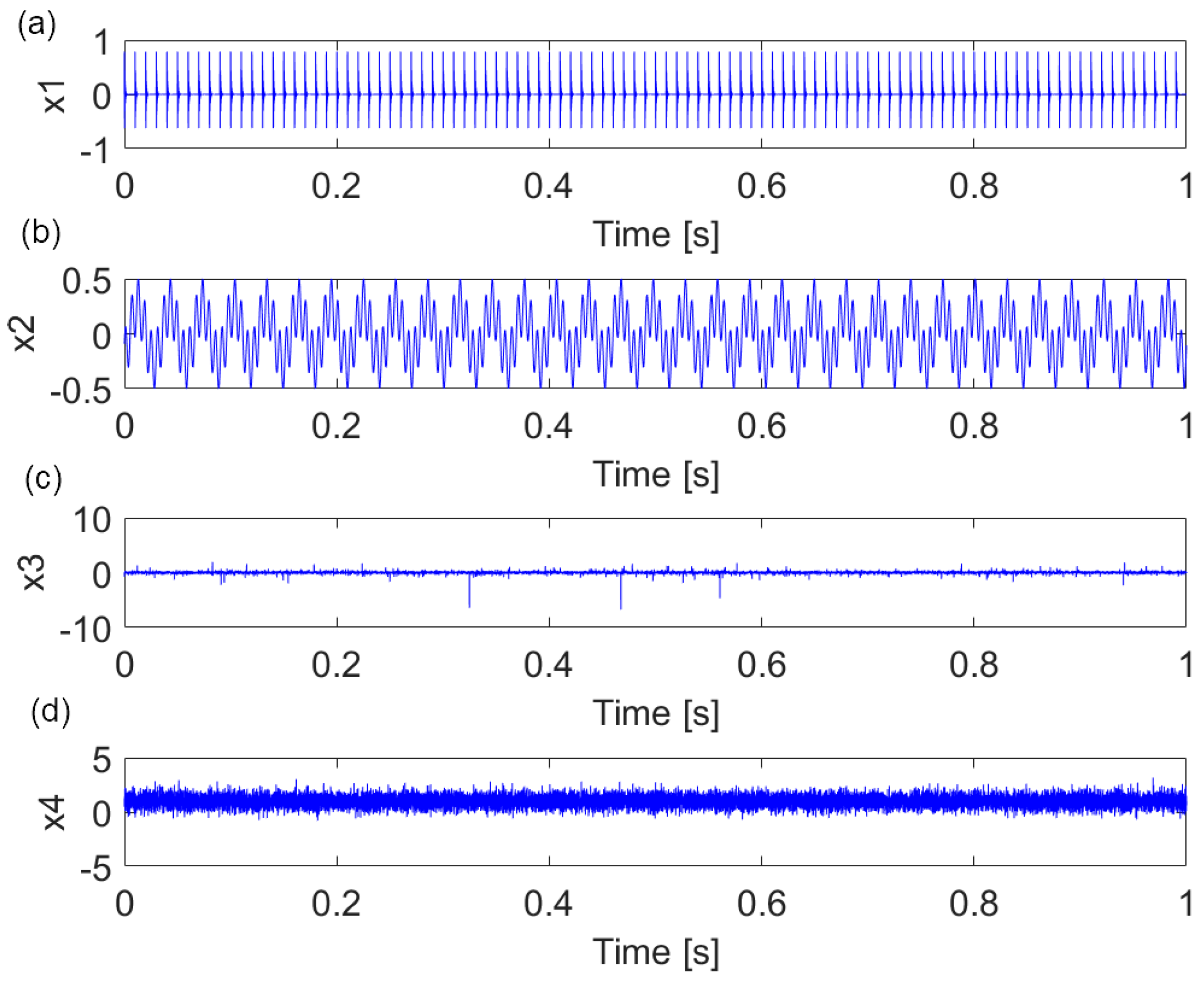
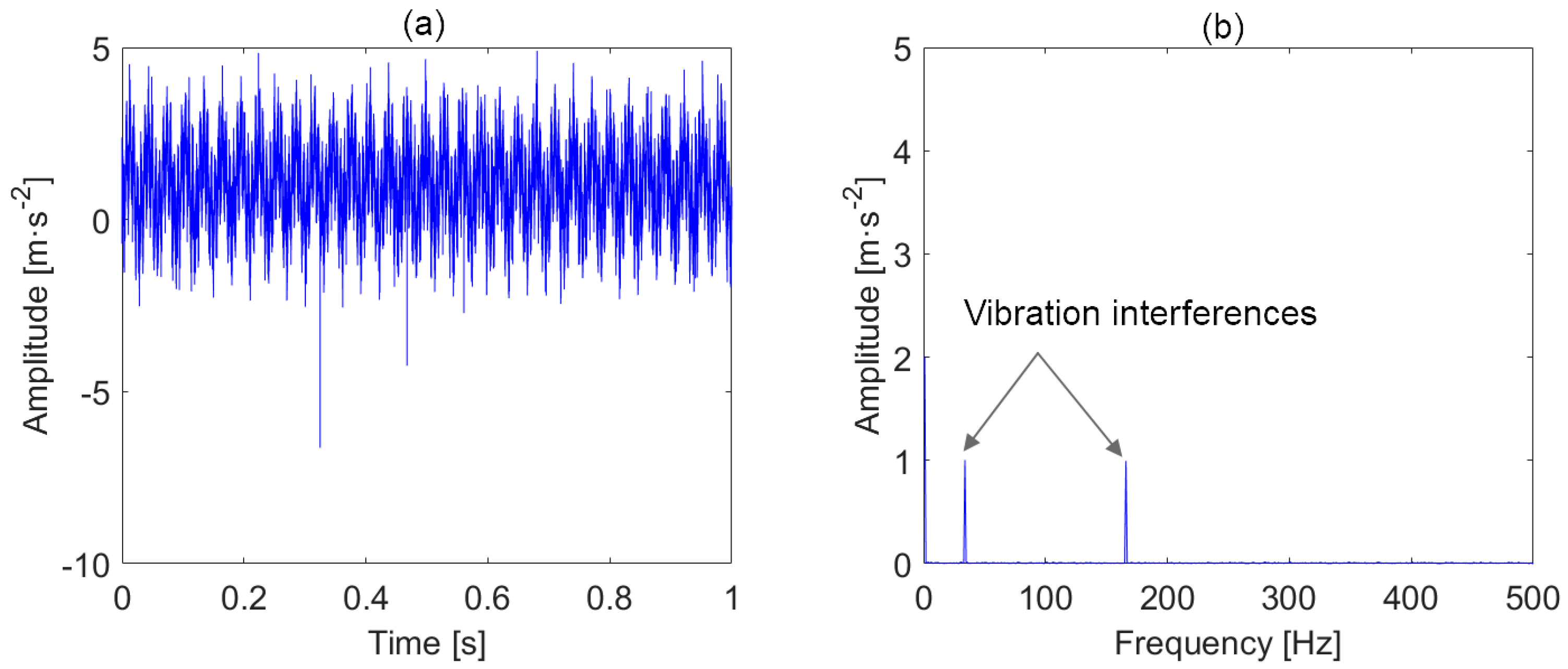
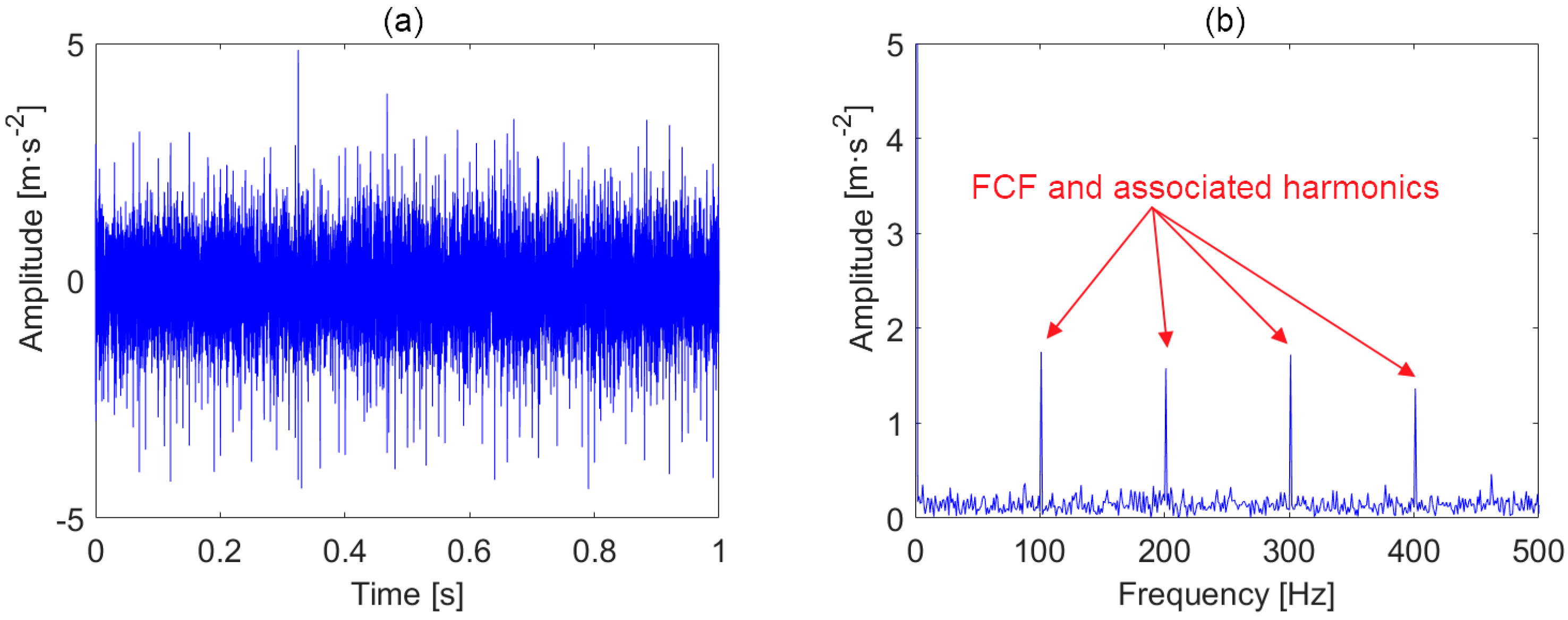
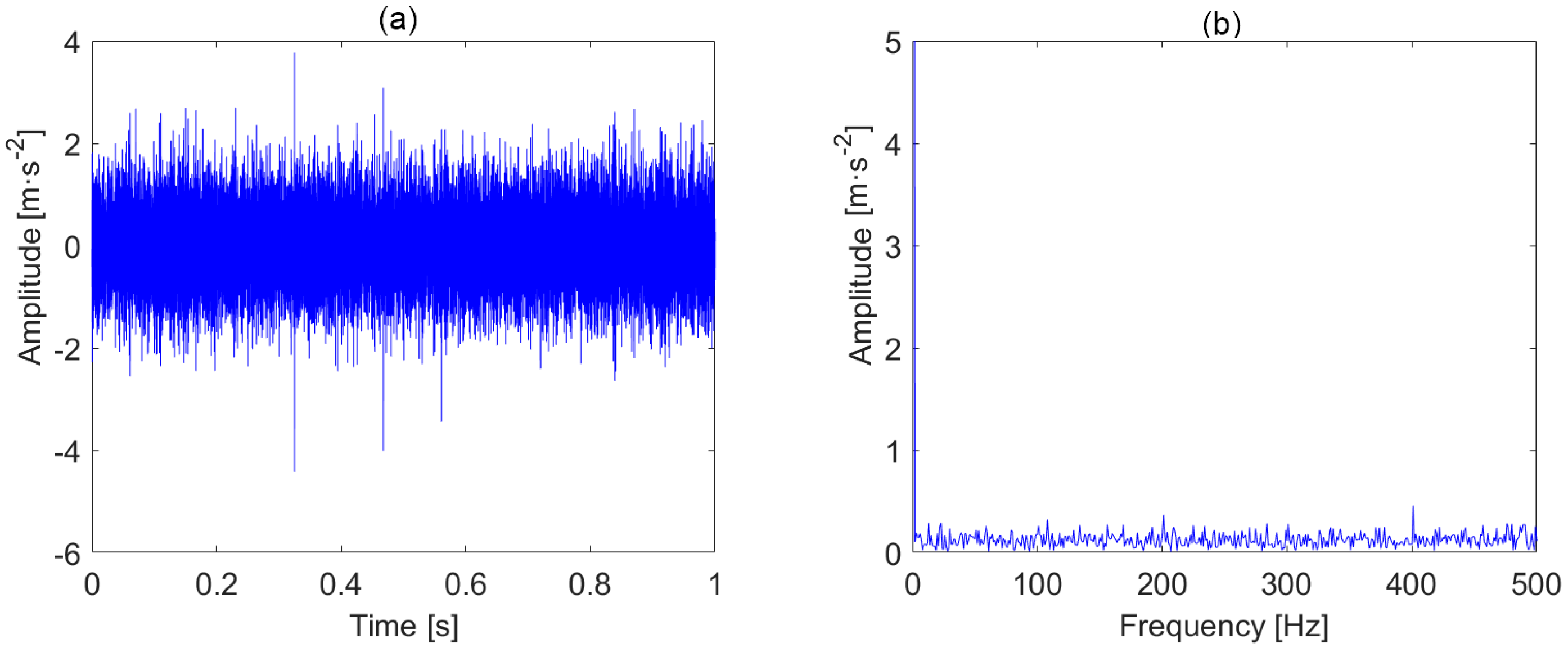



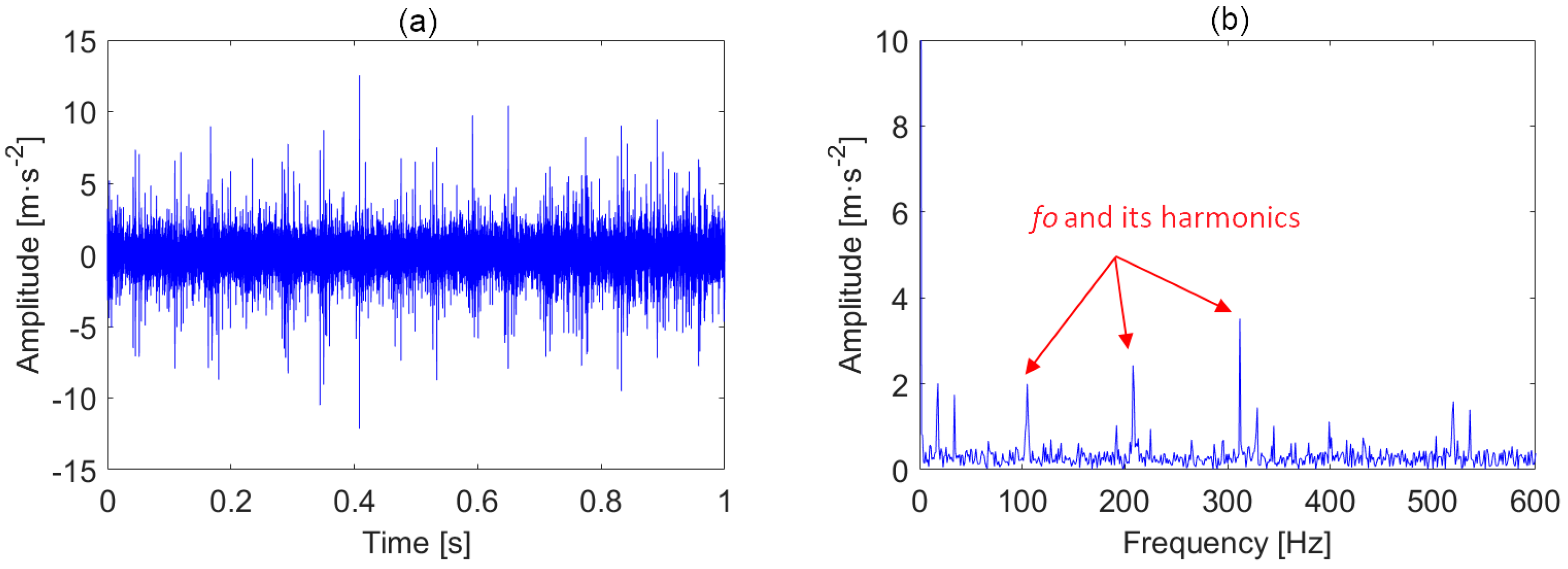

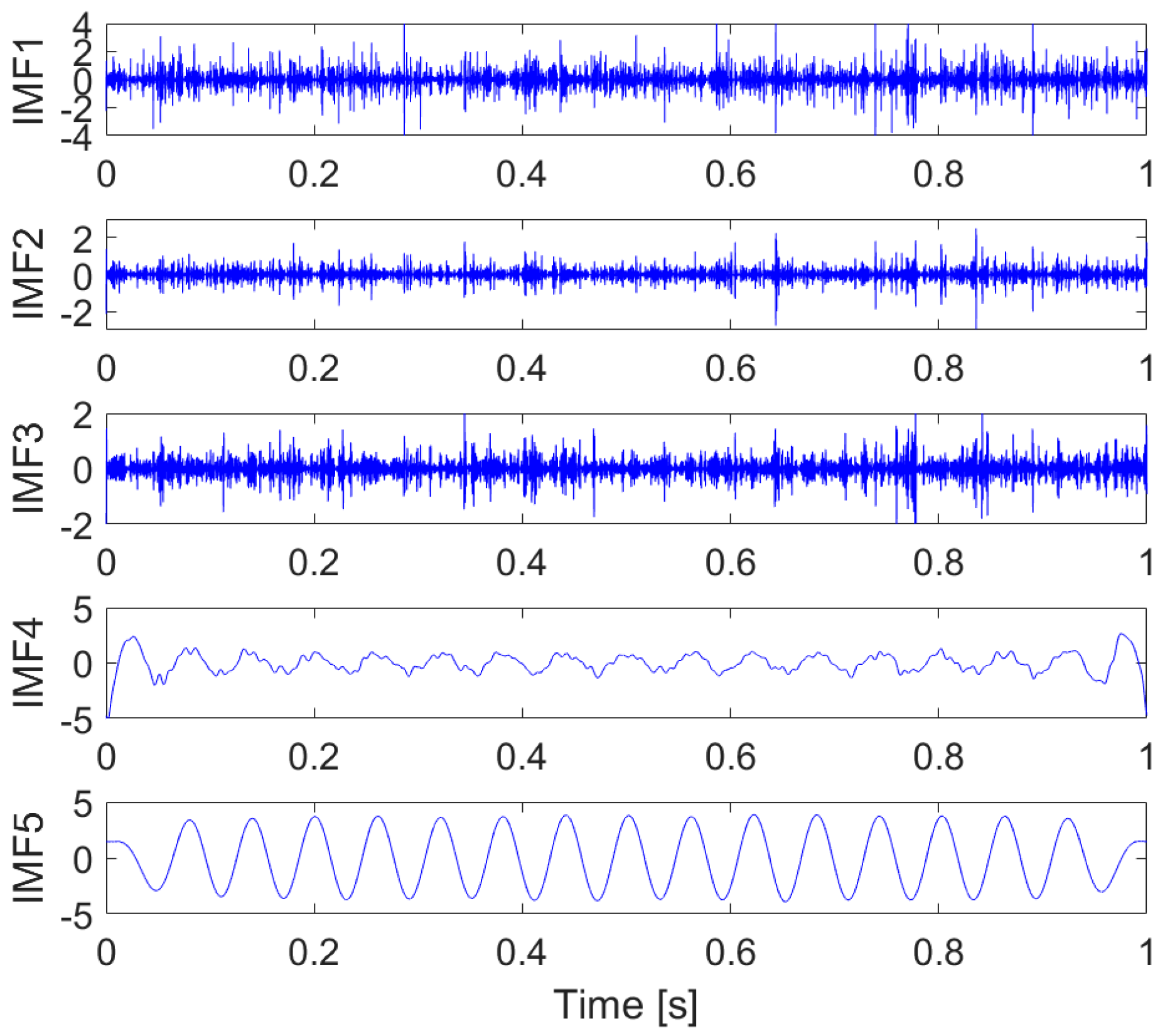
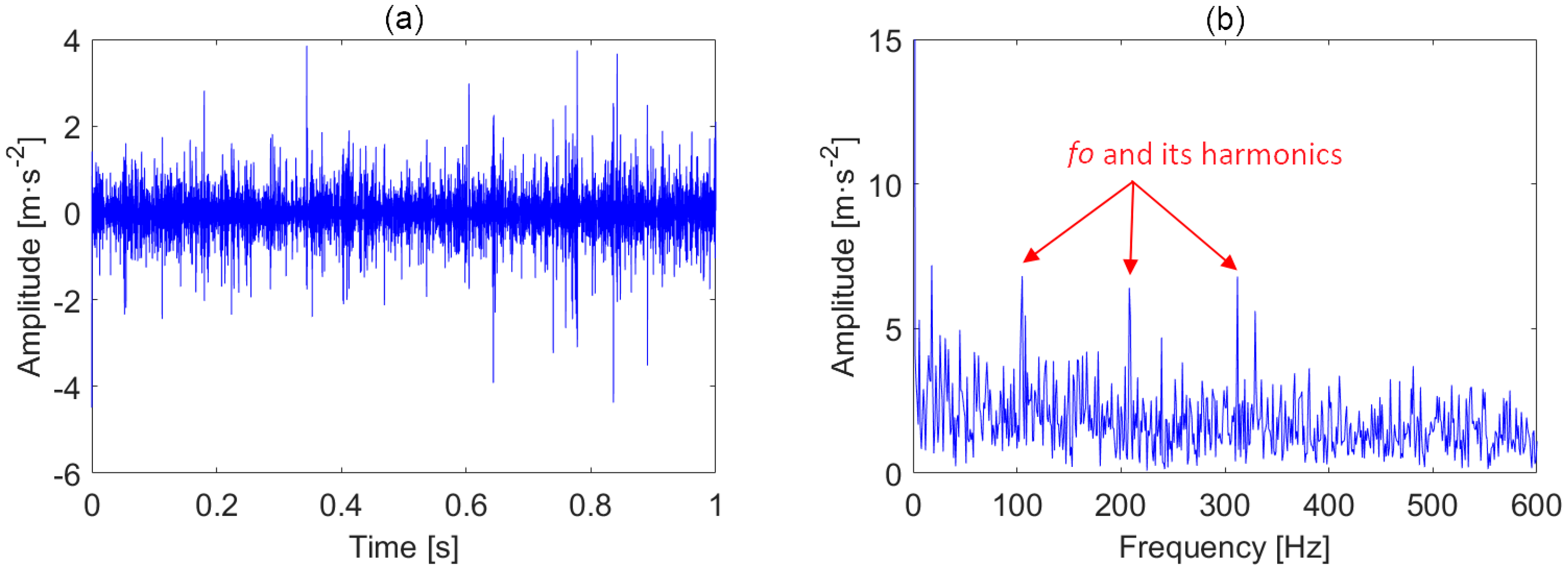
| Parameter | An (m·s−2) | (N·s/m) | Tp (s) | (Hz) |
|---|---|---|---|---|
| Value | 2 | 3000 | 0.01 | 2048 |
| Sampling frequency (Hz) | 51,200 |
| Rotational speed (Hz) | 29 |
| Bearing no. | MB ER-16K |
| Number of balls | 9 |
| Ball diameter (mm) | 7.9375 |
| Pitch diameter (mm) | 38.50 |
| Inner race fault characteristic frequency fi (Hz) | 157.4 |
| Outside diameter (mm) | 90 |
| Ball diameter (mm) | 12.5 |
| Pitch diameter (mm) | 65 |
| Number of rolling elements | 15 |
| Contact angle | 30° |
| Rotational speed (r/min) | 960 |
| Sampling frequency (kHz) | 20 |
| Outer race fault characteristic frequency fo (Hz) | 104.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, D.; Xu, Y.; Liu, X. Application of an Improved Laplacian-of-Gaussian Filter for Bearing Fault Signal Enhancement of Motors. Machines 2024, 12, 389. https://doi.org/10.3390/machines12060389
Tang D, Xu Y, Liu X. Application of an Improved Laplacian-of-Gaussian Filter for Bearing Fault Signal Enhancement of Motors. Machines. 2024; 12(6):389. https://doi.org/10.3390/machines12060389
Chicago/Turabian StyleTang, Dafeng, Yuanbo Xu, and Xiaojun Liu. 2024. "Application of an Improved Laplacian-of-Gaussian Filter for Bearing Fault Signal Enhancement of Motors" Machines 12, no. 6: 389. https://doi.org/10.3390/machines12060389
APA StyleTang, D., Xu, Y., & Liu, X. (2024). Application of an Improved Laplacian-of-Gaussian Filter for Bearing Fault Signal Enhancement of Motors. Machines, 12(6), 389. https://doi.org/10.3390/machines12060389





