Estimation of Tire Side-Slip Angles Based on the Frequency Domain Lateral Acceleration Characteristics Inside Tires

Abstract

The identification and control of tire side slip angle is the key to vehicle stability control. Intelligent tire technology based on the sensing of side-slip acceleration inside the tire provides a novel method for estimating the tire side-slip angle. This study proposed a method to estimate the tire side-slip angle by using the frequency domain lateral acceleration of the tire. First, an intelligent tire testing system was constructed by independently developing a special rim assembly and data collector. A three-axis accelerometer was placed on the right side of the tire, and the acceleration value was acquired by using a wired method with a sampling frequency of 50 kHz. Second, based on the constructed test system, a tire side deflection test was carried out on the Flat Trac bench. Through data analysis, it was found that the lateral acceleration was in the frequency domain of 400 Hz. As the side-slip angle increased from −4° to 4°, the vibration amplitude gradually decreased. Moreover, the vibration amplitude within 0.5~2 kHz was highly correlated with the side-slip angle. Subsequently, the vibration amplitude of the lateral acceleration within 2 kHz was extracted at an interval of 20 Hz as the feature point, and a frequency domain data set FDAy3 was established together with the vertical load and tire pressure. Finally, the support vector machine (SVM) algorithm was employed to make predictions on the data set. The grid search method was utilized to find the optimal parameter values of the model penalty factor c and radial basis kernel function coefficient g, which were 1.4142 and 0.0884, respectively. The results suggested that the root mean square error of the model prediction was 0.0806°, and the maximum estimated angle deviation of the prediction was 0.4587°. Meanwhile, the optimal prediction accuracy and real-time performance were achieved when the number of feature points and the feature frequency band were 25 and within 500 Hz, respectively. The findings of this study confirm that it is feasible to estimate the tire side-slip angle based on the frequency domain lateral acceleration of the tire, which provides a new method for tire side-slip angle estimation.

1. Introduction

Tire slip characteristics, especially the tire side-slip angle, are the key to vehicle stability control [1,2]. Currently, there are three main methods for obtaining tire side-slip angle: (1) designing vehicle dynamics and tire mechanics models, constructing linear or nonlinear observers based on sliding mode observers [3], and using Kalman filters [4,5,6,7]; (2) establishing a mapping observation model between side-slip angle and vehicle kinematics based on neural networks and deep learning [8,9,10]; and (3) developing a tire side-slip angle testing method based on machine vision, slip angle sensors, and experimental determination during actual driving processes [11,12,13,14,15]. However, the above methods have many defects, such as poor model adaptability, low accuracy, or high cost of additional equipment, making it difficult to use them in industrial applications.

In recent years, the development of sensing testing technology has made it possible to arrange sensors inside the tire to directly obtain the interaction status information between the tire and the road and then measure the tire side-slip angle [16,17]. For example, by placing an accelerometer on the center plane of the tire, Xu et al. [18] revealed that the acceleration vibration amplitude around 1000 Hz was highly correlated with the tire side-slip angle under a tire pressure of 220 kPa. Singh et al. [19] extracted the tire lateral displacement through quadratic integration of the lateral acceleration signal and found that the lateral displacement increased with the tire side-slip angle. Some studies also arranged accelerometers at positions deviated from the tire center plane. For instance, Mancosu et al. [20] estimated tire side-slip angle based on two pieces of ground contact characteristic information acquired under standard tire pressure. Some researchers arranged a polyvinylidene fluoride (PVDF) piezoelectric thin film sensor at a position deviated from the tire center plane. For example, Erdogan et al. [21] revealed that the linear slope of the signal collected by the piezoelectric sensor during the tire grounding process was correlated with the tire side-slip angle. This study developed a new method for estimating the tire side-slip angle using the lateral acceleration frequency domain signal of the sidewall position.

Our study aimed to design an intelligent tire testing system based on in-tire acceleration and conduct an experimental investigation of lateral deviation. First, an intelligent tire testing system with a sampling frequency of 50 kHz was constructed, and a three-axis accelerometer was placed near the sidewall. Then, lateral deviation tests were conducted on the Flat Trac bench under different side-slip angles, vertical loads, and tire pressures. After the tests, frequency domain data were extracted, and a data set was established. Finally, a support vector machine algorithm model was constructed to analyze the side-slip angle and verify its feasibility.

2. Experimental Device and Design

2.1. Design of Intelligent Tire Testing System

In order to accurately extract the in-tire acceleration signals to study the sidewall characteristics of the tires, a triaxial accelerometer (DYTRAN 333MT, range ±500 g) was arranged at the inner tire side near the outside of the vehicle, as illustrated in Figure 1. The sensor signal was transmitted in a wired manner. In Figure 1, the Z-axis of the accelerometer is perpendicular to the tire surface and points to the wheel axis. The X-axis is in the longitudinal direction of the tire and points in the opposite direction to the output end of the accelerometer signal. The Y-axis is the lateral direction of the tires, the pointing of which is determined by the right-hand rule, and the positive direction of the Y-axis points to the outside of the vehicle. The lateral acceleration of the accelerometer at the rightmost position is denoted as Ay3. It is noteworthy that the accelerometer is arranged in a symmetrical position on the far left, and the effect is the same as that on the far right.

The constructed intelligent tire testing system is shown in Figure 2. Bench testing was carried out on the Flat Trac testing machine. The self-developed special rim assembly [22] was installed on the rotating axis of the testing machine. The tire was driven to roll through the testing machine roadbed, and then the steering actuator was rotated to realize tire side deflection. The sensor signal line was fixed on the slip ring bracket and connected to the data collector. The host computer was responsible for real-time display and the storage of data. The entire intelligent tire testing system had a sampling frequency of 50 kHz.

2.2. Experimental Design

The test was conducted on the Flat Trac bench with a certain passenger car radial tire Giti 225/45 R17. The test surface was a Flat Trac bench bed system with 3 mite 120 grit sandpaper. The test conditions are listed in

Table 1. Design of side deflection test conditions.

No.	Vertical Load (N)	Tire Pressure (bar)	Speed (km/h)	Side-Slip Angle (°)	Duration of Each Side-Slip Angle (s)
1	2000	3.0	60	0 ±1 ±2 ±3 ±4	10
2	4000
3	6000
4	2000	2.5
5	4000
6	6000
7	2000	2.0
8	4000
9	6000

. In each set of tests, the tire pressure and vertical load were fixed, and the Flat Trac rotation steering actuator was controlled to achieve an incremental increase in the side-slip angle from 0° to ±4° at an interval of ±1°, where a positive side-slip angle represents that the tire is deflected to the right (in the Y positive direction of the axis); otherwise, it deviates to the left. To ensure that the tires can rotate a larger number of revolutions to extract samples for the estimation of the tire side bias angle, and to reduce the influence of tire wear on the acceleration signal, the duration of each side-slip angle test was set to 10 s. Between different test groups, the tire pressure and vertical load were changed, respectively. For example, the tire pressure decreased from 3.0 bar to 2.0 bar at an interval of 0.5 bar to investigate the effects of high pressure, normal pressure, and low pressure on tire contact. The setting of the vertical load was the same. Considering that when the side-slip angle is small, the speed has little impact on the side-slip characteristics of the tire [23], it was uniformly set to 60 km/h in this study.

3. Analysis of Lateral Acceleration-Related Side-Slip Angle Characteristics

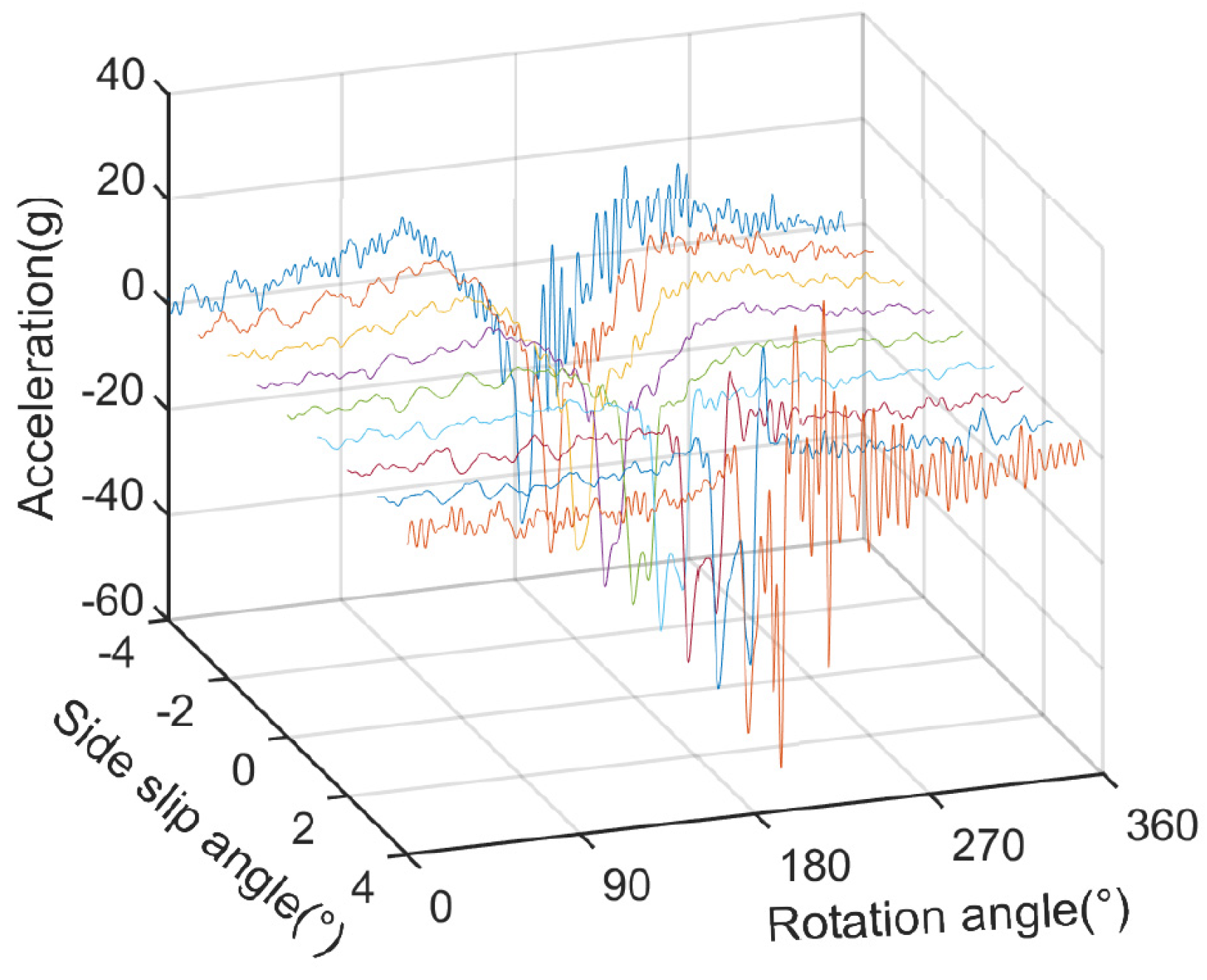
3.1. Effect of Side-Slip Angle on the Acceleration Ay3 in Time and Frequency Domains

Figure 3 demonstrates the relationship between the lateral acceleration Ay3 time-domain waveform and the side-slip angle in the side deflection test under a tire pressure of 2.5 bar, a vertical load of 4000 N, and a vehicle speed of 60 km/h. The lateral acceleration adopted a low-pass filter with a cutoff frequency of 400 Hz. It can be seen from Figure 3 that the signal amplitude of Ay3 was significantly correlated with the tire side-slip angle. When the side-slip angle was −4°, the Ay3 waveform exhibited a downward-facing peak. As the side-slip angle increased to 4°, this wave peak gradually turned into two downward wave peaks, and the absolute peak value gradually increased. This is mainly because the tire side deflection direction is opposite to the accelerometer sticking position. When the tire slip direction is consistent with the acceleration sensor pasting position, the lateral force in the tire contact patch increases with the slip angle, which is represented by a gradual increase in lateral acceleration. Additionally, when the side-slip angle was ±4°, the lateral acceleration of the tire during the ground-breaking process was significantly larger than the acceleration fluctuation during the tire-grounding process. This was mainly due to tire slip, i.e., tire slip starts from the ground-breaking process and gradually extends to the entire contact patch as the side-slip angle increases [18]. During a complete single rotation of a tire, the middle of the range of rotation angles from 90° to 270° includes the process of grounding and lifting the tire off the ground.

The influence of the side-slip angle on unfiltered lateral acceleration Ay3 was analyzed from the perspective of the frequency domain. It can be seen from Figure 4 that, within the frequency domain of 400 Hz, as the side-slip angle increased from −4° to 4°, the signal vibration amplitude gradually decreased, and multiple peaks appeared. The results indicated that when the tire deviated to the right side, the right sidewall gradually produced high-frequency vibration. Meanwhile, when the side-slip angle increased, there was a significant increase in the vibration amplitude of 500–1000 Hz, indicating that the side-slip angle affected the Ay3 at 500–1000 Hz. Moreover, when the side-slip angle was 4°, a total of three peaks appeared in the frequency domain of 400 Hz, with frequencies around 43 Hz, 180 Hz, and 342 Hz, respectively, corresponding to multiple downward-facing peaks in the time domain waveform of the tire grounding process. It is noteworthy that when the side-slip angle was 4°, the lateral acceleration also peaked near 1274 Hz, and this was mainly related to the slippage of the tire tread.

Considering that the acceleration signal in the frequency domain related to the side-slip angle has a higher signal-to-noise ratio than the acceleration signal in the time domain, this study selected to extract the frequency domain characteristics of the lateral acceleration Ay3 near the tire side for estimating the tire side-slip angle.

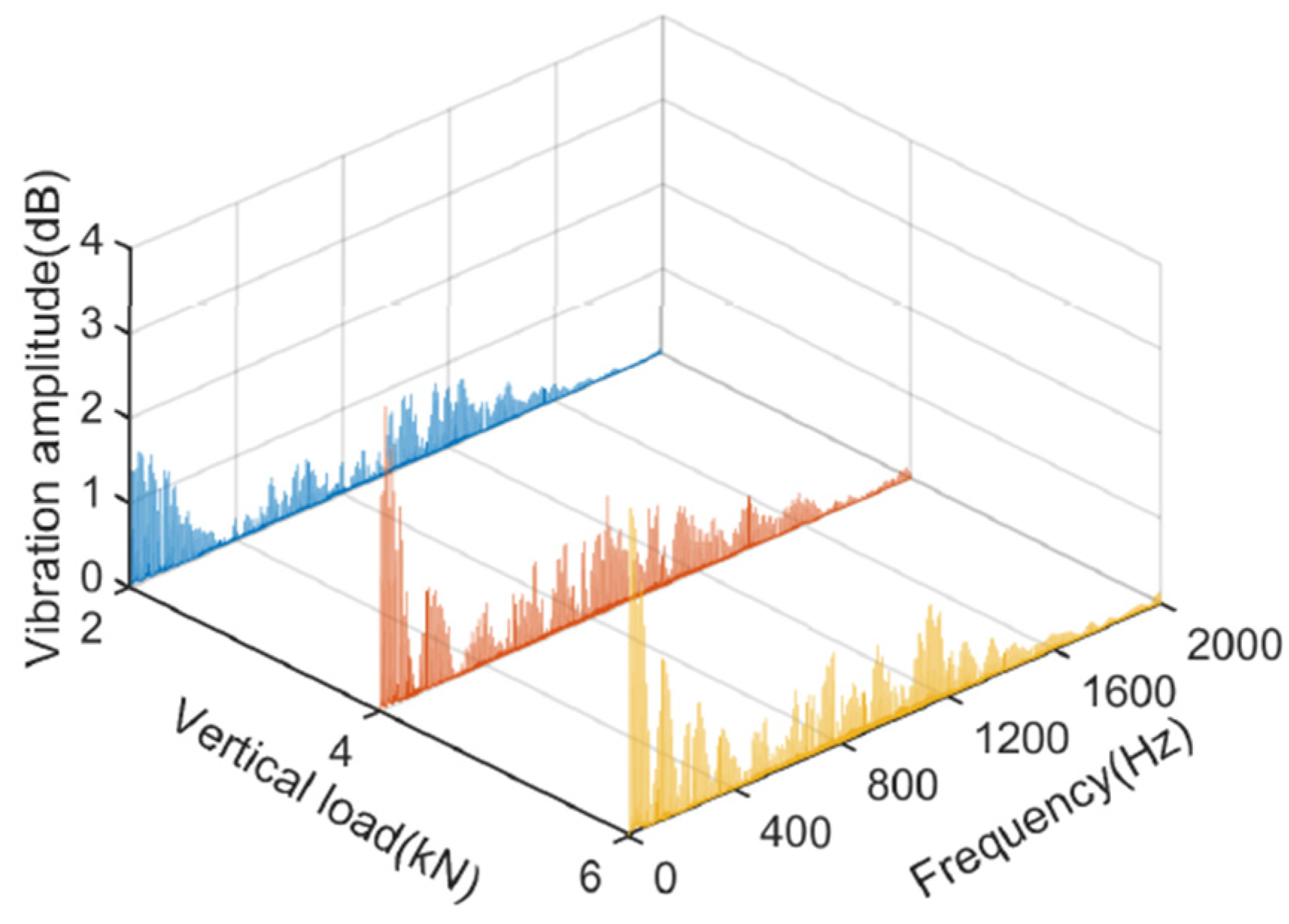
3.2. Effect of Vertical Load on Acceleration Frequency Domain Signal

Figure 5 shows the changes in lateral acceleration in the frequency domain under different vertical loads with a tire pressure of 2.5 bar, vehicle speed of 60 km/h, and side-slip angle of 2°. It was observed that as the vertical load increased from 2000 to 6000 N, the signal vibration amplitude of the Ay3 at low frequency around 25 Hz gradually increased. The main reason is that the as vertical load increases, the contact area between the tire and the road gradually increases, resulting in an increase in the lateral force generated by the tire under side deflection. As a result, the deformation of the sidewall position increased with the vertical load. When the vertical load increased from 4000 N to 6000 N, the increase in the signal vibration amplitude of Ay3 at a low frequency of around 25 Hz slowed down. This is because as the vertical load increases, the pressure at the sidewall position increases, causing the tire rubber material to reach the compression limit at this position, and the lateral force tends to stabilize.

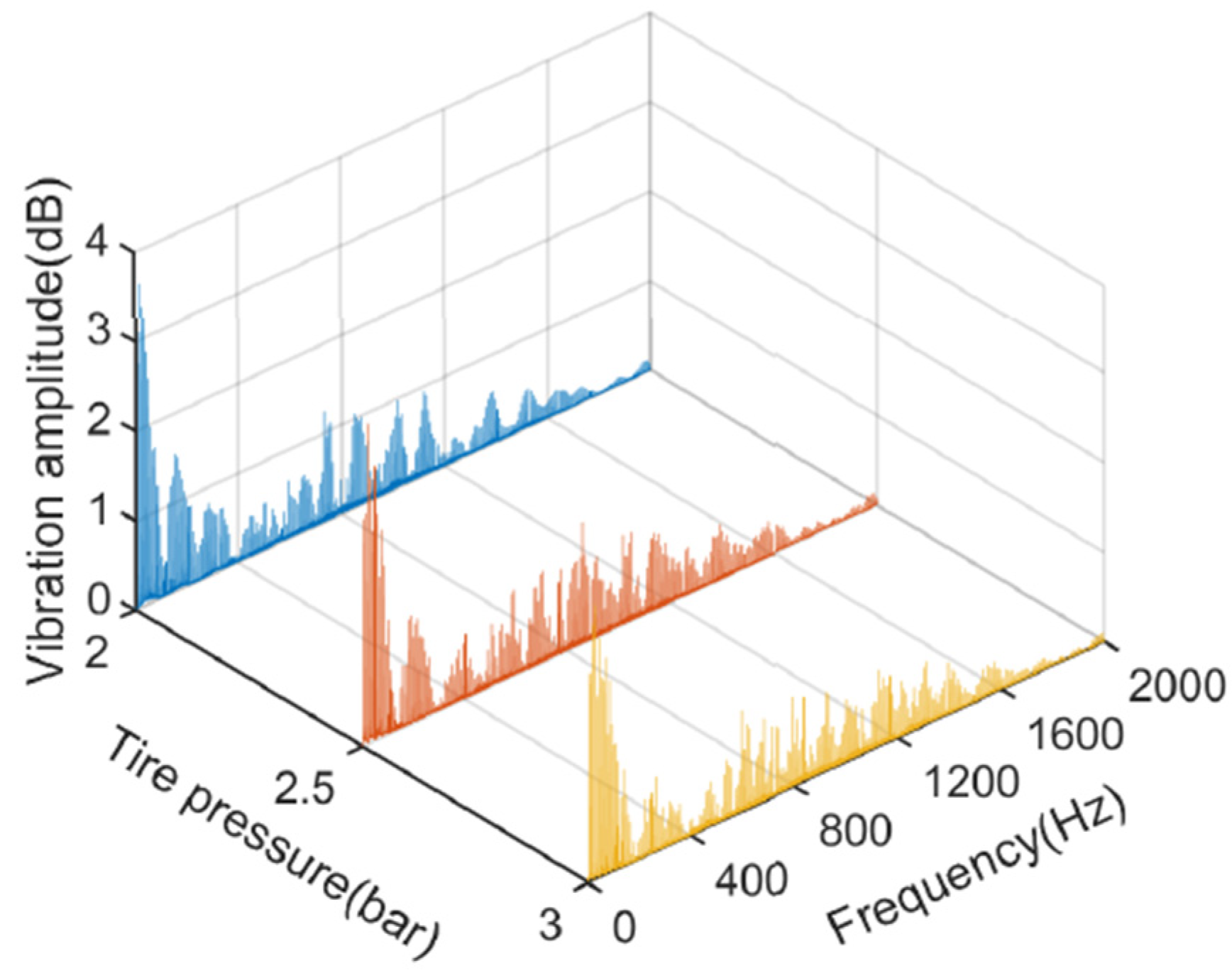
3.3. Effect of Tire Pressure on Acceleration Frequency Domain Signal

Figure 6 demonstrates the changes of lateral acceleration in the frequency domain under different tire pressures with a vertical load of 4000 N, vehicle speed of 60 km/h, and side-slip angle of 2°. As shown in Figure 6, as the tire pressure increased from 2.0 to 3.0 bar, the signal vibration amplitude of Ay3 at a low frequency of around 25 Hz gradually decreased. This is because the increase in tire pressure leads to increased tire stiffness, ultimately resulting in reduced lateral vibration at the sidewall position when the tire deflects sideways.

4. Estimating Side-Slip Angle Based on Support Vector Machines

The support vector machine (SVM) method based on statistical learning theory has strong learning and generalization capabilities in nonlinear regression, and it has been used in side-slip angle estimation, road slope prediction, and road surface recognition [11,24,25]. This study employed the SVM method to model the dynamic response parameters of tires under different side-slip angle excitations and estimate the side-slip angle.

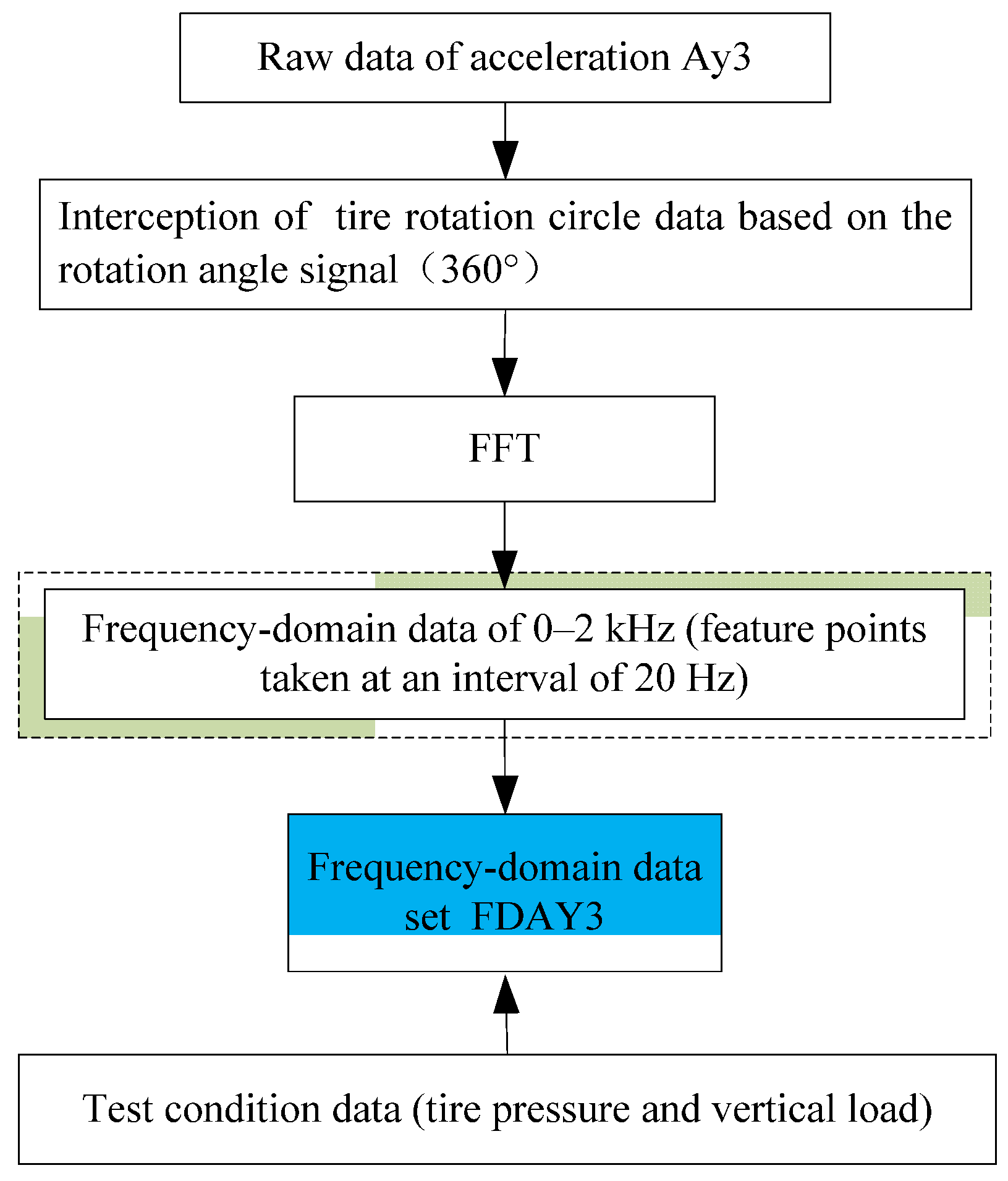
4.1. Data Set Construction

As mentioned above, the signal vibration amplitude of the lateral acceleration Ay3 in the frequency domain of 2 kHz was highly correlated with the side-slip angle. Therefore, the vibration amplitude within 2 kHz of the Ay3 frequency domain was extracted at an interval of 20 Hz as a feature to construct a data set. The data set construction process is shown in Figure 7. The lateral acceleration Ay3 of the tire rotation was intercepted through the corner signal, and the Fourier transform (FFT) was applied to perform a spectrum on the original acceleration data. Then, the vibration amplitude within 2 kHz of the frequency domain of Ay3 was extracted at an interval of 20 Hz, and the number of feature points was 100. Considering that the vertical load and tire pressure affected the vibration amplitude characteristics of Ay3 in the frequency domain, the above characteristics together with the vertical load and tire pressure were taken as the model input, and the side-slip angle was taken as the model output to establish the frequency domain data set FDAy3.

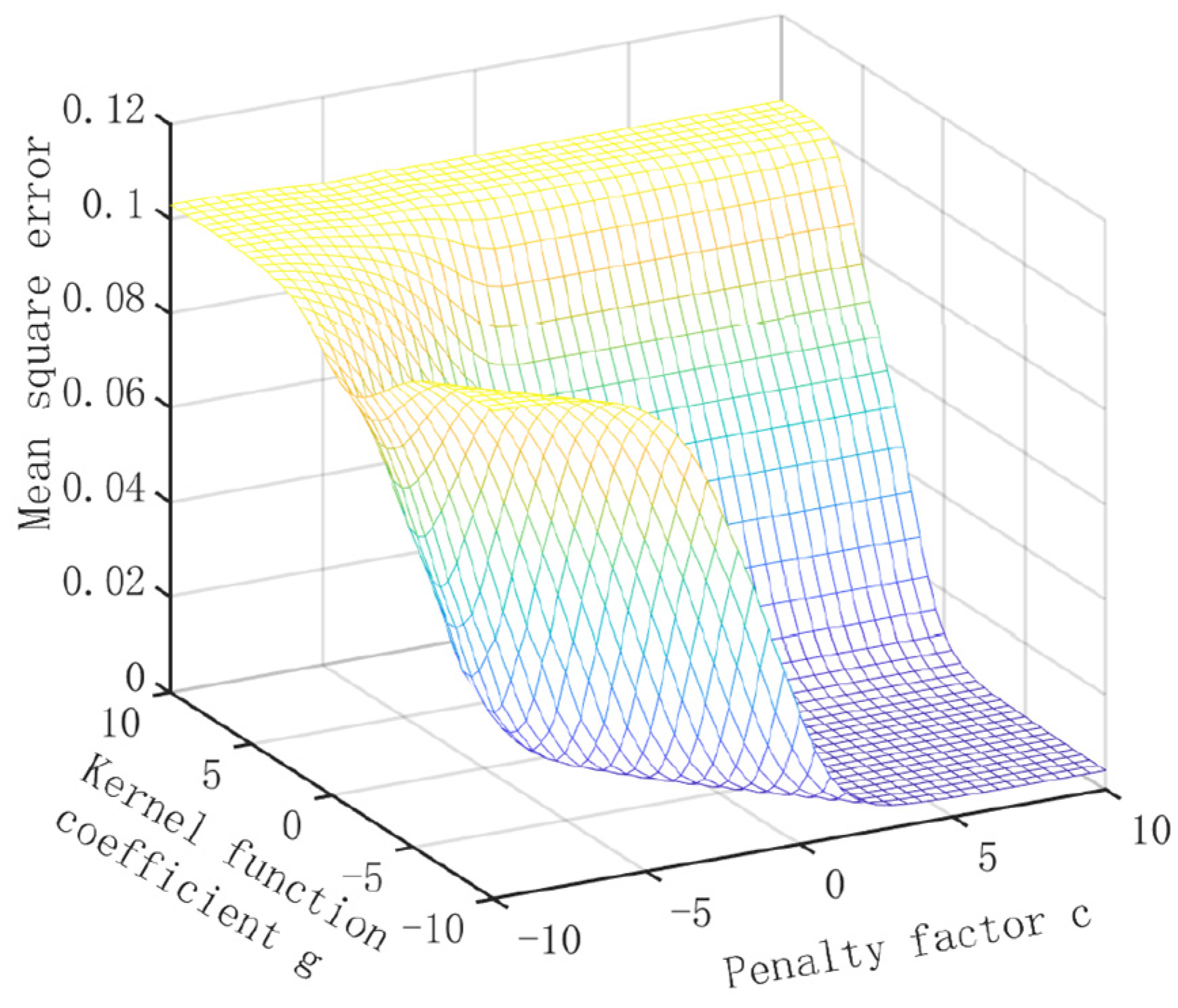
4.2. SVM Parameter Optimization

In this study, the SVM algorithm adopted the radial basis kernel function. The two parameters that have the most impact on the estimation effect are the penalty factor and the kernel function coefficient. The penalty factor c is the tolerance to errors. The higher the value of c, the less tolerant to errors, and the easier to overfit. In contrast, the smaller the value of c, the easier to underfit. Therefore, when the value of c is too large or too small, it can affect the generalization ability of the model. Additionally, the radial basis kernel function parameter g determines the distribution of data after mapping to a new feature space. The larger the value of g, the fewer support vectors, and the more the radial basis function acts near the support vector sample, resulting in worse model generalization ability. The smaller the value of g, the more the support vectors, but it will reduce the model’s training and prediction speed. Therefore, selecting appropriate values of the penalty factor c and radial basis kernel function coefficient g is crucial to the accuracy of SVM estimation.

The grid search method was utilized to find optimal parameter values [25]. Since the parameters c and g are constantly changing within a certain range, the method traversed all values, used the obtained parameter values for training prediction, and selected the parameter value with the smallest mean square error (MSE) as the optimal parameter. Figure 8 shows the MSE result obtained by the grid search method. In this paper, the tires used are Giti 225/45 R17 and the road surface is made of 3 mite 120 grit sandpaper, the optimal values of the parameters c and g obtained from the study are 1.4142 and 0.0884, respectively.

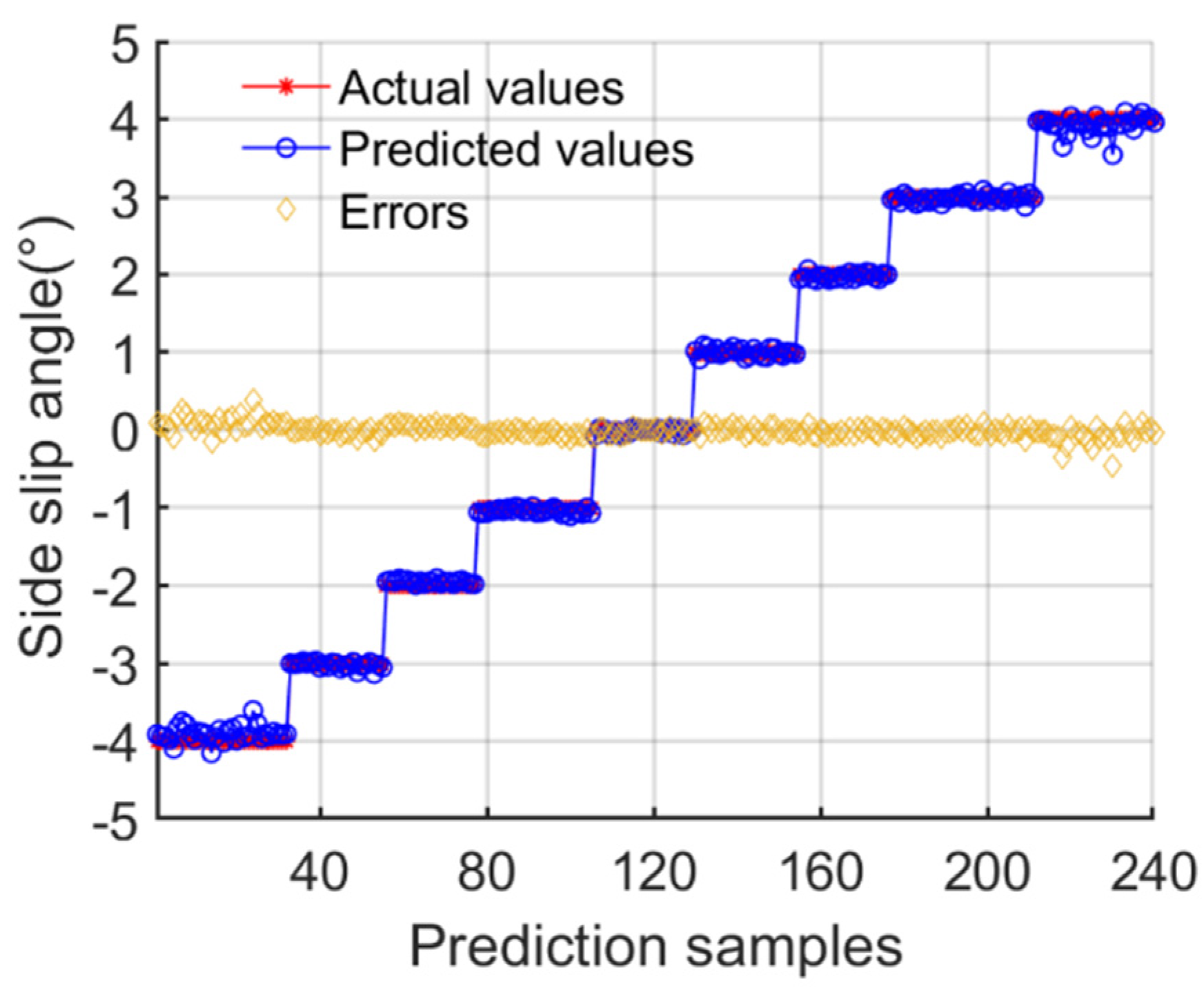
4.3. Model Estimation and Analysis

All samples were normalized to avoid the impact on the output contribution due to the different size ranges of the input elements and to improve calculation speed. This study used minimum and maximum normalization to standardize the data set. Minimum and maximum normalization is a linear transformation that can accurately retain all relationships between data values and facilitate SVM training. The calculation is shown in Equation (1):

$$x_{norm}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$$

(1)

where $x$ denotes the eigenvalue in the data set, $x_{\min }$ and $x_{\max }$, respectively, denote the minimum and maximum values in the eigenvalues, and $x_{norm}$ denotes the normalized eigenvalue. Meanwhile, the tire side-slip angle predicted by the model needs to be denormalized, and its mapping relationship coefficient remains consistent.

The data set was randomly divided into a training set and a test set at a ratio of 7:3, where the former was used to build an estimation model of input features and output values, and the latter was used to evaluate the performance of the model.

The slip angle prediction method after modeling was evaluated by root mean square error (RMSE). The calculation formula is as follows:

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{{\displaystyle \sum _{i=1}^n\left({\widehat{y}}_i-y_i\right)}}^2}$$

(2)

where $i$ represents the $i$-th data sample, ${\widehat{y}}_i$ and $y_i$ represent the model prediction value and the true value, respectively, and $n$ denotes the total number of samples. RMSE is used to measure the deviation between the observed value and the true value. The smaller the value, the smaller the model prediction error, and the more accurate the estimate.

The computer used in the experiment was equipped with an Intel i7 processor CPU @ 3.40 GHz. The processed data set was substituted into the SVM model for training. To avoid the contingency of the prediction results, the model was trained 10 times, and the values were averaged. The prediction results are shown in Figure 9. The RMSE was 0.0806, corresponding to an average angle error of 0.0049°. When the side-slip angle was ±4°, the estimation error of the side-slip angle exhibited more fluctuation, and the maximum estimated angle error was 0.4587°. Therefore, SVM can be used to predict tire side-slip angle based on the frequency domain data set FDAy3.

Within the frequency domain of 400 Hz, as the side-slip angle increased from −4° to 4°, the vibration amplitude varied greatly. Therefore, the frequency domain data set constructed by extracting the vibration amplitude in this frequency band as a feature can also be used to predict the tire side-slip angle. That is, the selection of the characteristic frequency band and the number of feature points can affect the model’s prediction accuracy and operation time.

Multiple sets of frequency domain data sets were constructed using the characteristic frequency band, with the number of feature points as independent variables. Then, the prediction accuracy RMSE and operation time of the constructed SVM estimation models were investigated. The number of selected characteristic frequency bands increased from 500 to 2000 with an interval of 500. The number of characteristic points had a middle value of 100, with an interval of 25 and 3 on the left and right. Similarly, to avoid the contingency of prediction results, the SVM model was trained 10 times, and the average value was taken.

As demonstrated in Figure 10, the number of feature points had a significant impact on the model’s prediction accuracy. As the number of feature points decreased, the model’s prediction accuracy increased. For example, when the number of feature points was 175 and the characteristic frequency band was 2000 Hz, the prediction error RMSE of the model was 0.1245. When the number of feature points was reduced to 25, the prediction error was reduced to 0.054, showing a decline of 56.63%. The main reason is that the higher the number of feature points, the more features irrelevant to the side-slip angle. These features will lead to a longer calculation time for the model and will cause the model’s accuracy to decrease. It should be noted that when the characteristic frequency band was 500 Hz, the number of feature points had a significant impact on the model’s prediction error. In contrast, the characteristic frequency band had less impact on the model’s prediction error than the number of feature points.

As shown in Figure 11, the number of feature points had a significant impact on the model’s calculation time, while the feature frequency band had a smaller impact. Meanwhile, as the number of feature points decreased, the model’s operation time was reduced. For example, when the number of feature points was 175 and the characteristic frequency band was 500 Hz, the model’s operation time was 20.402 ms. When the number of feature points was reduced to 25, the model’s operation time was reduced to 1.5394 ms.

To sum up, the characteristic frequency band should be selected within 500 Hz with 25 feature points. This can ensure the model’s prediction accuracy, decrease the model calculation time as much as possible, and reduce the requirements for hardware development.

Our research group developed an intelligent tire in tread module by cooperating with a tire company. It was found that the acceleration sampling frequency developed with Infineon’s SP40T controller can reach more than 1 kHz, and FFT calculations can be completed. These findings indicate that it is feasible to estimate the tire side-slip angle based on the SVM algorithm.

5. Conclusions

(1)

This paper conducted lateral deflection tests by arranging one triaxial acceleration at the right sidewall position of the tire and building a smart tire test system on a Flat Trac bench with 3 mite 120 grit sandpaper on the road surface. When the camber angle is 0, it is found that the vibration amplitude of lateral acceleration Ay3 decreases gradually with the increase in the lateral deflection angle from −4° to 4° in the frequency domain of 400 Hz, and the vibration amplitude is significantly correlated with the lateral deflection angle in the range of 0.5~2 kHz. The influence of rotational speed on frequency response is not checked in this paper and will be discussed in the future.

(2)

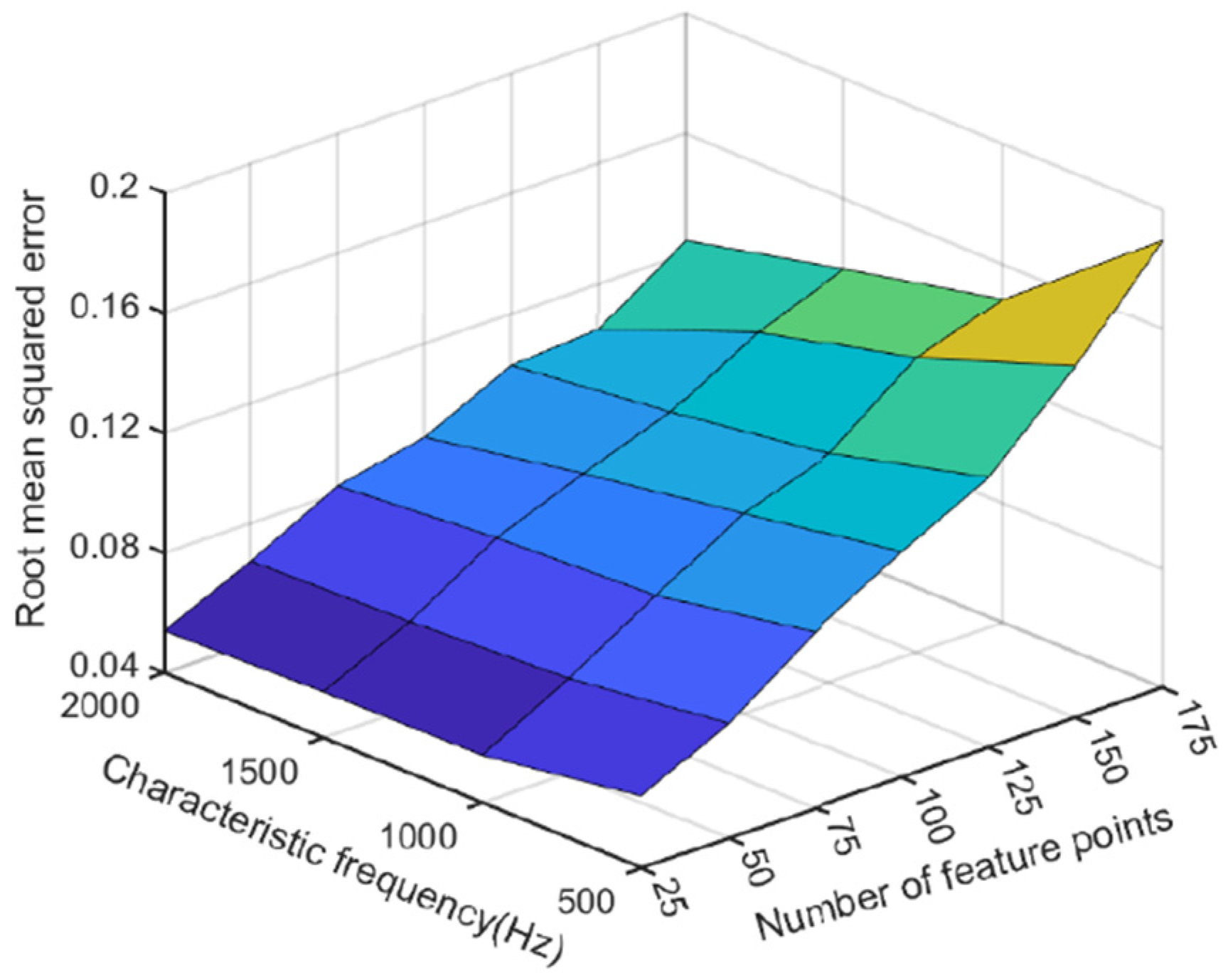
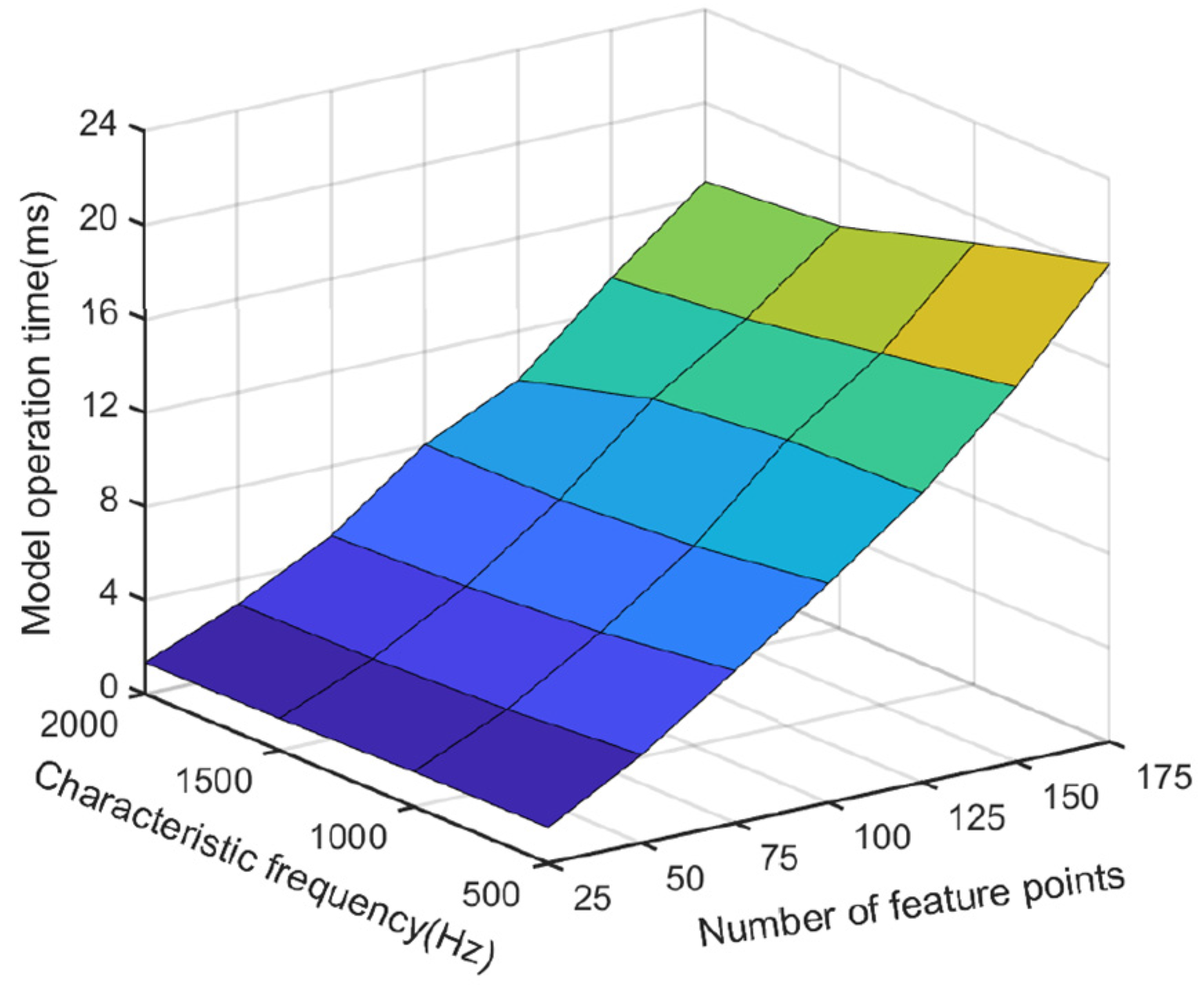
Based on the characteristic frequency band and the number of feature points, the frequency domain vibration amplitude of lateral acceleration Ay3 was extracted to construct a data set, and SVM was employed to predict the tire side-slip angle. Then, by taking the characteristic frequency band and the number of feature points as independent variables, multiple sets of frequency domain data sets were established and applied to the model. The results indicated that when the characteristic frequency band was selected within 500 Hz, the Ay3 data set with 25 feature points contributed to the optimal prediction accuracy and real-time performance. The tire side deflection angle estimation method proposed in this paper has been validated on the bench, but considering the applicability of the method on actual road surfaces, road studies will be carried out at a later stage for correcting the side deflection angle estimation model. In practice, the acceleration sampling frequency of the Infineon-based SP40T controller can reach more than 1 kHz. Therefore, this study provides a new method for side-slip angle estimation.