Discretionary Lane-Change Decision and Control via Parameterized Soft Actor–Critic for Hybrid Action Space
Abstract
1. Introduction
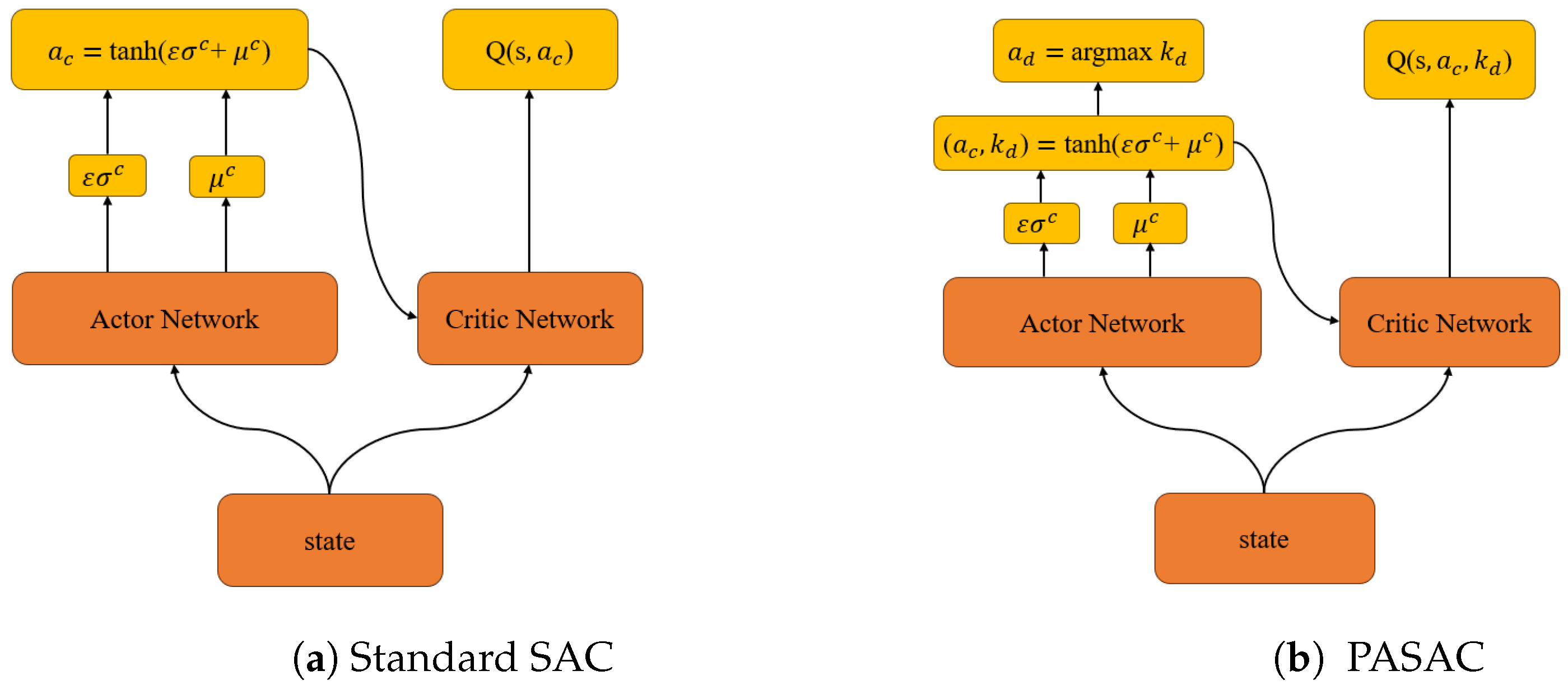
2. Parameterized Soft Actor–Critic
2.1. Reinforcement Learning
2.2. Soft Actor–Critic
2.3. Parameterized Soft Actor–Critic
| Algorithm 1 PASAC Algorithm Training Process. |
|
3. PASAC for Lane Changing
3.1. Scenario Settings
3.2. State
3.3. Action
3.4. Reward
4. Model Predictive Control Model
4.1. State-Space Equations
4.2. Cost Function
4.3. Future State Estimation
4.4. TLACC (Two-Lane Adaptive Cruise Control)
| Algorithm 2 TLACC Algorithm Process. |
|
5. Comparison Results of DRL and MPC
5.1. DRL Training
5.2. DRL Testing
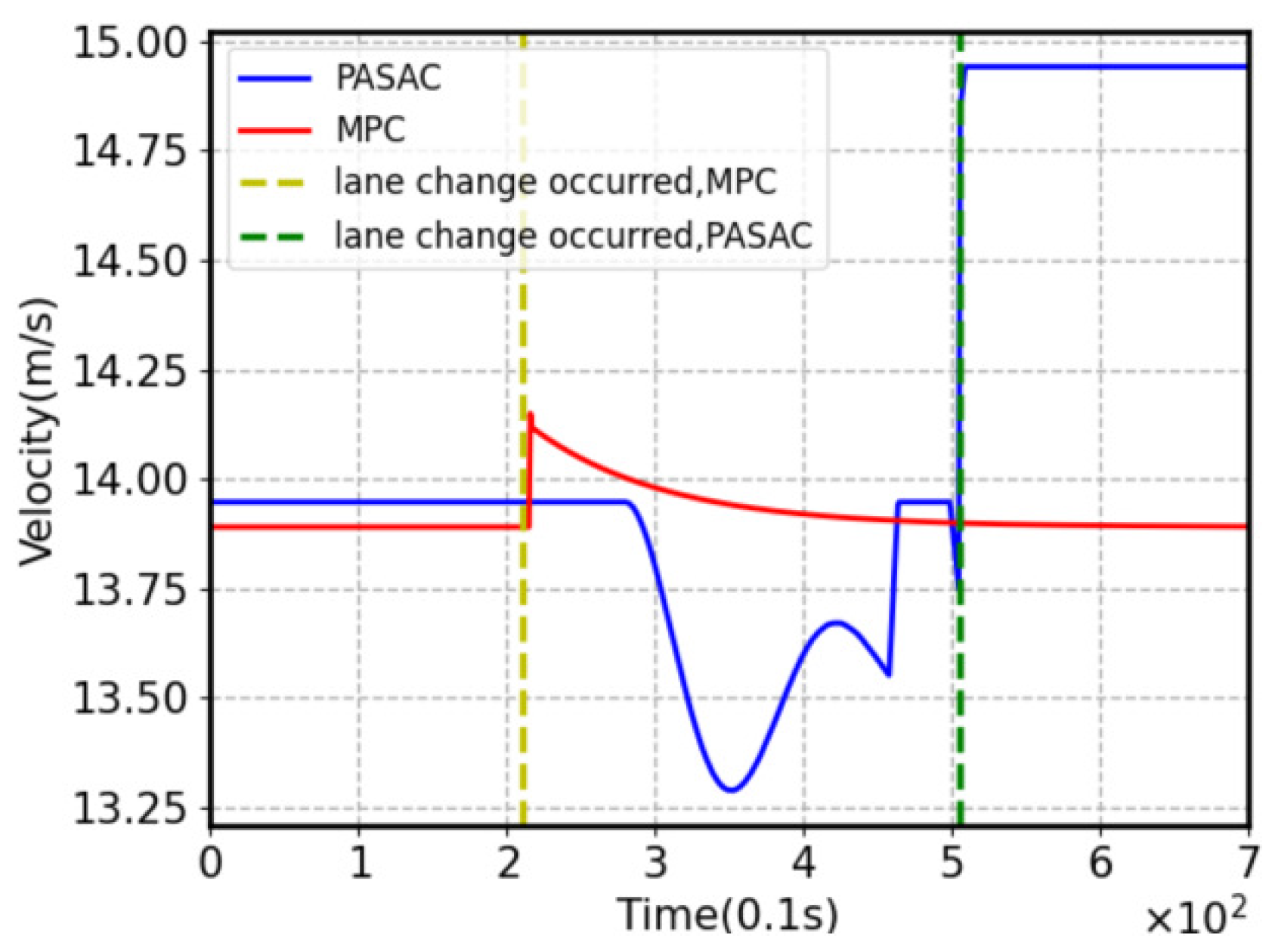
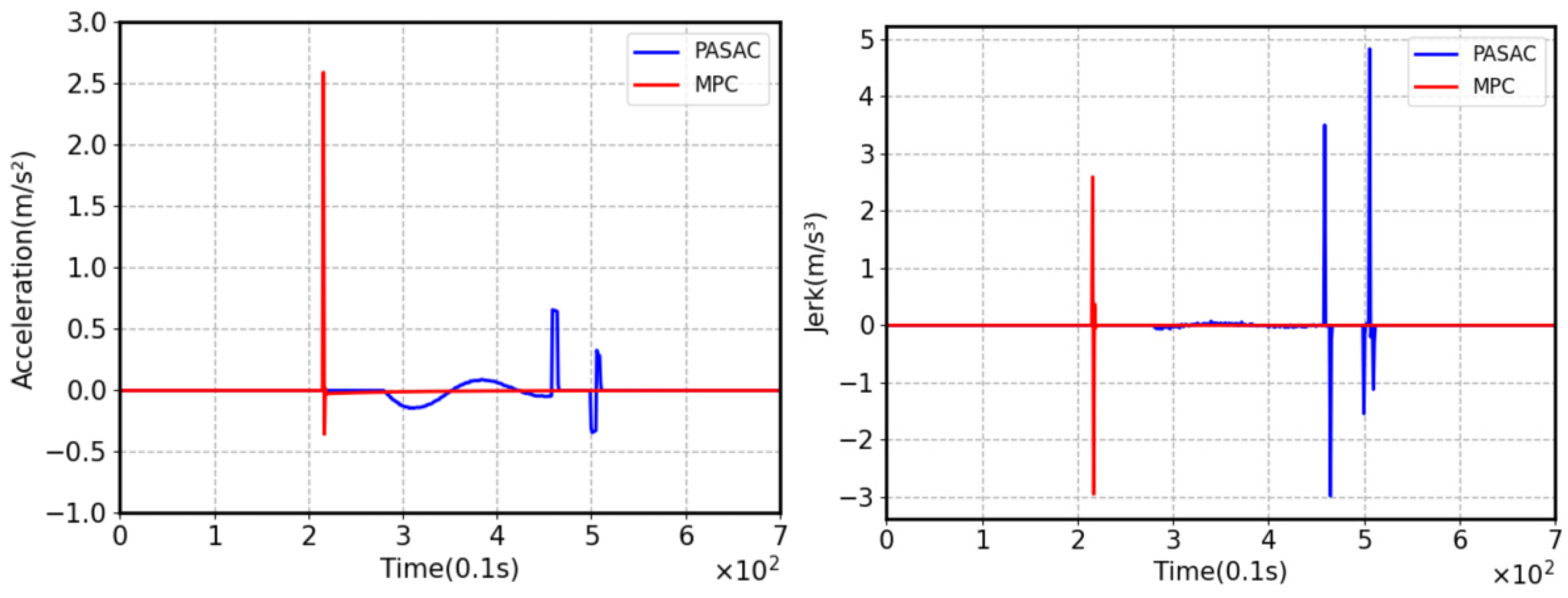
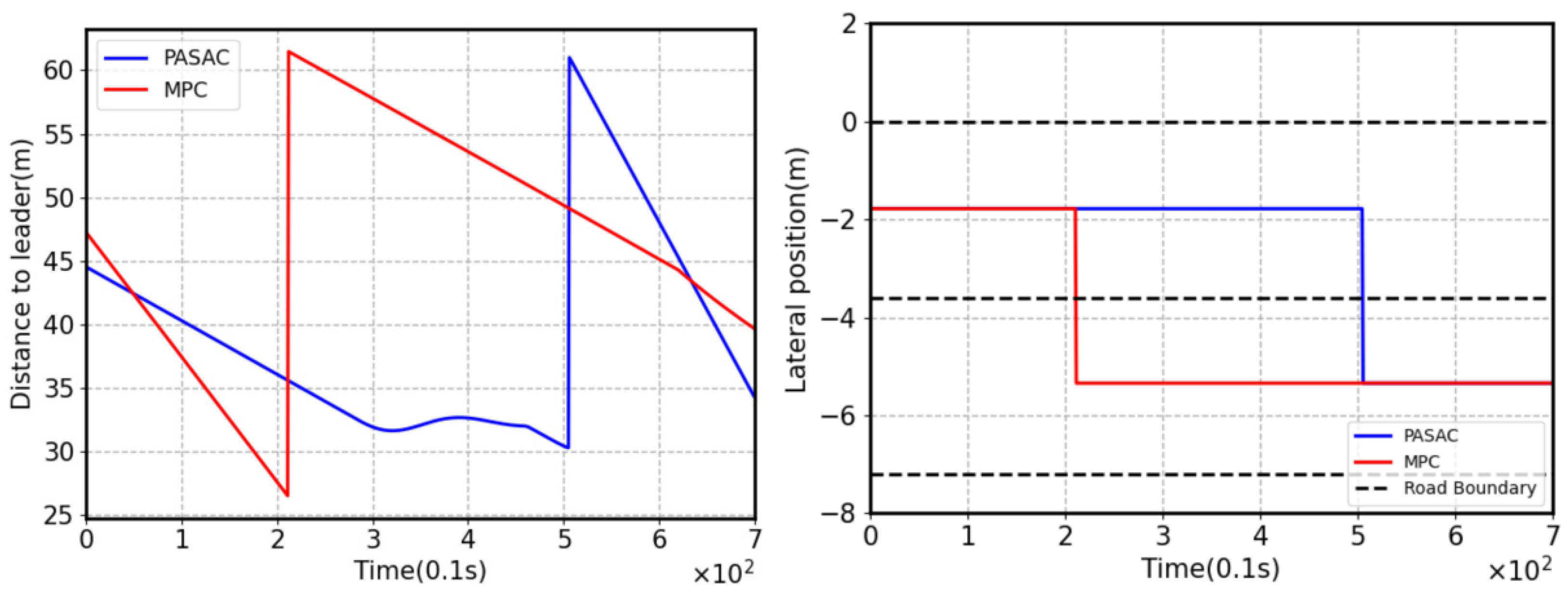
5.3. Comparison and Analysis
5.4. Generalization Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.N.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Hetrick, S. Examination of Driver Lane Change Behavior and the Potential Effectiveness of Warning Onset Rules for Lane Change or “Side” Crash Avoidance Systems. Master’s Dissertation, Virginia Polytechnic Institute & State University, Blacksburg, VA, USA, 1997. [Google Scholar]
- Nilsson, J.; Brännström, M.; Coelingh, E.; Fredriksson, J. Lane change maneuvers for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1087–1096. [Google Scholar] [CrossRef]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model predictive multi-objective vehicular adaptive cruise control. IEEE Trans. Control. Syst. Technol. 2010, 19, 556–566. [Google Scholar] [CrossRef]
- Ji, J.; Khajepour, A.; Melek, W.W.; Huang, Y. Path Planning and Tracking for Vehicle Collision Avoidance Based on Model Predictive Control With Multiconstraints. IEEE Trans. Veh. Technol. 2017, 66, 952–964. [Google Scholar] [CrossRef]
- Raffo, G.V.; Gomes, G.K.; Normey-Rico, J.E.; Kelber, C.R.; Becker, L.B. A Predictive Controller for Autonomous Vehicle Path Tracking. IEEE Trans. Intell. Transp. Syst. 2009, 10, 92–102. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, B.Y.; Shan, X.; Jia, W.H.; Lu, Z.F.; Xu, G. Model predictive control for lane keeping system in autonomous vehicle. In Proceedings of the 2017 7th International Conference on Power Electronics Systems and Applications-Smart Mobility, Power Transfer & Security (PESA), Hong Kong, China, 12–14 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Samuel, M.; Mohamad, M.; Hussein, M.; Saad, S.M. Lane keeping maneuvers using proportional integral derivative (PID) and model predictive control (MPC). J. Robot. Control (JRC). 2021, 2, 78–82. [Google Scholar] [CrossRef]
- Hang, P.; Lv, C.; Xing, Y.; Huang, C.; Hu, Z. Human-Like Decision Making for Autonomous Driving: A Noncooperative Game Theoretic Approach. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2076–2087. [Google Scholar] [CrossRef]
- Hang, P.; Lv, C.; Huang, C.; Cai, J.; Hu, Z.; Xing, Y. An Integrated Framework of Decision Making and Motion Planning for Autonomous Vehicles Considering Social Behaviors. IEEE Trans. Veh. Technol. 2020, 69, 14458–14469. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjel, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30, pp. 2094–2100. [Google Scholar]
- Hessel, M.; Modayil, J.; Van Hasselt, H.; Schaul, T.; Ostrovski, G.; Dabney, W.; Horgan, D.; Piot, B.; Azar, M.; Silver, D. Rainbow: Combining improvements in deep reinforcement learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32, pp. 3215–3222. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1587–1596. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1861–1870. [Google Scholar]
- Neunert, M.; Abdolmaleki, A.; Wulfmeier, M.; Lampe, T.; Springenberg, T.; Hafner, R.; Romano, F.; Buchli, J.; Heess, N.; Riedmiller, M. Continuous-discrete reinforcement learning for hybrid control in robotics. In Proceedings of the Conference on Robot Learning, Osaka, Japan, 30 October–1 November 2019; pp. 735–751. [Google Scholar]
- Hausknecht, M.; Stone, P. Deep reinforcement learning in parameterized action space. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Xiong, J.; Wang, Q.; Yang, Z.; Sun, P.; Han, L.; Zheng, Y.; Fu, H.; Zhang, T.; Liu, J.; Liu, H. Parametrized deep Q-networks learning: Reinforcement learning with discrete-continuous hybrid action space. arXiv 2018, arXiv:1810.06394. [Google Scholar]
- Bester, C.J.; James, S.D.; Konidaris, G.D. Multi-pass Q-networks for deep reinforcement learning with parameterised action spaces. arXiv 2019, arXiv:1905.04388. [Google Scholar]
- Li, B.; Tang, H.; Zheng, Y.; Jianye, H.A.O.; Li, P.; Wang, Z.; Meng, Z.; Wang, L.I. HyAR: Addressing Discrete-Continuous Action Reinforcement Learning via Hybrid Action Representation. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Mukadam, M.; Cosgun, A.; Nakhaei, A.; Fujimura, K. Tactical decision making for lane changing with deep reinforcement learning. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, P.; Chan, C.Y.; de La Fortelle, A. A reinforcement learning based approach for automated lane change maneuvers. In IEEE Intelligent Vehicles Symposium; IEEE: Piscataway, NJ, USA, 2018; pp. 1379–1384. [Google Scholar]
- Alizadeh, A.; Moghadam, M.; Bicer, Y.; Ure, N.K.; Yavas, U.; Kurtulus, C. Automated lane change decision making using deep reinforcement learning in dynamic and uncertain highway environment. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Auckland, New Zealand, 27–30 October 2019; pp. 1399–1404. [Google Scholar]
- Saxena, D.M.; Bae, S.; Nakhaei, A.; Fujimura, K.; Likhachev, M. Driving in dense traffic with model-free reinforcement learning. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 5385–5392. [Google Scholar]
- Wang, G.; Hu, J.; Li, Z.; Li, L. Harmonious lane changing via deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4642–4650. [Google Scholar] [CrossRef]
- Guo, Q.; Angah, O.; Liu, Z.; Ban, X.J. Hybrid deep reinforcement learning based eco-driving for low-level connected and automated vehicles along signalized corridors. Transp. Res. Part C Emerg. Technol. 2021, 124, 102980. [Google Scholar] [CrossRef]
- Vajedi, M.; Azad, N.L. Ecological adaptive cruise controller for plug in hybrid electric vehicles using nonlinear model predictive control. IEEE Trans. Intell. Transp. Syst. 2016, 17, 113–122. [Google Scholar] [CrossRef]
- Lee, J.; Balakrishnan, A.; Gaurav, A.; Czarnecki, K.; Sedwards, S. Wisemove: A framework to investigate safe deep reinforcement learning for autonomous driving. In Proceedings of the Quantitative Evaluation of Systems: 16th International Conference, QEST 2019, Glasgow, UK, 10–12 September 2019; pp. 350–354. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement learning. J. Cogn. Neurosci. 1999, 11, 126–134. [Google Scholar]
- Delalleau, O.; Peter, M.; Alonso, E.; Logut, A. Discrete and continuous action representation for practical RL in video games. arXiv 2019, arXiv:1912.11077. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent development and applications of SUMO-Simulation of Urban MObility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Wang, Z.; Cook, A.; Shao, Y.; Xu, G.; Chen, J.M. Cooperative merging speed planning: A vehicle-dynamics-free method. In Proceedings of the 2023 IEEE Intelligent Vehicles Symposium (IV), Anchorage, AK, USA, 4–7 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar]
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive active steering control for autonomous vehicle systems. IEEE Trans. Control Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]


| Parameters | Value | Weights | Value |
|---|---|---|---|
| −4.5 m/s2 | 3.13 | ||
| 2.6 m/s2 | 0.5 | ||
| 13.89 m/s | 0.4 | ||
| 25 m | 0.72 | ||
| −200 | 0.5 |
| Hyperparameters | Value | Hyperparameters | Value |
|---|---|---|---|
| Discount factor | 0.99 | Tau | 0.005 |
| Alpha | 0.05 | Learning starts | 500 |
| Actor learning rate | 0.0001 | Mini-batch size | 128 |
| Critic learning rate | 0.001 | Buffer size | 10,000 |
| Collision | Average Speed (m/s) | Lane Change Times | Reward (Cost) | Reward (Cost) Difference | |
|---|---|---|---|---|---|
| PASAC | 0% | 14.34 | 34 | −27.73 | 27.90% |
| MPC | 0% | 13.95 | 25 | −38.46 | 0% |
| Collision | Average Speed (m/s) | Lane Change Times | Reward (Cost) | Reward (Cost) Difference | ||
|---|---|---|---|---|---|---|
| Traffic flow density (veh/s ) | PASAC | 0% | 14.40 | 24 | −25.74 | 29.78% |
| MPC | 0% | 13.97 | 19 | −36.66 | 0% | |
| Traffic flow density (veh/s) | PASAC | 0.2% | 14.25 | 46 | −27.53 | 30.63% |
| MPC | 0% | 13.92 | 33 | −39.69 | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Liu, X.; Zheng, Z. Discretionary Lane-Change Decision and Control via Parameterized Soft Actor–Critic for Hybrid Action Space. Machines 2024, 12, 213. https://doi.org/10.3390/machines12040213
Lin Y, Liu X, Zheng Z. Discretionary Lane-Change Decision and Control via Parameterized Soft Actor–Critic for Hybrid Action Space. Machines. 2024; 12(4):213. https://doi.org/10.3390/machines12040213
Chicago/Turabian StyleLin, Yuan, Xiao Liu, and Zishun Zheng. 2024. "Discretionary Lane-Change Decision and Control via Parameterized Soft Actor–Critic for Hybrid Action Space" Machines 12, no. 4: 213. https://doi.org/10.3390/machines12040213
APA StyleLin, Y., Liu, X., & Zheng, Z. (2024). Discretionary Lane-Change Decision and Control via Parameterized Soft Actor–Critic for Hybrid Action Space. Machines, 12(4), 213. https://doi.org/10.3390/machines12040213







