Intelligent Numerical Control Programming System Based on Knowledge Graph

Abstract

With the wide application of computer-aided manufacturing (CAM) software, manufacturing enterprises have accumulated a wealth of numerical control (NC) programming data, providing valuable knowledge resources for new products’ development. Efficiently acquiring and reusing existing NC knowledge is essential for enhancing programming efficiency, improving product quality, and shortening manufacturing cycles. This study proposes an intelligent NC programming method based on knowledge graph. Firstly, the relevant knowledge in the NC programming domain is analyzed, and CAM knowledge elements are constructed to reduce the granularity of knowledge. Then, the ontology layer and data layer are constructed to achieve the development of the knowledge graph. Next, knowledge reasoning is performed on the knowledge graph through entity alignment and semantic rule-based reasoning. Furthermore, to address the issues of low reliability, limited applicability and need for frequent manual modifications in NC programming templates guided by the CAM knowledge graph, a CAM knowledge graph completion method based on neighborhood aggregation and semantic enhancement is proposed. Finally, an intelligent NC programming system based on knowledge graph is developed, and comparative experiments with mainstream algorithms on public datasets for few-shot knowledge graph completion are conducted, validating the effectiveness of the proposed method by experimenting with the key components of marine diesel engines.

1. Introduction

With the digital transformation of the manufacturing industry, computer-aided manufacturing (CAM) software has been widely used and has accumulated a substantial number of historical cases that provide valuable knowledge resources for the production of new products [1]. According to incomplete statistics, approximately 60% of workpieces with numerical control (NC) codes can reuse the existing ones, while less than 40% of workpieces require entirely new code development [2]. Currently, most enterprises rely on the subjective experience of programmers to select appropriate templates from NC programming template library based on manufacturing information of machining features during NC programming [3]. While this approach can reduce the number of programming interactions and improve efficiency to some extent, it is important to note that the accuracy and applicability of the templates may not be effectively guaranteed due to limitations in the experience of both developers and users of the NC programming templates. Moreover, the integration of computer-aided design (CAD)/computer-aided process planning (CAPP)/CAM systems remains limited, resulting in the dispersion of critical information required for NC programming across diverse manufacturing stages [4]. This fragmentation results in the independent storage of data, often in varied formats. The lack of a unified representation method and standardized interfaces for data transmission results in significant data dispersion, widespread distribution, and varied storage formats. This fragmentation hinders the effective reuse and sharing of data and knowledge, leading to significant resource wastage for enterprises [5]. Therefore, efficiently and accurately acquiring and reusing existing design achievement is a crucial strategy for enhancing programming efficiency and quality, as well as shortening the product manufacturing cycle.

Knowledge graph is a semantic knowledge description framework with a directed graph structure, characterized by its flexible semantic representation capabilities and rich knowledge structure models [6]. Compared to traditional relational databases, knowledge graph places greater emphasis on the semantic aspects of data [7]. Its emergence enables the representation of process knowledge models to encompass not only geometric features and manufacturing semantic information but also macro- and micro-level process knowledge for NC machining, along with the higher-level design intentions of designers [8]. Knowledge graphs not only overcome information barriers between data; they also leverage their advanced knowledge reasoning capabilities to significantly enhance enterprise knowledge management.

To address these problems, we propose an intelligent NC programming method based on knowledge graph. This method aims to deeply mine hidden information and rules from historical programming cases within enterprises, thereby enhancing the efficiency and quality of NC programming, while enabling effective reuse of existing NC programming achievements. Firstly, NC process knowledge is combined with existing NC machining cases from enterprises to analyze the characteristics of knowledge in the CAM domain, and CAM knowledge units are established. On this basis, the ontology layer and schema layer are modeled to achieve the construction of the CAM knowledge graph. Then, a CAM knowledge graph completion model based on neighborhood aggregation and semantic enhancement is proposed to address issues such as data sparsity and missing relationships within the CAM knowledge graph. Moreover, knowledge reasoning on the CAM knowledge graph is performed using the Jena reasoning framework and Semantic Web Rule Language (SWRL) to uncover implicit relationships between machining features and NC programming parameters. Finally, NC programming parameters for generated machining features are validated through practical examples, guided by the CAM knowledge graph.

In summary, this paper has the following merits:

• We propose CAM knowledge unit, which reduces the granularity of knowledge, and construct a CAM knowledge graph using the enterprise’s historical machining resource database, thus achieving the integration of manufacturing information.
• A CAM knowledge graph completion algorithm model based on neighborhood aggregation and semantic enhancement is proposed to address issues such as data sparsity and missing relationships between knowledge within the CAM knowledge graph.
• To improve the accuracy of knowledge graph applications, we define logical rules between entities to align and fuse multi-source descriptive information for the same entity across different knowledge graphs, and we construct a Jena-based reasoning framework to evaluate programming parameters.
• We develop a knowledge graph-based intelligent NC programming system, using actual machining parts from a diesel engine enterprise for experimentation. This system effectively enhances the reuse capability of historical case knowledge and improves the efficiency and intelligence level of NC programming.

The rest of the paper is organized as follows. In Section 2, we review the related works. In Section 3, some basic concepts and an overview of our approach are provided. Section 4 provides a detailed description of the method proposed in this paper. In Section 5, the experiments and analysis are provided. Section 6 covers the development of the prototype system and its application validation. Finally, we conclude the paper and present the future work in Section 7.

2. State of the Art

Intelligence NC programming is a prominent topic in the field of manufacturing automation, and a lot of research work has been carried out. After representing the NC process information as graph structure, knowledge graph is gradually introduced. Intelligence NC programming and knowledge graph are the key issues of the proposed work. To clearly present the innovation of this study, the related works can be grouped into four main sub-aspects: intelligence NC programming, knowledge graph application in intelligent manufacturing, knowledge graph completion, and knowledge graph reasoning.

2.1. Intelligence NC Programming

In recent years, propelled by advancements in 5G communication, big data, and artificial intelligence, NC programming has increasingly evolved towards greater levels of networking, integration, intelligence, and adaptability. CAD, CAPP, and CAM have long been widely utilized as separate modules within enterprises, operating independently with minimal interaction. However, as the concepts of collaborative and concurrent product design gain traction in the industrial sector, CAD, CAPP, and CAM are no longer isolated modules. The integration and sharing among these modules are becoming increasingly common, paving the way for the development of a fully integrated platform. This platform will ultimately enable the concurrent design and manufacturing of products.

Xiao W et al. [9] utilized the CATIA platform for secondary development and successfully achieved a comprehensive integration of CAD, CAM, and CNC systems by adopting STEP-NC as the data file model. Ferreira JCE et al. [10] designed and developed a CAD/CAPP/CAM-integrated system using the STEP-NC standard as the system’s data file model, enabling seamless integration from design to manufacturing for general surface parts. In the field of CAD/CAM/CAPP-integrated design technology, research has primarily utilized STEP-NC technologies to effectively address the challenges of information sharing across different domains in design and manufacturing. These technologies have facilitated information sharing between the CNC programming and process design stages. However, the systems primarily rely on standardized data formats and interfaces, which limit their scalability and interoperability. Additionally, they exhibit weak capabilities in understanding and associating semantic information.

Extensive research has been conducted on the NC programming knowledge reuse, achieving significant improvements in programming efficiency and quality. Asghar E et al. [11] employed a deep learning approach based on 3D convolutional neural networks to classify parts with similar geometric features and operational conditions. They created an operation library to facilitate the reuse of machining knowledge. Huang et al. [2] proposed an NC process planning method that integrates syntactic knowledge with deep learning techniques. This method constructs process knowledge and utilizes OR-graph representations of machining processes, incorporating attention mechanisms to learn the mapping rules between machining features and their corresponding processes. As a result, it facilitates the exploration of optimal process plans for various machining features. Deng et al. [12] introduced a part model retrieval method based on fuzzy subgraph matching, representing part models as attribute graphs. This approach transforms the model retrieval task into a fuzzy subgraph matching problem, effectively enabling the retrieval of complex part models and the reuse of process knowledge.

While these methods effectively leverage past case knowledge and achieve a certain degree of knowledge reuse, there are still issues with the granularity of knowledge. In practical production settings, NC programming tends to focus on building templates for specific machining steps based on particular machining features. Furthermore, the rigid format of these methods during knowledge reuse poses challenges for adapting to new types of machining features, thus limiting their applicability in practical scenarios.

2.2. Knowledge Graph Application in Intelligent Manufacturing

In recent years, knowledge graph-related technologies have been extensively researched and applied in the field of intelligent manufacturing, providing a new approach for the refined reuse of digital manufacturing outcomes [13]. Knowledge graphs offer significant advantages in knowledge representation, retrieval, storage, and reasoning. Li et al. [14] proposed a method for constructing a process knowledge graph for heterogeneous CAM models. They analyzed the characteristics of these models and developed a semantic representation through a schema layer, transforming multi-source, heterogeneous CAM knowledge into structured graph data. This approach enables the effective reuse of process knowledge. Hedberg et al. [15] utilized knowledge graphs as an information management tool to integrate manufacturing data across the design, manufacturing, and quality stages. This approach facilitates the construction of a digital thread covering the entire product lifecycle, supporting rapid traceability of product manufacturing context information and knowledge reuse tasks. GUO et al. [16] built a hybrid knowledge reasoning system on the foundation of an established process knowledge graph, overcoming obstacles related to the heterogeneity of process knowledge during decision-making. These studies demonstrate that the application of knowledge graph technology in intelligent manufacturing not only resolves information barriers between data but also significantly enhances enterprise knowledge management capabilities. Therefore, leveraging its superior knowledge reasoning capabilities to improve knowledge reuse and further deepen the application of knowledge graphs within enterprises is essential.

2.3. Knowledge Graph Completion

In practice, manually constructed knowledge graphs frequently suffer from significant omissions, and the continuous influx of large-scale information leads to numerous missing entities [17]. The issue of incomplete knowledge is a major constraint on the effectiveness of knowledge graphs in various application domains. Consequently, there has been growing interest in leveraging existing knowledge to predict missing entities, addressing this critical limitation. Extensive research has been conducted on knowledge graph completion (KGC), resulting in notable progress. This section discusses mainstream methods both in traditional knowledge graph completion and few-shot knowledge graph completion.

Traditional knowledge graph completion models generally project entities and relationships into low-dimensional continuous vector spaces to learn embeddings and infer missing facts. Recently, embedding models based on representation learning have been extensively studied. The TransE [18] model, for instance, was the first to use the translational invariance of word vectors to predict missing entities in triples, although it lacks the capacity to handle complex relationships such as one-to-many. To address this limitation, the Trans series models were subsequently proposed [19,20,21]. While these models improved predictive performance, they increased computational complexity and parameter scale. Dettmers et al. [22] introduced the ConvE model, which was the first to apply convolutional neural networks to knowledge graph completion tasks. As a non-linear model, ConvE output features are more expressive. Building on this, various convolutional models, such as ConvE [23], ConvKB [24], and ConvR [25], have been proposed to embed entities and relationships into complex vector spaces through different concatenations and reshaping of triples, capturing more features. Despite the significant progress in knowledge graph embedding models, these approaches rely heavily on abundant training instances, overlooking the common issue of insufficient training instances for dynamic feature updates in practical applications. Ma et al. [26] combined knowledge graph embedding models with pre-trained language models, utilizing textual descriptions of entities to significantly enhance knowledge representation capabilities. However, this approach treats textual information as independent instances, which makes it challenging to fully integrate knowledge graph structures with textual information, resulting in lower utilization of semantic features.

In knowledge graphs, a majority of the relationships contain only a small number of head–tail entity pairs. Traditional knowledge graph completion methods heavily rely on large training datasets, which can easily result in overfitting. Hence, it is imperative to develop few-shot completion techniques to improve the effectiveness and reliability of knowledge graphs in real-world applications. Current methods for few-shot knowledge graph completion can be categorized into two main types:

(1)

Metric Learning-Based Methods: These methods learn a similarity matching function between samples to identify the most similar samples to the reference ones. The GMatching [27] model was the first to define the few-shot knowledge graph completion task, using a neighbor encoder to aggregate one-hop neighbor structural information of entities and learning a metric function to match entity pairs. However, GMatching does not distinguish the importance of different neighbors, so it can introduce noise. To address this, FSRL [28] introduced a static attention mechanism to assign different weights to one-hop neighbors, obtaining richer entity information. Sheng et al. [29] proposed the FAAN model, which dynamically adjusts neighbor information weights based on different tasks, extending the previous methods but increasing task complexity.

(2)

Optimization-Based Meta-Learning Methods: These methods focus on learning the most crucial information from the support set to the query set. A typical model is MetaR [30], which defines the most important information in completion tasks through relational meta and gradient meta. Relational meta represents higher-order relations between entities, while gradient meta captures the loss gradients of relational meta information. Niu et al. [31] proposed the GANA model based on meta-learning, combining the Trans series models to aggregate neighbor information and fully considering complex relationships, such as 1-N, N-1, and N-N. Although these methods have made progress in few-shot knowledge graph tasks, they still face limitations, such as rigid or high computational cost in weighting aggregated neighborhood information and high dependency on pre-trained models when dealing with complex relationship types.

2.4. Knowledge Graph Reasoning

Knowledge reasoning is the process of deriving new knowledge from existing knowledge using specific methods. Through knowledge reasoning, hidden relationships between knowledge can be uncovered. Reasoning is the mental process of starting from reality, using existing knowledge and deriving new facts based on a certain strategy from the knowledge already obtained [32]. Currently, there are three main approaches to knowledge reasoning: reasoning based on representation learning, reasoning based on logical rules, and reasoning based on neural networks.

(1)

Knowledge reasoning based on representation learning: The core idea of reasoning algorithms based on representation learning is to find a mapping function that projects entities, relationships, and attributes in a semantic network into a low-dimensional real-valued vector space to obtain distributed representations. This approach captures implicit associations between entities and relationships. Researchers have proposed numerous reasoning methods based on representation learning, including those based on tensor decomposition [33,34], distance models [19,35], semantic matching [36,37], and multi-information models [38]. Representation learning has developed rapidly and shows great potential in knowledge representation and reasoning within large-scale knowledge graphs. This algorithm addresses the issue of data sparsity that logical rule-based algorithms cannot resolve, offering strong generalization capabilities and achieving reasonable results on large-scale knowledge graphs. However, it also has drawbacks, such as the lack of clear physical meaning in the vector values of entities and relationships, and poor interpretability. Additionally, reasoning based on representation learning only considers the constraints that the facts in the knowledge graph must satisfy, without considering deeper compositional information, thus limiting its reasoning capabilities.

(2)

Knowledge reasoning based on logical rules: Early knowledge reasoning primarily relied on logical rule-based reasoning. The fundamental idea is to leverage traditional rule-based reasoning methods and apply simple rules or statistical features to knowledge graphs. It mainly includes logical rule-based reasoning [39,40] and ontology-based reasoning [41]. The advantages of logical rule-based reasoning algorithms are their solid mathematical foundation and strong interpretability. When combined with large-scale parsed corpora and background knowledge, these algorithms can emulate human reasoning and capture hidden semantic information within knowledge graphs, making it possible to leverage prior knowledge to support and enhance reasoning. However, the nodes in knowledge graphs often follow a long-tail distribution, where only a small number of entities and relationships occur frequently, while a majority have low occurrence rates. Consequently, logical rule-based reasoning struggles to address data-sparsity issues, cannot effectively handle multi-hop reasoning, and significantly impacts reasoning performance.

(3)

Knowledge reasoning based on neural networks: The construction of deep learning models is partly inspired by the multi-layered biological neural networks structure of the human brain, simulating how the brain combines lower-level features to form more abstract, higher-level features. Neural network-based reasoning possesses stronger generalization and learning capabilities, combining the representation learning methods through multiple nonlinear layers and then representing their deep features for knowledge reasoning. This includes reasoning approaches based on convolutional neural networks [42], recurrent neural networks [43], and reinforcement learning [44]. Neural network-based methods have higher learning, reasoning, and generalization capabilities. They can leverage vast amounts of textual data, addressing the data-explosion problem posed by large-scale knowledge graphs, and directly model fact triples, thereby reducing computational complexity. Furthermore, with appropriate design and the use of auxiliary storage units, these methods can partially simulate the human brain’s process of reasoning and problem-solving. However, the increased complexity of these models also leads to poorer interpretability.

3. Basic Concepts and Overview of Proposed Approach

In this section, we first define some basic concepts and then briefly outline our approach

3.1. Basic Concepts

In the context of reusing historical NC programming cases, in order to reduce the granularity of knowledge and enhance the flexibility and versatility of knowledge reuse, we define the fundamental unit of NC programming knowledge as the CAM Knowledge Unit. It refines NC programming knowledge down to specific machining features of a part and their corresponding machining operations.

Definition 1

(CAM Knowledge Unit (CKU)). It is composed of machining features and their corresponding machining operations, encompassing manufacturing semantic information, such as geometric information, process planning, and machining requirements of the machining features. It can be denoted as follows:

$$CKU=\left[MF,PO\right],$$

(1)

where MF is the NC machining feature unit of a part, PO is the corresponding machining operation for the feature unit, and the relationship between features and machining operations is 1-N.

Definition 2

(Manufacturing feature (MF)). It is a set of features with specific machining attributes, such as machining methods, cutting tools, precision requirements, etc. It comprises manufacturing semantics, geometric information, and topological information. It can be denoted as follows:

$$MF=SI\cup GI\cup TI,$$

(2)

where SI is manufacturing semantic information, which includes basic attributes of the machining features, such as material type, tolerances, and roughness levels; GI is geometric information, which encompasses the shape, structure, dimensions, and positional details of the machining features; and TI is topological information, describing the connectivity between different parts of the machining features, including relationships such as adjacency, perpendicularity, and parallelism.

Definition 3

(Process operation (PO)). It is the specific cutting or forming steps required to achieve the machining features, consisting of NC process information, NC programming parameters, and workshop information. It can be denoted as follows:

$$PO=PI\cup NI\cup MI,$$

(3)

where PI is NC process information, including machining stages (roughing, finishing, semi-finishing), machining methods (turning, milling, drilling, etc.), and machining allowances. NI is NC programming parameters, including machining templates, strategies, and post-processors. MI denotes workshop information, encompassing tool details, machine model, and operator information.

Figure 1 shows the structure of the CAM knowledge unit, where a single machining feature serves as the fundamental unit. The NC machining process of a component is optimized and composed of multiple CAM knowledge units corresponding to various features to be processed.

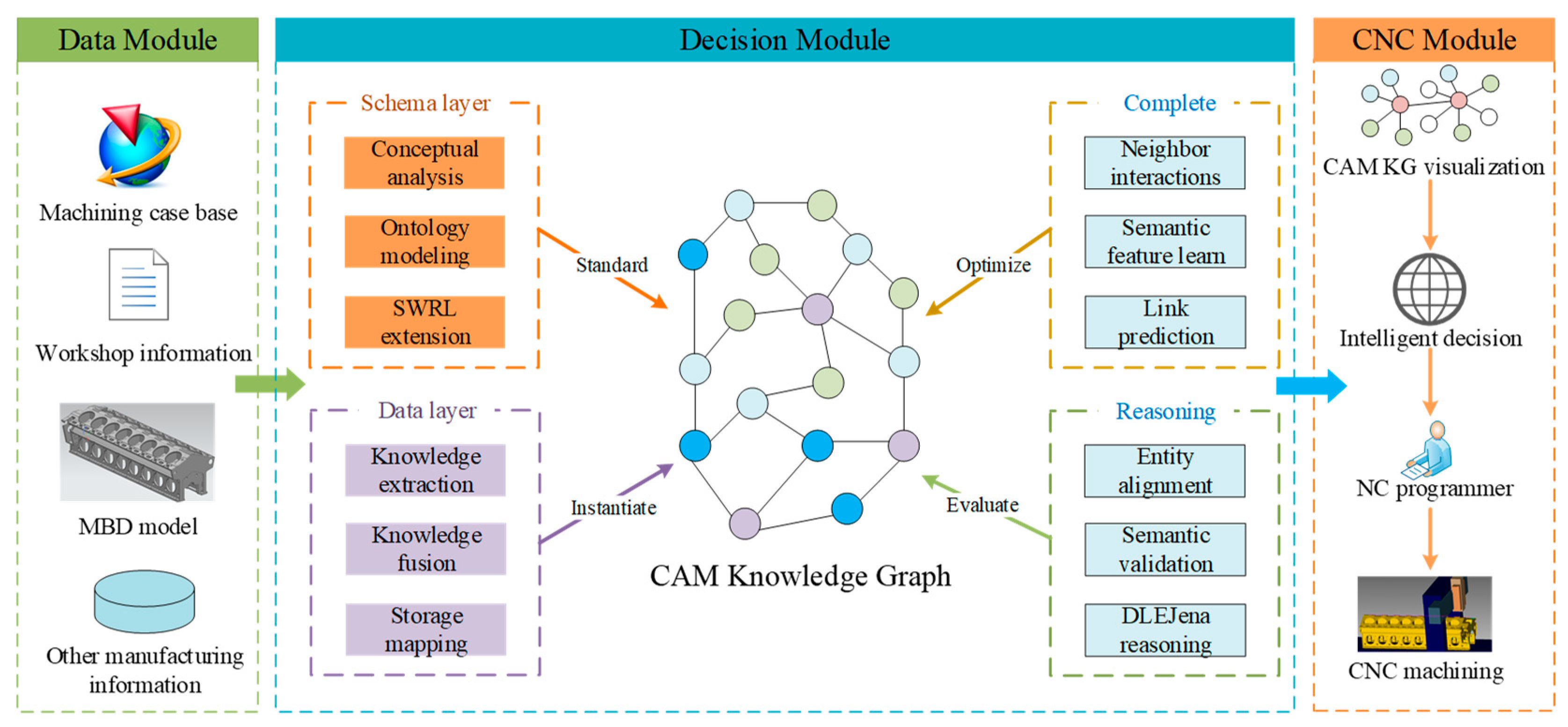
3.2. Overview of Approach

Figure 2 shows the general framework of our approach. This framework involves three parts: data module, decision module, and CNC module. Here, we give a brief description of each part:

(1)

(Data module: To support the knowledge graph decision module, it is essential to collect manufacturing information that influences NC programming decisions, as well as historical NC programming cases generated during manufacturing processes. This includes data such as MBD models (e.g., process planning and geometric features), workshop information (e.g., tooling and machine tool data), and other relevant manufacturing information (e.g., material properties and personnel details).

(2)

Decision module: Emulate the decision-making process of NC programming experts to determine optimal programming parameters for machining features. It includes the knowledge graph schema layer and ontology layer construction, and knowledge graph complete and reasoning. The knowledge graph construction module provides semantic and data support for the NC programming system. Knowledge graph complete and reasoning modules ensure the reliability of the generated NC programming parameters.

(3)

CNC module: Following evaluation and optimization, the CAM knowledge graph will be mapped to a machining template and visualized in graph format, accompanied by suggestions for further evaluation and optimization. Programmers will review the optimized template in conjunction with the knowledge graph and reasoning recommendations, and then the reviewed template is used for production machining.

4. Methodology

4.1. Knowledge Graph Construction

The construction methods of a knowledge graph are mainly divided into top-down and bottom-up approaches. The top-down approach begins with the top-level concepts, subsequently constructing the schema layer before building the data layer through information extraction. This method is suitable for the construction of knowledge graphs in specialized domains. The bottom-up approach involves extracting high-confidence entities from databases to be added to the knowledge base, followed by constructing the top-level ontology schema, and doing so is suitable for common-sense knowledge. The CAM knowledge graph is designed for professionals in the NC programming field, which demands a high level of expertise. Consequently, a top-down construction method is employed.

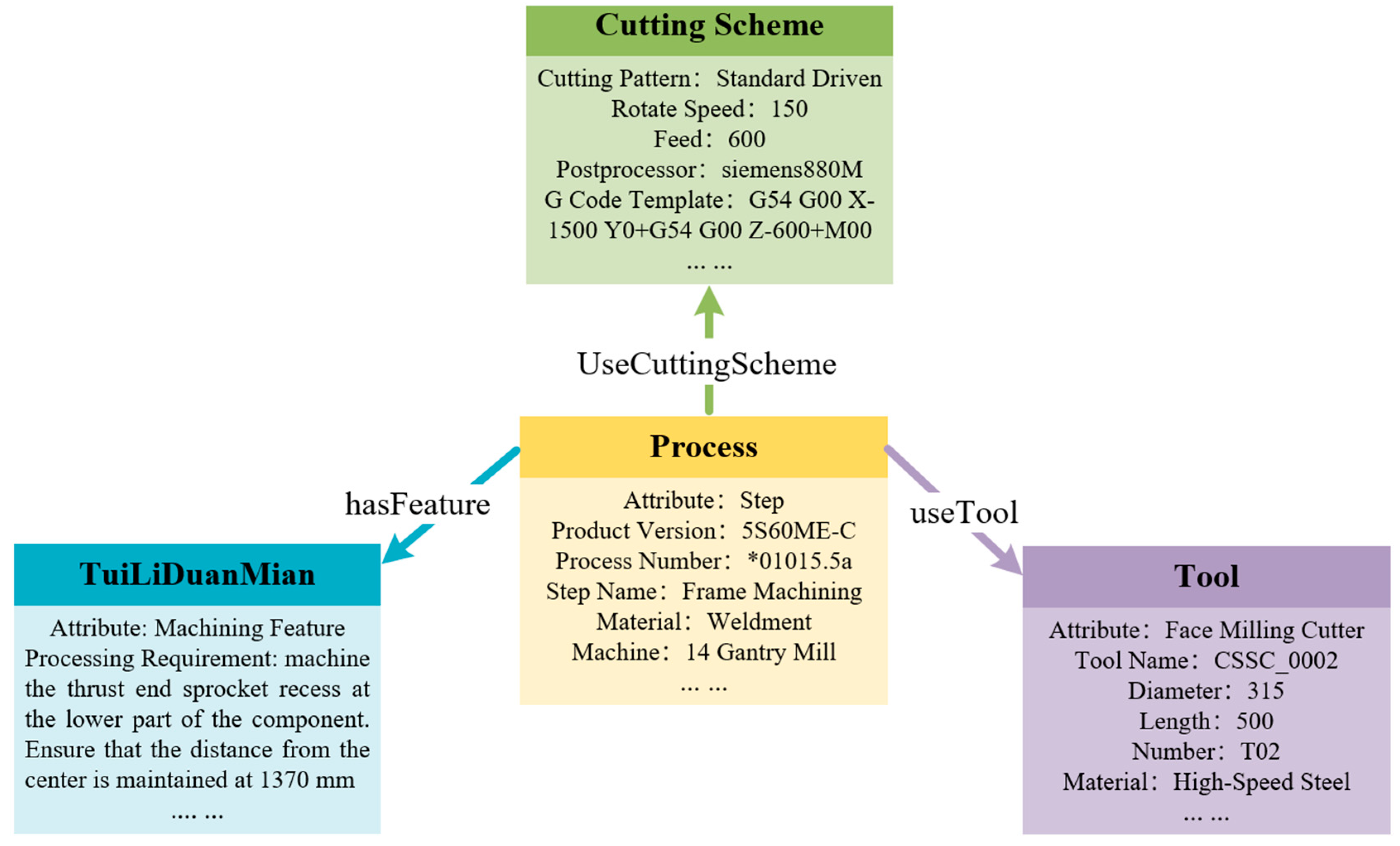
4.1.1. Ontology Modeling

Ontology model is a formal representation of multiple concepts and their interrelationships within a complex domain. By combining relevant data and historical NC programming cases from the CAM field, and considering the perspective of NC programmers, the workpiece to be machined can be used as a bridge to link various individual concepts in the CAM domain, enabling clear and effective expression of knowledge in the NC programming field. The ontology for the CAM knowledge graph can be modeled as follows:

$$O=〈C,R,P,I〉,$$

(4)

where O represents the ontology; C represents the basic classes, indicating sets of entities of the same type; R represents the logical relationships, indicating the interrelationships between concepts; P represents the properties, indicating the attributes and values that concepts possess; and I represents the instances, indicating specific instances of a basic class. The basic steps for constructing the ontology in the CAM domain are as follows: (1) determine the basic classes of the ontology model; (2) construct the object properties of the basic classes; (3) define the hierarchy of classes and subclasses; (4) define data property constraints; and (5) create ontology instances. Figure 3 show the CAM knowledge graph ontology model.

4.1.2. Semantic Rule Extension

Much of the knowledge in the CAM domain comes from the technical experience accumulated over time by NC programming personnel. This knowledge is often inferential and highly experiential, such as the rules for selecting cutting modes for the features to be machined, the methods for tool entry and exit in the machining area, and the selection of tools. Such knowledge is semantic and cannot be fully represented by a constructed ontology model alone, as it may not effectively express the relationships between class attributes. SWRL, a Semantic Web Rule Language that combines Web Ontology Language (OWL) and Rule Markup Language (RuleML), is used to extend the ontology with rules to uncover implicit knowledge. To enhance the semantic reasoning capabilities of the CAM knowledge graph, this paper analyzes and summarizes the experiential knowledge provided by experienced NC programming personnel and experts, and it constructs multiple SWRL semantic rules to capture the complex semantic relationships between ontology concepts. SWRL rules consist of a precondition and a conclusion, both of which are composed of several atoms. The rules are logically connected by ‘or’, and within each rule the atoms are connected by ‘and’. Figure 4 shows the partial NC programming parameter setting rules.

4.1.3. Feature Information Extraction

Feature information is composed of manufacturing semantics, geometric elements, and geometric topology relationships. The information that needs to be extracted for each component is as follows:

• Manufacturing semantics: Manufacturing semantics describe the intended meaning of the manufacturing feature, including the material of the part, the type of manufacturing feature, and the basic requirements of the feature. Typically, manufacturing semantic information is defined and stored in the MBD model during the CAD/CAPP stages.
• Geometric elements: Geometric elements encompass the geometric attributes of the manufacturing feature, including the basic dimensions of the feature and its basic positional information.
• Geometric topology: Geometric topology information is used to describe the geometric shape and structure of the feature, including the relative position of features, the basic structure of the feature, and the dependencies between features.

Using feature recognition technology, the geometric elements and topology information of features are obtained from CAD solid models. Through the API interface of CAM software, the process-planning information corresponding to machining features in the MBD model, as well as other relevant manufacturing information that influences CAM programming decisions (such as the status of machining equipment, like machine tools and tools), is retrieved. The acquired process information, feature dimensions, machining operation information, and other structured information are then stored in a relational database. As shown in Figure 5, the manufacturing information extraction process for the connecting rod feature of a marine diesel engine is illustrated.

4.1.4. Construction

Based on the structured characteristics of NC programming information in the relational database, an ontology-based DM mapping method is used to map the information in the database to an ontology, generating RDF triple files. These files contain all the information that influences NC programming decisions, including feature geometry information, process planning, material characteristics, tools, and machine tools. However, querying RDF triples by using the SPARQL language is relatively inefficient and lacks knowledge graph visualization capabilities. Neo4j graph database, on the other hand, offers better visualization and efficient retrieval capabilities, making it suitable for the visual display of the CAM knowledge graph in this study.

Due to the differences in representation between RDF triples and Neo4j graph databases, a mapping process is required, which follows these mapping rules: (1) The subject and object in RDF are mapped to nodes in Neo4j. (2) The attributes of RDF subjects and objects are mapped to attributes of Neo4j nodes. (3) Unique identifiers are assigned to RDF subjects and objects to facilitate association and querying. (4) The predicate in RDF is mapped to relationships in Neo4j. As shown in Figure 6, the instance knowledge graph of the ‘precision milling of the lower surface’ machining operation is stored in Neo4j after applying the RDF-Neo4j mapping rules.

4.2. Knowledge Reasoning

In practical NC machining processes, due to the complexity of machining features and the dynamic changes in the state of machining equipment, the NC programming templates generated from CAM knowledge graphs by directly retrieving instances of machining feature knowledge graphs often fail to fully meet the requirements of actual machining tasks. It is necessary to evaluate and adjust the parameters within the matched instance knowledge graphs based on specific conditions and requirements. Therefore, this paper proposes a knowledge reasoning method tailored to knowledge graphs.

4.2.1. Entity Alignment

In the process of information integration, it is common for a single real-world entity to correspond to multiple nodes within different knowledge graphs. This phenomenon often results in data redundancy and information ambiguity within the CAM knowledge graph. To address these issues, this paper proposes the fusion of multi-source descriptive information of the same entity or concept by defining logical rules between entities. As shown in Equation (5), the logical rules for entity alignment are established.

$$\begin{array}{l}\forall e_i,e_j,e_k,e_l\in E,\forall r{e}_1,r{e}_2,r{e}_3,r{e}_4\in Re\\ \exists (e_i,r{e}_1,e_j)\wedge (e_j,r{e}_2,e_k)\wedge (e_k,r{e}_3,e_l)\Rightarrow (e_i,r{e}_4,e_l),\end{array}$$

(5)

where $e$ represents individual entities in the knowledge graph, E is the set of all entities, $re$ denotes the relationships between entities, and $Re$ is the set of all relationships between entities. The rule can be expressed as follows: if entity $e_i$ has a relationship ($r{e}_1$) with entity $e_j$, entity $e_j$ has a relationship ($r{e}_2$) with entity $e_k$, and entity $e_k$ has a relationship ($r{e}_3$) with entity $e_l$, then it can be inferred that entity $e_i$ has a relationship ($r{e}_4$) with entity $e_l$. An example of this rule in the CAM knowledge graph is as follows: (hub surface, machining plan, and face milling); (face milling, cutting mode, and standard drive); (standard drive, cutting parameters, and climb milling); and (hub surface, cutting direction, and climb milling).

By defining logical rules between entities, entities in the CAM knowledge graph can be aligned with entities in the machining instance knowledge graph, thereby enabling knowledge expansion of the instance knowledge graph. For example, after knowledge expansion, if a tool node ‘CSSC_0031’ exists in the instance knowledge graph, it will be linked and associated with the entity named ‘CSSC_0031’ in the CAM knowledge graph. This association allows the retrieval of detailed information about the tool, such as its wear value, remaining service life, and other relevant data.

4.2.2. Knowledge Reasoning Based on Semantic Rules

In the ontology layer of the CAM knowledge graph, SWRL rules can express simple logical relationships and reasoning rules, but they still have limitations, particularly in terms of scalability in real-world production environments. The purpose of knowledge reasoning is to infer potential knowledge within the CAM knowledge graph under the support of OWL ontology and SWRL semantics in the schema layer. SWRL rules support user-defined plugins, and using a reasoner, complex reasoning operations can be performed in conjunction with the ontology, thereby enhancing the reasoning capabilities of the knowledge graph [21]. Jena is an open-source Java framework specifically designed for building semantic web and linked data applications. It supports the creation, querying, and manipulation of Resource Description Framework (RDF) graph data. This paper designs a reasoning framework, which integrates Jena’s RDF processing capabilities with Pellet’s logical reasoning capabilities, enabling complex logical reasoning.

By leveraging the RDF processing capabilities of the Jena semantic framework, semantic validation can be performed. Using the ‘ReasonerRegistry’ class in the Jena framework, an ontology reasoner (Reasoner) is created, and a Model data model is built to load the knowledge graph. The ‘Reasoner.validate().isValid()’ method is then called to conduct a semantic check. If the result indicates no ambiguities, knowledge reasoning is performed; however, if ambiguities are detected, the entities can be manually edited based on the reason provided to resolve the ambiguity before proceeding.

The reasoning process based on Jena can be divided into three steps:

(1)

Creating the Pellet reasoner: The ‘PelletReasonerFactory’ class is used in a factory pattern to create a Pellet reasoner. Pellet is a high-performance reasoner that supports SWRL rules, allowing it to conduct semantic reasoning based on strict inference rules. It is capable of quickly handling large-scale and complex reasoning tasks, and it provides an adaptation interface for the Jena framework.

(2)

Creating the ontology model: The Pellet reasoner is passed as a parameter to the ‘ModelFactory.Create’ function in the Jena framework, which is used to create the ontology model. Once the ontology model ‘InfoModel’ is obtained, SWRL rules from the schema layer are loaded into the ‘InfoModel’.

(3)

Binding the data model: The data model ‘Model’ is then bound, which triggers events. The ontology model ‘InfoModel’ automatically performs rule-based and ontology reasoning as a result of this process [22].

As illustrated in Figure 7, this describes the Jena reasoning framework.

During the reasoning process, new triple knowledge is generated. If the predicate of the newly inferred triples overlaps with the predicates of existing knowledge in the graph, it indicates that the original knowledge does not meet the current programming requirements. In such cases, knowledge replacement is necessary, meaning that the newly inferred triples should be used to overwrite the existing knowledge.

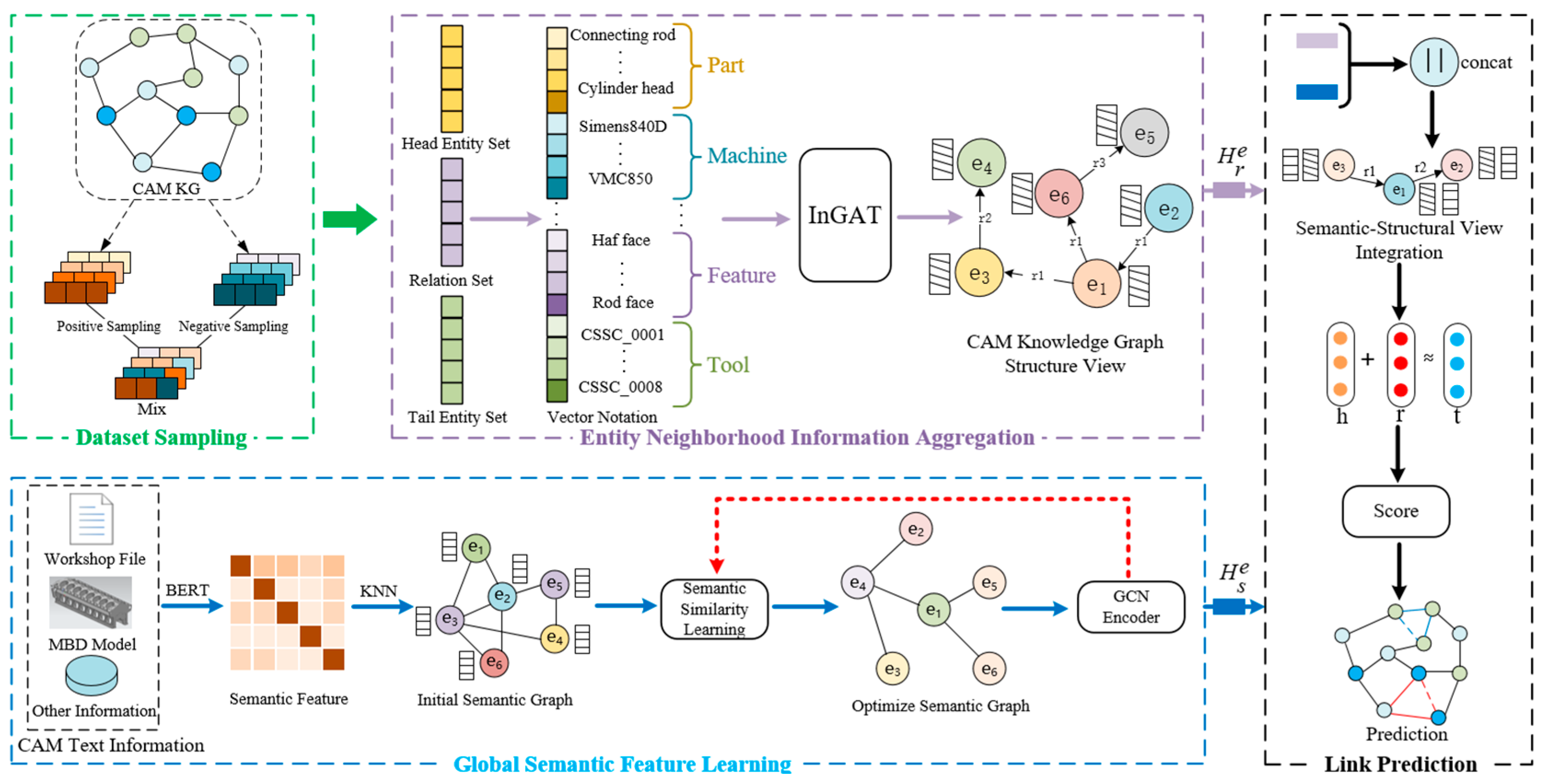
4.3. CAM Knowledge Graph Completion

In NC machining, the programming templates generated by the CAM knowledge graph are suitable for processing simple parts. However, NC programming knowledge is often dispersed across various stages of manufacturing, characterized by sparsity, complex relationships, and multi-source heterogeneity. Consequently, manually or automatically constructed CAM knowledge graphs often suffer from poor completeness, low accuracy in knowledge reuse, and missing relationships between entities. When applied to complex parts, the templates generated by the CAM knowledge graph may contain parameter errors, necessitating repeated manual adjustments by programmers and limiting their applicability.

To enhance the reliability of knowledge graph in NC programming applications, it is necessary to perform knowledge graph completion (KGC) on the constructed knowledge graph, enabling them to be effectively used in real-world NC programming tasks. KGC is a task focused on inferring and filling missing information within a knowledge graph. In this process, algorithms analyze existing entities and relationships to predict and incorporate missing links or attributes, thereby enhancing the graph’s overall completeness and utility. Figure 8 shows a case study of knowledge graph completion; for this CAM knowledge graph, the completion task is to infer the missing entity represented by ‘?’ in the triple (φ50Hole, hasOperation, and ‘?’). After completion, the top five candidate entities are obtained based on their scores, with the highest-scoring entity identified as the missing entity. The abovementioned method is the traditional method for knowledge graph completion, which predicts missing entities based on existing entities and relationships. This approach relies on a large number of training samples.

Given the limited number of triple samples and the presence of long-tail relationships in the CAM knowledge graph, traditional knowledge graph completion methods are prone to overfitting when applied to CAM knowledge graphs. Long-tail relationships refer to cases where a few relationships occur very frequently in the data, while a majority are rare, appearing only a few times. Therefore, it is crucial to adopt a few-shot completion method specifically for CAM knowledge graphs. This involves designing a few-shot triple learning model that leverages the existing knowledge graph structure and sparse data samples to effectively capture knowledge from heterogeneous information, such as textual information, image information, and temporal information. The model should establish a triple relationship scoring function to solve link prediction problems such as (‘h’, ‘r’, and ‘?’) or (‘?’, ‘r’, and ‘t’), where ‘?’ represents the missing part of the triple, thereby improving the effectiveness and reliability of the knowledge graph in practical applications.

In response to the above issues, this paper proposes a CAM knowledge graph completion model based on neighborhood aggregation and semantic enhancement (NS-KGC). The model comprises four modules: dataset sampling, entity neighborhood information aggregation, global semantic feature learning, and link prediction, as shown in Figure 9. (1) Dataset sampling module: This module primarily performs negative sampling on the CAM knowledge graph triples to generate negative example triples. By mixing positive and negative example triples, it expands the training dataset and enhances the model’s ability to distinguish and infer triples. (2) Entity neighborhood information aggregation module: This module incorporates a multi-head self-attention mechanism to aggregate neighborhood features. Through the attention function, it learns the importance of neighboring entities relative to the central entity based on relational paths, ultimately obtaining aggregated features at each layer. This process captures the structural information within the CAM knowledge graph, improving the representational capacity and effectiveness of feature aggregation. (3) Global semantic feature learning module: This module embeds manufacturing information from various stages of the NC programming process into word embeddings, creating a CAM semantic graph. It applies Graph Convolutional Networks (GCNs) for iterative learning and optimization, generating global semantic features for entities. (4) Link prediction module: This module integrates the feature vectors from the entity neighborhood information aggregation module with the global semantic features. Under a scoring function, it ranks candidate triples based on their scores to derive the best prediction results.

4.3.1. Dataset Sampling Module

In the CAM domain knowledge graph, the positive triples only describe factual knowledge related to the NC programming process. The quality of the triple training set is a key factor affecting the efficiency of knowledge graph completion algorithms. By performing negative sampling on the positive triples, the training set size can be expanded, which benefits the algorithm’s ability to efficiently learn the information between triples and enhance its reasoning capabilities [19,20]. Negative sampling of triples involves randomly replacing the head and tail nodes of triples, as shown in Equation (6):

$${\overline{S}}_{(h,r,t)}=\{(\overline{h},r,t)\notin S\left|\overline{h}\in \epsilon \right.\}\cup \{(h,r,\overline{t})\notin S\left|\overline{t}\in \epsilon \right.\},$$

(6)

where S denote the set of positive triples; $\overline{\mathrm{S}}$ denote the set of negative triples; E represents the set of entities; and $(\overline{h},r,t)$ and $(h,r,\overline{t})$ represent the negative triples generated by replacing the head entity or tail entity, respectively. During negative sample generation, replacing the relationship (r) can result in incorrect negative triples. Therefore, the replacement method shown in Equation (7) cannot be included in the set of negative triples.

$$\{(h,\overline{r},t)\notin S\left|\overline{r}\right.\in R\}$$

(7)

The mixed sampling module labels the obtained set of negative triples, introduces the set of positive triples, and combines the two using a certain mixing coefficient. A margin-based loss function is employed as the training objective to optimize the model. The loss function is shown in Equation (8):

$$\mathcal{L}={\displaystyle \sum _{(h,r,t)\in S}{\displaystyle \sum _{(\overline{h},r,\overline{t})\in \overline{S}}\max }}(\gamma +f(\overline{h},r,\overline{t})-f(h,r,t),0),$$

(8)

where the calculation method for $f(h,r,t)$ is shown in Equation (9):

$$f(h,r,t)=-{‖h+r-t‖}_1,$$

(9)

where $\gamma$ represents the margin between positive and negative samples. When $\left(\gamma +f(\overline{h},r,\overline{t})-f(h,r,t)\right)>0$, the loss function takes the original value; otherwise, it takes 0, aiming to maximize the distance between the most similar positive and negative triplets.

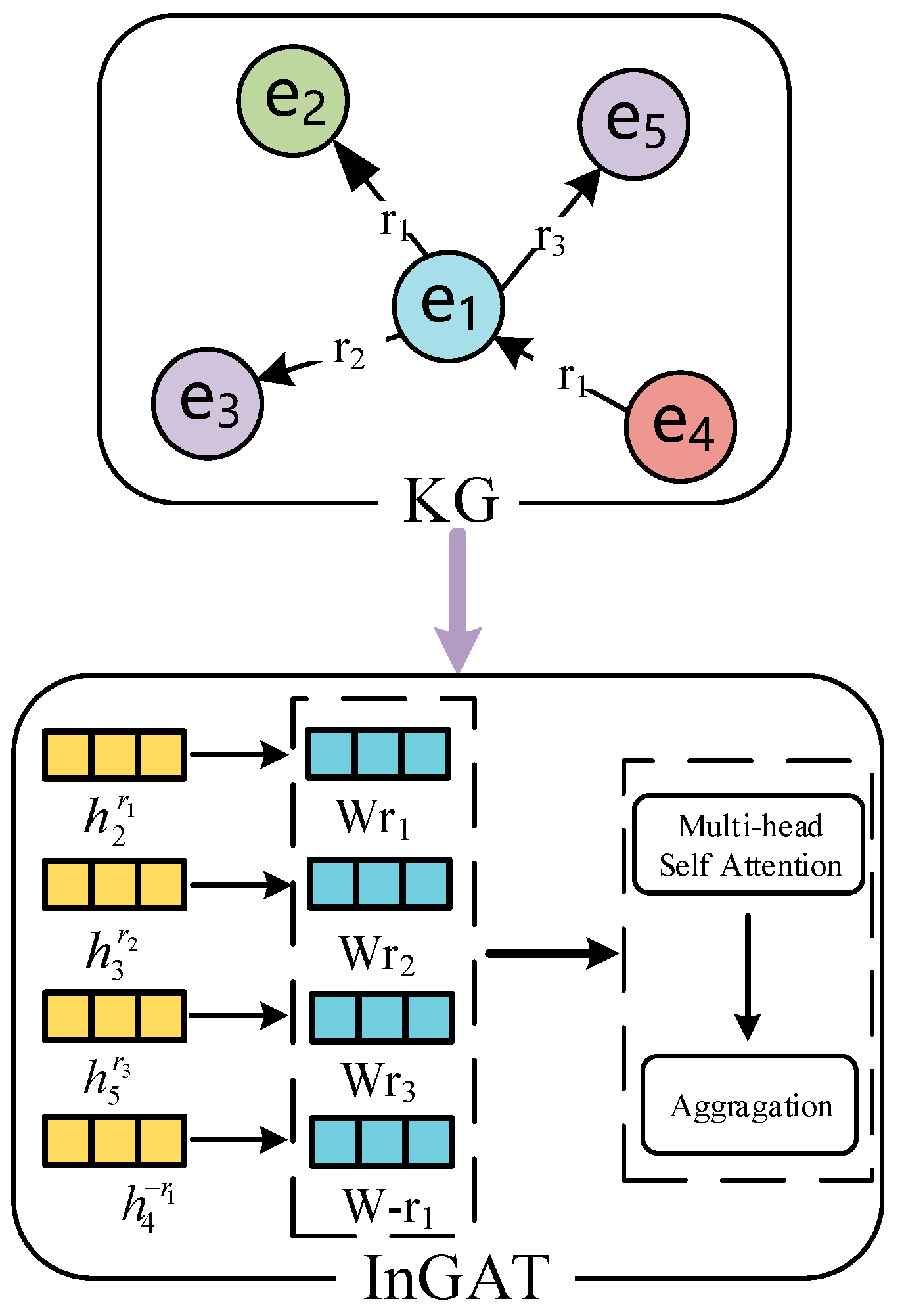
4.3.2. Entity Neighborhood Information Aggregation Module

In the CAM knowledge graph, there are various types of entities, and the relationships between entities are diverse and heterogeneous. Entities connected by different types of relationships may reside in different embedding spaces. Directly aggregating all neighboring entities can lead to semantic confusion, heterogeneous embedding spaces, and information redundancy. Therefore, this paper proposes a neighborhood information aggregation method based on relational paths. By leveraging an attention mechanism to select important neighboring features along relational paths, this approach effectively captures semantic information in complex relationships and enhances the model’s representation capability and performance in knowledge graph completion tasks. Figure 10 illustrates the principle of neighborhood information aggregation.

Firstly, entity $h_i^{\left(0\right)}$ and relation $h_r^{\left(0\right)}$ are taken as inputs, and entities within the neighborhood based on relations are aggregated, as shown in Equation (10).

$$H={\displaystyle \sum _{j\in N_i^r}{h}_j^{\left(l\right)}},$$

(10)

where $N_i^r$ represents the set of entities based on relation $r$ and central entity $i$, $h_j^{\left(l\right)}$ denotes the j-th entity in the l-th layer, and H represents the aggregated neighborhood entity features. The importance of neighborhood entities relative to the central entity is learned through an attention function, as shown in Equations (11) and (12):

$$e_{ij}^r={\alpha }^T\left(\left[W_n{h}_i^l\parallel W_n{h}_j^l\right]\right)$$

(11)

$${\alpha }_{ij}^r=\mathrm{softmax}\left(e_{ij}^r\right)={\displaystyle \frac{\exp \left(e_{ij}^r\right)}{{\displaystyle {\sum }_{k\in N_i^r}\exp (e_{ik}^r)}}},$$

(12)

where $e_{ij}^r$ denotes the attention score that measures the relevance or importance of entity j to entity i under the relation r; $e_{ij}^r$ higher value indicates a greater influence; ${\alpha }^T$ represents the transpose of the attention vector; $W_n$ is the weight matrix used for the linear transformation of entity features $h_i^l$ and $h_j^l$; $\parallel$ denotes the concatenation of the transformed features of entity i and entity j; and ${\alpha }_{ij}^r$ is the attention weight that signifies the importance of entity j to entity i. The attention scores are converted into a probability distribution using the softmax function, ensuring that the sum of the attention weights of all neighborhood entities is 1. The entity i neighborhood aggregation method based on relation r is given by Equation (13):

$$H_r^e={\displaystyle \frac{1}{\left|N_i^r\right|}}·{\displaystyle \frac{1}{K}}{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{j\in N_i^r}{\alpha }_{ij}^{r\left(k\right)}{h}_j^{\left(l\right)}}},$$

(13)

where $H_r^e$ represents the aggregated features of all neighborhood entities of entity i at layer l under relation path r, $\left|N_i^r\right|$ denotes the number of neighborhood entities of entity i under relation r, and K represents the number of attention heads in the multi-head attention mechanism. By applying the multi-head attention mechanism, the features of the neighborhood entities are weighted and summed, ultimately yielding the aggregated features of entity i at layer l.

This feature aggregation method, based on the multi-head attention mechanism, employs multiple independent attention mechanisms simultaneously. This allows the model to focus on and integrate the features of neighborhood entities from multiple perspectives, thereby enhancing the model’s stability and its capacity for semantic representation.

4.3.3. Global Semantic Feature Learning Module

The CAM domain encompasses a wide range of knowledge with diverse types. In knowledge graphs, entities correspond to manufacturing semantic information such as workshop details, feature information, and process planning in practical NC programming. By utilizing API functions provided by CAM software, process information, feature dimensions, and machining operation details can be extracted from NC programming cases and categorized and stored in a database [3]. Based on the extracted CAM manufacturing semantic information, a semantic graph is modeled and iteratively learned to obtain the optimal global semantic embeddings for entities. Figure 11 illustrates an example of a semantic graph for the machining feature ‘thrust end sprocket recess’. Tokenization is used to segment CAM text information, combining word embeddings, paragraph embeddings, and positional embeddings ([CLS] + Tok1 + Tok2 + … + Tokn + [SEP]) as inputs to the BERT model. The preprocessed text data are fed into the pre-trained BERT model to obtain encoded representations of the text information. The BERT model outputs hidden states for each word vector, which can be used to represent the initial semantic features of entities, $V_s$ [23].

In the global semantic feature learning module, the semantic graph visually represents the NC programming and manufacturing semantic relationships between entities, providing authentic and comprehensive manufacturing information for the CAM knowledge graph. An initial semantic graph is created using the K-Nearest Neighbors (KNNs) algorithm [24], where cosine similarity is used to measure the similarity between semantic features of each entity. Similarity scores are ranked, with the top K semantic feature values set to 1 and the remaining values set to 0. The calculation process is described in Equation (14):

$$A_{i,j}^0=\{\begin{array}{c}1, rank\left(S_{i,j}^0,S_i^0\right)\le k\\ 0, else\end{array},$$

(14)

where $S^0$ and $A^0$ represent the similarity matrix and adjacency matrix of the initial semantic graph, respectively; $S_i^0$ denotes the set of similarity matrix elements in the i-th row; $S_{i,j}^0$ represents the j-th element in the i-th row of the similarity matrix; and rank $\left(S_{i,j}^0,S_i^0\right)$ indicates the rank of $S_{i,j}^0$ when all elements in the i-th row are sorted in descending order. To obtain a semantic graph that best represents global semantic features, the created initial semantic graph is encoded using a Graph Convolutional Network (GCN) to generate entity representations. The weighted cosine similarity algorithm is then applied to calculate the semantic similarity between entity pairs, where independent similarity values are calculated based on different weights. Each weight corresponds to a distinct part of the entity’s semantic information. The calculation process is shown in Equations (15) and (16):

$$S_{ij}^n=\cos \left(w_n\odot v_i,w_n\odot v_j\right)$$

(15)

$$S_{ij}={\displaystyle \frac{1}{m}}{\displaystyle \sum _{n=1}^m{S}_{ij}^n},$$

(16)

where M is the adjacency matrix of $G^{\left(0\right)}$; and $G^{\left(1\right)}$ and $G^{\left(n\right)}$ represent the semantic graphs after the n-th and the first iteration of optimization, respectively. To combine $G^{*}$ and $G^{\left(0\right)}$ linearly, the final learned semantic graph is obtained by weighting the hyperparameter μ. During the fusion of $G^{*}$ and $G^{\left(0\right)}$, the trade-off hyperparameter, λ, is used to balance their contributions.

To output the optimal global semantic features, a two-layer GCN encoding is applied to perform two matrix transformations on the initial semantic features, $V_s$. The computation process for the output is described in Equation (17):

$$H_s^e=\sigma \left(\overline{G}\sigma \left(\overline{G}{V}_S{W}^{\left(0\right)}\right)W^{\left(1\right)}\right),$$

(17)

where $W^{\left(0\right)}$ and $W^{\left(1\right)}$ are the learnable weight matrices for the specific layers, σ is the ReLU activation function, and $H_s^e$ is the global semantic feature matrix output by the global semantic feature module.

4.3.4. Link Prediction Module

The link prediction module integrates global semantic features with structural information of CAM knowledge graph entities. The semantic features are used as one of the criteria for link prediction results, filtering out entities that do not conform to NC programming semantic rules. The entity features generated by the entity neighborhood information aggregation module and the global semantic feature learning module are fused to obtain the final vector representation for each entity. To prevent the loss of inherent properties in the CAM knowledge graph due to simple aggregation, learnable parameters, α (0 ≤ |α| ≤ 1), are used to optimize the aggregation process of each triplet vector with semantic features. During training, this is achieved through random initialization and iterative updates using linear transformations, ultimately resulting in a fused CAM triplet set that incorporates NC programming text information. The computation process is described in Equation (18):

$$S_{\left(h,r,t\right)}=H_r^e+\alpha H_s^e$$

(18)

The Adam optimizer is used to optimize the NS-KGC model, with the final training objective being to minimize the loss function. The loss function is described in Equation (19):

$$\mathcal{L}=-{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{y}_i·}\log \left(\phi \left(h,r,t\right)\right)+\left(1-y_i\right)·\log \left(1-\phi \left(h,r,t\right)\right),$$

(19)

where $y_i$ represents the missing triplet information entity–relation pairs (u,r), N is the number of entities in the CAM knowledge graph, and φ is the sigmoid function.

5. Experiments and Analysis

To evaluate the performance of the proposed knowledge graph completion algorithm, we selected the most representative and widely recognized models in the field for a fair comparison on two real-world datasets in the instance completion task. This selection enables a robust assessment of the advantages and improvements offered by our approach, ensuring that the comparison results align with the novel contributions of our work.

5.1. Dataset Description

In this experiment, we utilized datasets commonly used in few-shot knowledge graph completion tasks: FB15k237-One and NELL-One. These datasets are subsets of the FB15k237 and NELL datasets, consisting of entity pairs that share the same types of relations, with the number of entity pairs ranging from 50 to 500. Each dataset includes textual descriptions of entities and relations, thereby constructing semantic information for the entity pairs [26].

Table 1. Dataset information.

Dataset	#Ent	#Rel	#Tri	#Splits	#Sem
FB15k237-One	14,478	237	309,621	32/5/8	89
NELL-One	68,545	358	181,109	51/5/11	278

provides a detailed overview of the datasets, including the number of entities (#Ent); the number of relations (#Rel); the number of triples (#Tri); the ratio of training, validation, and test sets (#Splits); and the number of semantic information samples for entity pairs (#Sem).

Although these datasets do not directly reflect the specific characteristics of CAM knowledge graphs, their features—such as long-tail distributions, sparsity, and complex relationships—closely resemble the challenges encountered in CAM knowledge graphs. As a result, they provide a suitable basis for evaluating the robustness and generalizability of our proposed model. Furthermore, these datasets are widely adopted in the knowledge graph completion research community, ensuring that our comparisons with State-of-the-Art models are both fair and reproducible.

5.2. Baselines Model

We compare our model with two categories of baselines for comparative experiments.

Traditional knowledge graph completion models: TransE [10], which models relationships as translations, represents entities and relations as vectors in the same space. ComplEx [25] uses complex-valued embeddings for entities and relations, enabling the representation of asymmetric relationships through the complex inner product.

Few-shot knowledge graph completion models: GMatching [15] employs a graph-matching approach for knowledge graph completion, concentrating on aligning entity pairs and their relationships in a structured way. FSRL [16] introduces a static attention mechanism that assigns varying weights to one-hop neighbors. MetaR [6] adopts a meta-learning approach, enabling the model to learn a meta-strategy across tasks. FAAN [17] introduces an adaptive attention mechanism that dynamically adjusts attention weights. GANA [18] integrates a generative adversarial network (GAN) with graph embedding techniques.

The baseline models were selected for comparative experiments because they represent the most influential and innovative approaches in the field of knowledge graph completion. Comparing the proposed method with these established models allows for a more effective demonstration of the proposed model’s advanced capabilities and novel contributions.

5.3. Evaluation Metrics

In this study, we use two commonly employed evaluation metrics in knowledge graph completion tasks, Mean Reciprocal Rank (MRR) and $Hits@k$, to assess the performance of the proposed NS-KGC model.

Mean Reciprocal Rank (MRR) represents the average of the reciprocal ranks of the correct triples. Specifically, it computes the average of the reciprocal ranks of all correct predictions. A higher MRR value indicates that the model is more likely to rank the correct triple at a higher position, which is particularly important in practical applications where higher-ranked predictions are prioritized. MRR is widely used due to its ability to provide a concise, single-number assessment of a model’s effectiveness in correctly predicting and ranking triples. The calculation formula for MRR is given by Equation (20):

$$MRR={\displaystyle \frac{1}{S}}{\displaystyle \sum _{i=1}^{\left|S\right|}\frac{1}{ran{k}_i}},$$

(20)

where S represents the set of triples, |S| represents the number of triples in the set, and $ran{k}_i$ represents the rank of the i-th triple.

$Hits@k$ represents the proportion of correct triples among the top-k candidate triples. In this experiment, k values of 1, 5, and 10 are used. $Hits@1$ evaluates whether the correct triple is ranked first, $Hits@5$ assesses whether it is within the top 5, and $Hits@10$ checks if it appears in the top 10. These metrics are crucial because, in many real-world applications, the top-ranked predictions are prioritized. A higher $Hits@k$ value indicates that the model is more likely to rank the correct triple among the top-k candidates, thus directly reflecting the quality of the model’s predictions. The calculation formula for $Hits@k$ is given by Equation (21):

$$Hits@k={\displaystyle \frac{\left|Numk\right|}{\left|S\right|}},$$

(21)

where |Numk| represents the number of correct triples among the top-k candidate triples.

Both MRR and $Hits@k$ are widely recognized metrics in the field of knowledge graph completion, as they assess not only the accuracy of the model’s predictions but also its ability to effectively rank the correct predictions. These metrics are particularly suited for evaluating models in tasks where top-ranked predictions are crucial for real-world applications, such as recommendation systems, search engines, and automated reasoning.

5.4. Parameter Settings

During model training, after parameter tuning, the following configurations were applied: FB15k237-One dataset—batch size; 512, embedding dimensions for entities and relations, 200; learning rate, 0.001; margin between positive and negative samples, 1; number of iterations, 1000. NELL-One dataset—batch size, 256; embedding dimensions, 200; learning rate, 0.001; and number of iterations, 500.

5.5. Comparative Experimental Results

To evaluate the performance of the proposed NS-KGC model in the few-shot knowledge graph completion task, we conducted comparative analyses with State-of-the-Art models on publicly available few-shot knowledge graph datasets.

Table 2. Experimental results of various models on the FB15k237-One dataset.

Model	MRR (%)	Hits@1 (%)	Hits@5 (%)	Hits@10 (%)
TransE (2013)	15.9	8.9	21.2	31.2
ComplEx (2018)	27.8	19.2	31.2	41.0
GMatching (2018)	18.9	10.1	27.4	36.0
FSRL (2019)	22.3	10.2	36.4	48.6
MetaR (2019)	20.3	10.7	29.1	37.7
FAAN (2020)	20.9	10.7	33.4	41.8
GANA (2021)	25.9	17.8	42.4	54.1
Ours	29.0	21.3	46.8	59.0

and

Table 3. Experimental results of various models on the NELL-One dataset.

Model	MRR (%)	Hits@1 (%)	Hits@5 (%)	Hits@10 (%)
TransE (2013)	13.5	8.1	16.1	26.3
ComplEx (2018)	17.4	11.8	29.9	29.7
GMatching (2018)	18.4	12.9	23.0	27.9
FSRL (2019)	14.2	8.8	17.5	28.4
MetaR (2019)	22.7	16.4	28.2	34.0
FAAN (2020)	26.8	19.2	36.0	41.7
GANA (2021)	30.4	19.4	43.2	51.7
Ours	34.7	23.2	48.6	57.7

present the experimental results of various models on the FB15k237-One and NELL-One datasets, respectively.

Compared to the best-performing GANA model on the FB15k237-One dataset, the NS-KGC model shows an improvement of 3.1% in the MRR metric, with increases of 3.5%, 4.4%, and 4.9% in Hits@1, Hits@5, and Hits@10, respectively. On the NELL-One dataset, the NS-KGC model achieves a 4.3% increase in MRR, along with improvements of 3.8%, 5.4%, and 6% in Hits@1, Hits@5, and Hits@10, respectively.

5.6. Ablation Study

To investigate the impact of different components on the performance of the NS-KGC method, ablation studies were conducted on the FB15K237-One and NELL-One datasets using MRR, Hits@1, Hits@5, and Hits@10 as evaluation metrics. The baseline model is NS-KGC, with the following components removed: -DE indicates the removal of the data sampling module, -NA indicates the removal of the entity neighborhood information aggregation module, and -SF indicates the removal of the global semantic feature learning module. The results of the ablation study are shown in

Table 4. Ablation study results on the FB15k237-One dataset.

	MRR (%)	Hits@1 (%)	Hits@5 (%)	Hits@10 (%)
-DE	27.5	20.1	45.5	57.9
-NA	25.0	18.5	43.1	56.2
-SF	26.2	19.2	44.1	57.0
NS-KGC	29.0	21.3	46.8	59.0

and

Table 5. Ablation study results on the NELL-One dataset.

	MRR (%)	Hits@1 (%)	Hits@5 (%)	Hits@10 (%)
-DE	33.5	22.1	47.5	56.4
-NA	31.4	20.1	45.1	53.8
-SF	32.2	21.2	46.5	54.3
NS-KGC	34.7	23.2	48.6	57.7

.

According to the experimental results, removing the dataset sampling module, the entity neighborhood aggregation module, or the global semantic feature learning module leads to varying degrees of performance degradation, indicating that each of these components contributes to the knowledge graph completion task. Notably, the entity neighborhood aggregation module and the global semantic feature learning module have a more significant impact on the model’s performance.

5.7. Discussion and Analysis

The NELL-One dataset, having a larger training set compared to the FB15k237-One dataset, shows more pronounced experimental results. Based on the results from both public datasets, the NS-KGC model demonstrates strong performance on both FB15k237-One and NELL-One, proving its reliability and effectiveness in the knowledge graph completion task. The proposed NS-KGC model integrates entity neighborhood information and global semantic information, enriching the embeddings of entities and relations, and learning finer-grained link information, thereby improving the link prediction performance in knowledge graphs.

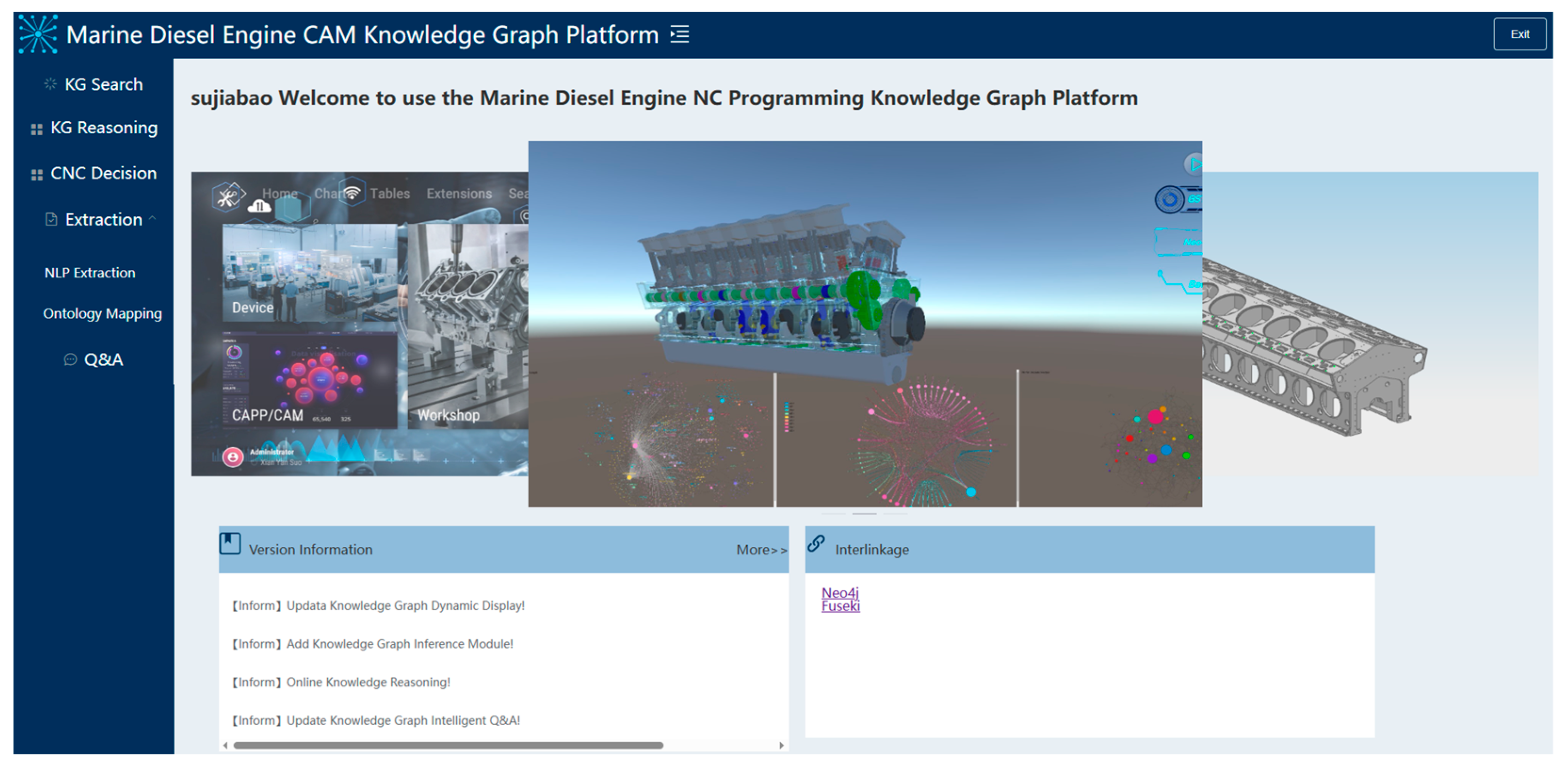
6. Prototype System Development and Application Validation

Based on the aforementioned theory, an intelligent NC programming system based on CAM knowledge graph was developed. Representative parts, such as connecting rods and frames from a marine diesel engine manufacturing company, were selected for case testing to validate the effectiveness of the principles and methods proposed in this research.

The main interface of this system is shown in Figure 12. The CAM module of this system is developed based on NX10.0 software. It includes an information preprocessing module, parameter decision module, and NC module. The information preprocessing module acquires all manufacturing data related to machining features and stores them in a database. The parameter decision module matches and infers NC programming parameters for the machining features. The NC module generates the tool paths and NC code for the machining features.

In Figure 13, the information flow between the modules is illustrated. The basic operating process is as follows: (1) The system retrieves the MBD model of the machining object, workshop information, and other manufacturing data. It traverses the information regarding processes, operations, and features to be machined. Then data are stored in a MySQL database, serving as the data layer for the knowledge graph. (2) The data from the database are loaded, and the CAM knowledge graph performs knowledge reasoning. Then, the programming parameters required for NC programming are obtained and passed into the UG CAM software in the form of an XML file. (3) The information in the XML file is parsed to guide the personnel in generating the tool paths and NC code for the machining features. The main interface of the knowledge graph platform is shown in Figure 14.

Taking the ‘large and small end faces and flat surfaces’ machining step of a diesel engine connecting rod as an example, Figure 15 shows the feature instance knowledge graph after knowledge reasoning and knowledge completion, which includes the template parameters required for NC programming of the machining features. As shown in Figure 16, the CAM template parameters are exported from the knowledge graph system in XML format. Figure 17 presents the tool paths and NC code generated by applying the knowledge graph to the machining features, validating the feasibility and effectiveness of the method. Figure 18 shows the virtual machining simulation based on Vericut.

7. Conclusions and Future Work

To effectively manage, reuse, and mine knowledge resources in the field of NC programming, enhancing the efficiency and quality of NC programming, this study proposes an intelligent NC programming method based on knowledge graph, in alignment with the actual work conditions and needs of enterprises. The main findings are as follows:

(1)

A method for constructing a knowledge graph in the CAM field is proposed. First, CAM knowledge elements are developed to reduce the granularity of knowledge reuse. Then, the thinking patterns of experts in the NC programming domain are analyzed to establish the ontology layer and semantic rules of the knowledge graph. Finally, knowledge extraction is performed using the enterprise’s historical machining resource database as the data source, leading to the construction of the CAM knowledge graph data layer.

(2)

A knowledge reasoning method for the CAM knowledge graph is proposed. First, rules for entity alignment are defined to integrate multi-source descriptive information of the same entity or concept, addressing issues of information redundancy, disorder, and ambiguity. Then, a reasoning framework based on Jena is designed to facilitate the inference and evaluation of programming parameters, thereby enhancing the accuracy of knowledge graph applications.

(3)

We propose a CAM knowledge graph completion algorithm model based on neighborhood aggregation and semantic enhancement. By employing a hybrid sampling method, the training set of the few-shot knowledge graph is expanded. A relationship path-based entity neighborhood information aggregation network is designed, and a multi-head self-attention network is introduced to address the limitations of traditional entity neighborhood aggregation networks. Additionally, a semantic graph is created to fully utilize textual information beyond structural views, combining triplet structural features and semantic characteristics of entities to enhance the performance of link prediction models.

(4)

Based on the aforementioned theoretical foundation, an intelligent NC programming system based on knowledge graphs was developed. Using actual machining parts from a diesel engine enterprise as experimental objects, the reliability of the tool paths and NC code generated by the system was validated. This effectively enhanced the reuse capability of historical case knowledge within the enterprise, reduced the workload of programming personnel, and improved the efficiency and intelligence of CAM programming.

There are also some discussions about the hypothesis, limitations, and future work of the proposed method:

(1)

In future work, efforts will be made to extract hierarchies from the type of information of entities, while considering the integration of multimodal information, thus further enhancing the performance of knowledge graphs in the field of NC programming.

(2)

Additionally, there is a need to expand the application scope and increase the scale of the knowledge graph, further leveraging its powerful reasoning capabilities to achieve greater generality.