Joint-Module Health Status Recognition for an Unmanned Platform: A Time–Frequency Representation and Extraction Network-Based Approach
Abstract
1. Introduction
- (1)
- Introduces a hybrid model based on the FMD, CWT, and capsule network for the fault diagnosis of joint modules in unmanned platforms.
- (2)
- Investigates the decomposition effectiveness of the FMD method on vibration signals. The signals processed by FMD are transformed into time–frequency representations using the CWT.
- (3)
- Proposes the multi-level feature enhancement (MLFE) module for integrating multi-scale features, and simultaneously utilizes the enhanced channel attention (ECA) module to adaptively extract crucial channel features to enhance the feature extraction capability of the capsule network.
2. Basic Theory
2.1. Continuous Wavelet Transform
2.2. Feature Mode Decomposition
- (1)
- Load the original signal, x, and preset the parameters for the FMD, such as the decomposition mode, K; the filter length, L; and the maximum iteration count, I.
- (2)
- Initialize the FIR filter bank using M Hanning windows and start the iteration with i = 1. Typically, M is set to be within the range of 5–10.
- (3)
- Use to obtain the filtered signal or decomposed mode components, where m = 1, 2, … M; represents the convolution operation.
- (4)
- Update the filter coefficients and estimate the fault period based on the input original signal and decomposed mode components. Here, is the time delay corresponding to the local maximum of the autocorrelation spectrum after the first zero crossing.
- (5)
- Check if the current iteration count has reached the maximum iteration count. If not, return to step (3); otherwise, proceed to step (6).
- (6)
- Compute the CC between two adjacent components and construct a correlation matrix. Select two adjacent mode components with the highest CC and calculate the CK values of the selected mode components based on the estimated fault period. Then, choose the mode component with the larger CK value as the FMD mode component and set M = M − 1.
- (7)
- Check if the current mode count has reached the preset mode count, K. If not, return to step (3); otherwise, stop the iteration and output the final decomposition results.
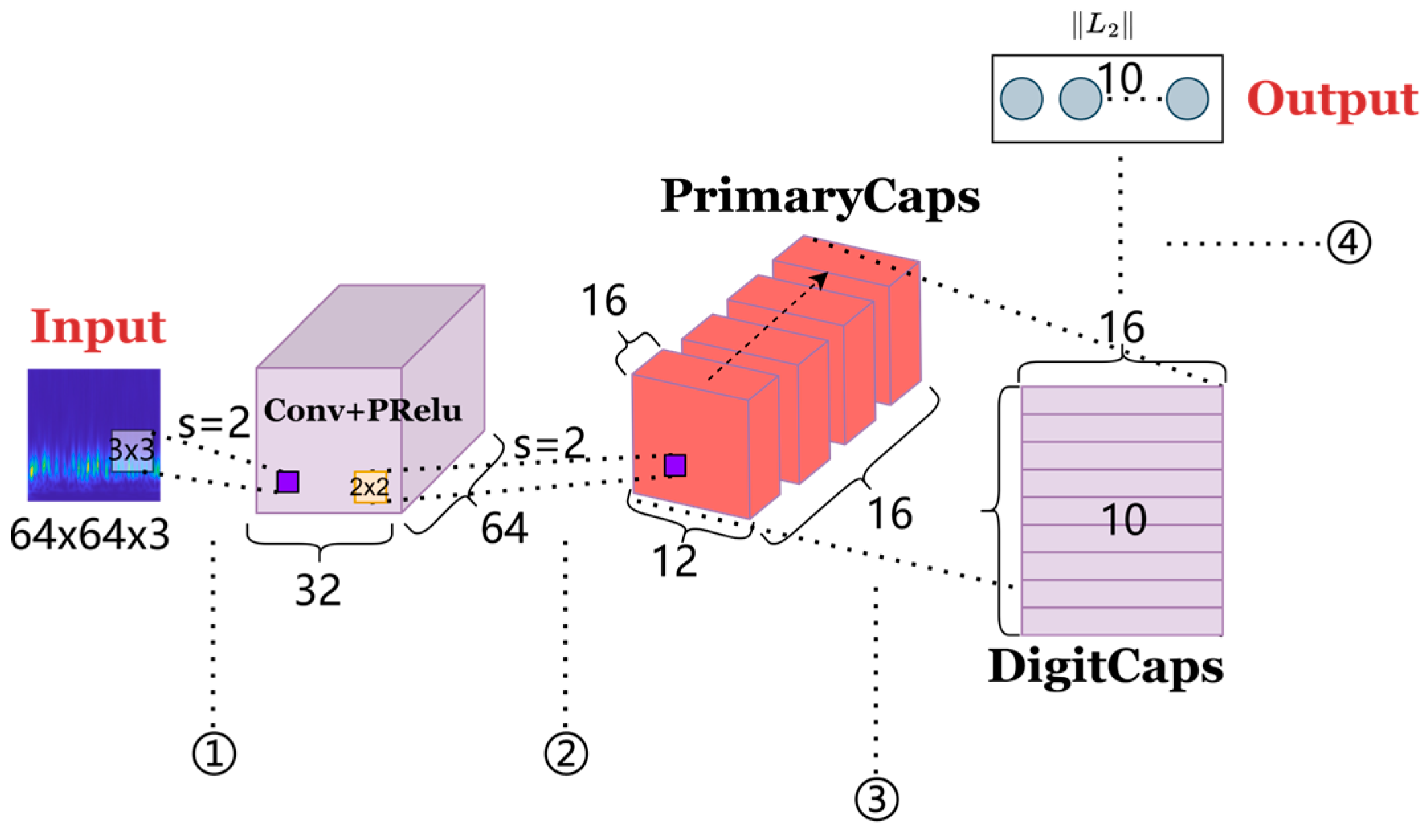
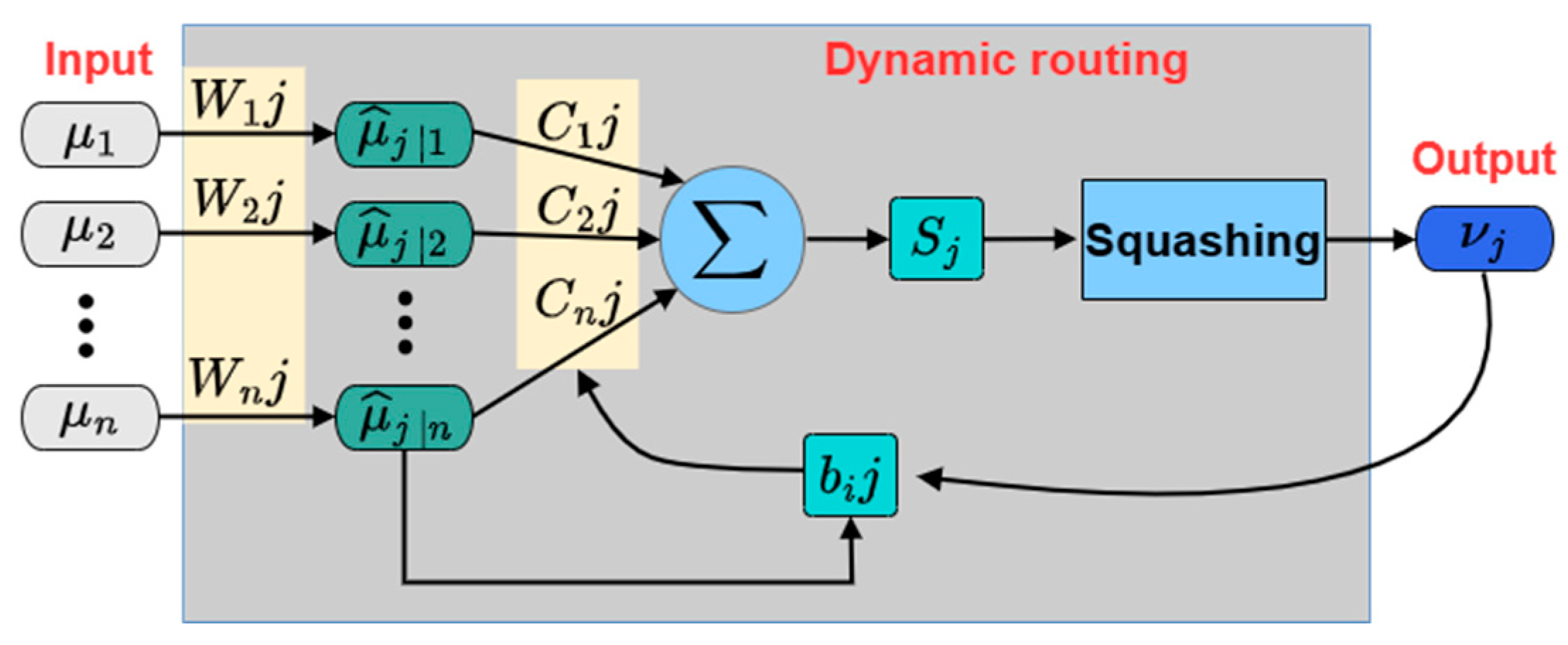
2.3. Capsule Network
- (1)
- The input is a set of lower-level capsules, where represents the number of capsules and represents the number of neurons in each capsule (vector length). Using a transformation matrix, , and representing the number of neurons in the output capsule, the input is transformed into the prediction vector:where .
- (2)
- The weighted sum of all the obtained prediction vectors is calculated as:where is the coupling coefficient and .
- (3)
- The final vector, , is obtained through non-linear mapping by the squeezing function:
2.4. Evaluation Metrics
- (1)
- Accuracy represents the proportion of correct predictions to the total number, with a higher ratio indicating a better classification performance.
- (2)
- For multi-class classifications, the loss function commonly used is the cross-entropy loss function, where a smaller value indicates a better performance.
- (3)
- The confusion matrix, also known as an error matrix, is a way to evaluate the performance of a classifier. It is an n × n matrix that describes the relationship between the true class attributes of the sample data and the predicted recognition classes, widely used for pattern recognition. Each row of the confusion matrix represents the true class attributes of the sample data, while each column represents the predicted recognition classes. It can be inferred that the higher the values on the diagonal of the confusion matrix, the better the classification recognition results.
3. Multi-Feature-Enhanced Efficient Channel Attention Fusion Capsule Network
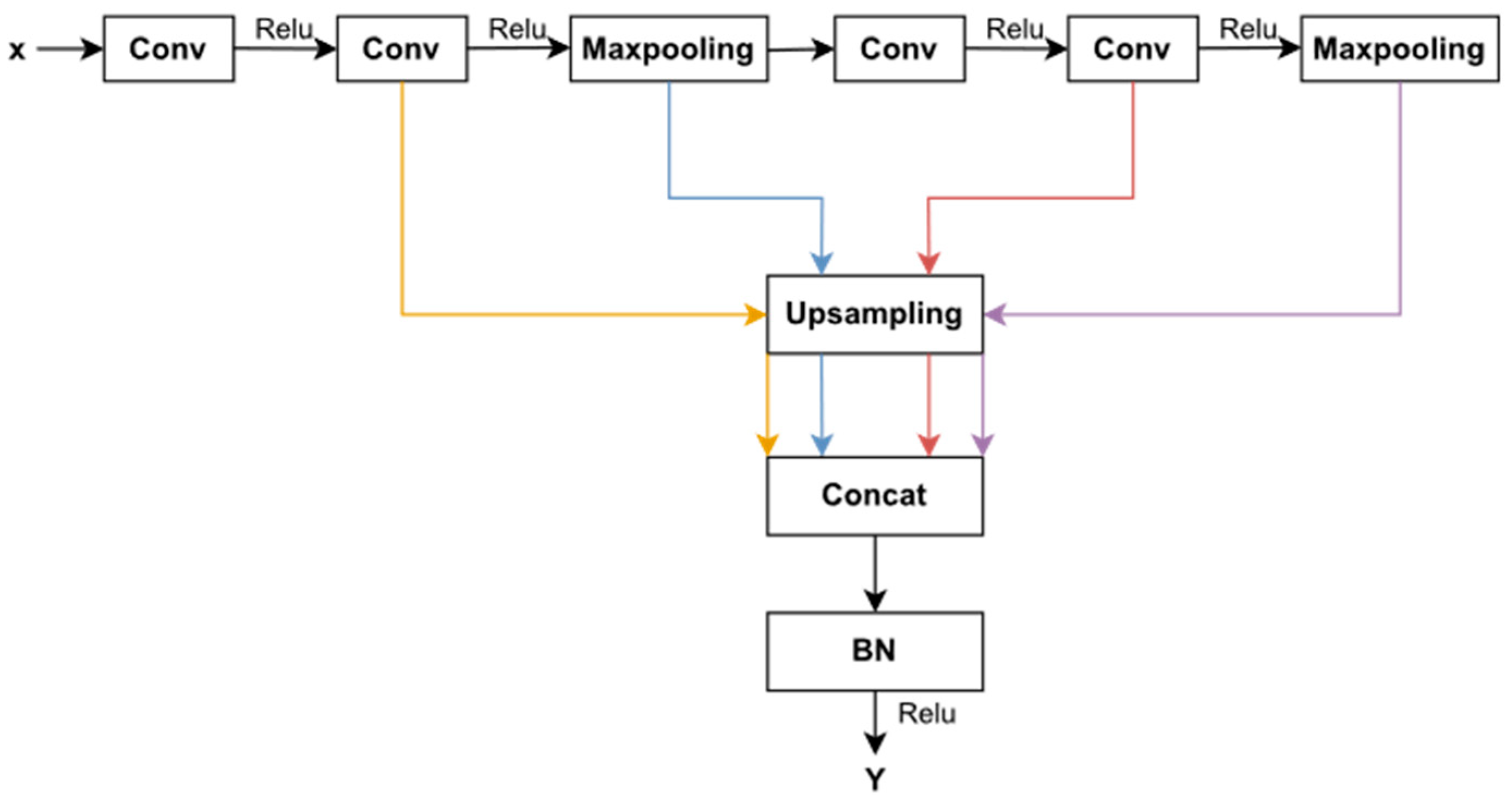
3.1. Multi-Scale Feature Enhancement Module
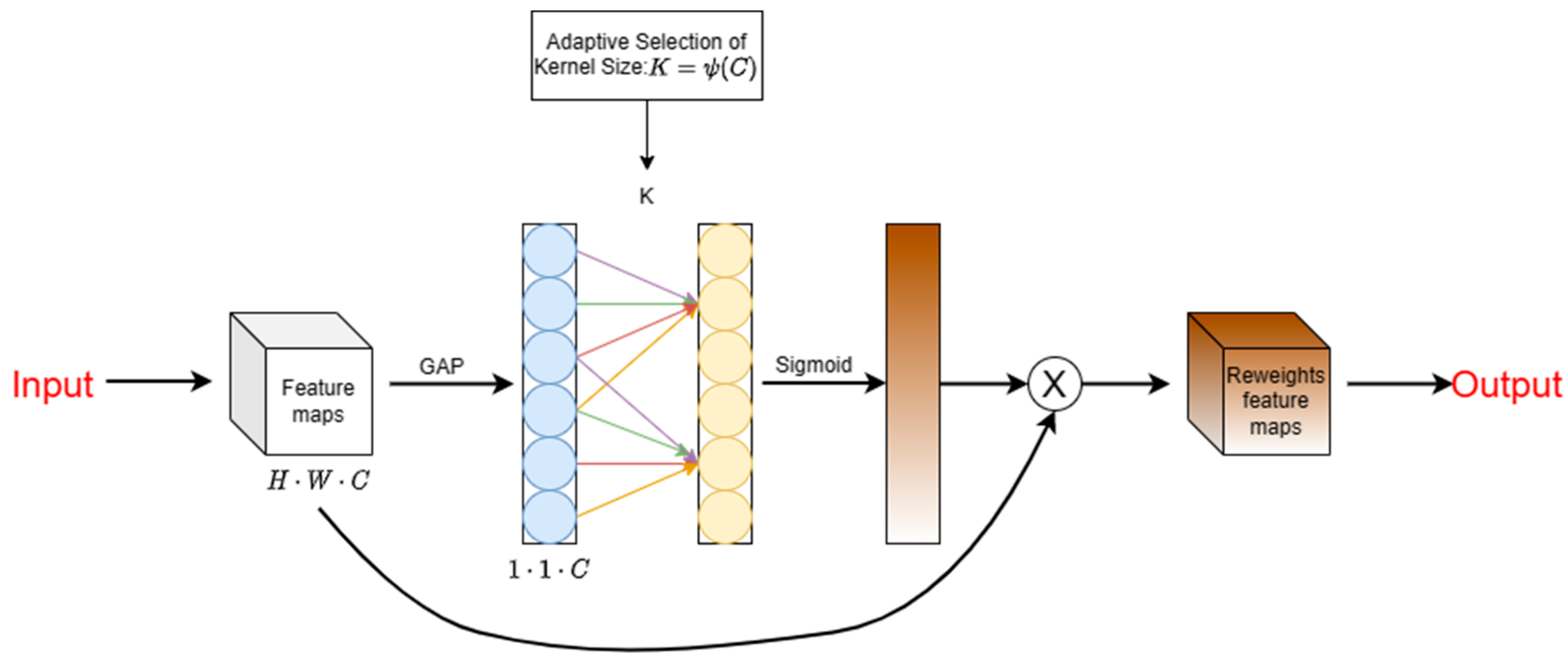
3.2. Efficient Channel Attention Module
3.3. The Proposed Network Structure
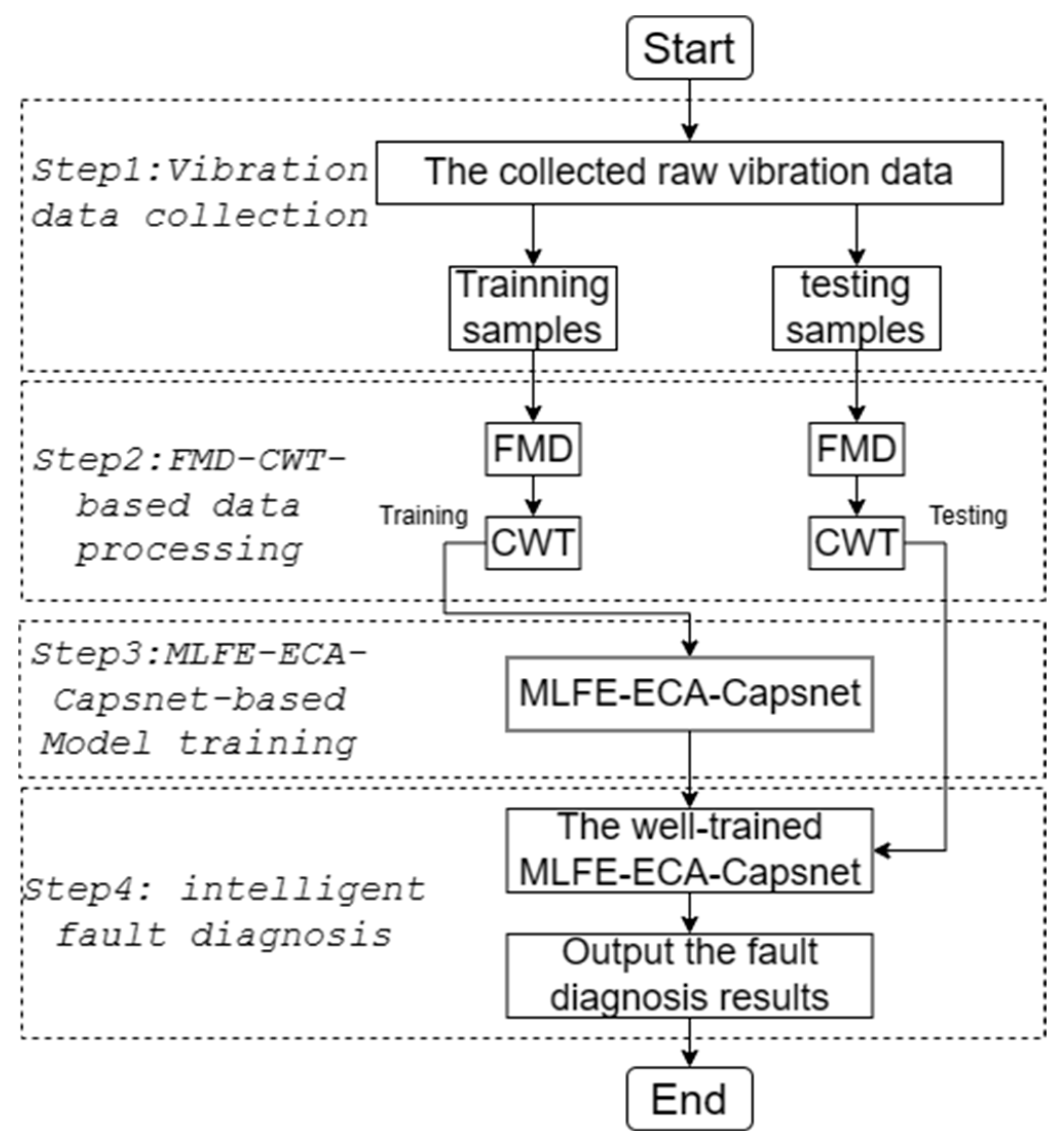
4. The Proposed Technological Framework
- (1)
- Vibration data collection. Firstly, the vibration data of the joint module of the unmanned platform were collected through an accelerometer installed on the upper end of the module’s casing.
- (2)
- Data processing based on FMD-CWT. The collected vibration data were processed through the FMD to extract effective signal components. The extracted components were then transformed into two-dimensional RGB images containing signal time–frequency features using the CWT. These data were then randomly divided into training and testing samples in a certain proportion.
- (3)
- Model training based on MLFE-ECA-Capsnet. The training samples were input into the MLFE-ECA-Capsnet for model training, utilizing the adaptive optimizer Adam and L2 regularization to optimize the training process and alleviate overfitting during model training.
- (4)
- Intelligent fault diagnosis. The testing samples were input into the trained MLFE-ECA-Capsnet to achieve the automatic fault recognition of mechanical faults and output the final diagnostic results.
5. Experimental Verification
5.1. Experimental Platform and Data Preparation
5.1.1. Experiment and Dataset Construction
5.1.2. Time–Frequency Representation
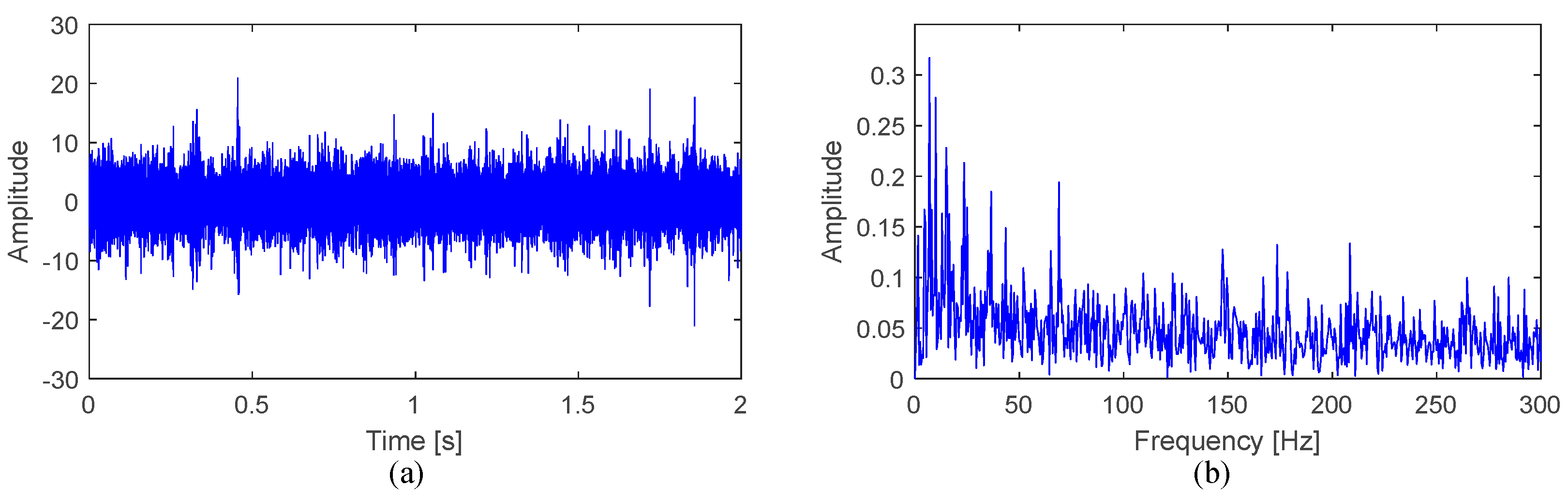
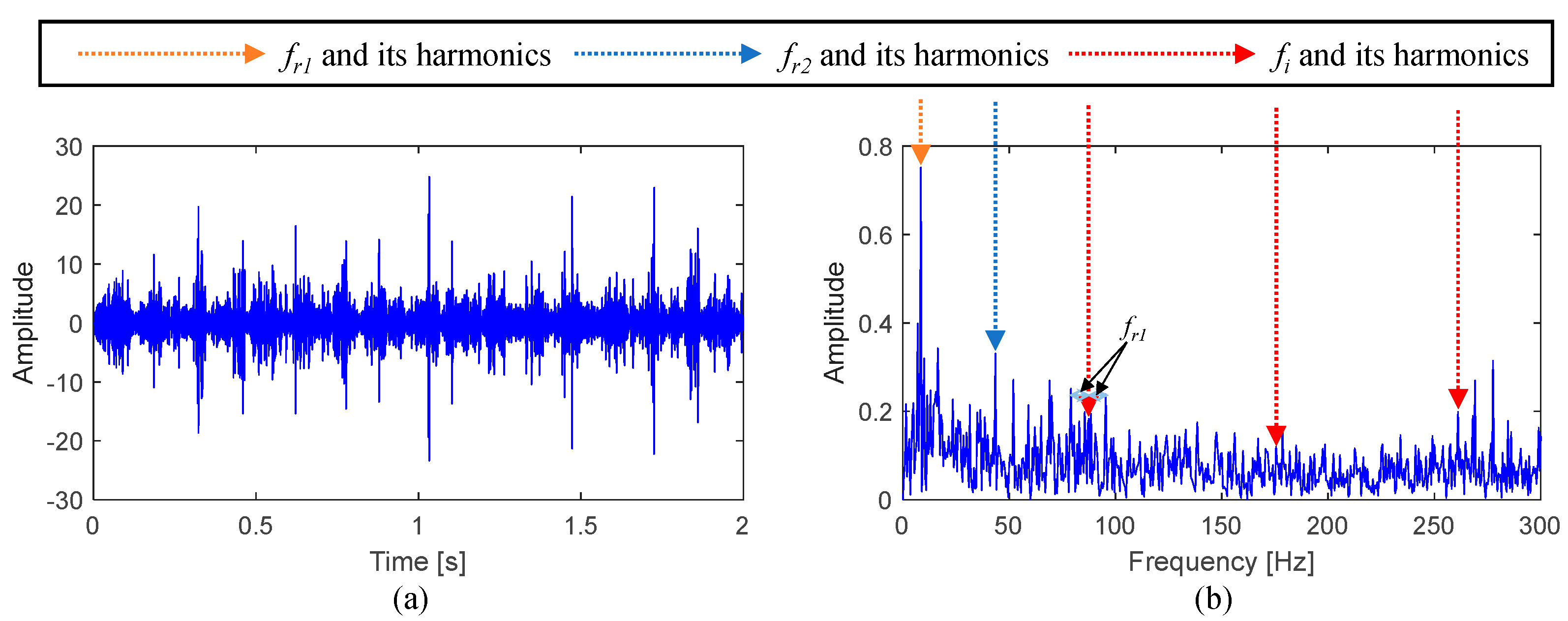
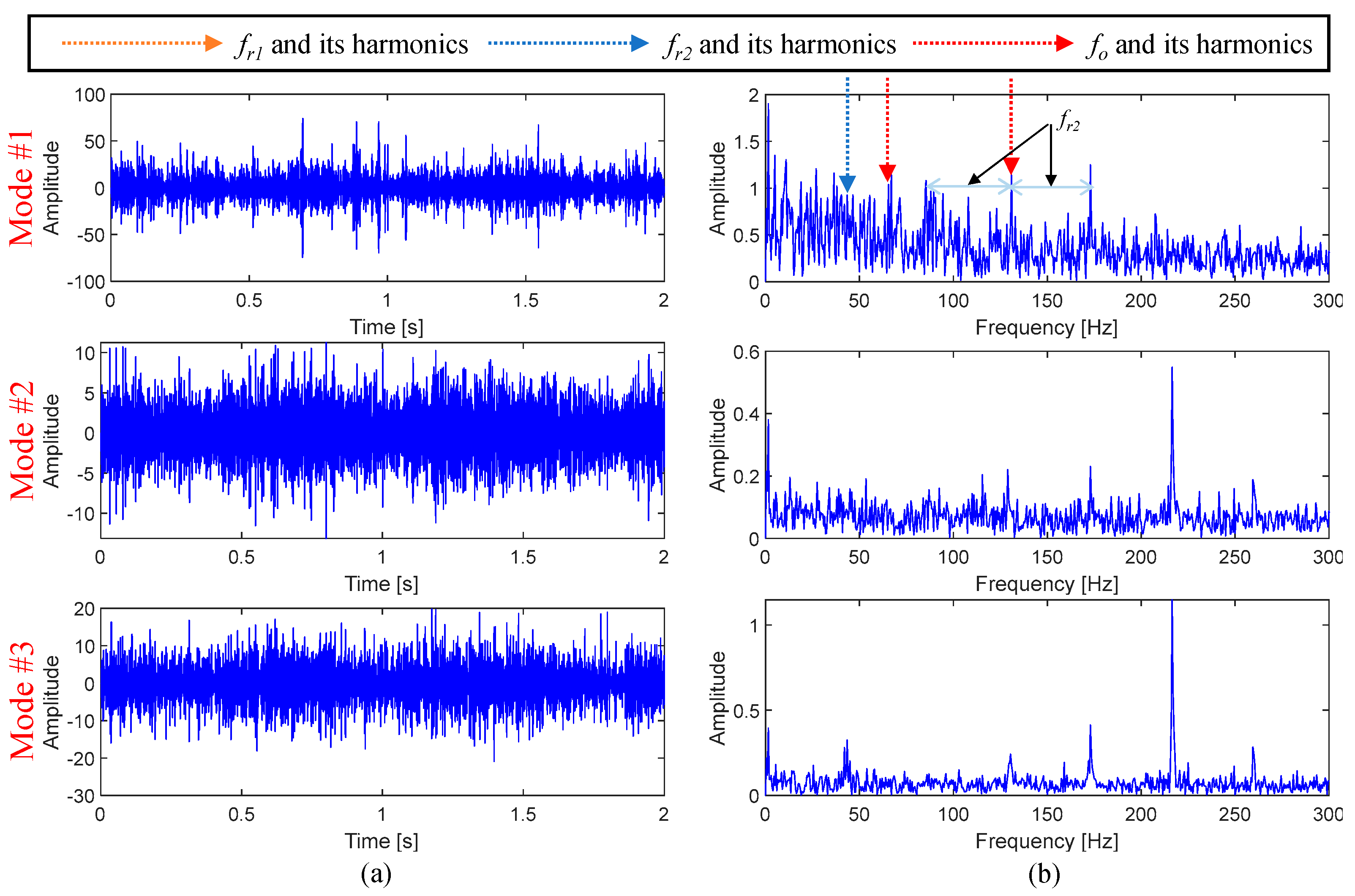
5.2. Effectiveness Verification of the FMD Method
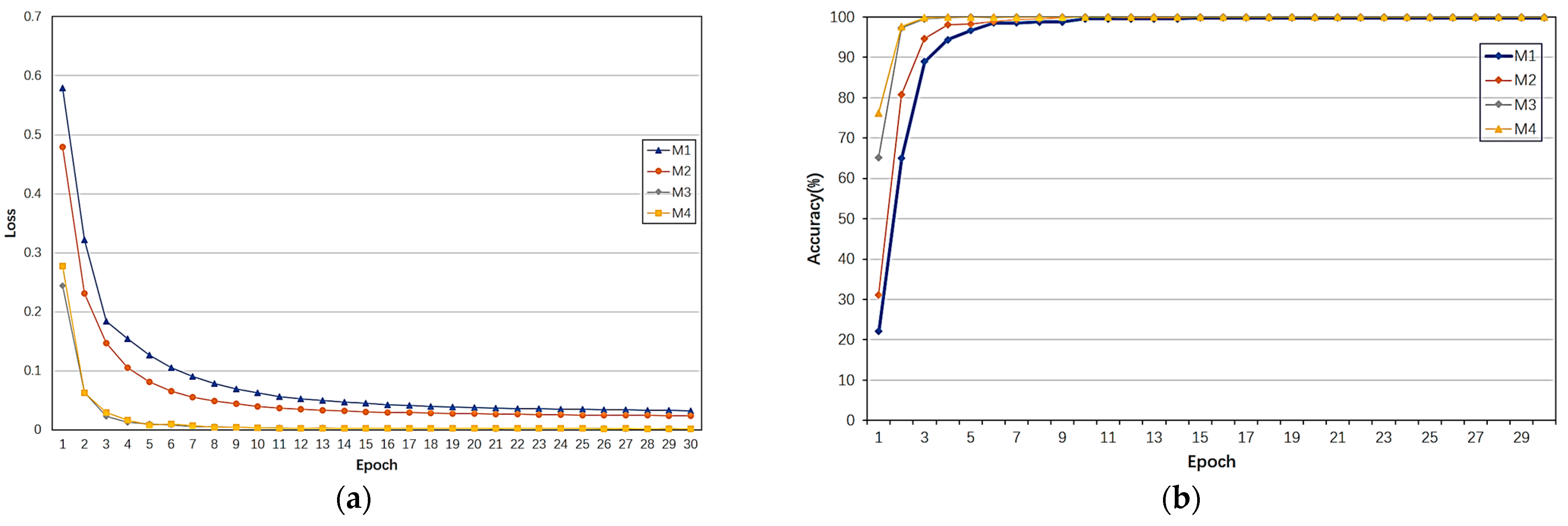
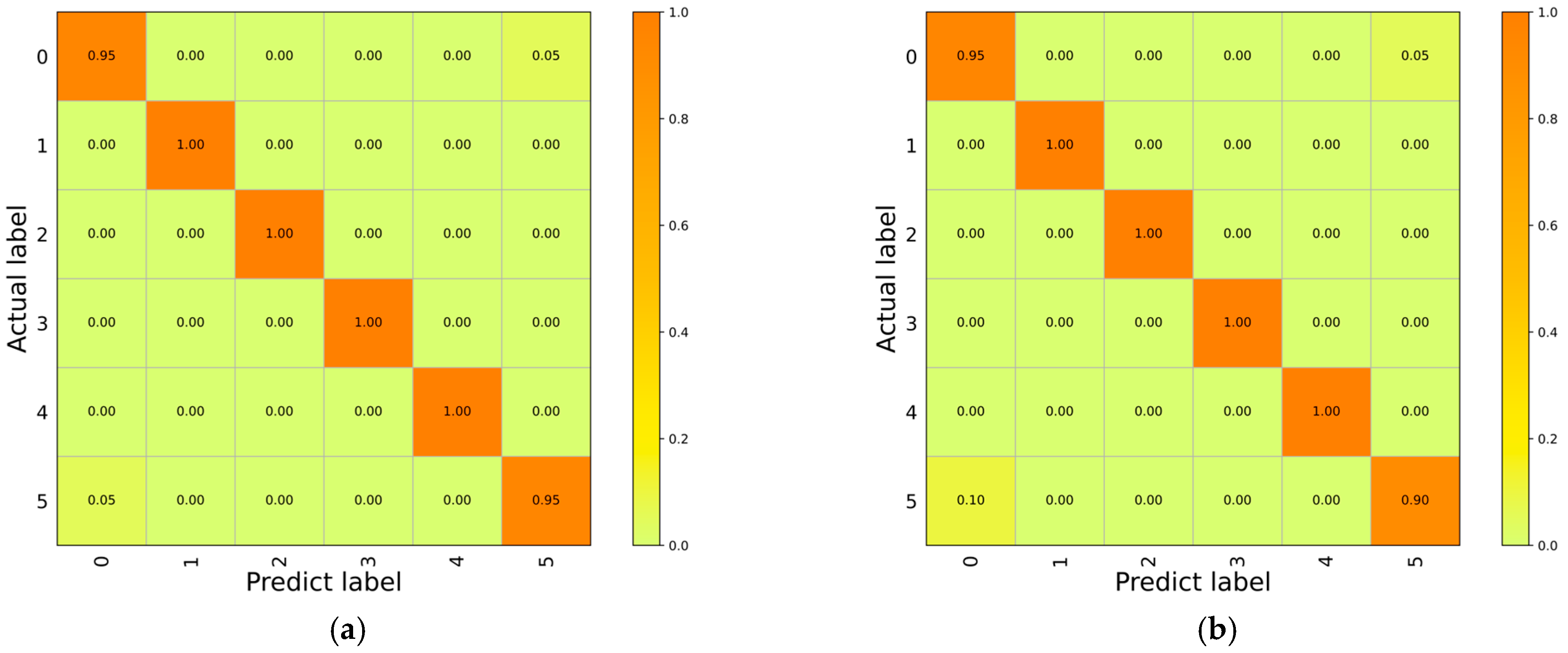
5.3. Ablation Analysis
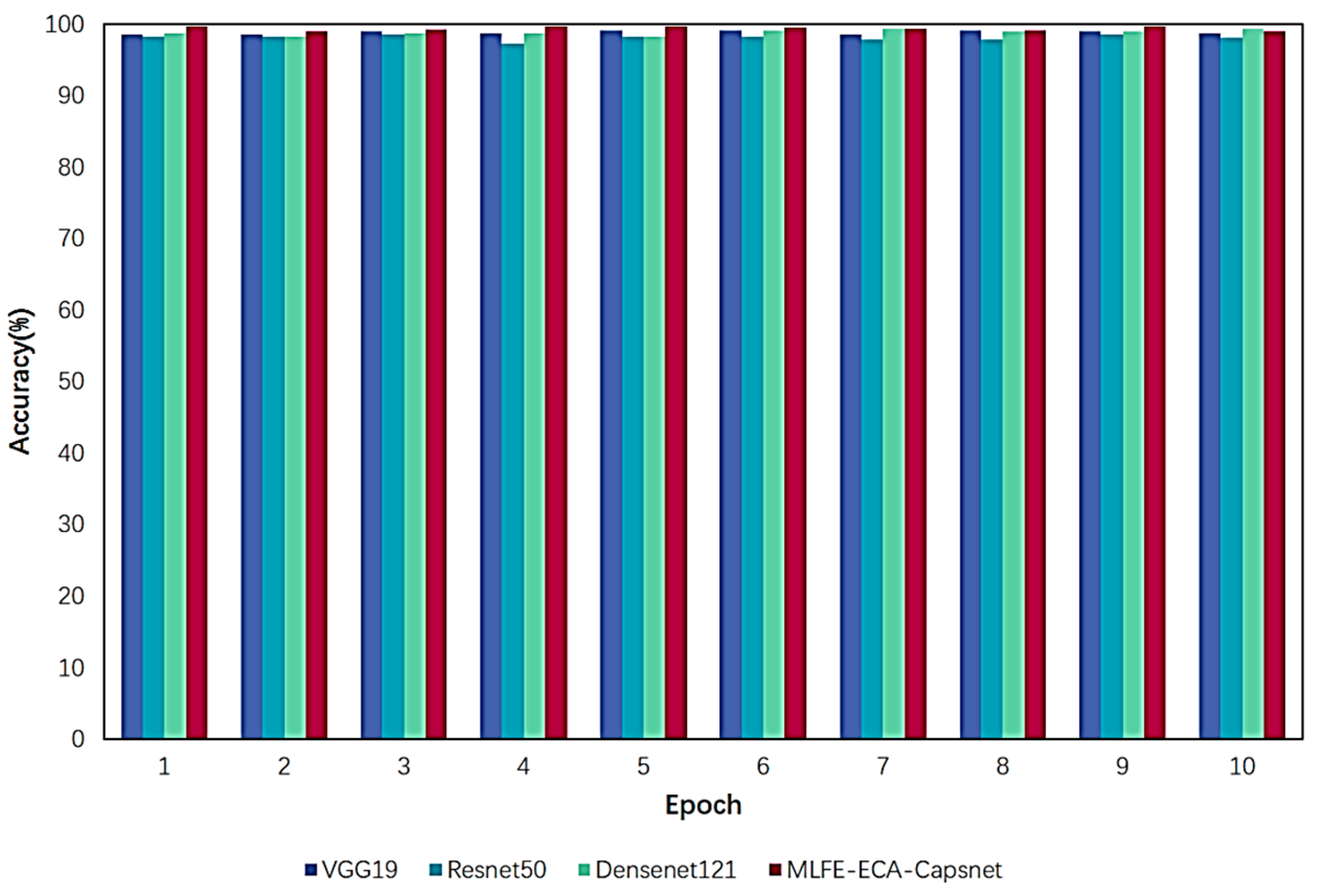
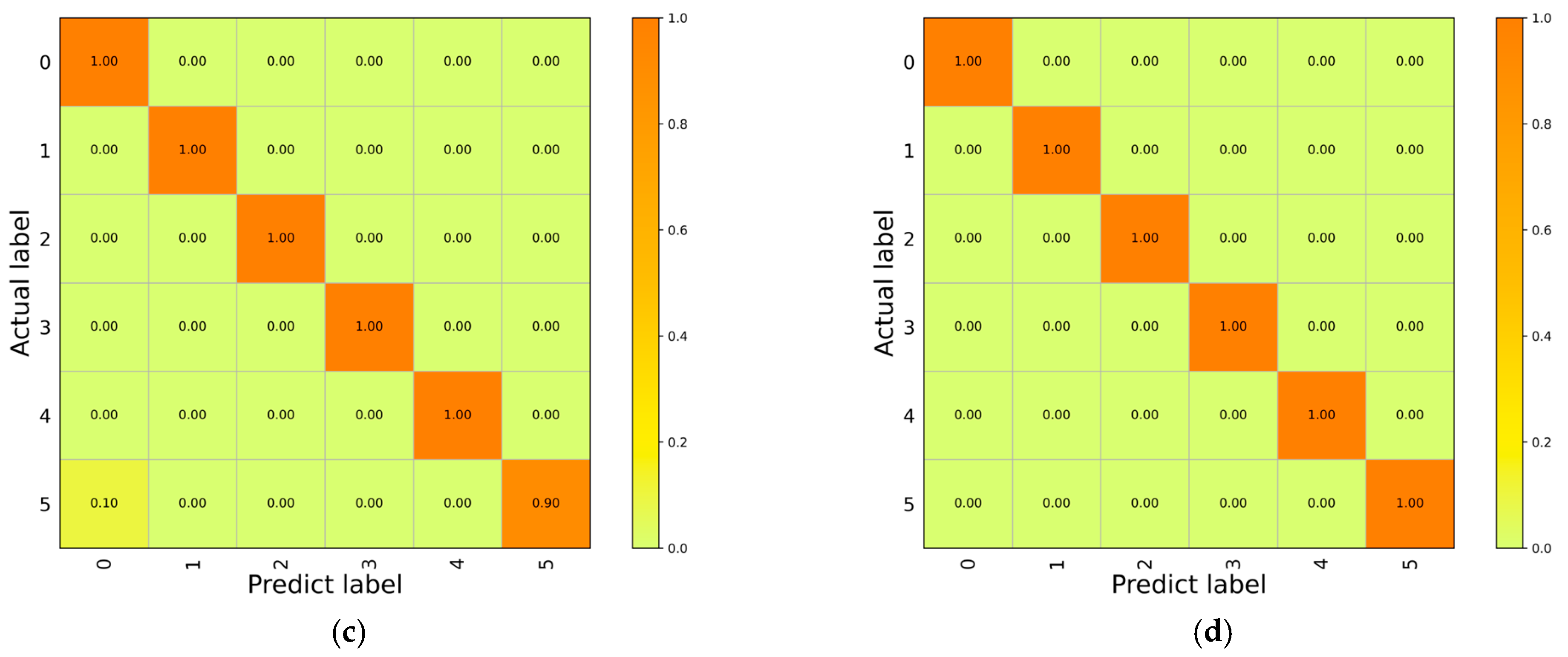
5.4. Network Comparisons
6. Conclusions
- (1)
- The time–frequency representation achieved through the continuous wavelet transform based on Morlet after filtering by the FMD method can obtain richer time-domain and frequency-domain information compared to the original time-domain signal, which is beneficial for the diagnostic performance of the diagnostic model.
- (2)
- Compared with the original capsule network, the MLFE and ECA modules included in the proposed method have different degrees of improvement for the original capsule network, with the MLFE module having the greatest improvement, but with increased parameters and training times. Overall, the proposed method is a good improvement compared to the original capsule network.
- (3)
- Compared with other advanced diagnostic networks, the proposed feature-enhanced diagnostic model exhibits a good performance in terms of its diagnostic accuracy and diagnostic stability, which also proves the effectiveness of the two proposed modules.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Assaad, R.H. The use of unmanned ground vehicles (mobile robots) and unmanned aerial vehicles (drones) in the civil infrastructure asset management sector: Applications, robotic platforms, sensors, and algorithms. Expert Syst. Appl. 2023, 232, 120897. [Google Scholar] [CrossRef]
- Laghari, A.A.; Jumani, A.K.; Laghari, R.A.; Nawaz, H. Unmanned aerial vehicles: A review. Cogn. Robot. 2023, 3, 8–22. [Google Scholar] [CrossRef]
- Xia, B.; Wang, K.; Xu, A.; Zeng, P.; Yang, N.; Li, B. Intelligent Fault Diagnosis for Bearings of Industrial Robot Joints Under Varying Working Conditions Based on Deep Adversarial Domain Adaptation. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Pan, J.; Qu, L.; Peng, K. Deep residual neural-network-based robot joint fault diagnosis method. Sci. Rep. 2022, 12, 17158. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Cheng, G.; Liu, C. Research on bearing fault diagnosis based on spectrum characteristics under strong noise interference. Measurement 2021, 169, 108509. [Google Scholar] [CrossRef]
- Yan, R.; Shang, Z.; Xu, H.; Wen, J.; Zhao, Z.; Chen, X.; Gao, R. Wavelet transform for rotary machine fault diagnosis:10 years revisited. Mech. Syst. Signal Process. 2023, 200, 110545. [Google Scholar] [CrossRef]
- Sylvain, M.; Duong-Hung, P.; Marcelo, A. On the use of short-time fourier transform and synchrosqueezing-based demodulation for the retrieval of the modes of multicomponent signals. Signal Process. 2021, 178, 107760. [Google Scholar]
- Cui, H.; Guan, Y.; Deng, W. Fault Diagnosis Using Cascaded Adaptive Second-Order Tristable Stochastic Resonance and Empirical Mode Decomposition. Appl. Sci. 2021, 11, 11480. [Google Scholar] [CrossRef]
- Yin, C.; Wang, Y.; Ma, G.; Wang, Y.; Sun, Y.; He, Y. Weak fault feature extraction of rolling bearings based on improved ensemble noise-reconstructed EMD and adaptive threshold denoising. Mech. Syst. Signal Process. 2022, 171, 108834. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Zi, Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Process. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Yu, J.; Lv, J. Weak Fault Feature Extraction of Rolling Bearings Using Local Mean Decomposition-Based Multilayer Hybrid Denoising. IEEE Trans. Instrum. Meas. 2017, 66, 3148–3159. [Google Scholar] [CrossRef]
- Pan, H.; Yang, Y.; Li, X.; Zheng, J.; Cheng, J. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 189–211. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, T.; Zhao, W.; Luo, Z.; Lin, H. Rotating Machinery Fault Diagnosis Based on Improved Multiscale Amplitude-Aware Permutation Entropy and Multiclass Relevance Vector Machine. Sensors 2019, 19, 4542. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Li, C.; Lin, J.; Zhang, D. Feature Mode Decomposition: New Decomposition Theory for Rotating Machinery Fault Diagnosis. IEEE Trans. Ind. Electron. 2023, 70, 1949–1960. [Google Scholar] [CrossRef]
- Li, L.; Meng, W.; Liu, X.; Fei, J. Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine. Electronics 2023, 12, 1290. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, F.; Hu, M.; Zhang, L.; Liu, H.; Li, M. A novel denoising algorithm based on TVF-EMD and its application in fault classification of rotating machinery. Measurement 2021, 179, 109337. [Google Scholar] [CrossRef]
- Jin, Z.; He, D.; Ma, R.; Zou, X.; Chen, Y.; Shan, S. Fault diagnosis of train rotating parts based on multi-objective VMD optimization and ensemble learning. Digit. Signal Process. 2022, 121, 103312. [Google Scholar] [CrossRef]
- Tong, Q.; Cao, J.; Han, B.; Zhang, X.; Nie, Z.; Wang, J.; Lin, Y.; Zhang, W. A Fault Diagnosis Approach for Rolling Element Bearings Based on RSGWPT-LCD Bilayer Screening and Extreme Learning Machine. IEEE Access 2017, 5, 5515–5530. [Google Scholar] [CrossRef]
- Tu, Z.; Gao, L.; Wu, X.; Liu, Y.; Zhao, Z. Rotate Vector Reducer Fault Diagnosis Model Based on EEMD-MPA-KELM. Appl. Sci. 2023, 13, 4476. [Google Scholar] [CrossRef]
- Chen, J.; Lin, C.; Yao, B.; Yang, L.; Ge, H. Intelligent fault diagnosis of rolling bearings with low-quality data: A feature significance and diversity learning method. Reliab. Eng. Syst. Saf. 2023, 237, 109343. [Google Scholar] [CrossRef]
- Tran, M.; Liu, M.; Tran, Q.; Nguyen, T. Effective Fault Diagnosis Based on Wavelet and Convolutional Attention Neural Network for Induction Motors. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Zaman, W.; Ahmad, Z.; Siddique, M.F.; Ullah, N.; Kim, J.-M. Centrifugal Pump Fault Diagnosis Based on a Novel SobelEdge Scalogram and CNN. Sensors 2023, 23, 5255. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault identification of hydraulic pump using deep adaptive normalized CNN and synchrosqueezed wavelet transform. Reliab. Eng. Syst. Saf. 2022, 224, 108560. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, W.; Guo, F.; Liu, W.; Shi, X. Wavelet Packet Decomposition-Based Multiscale CNN for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Cybern. 2023, 53, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Liu, M.; Li, C.; Cen, J.; Zhang, Q.; Liu, Q. A Bearing Fault Diagnosis Method Based on Improved Mutual Dimensionless and Deep Learning. IEEE Sens. J. 2023, 23, 18338–18348. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, P.; Han, D.; Jia, L. Research on rolling bearing fault diagnosis method based on AMVMD and convolutional neural networks. Measurement 2023, 217, 113028. [Google Scholar] [CrossRef]
- Kim, Y.; Na, K.; Youn, B. A health-adaptive time-scale representation (HTSR) embedded convolutional neural network for gearbox fault diagnostics. Mech. Syst. Signal Process. 2022, 167, 108575. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Wang, X.; Gu, H. A novel wind turbine fault diagnosis method based on compressed sensing and DTL-CNN. Renew. Energy 2022, 194, 249–258. [Google Scholar] [CrossRef]
- Gu, J.; Peng, Y.; Lu, H.; Chang, X.; Chen, G. A novel fault diagnosis method of rotating machinery via VMD, CWT and improved CNN. Measurement 2022, 200, 111635. [Google Scholar] [CrossRef]
- Xie, F.; Li, G.; Song, C.; Song, M. The Early Diagnosis of Rolling Bearings’ Faults Using Fractional Fourier Transform Information Fusion and a Lightweight Neural Network. Fractal Fract. 2023, 7, 875. [Google Scholar] [CrossRef]
- Liang, P.; Deng, C.; Yuan, X.; Zhang, L. A deep capsule neural network with data augmentation generative adversarial networks for single and simultaneous fault diagnosis of wind turbine gearbox. ISA Trans. 2023, 135, 462–475. [Google Scholar] [CrossRef] [PubMed]
- Siddique, M.F.; Ahmad, Z.; Kim, J.-M. Pipeline leak diagnosis based on leak-augmented scalograms and deep learning. Eng. Appl. Comput. Fluid Mech. 2023, 17, 1. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Santos, F.; Santos, E.; Vogado, L.; Ito, M.; Bianchi, A.; Tavares, J.; Veras, R. DFU-VGG, a Novel and Improved VGG-19 Network for Diabetic Foot Ulcer Classification. In Proceedings of the 2022 29th International Conference on Systems, Signals and Image Processing (IWSSIP), Sofia, Bulgaria, 1–3 June 2022; pp. 1–4. [Google Scholar]
- Huang, G.; Liu, Z.; Maaten, L.; Weinberger, K. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]


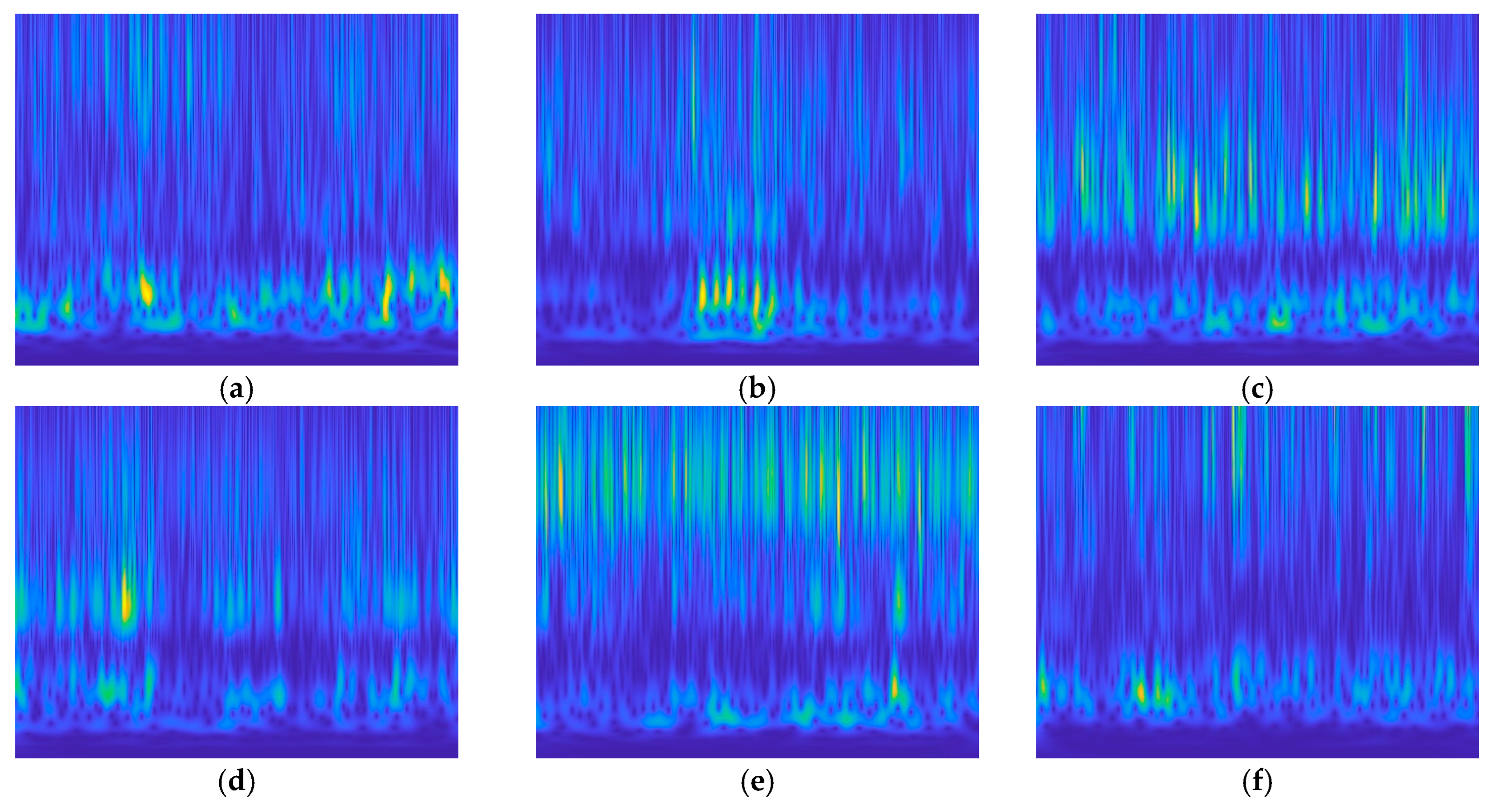

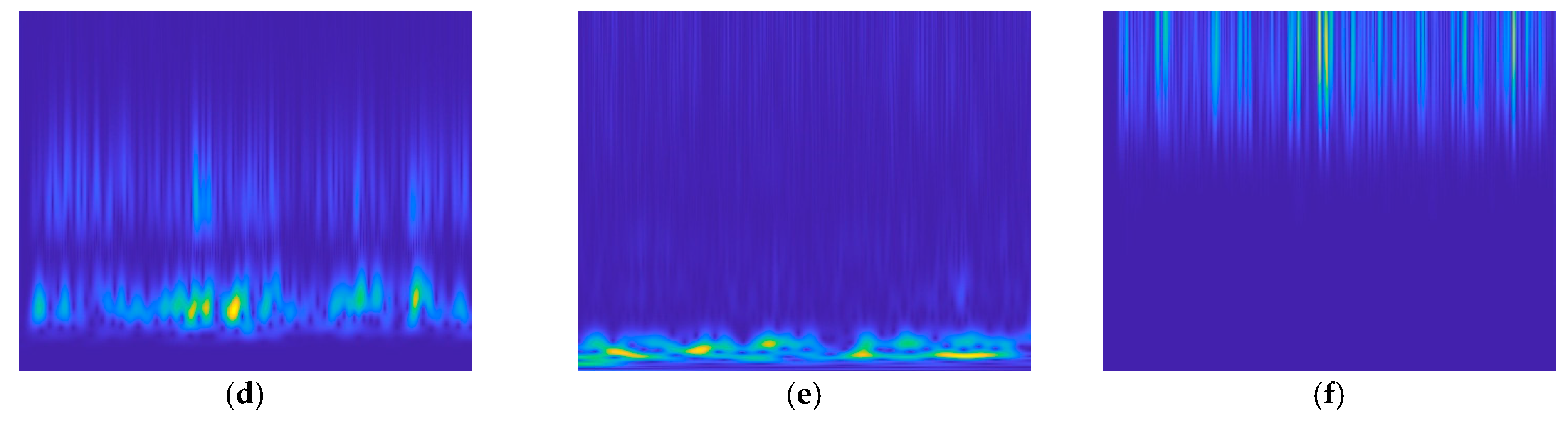




| Layers | Types | Output Size | Last Layer | |
|---|---|---|---|---|
| Input | Input layer | Input | (64,64,3) | \ |
| MLFE module | Conv1 | Conv(64,3,2) | (32,32,64) | Input layer |
| Activation1 | Relu | (32,32,64) | Conv1 | |
| Conv2 | Conv(128,3,2) | (16,16,128) | Activation1 | |
| Activation 2 | Relu | (16,16,128) | Conv2 | |
| Pooling1 | MaxPool(2,2) | (8,8,128) | Activation 2 | |
| Conv3 | Conv(256,3,2) | (4,4,256) | Pooling1 | |
| Activation 3 | Relu | (4,4,256) | Conv3 | |
| Conv4 | Conv(512,3,2) | (2,2,512) | Activation 3 | |
| Activation 4 | Relu | (2,2,512) | Conv4 | |
| Pooling2 | MaxPool(2,2) | (1,1,512) | Activation 4 | |
| Upsamlping1 | Upsampling(2,2) | (32,32,128) | Pooling2 | |
| Upsamlping2 | Upsampling(4,4) | (32,32,128) | Upsamlping1 | |
| Upsamlping3 | Upsampling(16,16) | (32,32,512) | Upsamlping2 | |
| Upsamlping4 | Upsampling(32,32) | (32,32,512) | Upsamlping3 | |
| Fusion1 | Contact | (32,32,1280) | Upsamlping4 | |
| BN1 | BN | (32,32,1280) | Fusion1 | |
| Activation 5 | Relu | (32,32,1280) | BN1 | |
| ECA module | Pooling3 | GAP | (1280) | Activation 5 |
| Reshape1 | Reshape | (1,1,1280) | Pooling3 | |
| Conv5 | Conv(2,2,1) | (1,1,1) | Reshape1 | |
| Activation6 | Sigmoid | (1,1,1) | Conv5 | |
| Fusion2 | Multiply | (15,15,256) | Activation6 | |
| Capsule network | Primary capsule | Primarycap | (14,16) | Fusion2 |
| Digit capsule | Digitcap | (14) | Primary capsule |
| Label | Types of Faults | Training/Validation/Test Samples |
|---|---|---|
| 0 | HSPBCF | 70/10/20 |
| 1 | HSGTM | 70/10/20 |
| 2 | HSPBIRF | 70/10/20 |
| 3 | LSGTM | 70/10/20 |
| 4 | NOR | 70/10/20 |
| 5 | HSPBORF | 70/10/20 |
| fr1 (Hz) | fr2 (Hz) | fi (Hz) | fo (Hz) |
|---|---|---|---|
| 8.58 | 43.33 | 87.75 | 65 |
| Different Approaches | Mode #1 | Mode #2 | Mode #3 |
|---|---|---|---|
| FMD | 0.0109 | 0.0038 | 0.0073 |
| VMD | 0.0048 | 0.0017 | 0.0057 |
| EEMD | 0.0053 | 0.0041 | 0.0067 |
| Model | Parameter | Training Time (s) |
|---|---|---|
| M1 | 18,916,325 | 122.3294 |
| M2 | 18,916,608 | 123.5110 |
| M3 | 24,617,856 | 200.7728 |
| M4 | 24,622,976 | 211.3169 |
| Model | Highest Value | Minimum Value | Mean Value | Standard Deviation |
|---|---|---|---|---|
| VGG19 | 99.16 | 98.54 | 98.85 | 0.263 |
| Resnet50 | 98.54 | 97.29 | 98.16 | 0.378 |
| Densenet121 | 99.37 | 98.34 | 98.88 | 0.366 |
| Proposed method | 100 | 99.33 | 99.61 | 0.251 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Yang, G.; Song, S.; Du, R.; Yuan, H. Joint-Module Health Status Recognition for an Unmanned Platform: A Time–Frequency Representation and Extraction Network-Based Approach. Machines 2024, 12, 79. https://doi.org/10.3390/machines12010079
Zhu S, Yang G, Song S, Du R, Yuan H. Joint-Module Health Status Recognition for an Unmanned Platform: A Time–Frequency Representation and Extraction Network-Based Approach. Machines. 2024; 12(1):79. https://doi.org/10.3390/machines12010079
Chicago/Turabian StyleZhu, Songbai, Guolai Yang, Sumian Song, Ruilong Du, and Haihui Yuan. 2024. "Joint-Module Health Status Recognition for an Unmanned Platform: A Time–Frequency Representation and Extraction Network-Based Approach" Machines 12, no. 1: 79. https://doi.org/10.3390/machines12010079
APA StyleZhu, S., Yang, G., Song, S., Du, R., & Yuan, H. (2024). Joint-Module Health Status Recognition for an Unmanned Platform: A Time–Frequency Representation and Extraction Network-Based Approach. Machines, 12(1), 79. https://doi.org/10.3390/machines12010079





