Supply Chain 4.0: A Machine Learning-Based Bayesian-Optimized LightGBM Model for Predicting Supply Chain Risk
Abstract
:1. Introduction
2. Literature Review
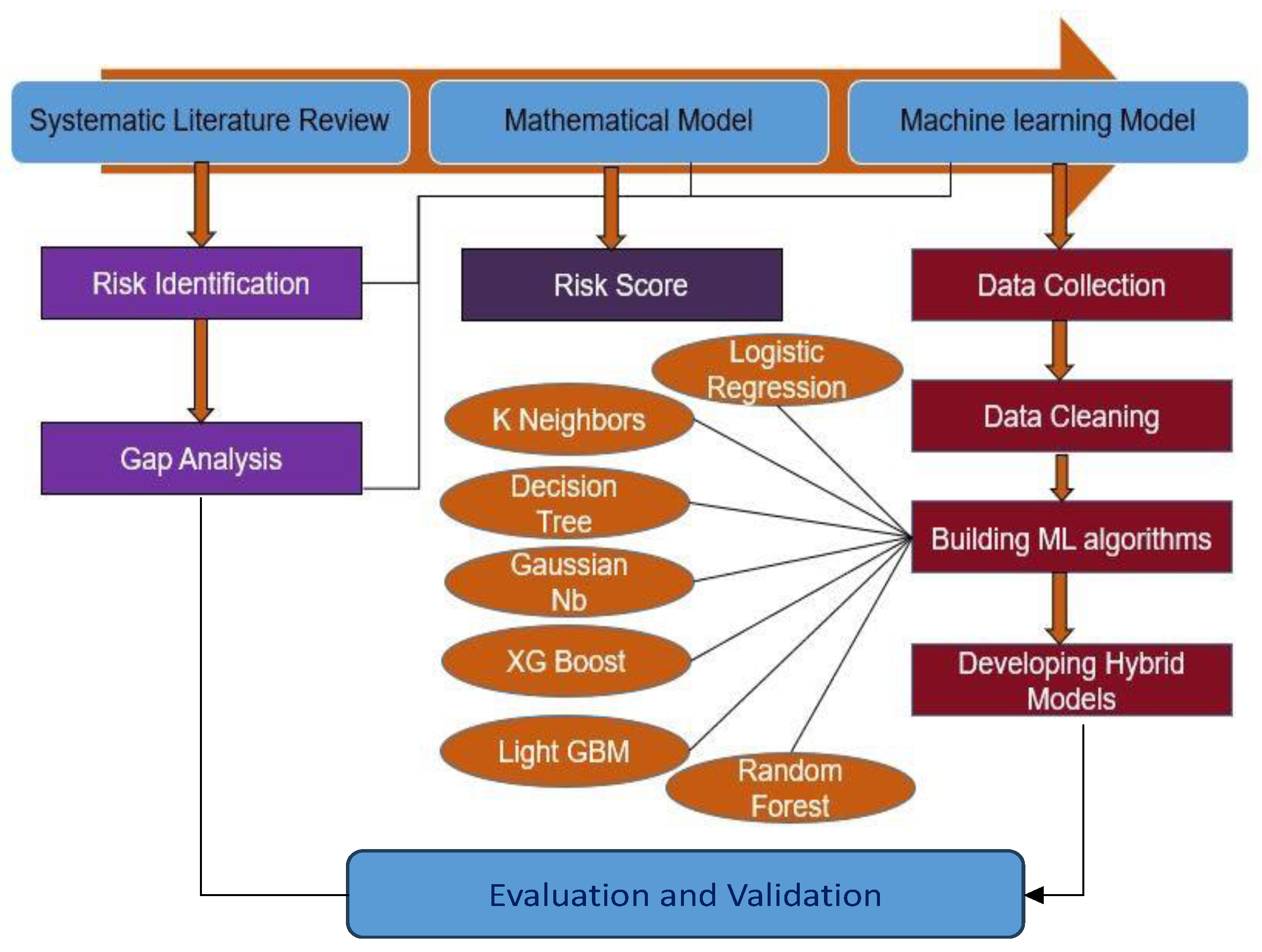
3. Methodology
3.1. Formulation of Mathematical Model
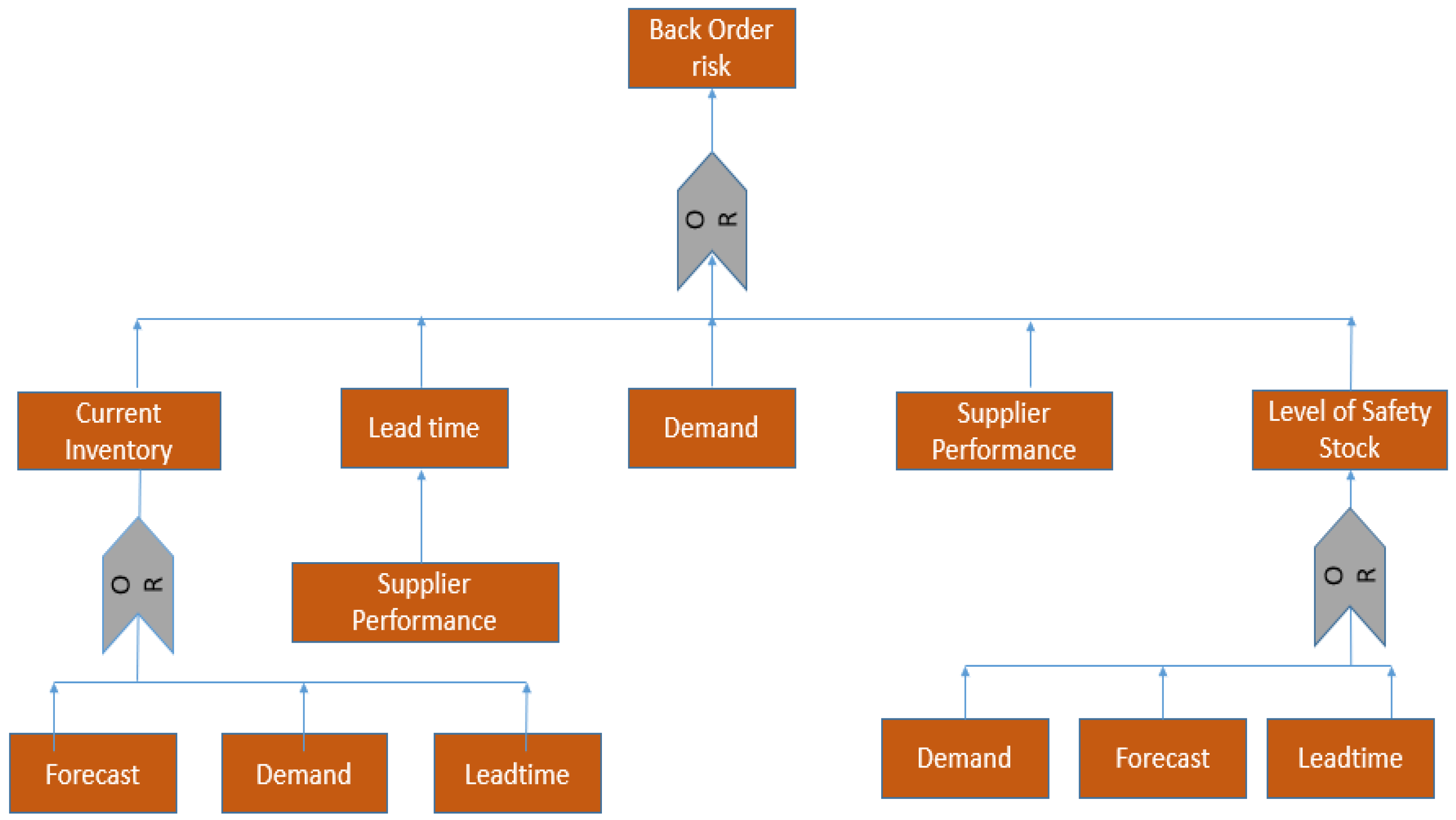
3.1.1. Fault Tree Analysis
3.1.2. Model Assumptions
- The input data used for training and testing the classification model are independent and identically distributed;
- The selected features (independent variables) used in the model are assumed to impact backorder risk significantly;
- The features (input variables) used for classification are independent;
- All relevant variables for predicting backorder risk are available and adequately measured;
- Relationships between predictors and backorder risk are consistent throughout the modelling period;
- Variables having binary values are ignored;
- Dependencies or interactions between different products or Store Keeping Units (SKUs) are not considered in the model.
3.1.3. Notations
- The notations required for the formulation of the backorder problem in mathematical terms enable one to solve the model to find optimal solutions for the occurrence of backorder risk. The set represents the SKUs with common properties or characteristics essential for the mathematical expressions. The parameters are the fixed values in the mathematical model that represent the risk score. The variable represents the values of supplier performance and actual demand to be determined.
Sets
- : Number of SKUs in the supply chain dataset.
- The row number of the SKU under consideration. (It is used as an index or label to identify a specific row or entry within the dataset. In the context of the equations, x takes values from 1 to n, representing each SKU in the dataset. For each SKU, the equations are calculated based on the values associated with that specific SKU, such as supplier performance and actual demand. Such an index helps one iterate through each SKU in the dataset to calculate risk scores, constraints, and other relevant quantities).
Parameters
- Threshold of Risk score;
- = Threshold of Total risk associated with Supplier Performance;
- = Threshold of Total risk associated with Demand;
- = Expected supplier performance for xth SKU;
- = Actual demand for SKU.
Variables
- = Variance in supplier performance for xth SKU;
- = Variance in demand risk of xth SKU;
- = Risk associated with Supplier Performance for the xth SKU;
- = Risk associated with Actual Demand for the xth SKU;
- = Total risk related to the SKU associated with the supply chain;
- = Average of total risk;
- = Total Risk associated with Supplier Performance;
- = Total Risk associated with Demand;
- = Risk score associated with both supplier performance and demand for the xth SKU;
- = Min value of ;
- = Max value of .
- = Actual Supplier Performance–Expected Supplier Performance;
- = Actual Demand–Expected Demand.
Constraints
3.2. Machine Learning-Based Prediction Model
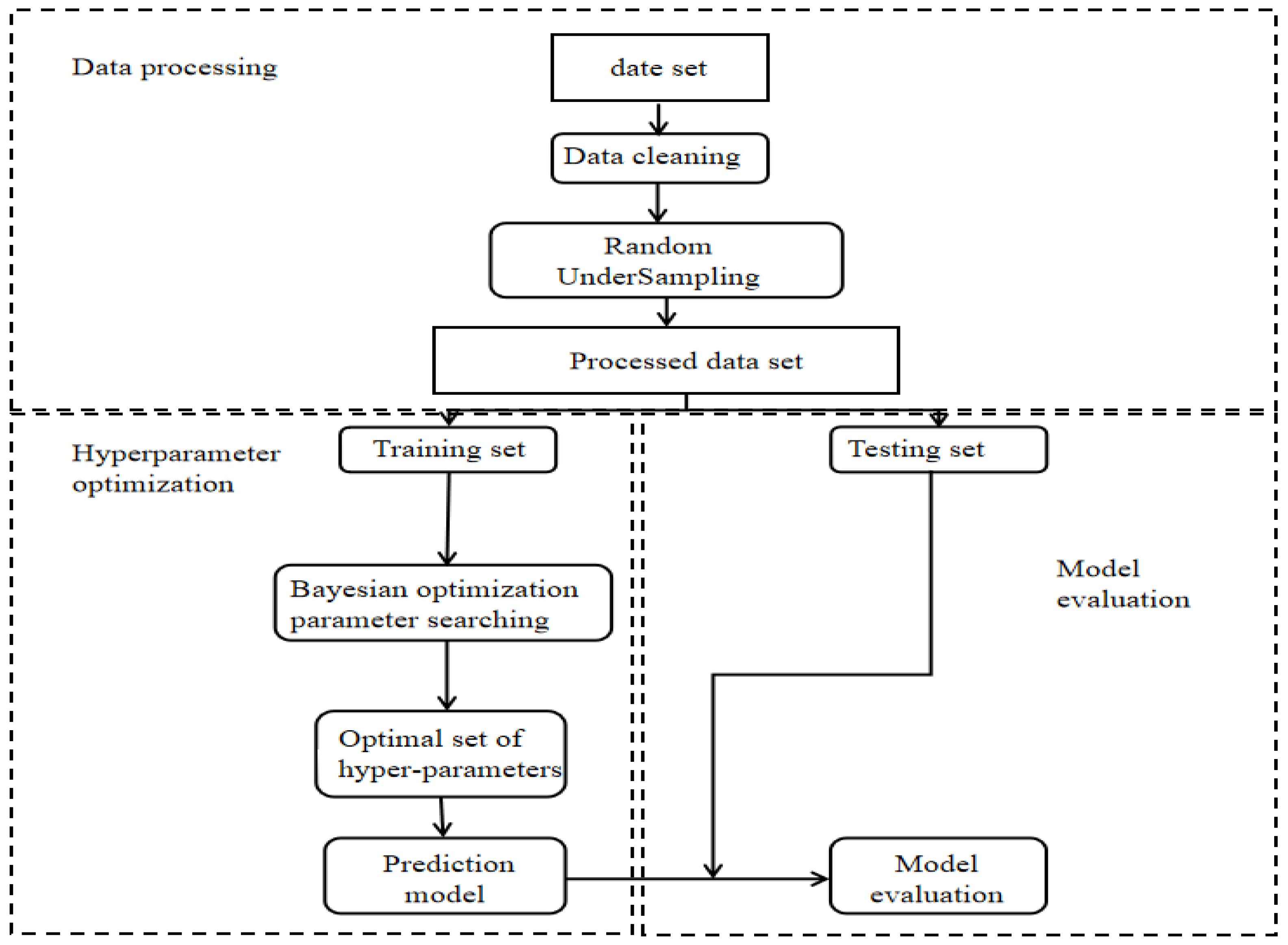
3.2.1. Data Pre-Processing
- Under-Sampling
- 2.
- Data Cleaning
3.2.2. LightGBM Algorithm
- 3.
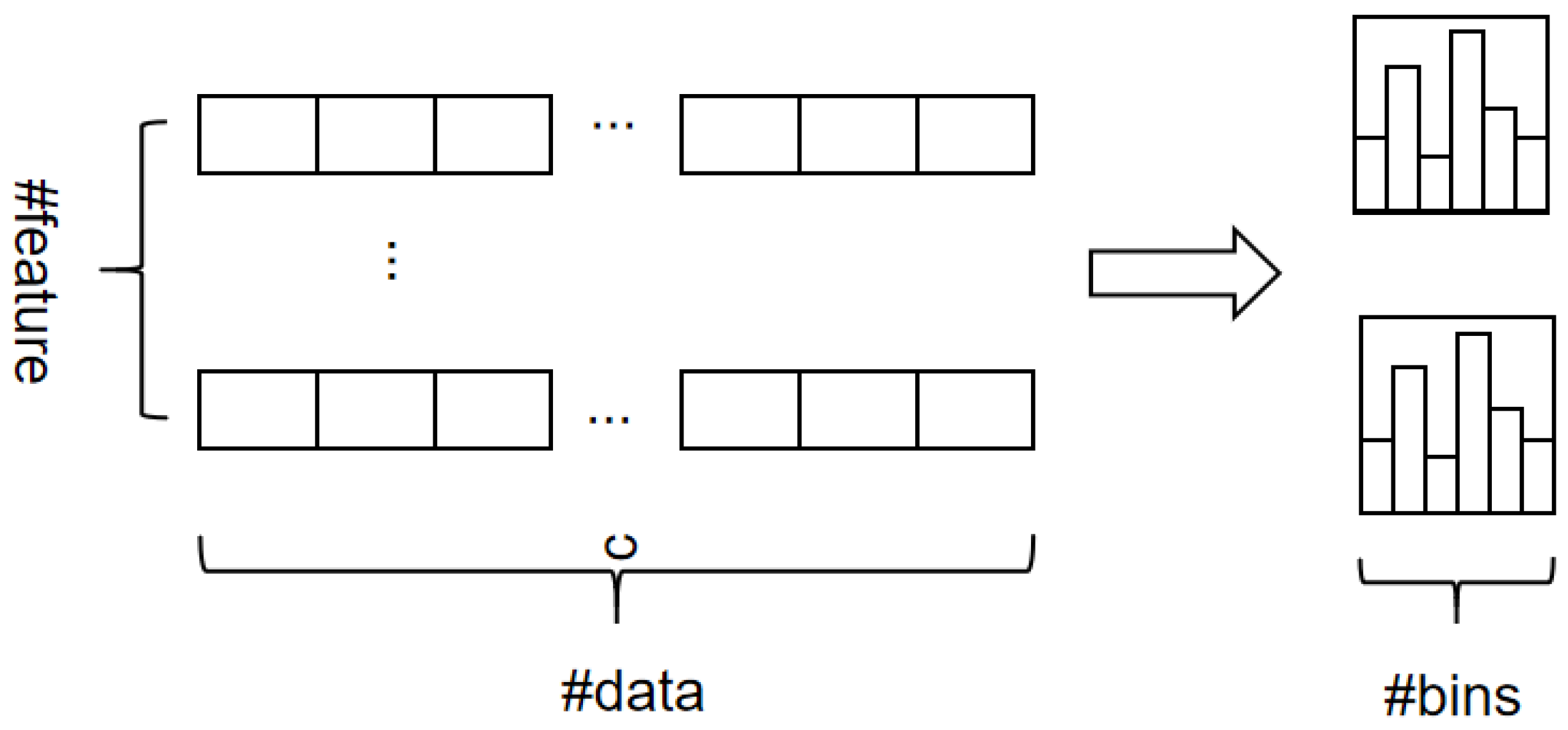
- The Histogram Algorithm
| Algorithm 1 Histogram-based Algorithm |
| Input: training data I, max depth d, feature dimension m 1: nodeSet ← {0} ▷ tree nodes in current level 2: rowSet ← {{0, 1, 2}} ▷ data indices in tree nodes 3: for i = 1 to d do 4: for node in nodeSet do 5: usedRows ← rowSet[node] 6: for k = 1 to m do 7: H ← new Histogram() 8: ▷ Build histogram 9: for j in usedRows do 10: bin ← I.f[k][j].bin 11: H[bin].y ← H[bin].y + I.y[j] 12: H[bin].y ← H[bin].y + 1 13: end for 14: Find the best split on histogram H 15: end for 16: end for 17: Update rowSet and nodeSet according to the best split points 18: end for |
- 4.
- The GOSS Algorithm
| Algorithm 2 Gradient-based One-side Sampling |
| Input: training data I, iterations d |
| Input: sampling ratio of large gradient data a |
| Input: sampling ratio of small gradient data b |
| Input: loss function loss, weak learner L |
| 1: models ← { }, fact ← |
| 2: topN ← a len(I), randN ← b len(I) |
| 3: for i = 1 to d do |
| 4: preds ← models.predict(I) |
| 5: g ← loss(I, preds), w ← {1, 1,…} |
| 6: sorted ← GetSortedIndices(abs(g)) |
| 7: topSet ← sorted[1: topN] |
| 8: randSet ← RandomPick(sorted[topN : len(I)]), randN) |
| 9: usedSet ← topSet + randSet |
| 10: w[randSet] fact ▷ Assign weight fact to small gradient data |
| 11: newModel ← L(I[usedSet]), −g[usedSet], w[usedSet]) |
| 12: model.append(newModel) |
| 13: end for |
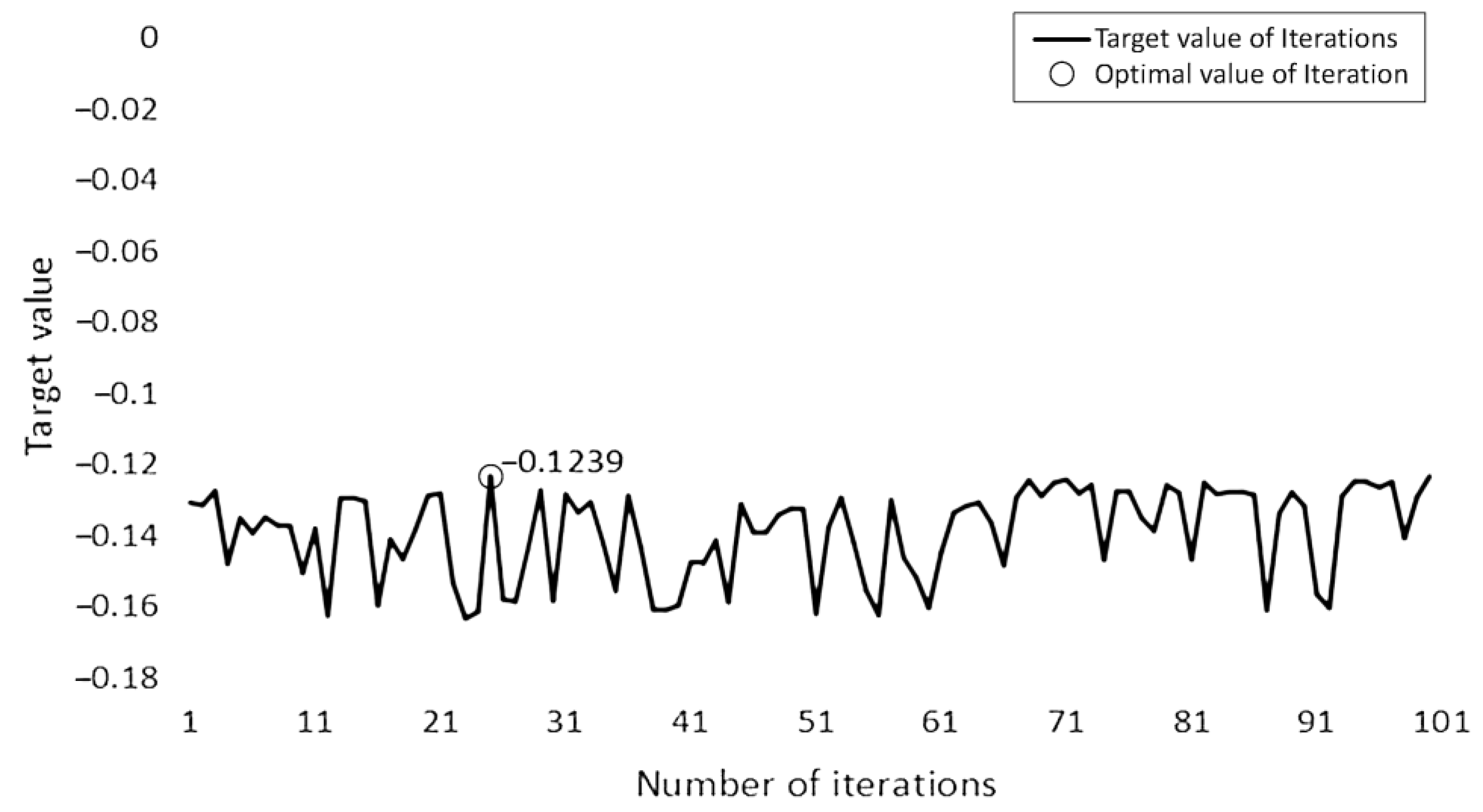
3.2.3. Bayesian Optimisation
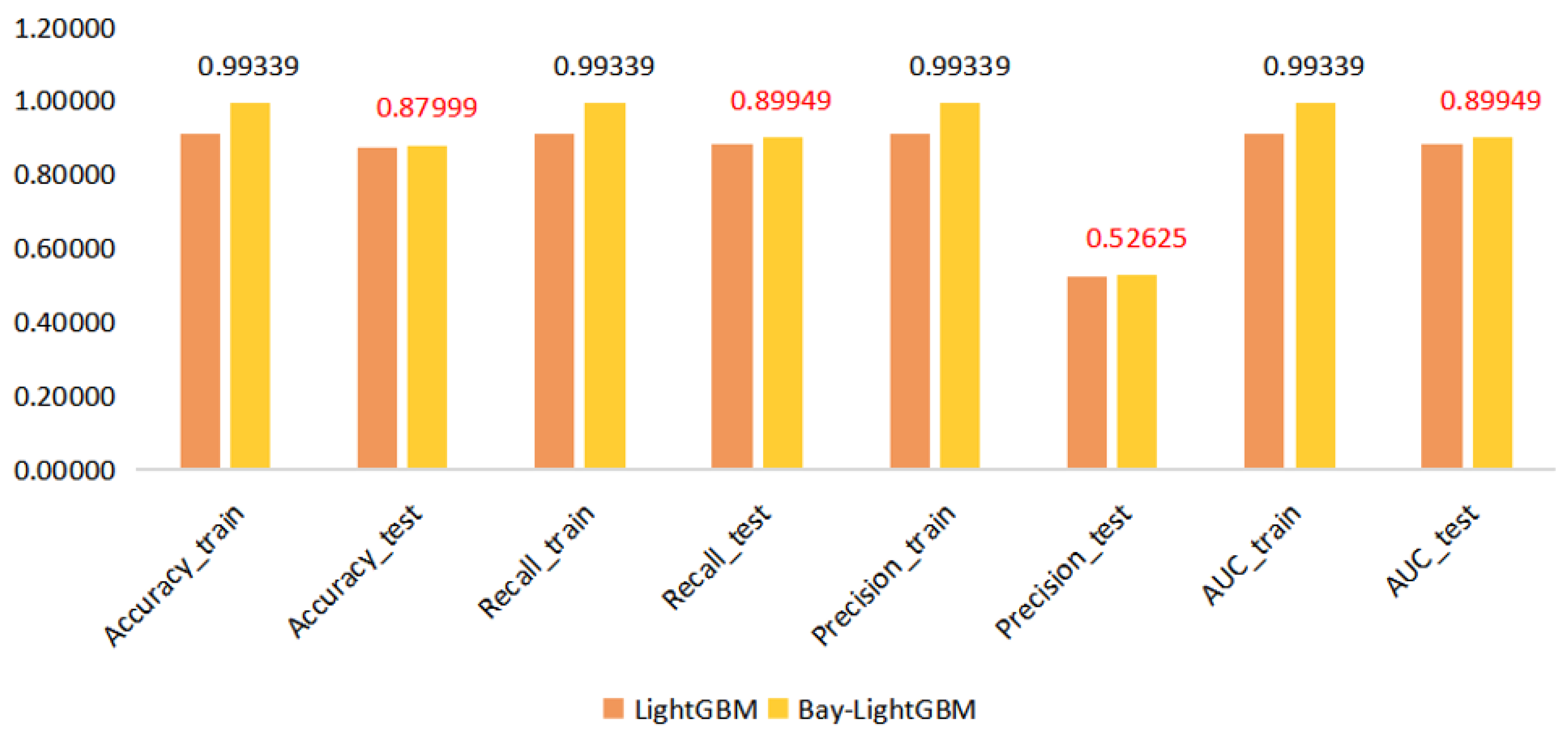
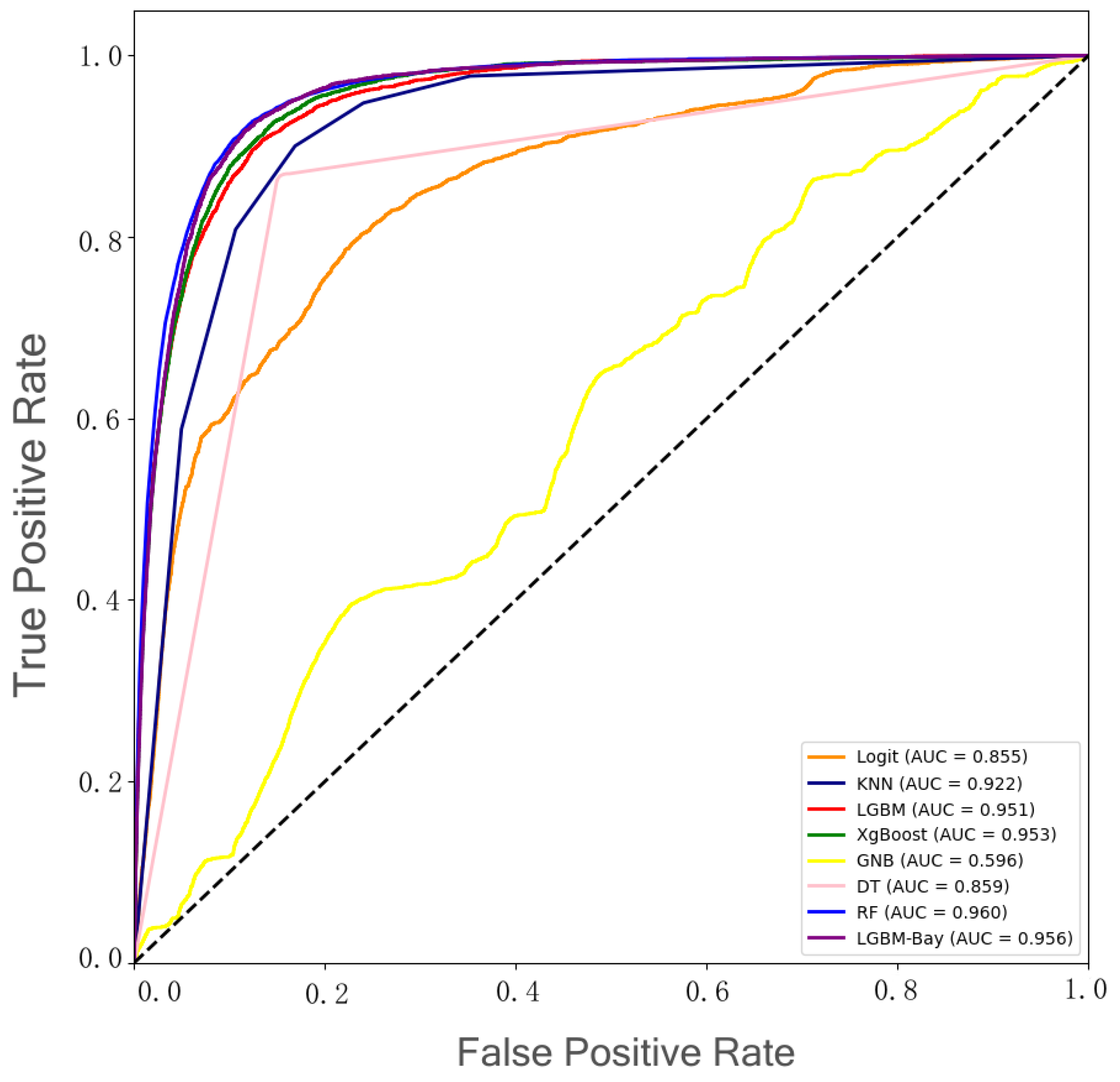
3.2.4. Model Evaluation
4. Empirical Study
4.1. Data Description
4.2. Data Pre-Processing
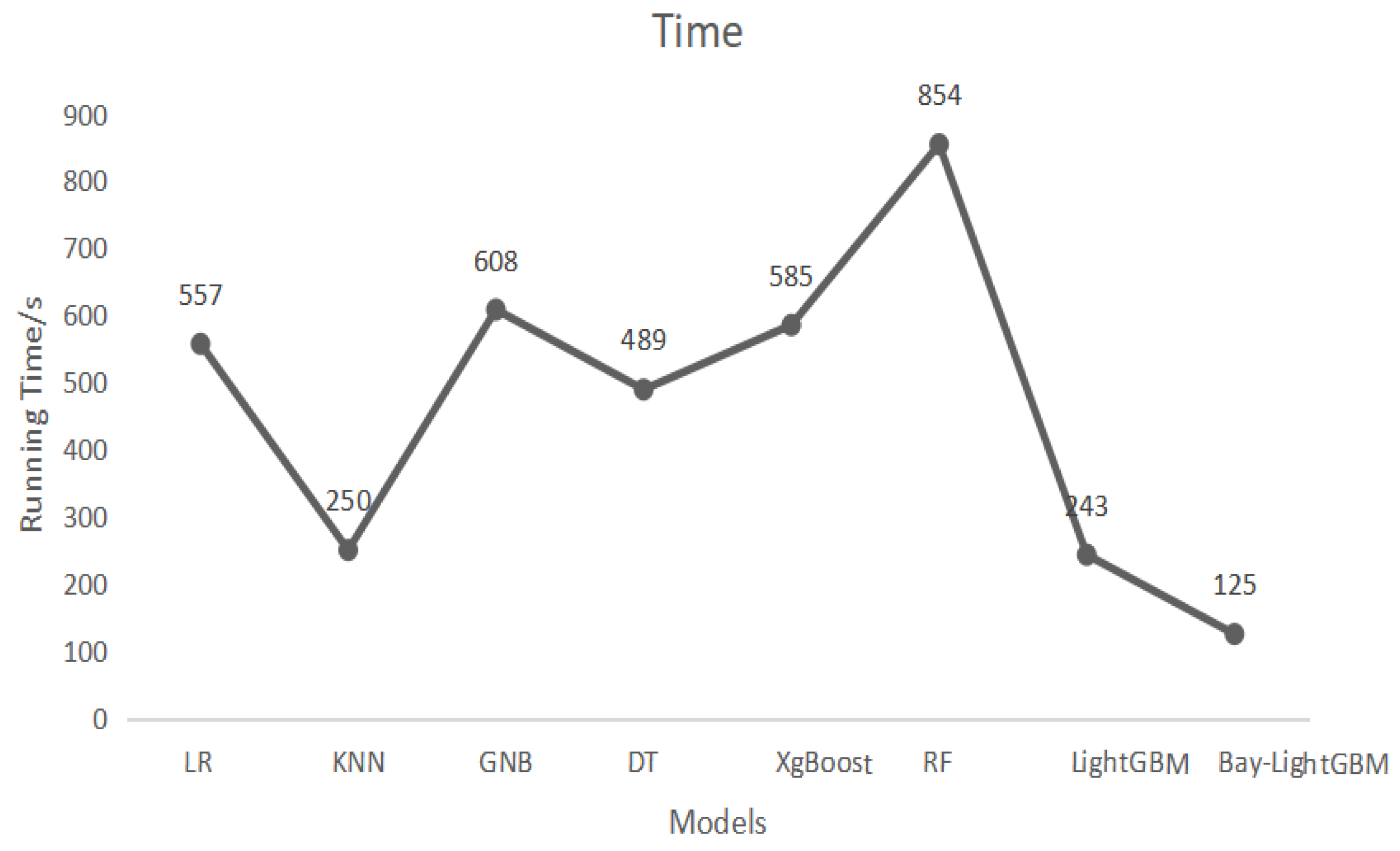
4.3. Model Building
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MacKenzie, C.A.; Barker, K.; Santos, J.R. Modeling a severe supply chain disruption and post-disaster decision making with application to the Japanese earthquake and tsunami. IIE Trans. 2014, 46, 1243–1260. [Google Scholar] [CrossRef]
- Ivanov, D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101922. [Google Scholar] [CrossRef] [PubMed]
- Arto, I.; Andreoni, V.; Rueda Cantuche, J.M. Global impacts of the automotive supply chain disruption following the Japanese earthquake of 2011. Econ. Syst. Res. 2015, 27, 306–323. [Google Scholar] [CrossRef]
- Burstein, G.; Zuckerman, I. Deconstructing Risk Factors for Predicting Risk Assessment in Supply Chains Using Machine Learning. J. Risk Financ. Manag. 2023, 16, 97. [Google Scholar] [CrossRef]
- Tang, J.; Haddad, Y.; Salonitis, K. Reconfigurable manufacturing system scheduling: A deep reinforcement learning approach. Procedia CIRP 2022, 107, 1198–1203. [Google Scholar] [CrossRef]
- Tang, J.; Salonitis, K. A deep reinforcement learning based scheduling policy for reconfigurable manufacturing systems. Procedia CIRP 2021, 103, 1–7. [Google Scholar] [CrossRef]
- Alrufaihi, D.; Oleghe, O.; Almanei, M.; Jagtap, S.; Salonitis, K. Feature reduction and selection for use in machine learning for manufacturing. Adv. Transdiscipl. Eng. 2022, 25, 289–296. [Google Scholar] [CrossRef]
- Almanei, M.; Oleghe, O.; Jagtap, S.; Salonitis, K. Machine learning algorithms comparison for manufacturing applications. Adv. Manuf. Technol. 2021, 34, 377–382. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Y.; Kong, D.; Zhang, Z.; Yang, Y. Decisions on spare parts allocation for repairable isolated system with dependent backorders. Comput. Ind. Eng. 2019, 127, 8–20. [Google Scholar] [CrossRef]
- Beam, A.L.; Kohane, I.S. Big data and machine learning in health care. JAMA 2018, 319, 1317–1318. [Google Scholar] [CrossRef]
- Ni, D.; Xiao, Z.; Lim, M.K. A systematic review of the research trends of machine learning in supply chain management. Int. J. Mach. Learn. Cybern. 2020, 11, 1463–1482. [Google Scholar] [CrossRef]
- Bavarsad, B.; Boshagh, M.; Kayedian, A. A study on supply chain risk factors and their impact on organizational Performance. Int. J. Oper. Logist. Manag. 2014, 3, 192–211. [Google Scholar]
- Schroeder, M.; Lodemann, S. A systematic investigation of the integration of machine learning into supply chain risk management. Logistics 2021, 5, 62. [Google Scholar] [CrossRef]
- Shekarian, M.; Mellat Parast, M. An Integrative approach to supply chain disruption risk and resilience management: A literature review. Int. J. Logist. Res. Appl. 2021, 24, 427–455. [Google Scholar] [CrossRef]
- Gaudenzi, B.; Borghesi, A. Managing risks in the supply chain using the AHP method. Int. J. Logist. Manag. 2006, 17, 114–136. [Google Scholar] [CrossRef]
- Salamai, A.; Hussain, O.K.; Saberi, M.; Chang, E.; Hussain, F.K. Highlighting the importance of considering the impacts of both external and internal risk factors on operational parameters to improve Supply Chain Risk Management. IEEE Access 2019, 7, 49297–49315. [Google Scholar] [CrossRef]
- Ho, W.; Zheng, T.; Yildiz, H.; Talluri, S. Supply chain risk management: A literature review. Int. J. Prod. Res. 2015, 53, 5031–5069. [Google Scholar] [CrossRef]
- MacKenzie, C.A.; Santos, J.R.; Barker, K. Measuring changes in international production from a disruption: Case study of the Japanese earthquake and tsunami. Int. J. Product. Econ. 2012, 138, 293–302. [Google Scholar] [CrossRef]
- DuHadway, S.; Carnovale, S.; Hazen, B. Understanding risk management for intentional supply chain disruptions: Risk detection, risk mitigation, and risk recovery. Appl. OR Disaster Relief Oper. 2019, 283, 179–198. [Google Scholar] [CrossRef]
- Nikookar, E.; Varsei, M.; Wieland, A. Gaining from disorder: Making the case for antifragility in purchasing and supply chain management. J. Purch. Supply Manag. 2021, 27, 100699. [Google Scholar] [CrossRef]
- Ponis, S.T.; Koronis, E. Supply Chain Resilience? Definition of concept and its formative elements. J. Appl. Bus. Res. 2012, 28, 921–935. [Google Scholar] [CrossRef]
- Ponomarov, S. Antecedents and Consequences of Supply Chain Resilience: A Dynamic Capabilities Perspective. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2012. [Google Scholar]
- Kleijnen, J.P.; Smits, M.T. Performance metrics in supply chain management. J. Oper. Res. Soc. 2003, 54, 507–514. [Google Scholar] [CrossRef]
- Björk, K.-M. An analytical solution to a fuzzy economic order quantity problem. Int. J. Approx. Reason. 2009, 50, 485–493. [Google Scholar] [CrossRef]
- Kazemi, N.; Ehsani, E.; Jaber, M.Y. An inventory model with backorders with fuzzy parameters and decision variables. Int. J. Approx. Reason. 2010, 51, 964–972. [Google Scholar] [CrossRef]
- Feng, G.; Chen-Yu, L.; Feng-Lei, X.; Wei-Ling, L. Demand Prediction of LRU Parts with Backorder for SRU. In Proceedings of the 2012 Fifth International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–29 October 2012; pp. 530–532. [Google Scholar] [CrossRef]
- Lee, H.L. The Triple-A Supply Chain. Harv. Bus. Rev. 2004, 82, 102–113. [Google Scholar]
- Disney, S.M.; Towill, D.R. On the bullwhip and inventory variance produced by an ordering policy. Omega 2003, 31, 157–167. [Google Scholar] [CrossRef]
- Nahmias, S.; Olsen, T.L. Production and Operations Analysis; Waveland Press: Long Grove, IL, USA, 2015. [Google Scholar]
- Monczka, R.M.; Handfield, R.B.; Giunipero, L.C.; Patterson, J.L. Purchasing and Supply Chain Management; Cengage Learning: Boston, MA, USA, 2020. [Google Scholar]
- Islam, S.; Amin, S.H. Prediction of probable backorder scenarios in the supply chain using Distributed Random Forest and Gradient Boosting Machine learning techniques. J. Big Data 2020, 7, 65. [Google Scholar] [CrossRef]
- Ntakolia, C.; Kokkotis, C.; Karlsson, P.; Moustakidis, S. An explainable machine learning model for material backorder prediction in inventory management. Sensors 2021, 21, 7926. [Google Scholar] [CrossRef]
- De Santis, R.B.; de Aguiar, E.P.; Goliatt, L. Predicting material backorders in inventory management using machine learning. In Proceedings of the IEEE Latin American Conference on Computational Intelligence (LA-CCI), Arequipa, Peru, 8–10 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Shajalal, M.; Hajek, P.; Abedin, M.Z. Product backorder prediction using deep neural network on imbalanced data. Int. J. Prod. Res. 2023, 61, 302–319. [Google Scholar] [CrossRef]
- Hajek, P.; Abedin, M.Z. A profit function-maximizing inventory backorder prediction system using big data analytics. IEEE Access 2020, 8, 58982–58994. [Google Scholar] [CrossRef]
- Sherwin, M.D.; Medal, H.; Lapp, S.A. Proactive cost-effective identification and mitigation of supply delay risks in a low volume high value supply chain using fault-tree analysis. Int. J. Prod. Econ. 2016, 175, 153–163. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault tree analysis: A survey of the state-of-the-art in modeling, analysis and tools. Comput. Sci. Rev. 2015, 15, 29–62. [Google Scholar] [CrossRef]
- Lee, W.-S.; Grosh, D.L.; Tillman, F.A.; Lie, C.H. Fault tree analysis, methods, and applications ߝ a review. ITR 1985, 34, 194–203. [Google Scholar] [CrossRef]
- Xing, L.; Amari, S.V. Fault Tree Analysis. In Handbook of Performability Engineering; Springer: London, UK, 2008; pp. 595–620. [Google Scholar]
- Hao, X.; Zhang, Z.; Xu, Q.; Huang, G.; Wang, K.J. Prediction of f-CaO content in cement clinker: A novel prediction method based on LightGBM and Bayesian optimization. Chemom. Intell. Lab. Syst. 2022, 220, 104461. [Google Scholar] [CrossRef]
- Prusa, J.; Khoshgoftaar, T.M.; Dittman, D.J.; Napolitano, A. Using random undersampling to alleviate class imbalance on tweet sentiment data. In Proceedings of the 2015 IEEE International Conference on Information Reuse and Integration, San Francisco, CA, USA, 13–15 August 2015; pp. 197–202. [Google Scholar] [CrossRef]
- Tanha, J.; Abdi, Y.; Samadi, N.; Razzaghi, N.; Asadpour, M. Boosting methods for multi-class imbalanced data classification: An experimental review. J. Big Data 2020, 7, 70. [Google Scholar] [CrossRef]
- Ramyachitra, D.; Manikandan, P. Imbalanced dataset classification and solutions: A review. Int. J. Comput. Bus. Res. 2014, 5, 1–29. [Google Scholar]
- Xu, S.; Lu, B.; Baldea, M.; Edgar, T.F.; Wojsznis, W.; Blevins, T.; Nixon, M. Data cleaning in the process industries. Rev. Chem. Eng. 2015, 31, 453–490. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Q.; Ma, Q.; Yu, B. LightGBM-PPI: Predicting protein-protein interactions through LightGBM with multi-information fusion. Chemom. Intell. Lab. Syst. 2019, 191, 54–64. [Google Scholar] [CrossRef]
- Al Daoud, E. Comparison between XGBoost, LightGBM and CatBoost using a home credit dataset. Int. J. Comput. Inf. Eng. 2019, 13, 6–10. [Google Scholar] [CrossRef]
- Zeng, H.; Yang, C.; Zhang, H.; Wu, Z.; Zhang, J.; Dai, G.; Babiloni, F.; Kong, W. A lightGBM-based EEG analysis method for driver mental states classification. Comput. Intell. Neurosci. 2019, 2019, 3761203. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 2017 Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; p. 30. [Google Scholar]
- Frazier, P.I. Bayesian Optimization. In Recent Advances in Optimization and Modeling of Contemporary Problems; Informs: Scottsdale, AZ, USA, 2018; pp. 255–278. [Google Scholar]
- Eriksson, D.; Pearce, M.; Gardner, J.; Turner, R.D.; Poloczek, M. Scalable global optimization via local bayesian optimization. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–14 December 2019; p. 32. [Google Scholar]
- Wang, Z.; Zoghi, M.; Hutter, F.; Matheson, D.; De Freitas, N. Bayesian Optimization in High Dimensions via Random Embeddings. In Proceedings of the IJCAI, Beijing, China, 3–9 August 2013; pp. 1778–1784. [Google Scholar] [CrossRef]
- Buckland, M.; Gey, F. The relationship between recall and precision. J. Am. Soc. Inf. Sci. 1994, 45, 12–19. [Google Scholar] [CrossRef]
- Ehrig, M.; Euzenat, J. Relaxed precision and recall for ontology matching. In Proceedings of the K-CAP 2005 Workshop on Integrating Ontology, Banff, AL, Canada, 2 October 2005; pp. 25–32. [Google Scholar]
- Tatbul, N.; Lee, T.J.; Zdonik, S.; Alam, M.; Gottschlich, J. Precision and recall for time series. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018; p. 31. [Google Scholar]
- Predictive Backorder Competition. Available online: https://github.com/rodrigosantis1/backorder_prediction (accessed on 1 March 2023).
- Tzanos, G.; Kachris, C.; Soudris, D. Hardware acceleration on gaussian naive bayes machine learning algorithm. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May; pp. 1–5. [CrossRef]
- Huang, Y.; Li, L. Naive Bayes classification algorithm based on small sample set. In Proceedings of the 2011 IEEE International Conference on Cloud Computing and Intelligence Systems, Beijing, China, 15–17 September 2011; pp. 34–39. [Google Scholar] [CrossRef]

| True Result | Prediction Result | |
|---|---|---|
| Negative | Positive | |
| Negative | True Negative (TN) | False Positive (FP) |
| Positive | False Negative (FN) | True Positive (TP) |
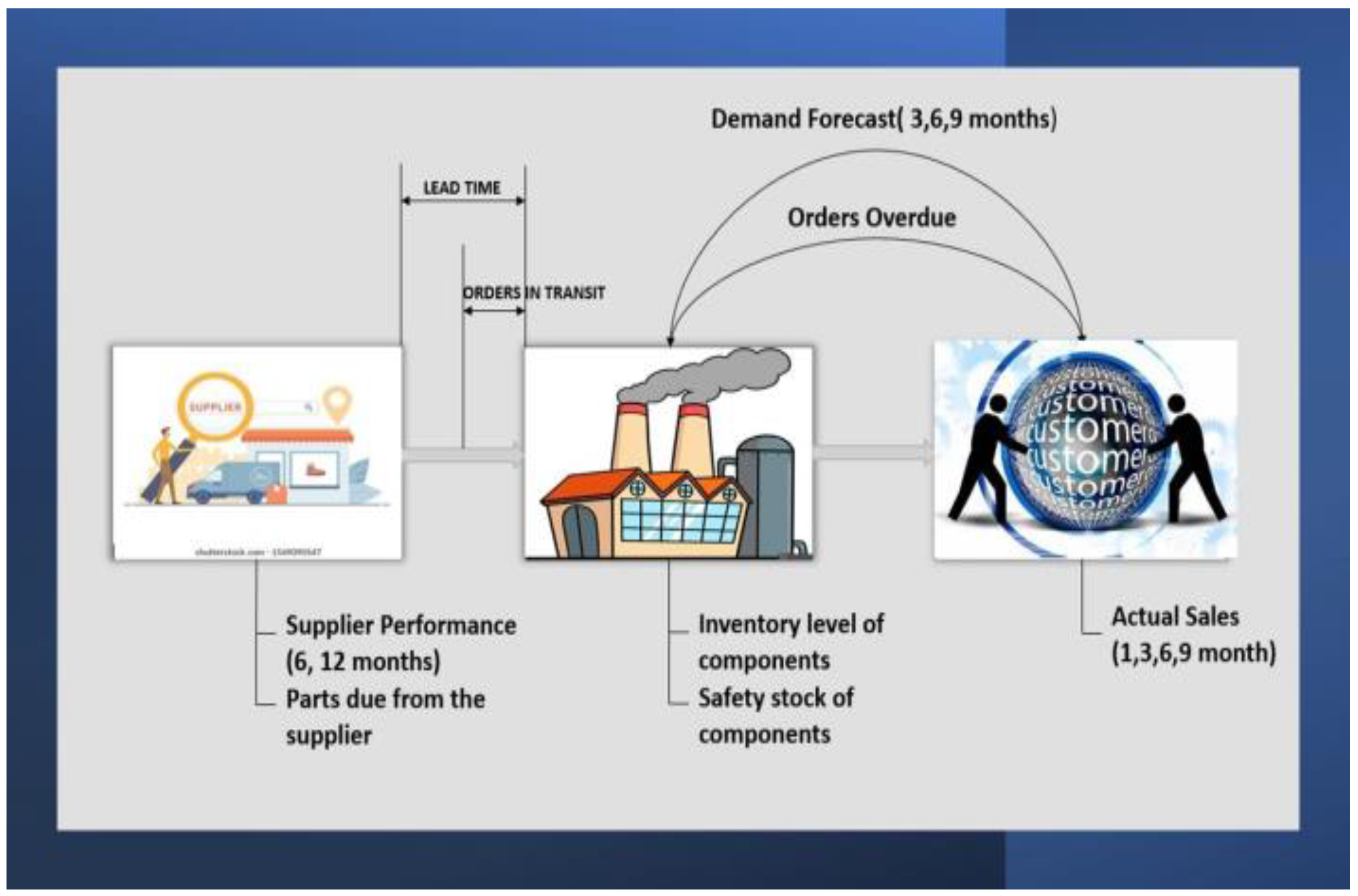
| Attributes | Ranges | Explanation |
|---|---|---|
| went_on_back_order (Binary) | Binary (0 or 1) | Product went on backorder |
| forecast_3_month, forecast_6_month, forecast_9_month (parts) | 0–138,240 | Sales forecast for next 3, 6, and 9 months |
| sales_1_month, sales_3_month, sales_6_month, sales_9_month (parts) | 0–132,068 | Sales volume in last 1, 3, 6, and 9 months |
| perf_6_month_avg, perf_12_month_avg (%) | 0 to 100% | Supplier performance in last 6 and 12 months |
| min_bank (parts) | 0–9672 | Minimum recommended stock amount |
| pieces_past_due (parts) | 0 | Number of parts overdue from supplier |
| local_bo_qty (parts) | 0 | Amount of stock overdue |
| in_transit_qtry (parts) | 0–5562 | Quantity in transit |
| lead_time (days) | 2 to 52 | Transit time |
| national_inv (parts) | 0–266,511 | Current inventory level |
| potential_issue (Binary) | Binary (0 or 1) | Identified source issue for the item |
| deck_risk, stop_auto_buy, rev_stop (Binary) | Binary (0 or 1) | General risk indicators |
| oe_constraint (Binary) | Binary (0 or 1) | Constraints on operating entities |
| ppap_risk (Binary) | Binary (0 or 1) | Risk associated with the production part approval process |
| Type | Original Dataset | Dataset after Random under Sampling | ||||
|---|---|---|---|---|---|---|
| True Sample | False Sample | Overall | True Sample | False Sample | Overall | |
| Training set | 1,341,197 | 9757 | 1,350,954 | 9757 | 9757 | 19,514 |
| Test set | 574,801 | 4180 | 578,981 | 574,801 | 4180 | 578,981 |
| Overall | 1,915,998 | 13,937 | 1,929,935 | 584,558 | 13,937 | 598,495 |
| Parameter | max_Depth | n_ Estimators | reg_alpha | min_child_ Samples | num_ Leaves | reg_ Lambda | Subsample |
|---|---|---|---|---|---|---|---|
| Value | 10 | 2930 | 0.1 | 47 | 20 | 1.0 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sani, S.; Xia, H.; Milisavljevic-Syed, J.; Salonitis, K. Supply Chain 4.0: A Machine Learning-Based Bayesian-Optimized LightGBM Model for Predicting Supply Chain Risk. Machines 2023, 11, 888. https://doi.org/10.3390/machines11090888
Sani S, Xia H, Milisavljevic-Syed J, Salonitis K. Supply Chain 4.0: A Machine Learning-Based Bayesian-Optimized LightGBM Model for Predicting Supply Chain Risk. Machines. 2023; 11(9):888. https://doi.org/10.3390/machines11090888
Chicago/Turabian StyleSani, Shehu, Hanbing Xia, Jelena Milisavljevic-Syed, and Konstantinos Salonitis. 2023. "Supply Chain 4.0: A Machine Learning-Based Bayesian-Optimized LightGBM Model for Predicting Supply Chain Risk" Machines 11, no. 9: 888. https://doi.org/10.3390/machines11090888
APA StyleSani, S., Xia, H., Milisavljevic-Syed, J., & Salonitis, K. (2023). Supply Chain 4.0: A Machine Learning-Based Bayesian-Optimized LightGBM Model for Predicting Supply Chain Risk. Machines, 11(9), 888. https://doi.org/10.3390/machines11090888








