1. Introduction
Since the Gough-Stewart configuration parallel platform was proposed in the 1960s [
1], there has been considerable research work by scholars on the theoretical modeling, motion simulation and mechanical testing of this interesting mechanism [
2]. Owing to the excellent multidimensional motion characteristic of the Stewart configuration mechanism, the application of the mechanism has spread across many fields, such as biomedical devices, aerospace engineering and industrial manufacturing [
3,
4,
5]. In the typical Stewart mechanism, the six legs are linked to the platform mainly by rigid joints, including ball joints and universal joints. Nevertheless, the relative movements of rigid parts occur during the working of rigid joints, which invariably cause nonlinear behavior of the system, such as clearances, friction and backlash [
6]. This results in lower accuracy, lower smoothness and higher uncertainty of dynamic characteristics in the system, which greatly limits the application of the Stewart mechanism in situations with high requirements for precision or stability of motion.
To address this shortcoming, researchers have gradually shifted their research direction towards flexible joints to substitute the function of rigid joints installed on the Stewart mechanism [
7,
8,
9,
10,
11,
12,
13,
14]. As a result, the working accuracy and dynamic characteristics of the Stewart mechanism have been substantially improved. Compared with the rigid joint, the flexible joint adopts an integrated design, which not only effectively avoids the inherent nonlinear behavior caused by structural clearances but also has the advantages of compactness and no lubrication [
15]. Nowadays, research and applications around the Stewart mechanism installed with flexible joints have covered many important areas in engineering, such as multidimensional motion control [
16,
17,
18], multidimensional disturbance suppression [
19,
20,
21] and precision measurement systems [
22,
23,
24]. However, with the usage of Flexible joints in the Stewart platform, a new difficulty had to be presented to the designers. It is well known that the flexible joint achieves relative motion between the connected parts through its own elastic deformation, and rebound forces are generated during the process, which leads to the introduction of the corresponding additional stiffness in the whole Stewart mechanism system. Consequently, the complexity of the dynamics theoretical analysis for the Stewart mechanism system is greatly increased.
Compared to the parallel legs in the Stewart platform, it is quite challenging to derive the additional stiffness matrix of the flexible joints. Therefore, when confronting the condition that the additional stiffness of Flexible joints has little effect, many researchers preferred to neglect the bending stiffness effect of Flexible joints during the theoretical study on Stewart configuration mechanisms [
9,
10,
25,
26,
27]. Despite so, in certain applications with higher stiffness sensitivity as well as demanding operational accuracy requirements [
28,
29], researchers need to emphasize the influence of the stiffness brought by flexible joints in the Stewart mechanism to ensure the mechanical accuracy of the whole system.
There are currently many theoretical studies on Stewart mechanisms with flexible joints that consider the effect of flexible joint stiffness. Wang [
30] represents the elastic bending and torsional deformation of the flexible joints by vector operations and establishes a standard dynamics formulation of the equivalent torque based on the principle of virtual work and the Lagrange method. Jiao [
11], based on the Kane equation, derived the complete dynamics equations of the Stewart active vibration isolation platform with flexible joints by combining the principle of virtual work. To research the performance of the 6-UPUR type Stewart configuration 6-axis force sensor, based on the screw theory, Zhao [
12] established a complete mathematical model of force transfer characteristics according to the relationship between stiffness and deformation compatibility conditions, which considers the stiffness of the flexible joints. To compensate for the added stiffness of the flexible joints in the control algorithm, Yang [
13] first obtained a linearized explicit dynamics model of the flexible joint stiffness in the Stewart platform based on the pseudo-rigid-body model and the principle of virtual power. Yao [
31] respectively constructed the overall stiffness matrix and the analytical mapping relationship of the 6-DOF force sensors based on the superposition principle under small deformations, which is certainly inspiring for the analysis of the stiffness of the flexure Stewart platform. As we can see from the above literature, it is a complicated and trying process to derive and analyze the stiffness participation of the flexible joints in a parallel mechanism through the dynamic theory approach. Additionally, due to the differences in application scenarios and designers’ mindsets, there can be a variety of position distribution and structural forms of flexible joints, which results in various types of Stewart mechanisms with different motion characteristics. Therefore, the theoretical model built for a particular structure type Stewart platform inevitably has limitations, which greatly reduce its availability.
In addition to the theoretical approach, it is worth mentioning that finite element method (FEM) simulation also provides a direct and effective approach for the analysis of rigid-flexible coupling systems. Furqan [
32] adopted the FEM simulation to solve the natural frequencies of the Stewart platform with flexible joints and obtained results comparable to the theory. DU [
33] analyzed the stiffness and dynamic characteristics of the Stewart configuration precision pointing mechanism by means of FEM simulation. Ranganath [
34] and Mohammed [
35] respectively conducted the force sensitivity analysis of the Stewart configuration six-dimensional force sensors with FEM simulation. Nevertheless, the single FEM simulation can only serve for the resultant analysis, which lacks the ability to solve the dynamic parameters of the system, so it cannot be used directly to obtain the numerical results regarding the stiffness effects of the flexible joints in the Stewart platform system.
This study mainly focuses on the effects of additional stiffness generated by flexible joints in Stewart platforms. Based on the dynamics modal characteristics of the Stewart platform system, a method for solving the additional stiffness of flexible joints is proposed depending on the FEM simulation. Based on theoretical research, the method is systematically analyzed and demonstrated together with simulation analysis and dynamics tests, which completely as well as sufficiently illustrate the correctness and effectiveness of the method for practical engineering applications. Compared with traditional dynamics methods such as the Newton-Euler method and Lagrange principle, the method proposed avoids the introduction of constraint forces and redundant derivative calculations. While avoiding complex kinematic analysis and formula derivation, it also reduces the involvement of calculated parameters, thus reducing the introduction of measuring deviations from the actual values of the system, which ensures high accuracy of the solution results in engineering. Moreover, the method holds a high degree of generality in practical applications. Theoretically, under the basic premise of stiffness symmetry, the additional stiffness caused by flexible joints with different position distributions or various structural forms in the Stewart mechanism can be solved by the method, which makes it fairly versatile for applications. The state of the art of this paper is creating a method with high generality and accuracy for solving the additional stiffness of flexible joints in the Stewart platform from a new perspective of combining theoretical analysis with FEM simulation methods, which has a high operational feasibility in practical engineering. Related parameter design methods are original and haven’t been proposed before. The paper provides certain technical references for the design and stiffness analysis of the Stewart configuration mechanism with flexible joints, further contributing to the Stewart configuration mechanism’s research and development in various engineering fields.
The paper contains five sections.
Section 2 elaborates on the method for solving the additional stiffness of flexible joints theoretically;
Section 3 solves and verifies the additional stiffness of Flexible joints in the Stewart platform through FEM modal analysis;
Section 4 presents the experimental work regarding the Stewart platform;
Section 5 concludes the overall work of this paper.
3. FEM Simulation of Stewart Platform
As an accurate and effective method for the dynamics analysis of complex systems, the finite element method has been well-established in various fields of engineering. Therefore, the FEM simulation was adopted in this paper to solve the modal results of the Stewart platform; the FEM model of the platform is shown in
Figure 2. All 6 degrees of freedom of the surface nodes below the Stewart platform are constrained during the process of modal analysis. For determining the stretching stiffness of legs and the bending stiffness of flexible joints in the FEM model of the Stewart platform, the dynamics calibration tests were conducted on the legs and flexible joints, respectively. According to the test results, the relevant material parameters of the leg springs and flexible joints’ FEM elements were set and adjusted so that the bending stiffness of the flexible joint in the FEM model is 146.72
, and the axial stretching stiffness of the legs is 324.57
, which match the test results. It is worth mentioning that the material of the flexible joint is steel, and its FEM model contains only the conventional body elements. After the calibration, the elastic modulus is
, Poisson’s ratio is
, and density is
. The specific contents of the tests are detailed in
Section 4 of this paper and will not be described here.
3.1. FEM Modal Analysis of Stewart Platform
During the establishment of the FEM model, a rectangular mass block was added and fixed to the upper platform of the Stewart platform’s FEM model, which aims to enable the difference of the mass distribution existing in the upper platform part between the
X and
Y axes, the parameters about the mass characteristics of the upper platform with the block can be referred to the
Appendix A. In addition, aiming to simplify the analysis process and reduce the error factor, the leg mass was set as 0 in the FEM model.
3.1.1. Modal Analysis of Stewart Platform with Ball Joints
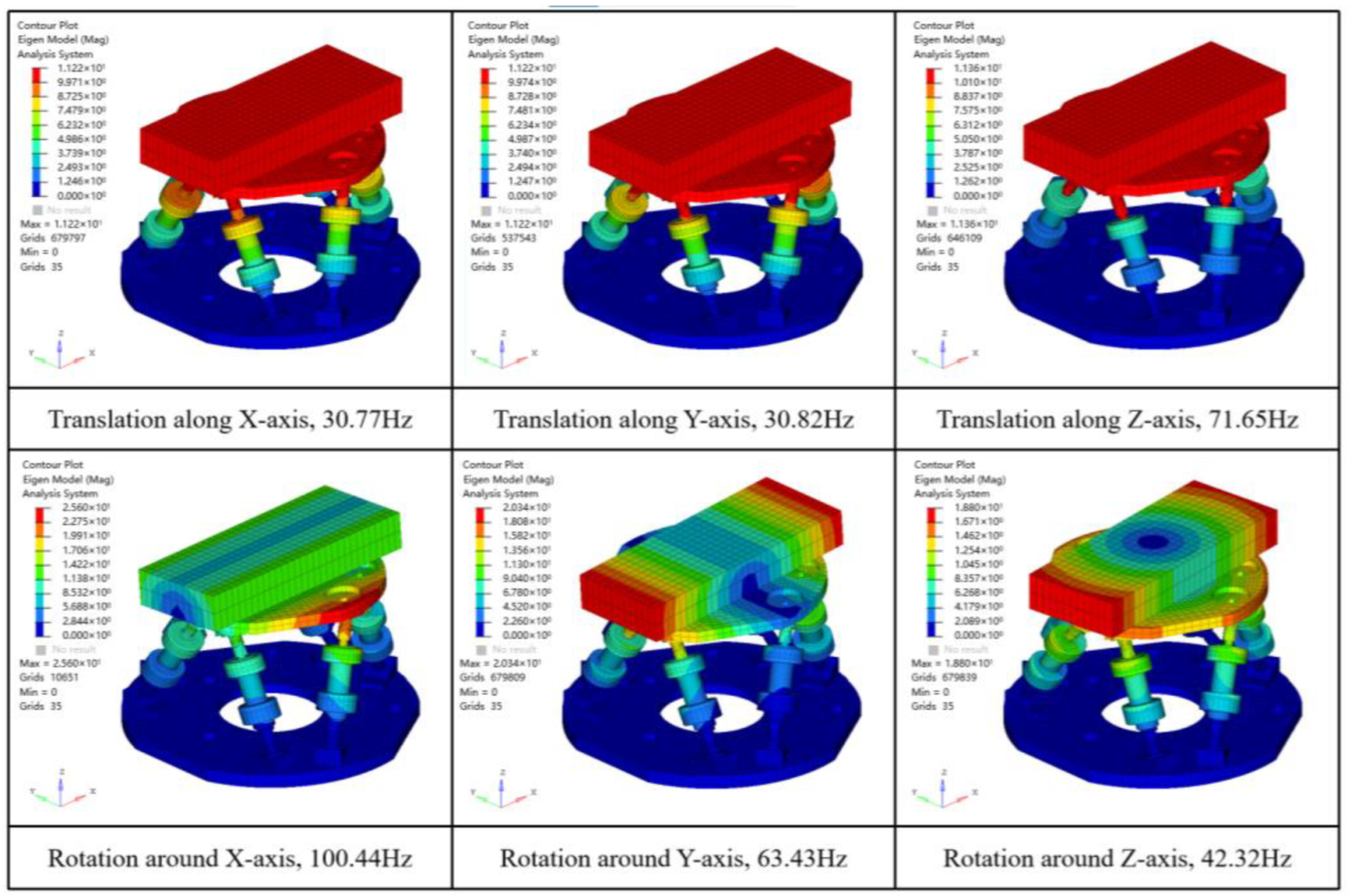
With the purpose of verifying the accuracy of the parameter settings in the FEM model and illustrating the consistency between the FEM simulation and the theoretical calculation results, the flexible joints in the model are first replaced by ball joints without additional stiffness, as shown in
Figure 2b, thereby eliminating the additional stiffness effect of the flexible joints on the Stewart platform. In terms of theoretical calculation, the generalized mass matrix
and stiffness matrix
of the system without the influence of the additional stiffness of flexible joints are calculated by Equations (2) and (6), respectively, and then the platform modes can be solved by Equation (1). The Stewart platform modes are solved by theoretical numerical calculation and FEM simulation, respectively, and the modal results obtained are shown in
Table 1.
Table 1 shows that the deviation of natural frequencies obtained by theoretical calculation and simulation is basically consistent. The maximum deviation of natural frequencies corresponding to the three order translational mode is only 0.04%, and the maximum deviation of natural frequency is the one corresponding to the rotational mode around the
X-axis, which is just 1.51%. The results can effectively reflect the accuracy of the FEM and the reliability of the modal solution of the FEM method.
3.1.2. Modal Analysis of Stewart Platform with Flexible Joints
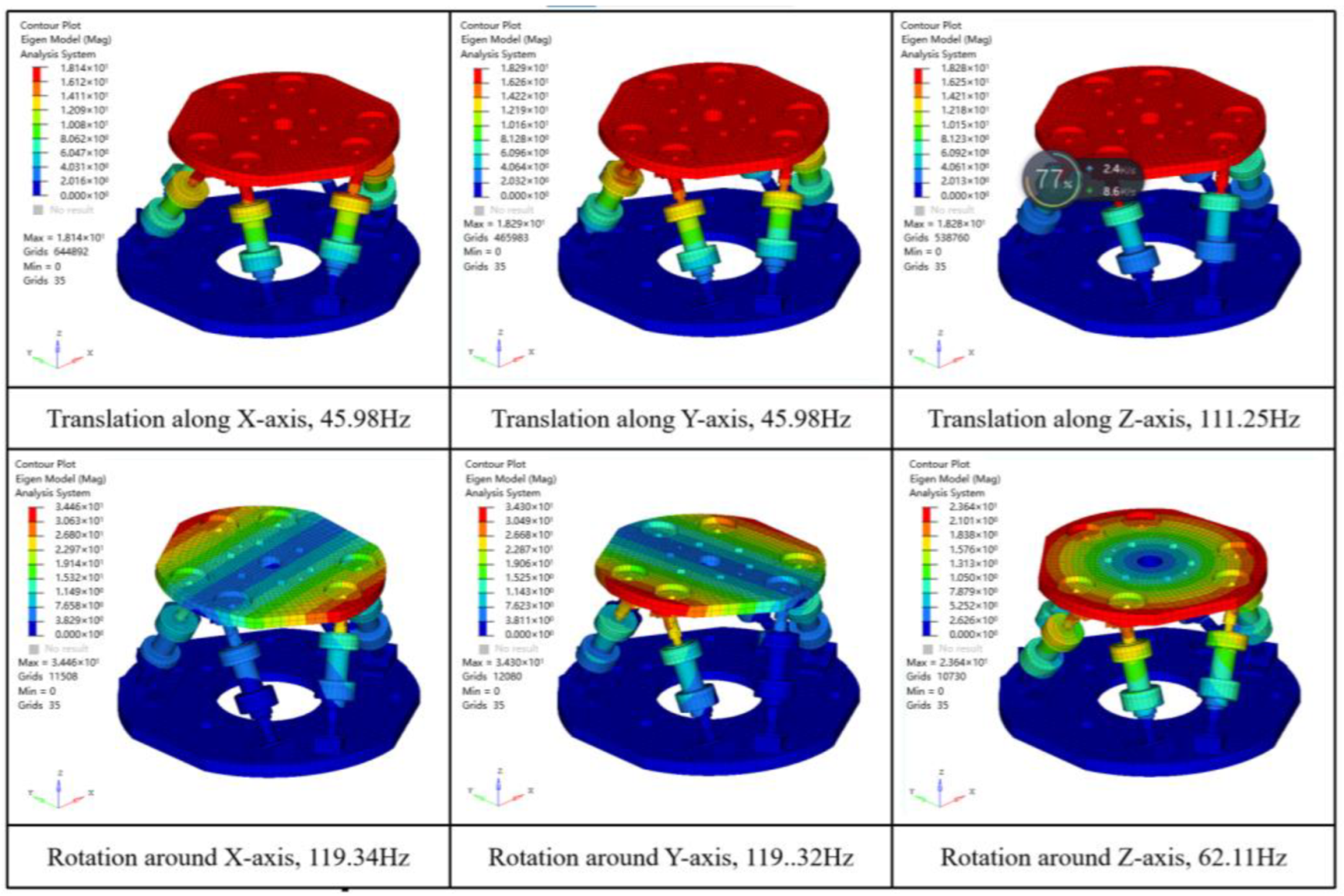
On the basis that the high accuracy of the Stewart platform’s FEM model has been ensured, the modal solution of the FEM model with flexible joints is further carried out; the modal results are shown in
Figure 3.
By substituting the corresponding natural frequencies of each mode in
Figure 3 into Equation (9), all parameters in the overall generalized stiffness matrix
of the system can be determined. Based on the solutions of stiffness matrix
and
, the additional stiffness
of the Stewart platform with flexible joints can be obtained by further using Equation (4). Finally, the solved additional stiffness matrix of the Stewart platform with flexible joints is:
3.2. Verification of Solving Results for Additional Stiffness of Flexible Joints
Further simulations are prepared around the Stewart platform in this paper based on the stiffness matrix obtained to verify the correctness of the theoretical method. In order to accomplish this, the following method is adopted in this paper: maintaining the stiffness characteristics of the flexible joints in the Stewart platform, the mass characteristics of the system and stretching stiffness values of legs are changed, and then the modal solution of the platform system under different mass states are calculation separately by theoretical numerical and FEM approach. Afterward, the accuracy of the solved can be verified by comparing the theoretical and simulation results. The specific conditions of characteristic change selected in this paper are:
- (a)
The mass of the rectangular load is changed to twice the original mass, and the leg stretching stiffness is changed to 1.5 times the original.
- (b)
The rectangular load of the upper platform is removed, and the corresponding mass characteristics of the legs are attached.
The corresponding modal results were respectively obtained after the FEM simulations. The modal results of condition (a) are basically similar to
Figure 3 and are not shown here to save space. The modal results corresponding to condition (b) are shown in
Figure 4.
It is worth noting that the main purpose of condition (b) is to correspond to the actual dynamic conditions of the Stewart platform for testing. The relevant parameters involved in the process are given in
Appendix A and are omitted here. The ultimate calculation results are shown in
Table 2.
As can be seen in
Table 2, the maximum deviation between the natural frequency results separately calculated by theory and FEM simulation under condition (a) is 2.26%, while the maximum deviation under condition (b) is just 0.87%. By comparing the natural frequency results under the characteristic conditions, the effectiveness of the proposed method for solving the additional stiffness of flexible joints can be verified.
5. Discussion
5.1. Additional Illustration of the Theoretical Method
It is observed from the previous contents that the method proposed in this paper reasonably depends on the symmetry of the Stewart configuration mechanism. Due to the structural axis-symmetric characteristics of the vertical
Z-axis, the dynamics of the mechanism exhibit theoretical consistency in the horizontal
X and
Y directions, which is particularly reflected in the generalized stiffness matrix K of the system. In addition, the mechanism exhibits the same symmetry characteristics regarding the dynamical coupling of both the
X and
Y axes. In many past studies, it can be found that the traditional type of Stewart configuration mechanism almost always has such properties of symmetry, and their stiffness matrix has the same parameter characteristics as Equation (7). Whenever this condition is satisfied, the solution of the additional stiffness of the flexible joint can be accomplished according to the theoretical method of this paper. According to the traditional kinematic theoretical method, it is inevitable to conduct different forms of kinematic analysis and theoretical derivation for the additional stiffness that exists in Stewart mechanisms with different types and distributions of flexible joints, and the derivation results can only be applied to one type of Stewart mechanism. In contrast, the method in this paper is more applicable and feasible for solving the additional stiffness of flexible joints in various forms of the Stewart mechanism. In addition, the theoretical idea of this paper can also be applied to the generalized Stewart mechanism mentioned by Jiang [
36], which contains a more complicated coupling relationship of stiffness characteristics compared to the traditional Stewart mechanism, including translational stiffness along the
X-axis and rotation stiffness around the
X-axis, translational stiffness along the
Y-axis and rotation stiffness around the
Y-axis, and translational stiffness along the
Z-axis and rotation stiffness around the
Z-axis. The generalized stiffness matrix of the system corresponding to the mechanism follows the equation:
where, apart from the same parameter characteristics as in Equation (7), the elements satisfy:
. This shows that there are two more values to be solved in the matrix
compared to the stiffness matrix
, which means there are seven parameters to be solved in the matrix
. However, the Stewart platform dynamics equations have only six modal solutions, which can only provide six eigenequations, which makes the set of equations unsolvable. The method given by the authors here follows. Before the step of the FEM modal solution for the Stewart platform, the upper platform shall be added to two different mass blocks successively and conducts the modal solution so that more eigenvalues and eigenequations can be obtained. Then the solution can be achieved when the number of eigenequations is more than that of solving parameters in fo matrix
. Although the usage of the method proposed for the generalized Stewart mechanism is more complicated than that of the traditional Stewart mechanism, it is still quite acceptable compared to the theoretical kinematic method with respect to the increased difficulty. The relevant content of this has not been studied deeply in the paper, and readers are encouraged to try it out.
Although the objective of the method in this paper is to find the additional stiffness induced by the flexible joints in the Stewart mechanism, the method proposed is essentially a solution for the overall stiffness of the system with the flexible joints. For conformity with the actual engineering situation and better illustration, the solution to the additional stiffness caused by the flexible joints in this paper is based on the premise that the generalized stiffness caused by the legs in the system is known. In fact, if the system stiffness caused by the legs is unknown, the additional stiffness caused by the flexible joint in the system can also be solved directly by setting the axial stretching stiffness of the legs in the FEM model to zero and keeping the flexible joint stiffness in the system. In practical situations, Stewart mechanisms may contain more than one type of flexible joint (e.g., bending-deformed flexible joints, torsion-deformed flexible joints). In this case, it is rather challenging to achieve a kinematic theoretical derivation to solve selectively for the additional stiffness caused by one or several groups of flexible joints in the system. However, it can be achieved straightforwardly by the method proposed, in which the corresponding stiffness of the irrelevant flexible components in the FEM model just needs to be set to zero before determining the FEM modal solution. Then the additional stiffness caused by the specified flexible joints can be obtained by bringing the obtained eigenvalues into the corresponding eigenequations to solve.
Furthermore, there are two issues need to be mentioned: 1. Since the method in this paper relies on the FEM modal solution results, a relatively good consistency between the established FEM model and the corresponding parameters in the set of eigenequations needs to be ensured, which determines the accuracy of the solution results. 2. During the process of adding additional load to the upper platform, it should be ensured that the overall mass distribution of the upper platform has differences in the X-axis and Y-axis directions to avoid the situation that and in the matrix , thus preventing the situation that the characteristic Equation (9a,b) is the same without solutions. Moreover, theoretically, the greater the difference between the upper platform part’s mass distribution about the X-axis and Y-axis directions, the better convergence and accuracy of the solution results can be obtained.
5.2. Damping Effects Analysis of Stewart Platform
The theoretical method proposed in this paper is primarily based on the modal analysis for the system stiffness solution, so the damping characteristics of the system are not considered during the theoretical analysis. However, during the actual tests, the dynamics behavior of the Stewart platform prototype will inevitably be affected by damping. For further clarification of the reasonableness of the test results under the influence of damping, the analysis and discussion around the influence of system damping follow.
Firstly, it should be specified that the Stewart platform tested adopts a gapless structure design, and the movements between the platform components depend on the elastic deformation of the flexible components (legs and hinges), which causes no frictional damping to occur in the system. Therefore, here we mainly consider the damping from the elastic deformation of the legs and the flexible joints, which is the main source of the damping compared to the structural damping and the air damping during the tests. Here, we temporarily assume linear damping; the specific values can be calculated using Equation (A2) in
Appendix A and the frequency response curves obtained from the tests in
Section 4.2. Then, the damping matrices of the system corresponding to the legs and the flexible joints are sequentially calculated by relevant dynamics theory, and the results are referred to in
Appendix A. Based on this, the dynamics equation of the system under unit sinusoidal excitation [
6] is given as follows:
where
denotes the system damping matrix, and given that the displacement of the payload platform is
, and the displacement of the base platform is
when a sinusoidal excitation is applied to the base platform, and the displacement of the base platform is:
. Here,
. Besides, the damping multiplication factor n is multiplied ahead of the damping matrix
. By changing the magnitude of
and solving Equation (13) sequentially, the frequency response curve of the Stewart platform with different damping can be obtained; the results are shown in
Figure 10.
After compilation, the natural frequencies of the Stewart platform with different damping are shown in
Table 5:
Figure 10 and
Table 5 show that the Stewart platform resonance peak decreases as the damping of the system increases, and the
X/
Y-direction second-order resonance peak disappears when the damping increases to a certain level. Meanwhile, the natural frequencies of each order of the system have different degrees of decline, in which the first-order natural frequency of
X/
Y direction with lower frequency has little change, and the second-order natural frequencies of
X/
Y direction and
Z direction with higher frequency have larger changes. Considering that the first-order natural frequencies of
X/
Y directions obtained from the tests are in strong agreement with the theoretical results, it can be considered that the first-order natural frequencies of the Stewart platform prototype in the tests are less affected by damping, and the negligence of the damping effect in the tests is justified to some extent.
Furthermore, we can observe that there is a large error in the higher
X/
Y-direction second-order natural frequencies and
Z-direction natural frequency under the assumption of linear damping. For this phenomenon, the authors give the following explanation after analysis. First, the curves in
Figure 10 are obtained under the premise that the damping of the system remains constant throughout the tests, but further observation shows that the actual second-order peak of the system is larger than the theoretical calculation, and the relatively first-order peak is significantly smaller than the theoretical result, so it can be concluded that the damping of the system during the second-order resonance is relatively smaller than that during the first-order resonance. Therefore, the actual second-order natural frequency is much closer to the theoretical natural frequency of 119
without damping, which indicates that the actual effect of damping on the second-order natural frequency of the system is obviously smaller. If so, a new problem arises here, the theoretical
Z-directional resonance amplitude is close to the test results, and the
Z-directional natural frequency is near the
X/
Y-directional second-order natural frequency, which contradicts the conclusion that the damping coefficient decreases in the high-frequency area. The authors speculate that it is due to the energy loss caused by the large-amplitude vibration of the system during the vibration process, which can also be confirmed by the fact that the theoretical
X/
Y first-order resonance amplitude is significantly larger compared to the test results. It is worth mentioning that the Stewart platform legs are equipped with damping components manufactured from viscoelastic materials, and the damping components may produce small creep on the surface of the closely attached parts while deforming during the system motion. Therefore, the author considers that the use of viscoelastic materials causes the complex damping characteristics of the system.
According to the theoretical analysis, the system-damping effect mainly acts in the higher frequency band. Under the assumption of constant damping in the full frequency band, the test error for the higher frequency X/Y-direction second-order natural frequency and Z-direction natural frequency is around 8%. However, the analysis of the test results shows that the damping in the high-frequency band is significantly lower than that in the low-frequency band, which entails that the damping-induced natural frequency error in the high-frequency band during the tests could be less than 8%. Therefore, the premise of the negligence of the damping effect can still be considered reasonable. Although the system damping has a certain influence on the test results, the overall correctness of the theoretical method of this paper can still be confirmed by the tests.