Wall Thickness Uniformity in ISF of Hydraulic Support: System Design, Finite Element Analysis and Experimental Verification
Abstract
1. Introduction
2. Materials and Methods
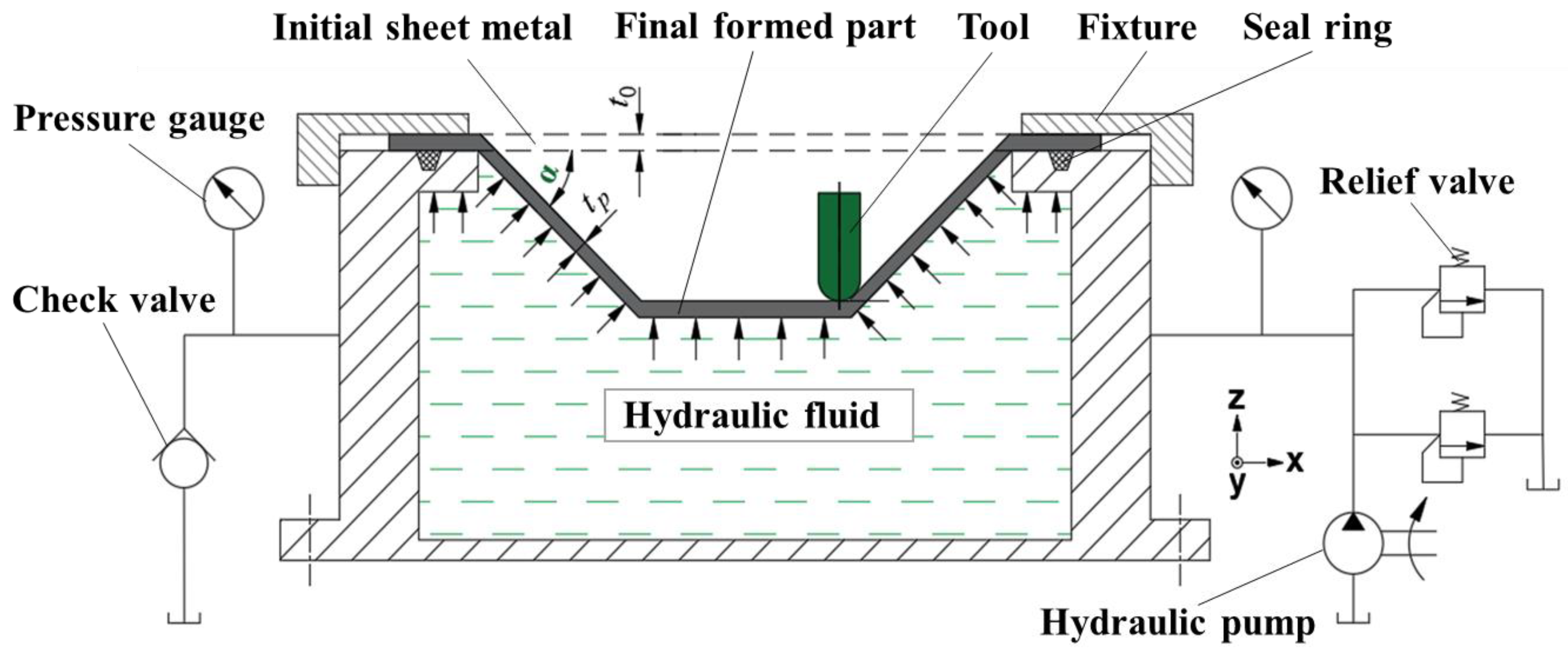
2.1. Design of HS-SPIF System
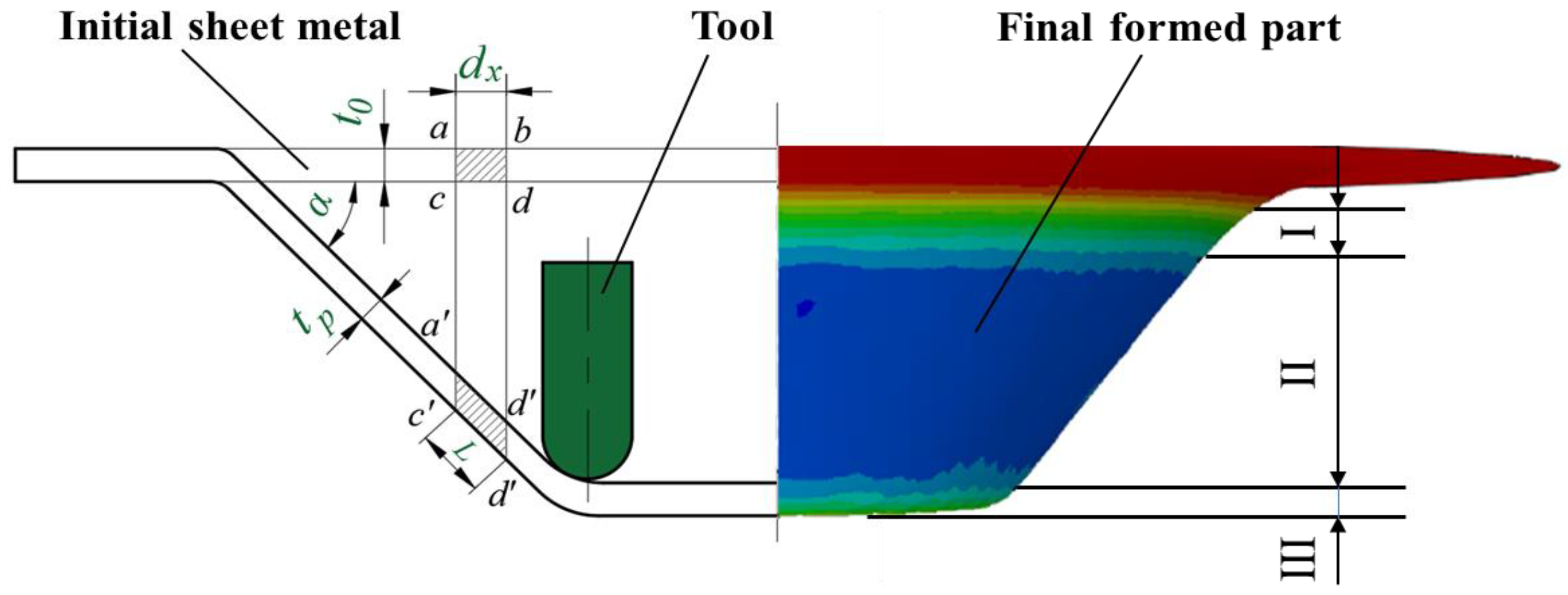
2.2. Critical Angle of Uniform Thickness
2.3. Finite Element Model and Analysis Method
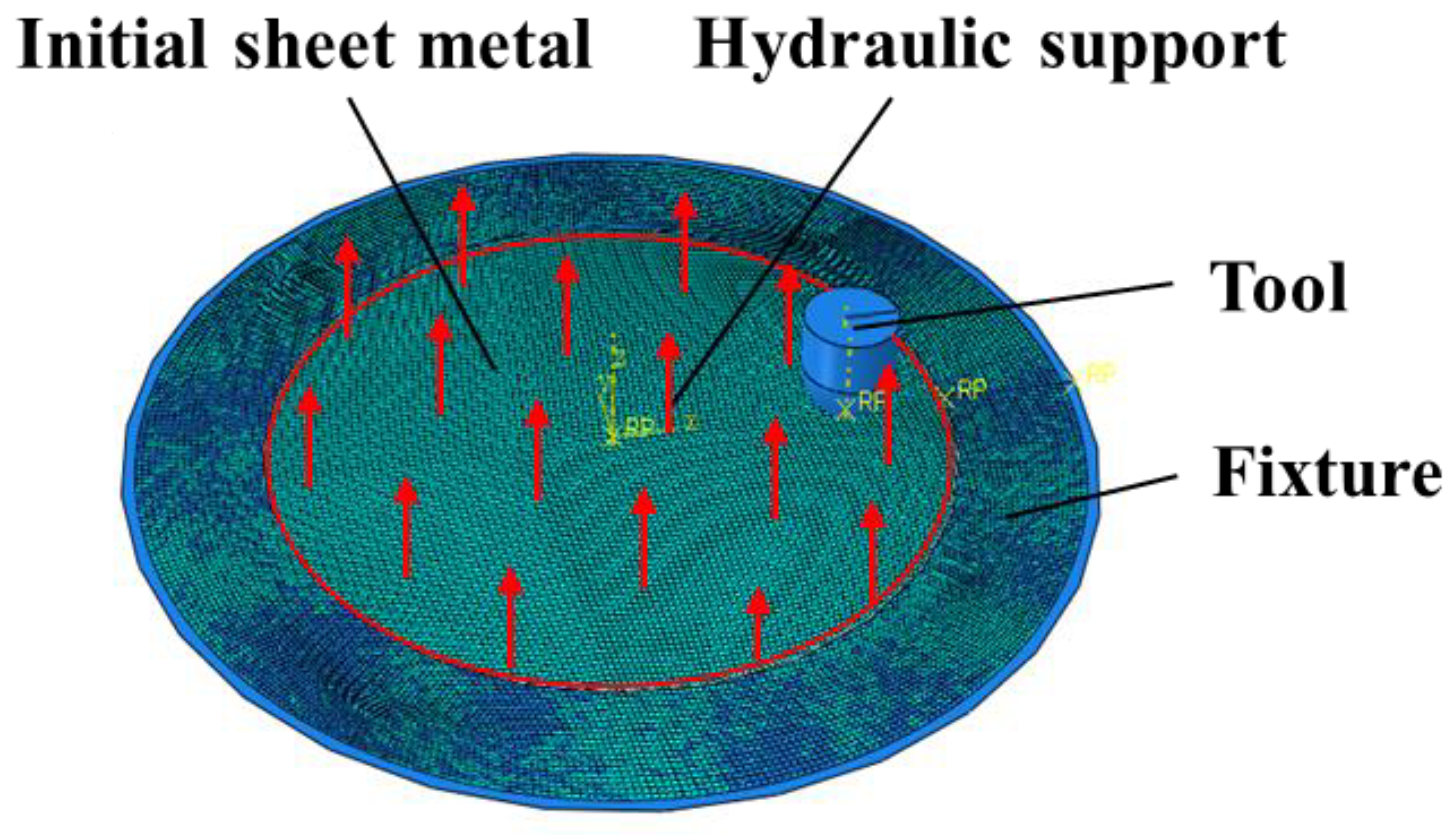
2.3.1. Establishment of Finite Element Model
2.3.2. Analysis Method
2.4. Experimental Equipment and Verification Scheme
2.4.1. Experimental Equipment
2.4.2. HS-SPIF Experimental Verification Scheme
3. Results
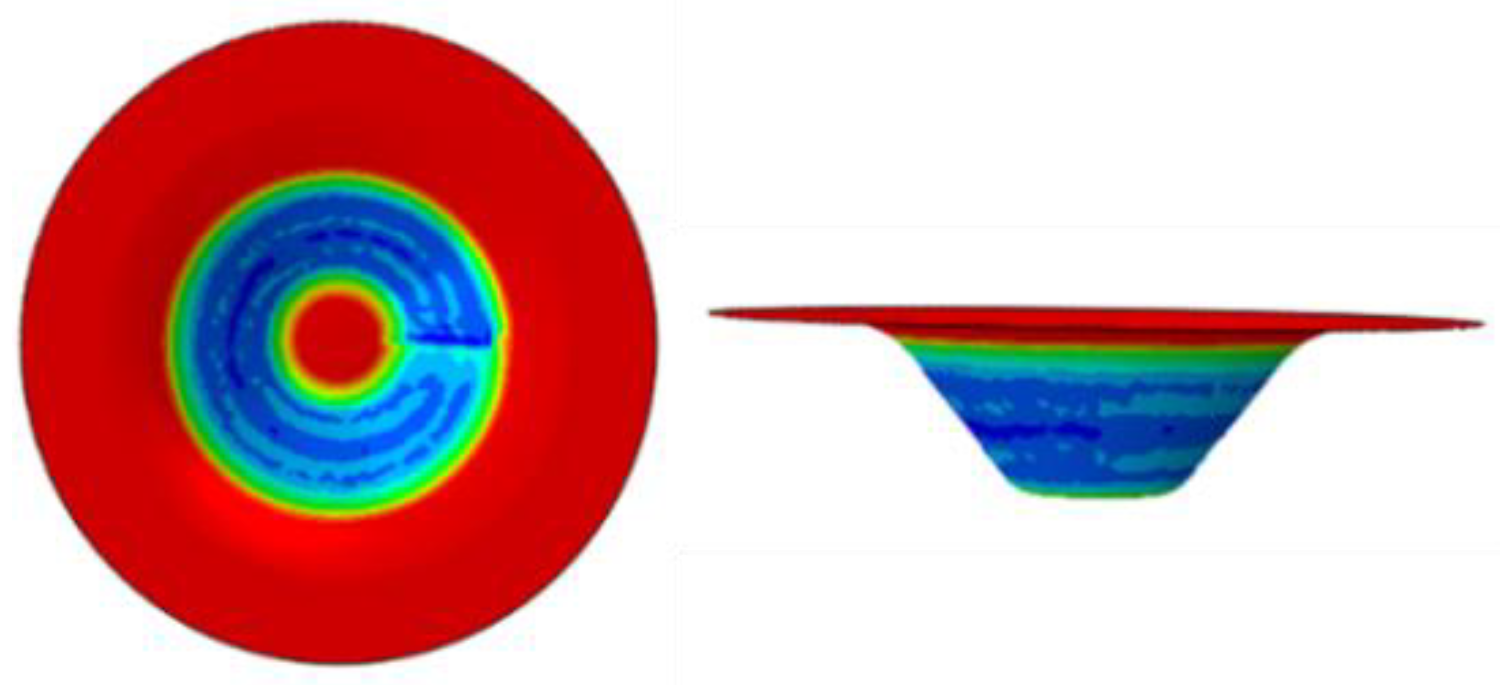
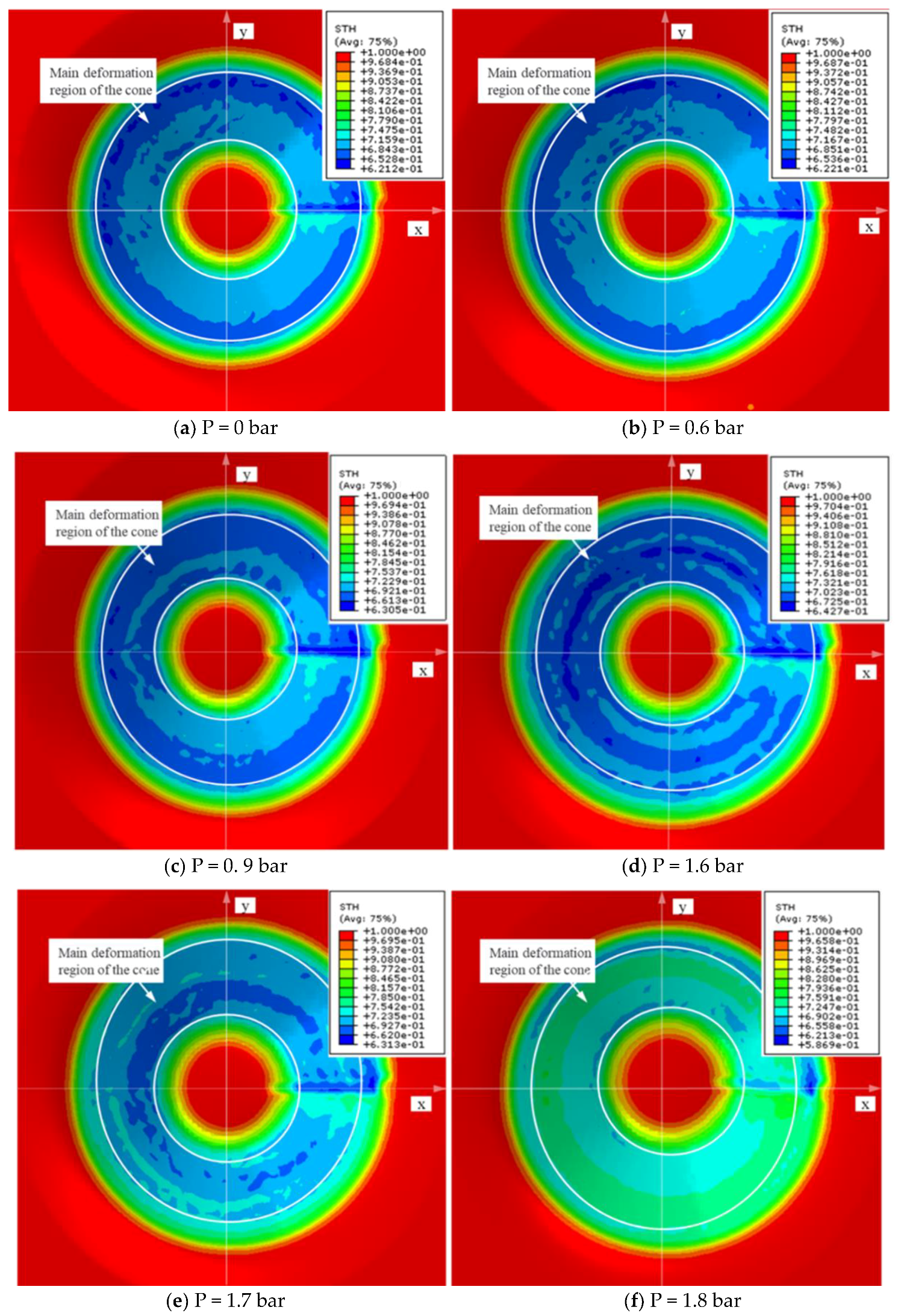
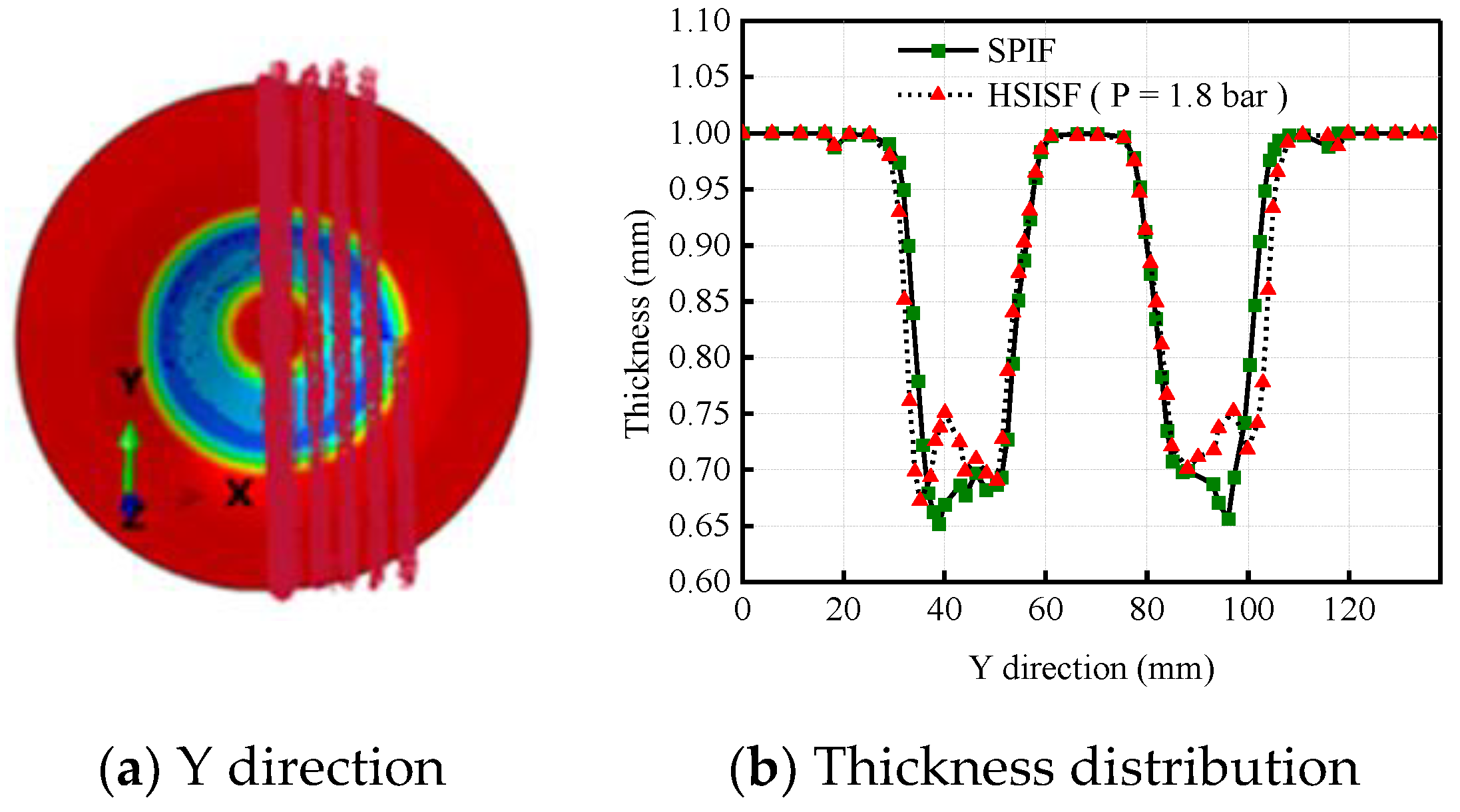
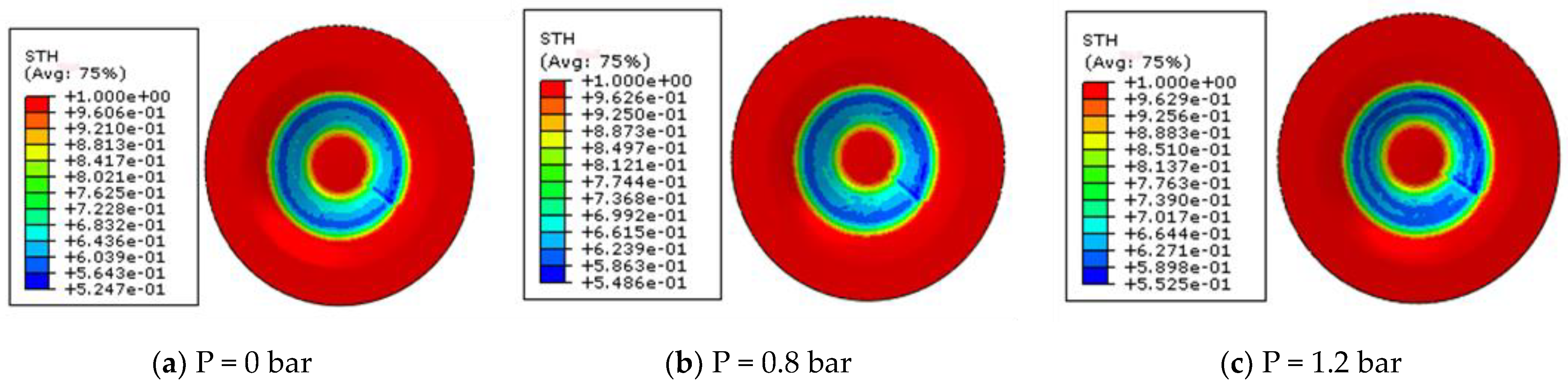
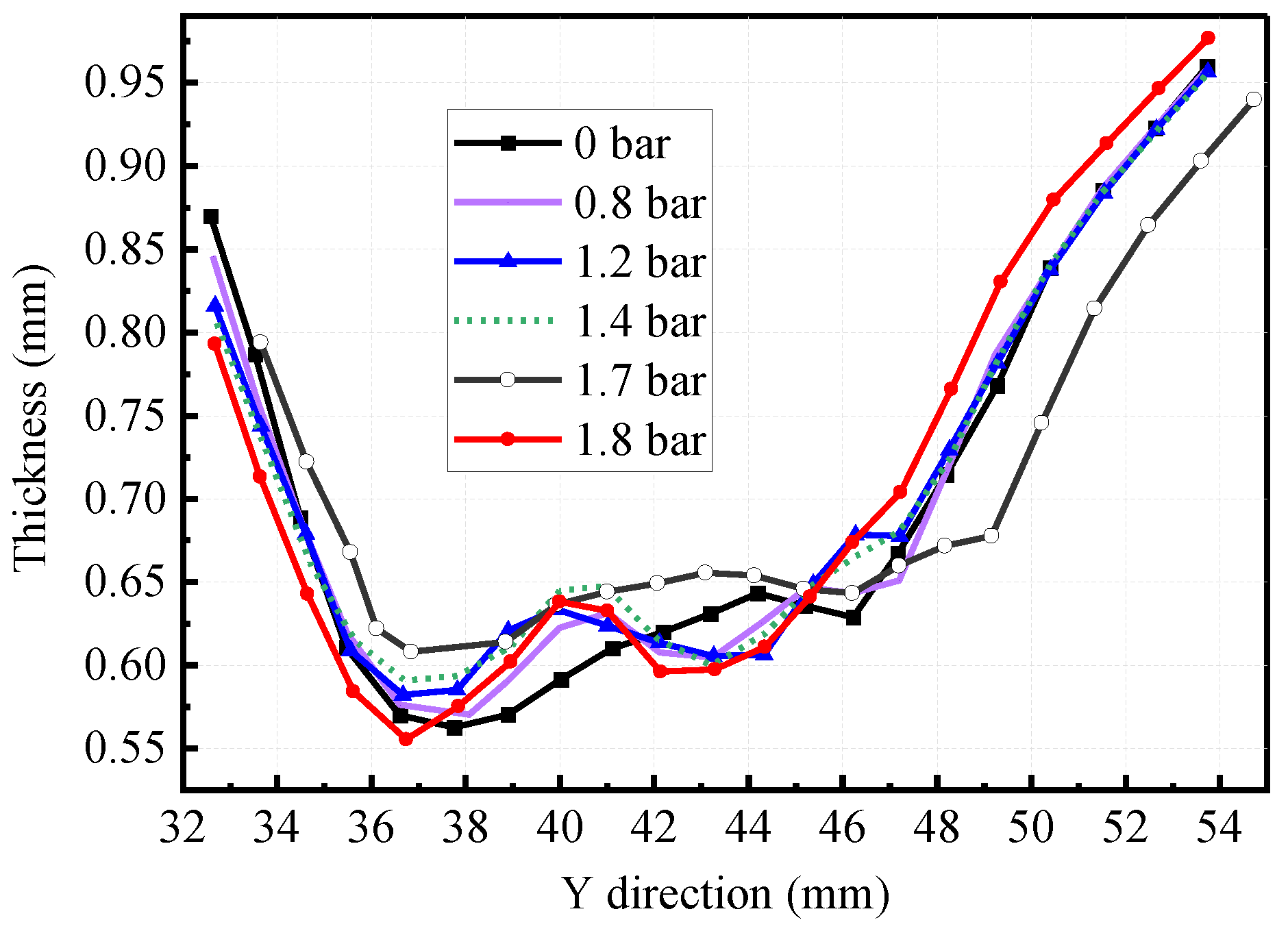
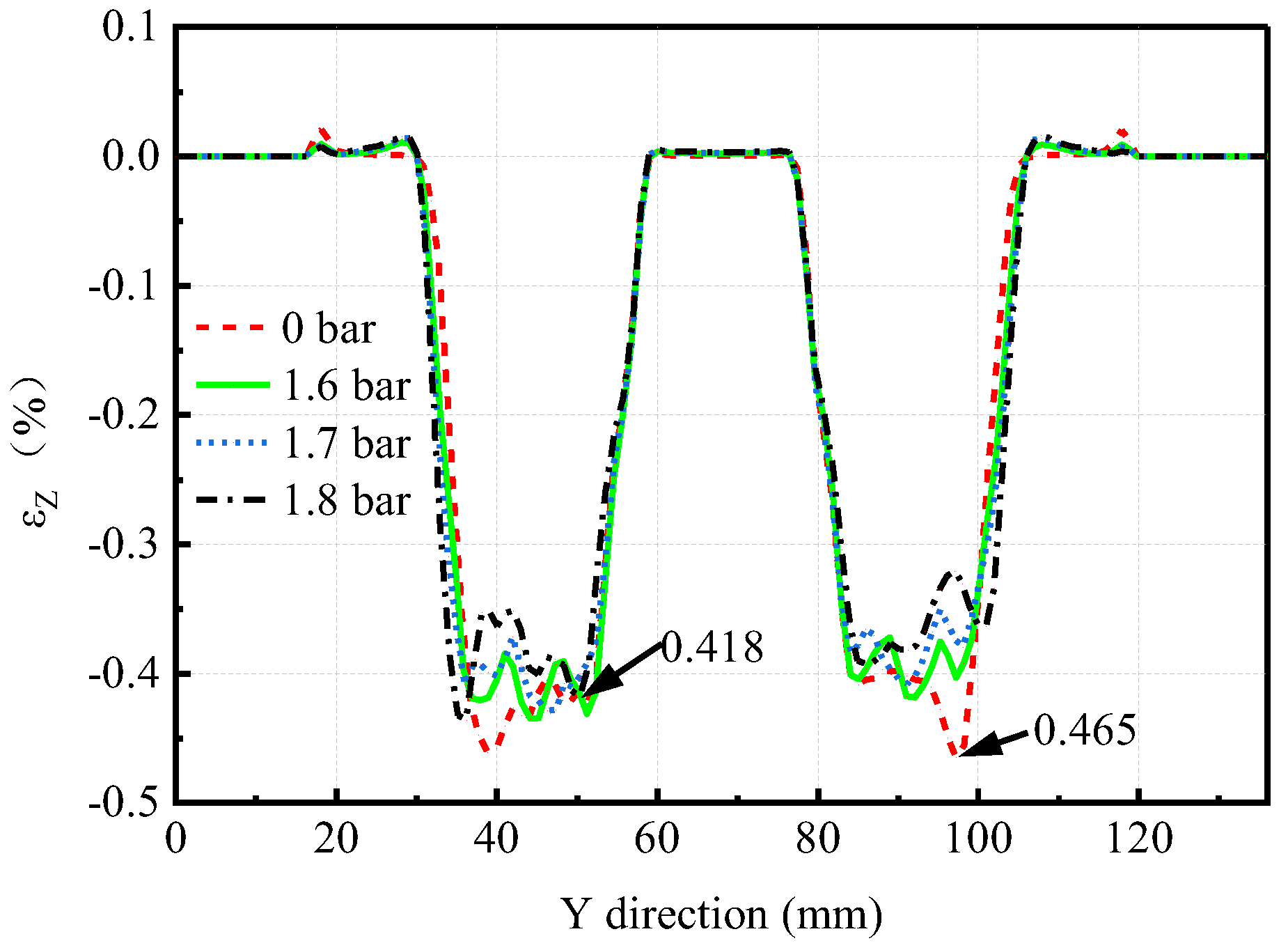
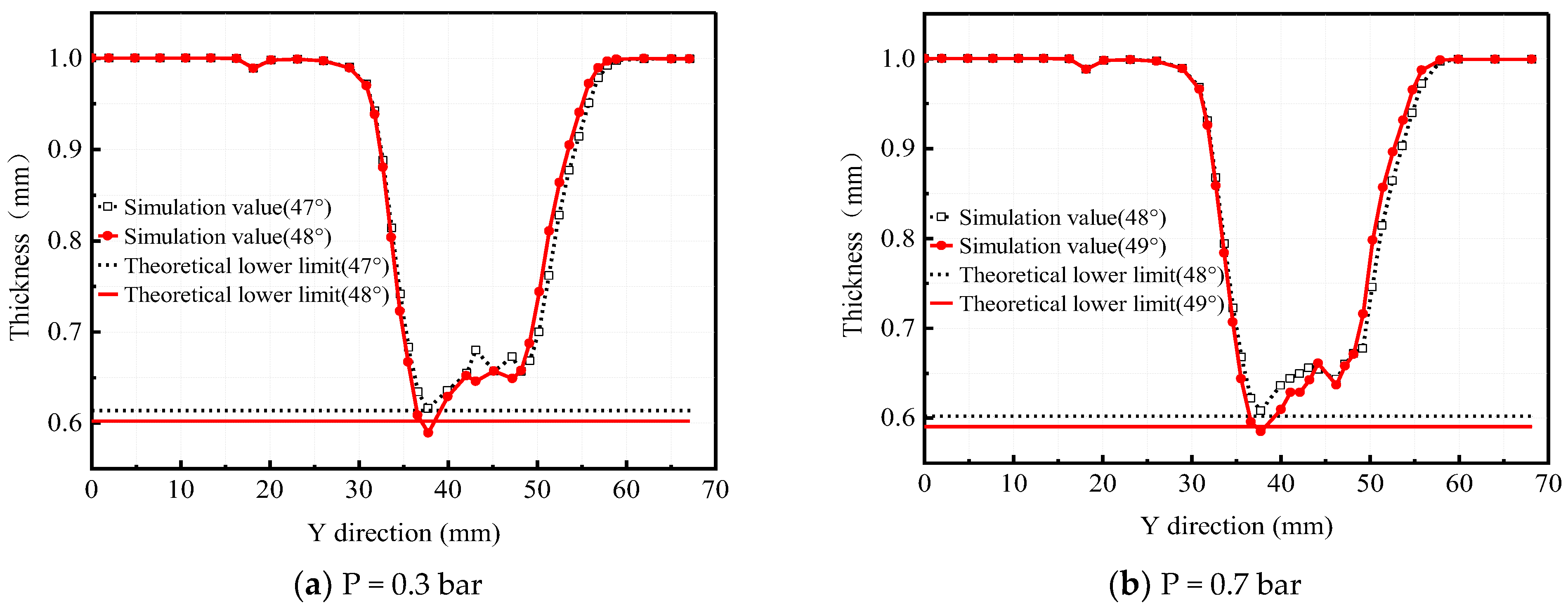
3.1. Simulation Results of Wall Thickness Distribution
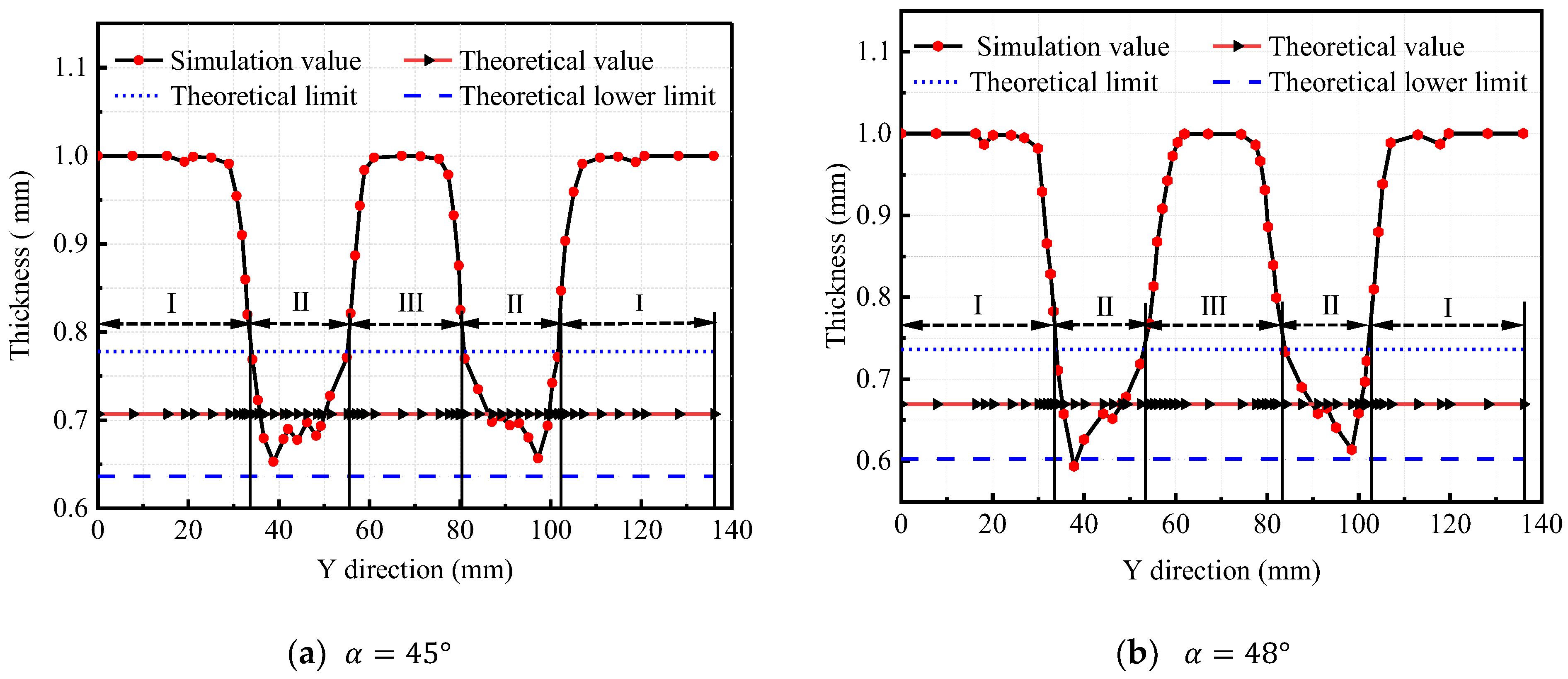
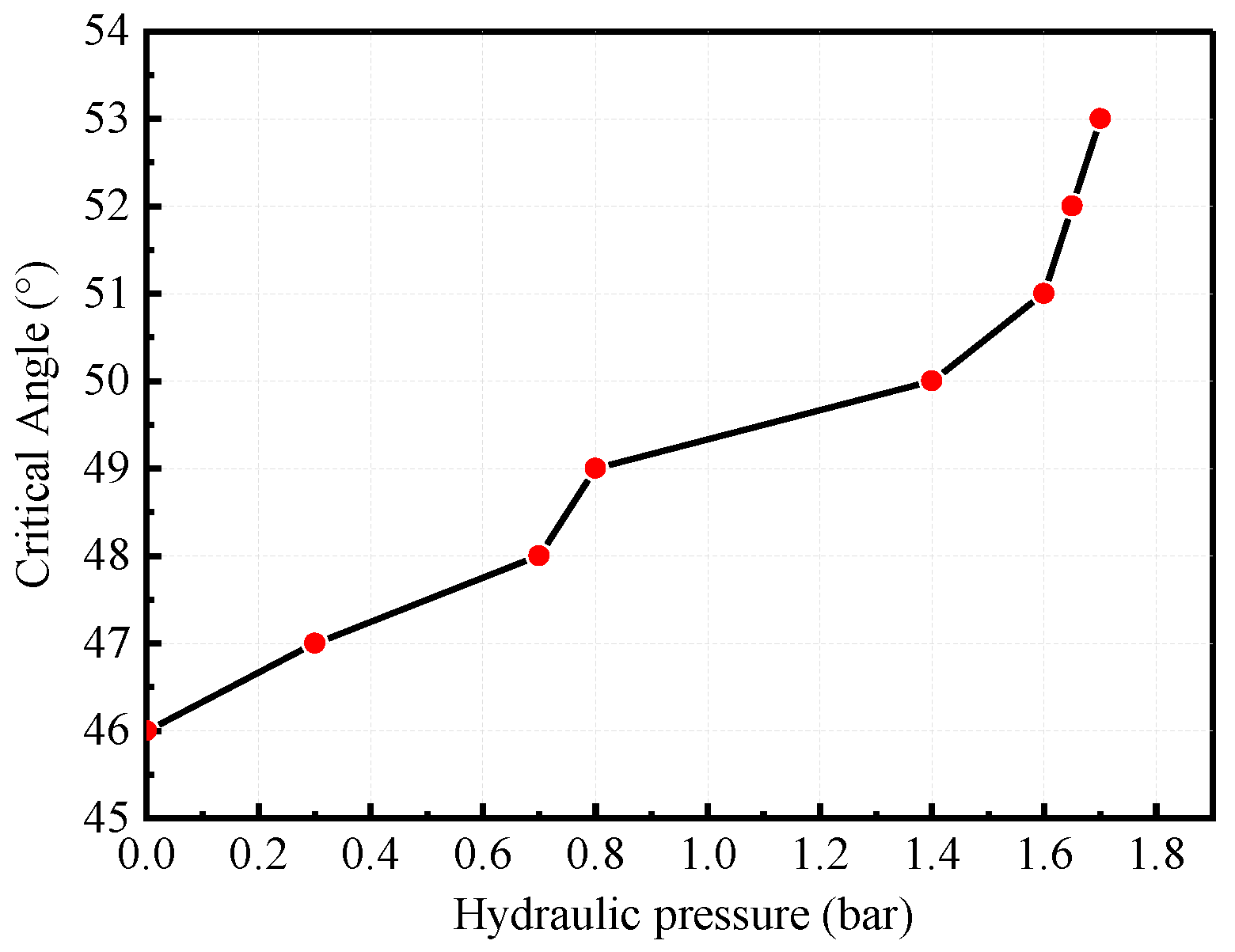
3.2. Simulation Results of Critical Angle
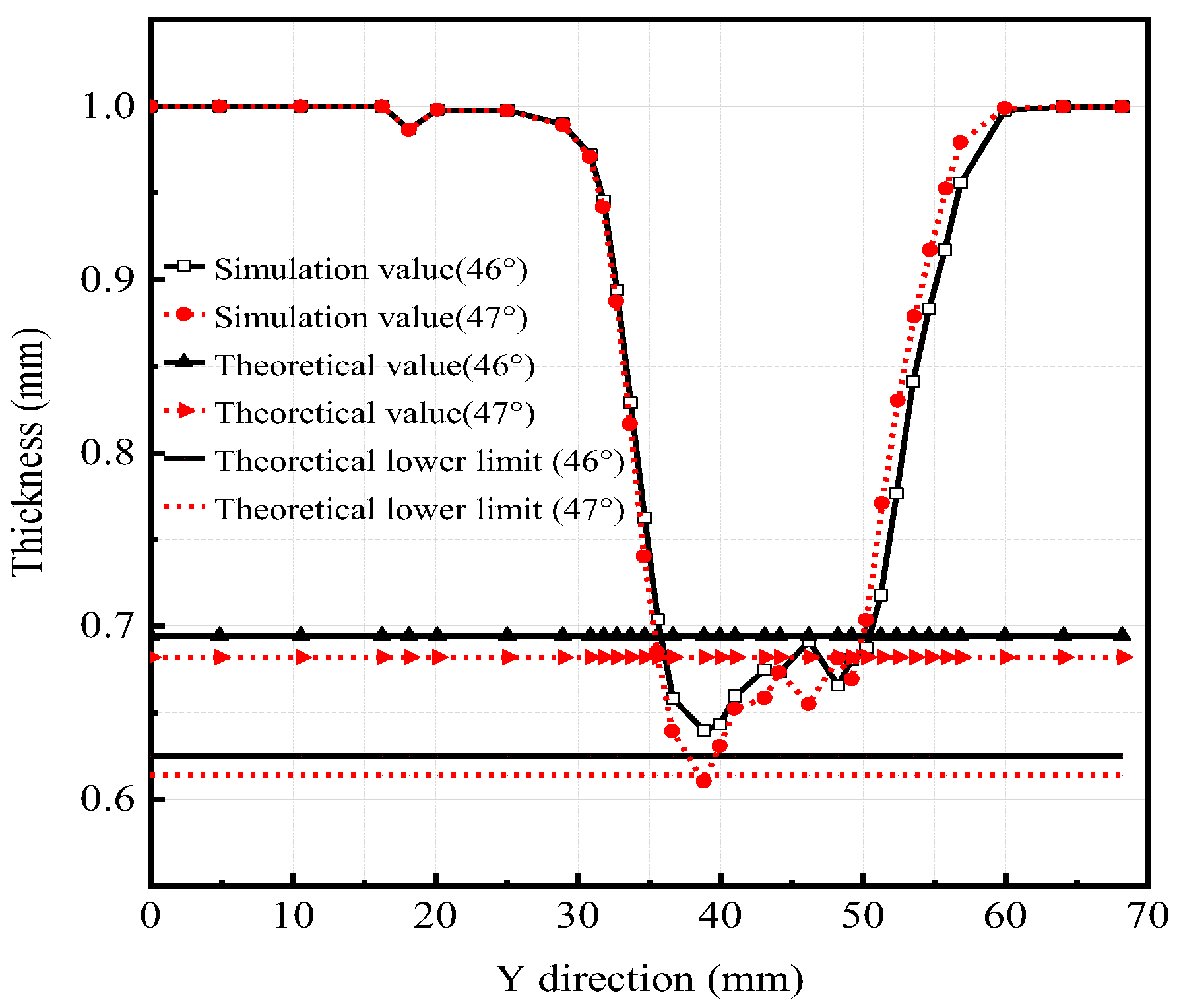
3.2.1. Assessment of SPIF Critical Angle
3.2.2. Assessment of HS-SPIF Critical Angle
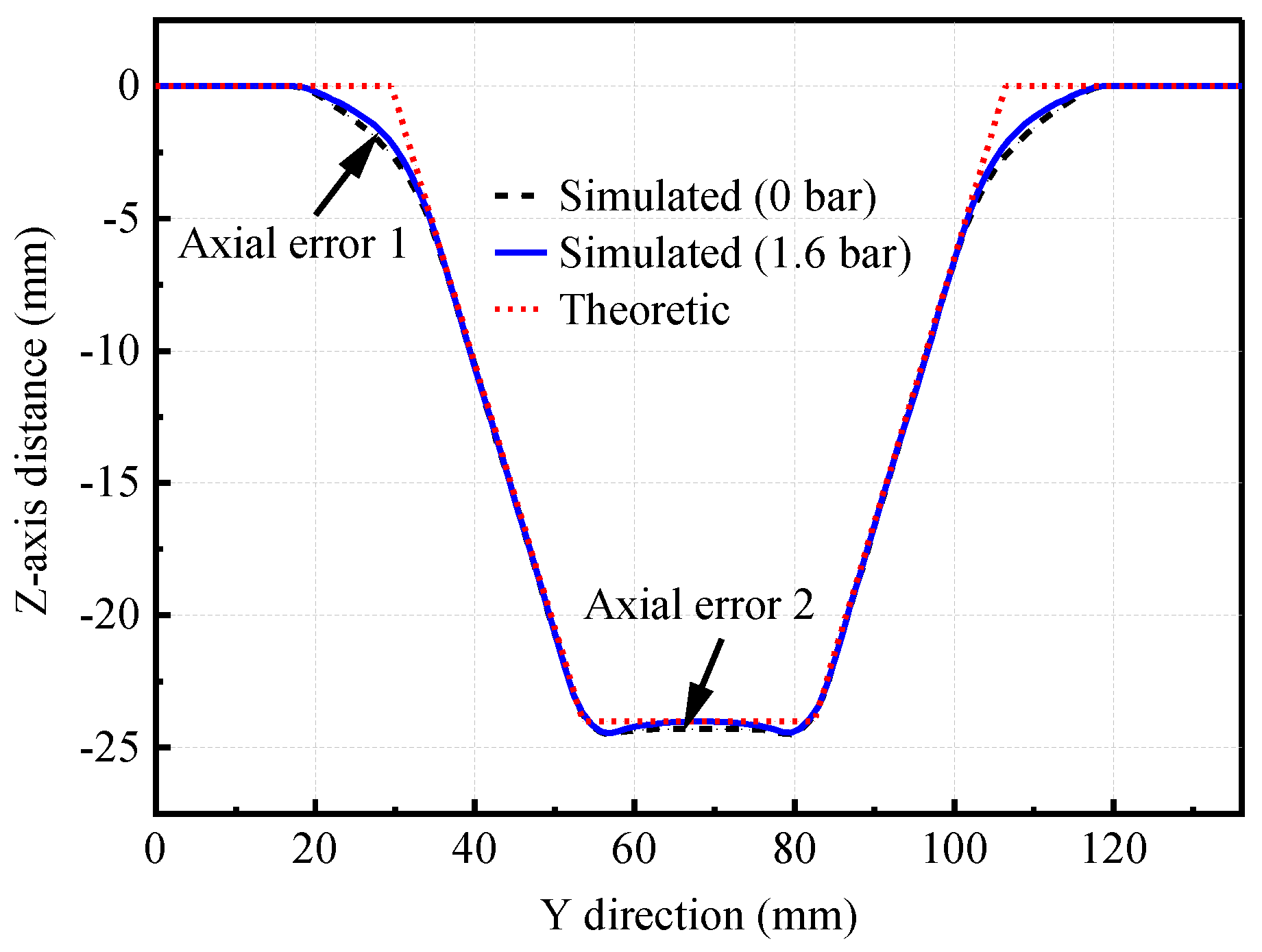
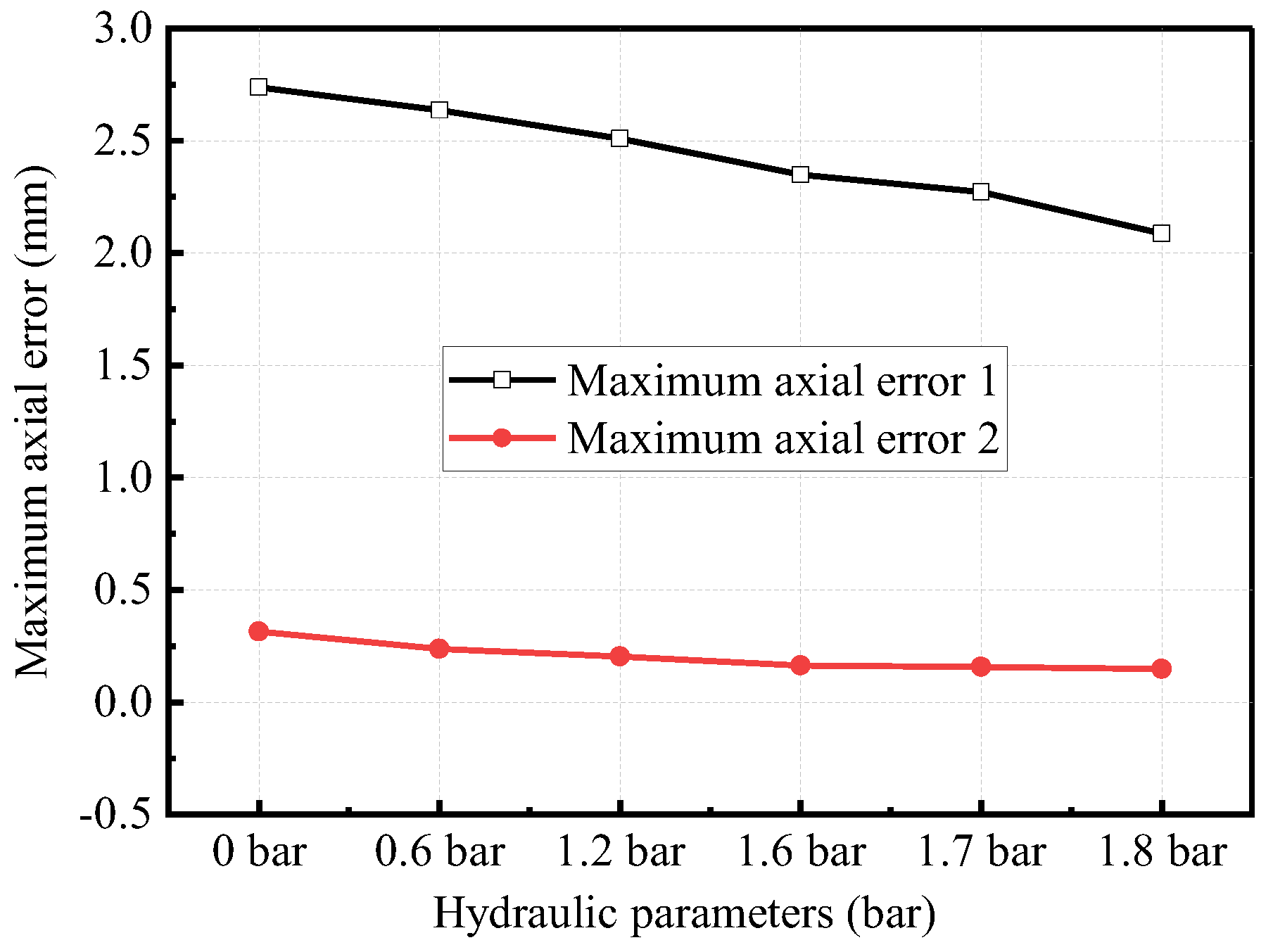
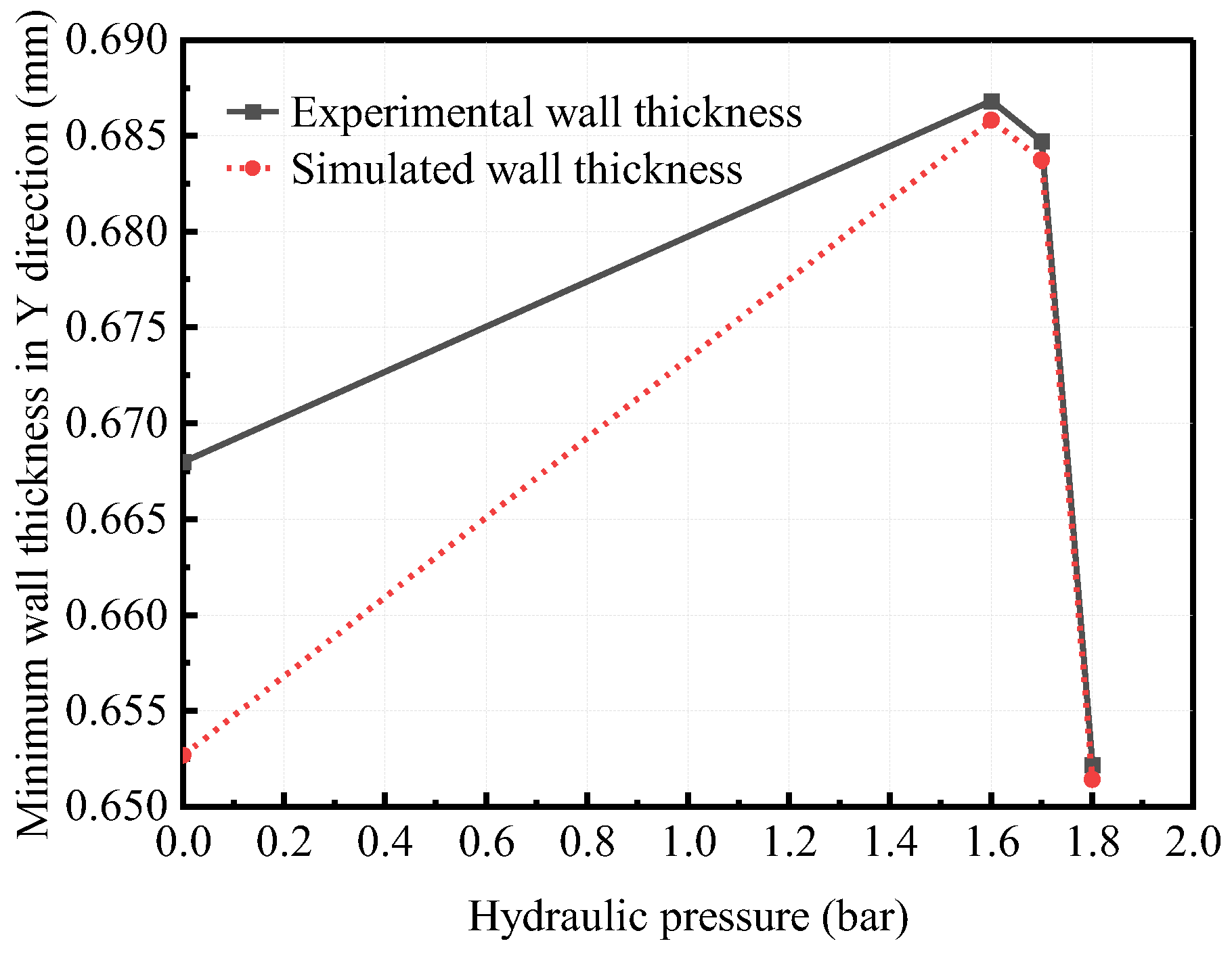
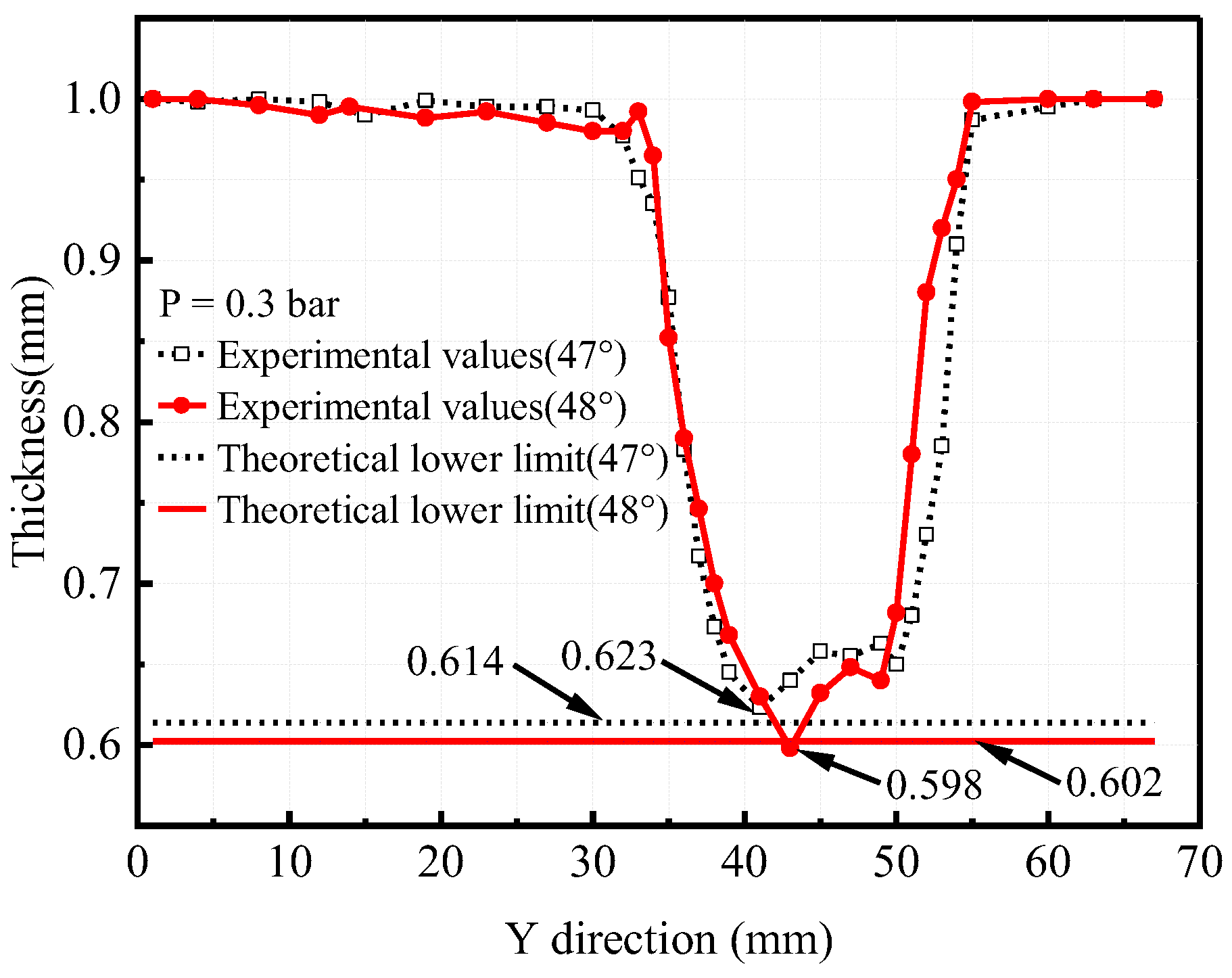
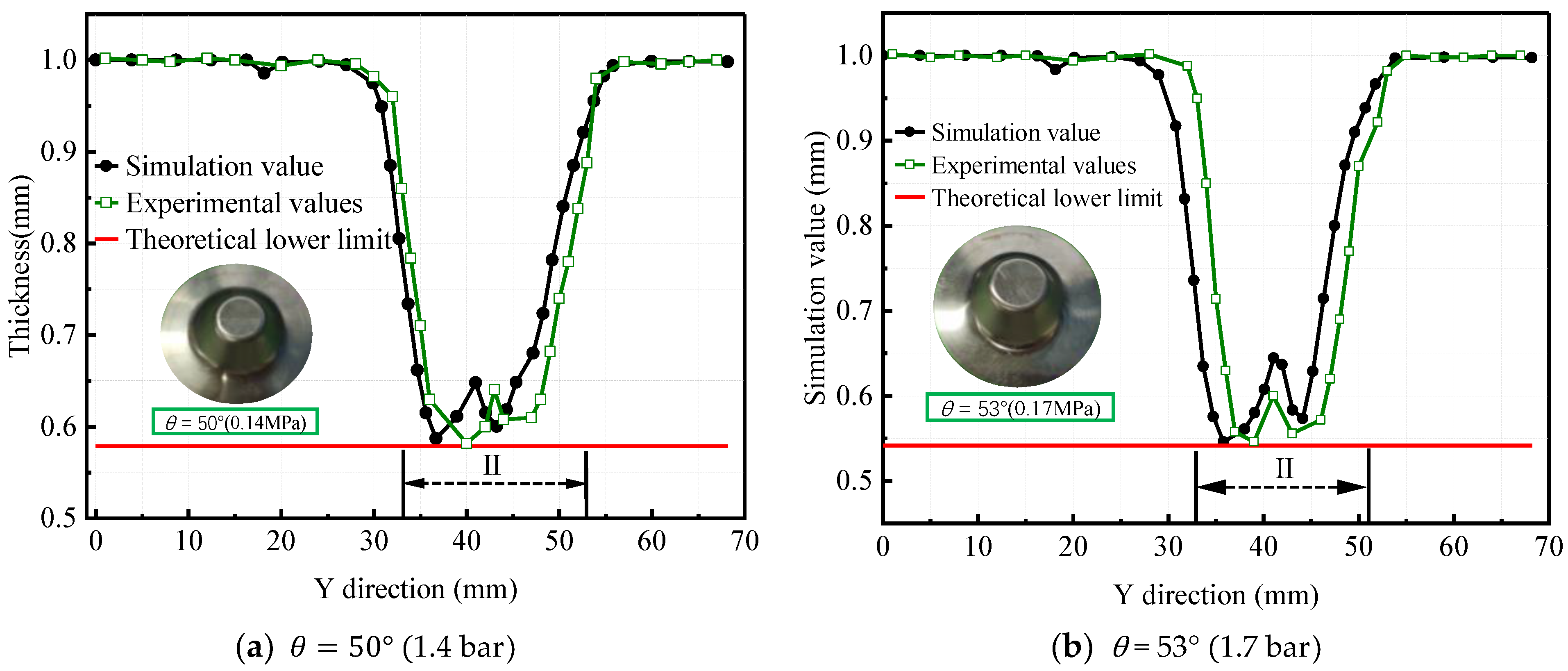
3.3. HS-SPIF Experimental Results
4. Discussion
5. Conclusions
- (1)
- The hydraulic sheet metal incremental sheet forming process can effectively promote the uniform distribution of sheet metal wall thickness. In the range of , with the pressure increase, the thinning zone gradually spreads in the main forming zone II, and the thickness distribution becomes more and more uniform. When the hydraulic pressure is 1.8 bar, the hydraulic support will hinder the uniform distribution of wall thickness in a few small local areas;
- (2)
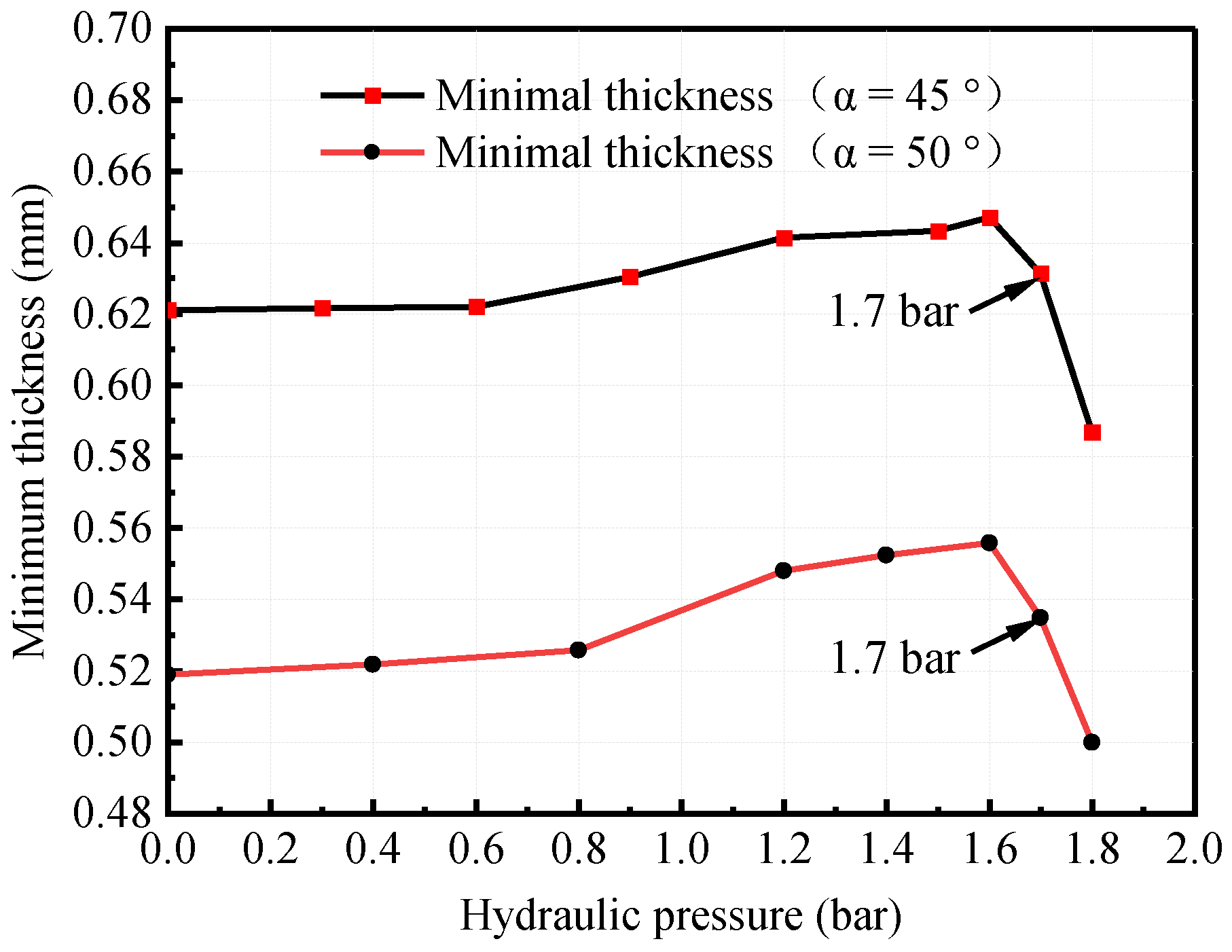
- When forming truncated pyramid parts with different angles, the influence trend of hydraulic parameters on wall thickness distribution is consistent. With increased hydraulic pressure, the minimum wall thickness increases first and then decreases. The favorable pressure range of the HS-SPIF process for uniform distribution of wall thickness is ;
- (3)
- The HS-SPIF process is helpful in improving the uniform critical angle of wall thickness. When the hydraulic pressure is at , the critical forming angle of HS-SPIF will increase with the pressure increase. When hydraulic pressure is used, the hydraulic pressure is the most sensitive to the critical forming angle. In the same other working conditions, the critical angle obtained by the ordinary SPIF process is 46°, while that obtained by the HS-SPIF process is ;
- (4)
- When the truncated pyramid with different forming angles is processed under different pressure, the most serious thinning part of the sheet is basically the same. Based on the assumption that there is only shear deformation, the occurrence of the minimum wall thickness of the experiment is 1.136–3.293 mm later than that of the finite element simulation, but these errors do not affect the determination of the final critical angle. As to the influence of hydraulic parameters on the uniform critical angle of wall thickness, the experimental results are consistent with the simulation results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Behera, A.K.; de Sousa, R.A.; Ingarao, G.; Oleksik, V. Single Point Incremental Forming: An Assessment of the Progress and Technology Trends From 2005 to 2015. J. Manuf. Process. 2017, 27, 37–62. [Google Scholar] [CrossRef]
- Li, P.Y.; He, J.; Liu, Q.; Yang, M.S.; Wang, Q.D.; Yuan, Q.L.; Li, Y. Evaluation of Forming Forces in Ultrasonic Incremental Sheet Metal Forming. Aerosp. Sci. Technol. 2017, 63, 132–139. [Google Scholar] [CrossRef]
- Liu, Z.B.; Daniel, W.; Li, Y.L.; Liu, S.; Meehan, P.A. Multi-Pass Deformation Design for Incremental Sheet Forming: Analytical Modeling, Finite Element Analysis and Experimental Validation. J. Mater. Process. Technol. 2014, 214, 620–634. [Google Scholar] [CrossRef]
- Vincze, G.; Pereira, A.B.; Lopes, D.; Yanez, J.; Butuc, M.C. Study on Asymmetric Rolling Process Applied to Aluminum Alloy Sheets. Machines 2022, 10, 641. [Google Scholar] [CrossRef]
- Liu, F.Y.; Li, Y.L.; Ghafoor, S.; Cheng, Z.N.; Li, F.Y.; Li, J.F. Sustainability Assessment of Incremental Sheet Forming: A Review. Int. J. Adv. Manuf. Technol. 2022, 119, 1385–1405. [Google Scholar] [CrossRef]
- Azaouzi, M.; Lebaal, N. Tool Path Optimization for Single Point Incremental Sheet Forming Using Response Surface Method. Simul. Model. Pract. Theory 2012, 24, 49–58. [Google Scholar] [CrossRef]
- Ben Said, L.; Mars, J.; Wali, M.; Dammak, F. Effects of the Tool Path Strategies on Incremental Sheet Metal Forming Process. Mech. Ind. 2016, 17, 411. [Google Scholar] [CrossRef]
- Nirala, H.K.; Agrawal, A. Fractal Geometry Rooted Incremental Toolpath for Incremental Sheet Forming. J. Manuf. Sci. Eng.-Trans. ASME 2018, 140, 021005. [Google Scholar] [CrossRef]
- Cao, T.T.; Lu, B.; Ou, H.G.; Long, H.; Chen, J. Investigation on a New Hole-Flanging Approach by Incremental Sheet Forming through a Featured Tool. Int. J. Mach. Tools Manuf. 2016, 110, 1–17. [Google Scholar] [CrossRef]
- Bouhamed, A.; Jrad, H.; Mars, J.; Wali, M.; Gamaoun, F.; Dammak, F. Homogenization of Elasto-Plastic Functionally Graded Material Based on Representative Volume Element: Application to Incremental Forming Process. Int. J. Mech. Sci. 2019, 160, 412–420. [Google Scholar] [CrossRef]
- Ben Said, L.; Mars, J.; Wali, M.; Dammak, F. Numerical Prediction of the Ductile Damage in Single Point Incremental Forming Process. Int. J. Mech. Sci. 2017, 131, 546–558. [Google Scholar] [CrossRef]
- Liu, Z.B.; Li, Y.L.; Meehan, P.A. Vertical Wall Formation and Material Flow Control for Incremental Sheet Forming by Revisiting Multistage Deformation Path Strategies. Mater. Manuf. Process. 2013, 28, 562–571. [Google Scholar] [CrossRef]
- Zhu, H.; Cheng, G.X.; Jung, D.W. Toolpath Planning and Generation for Multi-Stage Incremental Forming Based on Stretching Angle. Materials 2021, 14, 4818. [Google Scholar] [CrossRef] [PubMed]
- Mirnia, M.J.; Dariani, B.M.; Vanhove, H.; Duflou, J.R. Thickness Improvement in Single Point Incremental Forming Deduced by Sequential Limit Analysis. Int. J. Adv. Manuf. Technol. 2014, 70, 2029–2041. [Google Scholar] [CrossRef]
- Li, J.C.; Hu, J.B.; Pan, J.J.; Geng, P. Thickness Distribution and Design of a Multi-Stage Process for Sheet Metal Incremental Forming. Int. J. Adv. Manuf. Technol. 2012, 62, 981–988. [Google Scholar] [CrossRef]
- Ullah, S.; Li, X.Q.; Xu, P.; Li, D.S. Experimental and Numerical Investigation for Sheet Thickness Thinning in Two-Point Incremental Forming (Tpif). Int. J. Adv. Manuf. Technol. 2022, 122, 2493–2512. [Google Scholar] [CrossRef]
- Li, X.Q.; Han, K.; Xu, P.; Wang, H.B.; Li, D.S.; Li, Y.L.; Li, Q. Experimental and Theoretical Analysis of the Thickness Distribution in Multistage Two Point Incremental Sheet Forming. Int. J. Adv. Manuf. Technol. 2020, 107, 191–203. [Google Scholar] [CrossRef]
- Smith, J.; Malhotra, R.; Liu, W.K.; Cao, J. Deformation Mechanics in Single-Point and Accumulative Double-Sided Incremental Forming. Int. J. Adv. Manuf. Technol. 2013, 69, 1185–1201. [Google Scholar] [CrossRef]
- Praveen, K.; Shivaprasad, C.H.; Reddy, N.V. Effect of Support Force on Quality During Double-Sided Incremental Forming: An Experimental and Numerical Study. Int. J. Adv. Manuf. Technol. 2022, 122, 4275–4292. [Google Scholar] [CrossRef]
- Jin, Z.; Gao, J.; Zheng, L. Study on critical forming angle of progressive forming supported by punch of 1060 aluminum plate. Forg. Technol. 2022, 47, 99–106. [Google Scholar]
- Ben Khalifa, N.; Thiery, S. Incremental Sheet Forming with Active Medium. CIRP Ann.-Manuf. Technol. 2019, 68, 313–316. [Google Scholar] [CrossRef]
- Yu, J.H.; Jung, K.S.; Murugesan, M.; Chung, W.J.; Lee, C.W. Study on the Incremental Sheet Metal Forming Process Using a Metal Foam as a Die. Int. J. Mater. Form. 2022, 15, 71. [Google Scholar] [CrossRef]
- Kucukturk, G.; Yazgin, H.V. Improvement of Incremental Sheet Metal Forming with the Help of a Pressurised Fluid System. Mater. Test. 2022, 64, 1214–1222. [Google Scholar] [CrossRef]
- Hassan, A.A.; Kucukturk, G.; Yazgin, H.V.; Gurun, H.; Kaya, D. Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming. Machines 2022, 10, 941. [Google Scholar] [CrossRef]
- Kumar, Y.; Kumar, S. Experimental and Analytical Evaluation of Incremental Sheet Hydro-Forming Strategies to Produce High Forming Angle Sheets. Heliyon 2019, 5, e01801. [Google Scholar] [CrossRef] [PubMed]
- Bai, L. Study on Single Point Incremental Forming Accuracy and Influence Mechanism of Static Pressure Support and Ultrasonic Vibration. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2019. Available online: https://kns.cnki.net/kcms/detail/detail.aspx.FileName=1020306279.nh&DbName=CDFD2021 (accessed on 2 March 2022).
- Shi, W.; Gao, J. Study on the uniform critical angle of wall thickness in progressive forming supported by the outer contour of 1060 aluminum plate convex table. Forg. Technol. 2019, 44, 27–33. [Google Scholar]
- Ghorbel, O.; Koubaa, S.; Mars, J.; Wali, M.; Dammak, F. Non Associated-Anisotropic Plasticity Model Fully Coupled with Isotropic Ductile Damage for Sheet Metal Forming Applications. Int. J. Solids Struct. 2019, 166, 96–111. [Google Scholar] [CrossRef]
- Bouhamed, A.; Jrad, H.; Ben Said, L.; Wali, M.; Dammak, F. A Non-Associated Anisotropic Plasticity Model with Mixed Isotropic-Kinematic Hardening for Finite Element Simulation of Incremental Sheet Metal Forming Process. Int. J. Adv. Manuf. Technol. 2019, 100, 929–940. [Google Scholar] [CrossRef]
- Yang, M.S.; Xiao, X.D.; Yao, Z.Y.; Yuan, Q.L. Study on the limit of single-point incremental forming of ultrasonic vibration of 1060 aluminum plate. J. Ordnance Ind. 2019, 40, 601–611. [Google Scholar]
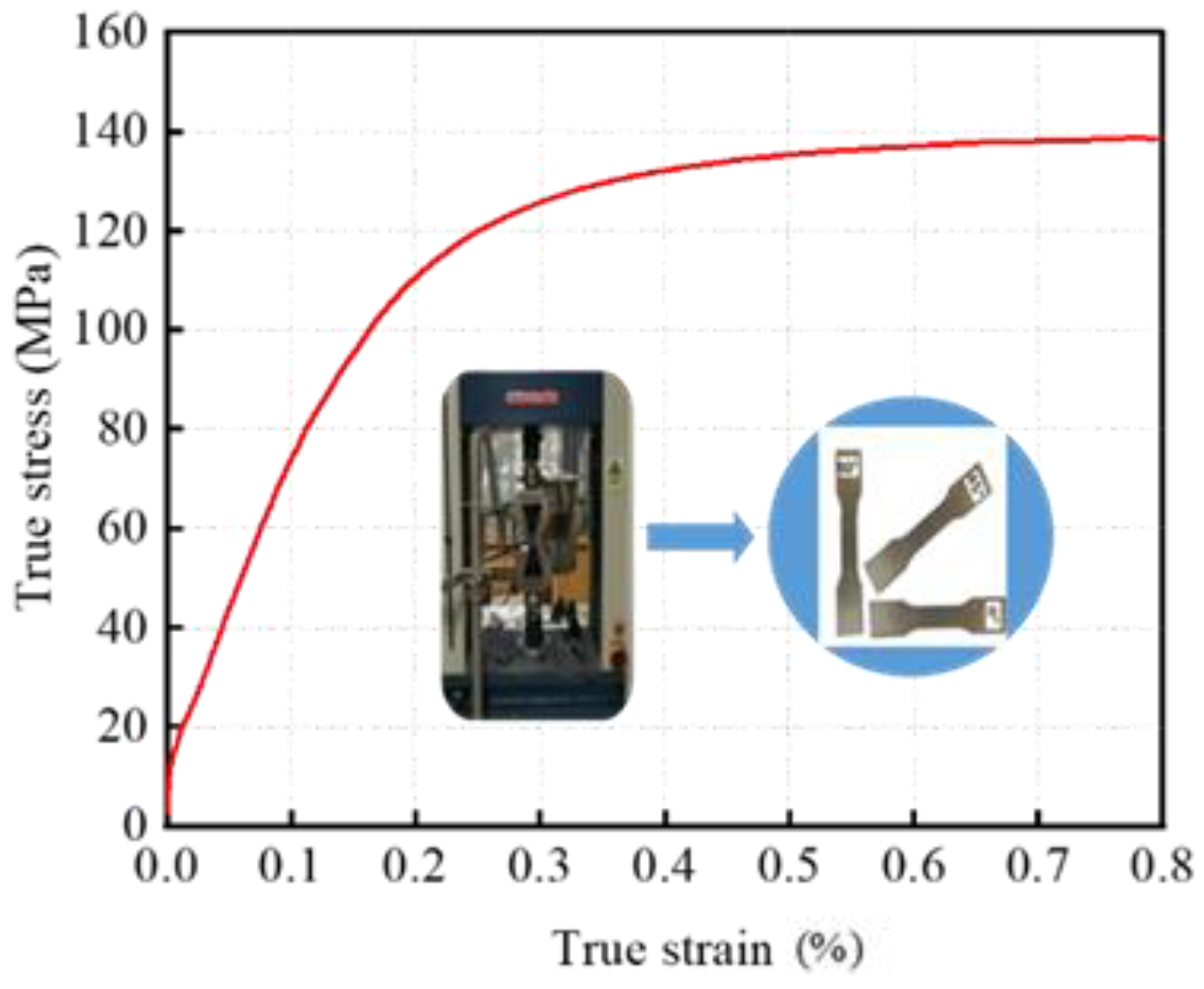
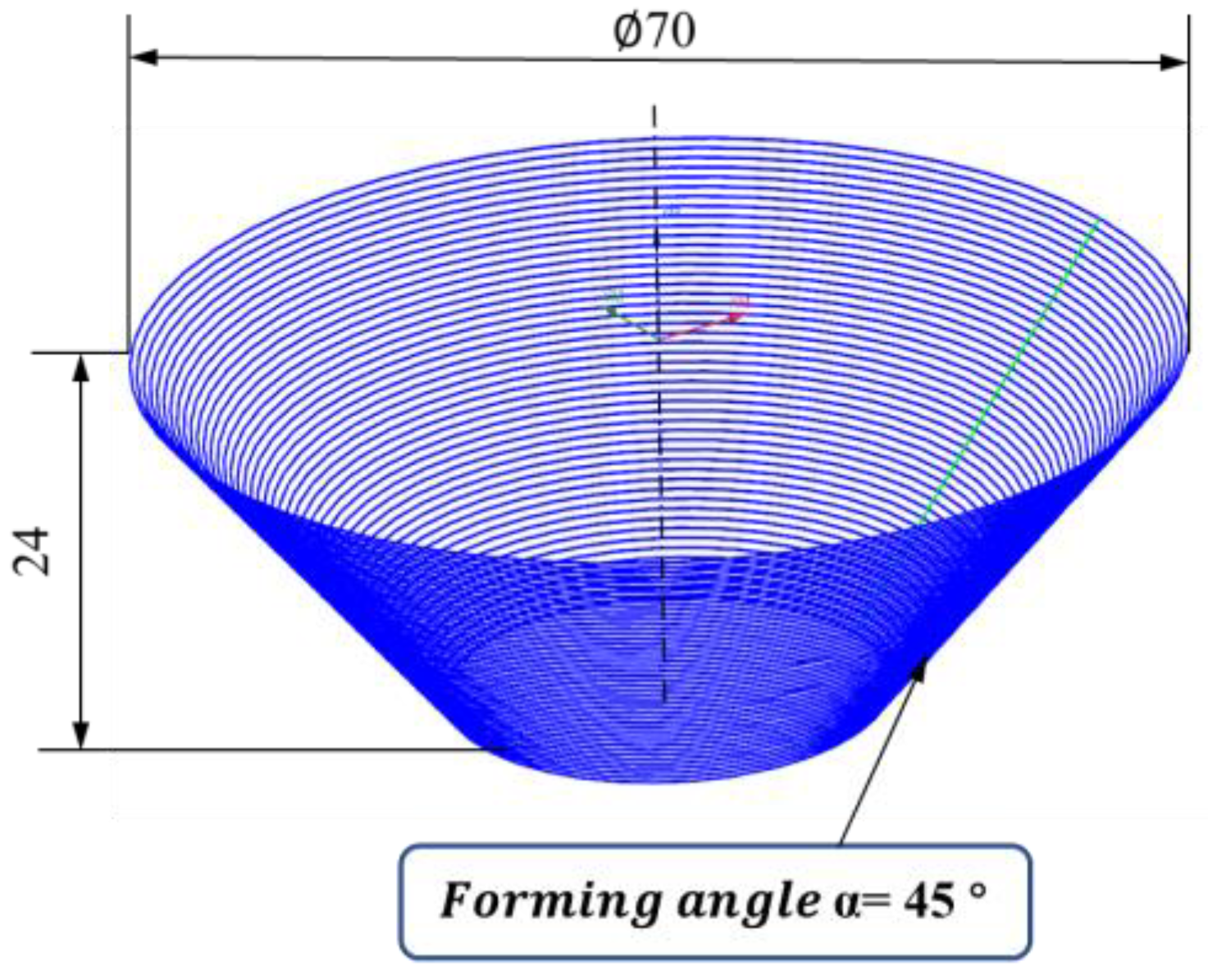





| Material | Al 1060 |
|---|---|
| Density (t/mm3) | 2.71 × 10−9 |
| Young’s modulus (MPa) | 68,000 |
| Poisson’s ratio | 0.33 |
| Yield strength (MPa) | 138 |
| Tensile strength (MPa) | 145 |
| Plastic coefficient K | 758.60 |
| Hardening exponent n | 0.31 |
| Experimental Equipment | Description |
|---|---|
| Forming device | The forming device includes the tool head and the MVC510 vertical CNC machine tool produced by Qinchuan Machine Tool Factory in China |
| Hydraulic system | The hydraulic system includes a fuel tank, hydraulic pump, pressure gauge, relief valve, one-way valve, and sealing ring |
| Sheet fixture | The sheet fixture is composed of an upper-pressing sheet and a lower-pressing sheet, which is used to fix the sheet |
| Oil cavity | The oil cavity and the lower pressure sheet are whole, which can be used to fix and support the sheet as well as for the storage of hydraulic oil so as to realize the change of the support pressure on the lower surface of the sheet |
| WEDM machine | WEDM machine generated by Sanguang Company, used for cutting formed parts |
| Double-pointed spiral micrometer | It is used to measure the wall thickness |
| Pressure (bar) | Forming Angle (°) | Minimum Thickness of Y Direction (mm) | Theoretical Minimum Thickness (mm) | Node Number | Y Direction Distance (mm) | |
|---|---|---|---|---|---|---|
| 0 | 46 | 0.63976 | 0.62519 | 41 | 38.834 | 46° |
| 47 | 0.61012 | 0.61380 | 41 | 38.864 | ||
| 0.3 | 47 | 0.61623 | 0.61380 | 40 | 37.721 | 47° |
| 48 | 0.58929 | 0.60222 | 40 | 37.774 | ||
| 0.7 | 48 | 0.60225 | 0.60222 | 40 | 37.741 | 48° |
| 49 | 0.58520 | 0.59045 | 40 | 37.737 | ||
| 0.8 | 49 | 0.59379 | 0.59045 | 40 | 37.737 | 49° |
| 50 | 0.56824 | 0.57870 | 40 | 37.770 | ||
| 1.4 | 50 | 0.58691 | 0.57870 | 39 | 36.706 | 50° |
| 51 | 0.55863 | 0.56639 | 39 | 36.742 | ||
| 1.6 | 51 | 0.56846 | 0.56639 | 39 | 36.795 | 51° |
| 52 | 0.55228 | 0.55409 | 39 | 36.772 | ||
| 1.65 | 52 | 0.55569 | 0.55409 | 39 | 36.855 | 52° |
| 53 | 0.53705 | 0.54164 | 38 | 35.750 | ||
| 1.7 | 53 | 0.54252 | 0.54164 | 38 | 35.786 | 53° |
| 54 | 0.50821 | 0.52900 | 38 | 35.776 |
| Pressure (Bar) | Forming Angle (°) | Initial Sheet Thickness (mm) | Theoretical Minimum Thickness (mm) |
|---|---|---|---|
| 1.6 | 45 | 1.002 | - |
| 1.7 | 45 | 1.004 | - |
| 1.8 | 45 | 1.002 | - |
| 0 | 45 | 1.002 | 0.636 |
| 46 | 1.006 | 0.625 | |
| 47 | 1.005 | 0.614 | |
| 0.3 | 46 | 1.002 | 0.625 |
| 47 | 1.004 | 0.614 | |
| 48 | 1.002 | 0.602 | |
| 0.8 | 48 | 1.002 | 0.602 |
| 49 | 1.004 | 0.590 | |
| 50 | 1.004 | 0.579 | |
| 1.4 | 49 | 1.002 | 0.590 |
| 50 | 1.002 | 0.579 | |
| 51 | 1.004 | 0.566 | |
| 1.7 | 52 | 1.002 | 0.554 |
| 53 | 1.002 | 0.542 | |
| 54 | 1.004 | 0.529 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, M.; Li, Y.; Yang, M.; Chen, Y.; Bai, L.; Li, P. Wall Thickness Uniformity in ISF of Hydraulic Support: System Design, Finite Element Analysis and Experimental Verification. Machines 2023, 11, 353. https://doi.org/10.3390/machines11030353
Shang M, Li Y, Yang M, Chen Y, Bai L, Li P. Wall Thickness Uniformity in ISF of Hydraulic Support: System Design, Finite Element Analysis and Experimental Verification. Machines. 2023; 11(3):353. https://doi.org/10.3390/machines11030353
Chicago/Turabian StyleShang, Miao, Yan Li, Mingshun Yang, Yunshuai Chen, Lang Bai, and Pengyang Li. 2023. "Wall Thickness Uniformity in ISF of Hydraulic Support: System Design, Finite Element Analysis and Experimental Verification" Machines 11, no. 3: 353. https://doi.org/10.3390/machines11030353
APA StyleShang, M., Li, Y., Yang, M., Chen, Y., Bai, L., & Li, P. (2023). Wall Thickness Uniformity in ISF of Hydraulic Support: System Design, Finite Element Analysis and Experimental Verification. Machines, 11(3), 353. https://doi.org/10.3390/machines11030353






