Research on Braking Energy Regeneration for Hybrid Electric Vehicles
Abstract
:1. Introduction
2. Mathematical Model and Objective Function
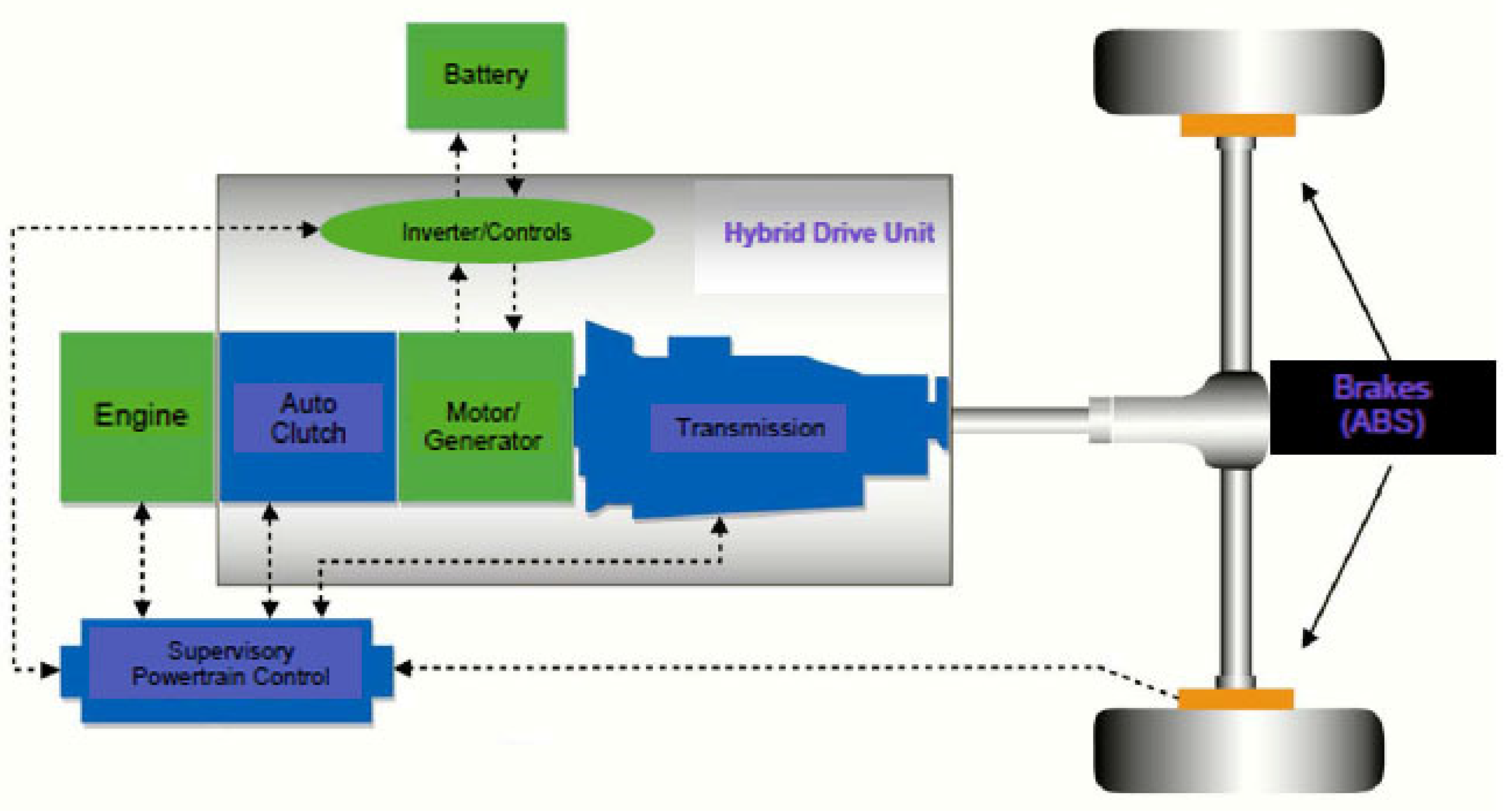
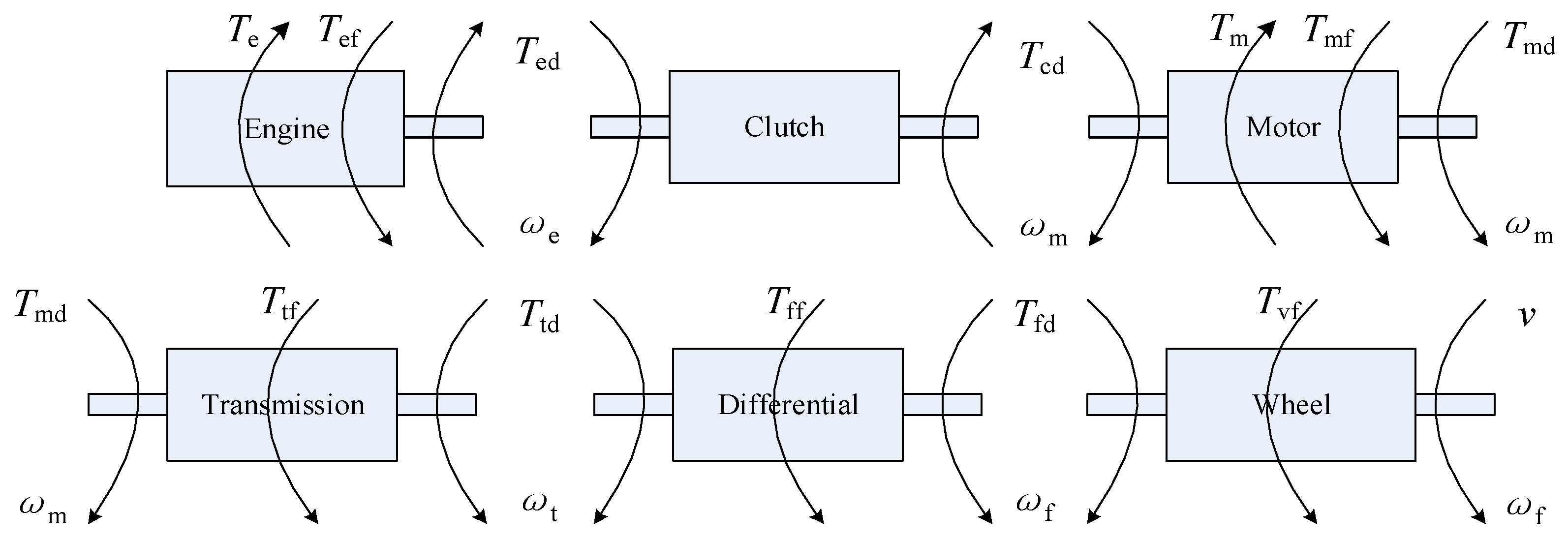
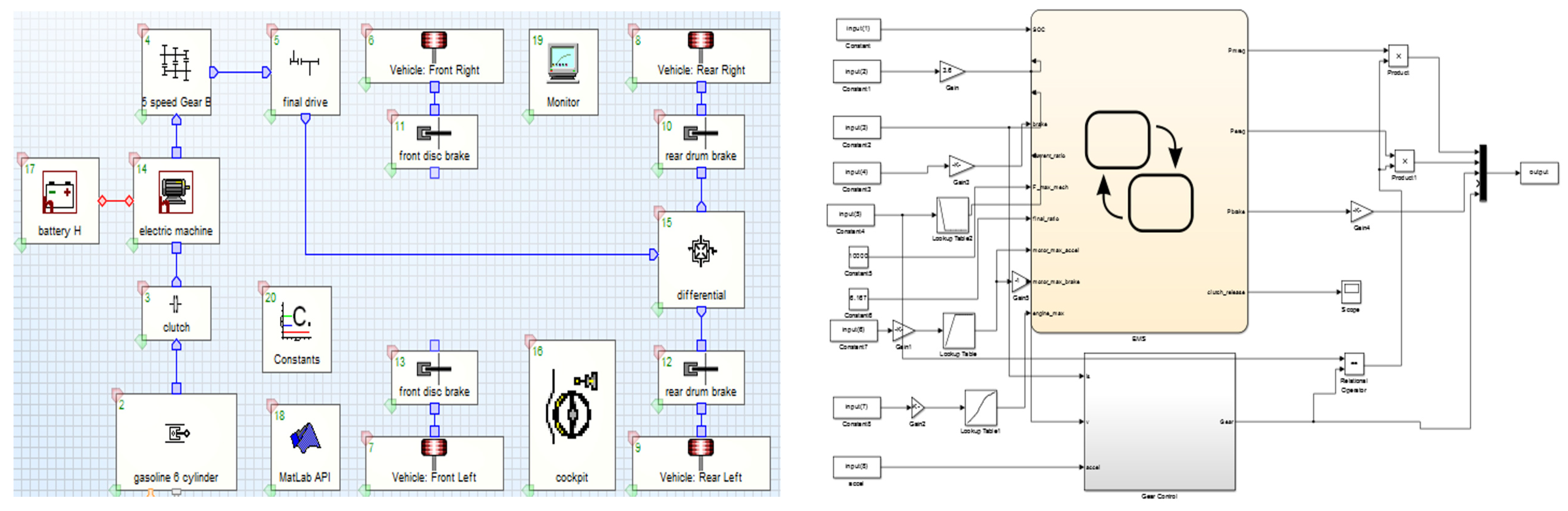
2.1. Vehicle System Model
- The torsional vibration of the engine and shaft and the effect of the clutch torsional damper on the system are neglected.
- The transverse vibration of the drive shaft and the driven shaft is neglected.
- Each component is a rigid inertial element without damping.
- The clearance of the kinematic pair is neglected.
2.1.1. Engine Model
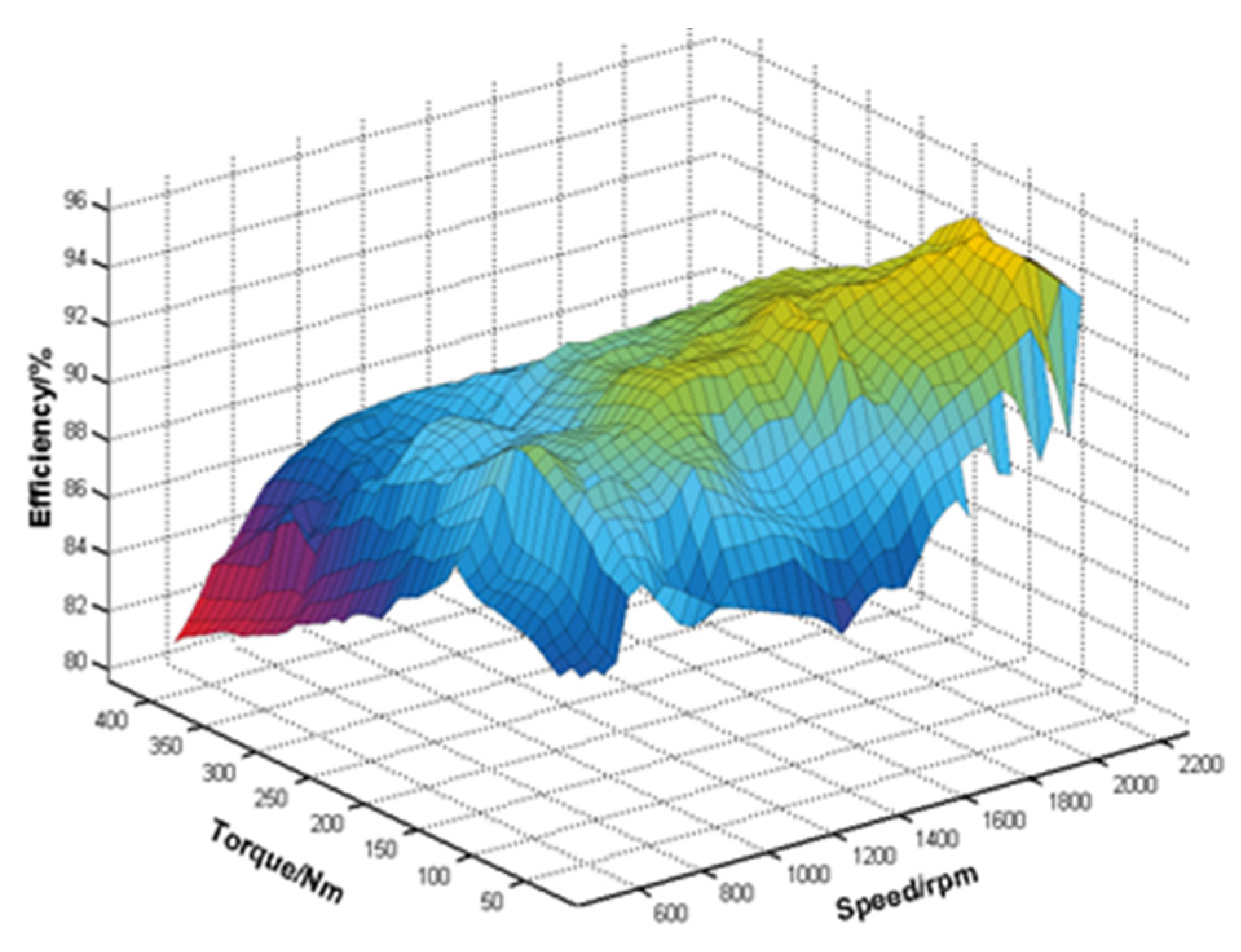
2.1.2. Motor Model
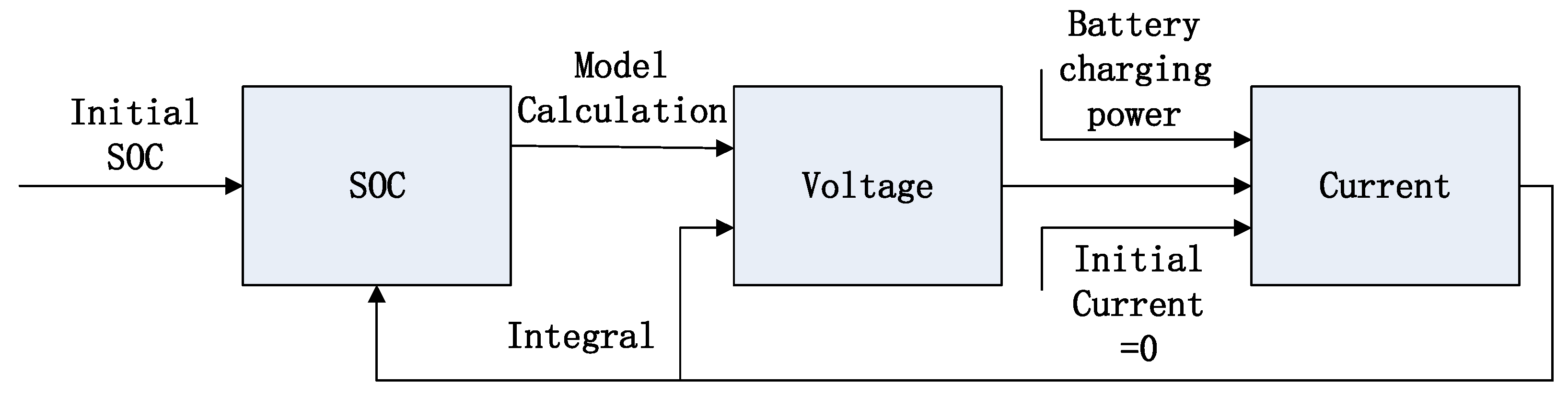
2.1.3. Battery Model
2.1.4. Other Mathematical Model
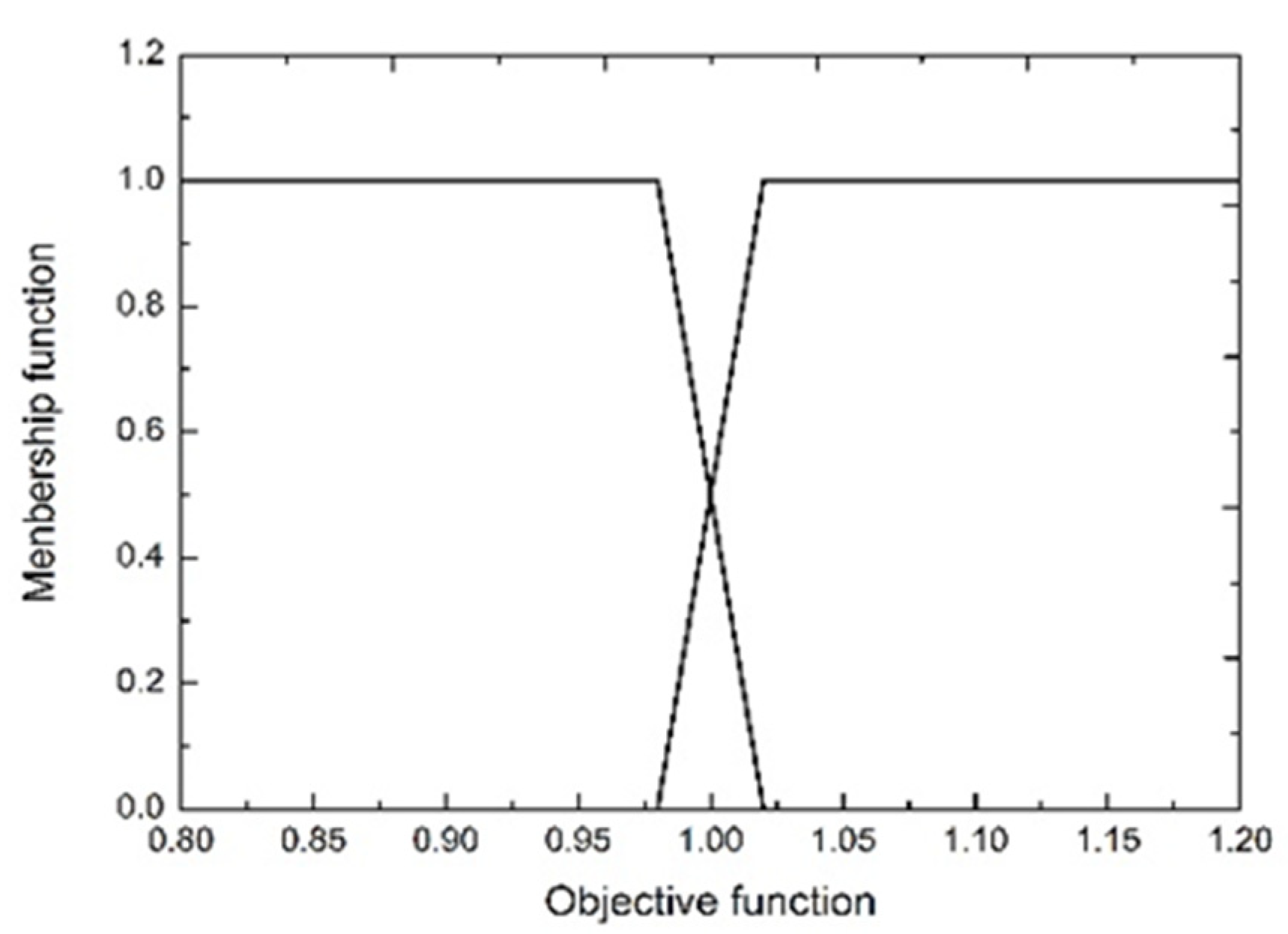
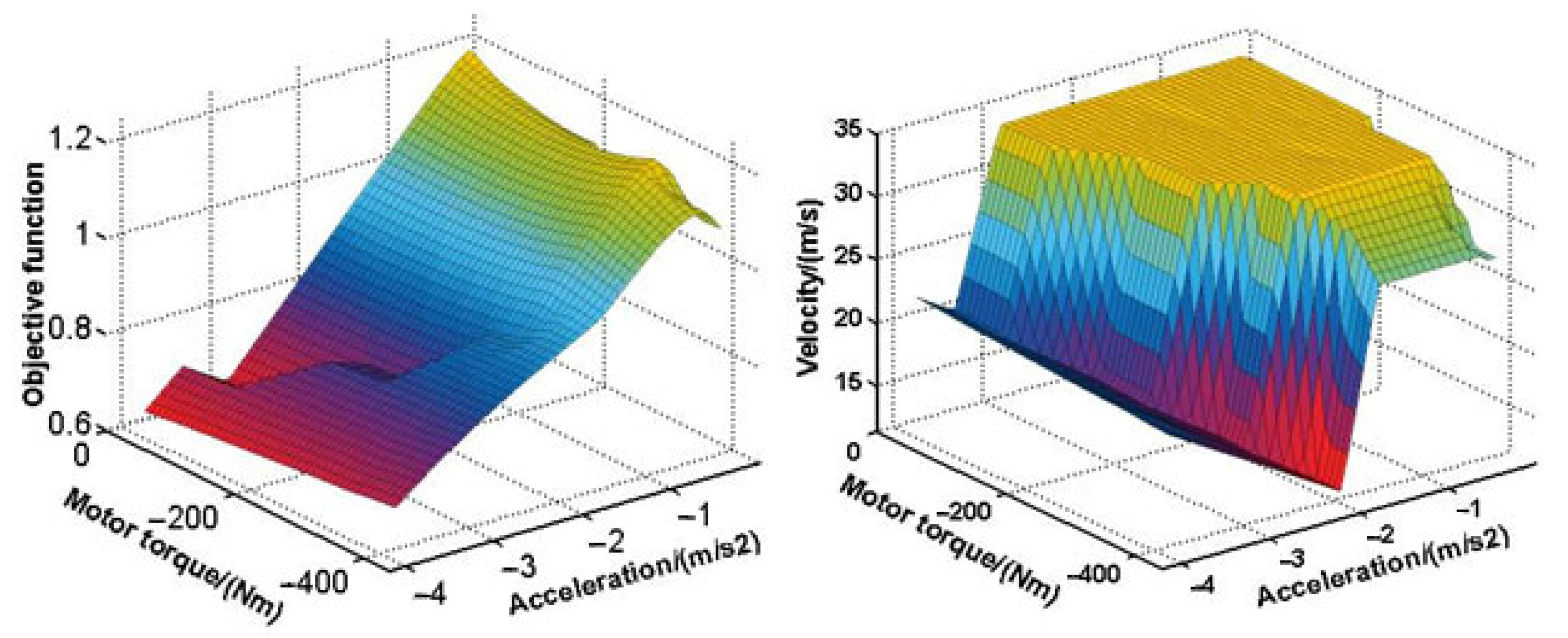
2.2. Objective Function
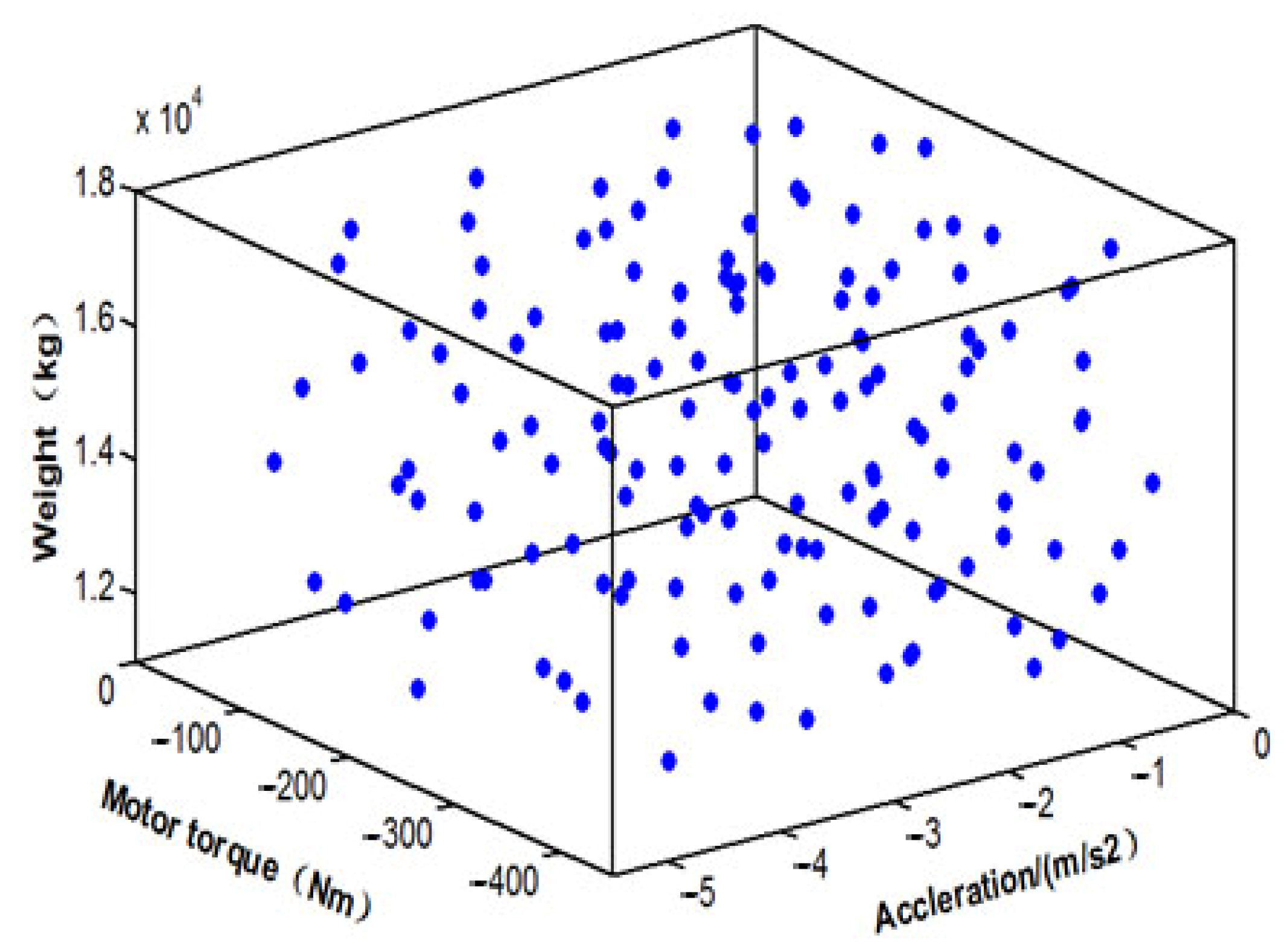
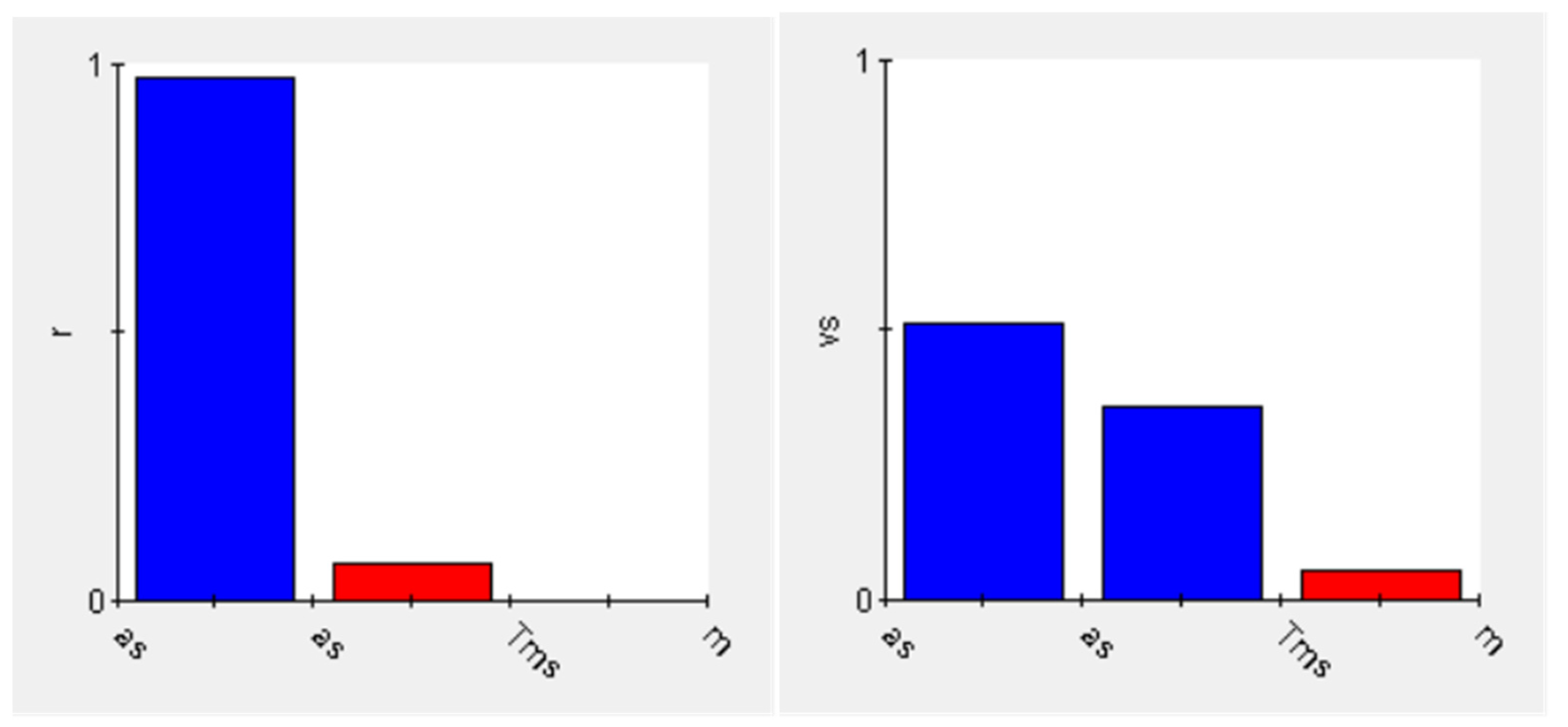
3. Solving Process of the Optimization Problem
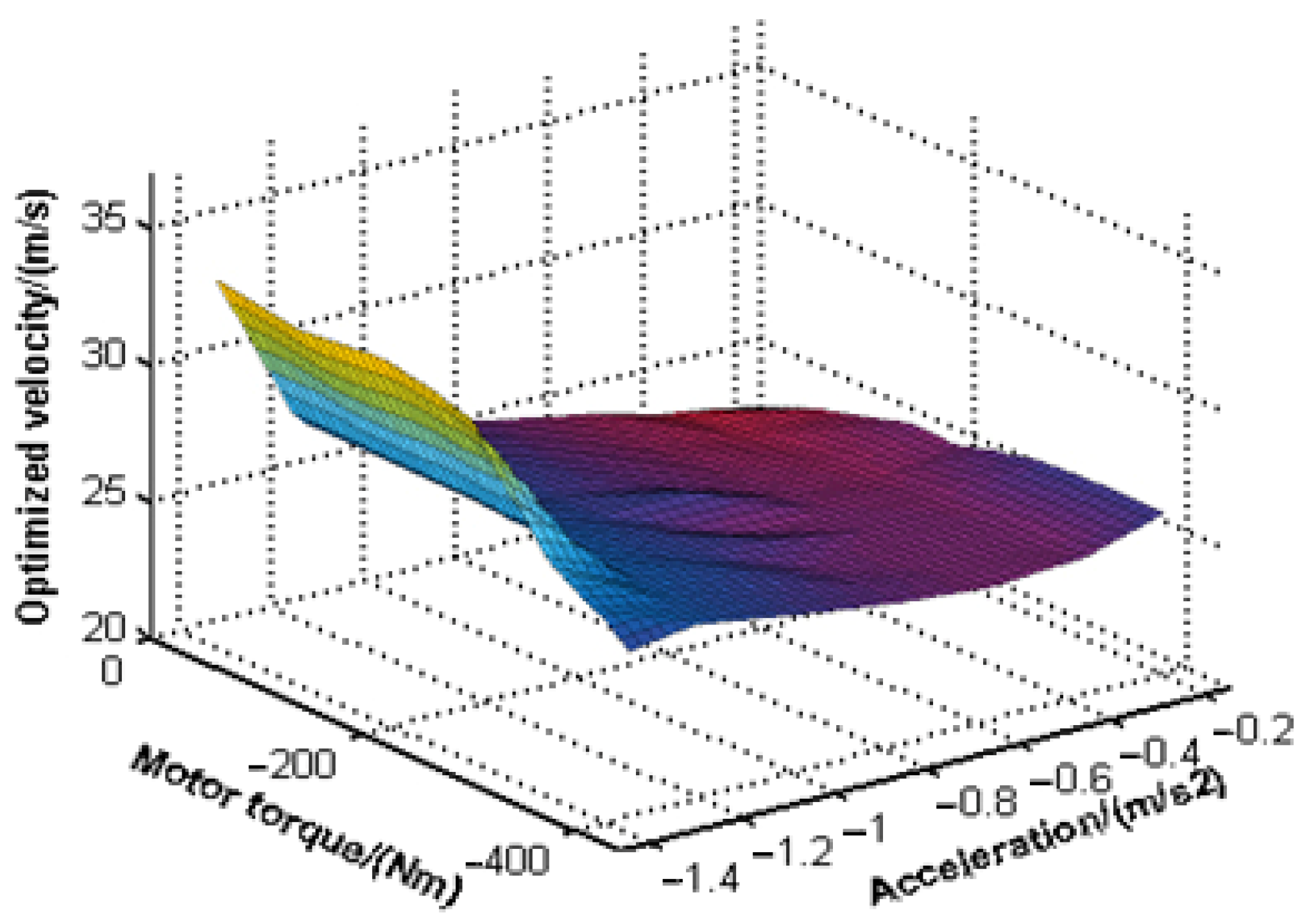
4. Optimization Results Analysis
5. Simulation and Validation of Optimization Results
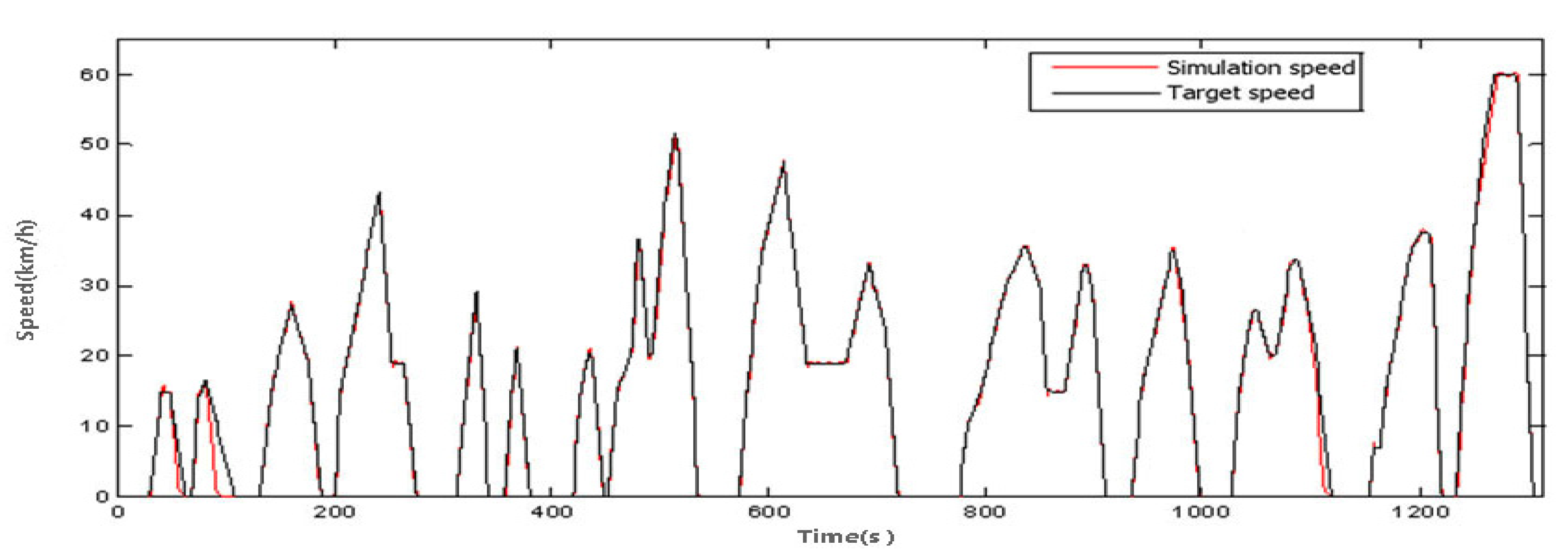
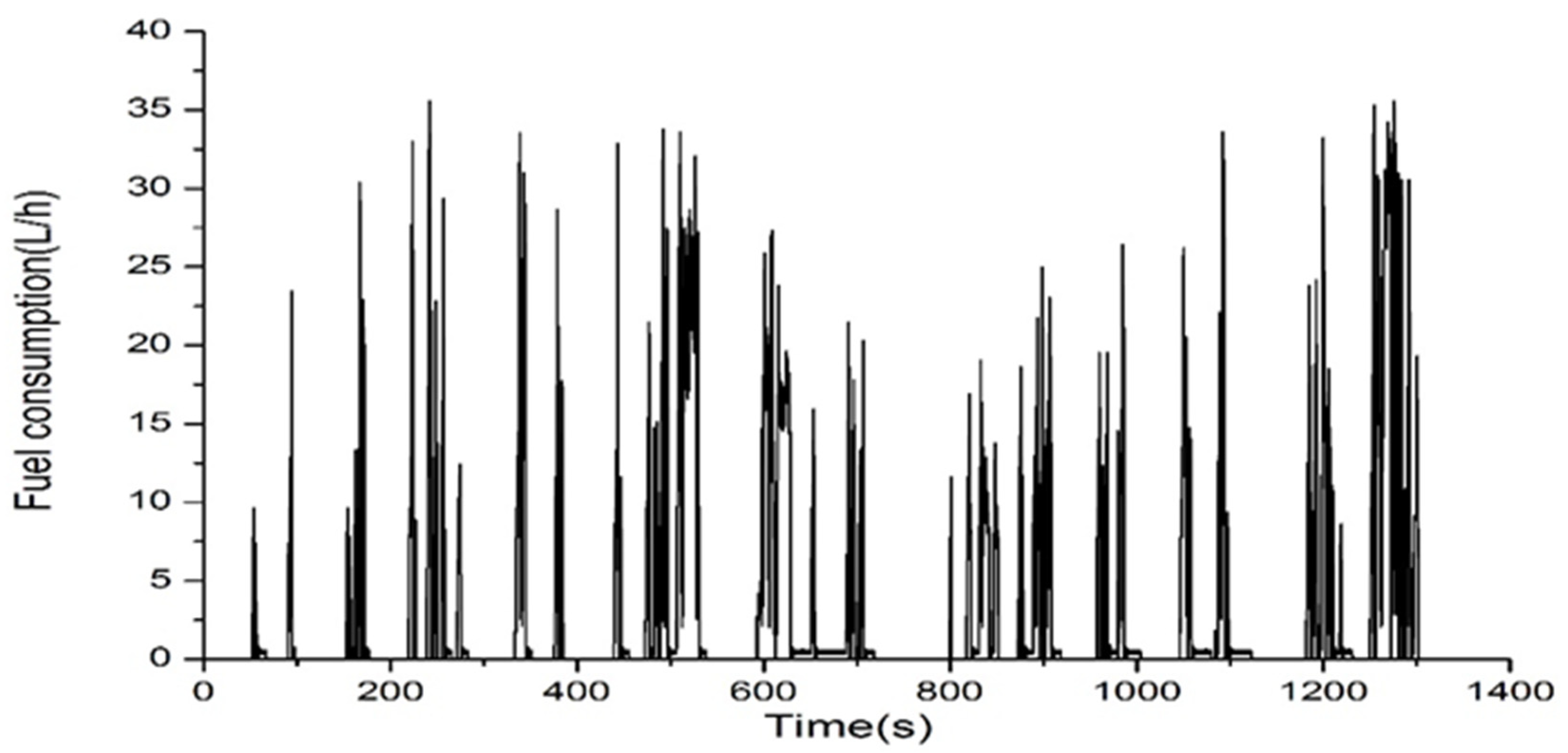
5.1. Model Validation
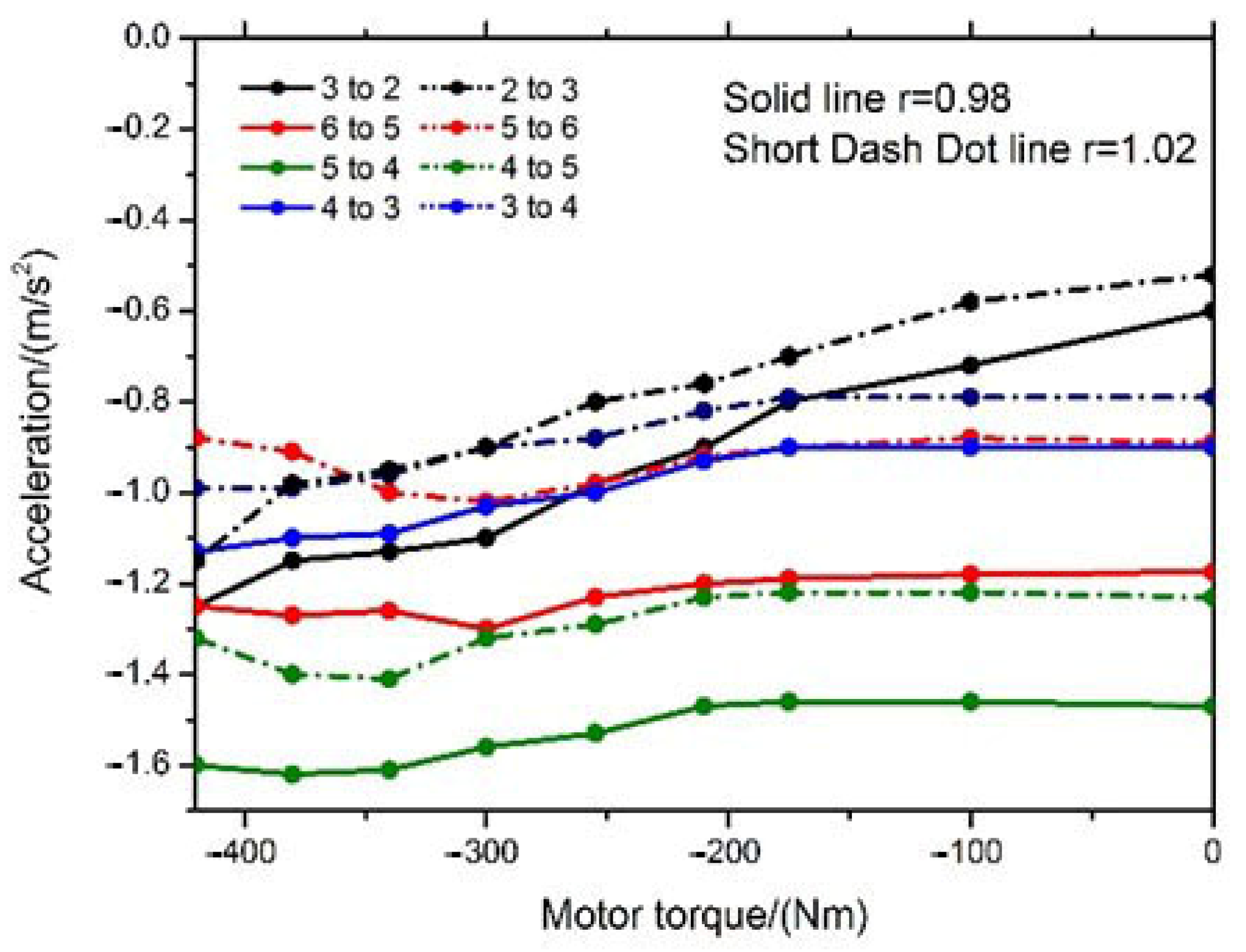
5.2. Validation of Gear Shifting Strategy in Braking Process
5.3. Validation of Gear Shifting Strategy under Different Braking Strengths
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berjoza, D.; Pirs, V.; Jurgena, I. Research into the regenerative braking of an electric car in urban driving. World Electr. Veh. J. 2022, 13, 202. [Google Scholar] [CrossRef]
- Hu, X.; Johannesson, L.; Murgovski, N.; Egardt, B. Longevity-conscious dimensioning and power management of the hybrid energy storage system in a fuel cell hybrid electric bus. Appl. Energy 2015, 137, 913–924. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Zhang, Z.; Ding, D.-L. Shift scheduling strategy development for parallel hybrid construction vehicles. J. Cent. South Univ. 2019, 26, 587–603. [Google Scholar] [CrossRef]
- Song, Q.; Ye, S.; Li, W. Research on AMT overall shift schedule for pure electric vehicles based on NSGA-II algorithm. Chin. J. Automot. Eng. 2017, 7, 44–51. [Google Scholar]
- Ngo, V.; Hofman, T.; Steinbuch, M.; Serrarens, A. Effect of gear shift and engine start losses on energy management strategies for hybrid electric vehicles. Int. J. Powertrains 2015, 4, 141–162. [Google Scholar] [CrossRef]
- Hua, Y. Research on Control Strategy for Double Synchronized Gear-Shift for Parallel Hybrid Electric Bus. Dalian University of Technology. 2014. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C475KOm_zrgu4lQARvep2SAkVNKPvpjdBoadmPoNwLRuZyEhqbyUdN4bwC47MsOtZnyuqNqdK5mVILBfBvr8lzDA&uniplatform=NZKPT (accessed on 1 February 2023).
- Qin, D.; Ye, X.; Hu, M.; Chen, Q. Optimization of Control Strategy for Medium Hybrid Electric Vehicle with ISG at Drive Condition. J. Mech. Eng. 2010, 46, 86–92. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Q.; Zeng, X. Research on Gear-shift Schedules in the Braking Process of Parallel Hybrid Electric Bus. J. Jilin Univ. 2009, 39, 10–13. [Google Scholar]
- Liu, W.; Chen, G.; Zong, C.; Li, C. Research on Electric Vehicle Braking Force Distribution for Maximizing Energy Regeneration. In Proceedings of the SAE 2016 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2016. [Google Scholar]
- Lu, J. Hill-Start Control Strategy of Heavy Off-Road Vehicles Equipped with AMT Based on Multi-Signal Integration; Beijing Institute of Technology: Beijing, China, 2014. [Google Scholar]
- Guo, H. Optimization Study on Control Strategy for the Cooperative Braking System in an Electric Vehicle with Independently Driven Front and Rear Axles; Beijing Institute of Technology: Beijing, China, 2014. [Google Scholar]
- Shen, W.; Hu, Y.; Yu, H. Shifting Process Control of AMT Based on Virtual Clutch Technology for Hybrid Electric Vehicle. J. Mech. Eng. 2014, 50, 108–117. [Google Scholar] [CrossRef]
- Mehrdad, E.; Yinin, G.; Ali, E. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals Theory, and Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lai, Y.; Jiang, X.; Fang, L. Optimization Theory and Examples of Parameters by Isight; Beihang University Press: Beijing, China, 2012. [Google Scholar]
- Zhong, Y.; Chen, B.; Wang, Z. Principles and Methods of Multidisciplinary Design Optimization; Huazhong University of Science and Technology Press: Wuhan, China, 2007. [Google Scholar]
- Yu, Z. Automobile Theory; Machinery Industry Press: Beijing, China, 2019. [Google Scholar]






| Component | Specification | Value | Unit |
|---|---|---|---|
| Engine | Type | Natural gas | - |
| Rated power/speed | 140/2500 | kW/rpm | |
| Maximum torque/speed | 650/1500 | Nm/rpm | |
| Motor | Type | Permanent magnet | - |
| Rated power/speed | 26/2600 | kW/rpm | |
| Maximum torque/speed | 420/1000 | Nm/rpm | |
| Battery | Voltage | 360 | V |
| Capacity | 8 | Ah | |
| Transmission | Gear ratio | 7.05/4.13/2.52/1.59/ 1.00/0.78/R6.75 | - |
| Coefficients | Scaled | Normalized | |
|---|---|---|---|
| Constant | 82.54907361 | ||
| nm | 0.007776876 | 3.796131489 | 31.01952404 |
| Tm | 0.022894698 | −1.328832684 | −10.8583587 |
| −2.07 × 10−6 | −1.49752163 | −12.23677534 | |
| −9.83 × 10−5 | −3.873657126 | −31.65301326 | |
| Tm − nm | 1.03× 10−5 | 1.741735007 | 14.23232865 |
| Major Component | Main Parameter | Parameter Value |
|---|---|---|
| Engine | Output volume (L) | 6.5 |
| Rated power/rotational speed (Kw/rpm) | 140/2500 | |
| Maximum torque/rotational speed (Nm/rpm) | 650/1500 | |
| Clutch | Type | Single-piece dry-type diaphragm spring clutch |
| Motor | Type | Permanent magnet synchronous motor |
| Voltage (V) | 340 | |
| Rated power/rotational speed (Kw/rpm) | 26/2600 | |
| Maximum torque/rotational speed (Nm/rpm) | 420/1000 | |
| Battery | Type | Aluminum–plastic film manganese oxide lithium-ion power battery |
| Voltage (V) | 360 | |
| Capacity | 8Ah | |
| Transmission | Manipulation mode | AMT |
| Speed ratio of each gear | 7.05/4.13/2.52/1.59/1.00/0.78/R6.75 |
| Acceleration (m/s2) | Regeneration Energy | Acceleration (m/s2) | Regeneration Energy | ||||
|---|---|---|---|---|---|---|---|
| D | Optimal Strategy | L | D | Optimal Strategy | L | ||
| −0.4 | 0.1229 | 0.1229 | 0.1229 | −1.2 | 0.0426 | 0.0439 | 0.0430 |
| −0.5 | 0.0974 | 0.1022 | 0.1022 | −1.3 | 0.0389 | 0.0391 | 0.0388 |
| −0.6 | 0.0802 | 0.0843 | 0.0843 | −1.4 | 0.0359 | 0.0359 | 0.0352 |
| −0.7 | 0.0719 | 0.0758 | 0.0755 | −1.5 | 0.0332 | 0.0332 | 0.0320 |
| −0.8 | 0.0657 | 0.0691 | 0.0687 | −1.6 | 0.0314 | 0.0314 | 0.0299 |
| −0.9 | 0.0556 | 0.0581 | 0.0561 | −2 | 0.0264 | 0.0264 | 0.0241 |
| −1.0 | 0.0496 | 0.0515 | 0.0509 | −3 | 0.0166 | 0.0166 | 0.0125 |
| −1.1 | 0.0470 | 0.0498 | 0.0480 | −4 | 0.0121 | 0.0121 | 0.0077 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Peng, J.; Ren, X.; Yang, X.; Hu, Y. Research on Braking Energy Regeneration for Hybrid Electric Vehicles. Machines 2023, 11, 347. https://doi.org/10.3390/machines11030347
Xu M, Peng J, Ren X, Yang X, Hu Y. Research on Braking Energy Regeneration for Hybrid Electric Vehicles. Machines. 2023; 11(3):347. https://doi.org/10.3390/machines11030347
Chicago/Turabian StyleXu, Mengtian, Jianxin Peng, Xiaochen Ren, Xuekun Yang, and Yuhui Hu. 2023. "Research on Braking Energy Regeneration for Hybrid Electric Vehicles" Machines 11, no. 3: 347. https://doi.org/10.3390/machines11030347
APA StyleXu, M., Peng, J., Ren, X., Yang, X., & Hu, Y. (2023). Research on Braking Energy Regeneration for Hybrid Electric Vehicles. Machines, 11(3), 347. https://doi.org/10.3390/machines11030347










