Self-Docking Characteristics and Sliding Mode Control on Space Electromagnetic Docking Mechanism
Abstract
1. Introduction
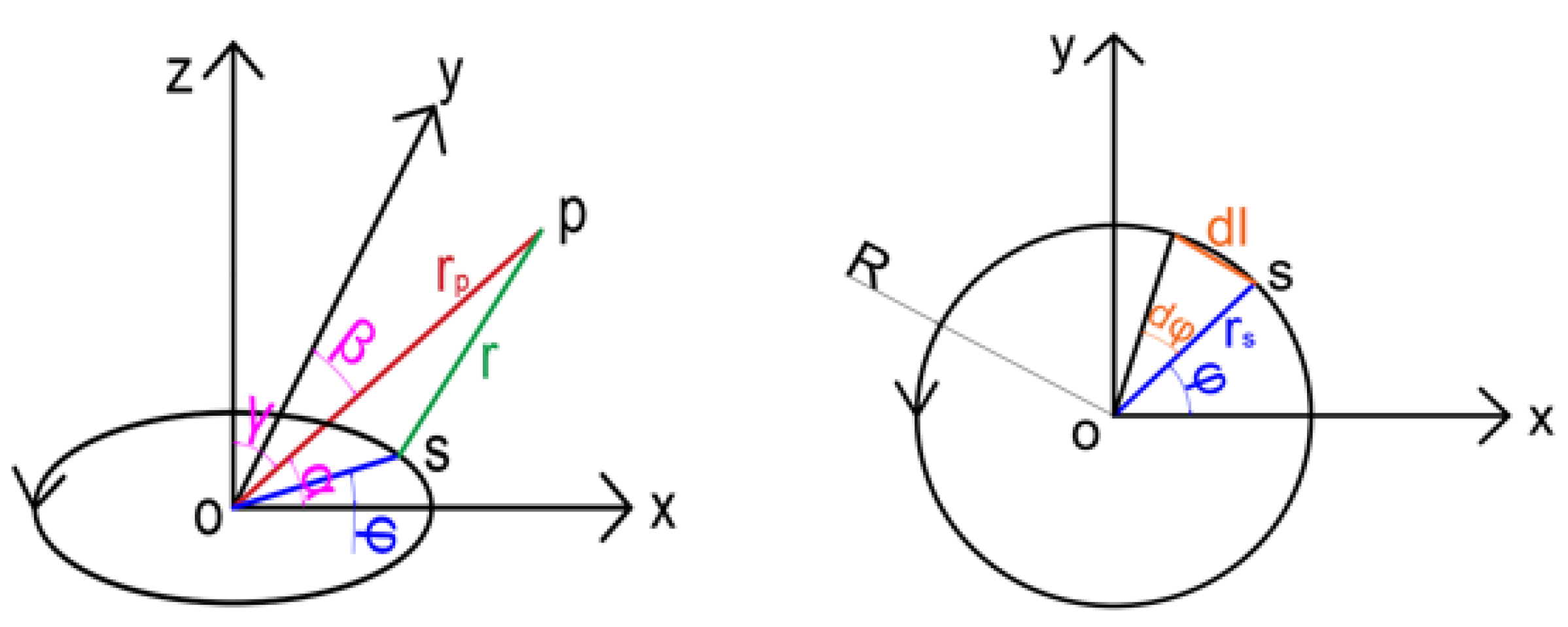
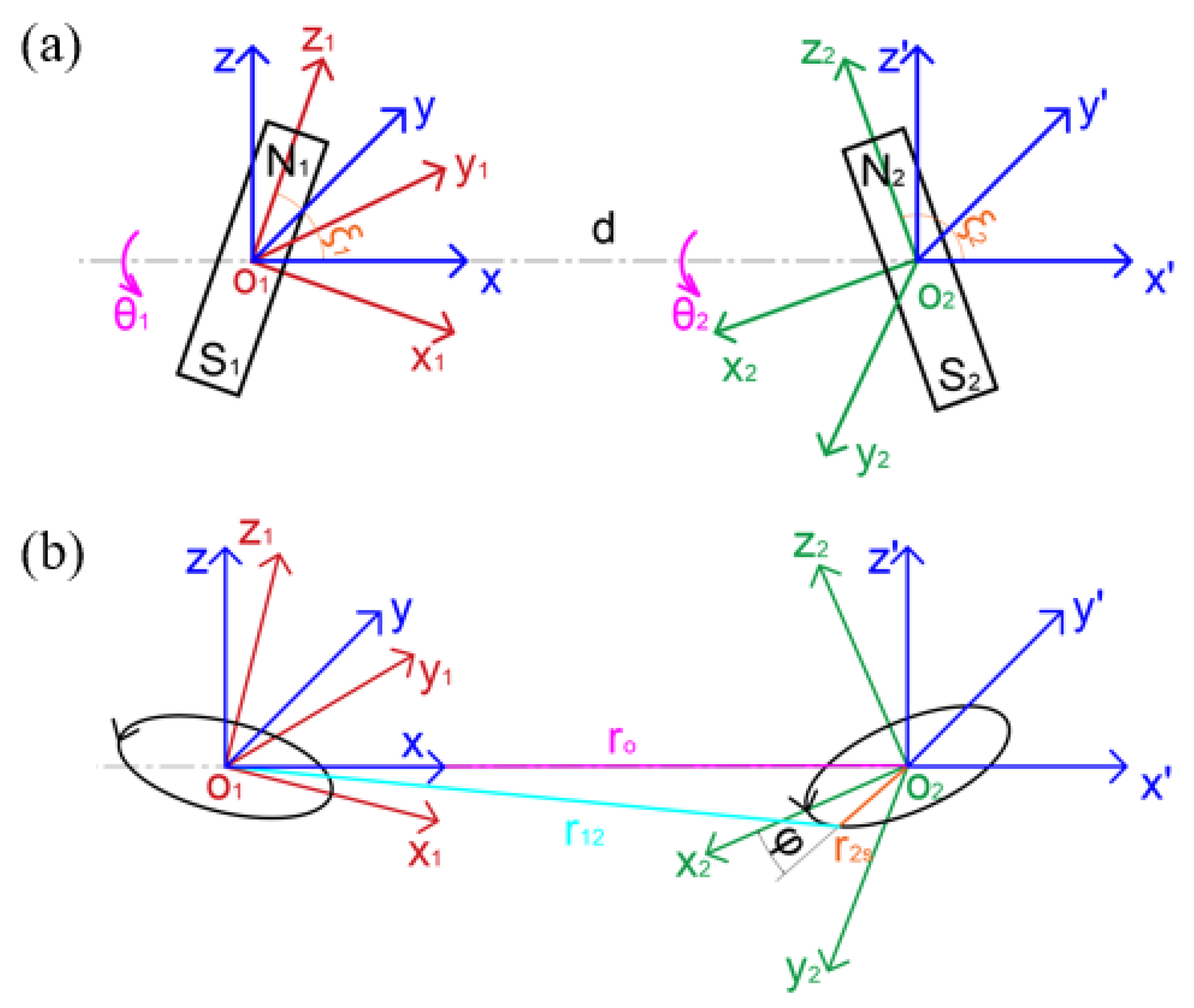
2. Mathematical Model of Electromagnetic Force and Torque in Space Electromagnetic Docking Process
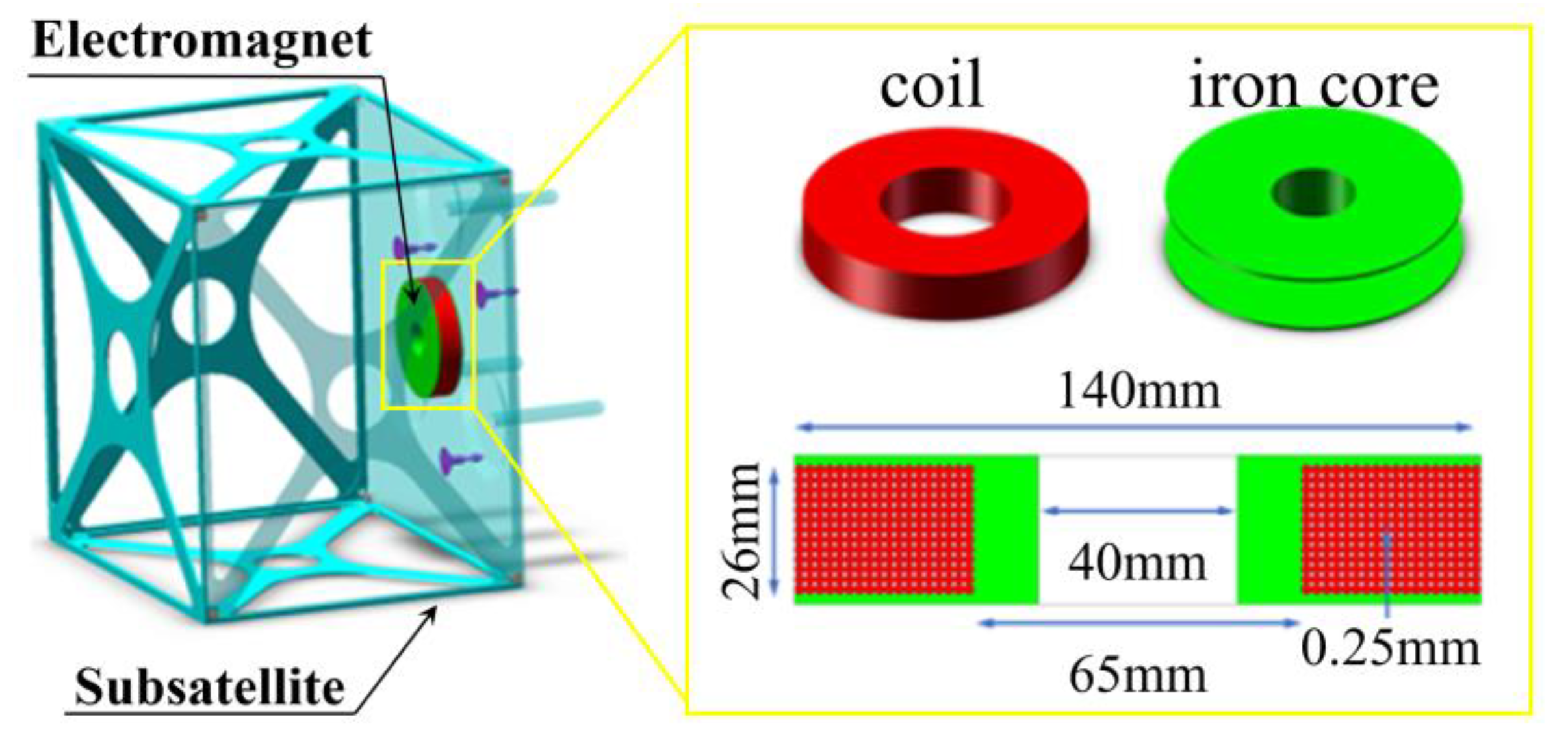
3. Self-Docking Characteristics of Space Electromagnetic
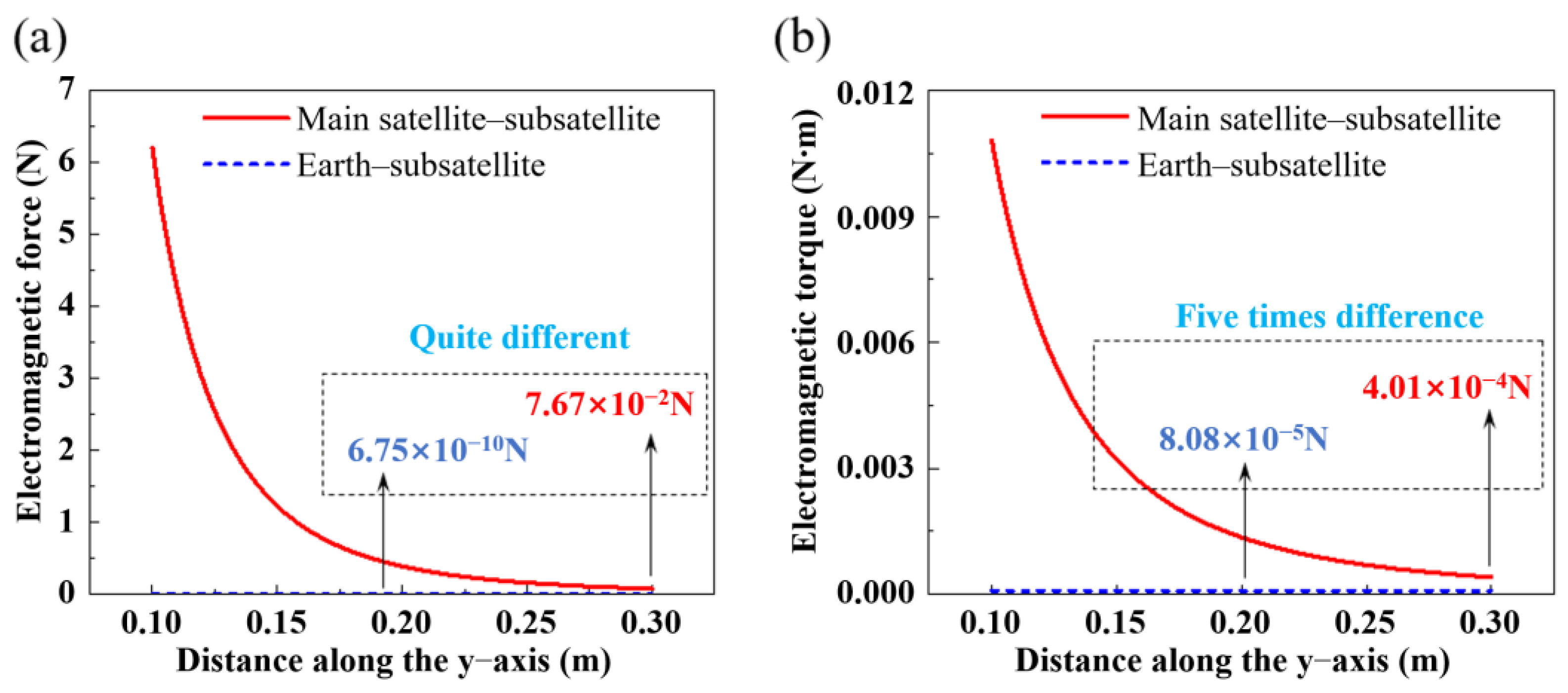
3.1. Analysis of the Interference Effect from the Geomagnetic Field
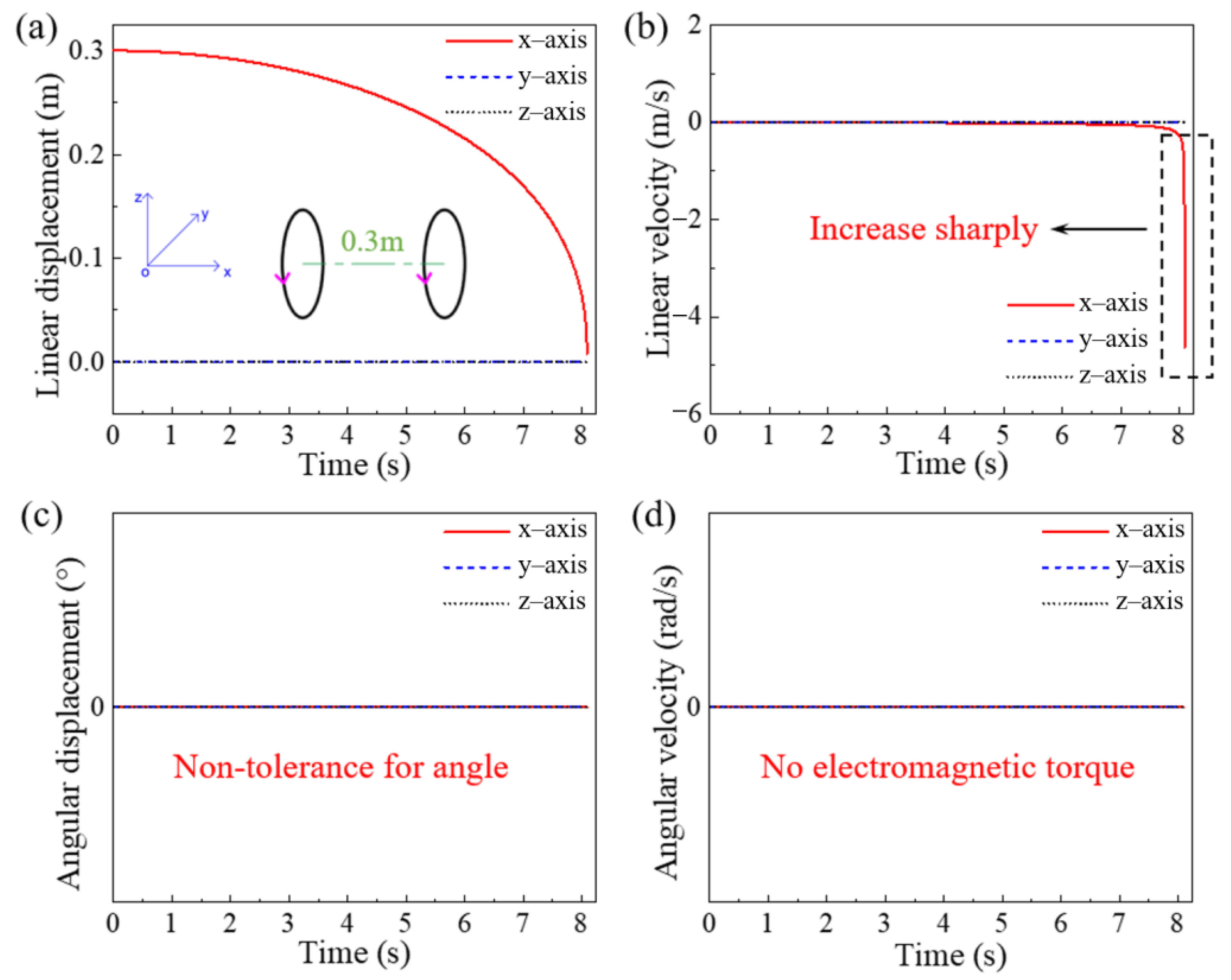
3.2. Electromagnetic Self-Docking Characteristics
4. The Strategy of Sliding Mode Variable Structure Control
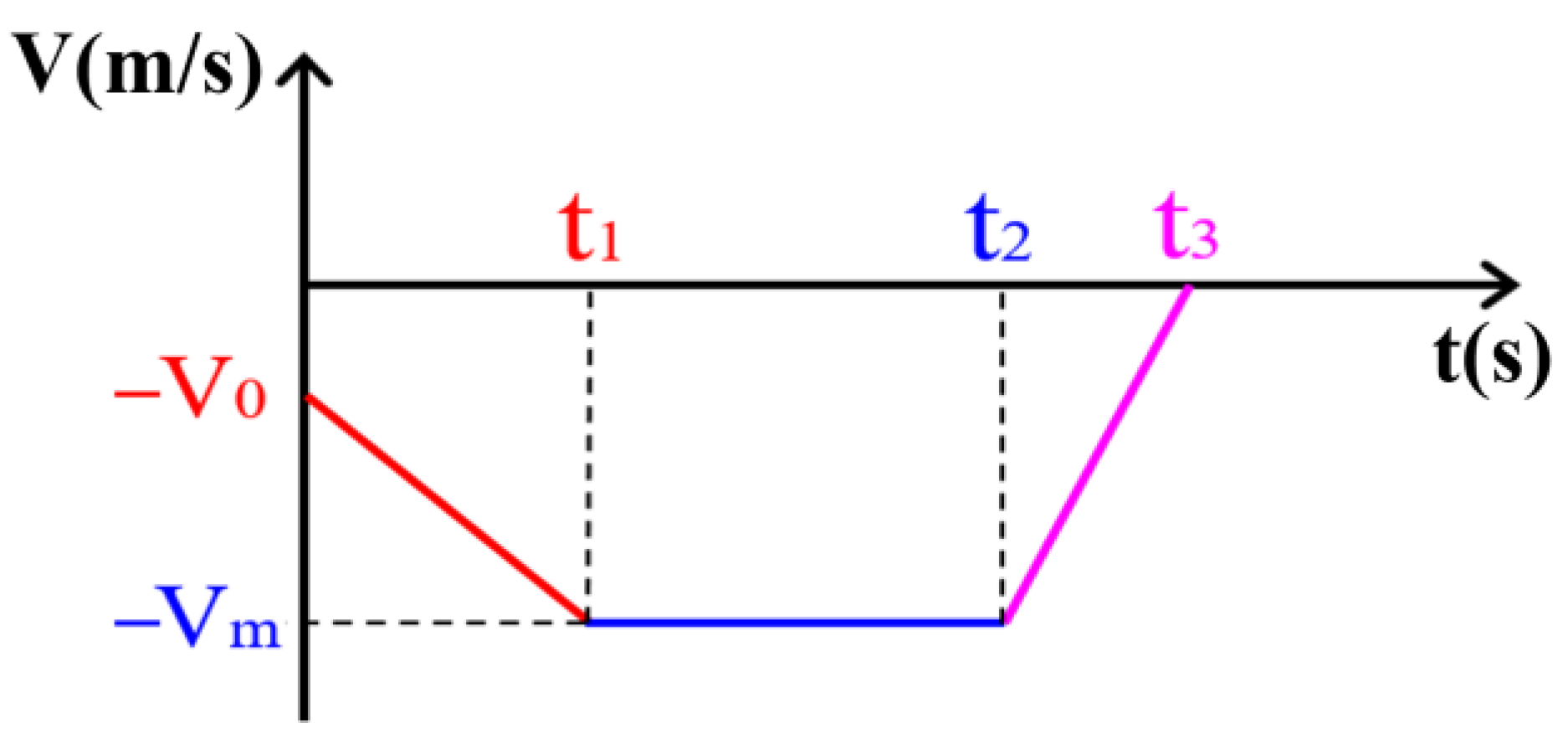
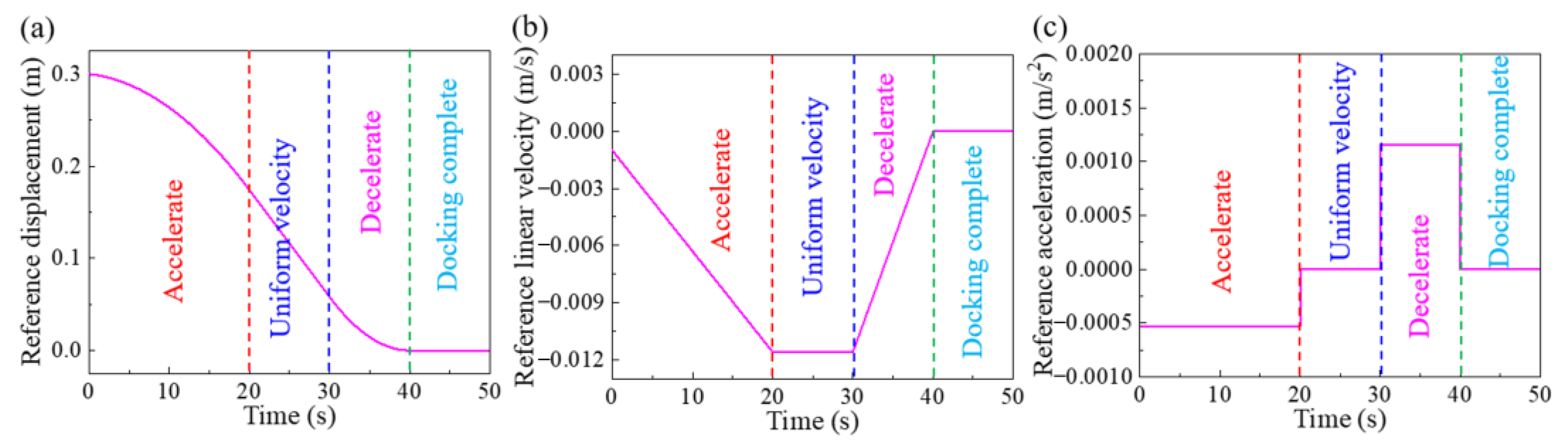
4.1. Design of Reference Trajectory for Non-Tolerance Docking Process
4.2. The Strategy of Sliding Mode Variable Structure Control Based on Exponential Reaching Law
4.3. The Strategy of Sliding Mode Variable Structure Control Based on Quasi Sliding Mode
5. Results and Discussion
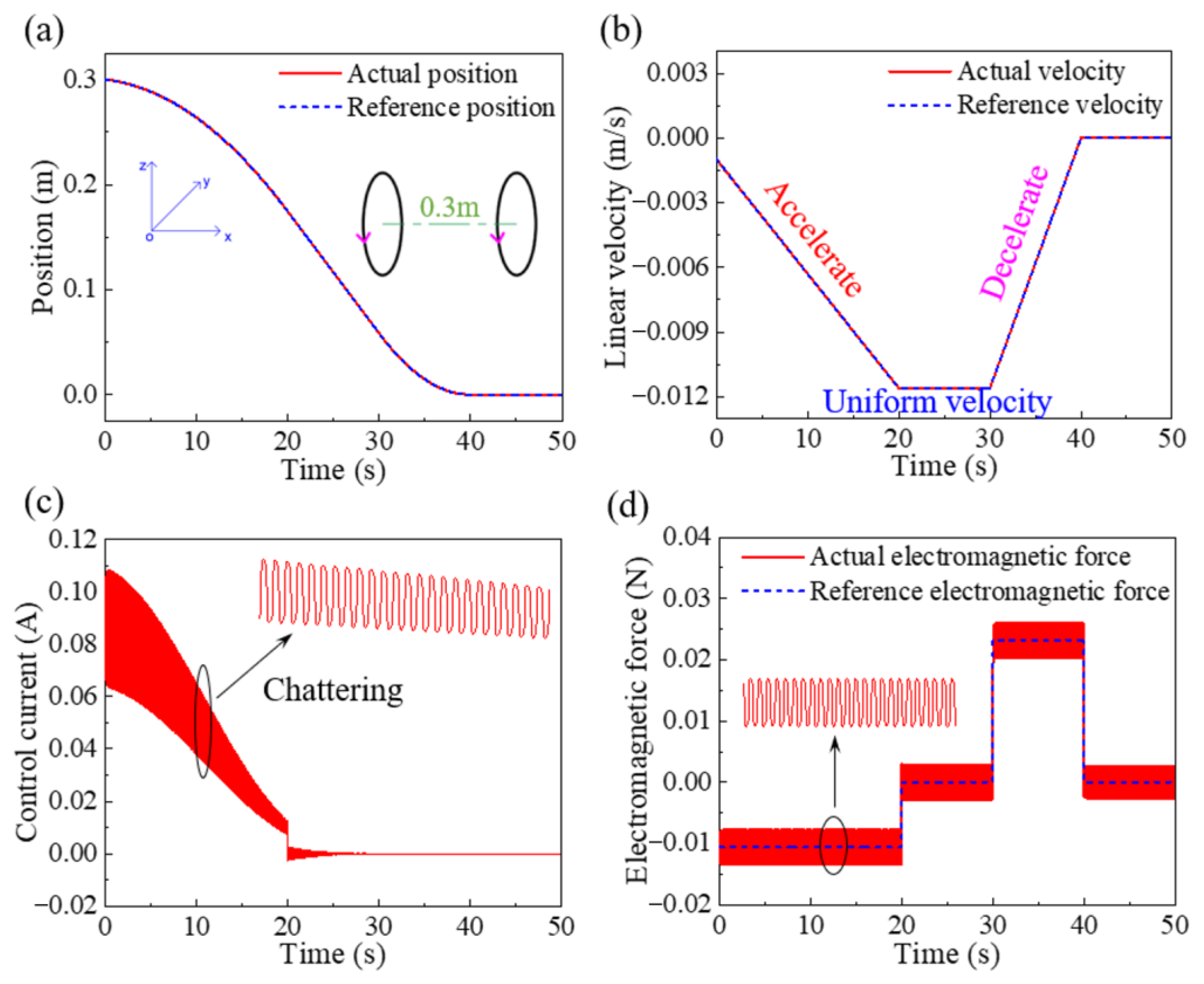
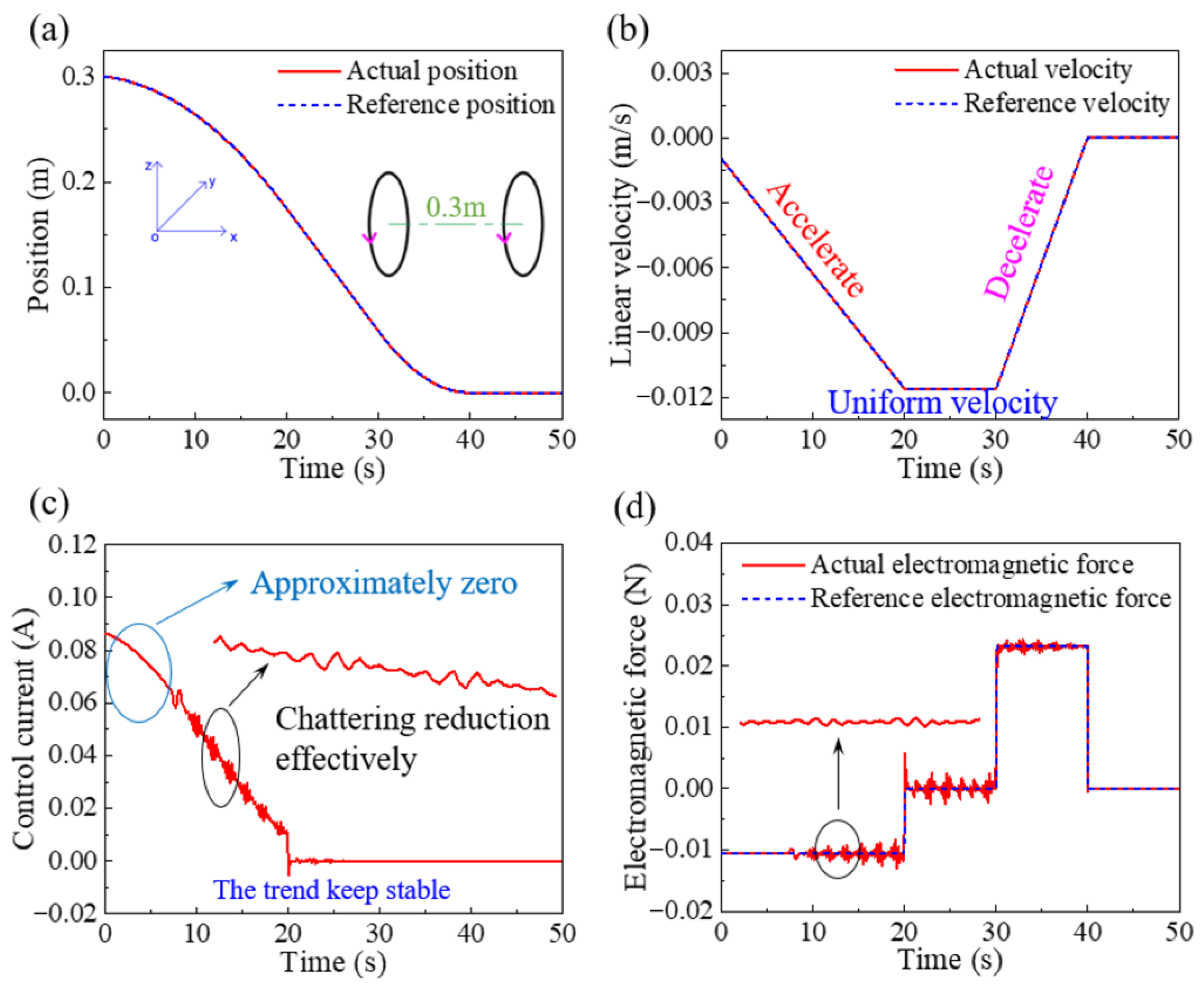
5.1. The Verification of Sliding Mode Variable Structure Control Based on Exponential Reaching Law
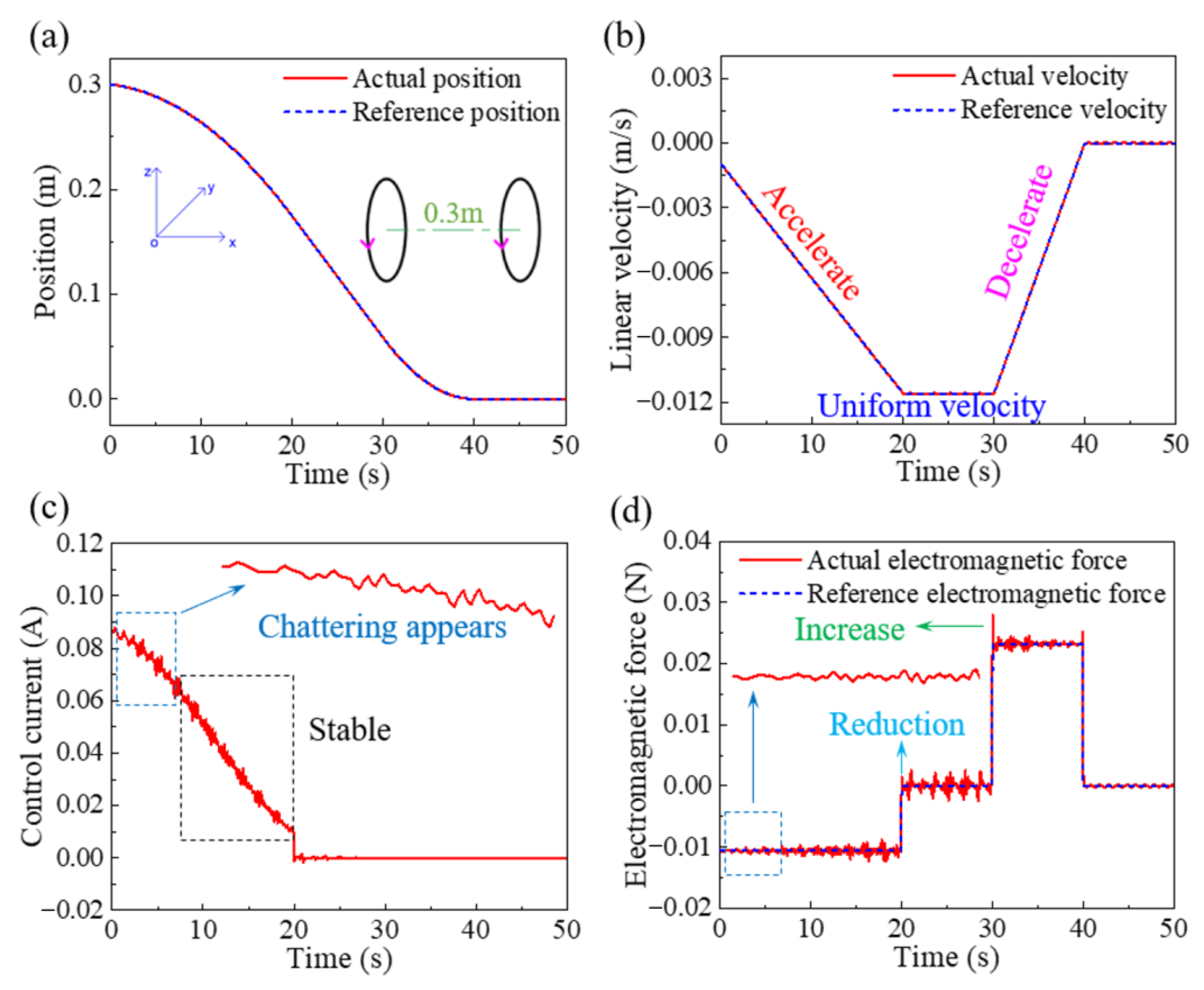
5.2. The Verification of Sliding Mode Variable Structure Control Based on Quasi Sliding Mode
6. Conclusions
- The electromagnetic force and electromagnetic torque models during electromagnetic docking were obtained based on the far-field model. The self-docking characteristics of the electromagnetic docking device were analyzed by using the established space electromagnetic docking dynamics model. It was necessary to design and add an electromagnetic controller to achieve flexible docking.
- According to the designed one-dimensional docking reference trajectory, the sliding mode variable structure control was proposed. The sliding mode variable structure control based on the exponential reaching law and quasi sliding mode showed good tracking effects on the reference trajectory, and could realize one-dimensional electromagnetic flexible docking.
- Compared with the control method based on exponential reaching law, the quasi sliding mode could effectively reduce the chattering phenomenon in the docking control process and presented good robustness. The sliding mode variable structure control with the quasi-sliding mode reduced the amplitude of current chattering by 80%, which was from 0.05 A to 0.01 A.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, Y.; Zhou, H.; Ma, S.; Gao, B.; Tan, L. Review of Spacecraft Exposed Payload Adapter Technology. Spacecr. Eng. 2019, 28, 104–111. [Google Scholar]
- Lu, Y.F.; Xie, Z.J.; Wang, J.; Yue, H.H.; Wu, M.; Liu, Y.W. A novel design of a parallel gripper actuated by a large-stroke shape memory alloy actuator. Int. J. Mech. Sci. 2019, 159, 74–80. [Google Scholar] [CrossRef]
- Vinals, J.; Urgoiti, E.; Guerra, G.; Valiente, I.; Esnoz-Larraya, J.; Ilzkovitz, M.; Franćeski, M.; Letier, P.; Yan, X.-T.; Henry, G.; et al. Multi-Functional Interface for Flexibility and Reconfigurability of Future European Space Robotic Systems. Adv. Astronaut. Sci. Technol. 2018, 1, 119–133. [Google Scholar] [CrossRef]
- Medina, A.; Tomassini, A.; Suatoni, M.; Aviles, M.; Solway, N.; Coxhill, I.; Paraskevas, I.S.; Rekleitis, G.; Papadopoulos, E.; Krenn, R.; et al. Towards a standardized grasping and refuelling on-orbit servicing for geo spacecraft. Acta Astronaut 2017, 134, 1–10. [Google Scholar] [CrossRef]
- Anthony, B.H.; Peter, T., Jr.; Jane, C.P.; Greg, A.R.; Gregory, J.W. Advancements in design of an autonomous satellite docking system. Proc. SPIE Spacecr. Platf. Infrastruct. 2004, 5419, 107–118. [Google Scholar] [CrossRef]
- Shi, K.K.; Liu, C.; Biggs, J.D.; Sun, Z.W.; Yue, X.K. Observer-based control for spacecraft electromagnetic docking. Aerosp. Sci. Technol. 2020, 99, 105759. [Google Scholar] [CrossRef]
- Steven, E.F.; Steve, D.; Nathan, H.; Jennifer, D.W. Application of the mini AERCam free flyer for orbital inspection. Proc. SPIE Spacecr. Platf. Infrastruct. 2004, 5419, 26–35. [Google Scholar] [CrossRef]
- Kong, E.M.C.; Kwon, D.W.; Schweighart, S.A.; Elias, L.M.; Sedwick, R.J.; Miller, D.W. Electromagnetic formation flight for multisatellite arrays. J. Spacecr. Rocket. 2004, 41, 659–666. [Google Scholar] [CrossRef]
- Underwood, C.; Pellegrino, S.; Lappas, V.J.; Bridges, C.P.; Baker, J. Using CubeSat/micro-satellite technology to demonstrate the Autonomous Assembly of a Reconfigurable Space Telescope (AAReST). Acta Astronaut 2015, 114, 112–122. [Google Scholar] [CrossRef]
- Abouzakhm, P.; Sharf, I. Guidance, Navigation, and Control for Docking of Two Cubic Blimps. IFAC-PapersOnLine 2016, 49, 260–265. [Google Scholar] [CrossRef]
- Schweighart, S.A.; Sedwick, R.J. Explicit Dipole Trajectory Solution for Electromagnetically Controlled Spacecraft Clusters. J. Guid Control Dynam. 2010, 33, 1225–1235. [Google Scholar] [CrossRef]
- Kwon, D.W. Propellantless formation flight applications using electromagnetic satellite formations. Acta Astronaut. 2010, 67, 1189–1201. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, X.L. Angular-Momentum Management of Electromagnetic Formation Flight Using Alternating Magnetic Fields. J. Guid. Control Dynam. 2016, 39, 1292–1302. [Google Scholar] [CrossRef]
- Shi, K.K.; Liu, C.; Sun, Z.W. Constrained fuel-free control for spacecraft electromagnetic docking in elliptical orbits. Acta Astronaut. 2019, 162, 14–24. [Google Scholar] [CrossRef]
- Huang, H.; Yang, L.P.; Zhu, Y.W.; Zhang, Y.W. Collective trajectory planning for satellite swarm using inter-satellite electromagnetic force. Acta Astronaut. 2014, 104, 220–230. [Google Scholar] [CrossRef]
- Huang, H.; Yang, L.; Zhu, Y.; Zhang, Y. Dynamics and relative equilibrium of spacecraft formation with non-contacting internal forces. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 1171–1182. [Google Scholar] [CrossRef]
- Huang, H.; Zhu, Y.W.; Yang, L.P.; Zhang, Y.W. Stability and shape analysis of relative equilibrium for three-spacecraft electromagnetic formation. Acta Astronaut. 2014, 94, 116–131. [Google Scholar] [CrossRef]
- Fabacher, E.; Lizy-Destrez, S.; Alazard, D.; Ankersen, F.; Profizi, A. Guidance of magnetic space tug. Adv. Space Res. 2017, 60, 14–27. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Yang, L.P.; Zhu, Y.W.; Huang, H. Dynamics and Solutions for Multispacecraft Electromagnetic Orbit Correction. J. Guid. Control Dynam. 2014, 37, 1604–1610. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Yang, L.P.; Zhu, Y.W.; Ao, H.J.; Qi, D.W. Self-docking analysis and velocity-aimed control for spacecraft electromagnetic docking. Adv. Space Res. 2016, 57, 2314–2325. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Yang, L.P.; Zhu, Y.W.; Ren, X.H.; Huang, H. Self-docking capability and control strategy of electromagnetic docking technology. Acta Astronaut. 2011, 69, 1073–1081. [Google Scholar] [CrossRef]
- Ahsun, U.; Miller, D.W.; Ramirez, J.L. Control of Electromagnetic Satellite Formations in Near-Earth Orbits. J. Guid. Control Dynam. 2010, 33, 1883–1891. [Google Scholar]
- Zhang, Y.W.; Yang, L.P.; Zhu, Y.W.; Huang, H. Dynamics and nonlinear control of space electromagnetic docking. J. Syst. Eng. Electron. 2013, 24, 454–462. [Google Scholar] [CrossRef]
- Kwon, D.W.; Sedwick, R.J.; Lee, S.I.; Ramirez-Riberos, J.L. Electromagnetic Formation Flight Testbed Using Superconducting Coils. J. Spacecr. Rocket. 2011, 48, 124–134. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Yang, L.P.; Zhu, Y.W.; Huang, H.; Cai, W.W. Nonlinear 6-DOF control of spacecraft docking with inter-satellite electromagnetic force. Acta Astronaut. 2012, 77, 97–108. [Google Scholar] [CrossRef]
- Zhao, W.; Underwood, C. Robust transition control of a Martian coaxial tiltrotor aerobot. Acta Astronaut. 2014, 99, 111–129. [Google Scholar] [CrossRef]
- Cai, W.W.; Yang, L.P.; Zhu, Y.W.; Zhang, Y.W. Formation keeping control through inter-satellite electromagnetic force. Sci. China Technol. Sci. 2013, 56, 1102–1111. [Google Scholar] [CrossRef]
- Torisaka, A.; Ozawa, S.; Yamakawa, H.; Kobayashi, N. Control of Electromagnetic Current at Final Docking Phase of Small Satellites. J. Space Eng. 2013, 6, 44–55. [Google Scholar] [CrossRef]
- Huang, X.L.; Zhang, C.; Lu, H.Q.; Li, M.M. Adaptive reaching law based sliding mode control for electromagnetic formation flight with input saturation. J. Frankl. I 2016, 353, 2398–2417. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.F.; Hexi, B.Y. Sliding mode control for low-thrust Earth-orbiting spacecraft formation maneuvering. Aerosp. Sci. Technol. 2006, 10, 636–643. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Hu, M. Finite-time control for electromagnetic satellite formations. Acta Astronaut. 2012, 74, 120–130. [Google Scholar] [CrossRef]
- Cai, W.W.; Yang, L.P.; Zhu, Y.W.; Zhang, Y.W. Optimal satellite formation reconfiguration actuated by inter-satellite electromagnetic forces. Acta Astronaut. 2013, 89, 154–165. [Google Scholar] [CrossRef]
- Fallaha, C.J.; Saad, M.; Kanaan, H.Y.; Al-Haddad, K. Sliding-Mode Robot Control With Exponential Reaching Law. IEEE Trans. Ind. Electron. 2011, 58, 600–610. [Google Scholar] [CrossRef]
- Weibing, G.; Hung, J.C. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, B.; Zhang, J.; Kong, N.; Ma, S.; Wang, B.; Han, R. Self-Docking Characteristics and Sliding Mode Control on Space Electromagnetic Docking Mechanism. Machines 2023, 11, 332. https://doi.org/10.3390/machines11030332
Wei B, Zhang J, Kong N, Ma S, Wang B, Han R. Self-Docking Characteristics and Sliding Mode Control on Space Electromagnetic Docking Mechanism. Machines. 2023; 11(3):332. https://doi.org/10.3390/machines11030332
Chicago/Turabian StyleWei, Boyu, Jie Zhang, Ning Kong, Shuai Ma, Bo Wang, and Runqi Han. 2023. "Self-Docking Characteristics and Sliding Mode Control on Space Electromagnetic Docking Mechanism" Machines 11, no. 3: 332. https://doi.org/10.3390/machines11030332
APA StyleWei, B., Zhang, J., Kong, N., Ma, S., Wang, B., & Han, R. (2023). Self-Docking Characteristics and Sliding Mode Control on Space Electromagnetic Docking Mechanism. Machines, 11(3), 332. https://doi.org/10.3390/machines11030332




