Thermal Model and Thermal Analysis of the Dual Drive Sliding Feed System
Abstract
:1. Introduction
2. Friction Torque Modeling of the Sliding Screw
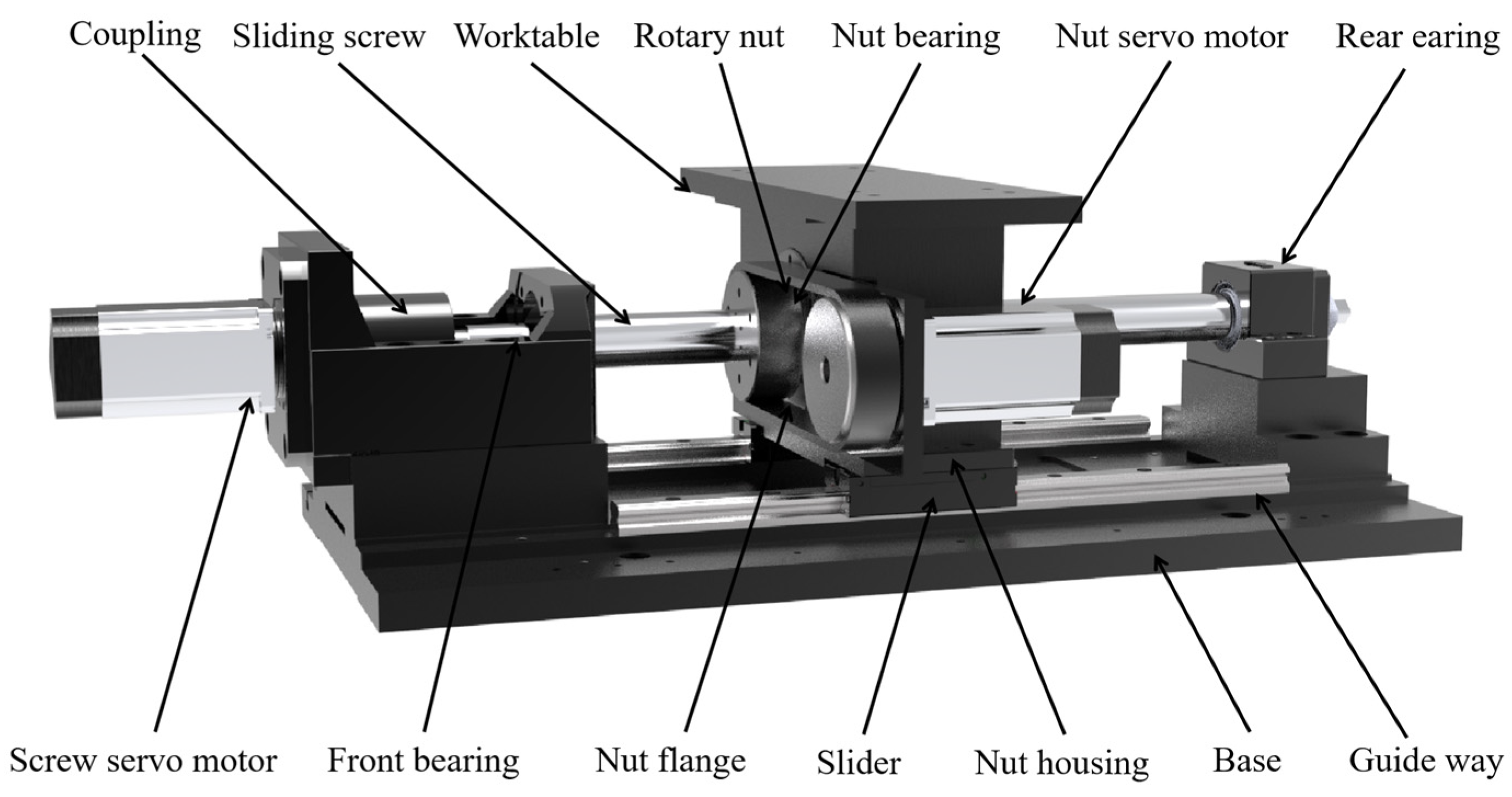
2.1. Dual Drive Sliding Feed System
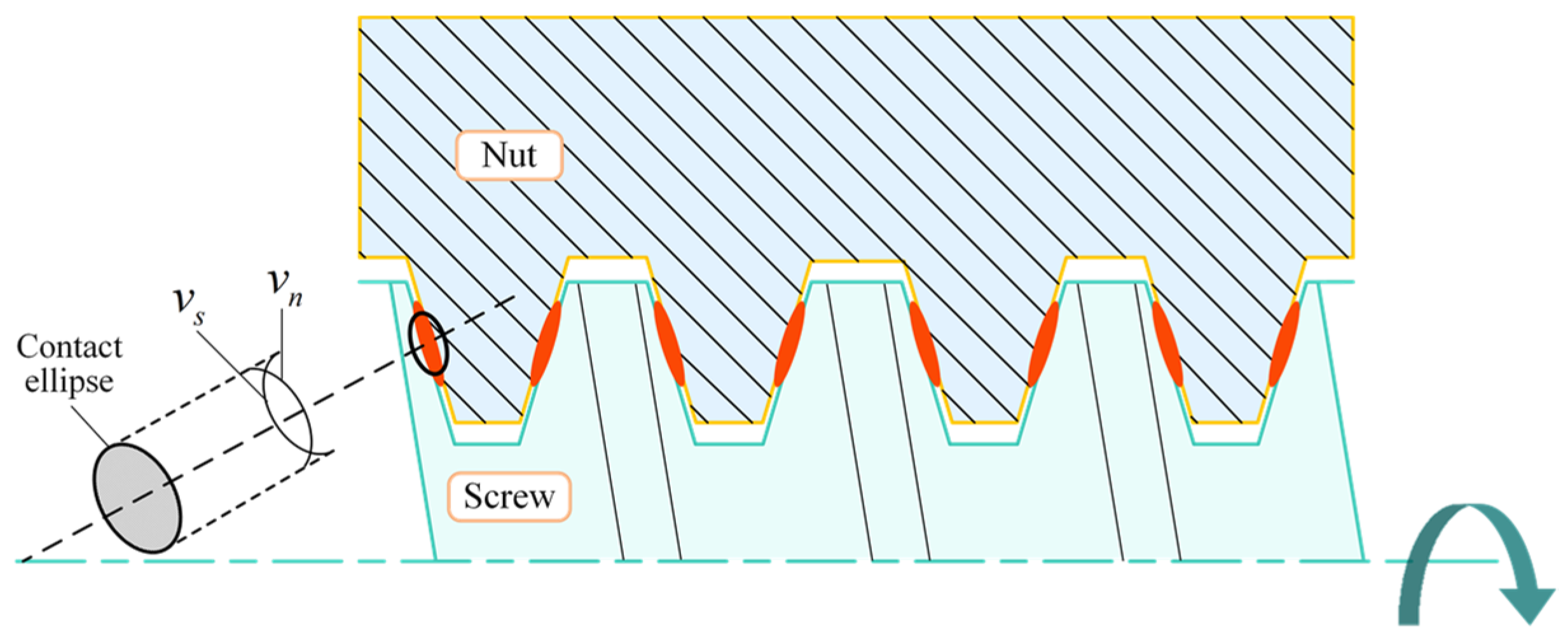
2.2. Friction Torque Caused by Differential Sliding
2.3. Frictional Moment Caused by Elastic Hysteresis
2.4. Friction Torque Caused by Lubrication Viscosity
3. Thermal Boundary Conditions of the Dual Drive Sliding Feed System
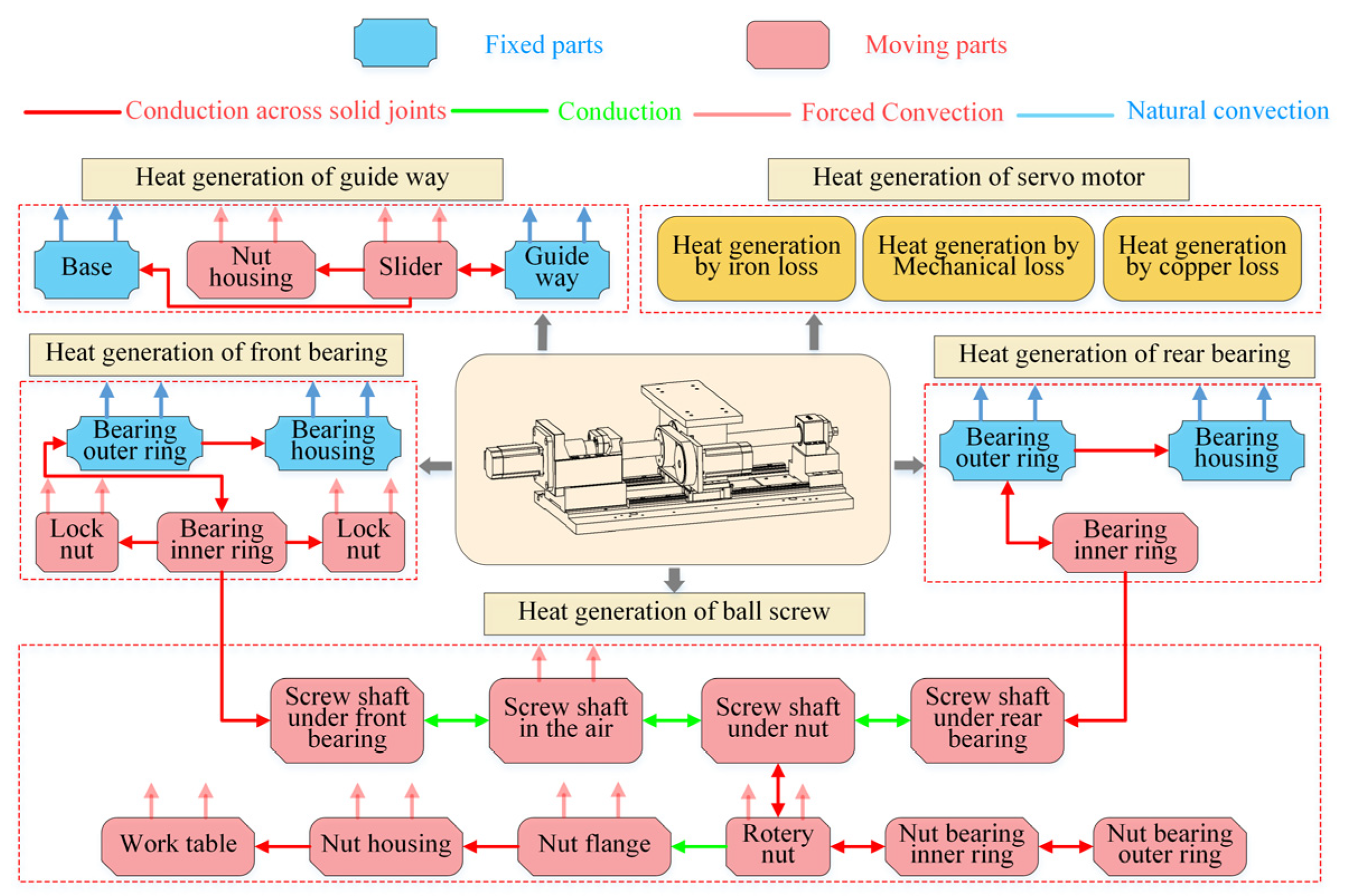
3.1. Analysis of Heat Generation
3.2. Analysis of Heat Transfer
3.3. TCRs between Rough Contact Surfaces
4. Establishment and Verification of the Thermal Model for Dual Drive Sliding Feed System
4.1. Finite Element Simulation Model of Dual Drive Sliding Feed System
- (1)
- The chamfers and some tiny parts inside the system were ignored;
- (2)
- The screw shaft ignores the grooves on its surface and treats it as a cylinder;
- (3)
- The parameters of heat generation and CHTCs obtained from the previous calculation do not vary with the movement or temperature rise of the components.
4.2. Experimental Verification Device and Scheme
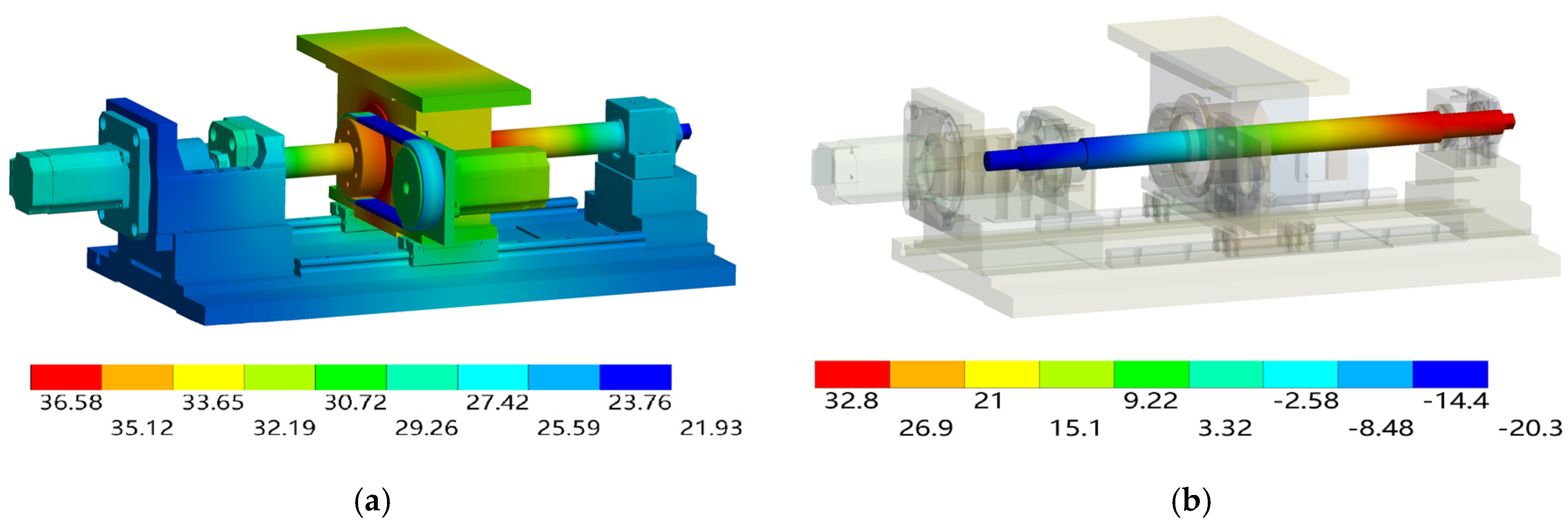
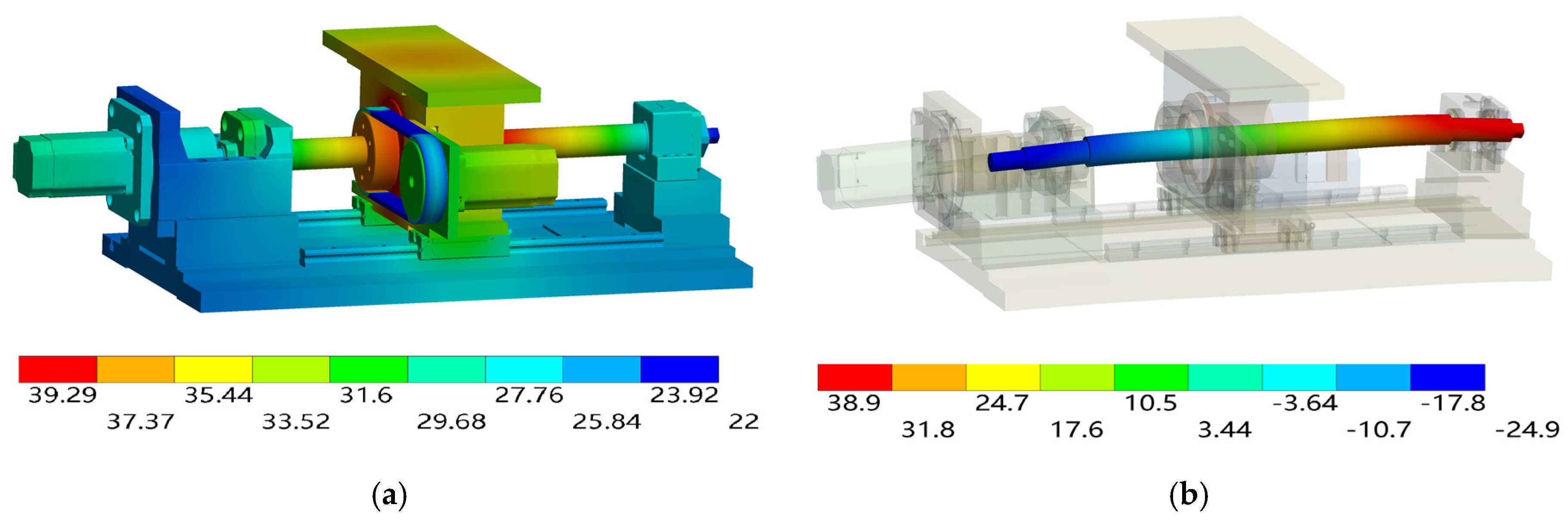
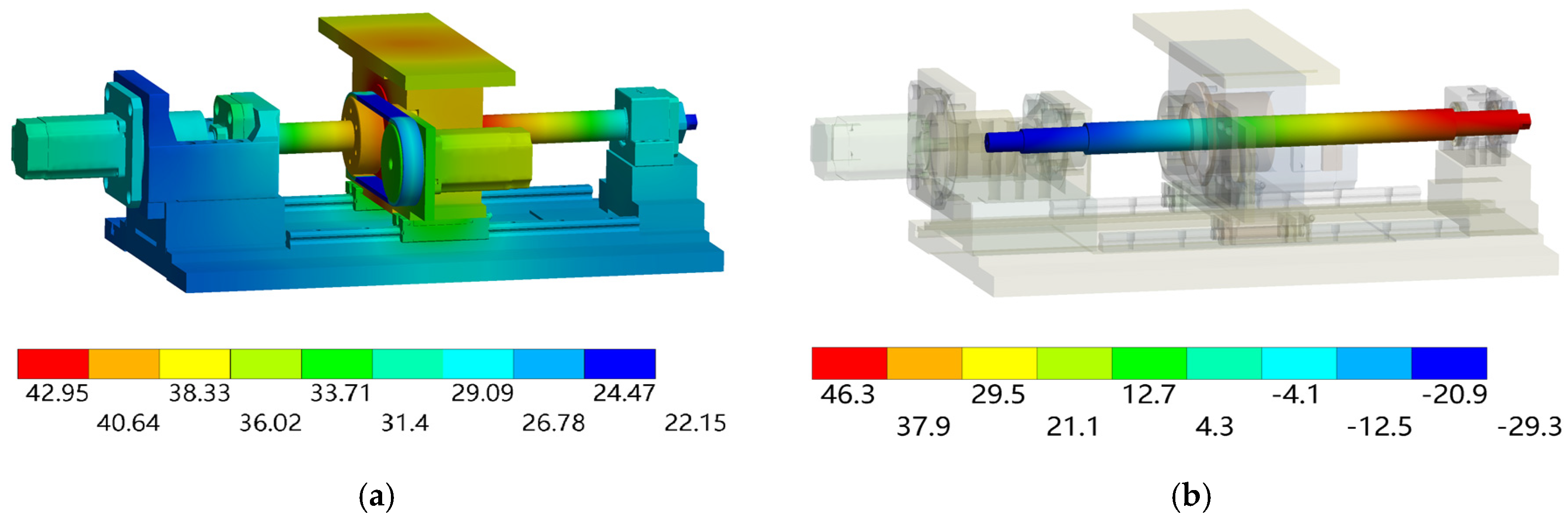
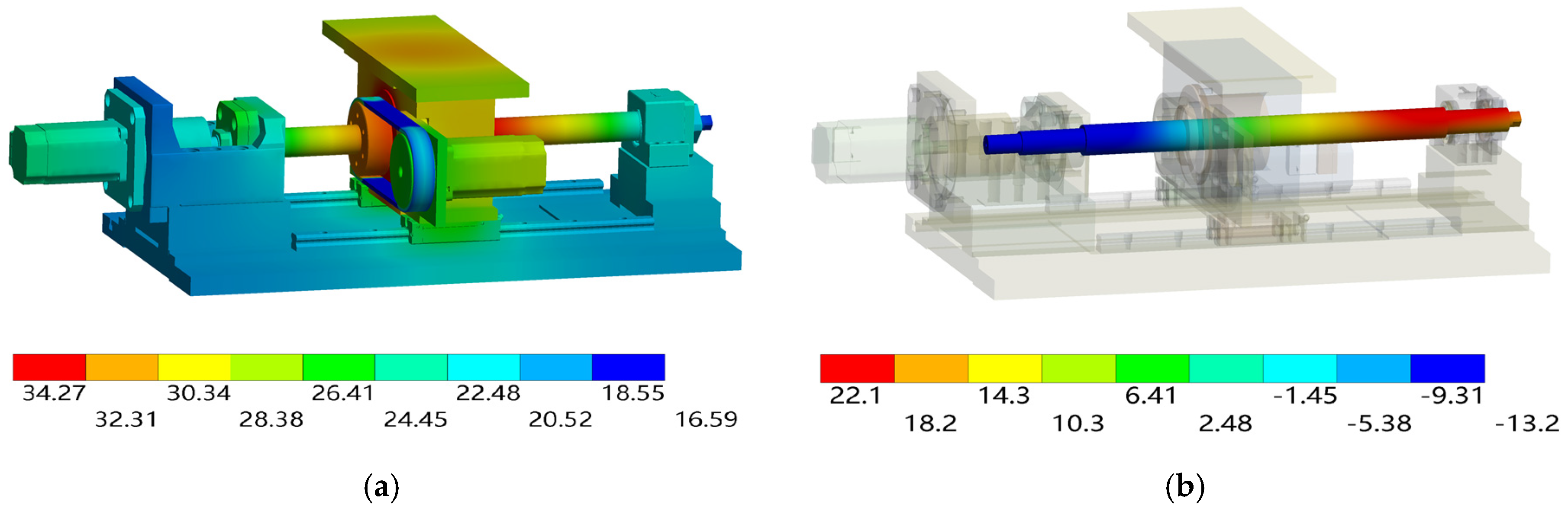
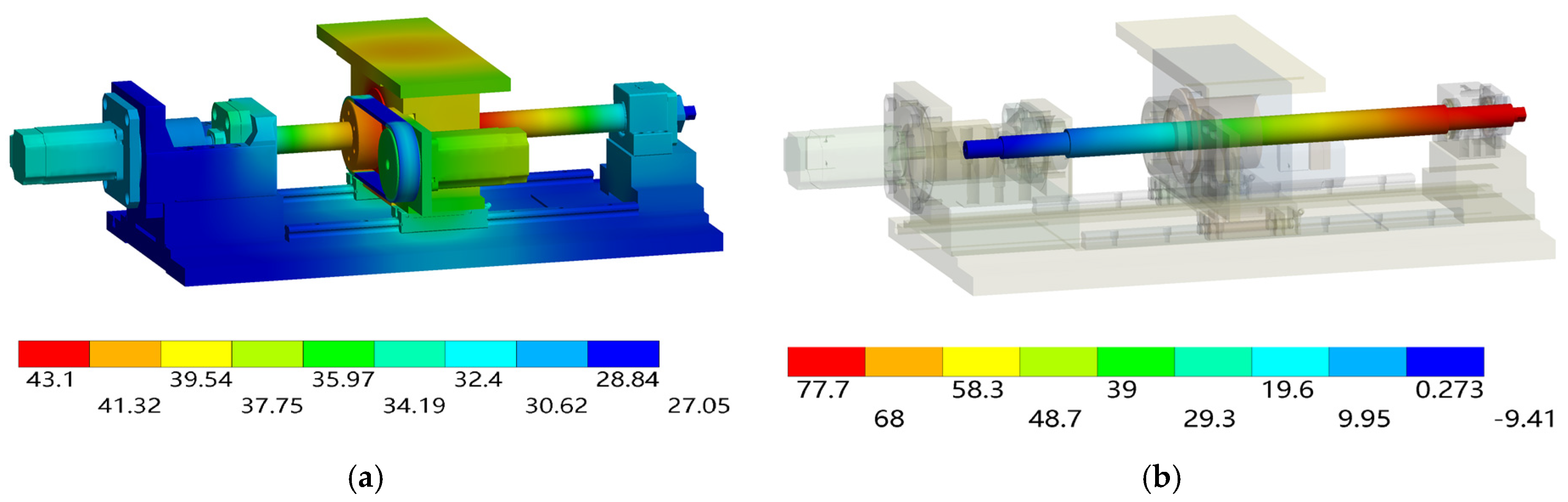
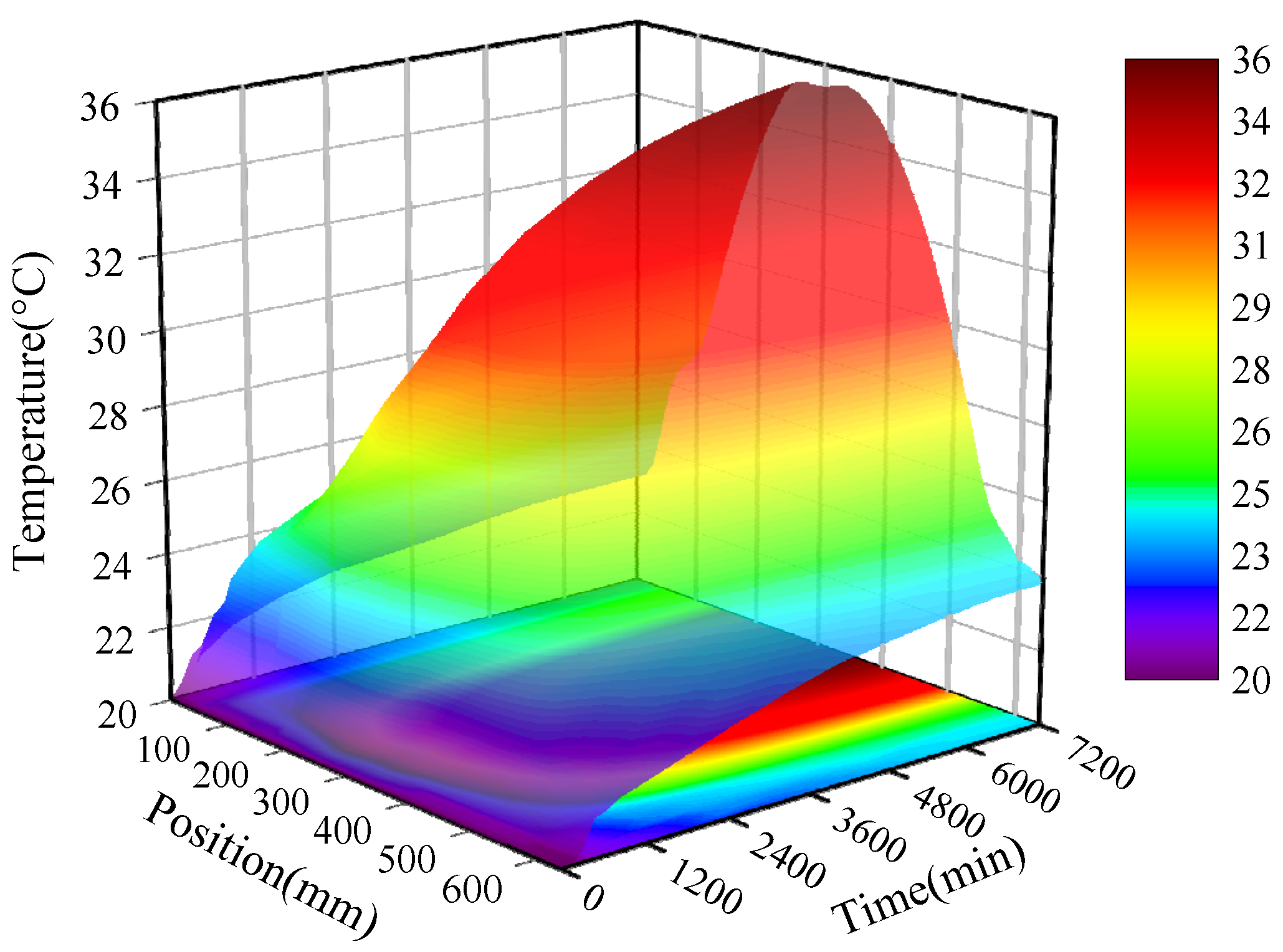
4.3. Comparison of the Simulation and Experimental Results
5. Conclusions
- The established thermal simulation model can effectively describe the dynamic thermal characteristics of the dual drive sliding feed system. By comparing the temperature rise and thermal elongation under simulation and experimental conditions, it can be concluded that the temperature rise deviation under five operating conditions is less than 2.1 °C, and the error in the axial thermal deformation of the screw is less than 6.2 µm. The established thermal characteristic simulation model can effectively describe the thermal dynamic response characteristics of the dual drive sliding feed system during operation.
- The thermal field distribution and axial deformation of the dual drive sliding feed system differ from those of conventional feed systems. Due to the difficulty of heat dissipation and the combined effect of the screw and nut bearings, the main heat distribution region of the dual drive feed system is at the nut. Given the numerous heat sources in the system and the significant temperature increase in the sliding screw, the axial deformation of the screw in the dual drive sliding feed system is greater than that in the conventional feed system under the same operating conditions.
- The thermal characteristics of a dual drive sliding system are significantly influenced by both rotational speed and ambient temperature. An increase in rotational speed results in a faster rate of temperature rise and a shorter time to reach thermal equilibrium. Conversely, higher ambient temperatures lead to a quicker temperature rise and a longer time to achieve thermal equilibrium. The ambient temperature also has a significant impact on the axial deformation of the screw. Even when the temperature field is similar, substantial differences in the axial thermal elongation of the screw can occur due to varying ambient temperatures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.-J.; Tan, Z.; Chen, Y.; Lu, Z.-C.; Fan, Y.-C. Thermal error prediction of ball screw feed system based on inverse heat transfer analysis. Int. J. Adv. Manuf. Technol. 2022, 122, 2607–2624. [Google Scholar] [CrossRef]
- Li, Y.; Wei, W.; Su, D.; Wu, W.; Zhang, J.; Zhao, W. Thermal characteristic analysis of ball screw feed drive system based on finite difference method considering the moving heat source. Int. J. Adv. Manuf. Technol. 2020, 106, 4533–4545. [Google Scholar] [CrossRef]
- Lei, M.; Yang, J.; Wang, S.; Zhao, L.; Xia, P.; Jiang, G.; Mei, X. Semi-supervised modeling and compensation for the thermal error of precision feed axes. Int. J. Adv. Manuf. Technol. 2019, 104, 4629–4640. [Google Scholar] [CrossRef]
- Liu, J.; Ma, C.; Wang, S.; Wang, S.; Yang, B.; Shi, H. Thermal boundary condition optimization of ball screw feed drive system based on response surface analysis. Mech. Syst. Signal Process. 2019, 121, 471–495. [Google Scholar] [CrossRef]
- Du, F.; Zhang, M.; Wang, Z.; Chen, Y.; Feng, X.; Li, P. Identification and compensation of friction for a novel two-axis differential micro-feed system. Mech. Syst. Signal Process. 2018, 106, 453–465. [Google Scholar] [CrossRef]
- Yang, H.; Xing, R.; Du, F. Thermal error modelling for a high-precision feed system in varying conditions based on an improved Elman network. Int. J. Adv. Manuf. Technol. 2020, 106, 279–288. [Google Scholar] [CrossRef]
- Lu, Z.; Feng, X.; Su, Z.; Liu, Y.; Yao, M. Friction Parameters Dynamic Change and Compensation for a Novel Dual-Drive Micro-Feeding System. Actuators 2022, 11, 236. [Google Scholar] [CrossRef]
- Xu, Z.Z.; Liu, X.J.; Kim, H.K.; Shin, J.H.; Lyu, S.K. Thermal error forecast and performance evaluation for an air-cooling ball screw system. Int. J. Mach. Tools Manuf. 2011, 51, 605–611. [Google Scholar] [CrossRef]
- Qiao, G.; Liu, G.; Ma, S.; Wang, Y.; Li, P.; Lim, T.C. Thermal characteristics analysis and experimental study of the planetary roller screw mechanism. Appl. Therm. Eng. 2019, 149, 1345–1358. [Google Scholar] [CrossRef]
- Zhao, C.J.; Yu, X.K.; Huang, Q.K.; Ge, S.D.; Gao, X. Analysis on the load characteristics and coefficient of friction of angular contact ball bearing at high speed. Tribol. Int. 2015, 87, 50–56. [Google Scholar] [CrossRef]
- Helmig, T.; Kneer, R. A novel transient infrared-thermography based experimental method for the inverse estimation of heat transfer coefficients in rotating bearings. Int. J. Therm. Sci. 2021, 167, 107000. [Google Scholar] [CrossRef]
- Bui, B.D.; Uchiyama, N.; Simba, K.R. Contouring control for three-axis machine tools based on nonlinear friction compensation for lead screws. Int. J. Mach. Tools Manuf. 2016, 108, 95–105. [Google Scholar] [CrossRef]
- Min, X.; Jiang, S. A thermal model of a ball screw feed drive system for a machine tool. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 186–193. [Google Scholar] [CrossRef]
- Ma, S.; Wu, L.; Liu, G.; Fu, X. Local contact characteristics of threaded surfaces in a planetary roller screw mechanism. J. Struct. Mech. 2020, 48, 1–26. [Google Scholar] [CrossRef]
- Du, C.; Liu, G.; Qiao, G.; Ma, S.; Cai, W. Transient thermal analysis of standard planetary roller screw mechanism based on finite element method. Adv. Mech. Eng. 2018, 10, 1687814018812305. [Google Scholar] [CrossRef]
- Houpert, L. Numerical and analytical calculation in ball bearings. Proc. Congr. Roulements Toulouse Toulouse 1999, 5–7, 1–15. [Google Scholar]
- Qiao, G.; Liu, G.; Ma, S.; Shi, Z.; Wang, Y.; Lim, T.C. An improved thermal estimation model of the inverted planetary roller screw mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4430–4446. [Google Scholar] [CrossRef]
- Yang, J.J. Effect of Preload on Axial Deformation and Friction of Planetary Roller Screw. J. Mech. Transm. 2011, 35, 16–22. [Google Scholar]
- Olaru, D.; Puiu, G.C.; Balan, L.C.; Puiu, V. A New Model to Estimate Friction Torque in a Ball Screw System. Prod. Eng. Eco-Des. Technol. Green Energy 2005, 333–346. Available online: https://link.springer.com/chapter/10.1007/1-4020-2933-0_20 (accessed on 12 November 2023).
- Kim, J.-J.; Jeong, Y.H.; Cho, D.-W. Thermal behavior of a machine tool equipped with linear motors. Int. J. Mach. Tools Manuf. 2004, 44, 749–758. [Google Scholar] [CrossRef]
- Su, D.; Li, Y.; Zhao, W.; Zhang, H. Transient thermal error modeling of a ball screw feed system. Int. J. Adv. Manuf. Technol. 2023, 124, 2095–2107. [Google Scholar] [CrossRef]
- Li, D.; Feng, P.; Zhang, J.; Wu, Z.; Yu, D. Method for modifying convective heat transfer coefficients used in the thermal simulation of a feed drive system based on the response surface methodology. Numer. Heat Transf. Part A Appl. 2015, 69, 51–66. [Google Scholar] [CrossRef]
- Oyanguren, A.; Larraaga, J.; Ulacia, I. Thermo-mechanical modelling of ball screw preload force variation in different working conditions. Int. J. Adv. Manuf. Technol. 2018, 97, 723–739. [Google Scholar] [CrossRef]
- Mao, X.; Mao, K.; Wang, F.; Yan, B.; Lei, S. A convective heat transfer coefficient algorithm for thermal analysis of machine tools considering a temperature change. Int. J. Adv. Manuf. Technol. 2018, 99, 1877–1889. [Google Scholar] [CrossRef]
- Wu, H.; Guan, Q.; Xi, C.; Zuo, D. Construction of dynamic temperature field model of ball screw based on superposition of positive and negative temperature fields. Numer. Heat Transf. Part A Appl. Int. J. Comput. Methodol. 2023, 83, 343–360. [Google Scholar] [CrossRef]


| Speed of Synthesis (m/Min) | Speed of Screw (Rpm) | Speed of Nut (Rpm) | Heat Production (W) | |||||
|---|---|---|---|---|---|---|---|---|
| Guideways | Screw Servo Motor | Nut Servo Motor | Front Bearing | Nut Bearing | Rear Bearing | |||
| 0.18 | 396 | 360 | 0.39 | 1.87 | 1.70 | 4.95 | 5.31 | 4.36 |
| Speed of Synthesis (m/Min) | Speed of Screw (Rpm) | Speed of Nut (Rpm) | CHTCS (W/m2·K) | |||||
|---|---|---|---|---|---|---|---|---|
| Screw Pair | Screw Shaft | Nut Servo Motor | Nut Housing | Slider | Worktable | |||
| 0.18 | 396 | 360 | 9.17 | 56.3 | 15.52 | 31.26 | 14.53 | 16.23 |
| Joint Component | TCR (m2·K/W) |
|---|---|
| Bearing outer ring-bearing housing | 1.25 × 10−3 |
| Bearing inner ring-screw shaft | 1.48 × 10−4 |
| Nut-screw | 1.65 × 10−4 |
| Guideway-slider | 6.89 × 10−4 |
| Nut servo motor-nut | 3.68 × 10−3 |
| Application Components | Material | Density (kg/m3) | Modulus of Elasticity (GPa) | Poisson’s Ratio | Linear Expansion Coefficient (10−5/K) | Thermal Conductivity (W/m·K) | Specific Heat Capacity (J/kg·K) |
|---|---|---|---|---|---|---|---|
| Nut | Copper alloy | 8400 | 110 | 0.34 | 1.7 | 115 | 387 |
| Screw/bearing | GCr15 | 7800 | 200 | 0.28 | 1.2 | 48 | 729 |
| Base/bearing housing | Q345B | 7850 | 206 | 0.3 | 1.2 | 46 | 460 |
| Guideways/slider | 40Cr | 7850 | 200 | 0.3 | 1.13 | 51 | 477 |
| Operating Condition | Speed of Synthesis (m/Min) | Speed of Screw (Rpm) | Speed of Nut (Rpm) | Ambient Temperature (°C) |
|---|---|---|---|---|
| I | 0.18 | 396 | 360 | 20 |
| II | 0.36 | 1116 | 1080 | 20 |
| III | 0.54 | 2214 | 2160 | 20 |
| IV | 0.36 | 1116 | 1080 | 15 |
| V | 0.36 | 1116 | 1080 | 25 |
| Operation Condition | Measured Position | Simulated Value (°C) | Measured Value (°C) | Deviation (°C) |
|---|---|---|---|---|
| I | T1 | 28.1 | 27.1 | 1.0 |
| T2 | 25.7 | 24.5 | 1.2 | |
| T3 | 35.9 | 34.5 | 1.4 | |
| T4 | 33.9 | 33.2 | 0.7 | |
| T5 | 33.7 | 31.9 | 1.8 | |
| II | T1 | 30.8 | 29.6 | 1.2 |
| T2 | 27.4 | 26.2 | 1.2 | |
| T3 | 38.5 | 37.1 | 1.4 | |
| T4 | 36.4 | 35.8 | 0.6 | |
| T5 | 36.2 | 34.2 | 2.0 | |
| III | T1 | 31.1 | 30.1 | 1.0 |
| T2 | 28.3 | 27.3 | 1.0 | |
| T3 | 42.1 | 40.1 | 2.0 | |
| T4 | 39.2 | 38.2 | 1.0 | |
| T5 | 38.7 | 36.6 | 2.1 | |
| IV | T1 | 24.7 | 23.6 | 1.1 |
| T2 | 21.9 | 20.9 | 1.0 | |
| T3 | 33.4 | 31.8 | 1.6 | |
| T4 | 30.2 | 29.5 | 0.7 | |
| T5 | 30.0 | 28.5 | 1.5 | |
| V | T1 | 34.5 | 33.2 | 1.3 |
| T2 | 31.7 | 30.5 | 1.2 | |
| T3 | 42.4 | 40.8 | 1.6 | |
| T4 | 39.9 | 38.8 | 1.1 | |
| T5 | 40.0 | 37.9 | 2.1 |
| Operation Condition | Simulated Value (µm) | Measured Value (µm) | Deviation (µm) |
|---|---|---|---|
| I | 32.8 | 29.9 | 2.9 |
| II | 38.9 | 35.5 | 3.4 |
| III | 46.3 | 42.5 | 3.8 |
| IV | 22.1 | 20.3 | 1.8 |
| V | 77.7 | 71.5 | 6.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, H.; Feng, X.; Liu, Y.; Yao, M.; Wang, A. Thermal Model and Thermal Analysis of the Dual Drive Sliding Feed System. Machines 2023, 11, 1084. https://doi.org/10.3390/machines11121084
Li H, Liu H, Feng X, Liu Y, Yao M, Wang A. Thermal Model and Thermal Analysis of the Dual Drive Sliding Feed System. Machines. 2023; 11(12):1084. https://doi.org/10.3390/machines11121084
Chicago/Turabian StyleLi, Hui, Haiyang Liu, Xianying Feng, Yandong Liu, Ming Yao, and Anning Wang. 2023. "Thermal Model and Thermal Analysis of the Dual Drive Sliding Feed System" Machines 11, no. 12: 1084. https://doi.org/10.3390/machines11121084
APA StyleLi, H., Liu, H., Feng, X., Liu, Y., Yao, M., & Wang, A. (2023). Thermal Model and Thermal Analysis of the Dual Drive Sliding Feed System. Machines, 11(12), 1084. https://doi.org/10.3390/machines11121084







