Efficient Autonomous Path Planning for Ultrasonic Non-Destructive Testing: A Graph Theory and K-Dimensional Tree Optimisation Approach
Abstract
:1. Introduction
2. Background Theory
2.1. Ultrasonic Inspection and Robotics for NDT
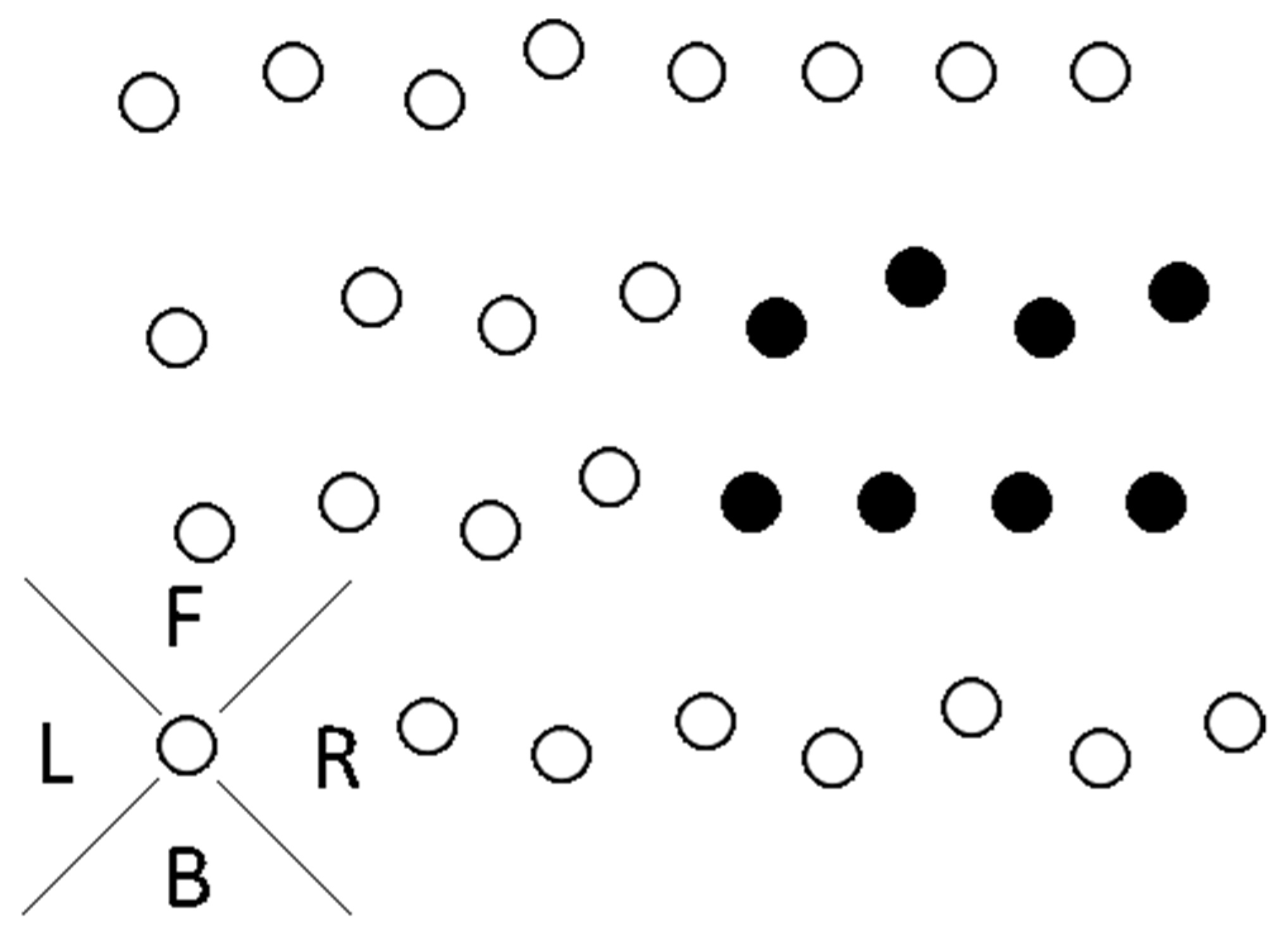
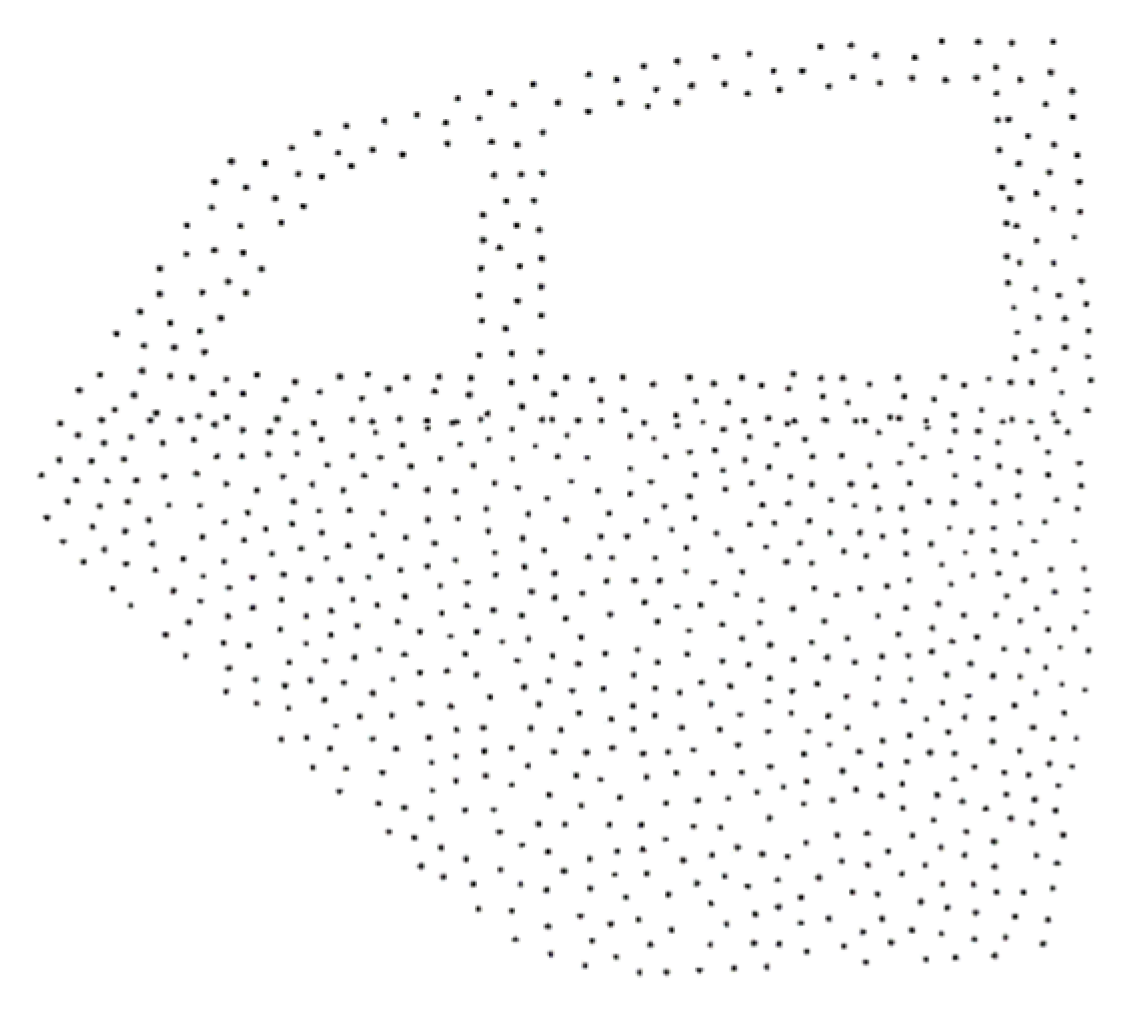
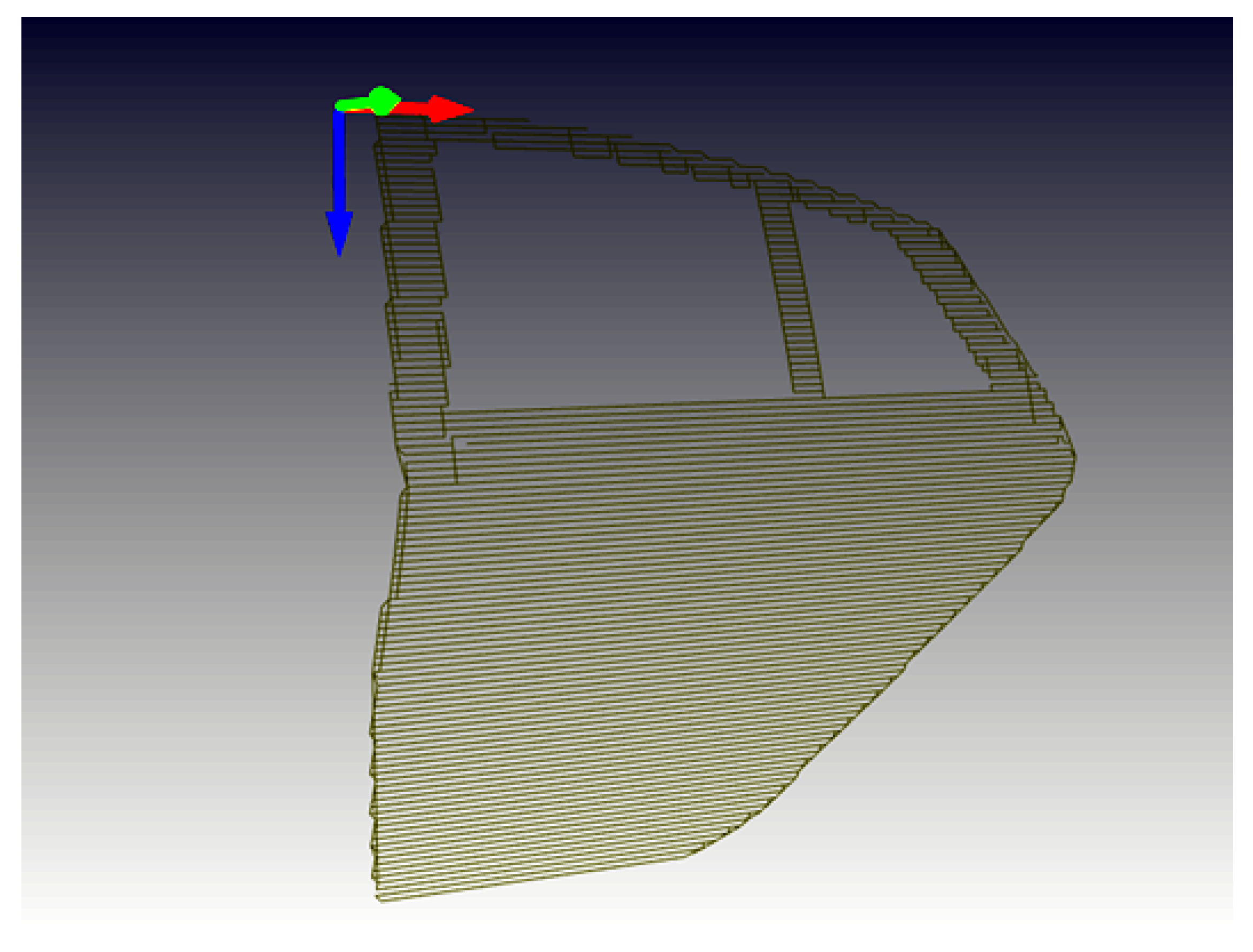
2.2. Decomposition of CAD Model
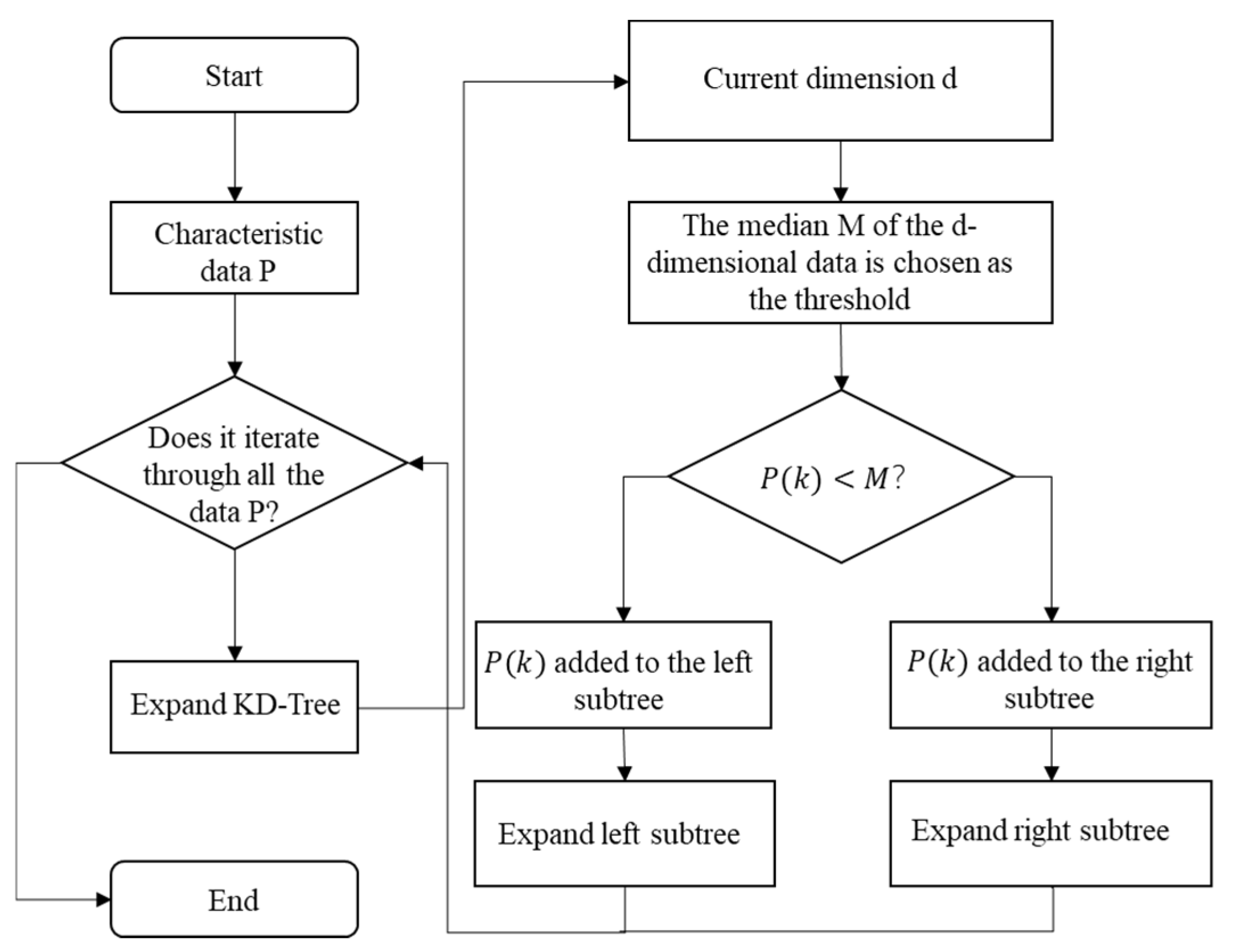
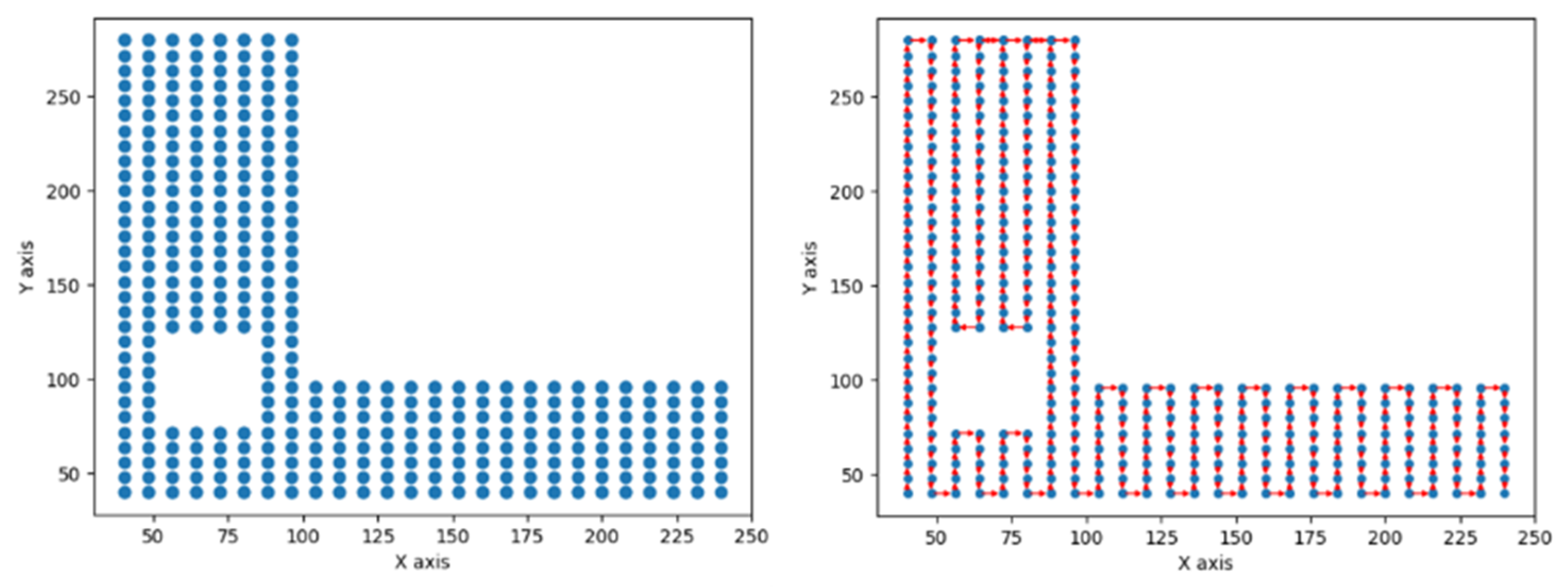
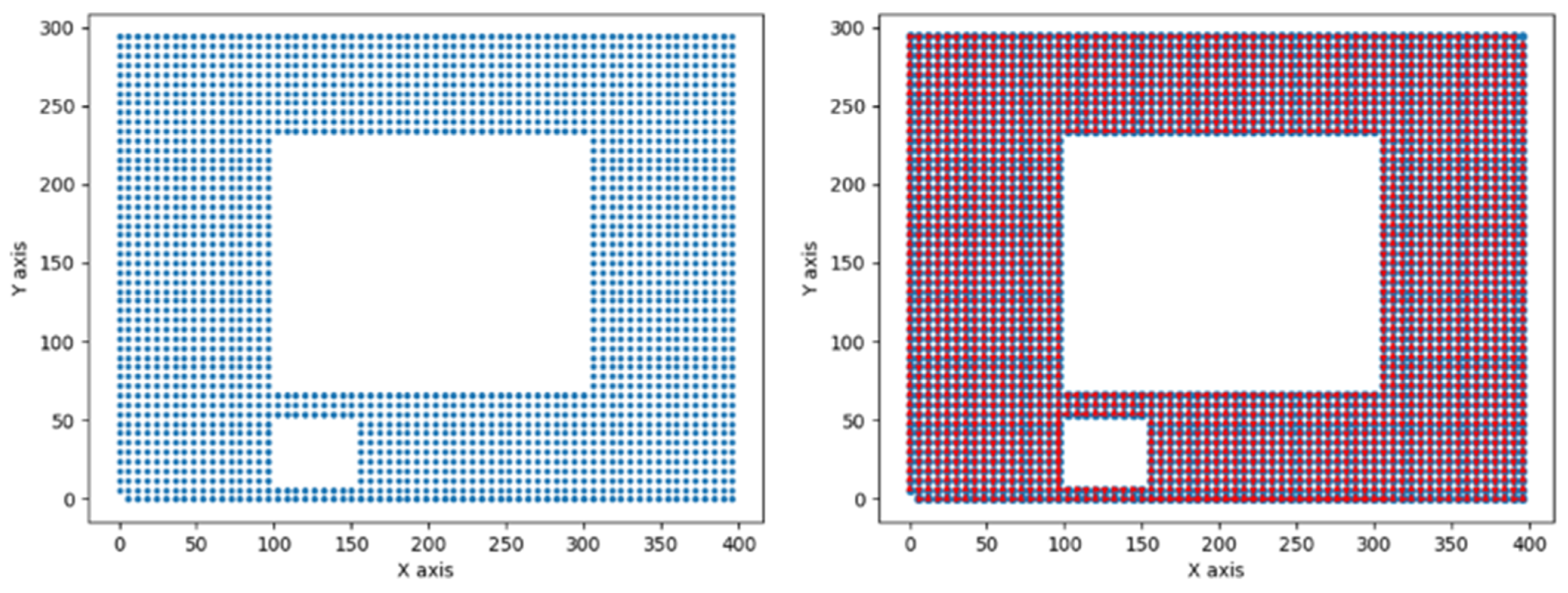
2.3. Graph Theory, KD-Tree Optimisation, and Dijkstra Algorithm
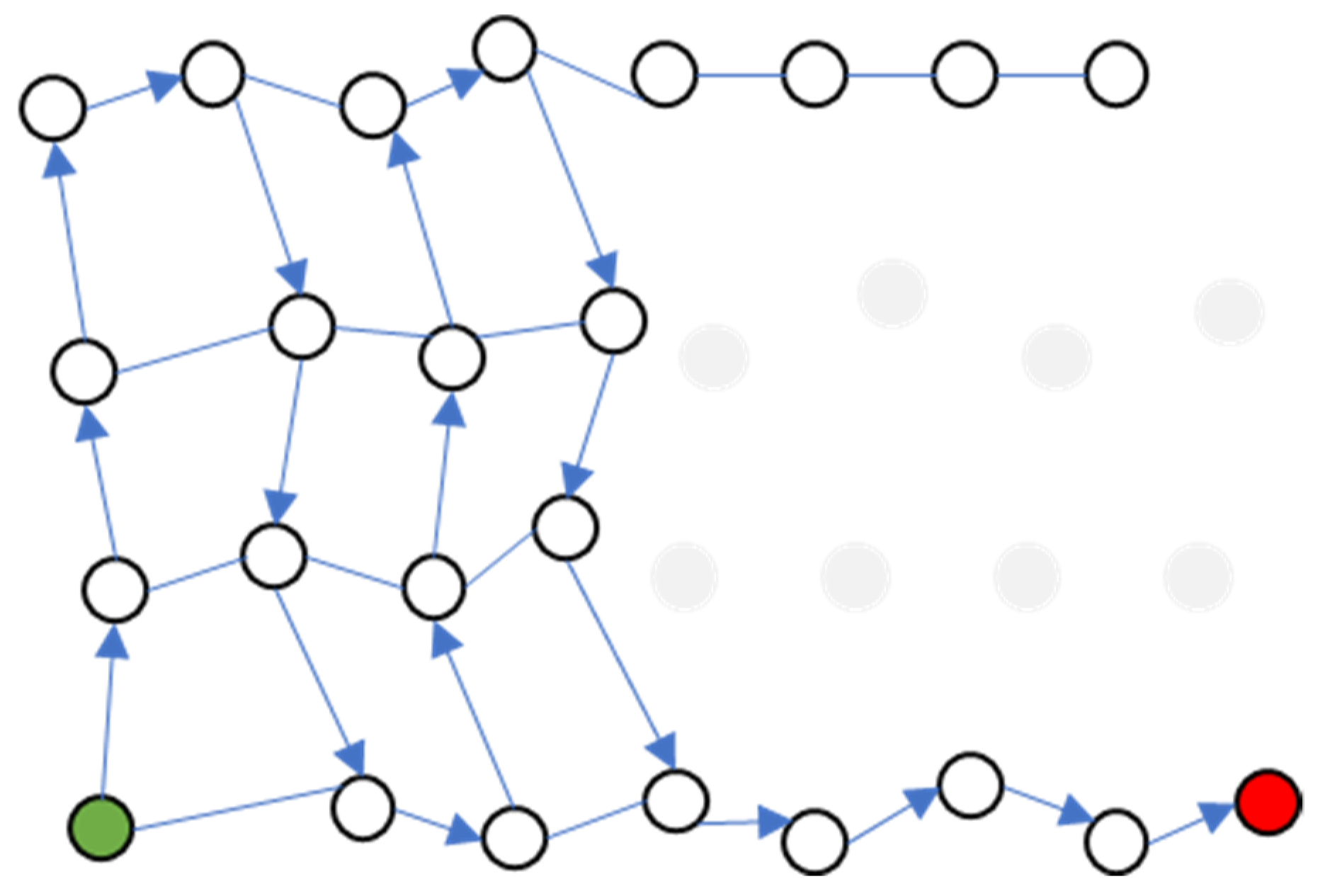
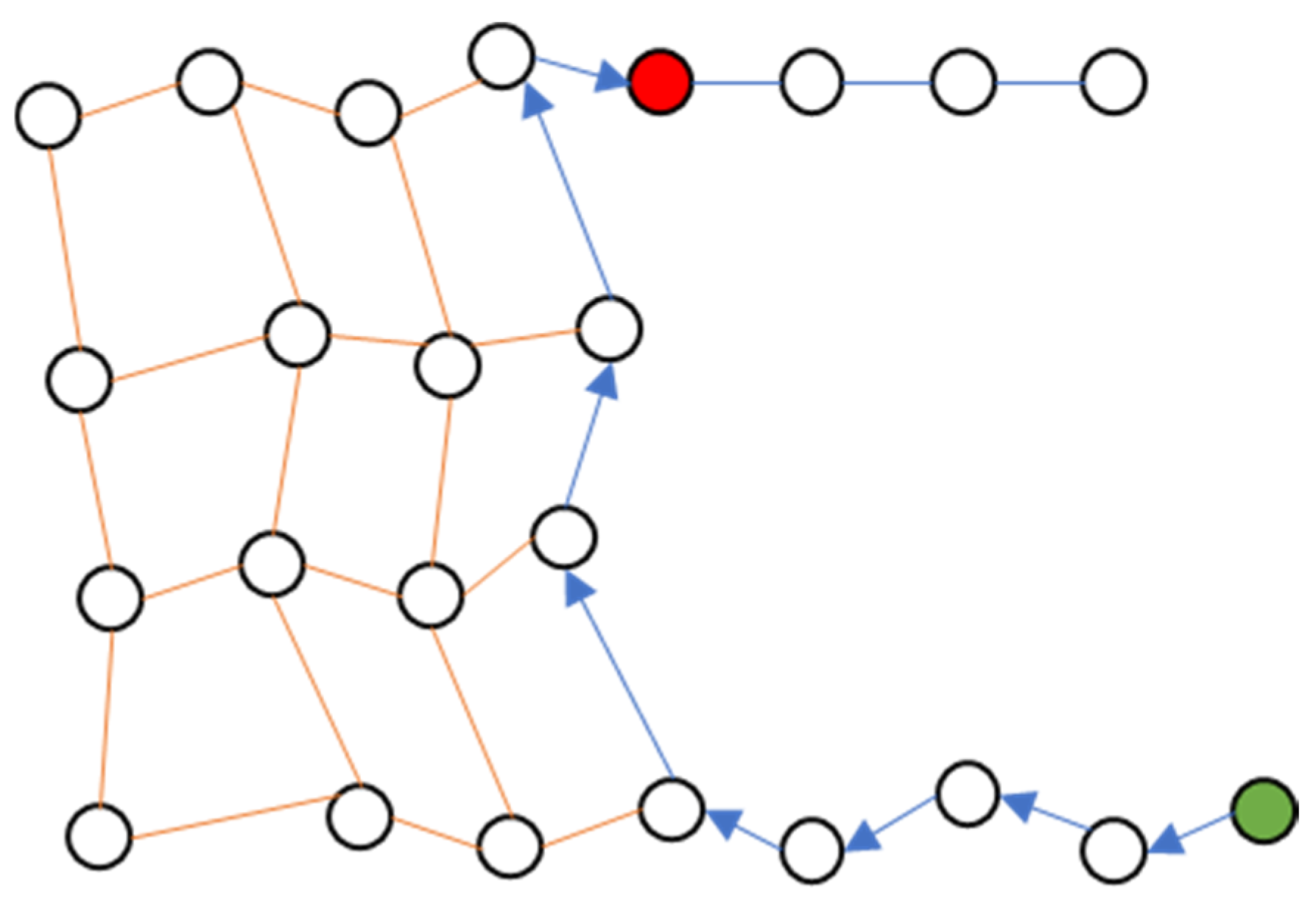
3. Method
- Initialisation
- 2.
- State Propagation
- 3.
- Data Structure Optimisation
- 4.
- State Update
- 5.
- Dead-end Escape
| Algorithm 1: The pseudocode of the hybrid algorithm |
| Function calculate_distance(nodeA, nodeB): return sqrt((x_b − x_a)² + (y_b − y_a)²) // Euclidean distance Function find_nearest_unvisited_node(n_current): n_unvisited = {n_i ∈ Node s | n_i.visited = false} // Set of unvisited nodes return argmin_{n ∈ n_unvisited} calculate_distance(n_current, n) Function update_robot_footprint(n_current): Nodes within the range of robot width from n_current -> visited = true Function move_robot(n_current, direction): n_current = n_current.direction if n_current.direction != null and n_current.direction.visited = false Function find_path(n_start, n_target): for each n ∈ Nodes: n.tested = false n.w = infinity n_start.w = 0 Queue = {n_start} while Queue != empty: n_current = dequeue(Queue) n_current.tested = true for each n_adjacent ∈ {n_current.forward, n_current.backward, n_current.left, n_current.right}: dist = n_current.w + calculate_distance(n_current, n_adjacent) if dist < n_adjacent.w: n_adjacent.w = dist if n_adjacent.tested = false: enqueue(Queue, n_adjacent) Path = empty stack n_current = n_target push(Path, n_current) while n_current ! = n_start: n_min = argmin_{n ∈ {n_current.forward, n_current.backward, n_current.left, n_current.right}} n.w n_current = n_min push(Path, n_current) return Path Main program: while there exist n ∈ Nodes such that n.visited = false: n_current = find_nearest_unvisited_node(n_current) if n_current exists: update_robot_footprint(n_current) move_robot(n_current, direction) // direction ∈ {forward, backward, left, right} find_path(n_current, n_target) |
| Algorithm 2: Application of Dijkstra’s Algorithm for Determining Shortest Path Lengths in a Graph |
| function Dijkstra(G, v0): // Initialize distance array and set of vertices S dist[] = {infinity} // An array to store the shortest distance from v0 to each vertex dist[v0] = 0 S = empty set while S does not contain all vertices in G: // Find the vertex u with minimum dist value and add it to S minDist = infinity u = None for each vertex v in G: if v not in S and dist[v] < minDist: minDist = dist[v] u = v add u to S // Update the shortest distance to other vertices through u for each neighbor w of u: if w not in S: newDist = dist[u] + cost(u, w) dist[w] = min(dist[w], newDist) return dist |
4. Simulation and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and Researches on Non Destructive Testing: A Review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Bogue, R. The Role of Robotics in Non-destructive Testing. Ind. Robot: Int. J. 2010, 37, 421–426. [Google Scholar] [CrossRef]
- Bakopoulou, K.; Michalos, G.; Mparis, K.; Gkournelos, C.; Dimitropoulos, N.; Makris, S. A Human Robot Collaborative Cell for Automating NDT Inspection Processes. Procedia CIRP 2022, 115, 214–219. [Google Scholar] [CrossRef]
- Sensors|Free Full-Text|Ultrasonic Non-Destructive Testing System of Semi-Enclosed Workpiece with Dual-Robot Testing System. Available online: https://www.mdpi.com/1424-8220/19/15/3359 (accessed on 18 October 2023).
- Cooper, I.; Nicholson, I.; Yan, D.; Wright, B.; Liaptsis, D.; Mineo, C. Development of a Fast Inspection System for Aerospace Composite Materials—The IntACom Project: 5th International Symposium on NDT in Aerospace. 13 November 2013. Available online: https://strathprints.strath.ac.uk/61717/ (accessed on 5 May 2023).
- Ma, P.; Xu, C.; Xiao, D. Robotic Ultrasonic Testing Technology for Aero-Engine Blades. Sensors 2023, 23, 3729. [Google Scholar] [CrossRef] [PubMed]
- Aparicio Secanellas, S.; Gauna León, I.; Parrilla, M.; Acebes, M.; Ibáñez, A.; De Matías Jiménez, H.; Martínez-Graullera, Ó.; Álvarez De Pablos, A.; González Hernández, M.; Anaya Velayos, J.J. Methodology for the Generation of High-Quality Ultrasonic Images of Complex Geometry Pieces Using Industrial Robots. Sensors 2023, 23, 2684. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Zhang, Y.; Tang, K. Sweep Scan Path Planning for Efficient Freeform Surface Inspection on Five-Axis CMM. Comput. -Aided Des. 2016, 77, 1–17. [Google Scholar] [CrossRef]
- Poole, A.; Sutcliffe, M.; Pierce, G.; Gachagan, A. Autonomous, Digital-Twin Free Path Planning and Deployment for Robotic NDT: Introducing LPAS: Locate, Plan, Approach, Scan Using Low Cost Vision Sensors. Appl. Sci. 2022, 12, 5288. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Xiang, Z. Optimal Inspection Path Planning of Substation Robot in the Complex Substation Environment. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5064–5068. [Google Scholar]
- Sun, Q.; Wan, W.; Chen, G.; Feng, X. Path Planning Algorithm under Specific Constraints in Weighted Directed Graph. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 635–640. [Google Scholar]
- Wayahdi, M.R.; Ginting, S.H.N.; Syahputra, D. Greedy, A-Star, and Dijkstra's Algorithms in Finding Shortest Path. Int. J. Adv. Data Inf. Syst. 2021, 2, 45–52. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.; Wilcox, P. Post-Processing of the Full Matrix of Ultrasonic Transmit-Receive Array Data for Non-Destructive Evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
- Liaptsis, D.; Yan, D.; Cooper, I.; Papadimitriou, V.; Roditis, G. Development of an Automated Scanner and Phased Array Ultrasonic Testing Technique for the Inspection of Nozzle Welds in the Nuclear Industry. In Proceedings of the 9th International Conference on NDE in Relation to Structural Integrity for Nuclear and Pressurized Components, Seattle, WA, USA, 22–24 May 2012; Available online: https://www.ndt.net/?id=14746 (accessed on 12 March 2023).
- Khan, A.; Mineo, C.; Dobie, G.; MacLeod, C.; Pierce, G. Vision Guided Robotic Inspection for Parts in Manufacturing and Remanufacturing Industry. J. Remanufacturing 2020, 11, 49–70. [Google Scholar] [CrossRef]
- Corsini, M.; Cignoni, P.; Scopigno, R. Efficient and Flexible Sampling with Blue Noise Properties of Triangular Meshes. IEEE Trans. Vis. Comput. Graph. 2012, 18, 914–924. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Luo, C.; Krishnan, M.; Paulik, M.; Tang, Y. An Enhanced Dynamic Delaunay Triangulation-Based Path Planning Algorithm for Autonomous Mobile Robot Navigation; Casasent, D.P., Hall, E.L., Röning, J., Eds.; Electronic imaging: San Jose, CA, USA, 2010; p. 75390P. [Google Scholar]
- Foulds, L.R. Graph Theory Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-1-4612-0933-1. [Google Scholar]
- Cheng, K.P.; Mohan, R.E.; Nhan, N.H.K.; Le, A.V. Graph Theory-Based Approach to Accomplish Complete Coverage Path Planning Tasks for Reconfigurable Robots. IEEE Access 2019, 7, 94642–94657. [Google Scholar] [CrossRef]
- Bento, L.M.S.; Boccardo, D.R.; Machado, R.C.S.; de Sá, V.G.P.; Szwarcfiter, J.L. Dijkstra Graphs. CoRR 2016, abs/1602.08653. Available online: http://arxiv.org/abs/1602.08653 (accessed on 4 April 2023).
- Pinkham, R.; Zeng, S.; Zhang, Z. QuickNN: Memory and Performance Optimization of k-d Tree Based Nearest Neighbor Search for 3D Point Clouds. In Proceedings of the 2020 IEEE International Symposium on High Performance Computer Architecture (HPCA), San Diego, CA, USA, 22–26 February 2020; pp. 180–192. [Google Scholar]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Hu, L.; Nooshabadi, S. Massive Parallelization of Approximate Nearest Neighbor Search on KD-Tree for High-Dimensional Image Descriptor Matching. J. Vis. Commun. Image Represent. 2017, 44, 106–115. [Google Scholar] [CrossRef]
- Poole, A.; Sutcliffe, M.; Pierce, G.; Gachagan, A. A Novel Complete-Surface-Finding Algorithm for Online Surface Scanning with Limited View Sensors. Sensors 2021, 21, 7692. [Google Scholar] [CrossRef] [PubMed]




| X | Y | KD-Tree Time (ms) | Non-KD-Tree Time (ms) | Performance Improvement |
|---|---|---|---|---|
| 500 | 800 | 336 | 3376 | 90.04% |
| 800 | 1000 | 1380 | 10,907 | 87.34% |
| 1200 | 1400 | 3000 | 45,251 | 93.37% |
| 1600 | 1800 | 5857 | 134,769 | 95.64% |
| 2400 | 2600 | 19,002 | 790,297 | 97.60% |
| 3200 | 3400 | 50,162 | 980,996 | 94.89% |
| 4000 | 4200 | 95,388 | 2,570,809 | 96.29% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Sutcliffe, M.; Nicholson, P.I.; Yang, Q. Efficient Autonomous Path Planning for Ultrasonic Non-Destructive Testing: A Graph Theory and K-Dimensional Tree Optimisation Approach. Machines 2023, 11, 1059. https://doi.org/10.3390/machines11121059
Zhang M, Sutcliffe M, Nicholson PI, Yang Q. Efficient Autonomous Path Planning for Ultrasonic Non-Destructive Testing: A Graph Theory and K-Dimensional Tree Optimisation Approach. Machines. 2023; 11(12):1059. https://doi.org/10.3390/machines11121059
Chicago/Turabian StyleZhang, Mengyuan, Mark Sutcliffe, P. Ian Nicholson, and Qingping Yang. 2023. "Efficient Autonomous Path Planning for Ultrasonic Non-Destructive Testing: A Graph Theory and K-Dimensional Tree Optimisation Approach" Machines 11, no. 12: 1059. https://doi.org/10.3390/machines11121059
APA StyleZhang, M., Sutcliffe, M., Nicholson, P. I., & Yang, Q. (2023). Efficient Autonomous Path Planning for Ultrasonic Non-Destructive Testing: A Graph Theory and K-Dimensional Tree Optimisation Approach. Machines, 11(12), 1059. https://doi.org/10.3390/machines11121059







