An Equilibrium Decision-Making Approach for Cutting Parameters of a Novel Five-Axis Hybrid Kinematic Machining Unit
Abstract
1. Introduction
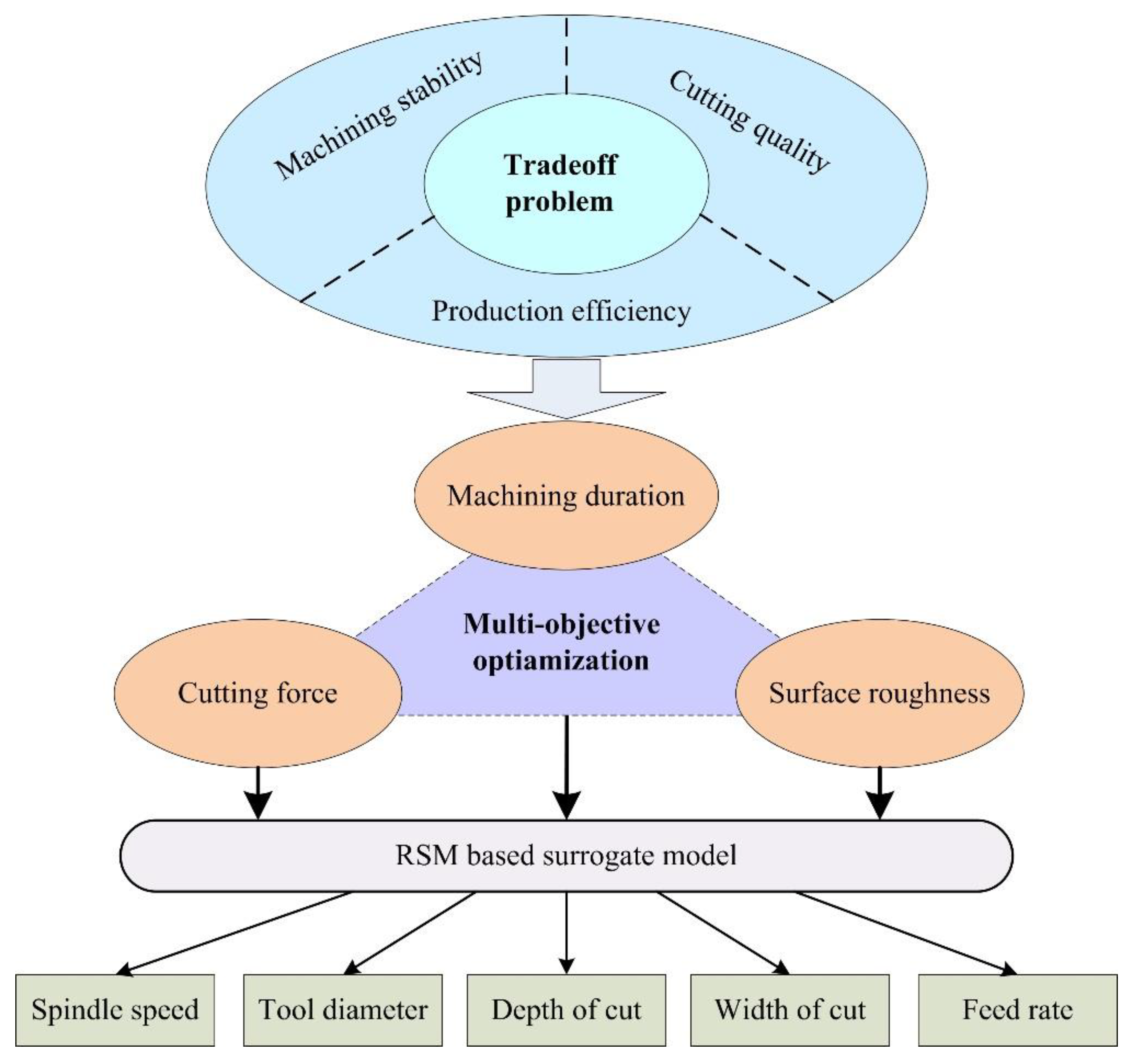
2. Equilibrium Decision-Making Approach
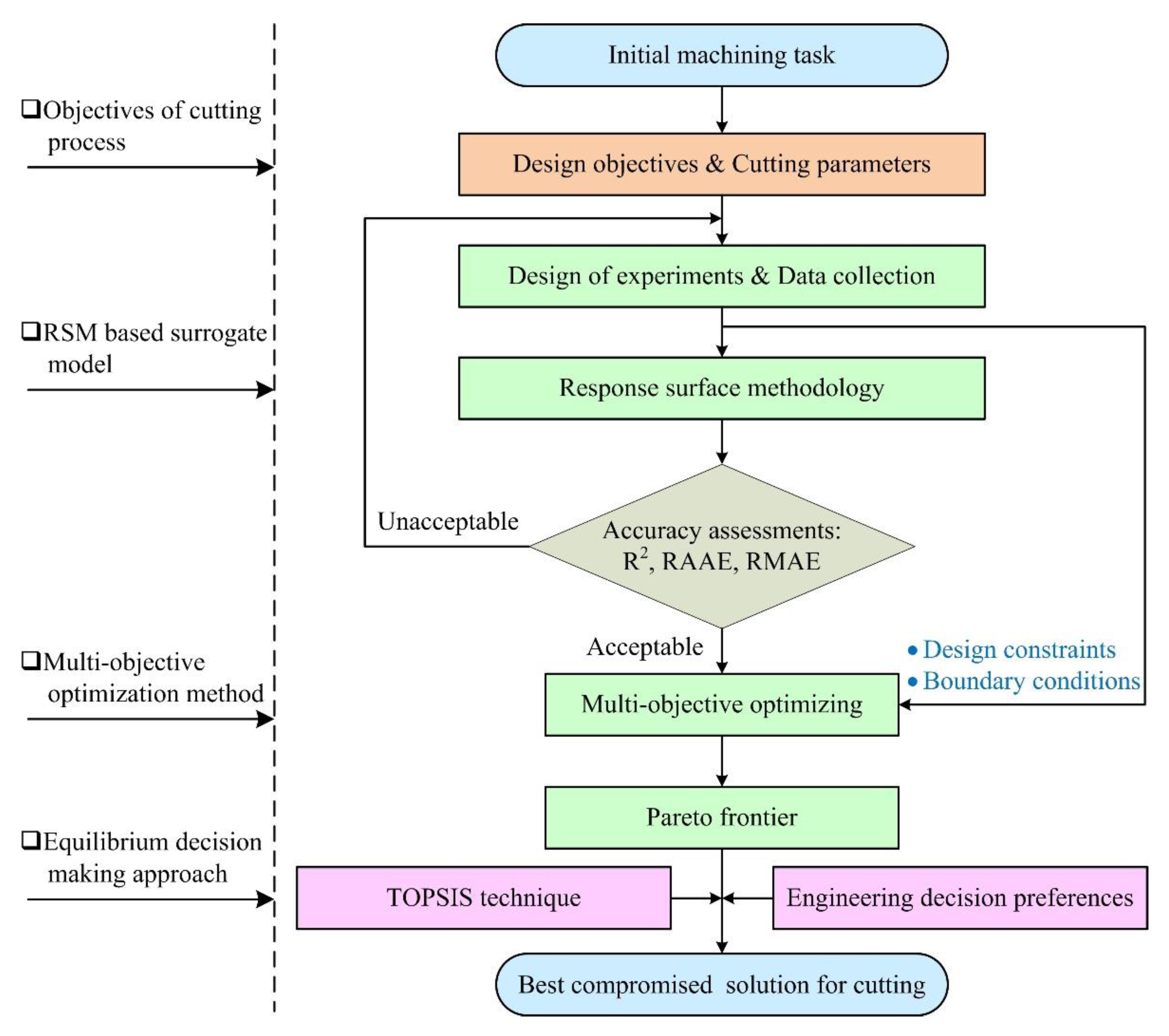
- (1)
- Firstly, the design objectives and cutting parameters of an HKMU are determined on the basis of the design criteria of the specified initial machining task.
- (2)
- Secondly, DoE is carried out to collect cutting responses. Based on this, the RSM technique [32] is adopted to establish a surrogate model in an accurate yet efficient manner. The surrogate model will be assessed in terms of regression accuracy, indicating whether it is acceptable for the following optimization.
- (3)
- Then, the acceptable surrogate model, as well as design constraints and boundary conditions, are employed in the multi-objective optimization design. By simultaneously optimizing the multiple objective functions, a cluster of solutions called the Pareto frontier is obtained for cutting parameters.
- (4)
- Finally, by combining the TOPSIS technique [41] and engineering decision preferences, a set of decision-making procedures is proposed to designate the best-compromised solution from the Pareto solutions.
2.1. Objectives of Cutting Process
- (1)
- Machining duration Te
- (2)
- Cutting force Fc
- (3)
- Surface roughness Ra
2.2. RSM-Based Surrogate Model
- (1)
- According to the dimensions of objectives and variables, select an experimental strategy that has as much information yet implementation convenience.
- (2)
- With the help of commercial software such as Design Expert or Isight, collect and manage the multiple responses to the design objectives of the cutting process.
- (3)
- On the basis of the statistical features obtained from experimental data, estimate the regression coefficients to fit the response surface of data.
2.3. Multi-Objective Optimization Model
2.4. Decision-Making Procedures
- (1)
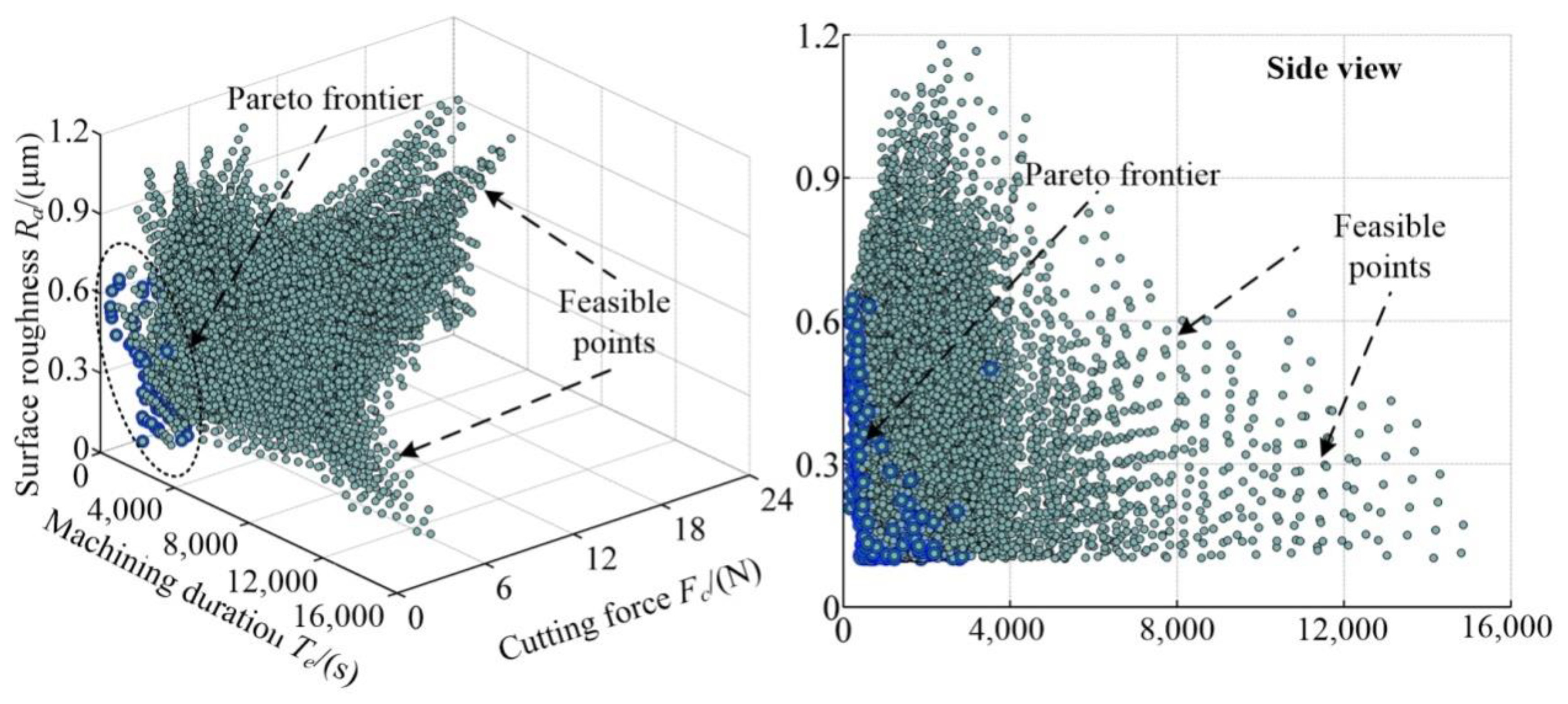
- Determine the Pareto frontier of feasible solutions, in which none of the objectives of a solution can be further improved without worsening other objectives. Taking a minimization problem as an example, the Pareto frontier can be described as:where n denotes the number of feasible solutions; m denotes the dimension of design objectives; yij (*) represents the j-th dimensional design objective of the i-th solution; Pnon and Pdom represent the design points that belong and do not belong to the Pareto frontier, respectively. Thus, it exists that the responses of Pnon are dominant over that of Pdom.
- (2)
- Perform the dimensionless processing on the j-th dimensional objective yij (i = 1,2,…Pn; j =1,2,…m) of Pareto points. Herein, the weighting factors are taken to weigh the design objectives. Thus, the weighted dimensionless response zij can be expressed as:where Pn denotes the number of Pareto points; wj is the weighting factor of the j-th dimensional design objective, which can be determined by the decision maker’s preferences.
- (3)
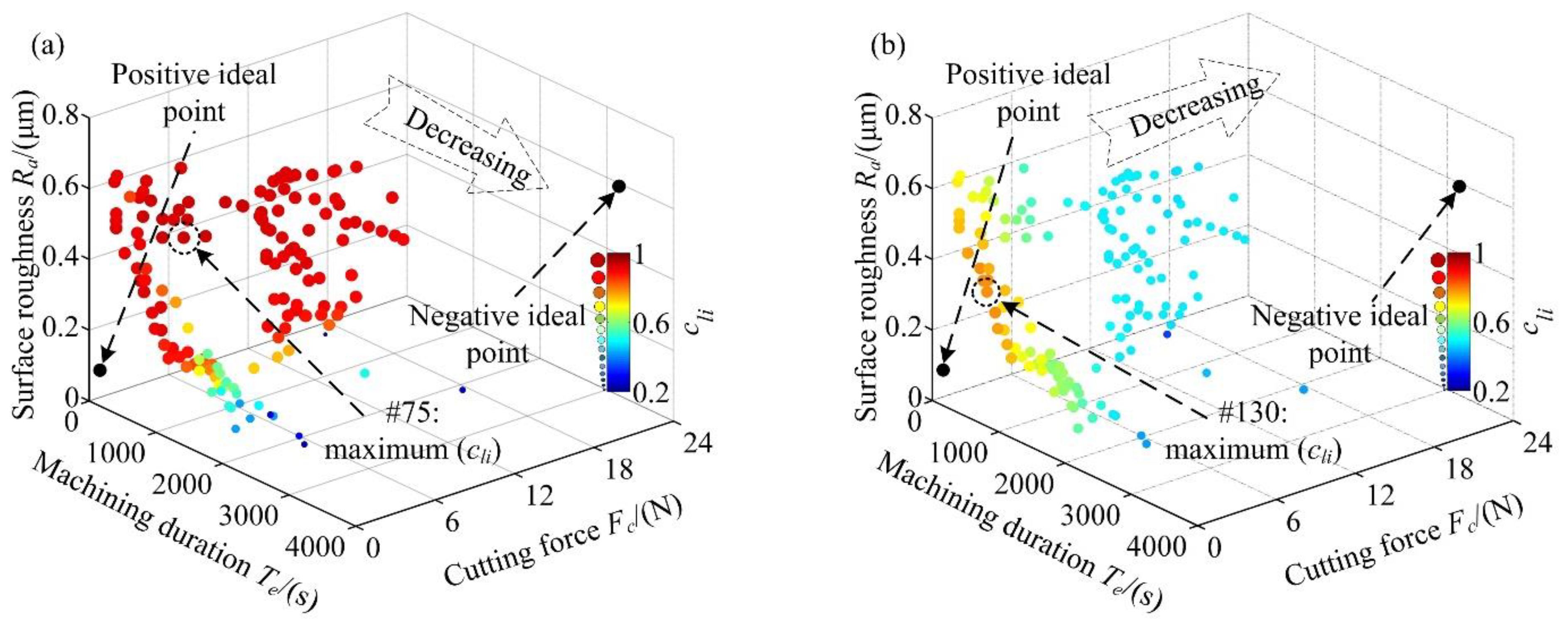
- Define the ideal points of the Pareto frontier. For clarity, the coordinates of the ideal points are discussed in two situations as follows.
- (1)
- If the design objective is desired to be minimum, it leads to:
- (2)
- If the design objective is desired to be maximum, it leads to:where and represent the j-th (j =1,2,…m) dimensional coordinate of the ‘positive ideal point’ and ‘negative ideal point’, respectively.
- (4)
- Calculate the Euclidean distances between the Pareto points and the ideal points. Mathematically, the distances of a Pareto point to the ideal points can be estimated by:And:where and (i = 1,2,…Pn) denote the Euclidean distances from the i-th Pareto point to the ‘positive ideal point’ and ‘negative ideal point’, respectively.
- (5)
- Adopt a comprehensive index to assess the relative distances of Pareto points to ideal points. According to the TOPSIS technique [43], the relative distance index is formulated as the following:where denotes the relative distance index of the i-th (i = 1,2,…Pn) Pareto point to the ideal points, and it is in the range of (0, 1).
3. Illustrative Example
3.1. Prototype Description
3.2. Design of Experiments
3.3. Multi-Objectives Optimization
3.4. Correlation Analysis
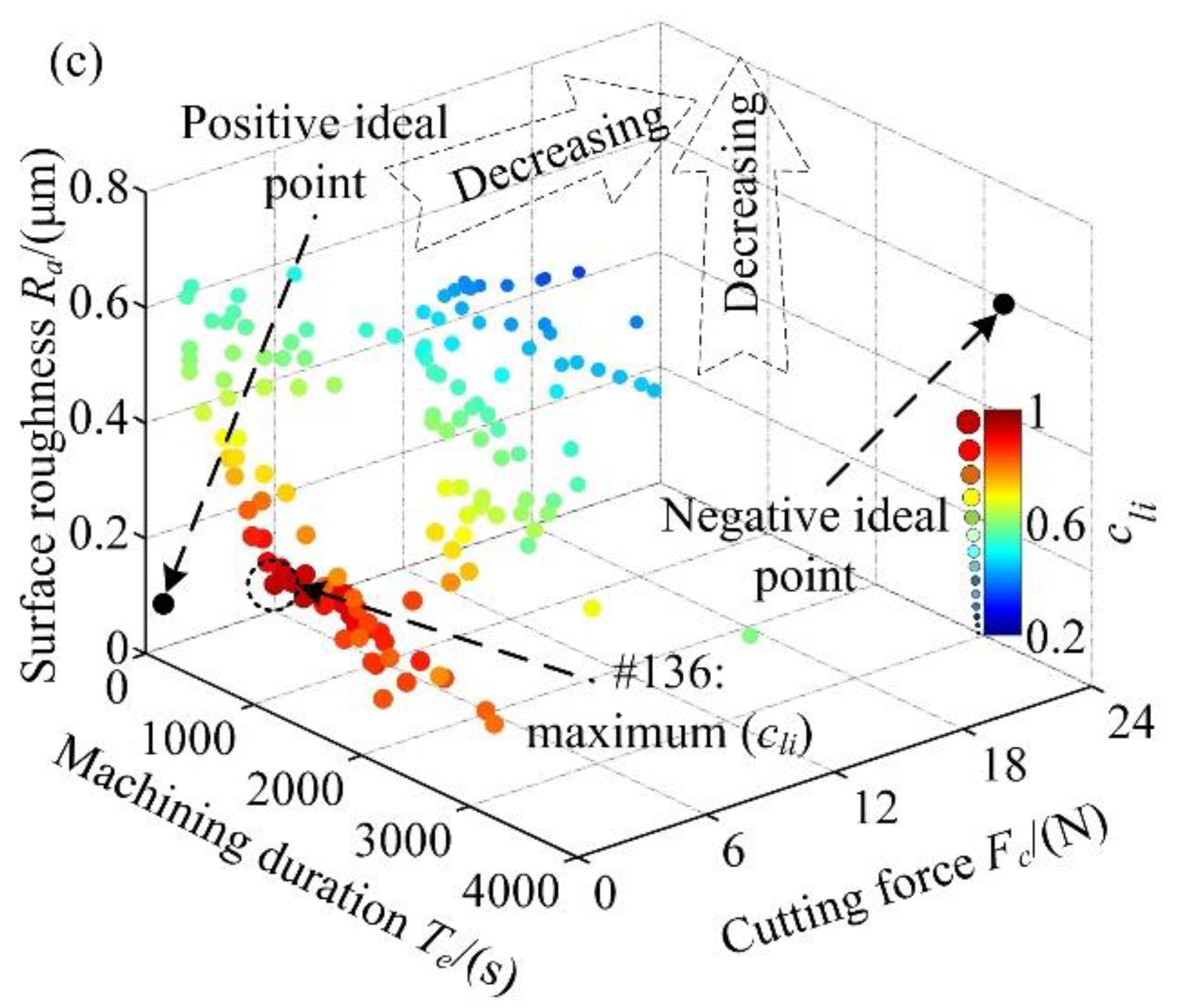
3.5. Equilibrium Decisions
4. Conclusions and Outlook
- (1)
- An equilibrium decision-making approach for cutting parameters of an HKMU is proposed with both multi-objective technological considerations and end users’ engineering decision preferences.
- (2)
- A total of 142 sets of compromised Pareto solutions and corresponding cutting parameters are determined for the typical face milling of the exemplary five-axis HKMU.
- (3)
- The correlation analysis reveals that machining duration is in a contradictory relationship with surface roughness while cutting force and surface roughness are in a collaborative relationship.
- (4)
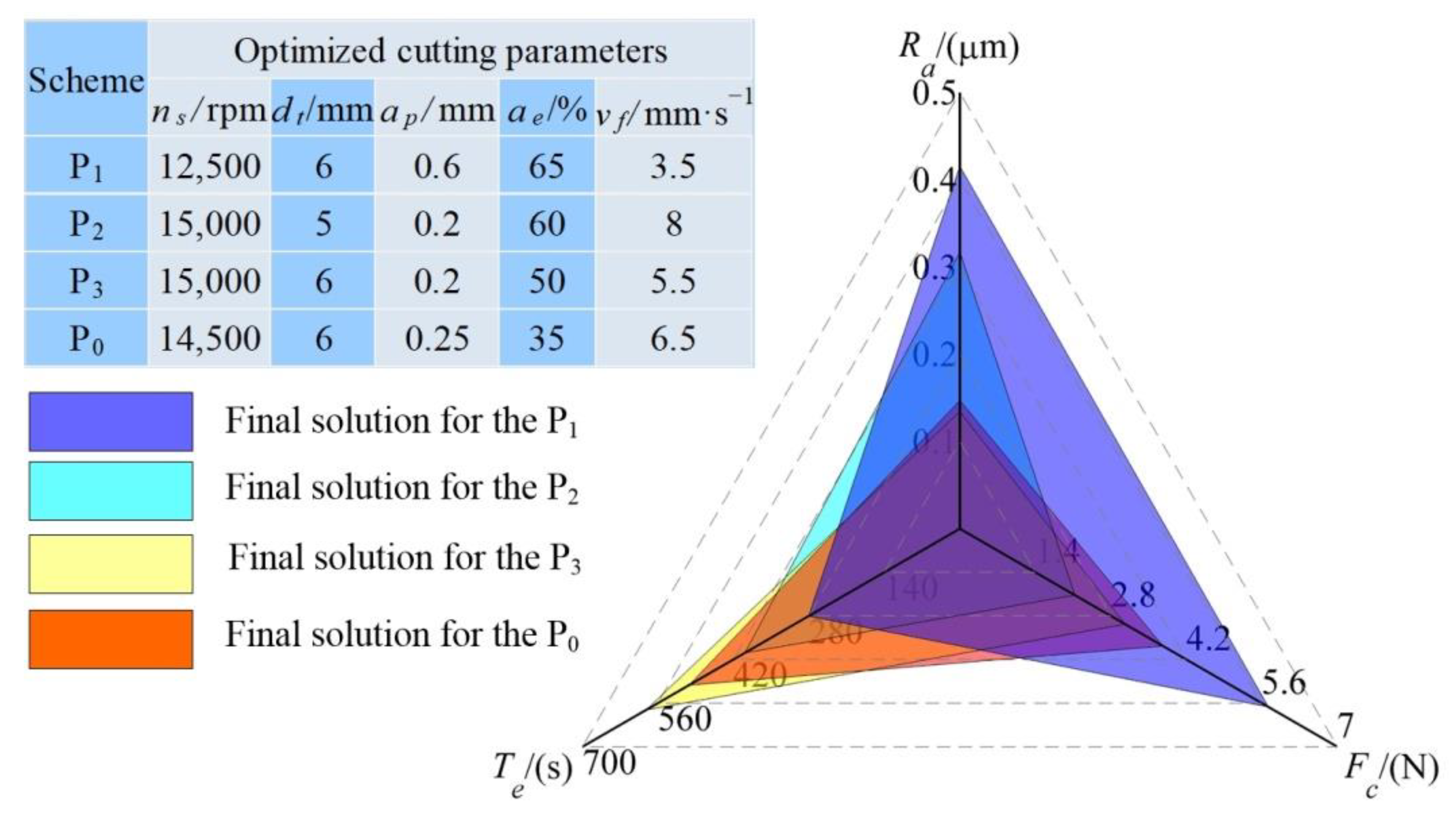
- Three customized machining schemes with different engineering decision preferences are analyzed to respectively designate the best-compromised solution on cutting parameters.
- (5)
- Compared to the scheme without engineering decision preferences, the three schemes reduce the machining duration, the cutting force, and the surface roughness by 44%, 43%, and 9%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uriarte, L.; Zatarain, M.; Axinte, D.; Yagüe-Fabra, J.; Ihlenfeldt, S.; Eguia, J.; Olarra, A. Machine tools for large parts. CIRP Ann. 2013, 62, 731–750. [Google Scholar] [CrossRef]
- Zhao, H.; Yu, X.; Li, X.; Ding, H. Weighted sum of vector norms based contouring control method for five-axis CNC machine tools. Precis. Eng. 2019, 60, 93–103. [Google Scholar] [CrossRef]
- Laryushkin, P.; Antonov, A.; Fomin, A.; Essomba, T. Velocity and Singularity Analysis of a 5-DOF (3T2R) Parallel-Serial (Hybrid) Manipulator. Machines 2022, 10, 276. [Google Scholar] [CrossRef]
- Zhao, Y.; Mei, J.; Jin, Y.; Niu, W. A new hierarchical approach for the optimal design of a 5-dof hybrid serial-parallel kinematic machine. Mech. Mach. Theory 2020, 156, 104160. [Google Scholar] [CrossRef]
- Lai, Y.-L.; Liao, C.-C.; Chao, Z.-G. Inverse kinematics for a novel hybrid parallel–serial five-axis machine tool. Robot. Comput. Manuf. 2018, 50, 63–79. [Google Scholar] [CrossRef]
- Qin, X.; Shi, M.; Hou, Z.; Li, S.; Li, H.; Liu, H. Analysis of 3-DOF Cutting Stability of Titanium Alloy Helical Milling Based on PKM and Machining Quality Optimization. Machines 2022, 10, 404. [Google Scholar] [CrossRef]
- Xu, P.; Cheung, C.; Wang, C.; Zhao, C. Novel hybrid robot and its processes for precision polishing of freeform surfaces. Precis. Eng. 2020, 64, 53–62. [Google Scholar] [CrossRef]
- Li, Q.; Wu, W.; Xiang, J.; Li, H.; Wu, C. A hybrid robot for friction stir welding. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 229, 2639–2650. [Google Scholar] [CrossRef]
- Oba, Y.; Kakinuma, Y. Simultaneous tool posture and polishing force control of unknown curved surface using serial-parallel mechanism polishing machine. Precis. Eng. 2017, 49, 24–32. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, Y.; Yao, J.; Zhao, Y. Design of a novel 5-DOF hybrid serial-parallel manipulator and theoretical analysis of its parallel part. Robot. Comput. Manuf. 2018, 53, 228–239. [Google Scholar] [CrossRef]
- Olazagoitia, J.L.; Wyatt, S. New PKM Tricept T9000 and Its Application to Flexible Manufacturing at Aerospace Industry; SAE Technical Paper 07ATC-94; SAE: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Hennes, N. Ecospeed—An innovative machinery concept for high performance 5 axis machining of large structural components in aircraft engineering. In Proceedings of the 3rd Chemnitz Parallel Kinematics Seminar, Chemnitz, Germany, 23–25 April 2002; pp. 763–774. [Google Scholar]
- Bi, Z.M. Kinetostatic modeling of Exechon parallel kinematic machine for stiffness analysis. Int. J. Adv. Manuf. Technol. 2014, 71, 325–335. [Google Scholar] [CrossRef]
- Jiang, S.; Chi, C.; Fang, H.; Tang, T.; Zhang, J. A minimal-error-model based two-step kinematic calibration methodology for redundantly actuated parallel manipulators: An application to a 3-DOF spindle head. Mech. Mach. Theory 2021, 167, 104532. [Google Scholar] [CrossRef]
- Tang, T.; Fang, H.; Zhang, J. Hierarchical design, laboratory prototype fabrication and machining tests of a novel 5-axis hybrid serial-parallel kinematic machine tool. Robot. Comput. Manuf. 2020, 64, 101944. [Google Scholar] [CrossRef]
- Fang, H.; Tang, T.; Zhang, J. Kinematic analysis and comparison of a 2R1T redundantly actuated parallel manipulator and its non-redundantly actuated forms. Mech. Mach. Theory 2019, 142, 103587. [Google Scholar] [CrossRef]
- Xu, X. Machine Tool 4.0 for the new era of manufacturing. Int. J. Adv. Manuf. Technol. 2017, 92, 1893–1900. [Google Scholar] [CrossRef]
- Calleja, A.; Bo, P.; González, H.; Bartoň, M.; de Lacalle, L.N.L. Highly accurate 5-axis flank CNC machining with conical tools. Int. J. Adv. Manuf. Technol. 2018, 97, 1605–1615. [Google Scholar] [CrossRef]
- Srivastava, V.S.; Gupta, T.K.; Srivastava, A.K.; Chauhan, S.; Chauhan, P.K. Effects of cutting parameters on aluminium alloys-A review. Mater. Today Proc. 2021, 47, 3823–3827. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Y.; Tang, J.; Tang, K.; Li, Z. Digital tooth contact analysis of face gear drives with an accurate measurement model of face gear tooth surface inspected by CMMs. Mech. Mach. Theory 2022, 167, 104498. [Google Scholar] [CrossRef]
- Zhou, Y.-S.; Tang, Z.-W.; Shi, X.-L.; Tang, J.-Y.; Li, Z.-M. Efficient and accurate worm grinding of spur face gears according to an advanced geometrical analysis and a closed-loop manufacturing process. J. Central South Univ. 2022, 29, 1–13. [Google Scholar] [CrossRef]
- Ghosh, G.; Mandal, P.; Mondal, S.C. Modeling and optimization of surface roughness in keyway milling using ANN, genetic algorithm, and particle swarm optimization. Int. J. Adv. Manuf. Technol. 2019, 100, 1223–1242. [Google Scholar] [CrossRef]
- Meral, G.; Sarıkaya, M.; Mia, M.; Dilipak, H.; Şeker, U.; Gupta, M.K. Multi-objective optimization of surface roughness, thrust force, and torque produced by novel drill geometries using Taguchi-based GRA. Int. J. Adv. Manuf. Technol. 2018, 101, 1595–1610. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, B.; Bao, H.; Huang, H. Optimization of Cutting Parameters for Minimizing Environmental Impact: Considering Energy Efficiency, Noise Emission and Economic Dimension. Int. J. Precis. Eng. Manuf. 2018, 19, 613–624. [Google Scholar] [CrossRef]
- Sofuoğlu, M.A.; Arapoğlu, R.A.; Orak, S. Multi objective optimization of turning operation using hybrid decision making analysis. Anadolu Univ. J. Sci. Technol. Appl. Sci. Eng. 2017, 18, 595–610. [Google Scholar] [CrossRef][Green Version]
- Sofuoglu, A. A Novel Hybrid Multi Criteria Decision Making Model: Application to Turning Operations. Int. J. Intell. Syst. Appl. Eng. 2017, 5, 124–131. [Google Scholar] [CrossRef]
- Utsumi, K.; Shichiri, S.; Sasahara, H. Determining the effect of tool posture on cutting force in a turn milling process using an analytical prediction model. Int. J. Mach. Tools Manuf. 2020, 150, 103511. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, B.; Jiang, Y.; Zhao, W. Cutting force modeling for non-uniform helix tools based on compensated chip thickness in five-axis flank milling process. Precis. Eng. 2018, 51, 659–681. [Google Scholar] [CrossRef]
- Zerti, A.; Yallese, M.A.; Meddour, I.; Belhadi, S.; Haddad, A.; Mabrouki, T. Modeling and multi-objective optimization for minimizing surface roughness, cutting force, and power, and maximizing productivity for tempered stainless steel AISI 420 in turning operations. Int. J. Adv. Manuf. Technol. 2018, 102, 135–157. [Google Scholar] [CrossRef]
- Balaji, M.; Rao, K.V.; Rao, N.M.; Murthy, B. Optimization of drilling parameters for drilling of TI-6Al-4V based on surface roughness, flank wear and drill vibration. Measurement 2018, 114, 332–339. [Google Scholar] [CrossRef]
- He, C.L.; Zong, W.J.; Zhang, J.J. Influencing factors and theoretical modeling methods of surface roughness in turning process: State-of-the-art. Int. J. Mach. Tools Manuf. 2018, 129, 15–26. [Google Scholar] [CrossRef]
- Zerti, A.; Yallese, M.A.; Zerti, O.; Nouioua, M.; Khettabi, R. Prediction of machining performance using RSM and ANN models in hard turning of martensitic stainless steel AISI 420. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4439–4462. [Google Scholar] [CrossRef]
- Li, C.; Xiao, Q.; Tang, Y.; Li, L. A method integrating Taguchi, RSM and MOPSO to CNC machining parameters optimization for energy saving. J. Clean. Prod. 2016, 135, 263–275. [Google Scholar] [CrossRef]
- Li, B.; Tian, X.; Zhang, M. Modeling and multi-objective optimization of cutting parameters in the high-speed milling using RSM and improved TLBO algorithm. Int. J. Adv. Manuf. Technol. 2020, 111, 2323–2335. [Google Scholar] [CrossRef]
- Yan, J.; Li, L. Multi-objective optimization of milling parameters—The trade-offs between energy, production rate and cutting quality. J. Clean. Prod. 2013, 52, 462–471. [Google Scholar] [CrossRef]
- Li, L.; Deng, X.; Zhao, J.; Zhao, F.; Sutherland, J. Multi-objective optimization of tool path considering efficiency, energy-saving and carbon-emission for free-form surface milling. J. Clean. Prod. 2018, 172, 3311–3322. [Google Scholar] [CrossRef]
- De Oliveira, L.G.; de Oliveira, C.H.; de Brito, T.G.; de Paiva, E.J.; de Paiva, A.P.; Ferreira, J.R. Nonlinear optimization strategy based on multivariate prediction capability ratios: Analytical schemes and model validation for duplex stainless steel end milling. Precis. Eng. 2020, 66, 229–254. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Jiang, P.; Gu, P. Experimental investigation and multi-objective optimization approach for low-carbon milling operation of aluminum. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2753–2772. [Google Scholar] [CrossRef]
- De Oliveira, L.G.; de Paiva, A.P.; Campos, P.H.D.S.; de Paiva, E.J.; Balestrassi, P.P. Prediction capability of Pareto optimal solutions: A multi-criteria optimization strategy based on model capability ratios. Precis. Eng. 2019, 59, 185–210. [Google Scholar] [CrossRef]
- Kumar, R.; Bilga, P.S.; Singh, S. Multi objective optimization using different methods of assigning weights to energy consumption responses, surface roughness and material removal rate during rough turning operation. J. Clean. Prod. 2017, 164, 45–57. [Google Scholar] [CrossRef]
- Jiang, Z.; Gao, D.; Lu, Y.; Liu, X. Optimization of Cutting Parameters for Trade-off Among Carbon Emissions, Surface Roughness, and Processing Time. Chin. J. Mech. Eng. 2019, 32, 1–18. [Google Scholar] [CrossRef]
- Kubler, S.; Robert, J.; Derigent, W.; Voisin, A.; Le Traon, Y. A state-of the-art survey & testbed of fuzzy AHP (FAHP) applications. Expert Syst. Appl. 2016, 65, 398–422. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Teti, R.; Mourtzis, D.; D’Addona, D.; Caggiano, A. Process monitoring of machining. CIRP Ann. 2022, 71, 529–552. [Google Scholar] [CrossRef]




| Factors | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| A: Spindle speed ns/rpm | 9000 | 11,000 | 13,000 | 15,000 |
| B: Tool radius dt/mm | 3 | 4 | 5 | 6 |
| C: Depth of cut ap/mm | 0.15 | 0.30 | 0.45 | 0.60 |
| D: Width of cut ae/% | 20 | 40 | 60 | 80 |
| E: Feed rate vf/mm·s−1 | 2 | 4 | 6 | 8 |
| Exp. No. | Spindle Speed ns/rpm | Tool Radius dt/mm | Depth of Cut ap/mm | Width of Cut ae/% | Feed Rate vf/mm·s−1 |
|---|---|---|---|---|---|
| 1 | 9000 | 3 | 0.15 | 20 (0.6 mm) | 2 |
| 2 | 9000 | 4 | 0.30 | 40 (1.6 mm) | 4 |
| 3 | 9000 | 5 | 0.45 | 60 (3.0 mm) | 6 |
| 4 | 9000 | 6 | 0.60 | 80 (4.8 mm) | 8 |
| 5 | 11,000 | 3 | 0.30 | 60 (1.8 mm) | 8 |
| 6 | 11,000 | 4 | 0.15 | 80 (3.2 mm) | 6 |
| 7 | 11,000 | 5 | 0.60 | 20 (1.0 mm) | 4 |
| 8 | 11,000 | 6 | 0.45 | 40 (2.4 mm) | 2 |
| 9 | 13,000 | 3 | 0.45 | 80 (2.4 mm) | 4 |
| 10 | 13,000 | 4 | 0.60 | 60 (2.4 mm) | 2 |
| 11 | 13,000 | 5 | 0.15 | 40 (2.0 mm) | 8 |
| 12 | 13,000 | 6 | 0.30 | 20 (1.2 mm) | 6 |
| 13 | 15,000 | 3 | 0.60 | 40 (1.2 mm) | 6 |
| 14 | 15,000 | 4 | 0.45 | 20 (0.8 mm) | 8 |
| 15 | 15,000 | 5 | 0.30 | 80 (4.0 mm) | 2 |
| 16 | 15,000 | 6 | 0.15 | 60 (3.6 mm) | 4 |
| Exp. No. | Machining Duration Te/s | Cutting Force Fc/N | Surface Roughness Ra/μm |
|---|---|---|---|
| 1 | 14,856 | 3.278 | 0.172 |
| 2 | 1440 | 13.475 | 0.213 |
| 3 | 380 | 17.061 | 0.532 |
| 4 | 159 | 23.315 | 0.180 |
| 5 | 738 | 11.661 | 0.219 |
| 6 | 1140 | 17.451 | 0.168 |
| 7 | 1020 | 8.204 | 0.149 |
| 8 | 1264 | 6.368 | 0.104 |
| 9 | 804 | 19.601 | 0.162 |
| 10 | 1071 | 17.285 | 0.231 |
| 11 | 1320 | 4.203 | 0.430 |
| 12 | 1128 | 4.312 | 0.126 |
| 13 | 684 | 22.585 | 0.160 |
| 14 | 888 | 12.410 | 0.298 |
| 15 | 1404 | 8.880 | 0.102 |
| 16 | 1428 | 3.958 | 0.118 |
| Value | Minimum/ Upper Bound | Maximum/ Lower Bound | Value | Minimum/ Upper Bound | Maximum/ Lower Bound |
|---|---|---|---|---|---|
| ns/rpm | 9000 | 15,000 | dt/mm | 3 | 6 |
| ap/mm | 0.15 | 0.60 | ae/% | 20 | 80 |
| vf/mm·s−1 | 2 | 8 | Te/s | 159 | 14,856 |
| Fc/N | 0.12 | 24 | Ra/μm | 0.101 | 3.2 |
| Assessment metrics | R2 | RAAE | RMAE | |
|---|---|---|---|---|
| Machining duration Te/s | Linear | 0.6572 | 0.505119284 | 1.7662867 |
| Quadratic | 0.9636 | 0.086900217 | 0.5213963 | |
| Cubic | 1 | 0.000170538 | 0.000244 | |
| Quartic | 1 | 0.0000503 | 0.000108 | |
| Cutting force Fc/N | Linear | 0.8571 | 0.310067858 | 0.9704946 |
| Quadratic | 0.9939 | 0.035263284 | 0.2109161 | |
| Cubic | 1 | 0.00011867 | 0.0013264 | |
| Quartic | 1 | 0.000117809 | 0.0013162 | |
| Surface roughness Ra/μm | Linear | 0.2727 | 1.213001375 | 4.4719211 |
| Quadratic | 0.7879 | 0.23523771 | 1.3923391 | |
| Cubic | 1 | 0.00308598 | 0.0188888 | |
| Quartic | 1 | 0.003055539 | 0.0191743 | |
| Point No. | Pareto Solutions | Cutting Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| Te/s | Fc/N | Ra/μm | ns/rpm | dt/mm | ap/mm | ae/% | vf/mm·s−1 | |
| #1 | 1614 | 0.812 | 0.266 | 9000 | 6 | 0.55 | 20 | 3.00 |
| #2 | 197 | 17.460 | 0.450 | 9000 | 6 | 0.55 | 65 | 6.50 |
| … | … | … | … | … | … | … | … | … |
| #50 | 326 | 12.637 | 0.410 | 11,500 | 5 | 0.55 | 6 | 5.00 |
| #51 | 974 | 10.169 | 0.103 | 11,500 | 5 | 0.60 | 35 | 3.00 |
| … | … | … | … | … | … | … | … | … |
| #100 | 269 | 2.707 | 0.511 | 13,750 | 6 | 0.60 | 75 | 3.50 |
| #101 | 407 | 18.099 | 0.106 | 14,000 | 3 | 0.50 | 45 | 6.50 |
| … | … | … | … | … | … | … | … | … |
| #141 | 363 | 2.025 | 0.347 | 15,000 | 6 | 0.25 | 40 | 7.50 |
| #142 | 753 | 1.715 | 0.358 | 15,000 | 6 | 0.25 | 45 | 7.00 |
| Correlation Coefficients | ns | dt | ap | ae | vf | Te | Fc | Ra |
|---|---|---|---|---|---|---|---|---|
| ns | 1 | 0 | 0 | 0 | 0 | −0.307 | −0.111 | −0.230 |
| dt | 0 | 1 | 0 | 0 | 0 | −0.329 | −0.337 | −0.063 |
| ap | 0 | 0 | 1 | 0 | 0 | −0.404 | 0.611 | −0.017 |
| ae | 0 | 0 | 0 | 1 | 0 | −0.366 | 0.534 | −0.049 |
| vf | 0 | 0 | 0 | 0 | 1 | −0.396 | 0.268 | 0.461 |
| Te | −0.307 | −0.329 | −0.404 | −0.366 | −0.396 | 1 | −0.414 | −0.120 |
| Fc | −0.111 | −0.337 | 0.611 | 0.534 | 0.268 | −0.414 | 1 | 0.123 |
| Ra | −0.230 | −0.063 | −0.017 | −0.049 | 0.461 | −0.120 | 0.123 | 1 |
| Schemes | Decision Maker’s Preferences | Weighting Factors | Engineering Decision Preferences | ||
|---|---|---|---|---|---|
| w10 (Te) | w20 (Fc) | w30 (Ra) | |||
| P1 | 0.5 | 0.1 | 0.1 | [0.714:0.143:0.143] | [Te] |
| P2 | 0.1 | 0.5 | 0.1 | [0.143:0.714:0.143] | [Fc] |
| P3 | 0.1 | 0.5 | 0.5 | [0.091:0.454:0.454] | [Fc, Ra] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, T.; Luo, H.; Tang, W.; Zhang, J. An Equilibrium Decision-Making Approach for Cutting Parameters of a Novel Five-Axis Hybrid Kinematic Machining Unit. Machines 2022, 10, 824. https://doi.org/10.3390/machines10090824
Tang T, Luo H, Tang W, Zhang J. An Equilibrium Decision-Making Approach for Cutting Parameters of a Novel Five-Axis Hybrid Kinematic Machining Unit. Machines. 2022; 10(9):824. https://doi.org/10.3390/machines10090824
Chicago/Turabian StyleTang, Tengfei, Haiwei Luo, Weimin Tang, and Jun Zhang. 2022. "An Equilibrium Decision-Making Approach for Cutting Parameters of a Novel Five-Axis Hybrid Kinematic Machining Unit" Machines 10, no. 9: 824. https://doi.org/10.3390/machines10090824
APA StyleTang, T., Luo, H., Tang, W., & Zhang, J. (2022). An Equilibrium Decision-Making Approach for Cutting Parameters of a Novel Five-Axis Hybrid Kinematic Machining Unit. Machines, 10(9), 824. https://doi.org/10.3390/machines10090824






