A Novel Numerical Method for Theoretical Tire Model Simulation

Abstract

Theoretical tire models are often used in tire dynamics analysis and tire design. In the past, scholars have carried out a lot of research on theoretical model modeling; however, little progress has been made on its solution. This paper focuses on the numerical solution of the theoretical model. New force and moment calculation matrix equations are constructed, and different iterative methods are compared. The results show that the modified Richardson iteration method proposed in this paper has the best convergence-stability in the steady and unsteady state calculation, which mathematically solves the problem of nonconvergence of discrete theoretical models in the published reference. A novel discrete method for solving the total deformation of tires is established based on the Euler method. The unsteady characteristics of tire models are only related to the path frequency without changing its parameters, so the unsteady state ability of the tire model can be judged based on this condition. It shows that the method in the references have significant differences at different speeds with the same path frequency under turn slip or load variations input, but the method proposed in this paper has good results.

1. Introduction

For tire and vehicle dynamics simulations and analyses, different types of tire models have been developed and categorized as empirical and theoretical models [1,2]. The empirical model, or combined theoretical and empirical model, is used for vehicle dynamics, and its model parameters are obtained by fitting measurements [2], including the MF/PAC2002 [2,3,4,5], TMeasy [6,7,8], UniTire [9,10], Hankook-Tire [11], TameTire [12,13], MF-Swift [14,15], FTire [16,17], CDTire [18,19] and RMOD-K [20,21] models, etc.

However, compared with the theoretical tire model, the empirical model is not suitable for the mechanical analysis of tire dynamics and tire design due to having too many model parameters and being dependent on experimental data. Tire design engineers should find the optimal design parameters that can satisfy the engineering requirements simultaneously and, for more efficient product development, a reliable theoretical model is essential because it enables systematic parameter study and design optimization. The theoretical models have advantages over the finite-element models in terms of computational efficiency, and they can be incorporated into the parameter study and optimization framework more easily [22]. Furthermore, combined with the static simulation data of the finite-element, using the theoretical model to achieve the steady and unsteady simulation should be a good prospect for future tire virtual development.

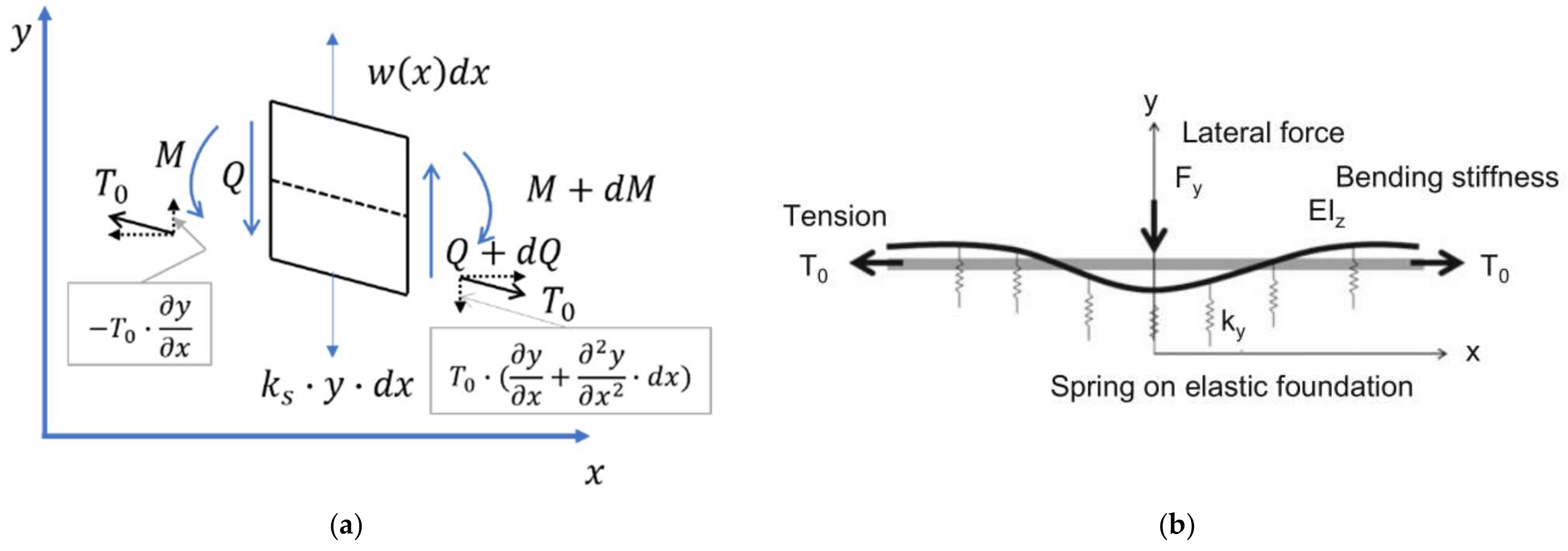
Fromm and Julien [3,23] proposed the brush tire model, which laid the foundation for tread modeling and tire theoretical analysis. The beam [1,3,24,25,26,27,28,29,30,31,32,33,34,35,36] and string models [3] are two classical belt/carcass modeling methods. Finally, the latest beam model includes belt tension, flexural rigidity, shear rigidity [1,22,25,26] and lateral shear force distribution [1], and the relationship between the parameters of the beam model and the design parameters of belts is established [1,22].

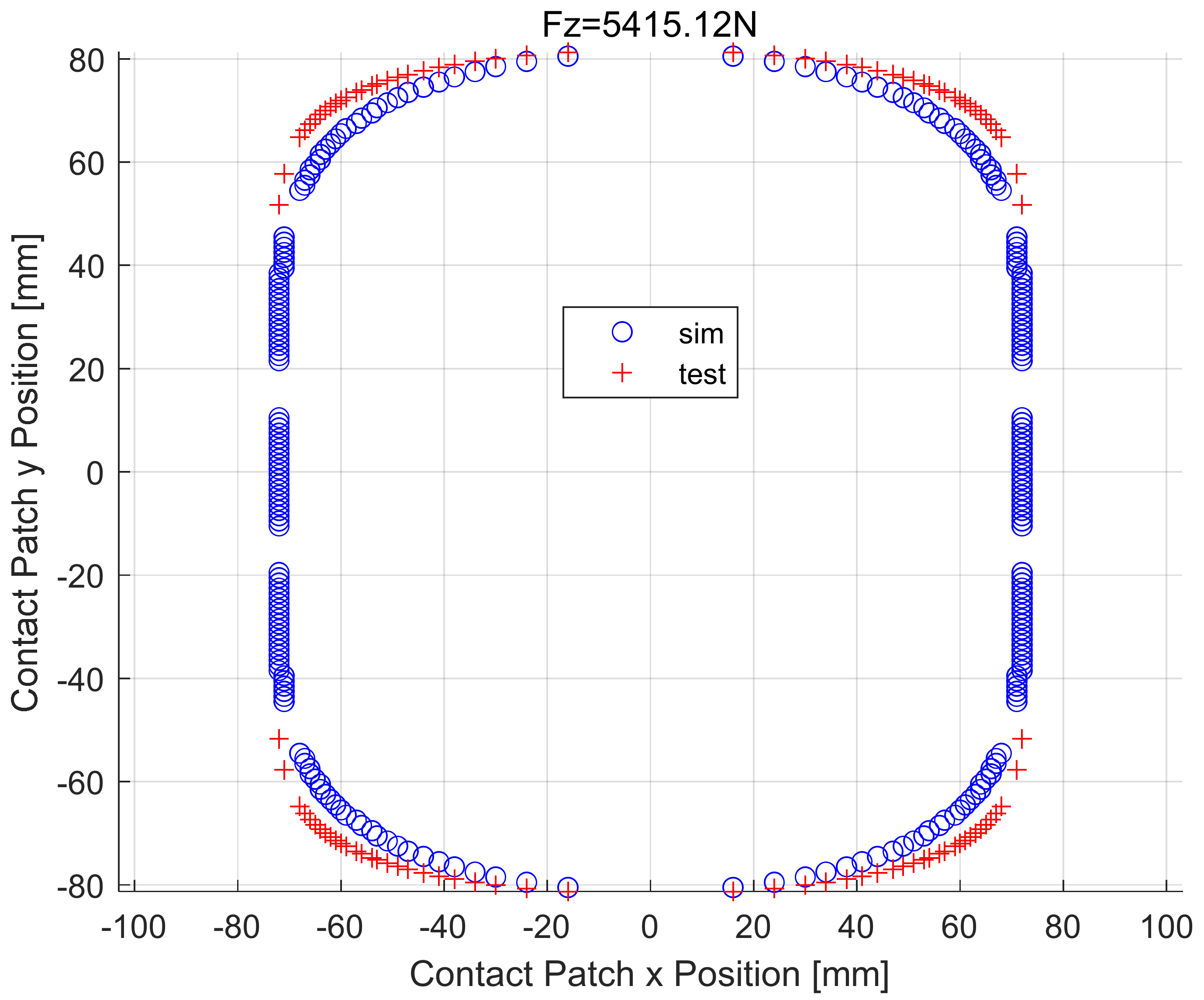
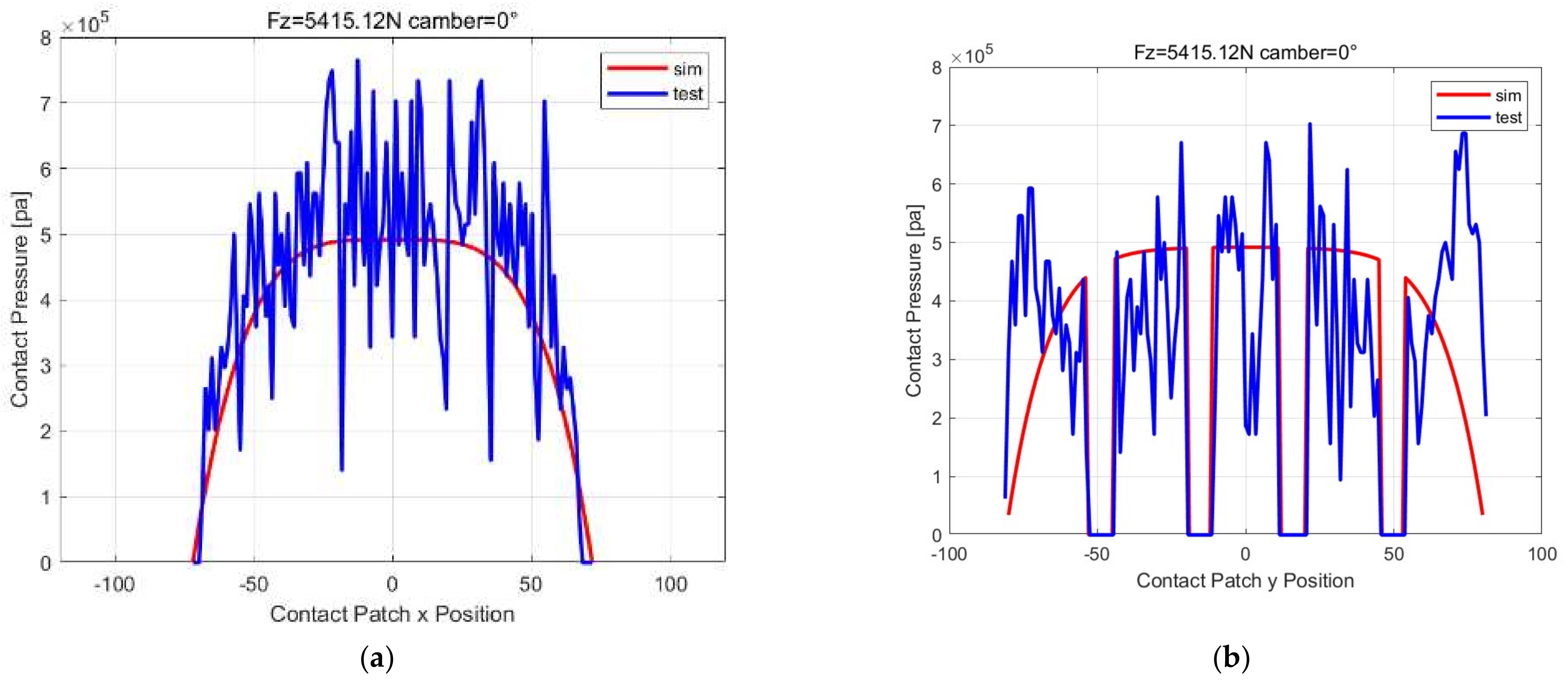
H. Sakai [28] pointed out that the previous practice of assuming the shape of the contact-patch as rectangular, the pressure distribution as lateral uniform and the longitudinal parabolic distribution does not reflect the reality; therefore, he studied the influence of different load, inflation pressure, camber, side slip angle and lateral force on the contact length in detail, and established a semi-empirical model of contact length with different rib along the width. Through the study of the distribution of contact patch-pressure on each rib, the empirical formula of contact patch pressure on each rib with load was established [29]. Guo Konghui established the general function of pressure distribution based on a rectangular contact patch in which the convexity, uniformity and fore-aft shift of pressure-distribution were considered [37,38,39]. Patrick Gruber, Robin S. Sharp and Andrew D studied normal and shear forces in the contact based on the finite-element model and established a 2D semi-empirical contact patch, considering longitudinal grooves as a function of vertical load and camber angle [40]. Ch. Oertel established the geometric relationship between the contact patch and vertical load, camber angle and tread profile curvature [41]; however, the contact patch length calculated by this method will be larger than the actual one, and the contact patch area caused by camber will be larger. Nakajima, Y. and Hidano, S. proposed two-dimensional contact patch considering that shear force, contact shape and contact pressure distribution are changed in the fore–aft and lateral direction caused by the camber, fore–aft and lateral external force [1,42], and the deficiency is that the contact patch shape is simply expressed as a rectangle or trapezoid.

Analytical [3,39,43,44,45,46,47,48,49,50] and numerical methods are usually used to solve theoretical models. The advantage of the former is high efficiency, but it is only suitable for simple theoretical models. With the increase of the complexity of the theoretical model, the numerical method becomes more and more important. TreadSim [3] is a typical representative for the steady-state numerical solution; however, the iteration process turned out to be unstable for certain combinations of vertical load, belt yaw and belt bend stiffness [51], and the method proposed in [51] does not actually solve the problem essentially by iteration. For unsteady-state numerical solutions, there are two different (but essentially the same) methods that are both based on the Lagrange description. An element that leaves the contact patch at one side is redefined in the model so that it will enter the contact patch at the opposite side. After a new element has entered the contact patch, the elements are also renumbered so that element number one is always the first element in the contact patch, and when the traveling distance in an increment time is larger than the distance between adjacent tread elements, a linear-interpolation method is used [52,53,54,55]. However, this method has some problems under the condition of turn slip or load variations inputs, which will be discussed in this paper. There are many methods for the iterative solution of matrix equations, including the traditional [56,57] and the latest [58,59], and different methods are suited for different application scenarios. For dynamic equations of tire models which usually consider mass, Newton’s method and the Newmark-beta method are always used [60,61]. However, in this paper, we do not intend to focus on the development of new iterative methods, but to reconstruct the matrix equations that can meet the application requirements of different iterative methods and compare several common iterative methods to select the most suitable for the discrete theoretical model and make appropriate optimizations.

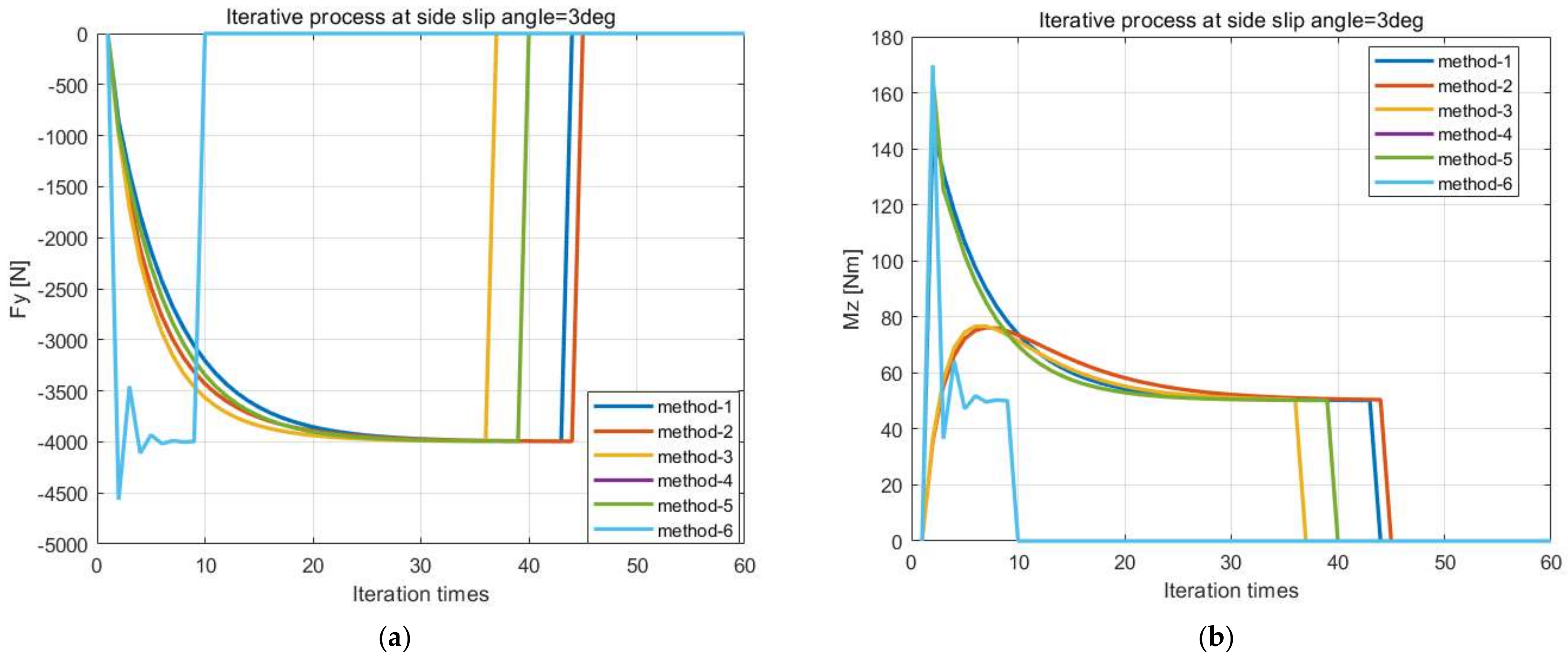
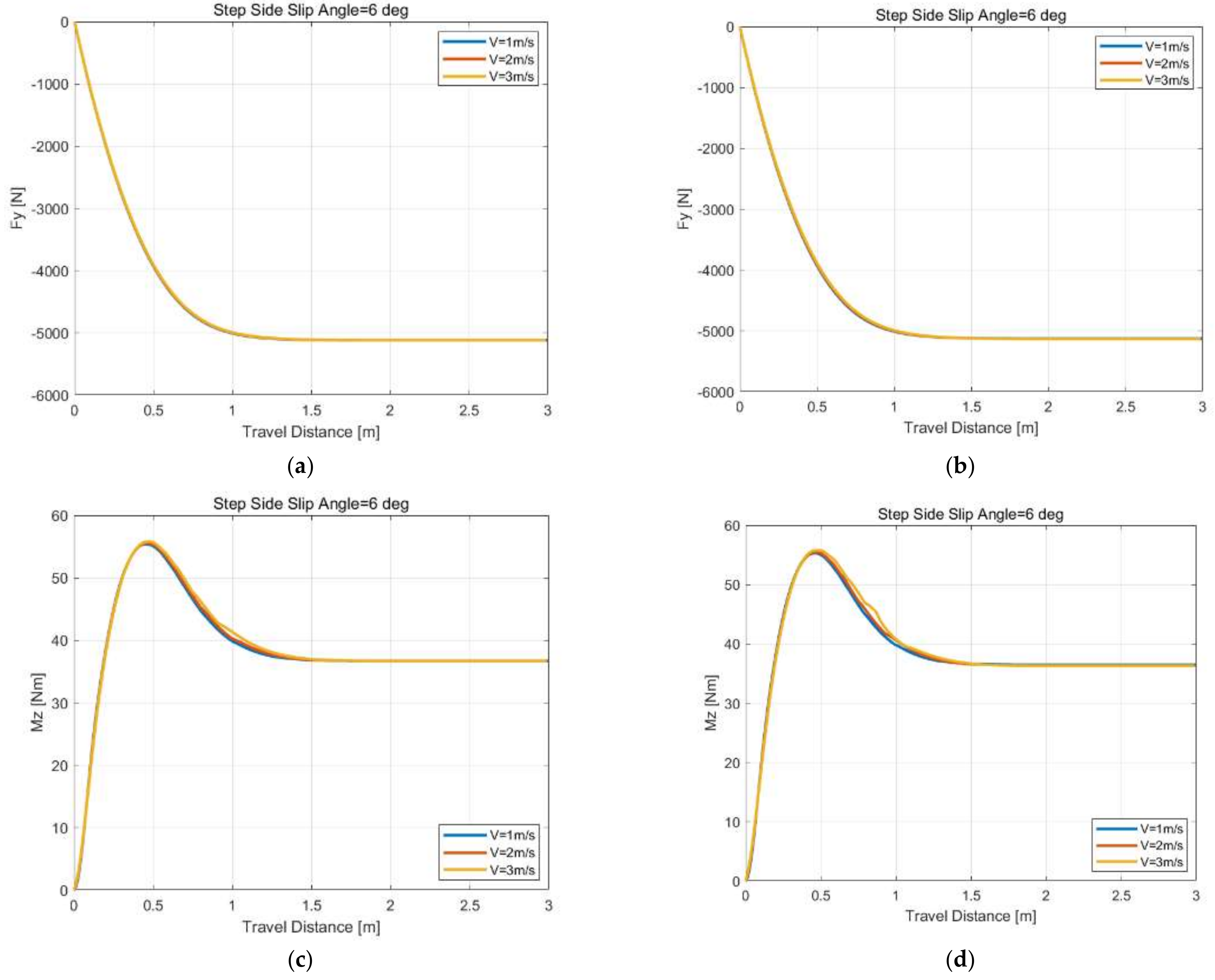
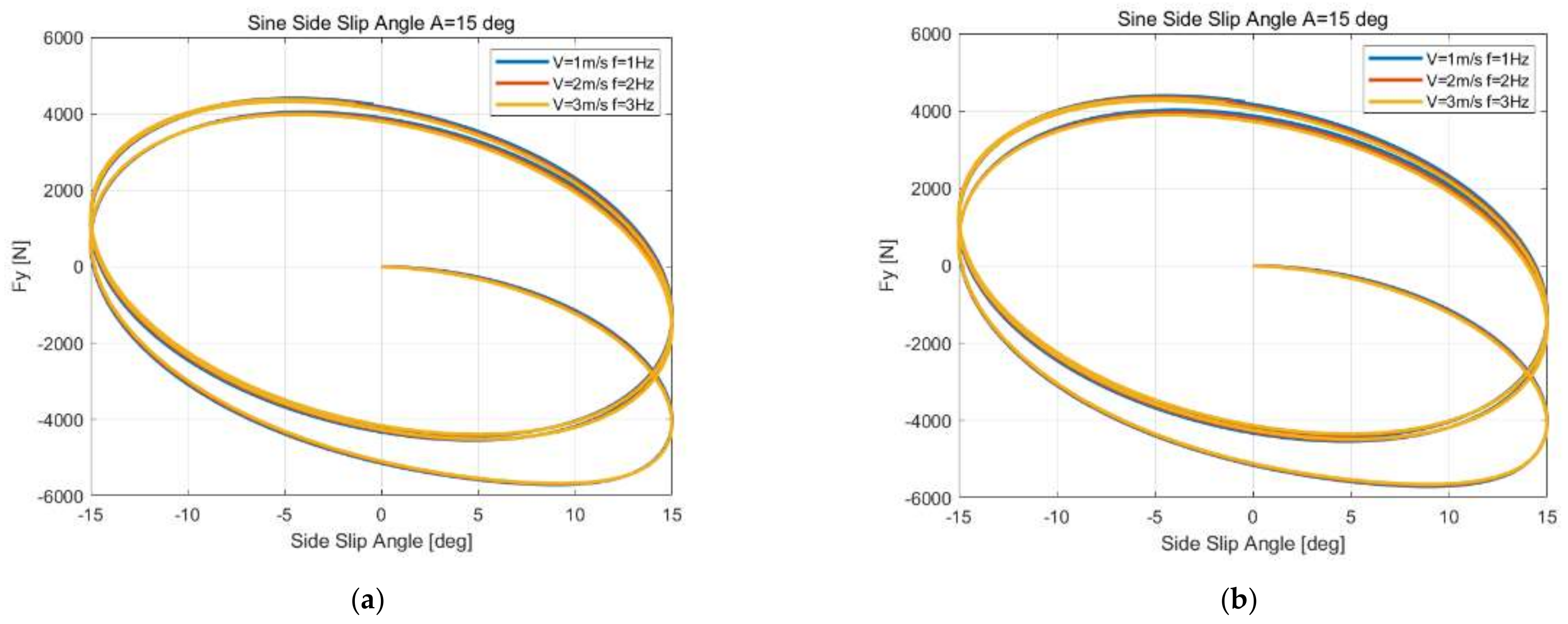
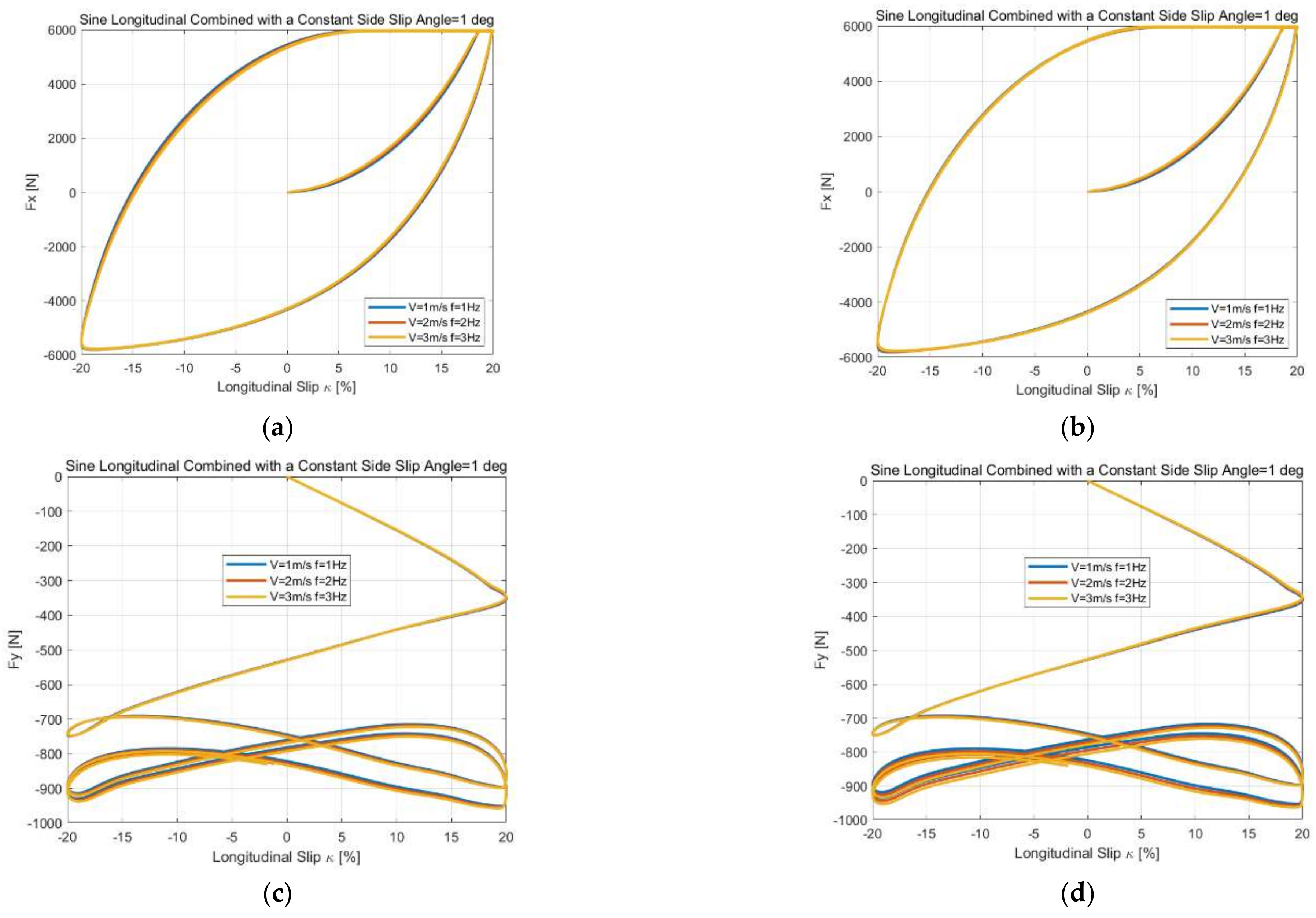
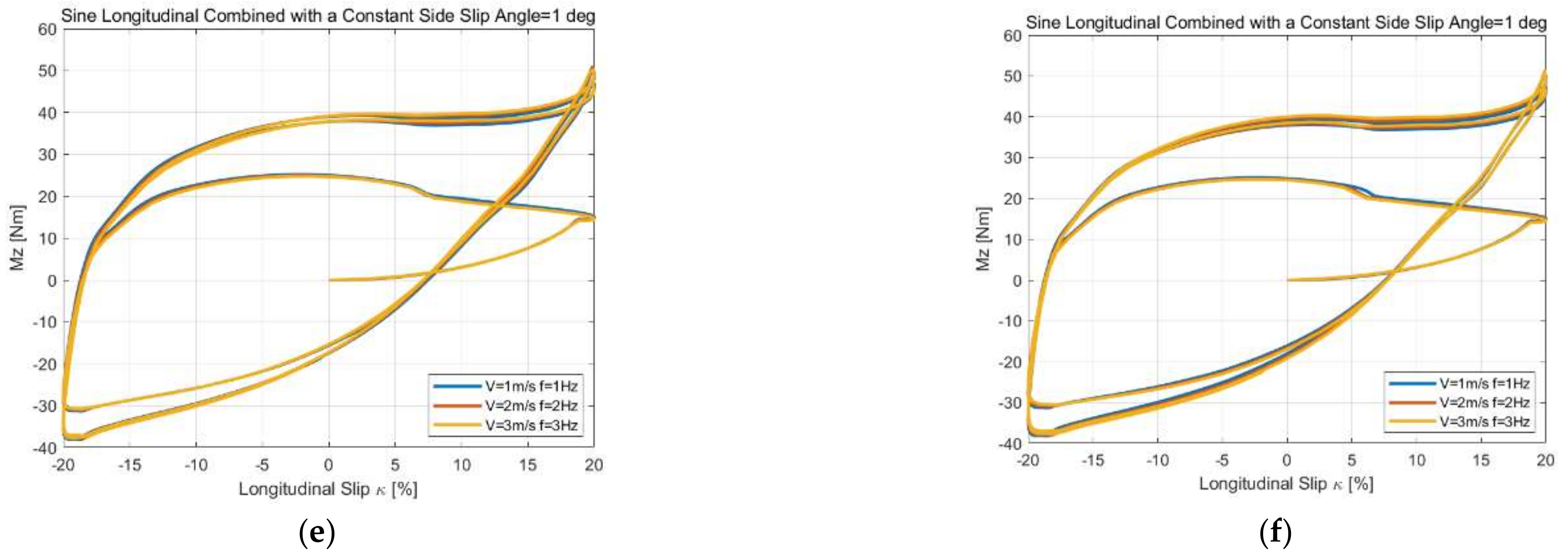
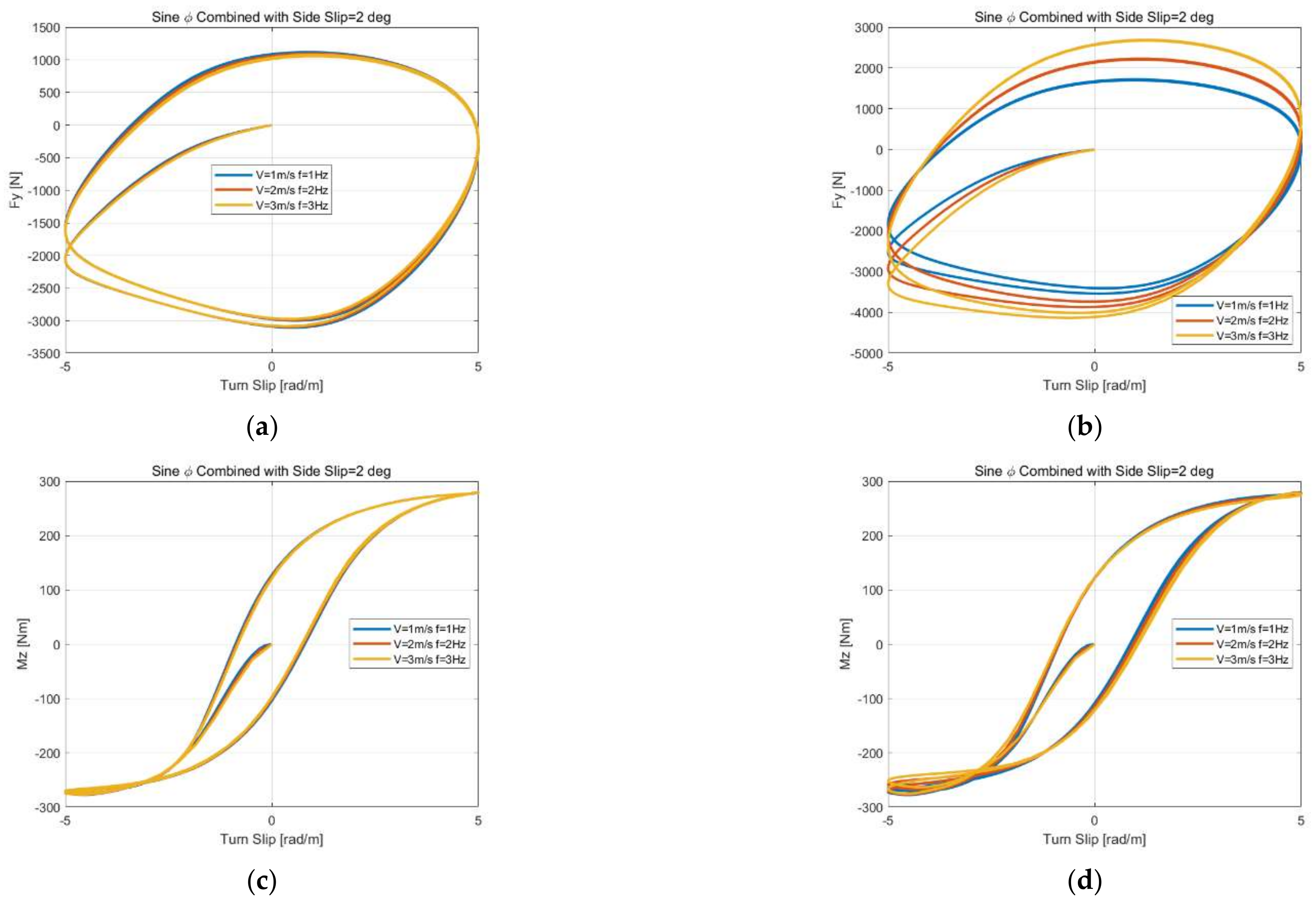
In this paper, a novel matrix equation for the force and moment calculation is constructed and different iterative methods are compared under steady-state constant side slip angle and unsteady-state conditions, including the step side slip, sine side slip, load variations at constant side slip, sine side slip angle at constant turn slip and sine longitudinal slip at constant side slip inputs. It shows that only the modified Richardson method proposed in this paper can complete all of the simulations without any convergence. A novel, discrete solution method for tire total deformation is proposed based on the Euler method, and time derivatives are replaced by spatial gradients. 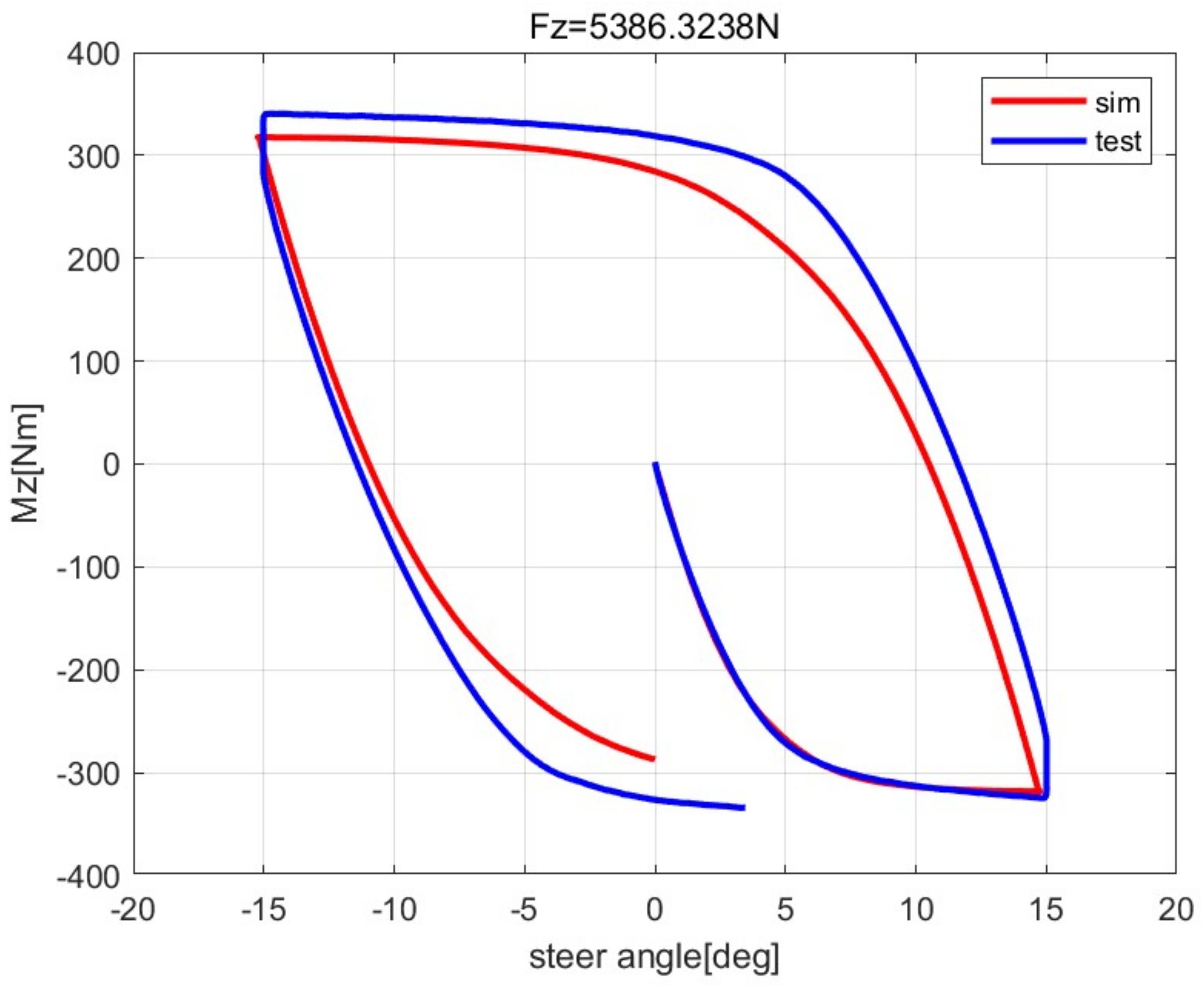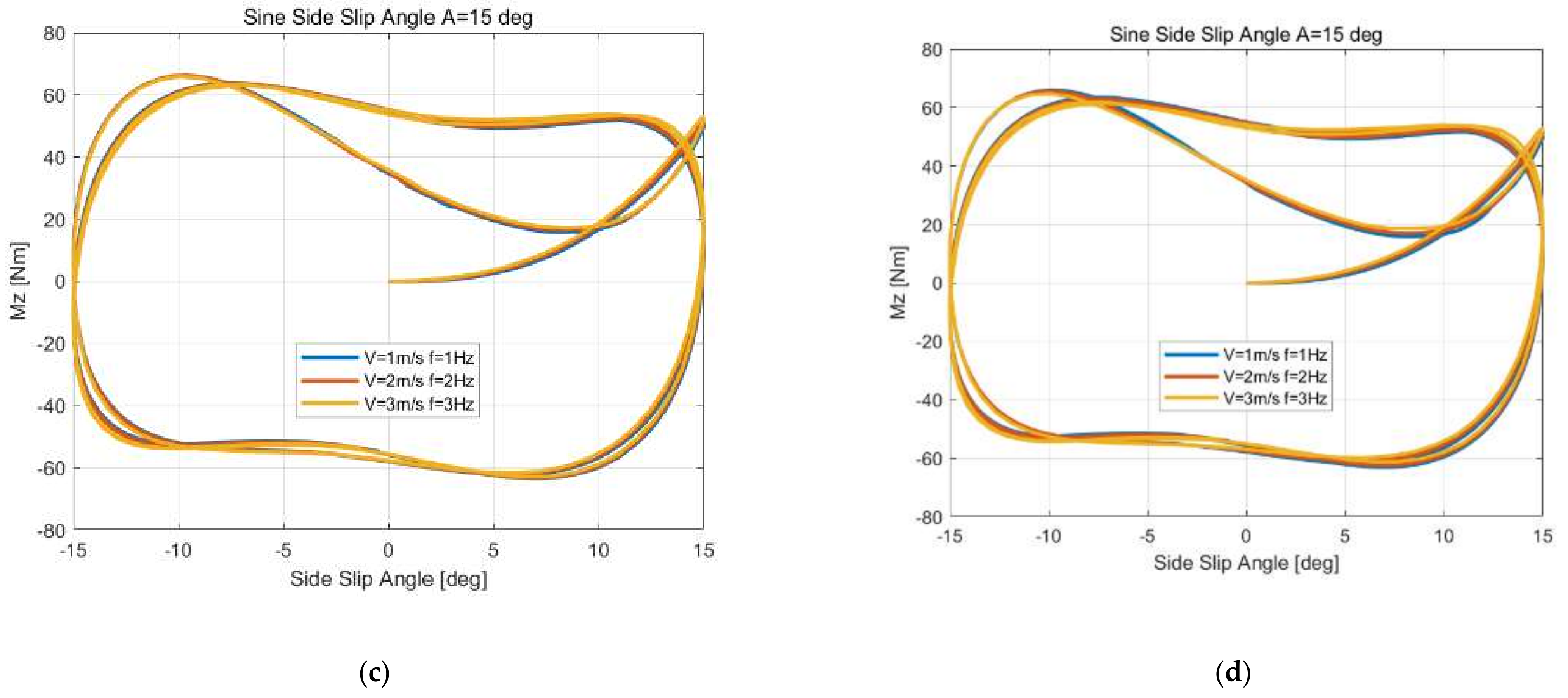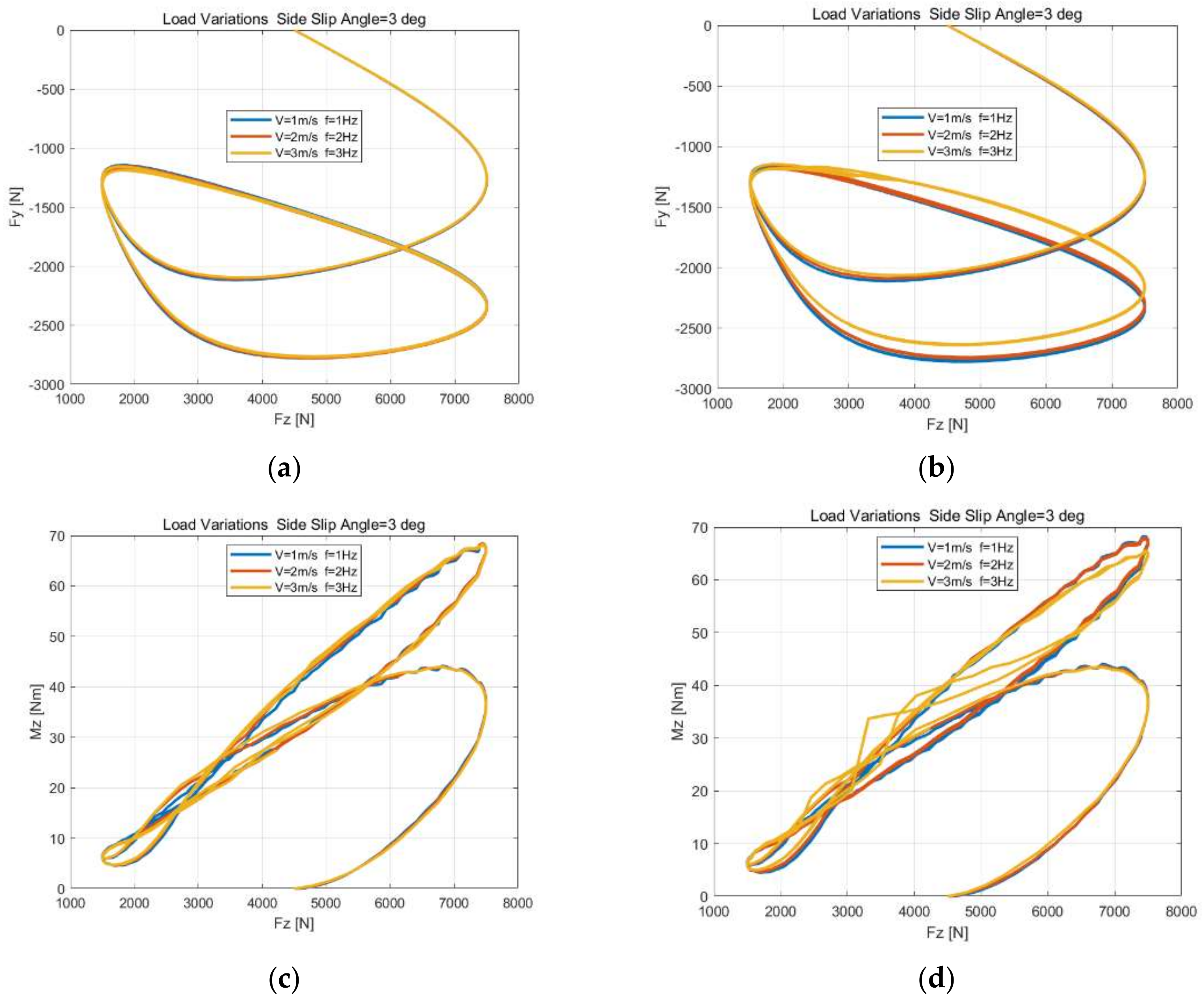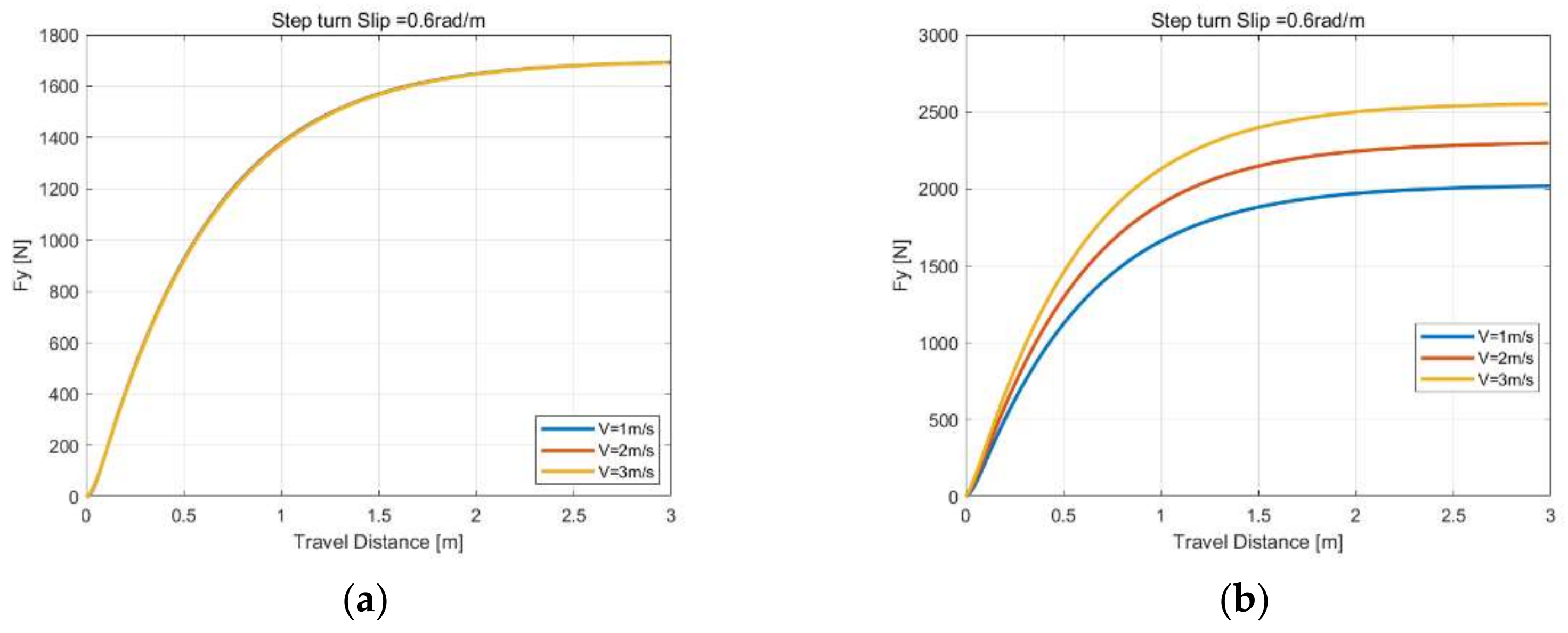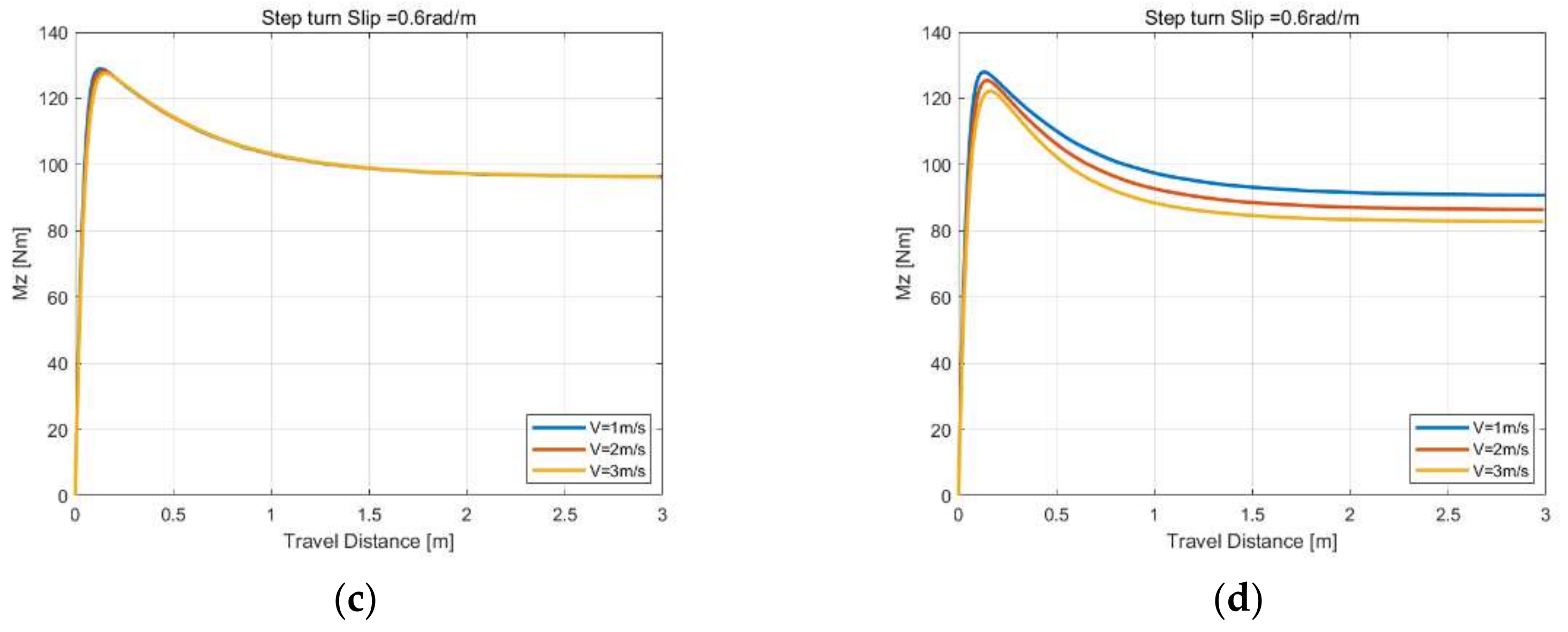Furthermore, based on the condition of the unsteady characteristics of tire models only relating to the path frequency without changing their parameters, the discrete solution method proposed is compared with reference [52,53,54,55] under different unsteady-state conditions, including the step side slip angle, sine side slip angle, load variations at constant side slip angle, step turn slip simulation, sine longitudinal combined with a constant side slip, sine turn combined with a constant side slip and load variations at constant longitudinal and side slip inputs. It shows that the simulation results have little difference by using the proposed method, but the reference method has a significant difference under turn slip or load variations inputs at different speed or, more precisely, the ratio between the distance of the contact patch center traveling in space within the time interval and distance between adjacent tread elements in the contact patch. However, this paper only studies the numerical solution method of the theoretical model in detail, and the results of the comparison between the model and the experiment show that a refined contact patch model considering camber and the influence of lateral force and longitudinal force on the contact patch model demonstrate the need for more in-depth research on the dynamic friction model, considering that the influences of contact pressure and slip velocity are added to the theoretical model.

The sections of this paper are arranged as follows. In Section 2, the tire total deformation discrete solution method based on the Euler method will be given. In Section 3, the modeling method of belt/carcass deformation, contact patch, stress direction in the sliding region and anisotropic of tread stiffness is described. In Section 4, according to the adhesion and sliding region, the matrix equations for the calculation of force and torque are established, and the advantages and disadvantages of different iterative methods are compared. 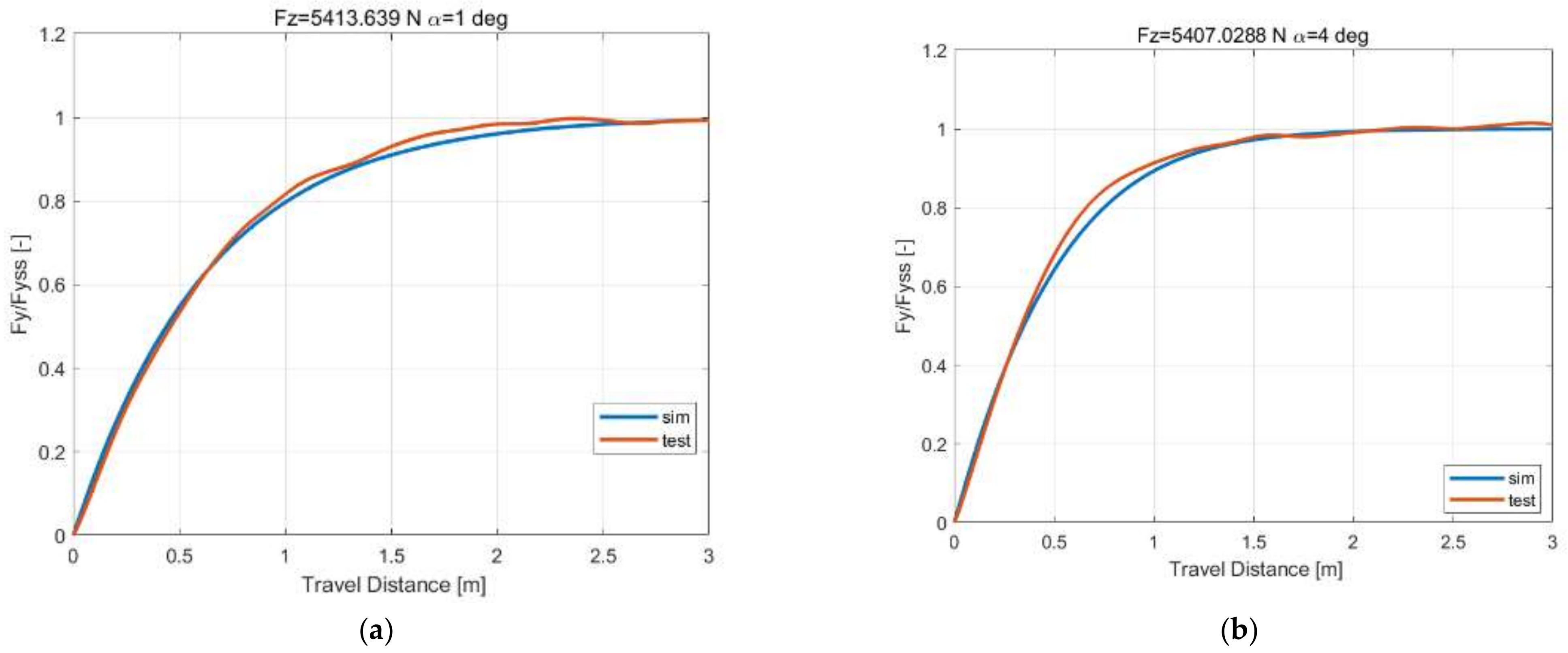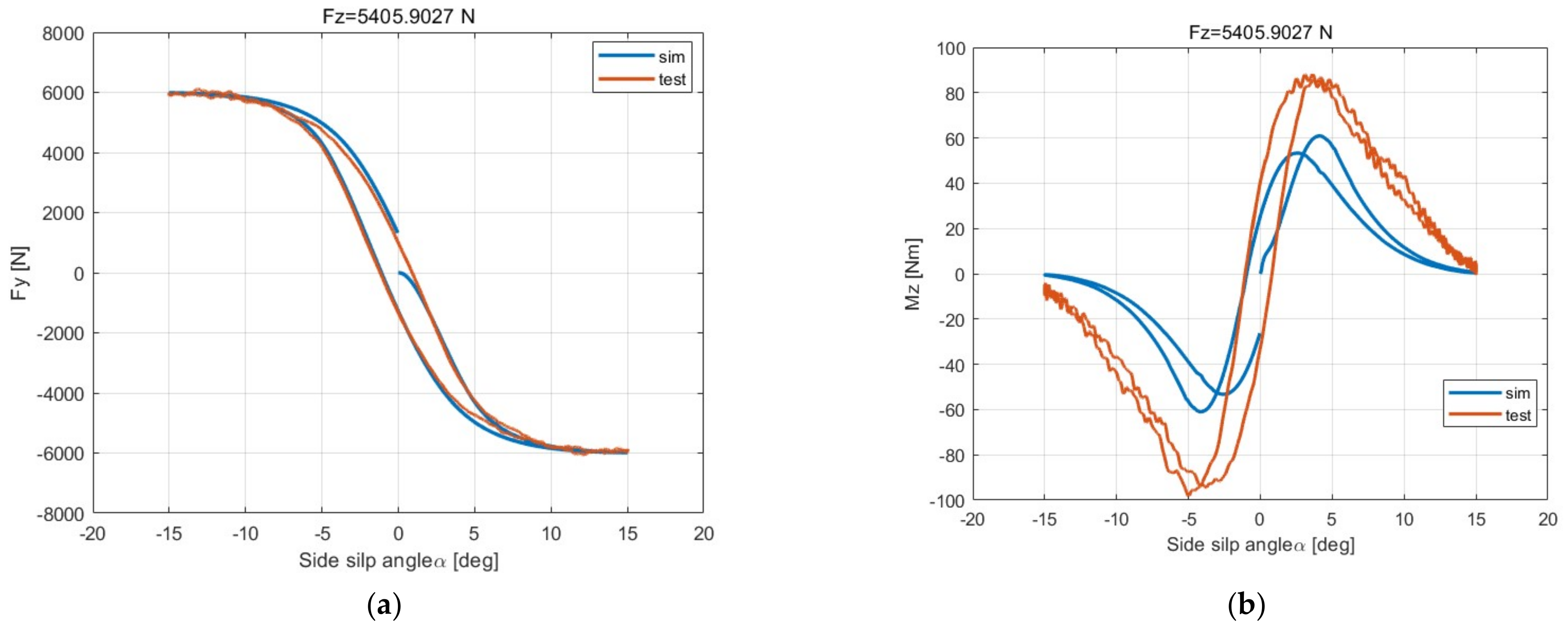In Section 5, the theoretical model is compared with the experiment to verify the rationality of the theoretical model parameters, and based on the principle that the unsteady state only depends on the path frequency, the discrete solution method proposed in this paper is compared with reference [52,53] unsteady-state conditions. Finally, the discussion and conclusions will be given in Section 6.

2. Tire Total Deformation Discrete Solution Method Based on the Euler Method

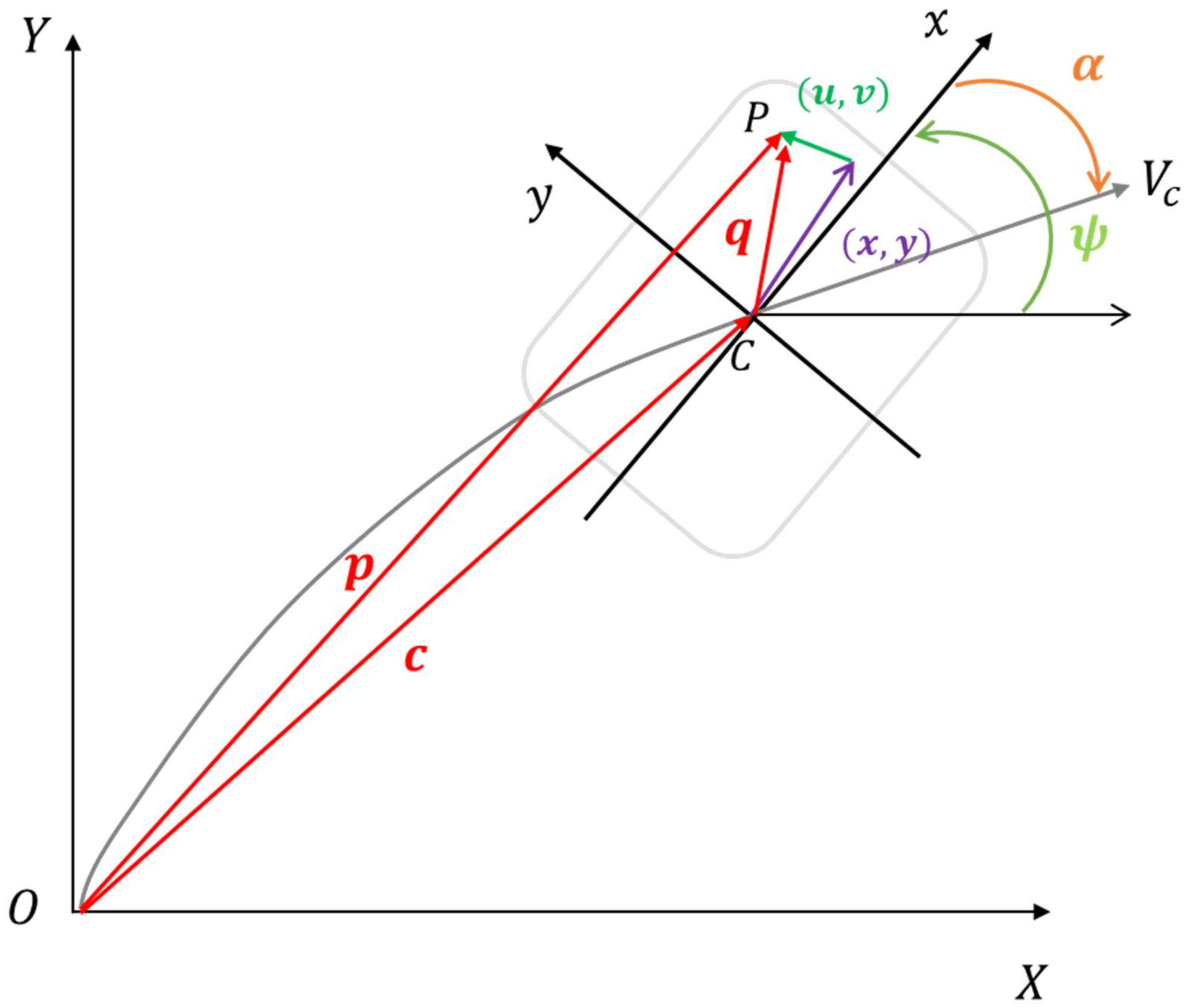
The total deformation of tires caused by friction consists of tread and carcass. When the tire deformation is described, two coordinate systems are used; one is the road coordinate system $(O,X,Y,Z)$ and the other is the contact patch coordinate system $(C,x,y,z)$, named as $ISO-W$. When the tire slips relative to the road surface, the friction forces makes the tire deform $(u,v)$ relative to the contact patch coordinates $(x,y)$, as shown in Figure 1. $P$ is the contact point at undeformed state and $p$ is the vector of $P$ relative to the $(O,X,Y,Z)$ system. $C$ represents the contact patch center and $c$ is the vector $C$ relative to the $(O,X,Y,Z)$ system. $(x,y)$ represents the contact point vector at undeformed state, $(u,v)$ represents the total tire deformation vector and $q$ is the vector of $P$ relative to $C$. $\alpha$ represents the sideslip angle and $\psi$ represents the yaw angle of the $x$-axis with respect to the $X$-axis.

The position of the tread location relative to $(O,X,Y,Z)$ can be expressed as the equation:

$$\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CP} \mathrm{or} p=c+q$$

(1)

Herein, $q=(x+u)e_x+(y+v)e_y$. So, there is the slip velocity of the tread relative to the road:

$$V_g=\dot{p}=\dot{c}+\dot{q}=V_c+(\dot{x}+\dot{u})e_x+(\dot{y}+\dot{v})e_y+\dot{\psi }\{(x+u)e_y-(y+v)e_x\}$$

(2)

where $V_c$ is the contact patch center velocity and $e_x$ and $e_y$ are the $(C,x,y,z)$ base vector. When there is no relative slip between the tread and the road surface, $V_g=0$, then

$$\dot{u}=-V_{sx}+\dot{\psi }\cdot (y+v)$$

(3)

$$\dot{v}=-V_{cy}-\dot{\psi }\cdot (x+u)$$

(4)

Herein, $\dot{x}=\frac{dx}{dt}=-\Omega R_e=V_r$, $V_{sx}=V_{cx}+\dot{x}$, $\dot{y}=0$, expression of Equations (3) and (4) by the Euler method

$$\dot{u}=\frac{\partial u}{\partial x}\cdot \frac{dx}{dt}+\frac{\partial u}{\partial y}\cdot \frac{dy}{dt}+\frac{\partial u}{\partial S}\cdot \frac{dS}{dt}=-V_{sx}+\dot{\psi }\cdot (y+v)$$

(5)

$$\dot{v}=\frac{\partial v}{\partial x}\cdot \frac{dx}{dt}+\frac{\partial v}{\partial y}\cdot \frac{dy}{dt}+\frac{\partial v}{\partial S}\cdot \frac{dS}{dt}=-V_{cy}-\dot{\psi }\cdot (x+u)$$

(6)

Then, there are:

$$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial S}\cdot \frac{V_c}{V_r}=-S_x+\phi \cdot (y+v)$$

(7)

$$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial S}\cdot \frac{V_c}{V_r}=-S_x+\phi \cdot (y+v)$$

(8)

Herein, $\frac{dS}{dt}=V_c$, $S_x=\frac{V_{sx}}{V_r}=\frac{\kappa }{\kappa +1}$, $S_y=\frac{V_{cy}}{V_r}=-\frac{1}{\kappa +1}\cdot \frac{V_{cy}}{V_x}=-\frac{1}{\kappa +1}\cdot \tan \alpha$, $\phi =\frac{\dot{\psi }}{V_r}$, and $\kappa$ is practical slip, $\alpha$ is side slip angle, $S_x$ is the longitudinal theoretical slip, $S_y$ is the lateral theoretical slip and $\phi$ is the turn theoretical slip. Equations (7) and (8) are only related to the coordinates of the contact patch $(x,y)$ and the space position of the contact patch center. The expression of Equations (7) and (8) in a discrete method:

$$\begin{array}{l}\frac{u\{S_{k+1}\}(x_{i+1},y_{j+1})-u\{S_{k+1}\}(x_i,y_{j+1})}{x_{i+1}-x_i}+\frac{u\{S_{k+1}\}(x_{i+1},y_{j+1})-u\{S_k\}(x_{i+1},y_{j+1})}{S_{k+1}-S_k}\cdot \frac{V_c}{V_r}\\ =-S_x+\phi \cdot [y_{j+1}+v\{S_{k+1}\}(x_{i+1},y_{j+1})]\end{array}$$

(9)

$$\begin{array}{l}\frac{v\{S_{k+1}\}(x_{i+1},y_{j+1})-v\{S_{k+1}\}(x_i,y_{j+1})}{x_{i+1}-x_i}+\frac{v\{S_{k+1}\}(x_{i+1},y_{j+1})-v\{S_k\}(x_{i+1},y_{j+1})}{S_{k+1}-S_k}\cdot \frac{V_c}{V_r}\\ =-S_y-\phi \cdot [x_{j+1}+u\{S_{k+1}\}(x_{i+1},y_{j+1})]\end{array}$$

(10)

According to Equations (9) and (10), there are tire total deformation:

$$u\{S_{k+1}\}(x_{i+1},y_{j+1})=p_{u1}\cdot [p_{u2}+\phi \cdot \frac{1}{\frac{1}{ds}\cdot \frac{V_c}{V_r}-\frac{1}{dx}}\cdot p_{u3}]$$

(11)

$$v\{S_{k+1}\}(x_{i+1},y_{j+1})=p_{v1}\cdot [p_{v2}-\phi \cdot \frac{1}{\frac{1}{ds}\cdot \frac{V_c}{V_r}-\frac{1}{dx}}\cdot p_{v3}]$$

(12)

Herein:

$dx=-(x_{i+1}-x_i)$ represents the distance between adjacent tread elements in the contact patch.

$ds=S_{k+1}-S_k$ represents the distance of the contact patch center traveling in space within the time interval $dt$.

$$p_{u1}=p_{v1}=\frac{1}{1+{(\frac{\phi }{\frac{1}{ds}\cdot \frac{V_c}{V_r}-\frac{1}{dx}})}^2}\cdot \frac{1}{\frac{1}{ds}\cdot \frac{V_c}{V_r}-\frac{1}{dx}}$$

$$p_{u2}=-S_x+\phi \cdot y_{j+1}-u\{S_{k+1}\}(x_i,y_{j+1})\cdot \frac{1}{dx}+u\{S_k\}(x_{i+1},y_{j+1})\cdot \frac{1}{ds}\cdot \frac{V_c}{V_r}$$

$$p_{u3}=-S_y-\phi \cdot x_{i+1}-v\{S_{k+1}\}(x_i,y_{j+1})\cdot \frac{1}{dx}+v\{S_k\}(x_{i+1},y_{j+1})\cdot \frac{1}{ds}\cdot \frac{V_c}{V_r}$$

$$p_{v2}=-S_y-\phi \cdot x_{i+1}-v\{S_{k+1}\}(x_i,y_{i+1})\cdot \frac{1}{dx}+v\{S_k\}(x_{i+1},y_{j+1})\cdot \frac{1}{dx}\cdot \frac{V_c}{V_r}$$

$$p_{v3}=-S_x+\phi \cdot y_{j+1}-u\{S_{k+1}\}(x_i,y_{j+1})\cdot \frac{1}{dx}+u\{S_k\}(x_{i+1},y_{j+1})\cdot \frac{1}{ds}\cdot \frac{V_c}{V_r}$$

If $\frac{V_c}{V_r}$ is set to zero, it can be transformed into a steady state.

3. Model Description

3.1. Belt/Carcass Deformation [23,54]

Assuming that longitudinal translation deformation only occurs under longitudinal force [54]:

$$u_c=\frac{F_x}{K_{cx0}}$$

(13)

where $K_{cx0}$ is the longitudinal translational stiffness of carcass. Under lateral force, the carcass is expressed as the deformation of an infinite beam under concentrated force. The beam has in-plane flexural rigidity $E{I}_z$, where $I_z$ is the moment of the inertia of the area, $E$ is the Young’s modulus of the belt in the circumferential direction, $k_s$ is the lateral fundamental spring rate per unit length in the circumferential direction and the tension $T_0$ is uniformly distributed in the belt width direction [23]. $M$ represents bending moment and $Q$ represents shear force, as shown in Figure 2. The left diagram shows the equilibrium of forces of the beam section and the right diagram shows model of the beam on the elastic foundation.

The equilibrium of forces acting on the element of length $dx$ along the belt width results in the following equation:

$$w(x)dx+Q+dQ+T_0\cdot (\frac{\partial y}{\partial x}+\frac{{\partial }^{2}y}{\partial x^2}\cdot dx)-Q-T_0\cdot \frac{\partial y}{\partial x}-k_s\cdot y\cdot dx=0$$

(14)

$$\mathrm{and} \mathrm{for} \mathrm{the} \mathrm{Euler} \mathrm{Bernoulli} \mathrm{beam}: Q=\frac{dM}{dx}$$

(15)

$$M=-E{I}_z\cdot \frac{d^{2}y}{d{x}^2}$$

(16)

Furthermore, according to (14)–(16), the differential equation of the lateral deformation of the beam can finally be expressed as:

$$E{I}_z\frac{{\partial }^{4}y}{\partial x^4}-T_0\frac{{\partial }^{2}y}{\partial x^2}+k_{s}y=w(x)$$

(17)

According to boundary conditions, (1) $x\to \infty ,y(x)\to 0$; (2) $x=0,\dot{y}(x)=0$; and (3) $F_y=2k_s{\displaystyle \underset{0}{\overset{\infty }{\int }}ydx}$, there is:

$$y(x)=\frac{\delta F_y}{4k_s}\cdot e^{-{\lambda }_1\left|x\right|}(\cos {\lambda }_{2}x+\frac{{\lambda }_1}{{\lambda }_2}\sin \left|{\lambda }_{2}x\right|)$$

(18)

Herein:

$${\lambda }_1=\sqrt[4]{\frac{k_s}{4E{I}_z}}\sqrt{(1+\frac{T_0}{\sqrt{4E{I}_z\cdot k_s}})}, {\lambda }_2=\sqrt[4]{\frac{k_s}{4E{I}_z}}\sqrt{(1-\frac{T_0}{\sqrt{4E{I}_z\cdot k_s}})}$$

$$\delta =\frac{{\lambda }_1^2+{\lambda }_2^2}{{\lambda }_1}, T_0=\xi \cdot \sqrt{4E{I}_z\cdot k_s}$$

Torsional deformation of carcass under aligning moment [54].

$$y(x)=\frac{M_z}{N_{\theta }}\cdot x$$

(19)

$N_{\theta }$ is the carcass torsion stiffness.

Therefore, the lateral deformation of the carcass under lateral force and an aligning moment can be expressed as

$$v_c=\frac{\delta F_y}{4k_s}\cdot e^{-{\lambda }_1\left|x\right|}(\cos {\lambda }_{2}x+\frac{{\lambda }_1}{{\lambda }_2}\sin \left|{\lambda }_{2}x\right|)+\frac{M_z}{N_{\theta }}\cdot x$$

(20)

3.2. Contact Patch

Reference [41] presents a method for calculating the shape of a contact patch based on vertical force. Due to the fact that this method usually leads to a large contact patch area following camber input, this paper does not consider camber.

$$G(x_i,y_j)=R_l-\sqrt{R^2-x_i^2-R^2{(\frac{y_j}{R_y})}^{n_y}}$$

(21)

$$R_l=R-d$$

(22)

$$F_z=p_{Fz1}\cdot d+p_{Fz2}\cdot d^2$$

(23)

where $R$ is free radius, $R_l$ is the loaded radius, $d$ is the vertical deflection, $R_y$ is the lateral radius and $n_y$ is the lateral direction curvature exponent.

However, directly according to this method, the obtained contact length will be larger. A correction method is proposed as follows:

$$G_{\lim }=G_1\cdot d^2+G_2\cdot d$$

(24)

Then, the contact patch can be obtained when $G(x_i,y_j)<G_{\lim }$.

The pressure distribution of ground imprinting is expressed as follows [41,54]:

$$\eta (\frac{x_i}{h_j})=A\cdot (1-{(\frac{x_i}{h_j})}^{2n})\cdot (1+\lambda \cdot {(\frac{x_i}{h_j})}^{2n})\cdot (1-B\cdot \frac{x_i}{h_j})$$

(25)

$$F_{zij}(x_i,y_j)=F_{0ij}\cdot \eta (\frac{x_i}{h_j})\cdot (1+a_{Fz1}{(\frac{y_j}{b_i})}^2-(a_{Fz1}+1)\cdot {(\frac{y_j}{b_i})}^6)$$

(26)

assuming that $F_{0ij}$ is a constant, which can be obtained according to $F_z={\displaystyle \sum F_{zij}(x_i,y_j)}$.

$h_j$ is the contact length at position $y_j$, $b_i$ is the contact width at position $x_i$ and $a_{Fz1}$ is the convexity factor along the contact width.

$$A=\frac{(2n+1)(4n+1)}{2n(4n+1+\lambda )}, B=-\frac{3(2n+3)(4n+3)(4n+1+\lambda )}{(2n+1)(4n+1)(4n+3+3\lambda )}\cdot \frac{\Delta }{h_j}$$

where $\lambda$ is convexity factor of contact pressure along contact length, $\frac{\Delta }{h_j}$ is the contact pressure center-offset factor and $n$ is the contact pressure-uniformity factor.

When considering the tread pattern longitudinal groove, the $F_{zij}(x_i,y_j)$ of the corresponding position is set to zero. The contact patch example is shown as in Figure 3.

3.3. Direction of Stress in the Sliding Regions

As shown in Figure 4, $B_i,P_i,T_i$ are the upper (which is attached to the belt) and lower end of the bristle and the bristle deformation, respectively, at previous times. $B_{i+1},P_{i+1},T_{i+1}$ correspond to the current time. $dG$ is the bristle slip displacement vector relative to the road.

$$dG=V_{g}dt=(V_B+V_T)dt=dB+dT=dB+T_{i+1}-T_i$$

(27)

then

$$dG-T_{i+1}=dB-T_i=\overrightarrow{P_i{B}_{i+1}}$$

(28)

For sliding regions, the sliding direction $V_g$ determines the direction of deformation, so the vector $dG$ is in the same direction as $T_{i+1}$ and $T_{i+1}$ is on vector $\overrightarrow{P_i{B}_{i+1}}$; that is to say $\overrightarrow{P_i{B}_{i+1}}$ determines the direction of $T_{i+1}$.

3.4. Stiffness of the Tread Element

The pattern block structure usually leads to the anisotropy of tread element stiffness. It is assumed that the stiffness satisfies the elliptic equation, as shown in Figure 5:

$${(\frac{k_t\cdot \cos \theta }{k_{tx}})}^2+{(\frac{k_t\cdot \sin \theta }{k_{ty}})}^2=1$$

(29)

then:

$$k_t=\sqrt{\frac{1}{{(\frac{\cos \theta }{k_{tx}})}^2+{(\frac{\sin \theta }{k_{ty}})}^2}}$$

(30)

where $\theta$ is the deformation direction angle of the tread element.

4. Iterative Method for Force and Moment Calculation

4.1. Deformation and Stress Calculation of Tread Element

When the tread element is in the adhesion region, the deformation is calculated as follows

$$u_T=u-u_c$$

(31)

$$v_T=v-v_c$$

(32)

Herein, $u$ and $v$ are obtained from Section 2, Equations (11) and (12); $u_c$ and $v_c$ are obtained from Section 3.1, Equations (13) and (17). The deformation direction angle of the tread element is expressed as

$$\tan \theta =\frac{v_T}{u_T}$$

(33)

The longitudinal and lateral stresses of tread element are expressed as

$$q_{xa}=k_t\cdot u_T, q_{ya}=k_t\cdot v_T, q_a=\sqrt{q_{xa}^2+q_{ya}^2}$$

(34)

If $q_a\le \mu \cdot q_z$

$$q_x=q_{xa}, q_y=q_{ya}$$

(35)

else

$$q_x=q_{xs}=\frac{q_{xa}}{q_a}\cdot \mu \cdot q_z=\mu \cdot q_z\cdot \cos \theta$$

(36)

$$q_y=q_{ys}=\frac{q_{ya}}{q_a}\cdot \mu \cdot q_z=\mu \cdot q_z\cdot \sin \theta$$

(37)

$$u_T=\frac{q_x}{k_t}, v_T=\frac{q_y}{k_t}; u=u_T+u_c, v=v_T+v_c$$

(38)

Above are the stress and deformation of tread element in the sliding region.

4.2. Calculation of Force and Moment

4.2.1. Fx Calculation

$$\begin{array}{l}{F}_x={{\displaystyle \iint q}}_{x}dA={\displaystyle \sum {\displaystyle \sum k_t{u}_{T}dA}}+{\displaystyle \sum {\displaystyle \sum q_{xs}dA}}\\ ={\displaystyle \sum {\displaystyle \sum k_{t}udA}-F_x\cdot }{\displaystyle \sum {\displaystyle \sum \frac{k_t}{K_{cx0}}dA}}+{\displaystyle \sum {\displaystyle \sum q_{xs}dA}}\end{array}$$

(39)

then:

$$(1+p_{Fx})F_x=F_{xr}$$

(40)

where:

$$p_{Fx}={\displaystyle \sum {\displaystyle \sum \frac{k_t}{K_{cx0}}dA}}, F_{xra}={\displaystyle \sum {\displaystyle \sum k_{t}udA}}, F_{xrs}={\displaystyle \sum {\displaystyle \sum q_{xs}dA}}, F_{xr}=F_{xra}+F_{xrs}$$

4.2.2. Fy Calculation

$$\begin{array}{l}{F}_y={{\displaystyle \iint q}}_{y}dA={\displaystyle \sum {\displaystyle \sum k_t{v}_{T}dA}}+{\displaystyle \sum {\displaystyle \sum q_{ys}dA}}\\ ={\displaystyle \sum {\displaystyle \sum k_{t}vdA}-F_y\cdot }{\displaystyle \sum {\displaystyle \sum k_t\eta dA-}}{M}_z{\displaystyle \sum {\displaystyle \sum k_t\varsigma dA}}+{\displaystyle \sum {\displaystyle \sum q_{ys}dA}}\end{array}$$

(41)

then:

$$(1+p_{Fy})F_y=F_{yr}+M_z\cdot p_{MTF}$$

(42)

where:

$$\eta =\frac{\delta }{4k_s}\cdot e^{-{\lambda }_1\left|x\right|}\cdot [\cos ({\lambda }_{2}x)+\frac{{\lambda }_1}{{\lambda }_2}\sin (\left|{\lambda }_{2}x\right|)], \varsigma =\frac{x}{N_{\theta }}$$

$$p_{Fy}={\displaystyle \sum {\displaystyle \sum k_t\eta dA}}, p_{MTF}=-{\displaystyle \sum {\displaystyle \sum k_t\varsigma dA}}, F_{yra}={\displaystyle \sum {\displaystyle \sum k_{t}vdA}}, F_{yrs}={\displaystyle \sum {\displaystyle \sum q_{ys}dA}}$$

$$F_{yr}=F_{yra}+F_{yrs}$$

4.2.3. Mz Calculation

$$\begin{array}{l}{M}_z={{\displaystyle \iint q}}_y(x+u)dA-{{\displaystyle \iint q}}_x(y+v)dA\\ ={\displaystyle \sum {\displaystyle \sum k_t{v}_T\cdot (x+u)}}+{\displaystyle \sum {\displaystyle \sum q_{ys}\cdot (x+u)}}-{\displaystyle \sum {\displaystyle \sum k_t{u}_T\cdot (y+v)-}}{\displaystyle \sum {\displaystyle \sum q_{xs}\cdot (y+v)}}\end{array}$$

(43)

then:

$$(1+p_{Mz})M_z=M_{zr}+F_y\cdot p_{FTM}$$

(44)

where:

$p_{Mz}={\displaystyle \sum {\displaystyle \sum k_t\varsigma \cdot (x+u)dA}}, p_{FTM}=-{\displaystyle \sum {\displaystyle \sum k_t\eta \cdot (x+u)}}dA$

$M_{zrxa}=-{\displaystyle \sum {\displaystyle \sum k_t{u}_T\cdot (y+v)}}dA, M_{zrxs}=-{\displaystyle \sum {\displaystyle \sum q_{xs}\cdot (y+v)}}dA$

$M_{zrya}={\displaystyle \sum {\displaystyle \sum k_{t}v}\cdot (x+u)}dA, M_{zrys}={\displaystyle \sum {\displaystyle \sum q_{ys}\cdot (x+u),}}$

$M_{zr}=M_{zrxa}+M_{zrxs}+M_{zrya}+M_{zrys}$

According to Equations (33) and (35), there are

$$(1+p_{Fy}-\frac{p_{FTM}\cdot p_{MTF}}{1+p_{Mz}})F_y=F_{yr}+\frac{p_{MTF}}{1+p_{Mz}}\cdot M_{zr}$$

(45)

$$(1+p_{Mz}-\frac{p_{FTM}\cdot p_{MTF}}{1+p_{Fy}})M_z=M_{zr}+\frac{p_{FTM}}{1+p_{Fy}}\cdot F_{yr}$$

(46)

Make:

$$A_{11}=1+p_{Fx}, A_{22}=1+p_{Fy}-\frac{p_{FTM}\cdot p_{MTF}}{1+p_{Mz}}, A_{33}=1+p_{Mz}-\frac{p_{FTM}\cdot p_{MTF}}{1+p_{Fy}}$$

$$B_1=F_{xr}, B_2=F_{yr}+\frac{p_{MTF}}{1+p_{Mz}}\cdot M_{zr}, B_3=M_{zr}+\frac{p_{FTM}}{1+p_{Fy}}\cdot F_{yr}$$

There are

$$\left[\begin{array}{ccc}{A}_{11}& 0& 0\\ 0& A_{22}& 0\\ 0& 0& A_{33}\end{array}\right]\left[\begin{array}{l}{F}_x\\ F_y\\ M_z\end{array}\right]=\left[\begin{array}{l}{B}_1\\ B_2\\ B_3\end{array}\right]$$

(47)

Make:

$$A=\left[\begin{array}{ccc}{A}_{11}& 0& 0\\ 0& A_{22}& 0\\ 0& 0& A_{33}\end{array}\right], B=\left[\begin{array}{l}{B}_1\\ B_2\\ B_3\end{array}\right], X=\left[\begin{array}{l}{F}_x\\ F_y\\ M_z\end{array}\right]$$

(48)

Finally, there are

$$AX=B$$

(49)

A reasonable iterative method can be constructed according to this matrix equation.

4.3. Iterative Strategy

4.3.1. Matrix Splitting Method

Make:

$$A=M-N$$

(50)

then:

$$X_{m+1}=M^{-1}N{X}_m+M^{-1}B$$

(51)

where $\frac{N_{ij}}{M_{ij}}=IR$, $IR<1$ and $M_{ij}=\frac{A_{ij}}{1-IR}$, $N_{ij}=\frac{IR}{1-IR}\cdot A_{ij}$.

4.3.2. Steepest-Descent Method

$$\begin{gathered} r_m=B-A{X}_m \\ {p}_m=r_m \\ {\alpha }_m=\frac{r_m^T{p}_m}{p_m^{T}A{p}_m} \\ {X}_{m+1}=X_m+{\alpha }_m{p}_m \end{gathered}$$

(52)

4.3.3. Richrdson Method

$$X_{m+1}=X_m+\omega (B-A{X}_m)$$

(53)

where $\omega =\frac{2}{{\lambda }_1+{\lambda }_n}$, ${\lambda }_1$ and ${\lambda }_n$ are the maximum and minimum eigenvalues of $A$, respectively.

4.3.4. Extrapolation Acceleration Method

According to matrixes $M$ and $N$ from Section 4.3.1, the extrapolation acceleration method can be made:

$$X_{m+1}=(1-\omega )X_m+\omega (M^{-1}N{X}_m+M^{-1}B)$$

(54)

where $\omega =\frac{2}{2-({\lambda }_1+{\lambda }_n)}$, ${\lambda }_1$ and ${\lambda }_n$ are the maximum and minimum eigenvalues of $M^{-}N$, respectively.

4.3.5. Method in References [54,55]

This method obtains the solution directly from the matrix equation:

$$X_{m+1}=A^{-1}B$$

(55)

This method is equivalent to Section 4.3.1 where $IR$ is equal to zero.

4.3.6. Method in References [3,51]

This method is equivalent to that of the matrix $M$ whose coefficients are equal to one, and the method is the same as in Section 4.3.1.

4.3.7. Iterative Error

$$ERR=B-A{X}_{m+1}$$

(56)

If $ER{R}^{T}ERR\le Tol$, the iterative reaches convergence, where $Tol$ is the iterative error tolerance.

4.3.8. Comparison of Iterative Methods

A comparison of the iterative methods at a steady state under a constant side slip angle = three deg is shown in Figure 6, and method 4 and 5’s iterative processes coincide completely.

The unsteady comparison results of different iterative methods are shown in

Table 1. The iterative CPU times of different methods at different conditions.

Iterative Method	Iterative CPU Time [s] and the Simulation Time Is Set to 3 s
	Step Side Slip	Sine Side Slip	Load Variations at Constant Side Slip	Sine Side Slip Angle at Constant Turn Slip	Sine Longitudinal Slip at Constant Side Slip
Method 1	35.11	94.10	69.40	no convergence	no convergence
Method 2	33.97	71.46	59.99	no convergence	no convergence
Method 3	55.34	136.21	141.71	154.96	280.46
Method 4	33.61	65.07	59.67	no convergence	no convergence
Method 5	32.50	66.26	60.14	no convergence	no convergence
Method 6	no convergence	no convergence	no convergence	no convergence	no convergence

.

Figure 6 shows that method 6 has the fastest iteration speed at a steady state, followed by method 3. It can be seen from Table 1 that although method 3 has the slowest iteration speed in unsteady state, it has the most stable convergence. As such, method 3 is selected as the iterative strategy of the discrete theoretical model. However, it should be noted that in the case of unsteady large slip, due to the fact that the coefficients of the $A$ matrix parameters tend to one but the $B$ matrix changes, the solution is sometimes not convergent, so it is necessary to improve the iterative method. Through research, it is found that the following equation can improve convergence:

$$\omega =\frac{2}{{\lambda }_1+{\lambda }_n+\frac{p_{\lambda }}{{\lambda }_1+{\lambda }_n}}$$

(57)

The adjustment of $p_{\lambda }$ can better improve the convergence, but it will reduce a certain convergence speed. The greater $p_{\lambda }$ is, the better the convergence will be, but the iteration speed will be reduced, and this parameter can be reasonably selected for specific situations. This paper recomments $p_{\lambda }=20$, and the simulation in Table 1 uses this parameter.

5. Simulation of the Discrete Theoretical Model

5.1. Model Parameters and Verification

The model parameters are listed in

Table 2. The discrete tire model parameters.

Parameters Name	Parameters Value	Parameters Name	Parameters Value
$k_{tx}[N/m^3]$	1.3377 × 108	$K_{cx0}[N/m]$	4.3735 × 105
$k_{ty}[N/m^3]$	1.0332 × 108	$E{I}_z[N{m}^2]$	1 × 103
$n[-]$	2	$k_s[N/m^2]$	1.25 × 105
$\lambda [-]$	0	$\xi [-]$	0.2
$\Delta [-]$	0	$N_{\theta }[Nm/rad]$	1.2994 × 104
$a{F}_{z1}[-]$	−0.05	$\mu [-]$	1.11
$p_{Fz1}[N/m]$	2.01 × 105	$R_0[m]$	0.3465
$p_{\lambda }[-]$	20	$n_y[-]$	5.4
$G_1[-]$	3.64	$R_y[m]$	0.145
$G_2[-]$	−0.74	Tol	10
$dx[mm]$	2	$dy[mm]$	2

, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show the comparison between the model and the test and the test information is shown in

Table 3. The test information.

Test No.	Test Conditions	Inflation Pressure	Road Speed	Steer Angle	Steer Cycle	Vertical Load
1	Contact Pressure	250 kPa	0	0	0 s	5415 N
2	Parking Maneuver	250 kPa	0	15~−15°	32 s (Slope)	5386 N
3	Sideslip Angle Step	250 kPa	0 → 10 kph	−1°	-	5414 N
		250 kPa	0 → 10 kph	−4°	-	5407 N
4	Sine Sideslip Angle	250 kPa	10 kph	−15~15°	20 s (0.05 Hz)	5406 N

.

The contact pressure is performed on the TekScan. The other three conditions are performed on the MTS CT Flat-trac machine (MTS System Corporation). For the sideslip angle step condition, the test procedure is to turn the steer angle first, then load and finally apply the belt speed of the MTS to 10kph within one second. It should be noted that the sign of steer angle in the table is the opposite to that of the slip angle which is determined by the MTS Flat-trac machine.

It should be noted that the response of normalized lateral force instead of lateral force with travel distance is used, which does not affect the assessment of transient behavior.

As shown in Figure 11, the aligning moment is quite different from the experimental data, and a reasonable reason is whether the local camber of the carcass caused by the lateral force is not considered, which can lead to greater aligning moment if taken into consideration.

The unsteady characteristics of tire models are only related to the path frequency without changing its parameters, so the unsteady state-ability of the tire model can be judged based on this condition and changing the ratio between the distance of the contact patch center traveling in space within the time interval and the distance between adjacent tread elements in the contact patch by changing speed. The path frequency is defined as:

$${\omega }_s=\frac{2\pi f}{V}$$

(58)

where ${\omega }_s$[$m^{-1}$] represents the path frequency, $f$[$s^{-1}$] represents the time frequency and $V$[$m/s$] represents the contact patch center velocity.

Next, the discrete method proposed for tire total-deformation calculation in this paper (Section 2) will be compared with the references [52,53], and the comparison results of two methods are given. The comparison error calculation method is as follows:

$$err=\sqrt{\frac{{\displaystyle \sum {(y_p-y_r)}^2}}{{\displaystyle \sum y_p^2}}}\times 100\%$$

(59)

where $y_p$ represents the proposed method in this paper and $y_r$ represents the proposed method in reference [52,53].

5.2. Pure Side Slip Simulation

5.2.1. Step Side Slip Angle

The simulation results of step side slip angle with the proposed method and the reference method are as shown in Figure 12.

5.2.2. Sine Side Slip Angle

The simulation results of sine side slip angle with the proposed method and the reference method are as shown in Figure 13.

5.2.3. Load Variations at Constant Side Slip Angle

The simulation results of load variations at constant side slip angle with the proposed method and the reference method are as shown in Figure 14.

5.2.4. Discussion

The above simulations have the same path frequency, and the simulation results for different speeds should also be the same, in theory. The simulation results of the proposed method are slightly different, but significant differences occur in reference methods under the load variations condition at different speeds. The simulation errors of the two methods at 3m/s are listed in

Table 4. The simulation errors at pure side slip simulation.

Simulation Conditions	Compare Items	Error [%]
Step Side Slip Angle	$F_y$	0.28
	$M_z$	1.12
Sine Side Slip Angle	$F_y$	1.37
	$M_z$	2.18
Load Variations at Constant Side Slip Angle	$F_y$	5.86
	$M_z$	7.59

.

5.3. Step Turn Slip Simulation

The simulation results of step turn slip with the proposed method and the reference method are as shown in Figure 15.

The method proposed in the references is obviously not suitable for the turn slip simulation because the steady-state simulation results at different speeds are quite different. The reason is that the method proposed in the reference is based on the principle of linear interpolation in the leading edge, while the tread deformation is nonlinear during turn slip and the method fails when $ds$ is much larger than $dx$. At the same time, it can be seen that the aligning moment responds quickly in the initial position, which is explained in Section 5.5.2. The simulation errors of the two methods at 3m/s are listed in

Table 5. The simulation errors at the step turn slip simulation.

Simulation Conditions	Compare Items	Error [%]
Step Turn Slip Simulation	$F_y$	141.40
	$M_z$	142.20

.

5.4. Combined Slip Simulation

5.4.1. Sine Longitudinal Combined with a Constant Side Slip

The simulation results of sine longitudinal combined with a constant side slip with the proposed method and the reference method are as shown in Figure 16.

5.4.2. Sine Turn Combined with a Constant Side Slip

The simulation results of sine turn combined with a constant side slip with the proposed method and the reference method are as shown in Figure 17.

5.4.3. Load Variations at Constant Longitudinal and Side Slip

The simulation results of load variations at constant longitudinal and side slip with the proposed method and the reference method are as shown in Figure 18.

5.4.4. Discussion

In the case of load variations or turn slip input the reference method has obvious problems, and the conclusions are consistent with Section 5.2 and Section 5.3. The simulation errors of the two methods at 3m/s are listed in

Table 6. The simulation errors at combined slip simulation.

Simulation Conditions	Compare Items	Error [%]
Step Turn Slip Simulation	$F_x$	2.54
	$F_y$	1.23
	$M_z$	3.67
Sine Turn Combined with a Constant Side Slip	$F_y$	61.01
	$M_z$	6.43
Load Variations at Constant Longitudinal and Side Slip	$F_x$	3.95
	$F_y$	8.49
	$M_z$	8.86

.

5.5. Deformation Analysis of Tread Element

5.5.1. Deformation of Tread Element under Step Side Slip Angle

In the side slip angle step condition, with the increase of the travel distance, the deformation of the tread element approximately changes shape from rectangular to trapezoidal and finally to triangular, as shown in Figure 19.

5.5.2. Deformation of the Tread Element under Step Turn Slip

In the turn slip step condition, the lateral deformation is first symmetrically distributed relative to the longitudinal center of contact patch, which is the reason why the slope of lateral force with the travel distance is zero at the starting position and also explains why aligning moment responds so quickly, as shown in Figure 20.

With the increase of the travel distance, the intersection point of the lateral deformation curve with the contact patch longitudinal axis gradually shifts from the center to the intersection point of the steady state. In this process, the lateral force increases continuously, and the increment gradient of the aligning moment caused by the lateral deformation decreases, which leads to a peak of the aligning moment which then decreases and finally tends to the steady state value.

At the same time, the lateral deformation is approximate to the nonlinear change of the parabolic shape, which also explains why the reference method will have problems in the turn slip input simulation.

5.5.3. Deformation of the Tread Element under Load Variations at a Constant Side Slip Angle

Figure 21 shows the that the lateral deformation of the proposed method is more regular and stable than reference. It explains why under load variations conditions at the same path frequency, when the traveling distance in an increment time is larger than the distance between adjacent tread elements, the lateral force and aligning moment of the reference method will be different.

6. Discussion and Conclusions

6.1. Discussion

Figure 7 and Figure 8 show that the contact patch parameters are reasonable, and the simulation results are consistent with the experiments. Figure 9, Figure 10 and Figure 11a show that the belt/carcass parameters are reasonable, and simulation and test results are consistent as well. However, Figure 11b shows that the aligning moment is quite different from the experimental data, and a reasonable reason is that the local camber of the carcass caused by the lateral force is not considered, which can lead to greater aligning moment if considered.

Figure 6 shows that different iterative methods converge to the same value and that the iterative method in reference [54,55] has the fastest iteration speed, followed by the modified Richardson method proposed in this paper. Table 1 shows that the modified Richardson has the best convergence and then method in reference [54,55] and the worst is the method in reference [3,51].

Figure 12, Figure 13 and Figure 16 show that whether the discrete method proposed or the references [52,53,54,55] are considered, the simulation results at different speeds with the same path frequency are only slightly different under side slip angle or longitudinal slip input. Figure 14, Figure 15, Figure 17 and Figure 18 show that for the discrete proposed method the simulation results still have slight differences, but the results of the method in the references [52,53,54,55] have significant differences at different speeds with the same path frequency, and the greater the speed difference, or more precisely the greater the ratio between the distance of the contact patch center traveling in space within the time interval and distance between adjacent tread elements in the contact patch, the greater the simulation difference. The calculation errors in Table 4, Table 5 and Table 6 also confirm the above analysis. Figure 19 shows that the tread deformation varies nearly linearly at the leading edge of the contact patch under step side slip angle, but Figure 20 shows that the tread deformation varies nonlinearly in an approximate parabolic under step turn slip. Figure 21 shows that the tread deformation is more stable by using the proposed method under the load variations input. Tread deformation explains why the methods in the reference [52,53,54,55] have problems under the turn slip or load variations inputs, since the method performs a linear interpolation process at the leading edge which is not suitable for nonlinear deformation and deformation instability. The above conclusions may be able to explain the reasons for the reference [3] “at each time step in which the wheel is rolled further over a distance equal to the interval between two successive tread elements” simulation settings.

6.2. Conclusions

In this paper, novel numerical methods for discrete theoretical tire model steady- and unsteady-state simulations are proposed. Some conclusions are as follows.

The comparison between the theoretical model and the experiment shows that the accuracy of the aligning moment needs further improvement, which may be affected by tire local carcass camber caused by lateral force, but the model parameters are reasonable.

New basic matrix equations for force and moment calculation are constructed for the convenient application of different iterative methods. Different iterative methods are studied and compared. The results show that the new modified Richardson iteration method proposed in this paper has the best convergence stability in the unsteady calculation, which mathematically solves the problem of nonconvergence of discrete theoretical models in the published references [3,51,55].

A novel discrete method for solving the total deformation of tires is established based on the Euler method. The unsteady characteristics of tire models are only related to the path frequency without changing its parameters, so the unsteady-state ability of the tire model can be judged based on this condition. It shows that the methods in the references [52,53,54,55] have significant differences at different speeds with the same path frequency, and the greater the speed difference, or more precisely the greater the ratio between the distance of the contact patch center traveling in space within the time interval and distance between adjacent tread elements in the contact patch, the greater the simulation difference under the turn slip or load variations inputs. However, the method proposed in this paper has good results.

This paper only studies the numerical solution method of the theoretical model in detail. In the future, the following work needs to be carried out. The establishment of a refined contact patch model considering camber and the influence of lateral force and longitudinal force on the contact patch model and of a dynamic friction model considering the influence of contact pressure and slip velocity is added to the theoretical model. System verification of theoretical models with experiments. Furthermore, it is hoped that theoretical models can be used in tire virtual development, since the computational efficiency of the finite element model is low and virtual data simulation, especially for turn slip input because the existing test machines cannot carry out this condition. Combined with the static simulation data of the finite element, using the theoretical model to achieve the steady and unsteady simulations should be a good prospect for the future of tire virtual development.