Self-Attention and Multi-Task Based Model for Remaining Useful Life Prediction with Missing Values

Abstract

Remaining useful life (RUL) prediction is recently a hot spot in industrial big data analysis research. It aims at obtaining the health status of the equipment in advance and making intelligent maintenance decisions. However, values missing is a common problem in real industrial applications which severely restricts the performance and application scope of RUL prediction. To deal with this problem, a novel prediction model called self-attention-based multi-task network (SMTN)is proposed. The spatiotemporal feature fusion module utilizes the self-attention mechanism and long short-term memory to fully exploit the information in space and time dimensions, multi-task learning module tries to learn a complete representation from incomplete data by performing the missing values imputation task, and the representation is simultaneously used for RUL prediction. Comparison experiments conducted on the C-MAPSS dataset verified the effectiveness of the proposed SMTN.

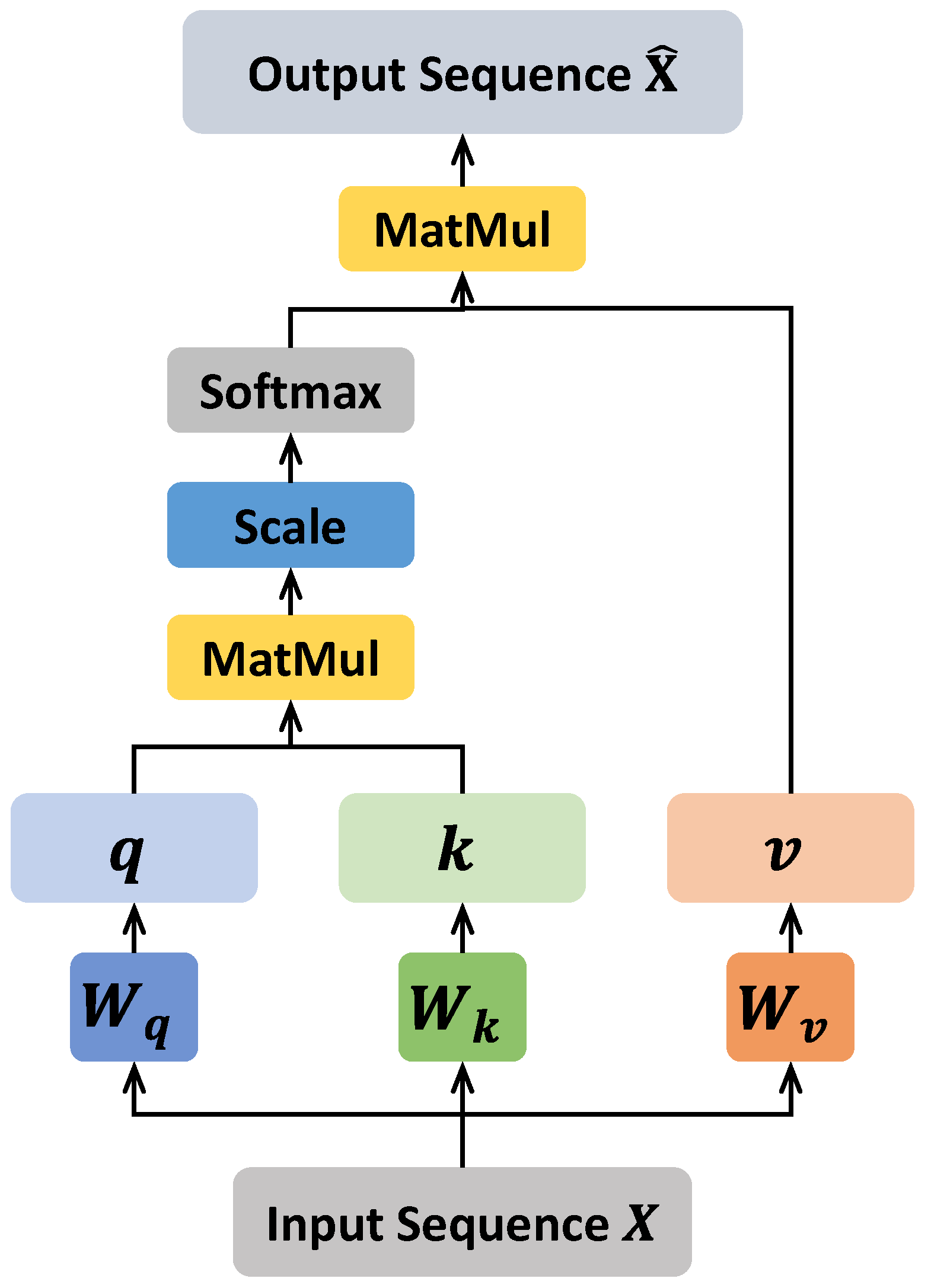
1. Introduction

Recently, prognostics and health management (PHM) has played a crucial role in the complex and sophisticated modern industrial system, which helps to improve the reliability of equipment [1,2,3], reduce the maintenance cost of industrial systems, and even avoid severe safety accidents. Remaining useful life (RUL) prediction is important part of PHM. RUL is defined as the time that the monitored equipment can work before it fails completely [4]. The goal of RUL prediction is to model the degradation process and predict the RUL of the system accurately, thus some measures can be taken before the equipment fails completely. RUL prediction has attracted more and more attention from researchers since it helps in improving the intelligent level of operation and maintenance of industrial systems.

Generally, RUL prediction methods can be roughly classified into model-based methods, data-driven methods, and hybrid methods. Model-based methods build a physical model based on the failure mechanism of the system, which describes the degradation process. Thereby the RUL of the system can be predicted. Paris-Erdogan (PE) model is the most widely used physical model in industrial RUL prediction, which is built to describe the crack propagation process of a component [5]. However, as modern industrial systems become more complex, it becomes more and more difficult to build accurate physical models, and the researchers pay more attention to data-driven RUL prediction methods. Data-driven RUL prediction aims to utilize machine learning methods to model the degradation process of the system and extract informative degradation features from the multi-source data, thus predicting the RUL of the system from the monitoring signals. Hybrid methods try to integrate the advantages of both data-driven and model-based approaches, however, they still face difficulties because still require physical knowledge to model the system, so this approach covers the least publications in past research.

In recent years, thanks to the cheap and high-performance sensors and the development of big data analysis technology, a large amount of monitoring data have become cheap and easy to obtain. These informative monitoring data provide the possibility to construct data-driven RUL prediction methods. Thereby, the data-driven RUL prediction methods have become the most promising RUL prediction method, and attracted many researchers’ focus on this field. Data-driven approaches attempt to use machine learning techniques to learn the degradation patterns of machines from monitoring data [6]. Researchers have proposed many data-driven RUL prediction methods including some typical methods such as SVR-based methods [7], hidden Markov model (HMM) methods [8], convolutional neural network (CNN) [9] based methods [10,11], recurrent neural network (RNN) and long short-term memory (LSTM) [12] based methods [13], etc. Deep learning-based methods are currently a popular data-driven RUL prediction method. Deep learning techniques can extract deep features from data without any manually operations. The auto extracted features can be more specific to the task and loss less information, therefore it usually performs well on RUL prediction. For example, in [10] the researchers proposed a novel deep convolutional neural network-bootstrap-based integrated prognostic approach for RUL prediction, which utilized a deep convolutional neural network–multilayer perceptron (i.e., DCNN–MLP) dual network to simultaneously extract informative representations hidden in both time series-based and image-based features and to predict the RUL. Despite some shortcomings of deep learning technology, such as poor interpretability and high requirements on data and computing resources, it is still been widely studied.

Transformer [14] is a popular model which has made excellent progress in both natural language processing (NLP) [15] and computer vision (CV) [16], where self-attention mechanism is the crucial part of it. The self-attention mechanism can model the global correlation of sequence data or image data, it has a larger receptive field and generalization than CNN-based and RNN-based methods, which is the reason why the self-attention mechanism performs well in both CV and NLP. Due to the outstanding performance of the self-attention mechanism and its naturally suitable for modeling sequence data, many researchers try to apply transformer and self-attention mechanism in RUL prediction [17,18,19,20,21]. In [18], the author proposed a two-stage RUL prediction method based on transformer. Specifically, in the first stage, a feature pre-extraction mechanism is designed to replace manual feature extraction and selection, which will retain more detailed information. In the second stage, an adaptive transformer (AT) model is proposed to achieve RUL prediction from low-level features which combines the advantages of the recurrent model and the novel attention mechanism, which can adaptively and accurately model the complex relationship between high-dimensional features and RUL compared to traditional recurrent models. To overcome the shortcomings of CNN and RNN-based traditional methods, ref. [20] proposed a full self-attention RUL prediction model without any CNN or RNN module. This model consists of an encoder and decoder, the encoder utilized two paralleled self-attention modules to explore the data from time and sensor aspects and adaptively fuses the feature maps of the two aspects, and the fused feature map is sent to the decoder for RUL prediction.

Although the above mentioned methods provide new ideas and perspectives for RUL prediction, there are still some shortcomings. The problem of corruption data is a common problem in industrial applications. In practice, the common used measure is to directly discard samples with corrupted values and then perform RUL prediction, but this will lead to few-shot problem in the training process. Simply filling the missing values is another way to deal with this problem, such as mean value filling, last value filling, clustering-based missing value filling etc. But these methods often lead to filling errors and are not quite effective in the following prediction task. To deal with this problem, some researchers have proposed a few studies [22,23,24]. For example, in [22], the author proposed an integrated imputation and prediction scheme based on extreme learning machines. First, missing value imputation is performed using single imputation and multiple imputation. Next, the imputed data is used for RUL prediction using various prediction modules. In [23], multivariate functional principal component analysis (MFPCA) is used for missing value imputation and multi-sensor feature fusion, and the fused metrics are used in log-location-scale regression for RUL prediction. The above methods are essentially two-stage methods, which include two stages: first performing the missing values imputation, and then use the filled data for RUL prediction. There are some drawbacks in these methods: the missing value imputation stage does not fully exploit the effective information in the available data, which will lead to filling error, and this will lead to poorly RUL prediction performance. What’s more, the goals of the two stages of these methods are inconsistent, that is, the goal of the data imputation stage is inconsistent with the goal of the RUL prediction stage, which will cause the model to fail to achieve optimal.

To handle the problems mentioned above, a novel deep learning model is proposed in this work, which is named self-attention-based multi-task network (SMTN). There are two main modules in SMTN to deal with the missing values problem, namely the spatiotemporal feature fusion module and the multi-task learning module. The former module aims at fully exploiting the deep information in the available data, and the latter one tries to recover the complete representation for better RUL prediction. The novelty of this work lies in proposing a novel multi-task deep learning framework dealing with missing values in RUL prediction. The object of the proposed method is to predict the RUL accurately with missing values in the input data, which is common in real world applications. Specifically, in order to accurately predict RUL when there are missing values in the input data, the missing value imputation task is implemented to extract features containing complete degradation information, and such features are utilized for RUL prediction. In order to fully exploit the information in incomplete data, a spatiotemporal feature fusion mechanism combining self-attention mechanism and LSTM is proposed, which can effectively fully extract information from complete and incomplete data. In general, the novelty of the work is to propose a new paradigm that helps a lot in RUL prediction under missing values. The contributions of this work are summarized as follows:

• A novel self-attention-based deep learning model is proposed which can effectively handle the missing values problem in RUL prediction.
• Two mechanisms are designed in the proposed SMTN to deal with the missing values in different ways, namely the spatiotemporal feature fusion module and multi-task learning module.
• Extensive experimental studies verified the effectiveness of the proposed method.

The rest is organized as follows: the details of the proposed method are described in Section 2, Section 3 shows the experimental studies and the results, and finally, Section 4 concludes this work.

2. Proposed Method

In this section, we describe the proposed method in detail. The structure of SMTN is illustrated in Figure 1. The key part of the proposed method is a multi-task learning model based on the self-attention mechanism. Spatiotemporal feature extraction and fusion are first performed before multi-task learning. The classic CNN layer is utilized for feature extraction from the data of each sensor. Since the self-attention mechanism has the ability to fully explore the correlation of the input data, here we utilized it for spatial feature fusion, which means the correlation between sensors is modeled using a self-attention module. LSTM layers are used to model the temporal correlations of the input sequence to fuse features along the temporal dimension. After feature extraction and fusion, a multi-task module is performed, in which the missing values imputation and RUL prediction tasks are performed in parallel. The role of multi-task learning is to recover the complete signal from the input data with missing values and use the representation of the intermediate layer containing complete information for RUL prediction. Compared with directly predicting using data with missing values, better RUL prediction performance can be obtained using multi-task learning.

2.1. Self-Attention Mechanism

Here, we first detail the computational process of the self-attention mechanism and incorporate it into our method later. The self-attention mechanism was originally used for modeling sequence data [14], and later researchers extended it to image data in [16], which proves that self-attention is actually not only effect for sequence data, but can also model the correlations of various types of data. Given an input sequence data $\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N]\in {\mathbb{R}}^{d\times N}$, the self-attention layer will output an sequence $\widehat{\mathbf{X}}=[{\widehat{\mathbf{x}}}_1,{\widehat{\mathbf{x}}}_2,\cdots ,{\widehat{\mathbf{x}}}_N]$ with the same shape as $\mathbf{X}$. For the vector ${\widehat{\mathbf{x}}}_i$ at position i, the information of the input data of other positions is fused in it so that the information of the data at different positions can be fully explored. For each ${\mathbf{x}}_i$, linear transformation is firstly used to map it into the query space, key space, and value space as follows:

$${\mathbf{q}}_i={\mathbf{W}}_q·{\mathbf{x}}_i,{\mathbf{k}}_i={\mathbf{W}}_k·{\mathbf{x}}_i,{\mathbf{v}}_i={\mathbf{W}}_v·{\mathbf{x}}_i,$$

(1)

where ${\mathbf{W}}_q\in {\mathbb{R}}^{D\times d}$, ${\mathbf{W}}_k\in {\mathbb{R}}^{D\times d}$, and ${\mathbf{W}}_v\in {\mathbb{R}}^{D\times d}$ denote the transformation matrices which are learnable.

To model the correlation between ${\mathbf{x}}_i$ and other positions, dot product is performed on ${\mathbf{q}}_i$ and $\mathbf{K}=[{\mathbf{k}}_1,{\mathbf{k}}_2,\cdots ,{\mathbf{k}}_N]$, followed by the scale and softmax operation to produce the attention score of ${\mathbf{x}}_i$ to each other position:

$${\mathbf{a}}_i=softmax\left(\frac{{\mathbf{q}}_i^T·\mathbf{K}}{\sqrt{D}}\right)$$

(2)

Then for the purpose of fusing the information from other positions, element-wise product is performed on the attention score ${\mathbf{a}}_i=[a_{i1},a_{i2},\cdots ,a_{iN}]$ and the value matrix $\mathbf{V}=[{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_N]$, then sum all the vectors to produce the fused vector ${\widehat{\mathbf{x}}}_i$ of position i:

$${\widehat{\mathbf{x}}}_i=sum({\mathbf{a}}_i\otimes \mathbf{V})$$

(3)

Intuitively, we illustrate the calculation process in Figure 2.

2.2. Spatiotemporal Feature Fusion

The first part of the proposed SMTN is the spatiotemporal feature fusion module based on self-attention mechanism. Here the self-attention mechanism described in Section 2.1 is introduced to perform the spatial feature fusion due to its outstanding modeling ability. built the feature extraction and fusion module. First we employed 1D CNN layers to extract the deep features of the input sample data ${\mathbf{x}}_s^{\left(t\right)}\in {\mathbb{R}}^{w\times 1}$ of each sensor s at time t, where w denotes the sample length or sliding window size which will be described in Section 3.1. CNN is a classic model which is widely used in computer vision due to its strong feature extraction ability. In PHM, CNN has also been widely applied and performs well [25], since it can capture the local correlation in the time-series data. For the signals on each sensor, feature extraction is performed using 1D CNN layers with kernel size is $4\times 1$, striding is 2 and padding is 0. The extracted feature maps are expanded into a sequence of feature vectors. This means that each feature vector only contains the information of the corresponding sensor, and does not fully fuse the information among all sensors. This is detrimental to RUL prediction, especially if there are missing values in the input data. Therefore, in order to fully explore the available information, we introduce the self-attention mechanism for the spatial fusion of features.

For a set of feature vectors ${\mathbf{F}}_t=[{\mathbf{f}}_1^{\left(t\right)},{\mathbf{f}}_2^{\left(t\right)},\cdots ,{\mathbf{f}}_S^{\left(t\right)}]$ corresponding to S sensors at time t after 1D CNN layers, the correlations of sensors can be captured by sending it to the stacked self-attention layers mentioned in Section 2.1. The self-attention mechanism is essentially a weighted sum operation of features from a different sensor, and the weights of each sensor contain the correlation information between it and other sensors. This mechanism can fully explore the correlation between each sensor so that the output feature vector of each sensor after self-attention layers is fully considered the information from other sensors. Thus, these fused features lead to better RUL prediction than unfused features especially encountering the value missing problem. After stacked self-attention layers, residual connections are utilized to alleviate the vanishing gradient problem and speed up the training process.

After the spatial feature fusion, the classical LSTM layers are utilized for temporal feature fusion. LSTMs can model the correlation of sequence data effectively, and it’s also widely utilized in RUL prediction [13,26]. Specifically, the feature matrix ${\widehat{\mathbf{F}}}_t=[{\widehat{\mathbf{f}}}_1^{\left(t\right)},{\widehat{\mathbf{f}}}_2^{\left(t\right)},\cdots ,{\widehat{\mathbf{f}}}_S^{\left(t\right)}]$ output by the self-attention layers is firstly expanded into a feature vector ${\mathbf{f}}_t$, then iteratively input the feature vector to the LSTM cell at each time step, the features before current iteration is naturally fused and passed to the next iteration. The output vector ${\mathbf{f}}_t^{{}^{\prime }}$ of time step t naturally contains the information of previous time steps $1\sim t-1$.

2.3. Multi-Task Learning

To further improve the performance of RUL prediction under missing values, we propose a multi-task learning module in our model. The overall structure of this module is that two tasks share some layers of the network and perform different tasks after the last common layer, which means that the latent representation output by the last common layer will be shared by both tasks, as illustrated in the right of Figure 1. The advantage of this approach lies in that the model will be lead to capture the correlation between different tasks by the parallel performing of different but related tasks, and this will positively promote the performance of tasks. More intuitively, task A can be benefited by the information of task B due to the correlation information, and so can task B. Thereby, a better representation can be learned by the model than if the two tasks were performed separately.

In the case of RUL prediction under missing values, the motivation for using the multi-task learning module lies in that simply feeding the features extracted by the previous fusion module into the RUL prediction module can hardly achieve good performance when encountering a large number of missing values in the input data, since there is severe information loss in the features. Although the spatiotemporal feature fusion module had obtained available information from the limited data, limited by the insufficient capabilities of the model, without guidance and assistance, the model cannot predict the RUL accurately from the low-quality representations.

Specifically, based on the idea of multi-task learning, a missing value imputation task module is introduced after the feature fusion module, where the purpose is to lead the model to learn a latent representation that contains complete information since it can recover the complete signal. Simultaneously, this latent representation will be used for RUL prediction task in the parallel module, so the system RUL can be better predicted with this latent representation containing complete information. The missing value imputation module is implemented by a multi-layer fully connected neural network, which maps the latent representation to the observation signal space. And the RUL prediction using the latent representation is also performed with a multi-layer fully connected neural network. The above two tasks are conducted in parallel, and combined by sharing the preceding network layers.

There are two terms in the final objective function, namely the RUL prediction loss term and the missing values imputation loss term, respectively. So the final objective function is

$$\mathcal{L}=(1-\alpha )·{Loss}_{RUL}+\alpha ·{Loss}_{IMP}$$

(4)

where $\alpha$ trade off the two tasks, and ${Loss}_{RUL}$ and ${Loss}_{IMP}$ denote the loss of the RUL prediction task and missing values imputation task, respectively. Here, we use the mean square error (MSE) to be the loss function of both two tasks since they are all regression tasks, then we have

$$\mathcal{L}=\frac{1-\alpha }{N}\sum _{n=1}^N{({\widehat{y}}_n-y_n)}^2+\frac{\alpha }{wSN}\sum _{n=1}^N\left|\right|{\widehat{\mathbf{X}}}_n-{\tilde{\mathbf{X}}}_n{\left|\right|}_F^2$$

(5)

where N, w, and S stand for the number of samples, sliding window size, and the number of sensors, respectively. ${\widehat{\mathbf{X}}}_n$ and ${\tilde{\mathbf{X}}}_n$ means the output and the ground-truth complete value of sample n, ${\widehat{y}}_n$ and $y_n$ denotes the predicted RUL and the real RUL of sample n, respectively.

3. Experimental Study

To comprehensively verify the performance of the proposed method, we conduct experimental studies, including comparative experiments, ablation studies, and parameter sensitivity analysis. A detailed description will be given in the following sections.

3.1. Data Description and Preprocessing

The dataset used in our experimental study is the simulated aero-engine degradation data [27] created by NASA, which is also named C-MAPSS. Four sub-datasets are included in the C-MAPSS dataset, namely FD001, FD002, FD003, and FD004 which consists of training set and testing set in each of them. Each training set contains a sets of multi-sensor degradation signals corresponding to different engines under different fault modes and operation conditions, and the same is true for the test set. The difference is that the signal in the training set is collected from minor initial fault until it fails completely, while the signal in the testing set are ended at some time point before it fails completely. The real RUL is provided in all training and testing samples, and we applied piece-wise RUL as the target RUL according to [28]. The details of C-MAPSS are shown in

Table 1. The details of C-MAPSS dataset [29].

Subsets	FD001	FD002	FD003	FD004
Training engines	100	260	100	249
Testing engines	100	259	100	248
Fault modes	1	1	2	2
Operation conditions	1	6	1	6

.

As the previous studies [21,30], we performed sensor selection on this dataset which means removing the meaningless sensor data that has no degradation information.

The max-min normalization is utilized after sensor selection, which is a commonly used method in previous studies. The purpose of normalization is to map the features in different scales to the same scale, thereby the model can be well trained instead of failure due to pay too much attention on the large scale features and ignore the small scale features. Here, we map the features to $[0,1]$ using the following formula:

$$x_{\mathrm{norm}}^{(i,j)}=\frac{x^{(i,j)}-x_{\min }^{\left(i\right)}}{x_{\max }^{\left(i\right)}-x_{\min }^{\left(i\right)}}\forall i,j,$$

(6)

where i and j stands for the number of sensor and data point, $x^{(i,j)}$ and $x_{\mathrm{norm}}^{(i,j)}$ denotes the raw data and normalized data, $x_{\max }^{\left(i\right)}$ and $x_{\min }^{\left(i\right)}$ are the maximum and minimum values of sensor i, respectively.

In the proposed method, both the data with missing values and the corresponding ground-truth of the complete data are required, which is determined by the proposed method since missing value imputation is a supervised task. Or simply put, the complete values corresponding to the missing values are needed in calculating the loss function of missing values imputation task. Thus, the dataset with real world missing values are not applicable in the proposed method, since there are no complete values corresponding to the missing values can be obtained as the label in missing values imputation task, as a result we perform artificial missing value simulation on the complete data to construct the dataset we need. To some extent, the simulation of missing values is part of the proposed method, not only for experimental studies.

A variety of datasets with different overall missing rates are constructed, where the missing rates range from 0 to 0.8. There is a assumption that the missing values can be detected, and the missing values are simply set to 0. In order to improve the robustness of the model, instead of simply removing values randomly, we perform different degrees of value missing according to the sensor importance given in the literature [31]. That is, the more important the sensor is, the higher the missing rate is set. By recovering the important sensor data, the model can learn to capture the important information.

After normalization and missing values simulation, we implement sliding window processing with step size 1 to slice the time series signals to a series of samples. That is, each sample is a matrix $S\in {\mathbb{R}}^{w\times S}$, where w is the length of the sliding window and S is the number of sensors, and there are $w-1$ overlapping time points between adjacent samples. In our experiments, w and S are set to 30 and 14, respectively.

3.2. Experimental Settings and Metrics

In our experiments, there are several hyperparameters in the proposed method to be selected, we performed the grid searching method to select the proper value. Specifically, the number of the self-attention layers is 3, the number of LSTM layers is 2, and the hidden size in the LSTM is 512. In the objective function, the α is set to be 0.35. We used the Adam optimizer to perform the model training, and the learning rate, batch size, and epochs are 0.001, 128, and 300, respectively. The model is initialized with the Xavier uniform initializer [32]. In the selected comparison methods in Section 3.4, the support vector regression (SVR) and multi layer perceptron (MLP) are implemented using the classic machine learning library $scikit–learn$ with default values of the training parameters. For the deep long-short term memory (DLSTM) [33], we implement it according to the paper and adapt it to our data dimension. For the feature-attention based bidirectional gated recurrent unit CNN model (AGCNN) [29] and deep convolution neural network (DCNN) [34], we constructed the models with the given parameters in the paper, then applied them to our datasets. All experiments are performed on a server with 64-bit Ubuntu 18.04, which has a GeForce RTX 2080 Ti GPU with 12 GB memory. All the reported results are an average of five times.

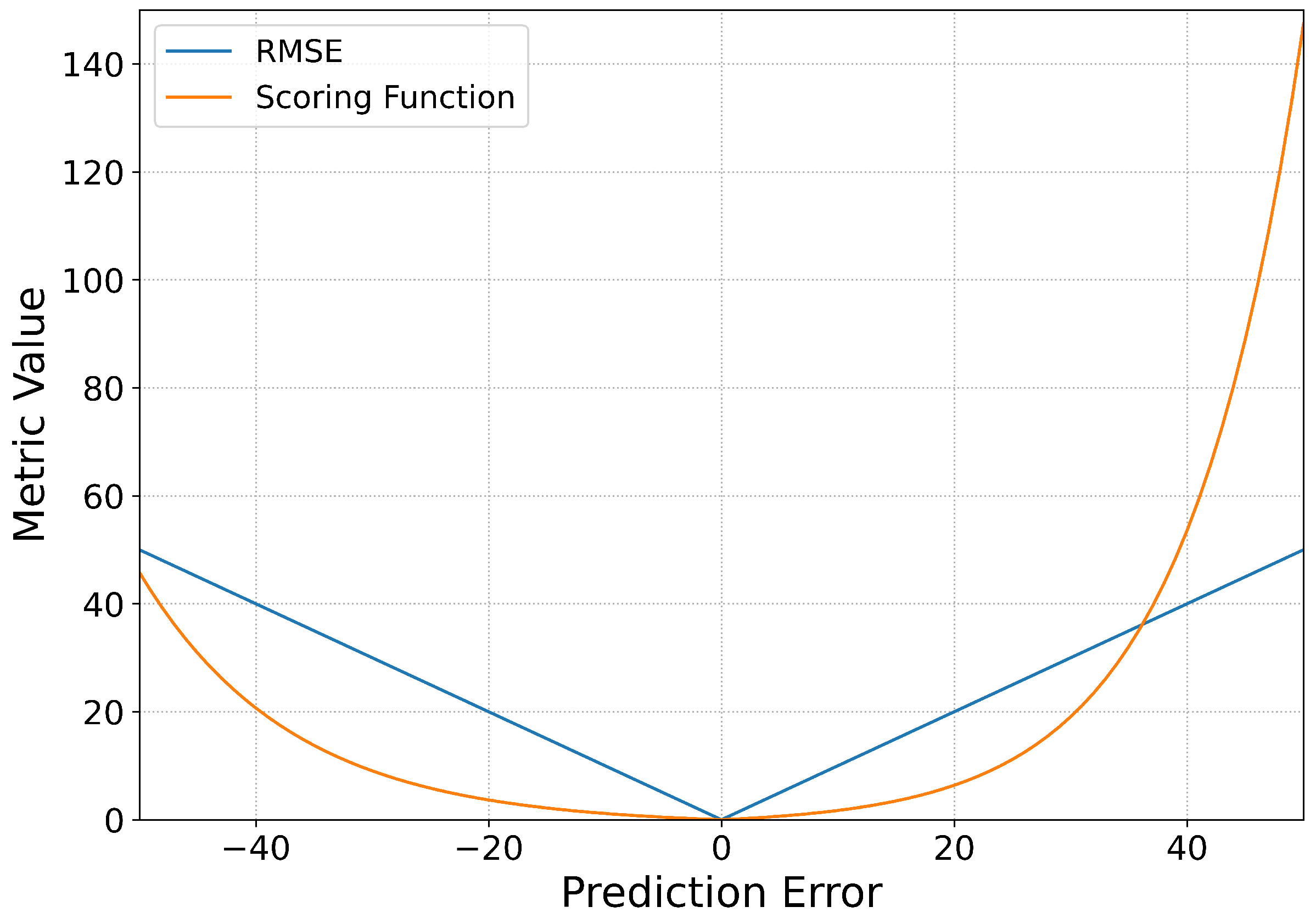
To evaluate and compare the performance of the proposed model, two metrics are used here which are root mean square error (RMSE) and the scoring function in [27]. RMSE is widely used to evaluate the performance of regression task, and the scoring function is a specially designed metric for RUL prediction task. The RMSE is calculated with

$$RMSE=\sqrt{\frac{1}{N}\sum _{n=1}^N{({\widehat{y}}_n-y_n)}^2},$$

(7)

where N means the number of samples, ${\widehat{y}}_n$ and $y_n$ denote the predicted value and the target RUL of sample n, respectively.

The scoring function is designed to overcome the shortcomings of RMSE, which can penalize the earlier and later prediction in different degrees, this is important in real industrial applications. The scoring function is defined as

$$SCORE=\left\{\begin{array}{cc}\hfill & \sum _{e=1}^E(e^{-\frac{{\widehat{y}}_e-y_e}{13}}-1),\mathrm{when}{\widehat{y}}_e<y_e\hfill \\ \hfill & \sum _{e=1}^E(e^{\frac{{\widehat{y}}_e-y_e}{10}}-1),\mathrm{when}{\widehat{y}}_e\ge y_e\hfill \end{array}\right.,$$

(8)

where E denotes the total number of testing engines, ${\widehat{y}}_e$ and $y_e$ denote the predicted RUL and the target RUL of the last sample of engine e, respectively. As it defined, the scoring function penalizes more severe on late prediction. RMSE and the scoring function are visualized in Figure 3.

Intuitively, it can be seen on the positive axis of prediction error in Figure 3 that when the predicted RUL is larger than the actual RUL, which means late prediction and usually leads to severe accidents, the scoring function imposes a larger penalty on the error. While under the situation of earlier prediction on the negative axis of prediction error, the scoring function penalizes less than the former case. However, the RMSE is symmetrical about 0 which means paying equal attention to the earlier and later prediction cases that lead to different degrees of harm.

3.3. Ablation Study

To deal with the RUL prediction problem under missing values, there are two main measures in SMTN: spatiotemporal feature fusion based on self-attention mechanism and multi-task learning. To verify the effectiveness of these designs, we conduct ablation studies on FD003 subset. Specifically, first we validate the role of the spatiotemporal feature fusion module in RUL prediction. By removing the spatiotemporal fusion module from SMTN, which is named SMTN${}^{*}$, we directly input the features extracted by the CNN into the multi-task learning module and compare the prediction performance under different missing rates with the standard version SMTN. Next, to study the effectiveness of the multi-task learning module, we implement the ablation study by setting the hyperparameter alpha to 0, which is named SMTN${}^{†}$. That is, the missing value imputation module is not optimized, which is equivalent to using only the RUL prediction module. The performance is also compared with the standard version. The experimental results of the above two cases are shown in

Table 2. The performance comparison of SMTN${}^{*}$ and SMTN on FD003 using RMSE under different missing rates (MR).

MR	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
SMTN${}^{*}$	13.56	13.82	14.19	14.23	15.87	19.02	19.72	21.32	21.55
SMTN	10.74	11.12	10.96	11.35	12.88	15.83	17.37	18.99	19.35
Improvement	20.80%	19.54%	22.76%	20.24%	18.84%	16.77%	11.92%	10.93%	10.21%

and

Table 3. The performance comparison of SMTN${}^{†}$ and SMTN on FD003 using RMSE under different MR.

MR	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
SMTN${}^{†}$	11.03	11.21	11.89	13.79	15.34	17.10	18.94	20.21	20.57
SMTN	10.74	11.12	10.96	11.35	12.88	15.83	17.37	18.99	19.35
Improvement	2.63%	0.80%	7.82%	17.69%	16.04%	7.43%	8.29%	6.04%	5.93%

, respectively.

Note that the $Improvement$ is defined as

$$Improvement=\left(\frac{RMS{E}_{ablated}-RMSE}{RMS{E}_{ablated}}\right)\times 100\%$$

(9)

where $RMS{E}_{ablated}$ denotes the RMSE of the two ablated models, namely SMTN${}^{*}$ and SMTN${}^{†}$ in Table 2 and Table 3, respectively, and $RMSE$ stands for the RMSE of standard version model, namely $SMTN$.

The results in Table 2 show that the RUL prediction performance under missing values of SMTN${}^{*}$ is much lower than that of the standard version. In terms of RMSE, even though there are no missing values in the data, the standard version SMTN is improved by about 20% compared with SMTN${}^{*}$. As the increase of the missing rate, the improvement of the RMSE value remains at about 20%, until the missing rate reaches more than 0.6, the improvement ratio is reduced to about 10%. The reason lies in that the spatiotemporal fusion module can effectively fully explore and fuse the available information in the input data from both the time and space dimensions, and this is critical to RUL prediction both under and no under missing values. However, without the mechanism of effective fusion of spatiotemporal features, the RUL prediction accuracy of the model is greatly reduced. Thus, the results fully demonstrate that the spatiotemporal module is crucial in the proposed model.

Table 3 compared the RUL prediction performance under different missing rates using multi-task learning and not using multi-task learning. In general, the performance of SMTN that using multi-task learning improves a lot than SMTN${}^{†}$ that not using it, but the improvement is not significant when the missing rate is too low or too high. For the former case, there are less information losing in the data and the general method is sufficient for dealing with this problem, multi-task learning cannot give full play to its advantages. When the missing rate is too high, the excessive information loss makes multi-task learning unable to obtain better prediction performance because it cannot recover the missing values with few available data. In general, the multi-task learning can achieve better RUL prediction when the missing rate is not too high or too low, because multi-task learning can obtain a hidden representation containing complete information by recovering the missing values with the available data, and this representation can lead to better RUL prediction performance.

3.4. Comparative Experiment

To investigate the performance of the proposed method for RUL prediction in values missing scenarios, comparative experiments are conducted between the proposed method and some typical methods. We selected a variety of typical comparison methods including SVR, MLP, DLSTM, DCNN, and AGCNN, and reproduced the results reported in the paper as much as possible, and then applied them to our dataset. The comparison results using RMSE and the score are shown in

Table 4. RMSE and the score of compared methods on C-MAPSS under different MR.

Metrics	Subset	MR	SVR	MLP	DLSTM	DCNN	AGCNN	SMTN
RMSE	FD001	0	15.58	20.62	13.48	13.71	13.09	12.38
		0.1	19.03	21.07	17.61	13.75	13.94	12.79
		0.2	19.60	21.82	21.20	13.38	14.13	12.83
		0.3	20.87	24.40	22.21	15.09	15.25	13.35
		0.4	21.85	26.16	22.80	16.85	16.87	15.21
		0.5	22.96	28.67	23.27	19.94	19.76	18.02
		0.6	24.15	29.87	25.02	21.39	19.85	19.23
		0.7	24.01	36.43	24.83	20.31	20.73	20.54
		0.8	24.14	46.13	24.36	22.32	21.14	21.43
	FD003	0	15.49	17.66	11.31	11.66	12.08	10.74
		0.1	17.36	18.68	13.69	11.66	13.07	11.12
		0.2	17.84	19.55	14.54	12.32	13.76	10.96
		0.3	18.84	21.72	17.96	13.62	13.82	11.35
		0.4	20.15	24.86	18.69	15.27	14.53	12.88
		0.5	21.67	26.04	20.21	17.64	17.81	15.83
		0.6	22.41	28.61	22.79	16.39	17.87	17.37
		0.7	23.00	31.32	20.74	17.62	19.43	18.99
		0.8	23.60	35.79	21.38	19.63	19.43	19.35
SCORE	FD001	0	475.17	1723.54	319.89	282.85	233.34	245.89
		0.1	1186.65	1384.44	752.17	416.98	528.26	372.11
		0.2	1243.58	1425.77	2023.09	472.05	411.62	351.82
		0.3	1916.70	1869.10	3719.53	799.67	497.74	422.65
		0.4	2222.08	10,610.61	4085.67	848.41	509.87	472.74
		0.5	6985.87	8626.61	3590.35	1772.34	795.78	925.54
		0.6	3032.66	1955.51	8044.69	1350.10	1268.10	920.25
		0.7	2428.92	4272.51	10,798.33	2655.43	1479.28	2104.73
		0.8	5246.20	22,689.29	15,817.78	5116.64	2292.33	2461.81
	FD003	0	1257.49	2236.46	732.43	282.23	240.08	238.98
		0.1	2007.97	2171.79	820.59	430.03	327.57	332.57
		0.2	1997.12	2194.71	2416.02	598.96	360.95	357.89
		0.3	2181.85	3280.49	3889.62	563.09	530.96	493.21
		0.4	2715.29	2761.14	5809.09	1194.57	857.15	793.62
		0.5	3115.46	5423.23	8890.98	3215.52	3135.02	2508.24
		0.6	4508.54	33,535.98	6881.44	2533.28	4944.36	2894.04
		0.7	3240.60	12,069.38	7501.80	3217.82	4538.29	3104.93
		0.8	4927.10	42,927.81	17,348.62	4373.71	3879.53	4020.19

.

It can be seen that the proposed method comprehensively outperforms the compared methods. Generally, the classical SVR and MLP methods perform far less well than relatively advanced methods, especially when encountering the missing values. The reason is that they cannot effectively exploit the abstract deep features in the data. The typical deep learning methods such as DCNN and AGCNN are basically the same as the proposed method when there are no missing values, but when encountering a lot of missing values in the data, the proposed method surpasses other compared methods. The reason is that there are various designed mechanisms for values missing problem in the proposed method.

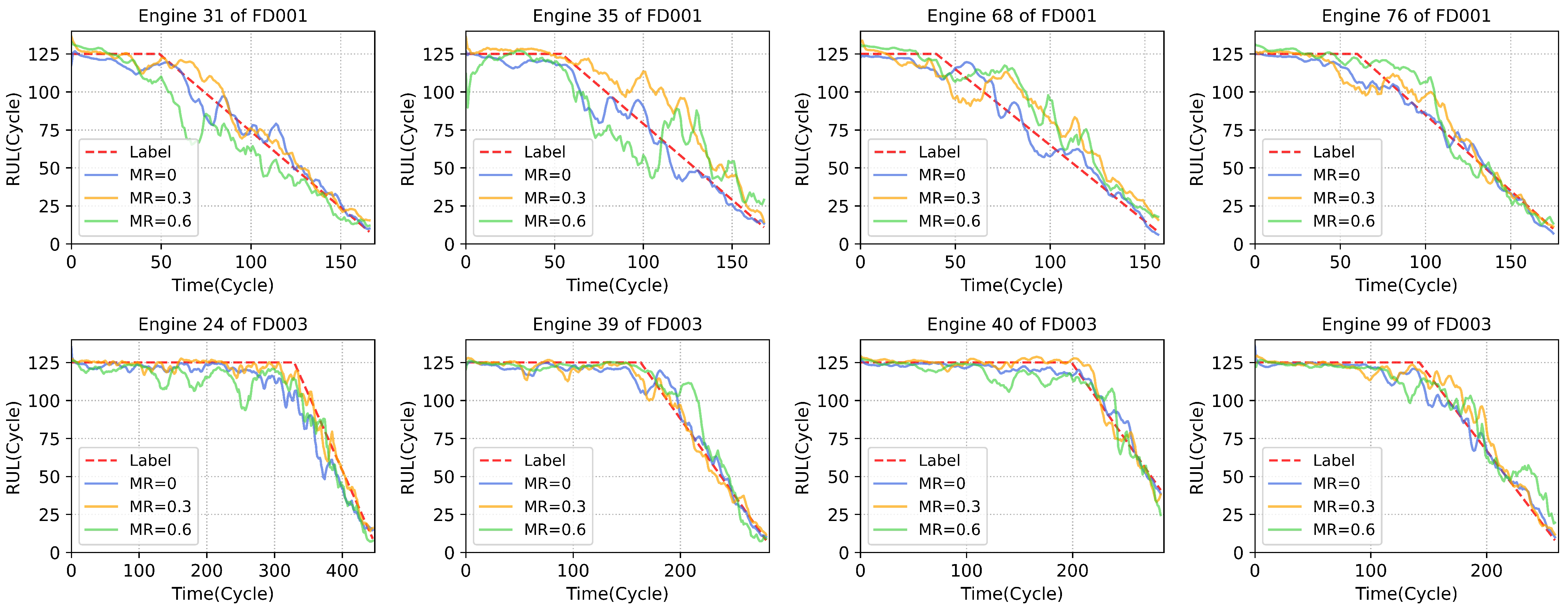
Firstly, the spatiotemporal feature extracting and fusion module can effectively exploit and integrate the information in the available data, which provides the guarantee for high-performance RUL prediction under values missing. The effectiveness is guaranteed by the ability of the self-attention mechanism to model the correlations between different sensors, which contains the spatial information, and the LSTM layers can fuse the features along time steps in the output representations which utilizes the history information of degradation. The multi-task learning further improves the performance under missing values. The missing value imputation task can recover the missing values, thus with the assistance of the missing values imputation task, the representations containing complete information can be effectively extracted by the model, which is not available in the compared methods. To demonstrate the RUL prediction performance of the proposed method intuitively, we select some typical samples to show the prediction performance of SMTN in Figure 4.

3.5. Parameter Sensitivity Analysis

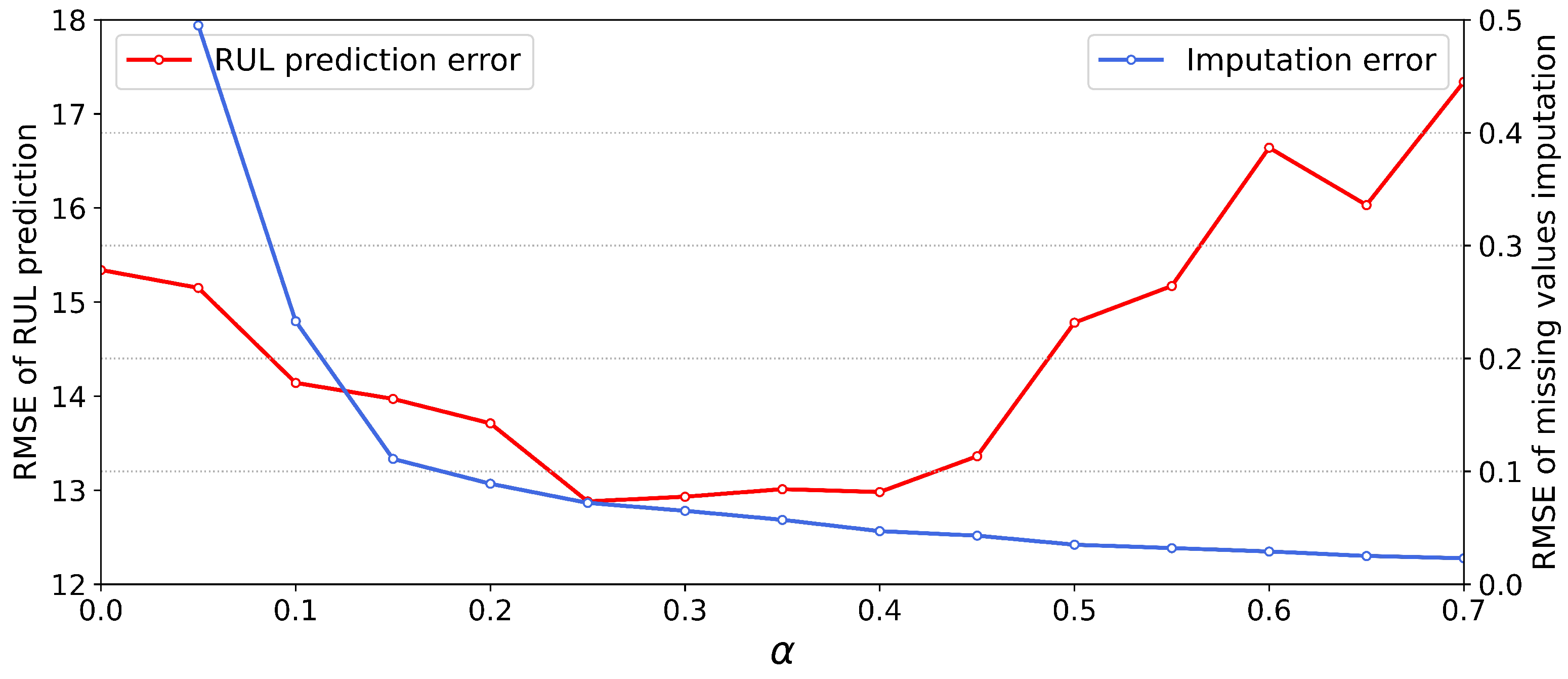
In our multi-task approach, the contribution of the two tasks to the model optimization process is controlled by the hyper-parameter alpha, which determines the proportion of loss in the objective function for the missing values imputation task and the RUL prediction task. The inappropriate parameters will lead to the degradation of the performance of the model because there need a trade-off between two tasks. In order to investigate the impact of the choice of $\alpha$ on the model performance, we conducted experiments on the FD003 dataset under missing rate of 0.4. We set different $\alpha$ and then training and testing the model, the RUL prediction error and missing values imputation error are shown in Figure 5.

The blue and red line represents the RMSE value of missing values imputation task and RUL prediction task, respectively. When $\alpha =0$ which means the missing values imputation module is not trained, the output by the missing values imputation module is equivalent to a random value, and the RMSE is very large and meaningless. When $\alpha =0.05$, the imputation error is significantly reduced, and the RUL prediction performance is slightly improved. This indicates that the missing value imputation module is effectively optimized and recovers the missing values to a certain degree. When $\alpha$ is further increased, the performance of the model is also improved accordingly and reaches its peak until $\alpha =0.25$, and the missing value imputation error tends to stabilize. When $\alpha$ is further increased, it can be seen that the error of missing value imputation is still slowly decreasing, but the performance of RUL prediction becomes worse. This is because an excessively large alpha value makes the model pay too much attention to the accuracy of missing value imputation, which leads to overfitting of the missing value imputation module. Thus, the hidden representation of the middle layer contains too much noise information that is useless for RUL prediction, which leads to the deterioration of RUL prediction performance. Note that the results we show were obtained with a certain missing rate of 0.4 for FD003, and in fact we have experimented with a variety of missing rates and the results show that the optimal value of $\alpha$ is close under different missing rates, and the best $\alpha$ is set to 0.25 accordingly.

4. Conclusions

In this work, we focus on the missing values problem in RUL prediction. A novel prediction model named SMTN is proposed to deal with this problem. There are two key parts in SMTN, namely spatiotemporal feature fusion module and multi-task learning module, the former one using the self-attention mechanism and classical LSTM to perform the feature fusion in space dimension and time dimension, the deep features and information can be fully exploit from the available data. The multi-task learning module try to learn a complete representation from the incomplete data by implement the missing values imputation task, and the complete representation are simultaneously used for RUL prediction under missing values. Experiments conducted on C-MAPSS verified the effectiveness of SMTN.

The performance of RUL prediction under missing values can be effectively improved, which is conducive to the application of RUL prediction in wider industrial scenarios, this will further improve the intelligence level of industrial maintenance and management. In future work, we will focus on the high performance RUL prediction under sensor faults which is a more common problem in real industrial applications.