Fault-Tolerant Predictive Current Control of Six-Phase PMSMs with a Single Isolated Neutral Configuration

Abstract

Six-phase machines are increasingly used in safety-critical applications due to their inherent fault-tolerant capabilities. Due to the greater complexity of controlling six-phase machines and the fast dynamics required in safety-critical applications, finite control set model predictive control (FCS-MPC) emerged as an ideal candidate for the control of six-phase machines. However, most of the available FCS-MPC strategies only apply to six-phase machines where the two sets of three-phase windings are star-connected with isolated neutral points (2N). Nevertheless, the 2N configuration does not take full advantage of the machine’s capabilities in terms of fault tolerance. Hence, this paper proposes a predictive current control strategy based on virtual vectors for six-phase permanent magnet synchronous (PMSM) drives with a single isolated neutral point (1N) configuration. The proposed method reduces the current harmonic distortion, decreases the copper losses, and is suitable to operate the six-phase drive in fault-tolerant conditions. The included simulation and experimental results demonstrate the good performance obtained with the proposed strategy.

1. Introduction

Multiphase machines are ideal for offshore wind energy and safety-critical applications, such as aerospace, aircraft, and electric traction [1,2,3]. Among the many advantages of multiphase machines is their improved fault tolerance capability, which is often highlighted as their main advantage over three-phase machines [4].

Among the different multiphase machine topologies, the six-phase machine is one of the most adopted due to its simple design and compatibility with existing three-phase power converter technology [5]. Furthermore, the six-phase asymmetrical winding configuration with two isolated neutral points (2N) is often preferred as it provides higher utilization of the dc bus voltage and restricts the circulation of zero-sequence currents [6]. However, the single isolated neutral point (1N) configuration provides a better torque range during fault-tolerant operation [7]. Furthermore, the six-phase machine with the 1N configuration can remain in operation with up to three open-phase faults (OPFs), independent of their location [8].

In recent years, the scientific community has pointed out finite control set model predictive control (FCS-MPC) as a solid alternative to classical control strategies, such as field-oriented control and direct torque control, in the control of six-phase drives [9,10]. In addition to excellent dynamic performance, FCS-MPC provides a straightforward design and has low tuning requirements [11,12]. Regarding the application of FCS-MPC strategies to six-phase drives, emphasis has been given to the use of virtual vectors to minimize the current harmonic distortion in six-phase induction machines (IMs) [13,14,15] or six-phase permanent magnet synchronous machines (PMSMs) [16,17,18,19]. In addition to its excellent transient performance, the ease of inclusion of different control objectives and constraints on the cost function are the main reasons why the FCS-MPC has been widely studied for fault-tolerant control in six-phase drives [20,21,22,23]. However, existing fault-tolerant FCS-MPC strategies based on virtual vectors only apply to six-phase machines with a 2N configuration [24,25,26].

This paper proposes a new fault-tolerant predictive current control (FT-PCC) strategy based on virtual vectors for six-phase PMSM drives operating with a 1N configuration. In addition to providing a low current harmonic distortion, the proposed technique can operate the six-phase drive in fault-tolerant conditions by adequately adjusting the reference currents after the fault occurrence while maintaining the same control structure. The efficacy of the control strategy proposed here for improving the drive performance is demonstrated through simulation and experimental results.

2. System Model

The diagram of the adopted six-phase PMSM drive is shown in Figure 1, where the machine is powered by two-level voltage source inverters (2L-VSIs), and the PMSM stator windings are wye-connected with a single isolated neutral point (1N).

Figure 1. Diagram of a six-phase PMSM drive with a 1N configuration.

The output voltages of the 2L-VSIs in Figure 1, measured between phase u and the negative dc rail N are given by:

$${\mathbf{u}}_{sN}^{abc}=U_{dc}\mathbf{s},$$

(1)

with:

$${\mathbf{u}}_{sN}^{abc}={\left[\begin{array}{cccccc}{u}_{a1N}& u_{b1N}& u_{c1N}& u_{a2N}& u_{b2N}& u_{c2N}\end{array}\right]}^{\mathrm{T}}$$

(2)

$$\mathbf{s}={\left[\begin{array}{cccccc}{s}_{a1}& s_{b1}& s_{c1}& s_{a2}& s_{b2}& s_{c2}\end{array}\right]}^{\mathrm{T}},$$

(3)

where $U_{dc}$ is the dc-link voltage and $s_u=\left\{0,1\right\}$ is the switching state of the converter leg of phase u with $u=\left\{a1,b1,\dots ,c2\right\}$. If $s_u=1$, the upper switch of phase u is ON and the lower switch of phase u is OFF, while the opposite is verified if $s_u=0$.

Considering (1), the PMSM phase voltages are given by:

$$\begin{array}{cc}\hfill {\mathbf{u}}_s^{abc}=& {\mathbf{u}}_{sN}^{abc}-u_{nN}·{\left[\begin{array}{cccccc}1& 1& 1& 1& 1& 1\end{array}\right]}^{\mathrm{T}}\hfill \\ \hfill & {\mathbf{u}}_c^{abc}+{\mathbf{u}}_0^{abc}\hfill \end{array},$$

(4)

where $u_{nN}$ is the voltage measured between the isolated neutral point n and the negative dc rail N (see Figure 1):

$$u_{nN}=\frac{1}{6}\sum _{u=\{a1,\dots ,c2\}}{u}_{uN}-\frac{1}{6}\sum _{u=\{a1,\dots ,c2\}}{u}_u,$$

(5)

and vectors ${\mathbf{u}}_c^{abc}$ and ${\mathbf{u}}_0$ are defined as:

$${\mathbf{u}}_c^{abc}={\mathbf{u}}_{sN}^{abc}-\frac{1}{6}\sum _{u=\{a1,\dots ,c2\}}{u}_{uN}·{\left[\begin{array}{cccccc}1& 1& 1& 1& 1& 1\end{array}\right]}^{\mathrm{T}}$$

(6)

$${\mathbf{u}}_0^{abc}=\frac{1}{6}\sum _{u=\{a1,\dots ,c2\}}{u}_u·{\left[\begin{array}{cccccc}1& 1& 1& 1& 1& 1\end{array}\right]}^{\mathrm{T}}.$$

(7)

In (4), vector ${\mathbf{u}}_c^{abc}$ corresponds to the component of the PMSM voltages imposed by the 2L-VSIs, while vector ${\mathbf{u}}_0^{abc}$ corresponds to the PMSM zero-sequence voltage components (ZSVCs). Considering the $2^6=64$ possibilities for vector $\mathbf{s}$ in (1) and (6), the 2L-VSIs can apply forty-nine distinct voltage vectors to the PMSM, whose mapping in the $\alpha$-$\beta$, x-y and $z1$-$z2$ subspaces is shown in Figure 2.

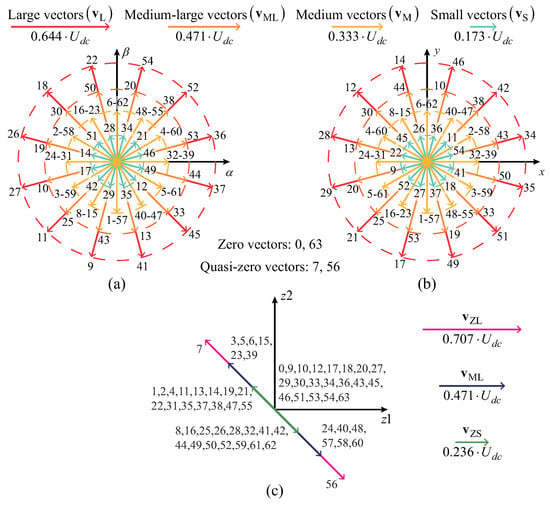
Figure 2. Mapping of the voltage vectors imposed by the 2L-VSIs to a six-phase machine with a 1N configuration: (a) $\alpha$-$\beta$; (b) x-y; (c) $z1$-$z2$ subspaces.

Considering the vector space decomposition (VSD) matrix in (8) and the rotational matrix $\mathbf{R}$ in (9):

$$\mathbf{T}=\frac{1}{3}\left[\begin{array}{cccccc}1& -\frac{1}{2}& -\frac{1}{2}& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}& 0\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}& \frac{1}{2}& \frac{1}{2}& -1\\ 1& -\frac{1}{2}& -\frac{1}{2}& -\frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}& 0\\ 0& -\frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}& \frac{1}{2}& \frac{1}{2}& -1\\ 1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\end{array}\right]$$

(8)

$$\mathbf{R}=\left[\begin{array}{ccc}{\mathbf{T}}_r& 0_2& 0_2\\ 0_2& {\mathbf{T}}_r^{-1}& 0_2\\ 0_2& 0_2& {\mathbf{I}}_2\end{array}\right],{\mathbf{T}}_r=\left[\begin{array}{cc}cos\left(\theta \right)& sin\left(\theta \right)\\ -sin\left(\theta \right)& cos\left(\theta \right)\end{array}\right],$$

(9)

where $\theta$ is the rotor electrical position, the model of the six-phase PMSM in the rotor reference frame, including model uncertainties, is given by [19]:

$$\frac{\mathrm{d}{\mathbf{i}}_s}{\mathrm{dt}}=\mathbf{A}·{\mathbf{i}}_s+\mathbf{B}·{\mathbf{u}}_s-\mathbf{B}·{\mathbf{e}}_s+\mathbf{B}·{\mathbf{d}}_s,$$

(10)

with matrices $\mathbf{A}$ and $\mathbf{B}$ being defined as:

$$\mathbf{A}=\left[\begin{array}{cccccc}-\frac{R_s}{L_{dq}}& {\omega }_r& 0& 0& 0& 0\\ -{\omega }_r& -\frac{R_s}{L_{dq}}& 0& 0& 0& 0\\ 0& 0& -\frac{R_s}{L_{xy}}& -{\omega }_r& 0& 0\\ 0& 0& {\omega }_r& -\frac{R_s}{L_{xy}}& 0& 0\\ 0& 0& 0& 0& -\frac{R_s}{L_{z12}}& 0\\ 0& 0& 0& 0& 0& -\frac{R_s}{L_{z12}}\end{array}\right]$$

(11)

$$\mathbf{B}=\mathrm{diag}\left\{\frac{1}{L_{dq}},\frac{1}{L_{dq}},\frac{1}{L_{xy}},\frac{1}{L_{xy}},\frac{1}{L_{z12}},\frac{1}{L_{z12}}\right\},$$

(12)

where ${\omega }_r$ is the rotor electrical speed, $R_s$ is the stator resistance, and $L_{dq}$, $L_{xy}$, and $L_{z12}$ are the inductances of d-q, $x^{\prime }$-$y^{\prime }$, and $z1$-$z2$ subspaces, respectively.

In (10), ${\mathbf{u}}_s$, ${\mathbf{i}}_s$, ${\mathbf{e}}_s$, and ${\mathbf{d}}_s$ are the voltage, current, back-EMF, and disturbance vectors. These vectors have the following format:

$${\mathbf{f}}_s={\left[\begin{array}{cccccc}{f}_d& f_q& f_{x^{\prime }}& f_{y^{\prime }}& f_{z1}& f_{z2}\end{array}\right]}^{\mathrm{T}}.$$

(13)

The inclusion of vector ${\mathbf{d}}_s$ in (10) increases the robustness of the FCS-MPC strategy against parameter mismatch errors or unmodeled dynamics due to the fifth and seventh back-EMF harmonics as well as deadtime effects. The disturbances in the d-q and $x^{\prime }$-$y^{\prime }$ subspaces are estimated by the disturbance observer (DOB) proposed in [19], whereas the disturbances in the $z1$-$z2$ subspace are assumed zero for simplicity, i.e., $d_{z1}=d_{z2}=0$. As discussed in [27], the dominant harmonics in the phase back-EMF of six-phase PMSMs with a 1N configuration are the third, fifth, and seventh. Since the DOB proposed in [19] already compensates for the fifth and seventh harmonics, vector ${\mathbf{e}}_s$ in (10) should take into account the third harmonic of the back-EMF:

$${\mathbf{e}}_s=\left[\begin{array}{c}{e}_d\\ e_q\\ e_{x^{\prime }}\\ e_{y^{\prime }}\\ e_{z1}\\ e_{z2}\end{array}\right]=\left[\begin{array}{c}0\\ {\omega }_r{\psi }_{\mathrm{PM}1}\\ 0\\ 0\\ -{\omega }_r{\psi }_{\mathrm{PM}3}sin\left(3\theta +{\varphi }_3\right)\\ {\omega }_r{\psi }_{\mathrm{PM}3}cos\left(3\theta +{\varphi }_3\right)\end{array}\right],$$

(14)

where ${\omega }_r$ is the rotor electrical speed, while ${\psi }_{\mathrm{PM}h}$ and ${\varphi }_h$ are the amplitude and initial phase of the h-order harmonic of the no-load flux linkage.

By combining (4) transformed into the synchronous reference frame and (10), the six-phase PMSM model becomes:

$$\frac{\mathrm{d}{\mathbf{i}}_s}{\mathrm{dt}}=\mathbf{A}·{\mathbf{i}}_s+\mathbf{B}·{\mathbf{u}}_c-\mathbf{B}·\underset{{\mathbf{e}}_s^{1\mathrm{N}}}{\underbrace{\left({\mathbf{e}}_s-{\mathbf{u}}_0\right)}}+\mathbf{B}·{\mathbf{d}}_s.$$

(15)

Since the currents are constrained by ${\sum }_u{i}_u=0$ with $u\in \left\{a1,\dots ,c2\right\}$ for the 1N configuration, which is equivalent to the restriction $i_{z1}=-i_{z2}$, vector ${\mathbf{u}}_0$ is given by:

$$\begin{array}{cc}\hfill {\mathbf{u}}_0=& \left(\mathbf{R}\mathbf{T}\right){\mathbf{u}}_0^{abc}\hfill \\ \hfill =& {\left[\begin{array}{cccccc}0& 0& 0& 0& \frac{1}{2}\left(e_{z1}+e_{z2}\right)& \frac{1}{2}\left(e_{z1}+e_{z2}\right)\end{array}\right]}^{\mathrm{T}}\hfill \end{array},$$

(16)

and vector ${\mathbf{e}}_s^{1\mathrm{N}}$ becomes:

$${\mathbf{e}}_s^{1\mathrm{N}}={\left[\begin{array}{cccccc}{e}_d& e_q& e_{x^{\prime }}& e_{y^{\prime }}& \frac{1}{2}\left(e_{z1}-e_{z2}\right)& -\frac{1}{2}\left(e_{z1}-e_{z2}\right)\end{array}\right]}^{\mathrm{T}}.$$

(17)

Since the constraint $i_{z1}=-i_{z2}$ is verified for the 1N configuration and the $z1$-$z2$ components in (17) are symmetric, the z1-$z2$ components of ${\mathbf{u}}_c$ are also symmetric. This symmetry is verified for all voltage vectors shown in Figure 2c.

3. Ft-Pcc Strategy

In order to keep the control strategy in [19] valid for six-phase PMSMs with the 1N configuration, it is necessary to redefine the virtual vectors and the dual virtual vectors to provide average zero voltage components in the $z1$-$z2$ subspace. Furthermore, it is necessary to design an additional control stage to regulate the $z1$-$z2$ currents.

As discussed in [28], the virtual vectors for six-phase machines with the 1N configuration $\left\{{\mathbf{v}}_{\mathrm{v}1}^{1\mathrm{N}},\dots ,{\mathbf{v}}_{\mathrm{v}12}^{1\mathrm{N}}\right\}$ are obtained by combining one large and one medium-large vector in the $\alpha$-$\beta$ subspace, with coinciding phases, as well as a zero or quasi-zero vector using the following duty cycles:

$$d_L^{1\mathrm{N}}=\frac{\sqrt{3}}{\sqrt{3}+1},d_{ML}^{1\mathrm{N}}=\sqrt{3}-\frac{3}{2},d_Z^{1\mathrm{N}}=1-\frac{\sqrt{3}}{2},$$

(18)

where $d_L^{1\mathrm{N}}$, $d_{ML}^{1\mathrm{N}}$, and $d_Z^{1\mathrm{N}}$ are the duty cycles of the large, medium-large, and zero or quasi-zero vectors, respectively.

The vectors $\left\{{\mathbf{v}}_{\mathrm{v}1}^{1\mathrm{N}},\dots ,{\mathbf{v}}_{\mathrm{v}12}^{1\mathrm{N}}\right\}$ shown in Figure 3a have an amplitude of $\left(\sqrt{3}-1\right)/\sqrt{2}·U_{dc}\approx 0.518·U_{dc}$ in the $\alpha$-$\beta$ subspace and zero components in both the x-y and $z1$-$z2$ subspaces. In the same manner, the dual virtual vectors $\left\{{\mathbf{v}}_{\mathrm{d}1}^{1\mathrm{N}},\dots ,{\mathbf{v}}_{\mathrm{d}12}^{1\mathrm{N}}\right\}$ are obtained by combining one large and one medium-large vector in the x-y subspace, with coinciding phases, as well as a zero or quasi-zero vector using the duty cycles in (18). Similarly, the dual virtual vectors shown in Figure 3b have an amplitude of $0.518·U_{dc}$ in the x-y subspace and zero components mapped into the remaining subspaces.

Figure 3. Mapping into the $\alpha$-$\beta$, x-y, and $z1$-$z2$ subspaces of: (a) virtual vectors; (b) dual virtual vectors.

By adopting the synchronized sampling approach used in [19] to reduce the noise in measured signals, the proposed control strategy first predicts the PMSM current for instant $k+0.5$ using:

$$\begin{array}{cc}\hfill {\mathbf{i}}_s^{k+0.5}=& \left[{\mathbf{I}}_6+\mathbf{A}·T_s\right]·{\mathbf{i}}_s^k+\hfill \\ \hfill & \mathbf{B}·T_s\left[{\mathbf{u}}_c^{k-0.5}-{\mathbf{e}}_s^{1\mathrm{N},k}+{\widehat{\mathbf{d}}}_s^k\right]\hfill \end{array},$$

(19)

where the estimate for ${\widehat{\mathbf{d}}}_s^k$ is obtained with the DOB proposed in [19], and whose expressions are given in Appendix A (A1).

The predicted current for instant $k+1.5$ is given by [19]:

$$\begin{array}{cc}\hfill {\mathbf{i}}_s^{k+1.5}=& \left[{\mathbf{I}}_6+\mathbf{A}·T_s\right]·{\mathbf{i}}_s^{k+0.5}+\hfill \\ \hfill & \mathbf{B}·T_s\left[{\mathbf{u}}_c^{k+0.5}-{\mathbf{e}}_s^{1\mathrm{N},k+0.5}+{\widehat{\mathbf{d}}}_s^{k+0.5}\right]\hfill \end{array},$$

(20)

where ${\widehat{\mathbf{d}}}_s^k$ is calculated using (A5).

Since $i_{z1}=-i_{z2}$, the zero control stage evaluates the following cost function for two quasi-zero candidate vectors $\left\{{\mathbf{v}}_7^{1\mathrm{N}},{\mathbf{v}}_{56}^{1\mathrm{N}}\right\}$, which only contain non-zero $z1$-$z2$ components:

$$g_{z,a}={\left(i_{z1}^{*}-i_{z1,a}^{k+1.5}\right)}^2,$$

(21)

where $i_{z1,a}^{k+1.5}$ is calculated by (20) for ${\mathbf{u}}_c^{k+0.5}=\mathbf{R}·{\mathbf{v}}_a$ with $a\in \left\{7,56\right\}$. The vector that minimizes (21) is given by:

$$w=\arg \underset{a}{\min }\left(g_{z,a}\right),a\in \{7,56\}.$$

(22)

The duty cycle $d_{z12}$ of the w-index vector is then obtained by minimizing:

$$f_{z,a}={\left(i_{z1}^{*}-\left[\left(1-d_{z12}\right)i_{z1,0}^{k+1.5}+d_{z12}·i_{z1,w}^{k+1.5}\right]\right)}^2,$$

(23)

which gives the following expression:

$$d_{z12}=\left(i_{z1,0}^{k+1.5}-i_{z1}^{*}\right)/\left(i_{z1,0}^{k+1.5}-i_{z1,w}^{k+1.5}\right),$$

(24)

where $i_{z1,0}^{k+1.5}$ is the predicted $z1$-axis current for instant $k+1.5$ due to a zero vector and $i_{z1,w}^{k+1.5}$ is the predicted $z1$-axis current for instant $k+1.5$ due to the w-index vector.

The flowchart of the proposed control strategy is shown in Figure 4, where the algorithm behind the fundamental and secondary control stages can be found in [19]. Due to the voltage limit of the 2L-VSIs, the duty cycles provided by the fundamental, secondary, and zero control stages must verify:

$$0\le d_i+d_j+d_m+d_n+d{}_{z12}\le 1,$$

(25)

where $d_{z12}$ is obtained by (24) and bounded to the range $\left[0,d_{z12}^{\max }\right]$, where $d_{z12}^{\max }$ is calculated by:

$$d_{z12}^{\max }=1-\left(d_i+d_j\right)-\left(d_m+d_n\right).$$

(26)

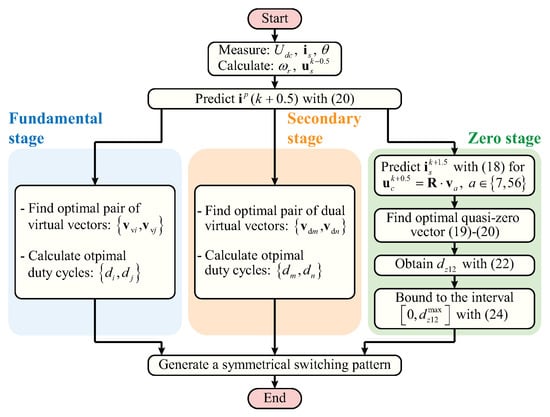
Figure 4. Flowchart of the proposed fault-tolerant control strategy.

The voltage vector ${\mathbf{u}}_c^{k+0.5}$ is calculated by:

$${\mathbf{u}}_c^{k+0.5}=\mathbf{R}\left[{\mathbf{v}}_{\mathrm{v}i}·d_i+{\mathbf{v}}_{\mathrm{v}j}·d_j+{\mathbf{v}}_{\mathrm{d}m}·d_m+{\mathbf{v}}_{\mathrm{d}n}·d_n+{\mathbf{v}}_w·d_{z12}^{\prime }\right]$$

(27)

and ${\mathbf{u}}_c^{k-0.5}$ is obtained by delaying (27) one sampling period.

After the execution of all three control stages, the duty cycles $\left\{d_i,d_j,d_m,d_n,d_{z12}^{\prime }\right\}$ of vectors $\left\{{\mathbf{v}}_{\mathrm{v}i},{\mathbf{v}}_{\mathrm{v}j},{\mathbf{v}}_{\mathrm{d}m},{\mathbf{v}}_{\mathrm{d}n},{\mathbf{v}}_w\right\}$ are summed on a per-leg basis to generate a symmetrical switching pattern that produces a fixed-switching frequency of $f_{sw}=1/T_s$ Hz, following a similar procedure as in [19].

4. Simulation Results

This section presents simulation results, obtained from MATLAB/Simulink, of a six-phase PMSM drive under the proposed FT-PCC strategy under healthy and fault-tolerant operating conditions for two distinct neutral configurations: 2N and 1N. The parameters of the considered six-phase drive are listed in Table 1, where $P_s$, $U_s$, $I_s$, $n_m$, and $t_n$ are the PMSM rated power, voltage, current, speed, and torque. The PMSM pole-pair number is represented by p, whereas $t_d$ is the deadtime considered in the power converter switches. The FT-PCC strategy is executed with a sampling period of $T_s=125$$\mathsf{\mu }$s, which leads to a fixed switching frequency of 8 kHz.

Table 1. Parameters of the six-phase PMSM drive.

Parameter	Value	Parameter	Value	Parameter	Value
$P_s$ (kW)	4	p	2	${\psi }_{\mathrm{PM}3}$ (mWb)	53.3
$U_s$ (V)	340	$R_s$ ($\mathsf{\Omega }$)	1.6	${\varphi }_3$ (deg)	0.52
$I_s$ (A)	3.4	$L_{dq}$ (mH)	53.8	$U_{dc}$ (V)	650
$n_m$ (rpm)	1500	$L_{xy}$ (mH)	2.1	$t_d$ ($\mathsf{\mu }$s)	2.2
$t_n$ (N.m)	28.4	${\psi }_{\mathrm{PM}1}$ (mWb)	973.7	$T_s$ ($\mathsf{\mu }$s)	125

To verify the good performance of the proposed control strategy, the total harmonic distortion (THD) of phase-u current is calculated by:

$${\mathrm{THD}}_u=\frac{1}{6}\sum _{u=\left\{a1,\dots ,c2\right\}}\frac{\sqrt{i_{u,2}^2+\cdots +i_{u,50}^2}}{i_{u,1}}\times 100\%,$$

(28)

where $i_{u,n}$ is the n-order harmonic of the phase-u current with $u\in \left\{a1,b1,c1,a2,b2,c2\right\}$.

The simulation results for a step-change in q-axis reference current from −1.2 A (25% load level) to −4.8 A (100% load level) are shown in Figure 5, where the PMSM is operated at 750 rpm with a 1N configuration. The zero control stage is disabled for the results shown in Figure 5a, which causes the $z1$-$z2$ currents to flow uncontrolled for a 1N configuration. In this scenario, the mean current THD for all six phases is calculated as 79.66%. In contrast, the zero control stage is enabled in Figure 5b, demonstrating its ability to reduce the $z1$-$z2$ currents to zero and eliminate torque ripple. In this second scenario, the mean current THD is effectively reduced to 2.46%.

Figure 5. Simulation results for a step change in the q-axis current at 750 rpm, considering the six-phase drive operating under the proposed control strategy with the zero control stage: (a) disabled; (b) enabled.

The simulation results for the PMSM drive under fault-tolerant mode due to an OPF in phase $a1$ are shown in Figure 6, which shows a side-by-side comparison of the machine operating with a 2N configuration in Figure 6a and a 1N configuration in Figure 6b. The results of Figure 6a are obtained using the DOB-PCC strategy in [19], while the results of Figure 6b are obtained with the proposed FT-PCC strategy. The THD calculated for the phase currents of the results shown in Figure 6 is listed in Table 2. In both cases, the current references are modified as in [8] to allow the six-phase drive operation in fault-tolerant conditions in maximum torque (MT) mode. In the case of Figure 6a, the PMSM is operated without any torque ripple, and the current harmonic content is minimized as demonstrated by the low values of THD for phase currents listed in Table 2. Alternatively, in the case of Figure 6b, the FT-PCC strategy minimizes the current harmonics and provides a reasonably low torque ripple around 1.4 N.m (5% of the rated torque). This torque ripple is due to not considering the contribution to the torque of the $z1$-$z2$ components of the current and back-EMF when optimizing the post-fault current references in [8] for six-phase machines. The torque ripple could be further minimized by optimizing the reference currents online, which would increase the computational burden of the proposed strategy. However, this topic is outside the scope of this paper.

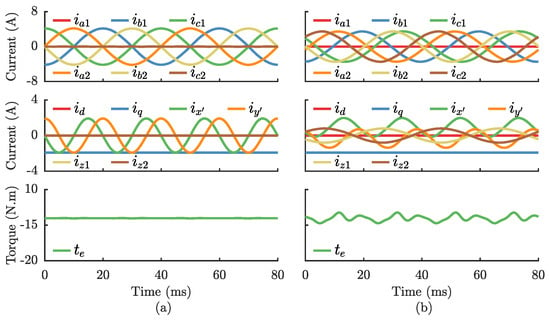
Figure 6. Simulation results for the six-phase drive under fault-tolerant mode due to an OPF in phase $a1$, operating at 750 rpm, 50% load level, and under: (a) 2N configuration; (b) 1N configuration.

Table 2. Simulation results: current THD for fault-tolerant mode due to an OPF in phase $a1$ at 750 rpm.

Strategy	Phase	Phase	Phase	Phase	Phase	Phase
	$\mathit{a}\mathbf{1}$	$\mathit{b}\mathbf{1}$	$\mathit{c}\mathbf{1}$	$\mathit{a}\mathbf{2}$	$\mathit{b}\mathbf{2}$	$\mathit{c}\mathbf{2}$
FT-PCC (2N)	-	0.63%	0.62%	0.48%	0.27%	-
FT-PCC (1N)	-	0.54%	0.89%	0.42%	0.47%	0.88%

The copper loss curves in p.u. as a function of the torque in p.u. are shown in Figure 7, considering the PMSM in healthy conditions and in fault-tolerant operation mode due to an OPF in phase a1 in minimum loss (ML) and MT modes. Figure 7a shows the loss curves when considering a 2N configuration, while Figure 7b shows the loss curves for the 1N case. The ML mode provides the lowest losses in both cases, limiting the maximum torque to 0.555 p.u. (55.5% load level) and 0.542 p.u. (54.2%) for 2N and 1N configurations, respectively. Alternatively, the MT mode extends the operational limits of the PMSM, allowing a maximum torque of 0.577 p.u. and 0.695 p.u. for 2N and 1N configurations, respectively.

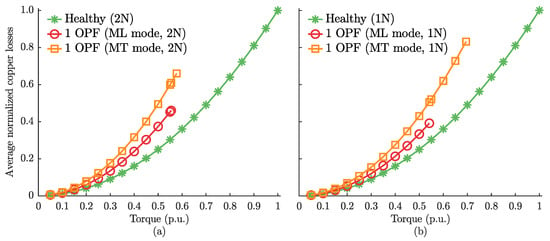
Figure 7. Simulation results for the average copper losses at different load levels obtained for the six-phase drive under: (a) 2N configuration; (b) 1N configuration.

5. Experimental Results

In order to validate the proposed FT-PCC strategy, this section contains experimental results obtained with a 4 kW six-phase PMSM drive with the same parameters as the ones listed in Table 1. The experimental setup used to obtain the results here included is shown in Figure 8.

Figure 8. Experimental setup.

Figure 9 shows the experimental results obtained for a step response in the q-axis current. The zero control stage is disabled for the case of Figure 9a, i.e., $d_{z12}$ is set to zero. Conversely, the zero control stage is enabled in Figure 9b. By disabling the zero control stage, the $z1$-$z2$ currents become uncontrolled and can reach relatively high magnitudes, as seen in Figure 9a. In this case and after the step change in q-axis current, the mean current THD is calculated as 66.77%. Besides the increase in the harmonic content of PMSM currents, the torque ripple also increases as $z1$-$z2$ current components produce non-negligible torque in six-phase PMSMs with a 1N configuration [27]. However, by enabling the zero control stage, the proposed strategy reduces the $z1$-$z2$ currents and minimizes the current harmonics and torque ripple. In this scenario, the current THD is calculated as 2.16% after the step change in the q-axis current.

Figure 9. Experimental results for a step change in the q-axis current at 750 rpm, considering the six-phase drive operating under the proposed control strategy with the zero control stage: (a) disabled; (b) enabled.

Figure 10 shows the experimental results obtained for the PMSM drive in fault-tolerant operation in MT mode due to an OPF in phase $a1$ for two neutral configurations: 2N and 1N. Table 3 lists the calculated values for the current THD for each scenario shown in Figure 10. Even though the PMSM is operated at 50% load level in both cases shown in Figure 10, the rms value of currents in the healthy phases is lower for the 1N configuration (0.86 p.u. vs. 0.72 p.u.). Since the rated current of the drive typically limits the maximum torque, the 1N configuration provides a higher torque range than the 2N configuration [8]. In terms of losses, the average normalized losses for MT mode for the cases shown in Figure 10 (50% load level) are 0.50 and 0.39 for 2N and 1N configurations, respectively. As far as the current harmonic content is concerned, the FT-PCC strategy guarantees minimal harmonic content for both 2N and 1N configurations, as demonstrated by the low THD values listed in Table 3.

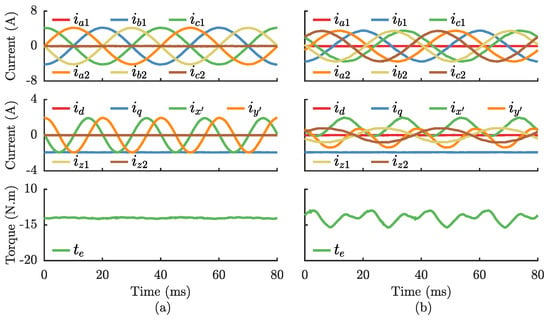
Figure 10. Experimental results for the six-phase drive under fault-tolerant mode due to an OPF in phase $a1$, operating at 750 rpm, 50% load level, and under: (a) 2N configuration; (b) 1N configuration.

Table 3. Experimental results: current THD for fault-tolerant mode due to an OPF in phase $a1$ at 750 rpm.

Strategy	Phase	Phase	Phase	Phase	Phase	Phase
	$\mathit{a}\mathbf{1}$	$\mathit{b}\mathbf{1}$	$\mathit{c}\mathbf{1}$	$\mathit{a}\mathbf{2}$	$\mathit{b}\mathbf{2}$	$\mathit{c}\mathbf{2}$
FT-PCC (2N)	-	0.78%	0.82%	0.46%	0.75%	-
FT-PCC (1N)	-	2.15%	2.02%	0.96%	2.60%	1.70%

The experimental results for the PMSM drive under fault-tolerant operation at 1200 rpm and 50% load are shown in Figure 11 due to an OPF in phase $a1$ (Figure 11a) and an OPF in phase $c2$ (Figure 11b) while the calculated values for the current THD in these scenarios are listed in Table 4. As observed in the case of Figure 10, the proposed FT-PCC strategy is able to maintain the six-phase drive operating after the occurrence of an OPF, independent of its location, while minimizing the current harmonic distortion.

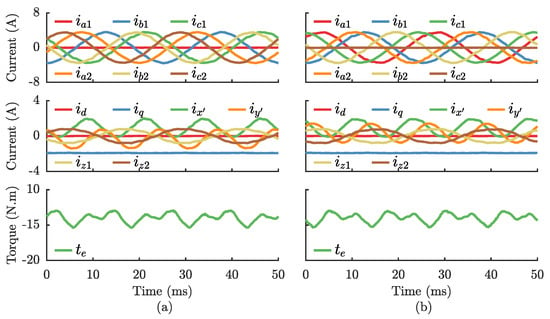
Figure 11. Experimental results for the six-phase drive under fault-tolerant mode, operating at 1200 rpm, 50% load level, under 1N configuration due to: (a) OPF in phase $a1$; (b) OPF in phase $c2$.

Table 4. Experimental results: current THD for fault-tolerant mode due to an OPF in phases $a1$ and $c2$ at 1200 rpm.

Strategy	Phase	Phase	Phase	Phase	Phase	Phase
	$\mathit{a}\mathbf{1}$	$\mathit{b}\mathbf{1}$	$\mathit{c}\mathbf{1}$	$\mathit{a}\mathbf{2}$	$\mathit{b}\mathbf{2}$	$\mathit{c}\mathbf{2}$
FT-PCC (1N): OPF in $a1$	-	3.28%	3.44%	1.69%	3.75%	2.74%
FT-PCC (1N): OPF in $c2$	2.83%	3.72%	1.27%	3.38%	3.73%	-

The copper loss curves obtained through experimental results for different load levels are shown in Figure 12. During fault-tolerant conditions in ML mode, operating the drive with a 1N configuration leads to lower copper losses. For example, with a torque of 0.5 p.u. (50% load level), the average normalized losses for ML mode are 0.38 and 0.31 for the 2N and 1N configurations, respectively. In terms of torque range during fault-tolerant conditions, MT mode provides the highest achievable torque compared to ML mode. Compared to the 2N configuration, the 1N configuration allows to increase of the maximum torque from 0.577 p.u. to 0.695 p.u., representing an increase of 20.45%. This increase in the torque range is the main reason why the 1N configuration is usually preferred for fault-tolerant operation [5,7,8].

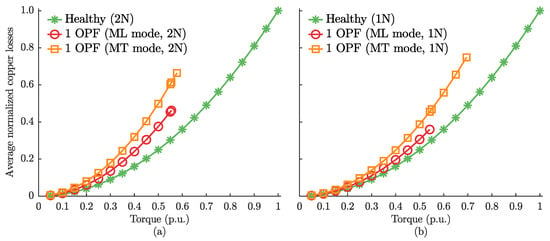
Figure 12. Experimental results for the average copper losses at different load levels obtained for the six-phase drive under: (a) 2N configuration; (b) 1N configuration.

6. Conclusions

A novel FT-PCC technique has been presented in this paper for application in six-phase PMSM drives, along with new virtual and dual virtual vectors suitable for a 1N configuration. The proposed technique provides a decoupled control of the currents in the d-q, $x^{\prime }$-$y^{\prime }$, and $z1$-$z2$ subspaces, carried out by the fundamental, secondary, and zero control stages. The proposed technique has minimal reconfiguration requirements and, when transitioning from normal to fault tolerant conditions, only requires changing the current references mapped in the $x^{\prime }$-$y^{\prime }$ subspace and $z1$-axis.

The presented results demonstrate that the proposed technique reduces current harmonic distortion and can operate the system in fault-tolerant conditions with good performance. Furthermore, it is also shown that the 1N configuration produces lower copper losses than the 2N configuration to generate the same torque during fault-tolerant conditions. However, due to its complexity, the optimization of reference currents to reduce torque oscillations for the 1N configuration during fault-tolerant conditions will be the subject of future work.