Development of the Cost-Based Model for Monitoring the Lifetime of the Earth Moving Machines
Abstract
1. Introduction
- In the first model, the company operates its equipment or part of it and takes care of it. The advantage of this model is that a company can manage and optimize the costs in relation to time, unify the fleet, implement its own maintenance policy and reduce operational costs that are generated only during the operation of the machine;
- In the second model, equipment is rented from a subcontractor specialized for the task at hand. In this case, the costs are fixed regardless of the age of the machine. The company does not have to organize the maintenance. The disadvantage of this model is that costs are incurred regardless of whether the machine is operating or not. Namely, in addition to the costs of active work, the costs of passive engagement are also generated since the machine cannot be engaged with another company during the time defined by the contract;
- The third model is a combination of the previous two models, where the company owns the equipment while the specialized subcontractor is engaged in the maintenance.
2. Materials and Methods
2.1. Lifetime Stages of the Machines
2.2. Machine’s Operational Costs
- Ownership costs: equipment depreciation and insurance;
- Operational costs: energy, lubricants, wearing parts, maintenance and other specific costs;
- Labor costs: operators and maintenance staff.
2.2.1. Total and Specific Costs
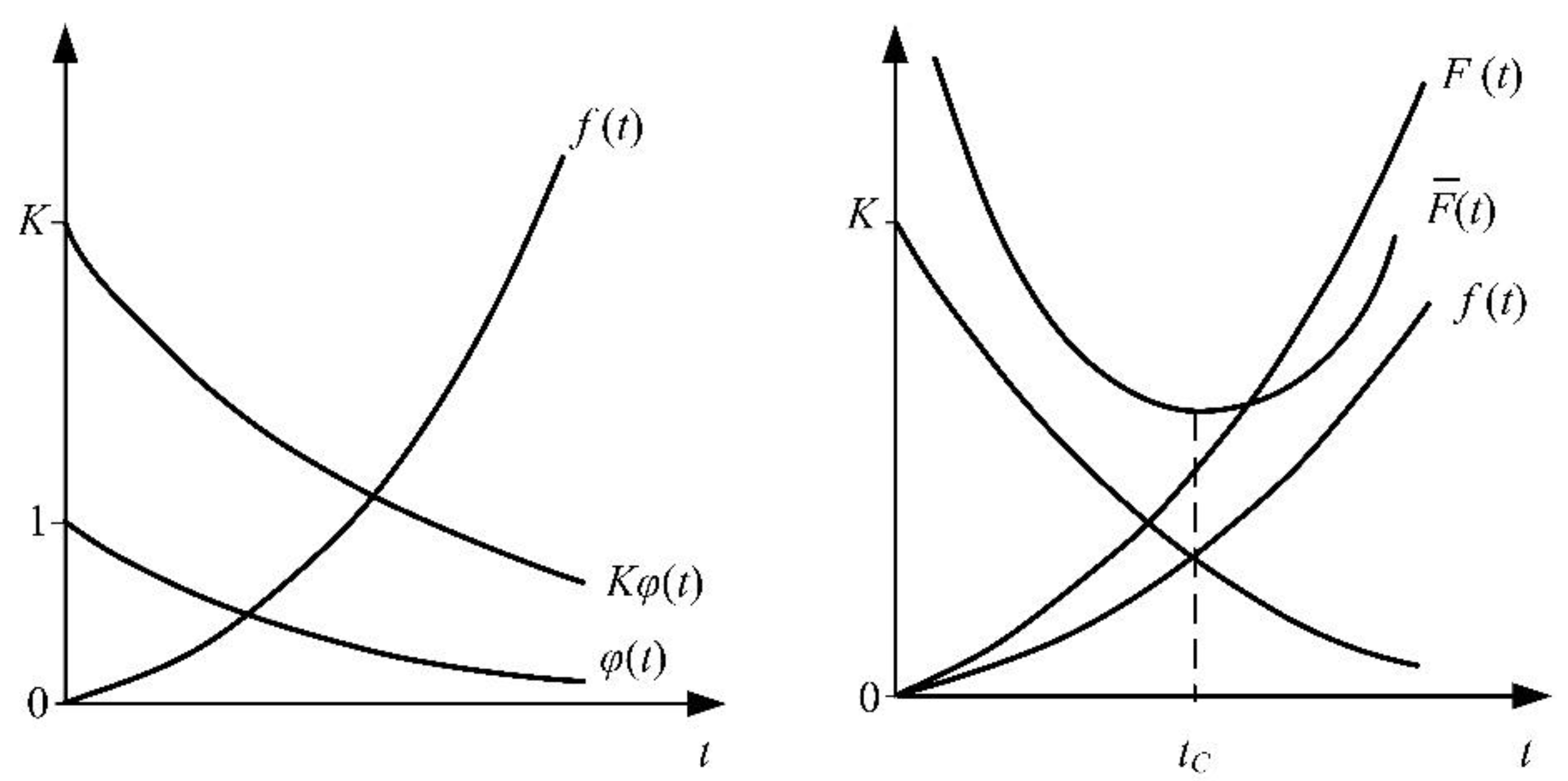
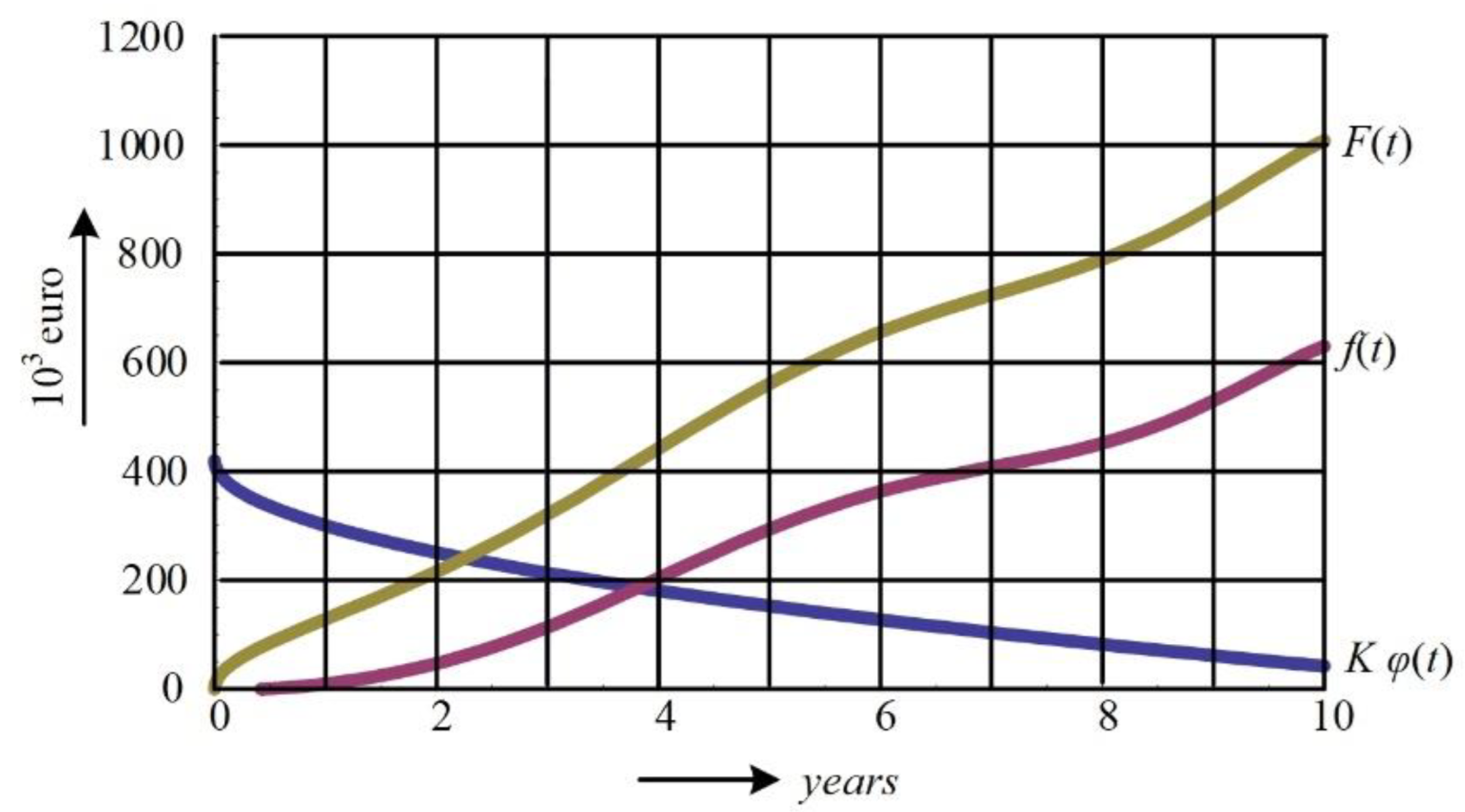
2.2.2. Determination of Costs Function
3. Results—Case Study
3.1. Data Collection
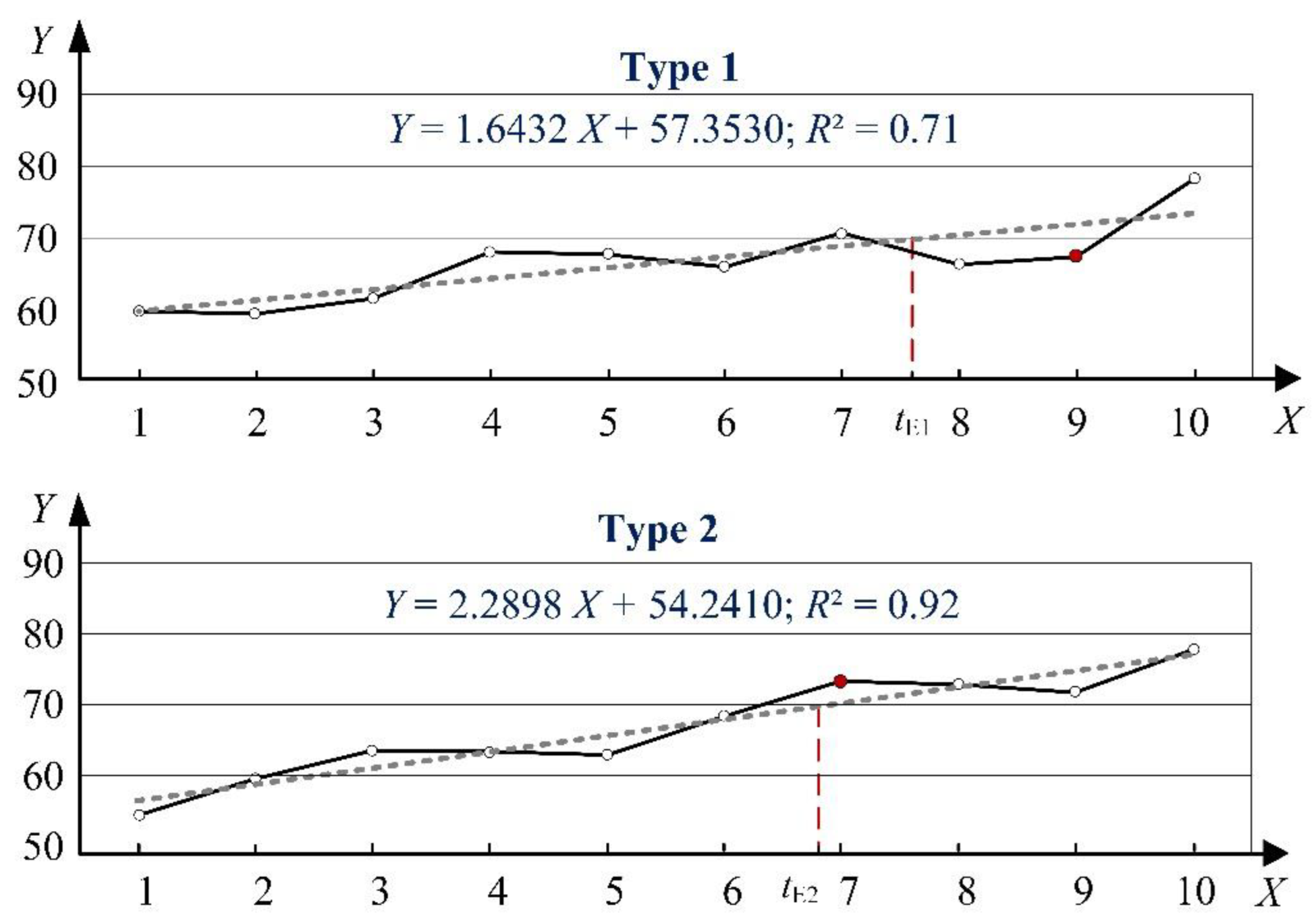
3.2. Reference Points of Economic Lifetime (tE)
- Machine type 1: 70 = 1.64 · tE1 + 57.35 → tE1 = 7.70 years;
- Machine type 2: 70 = 2.29 · tE2 + 54.24 → tE2 = 6.88 years.
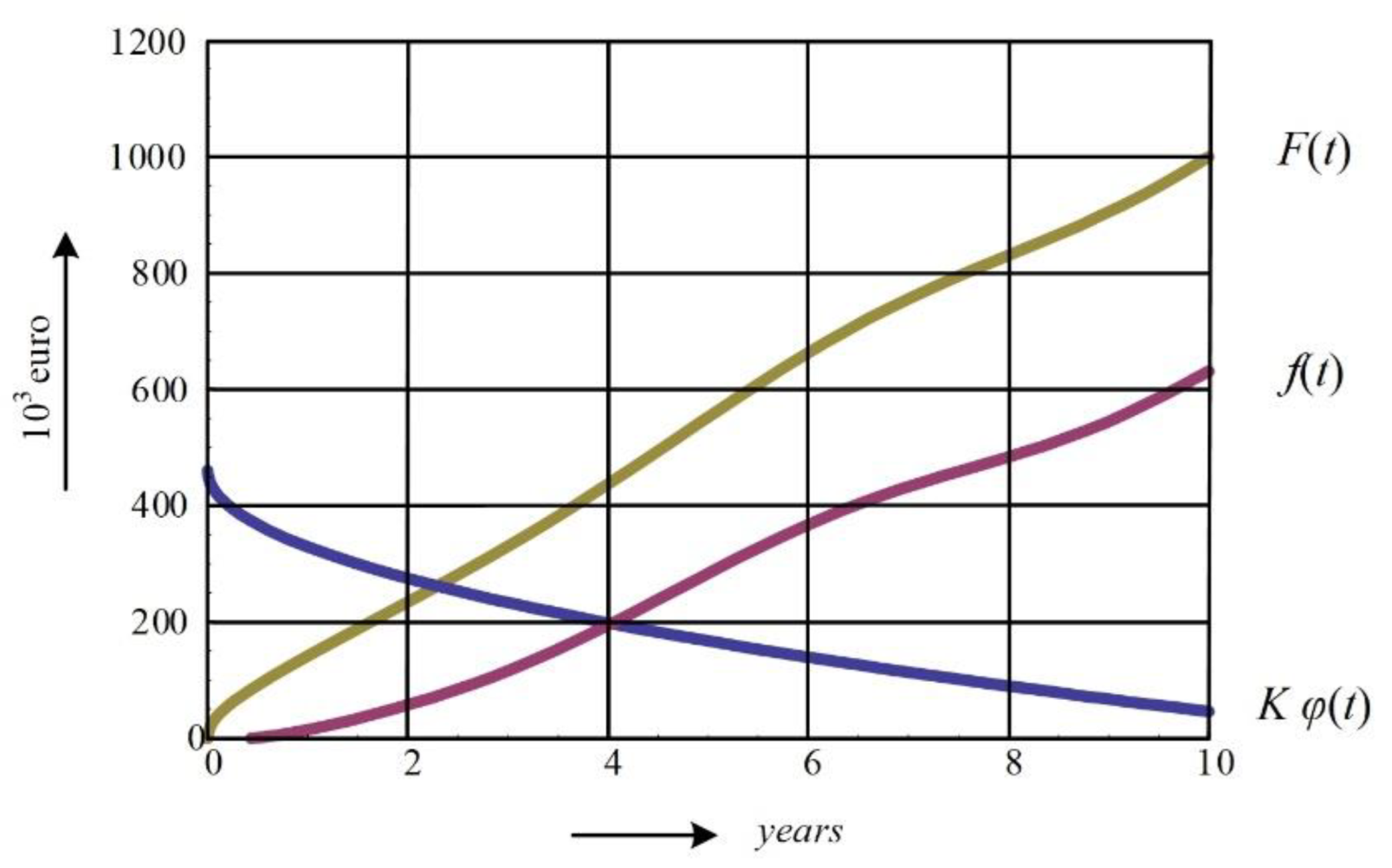
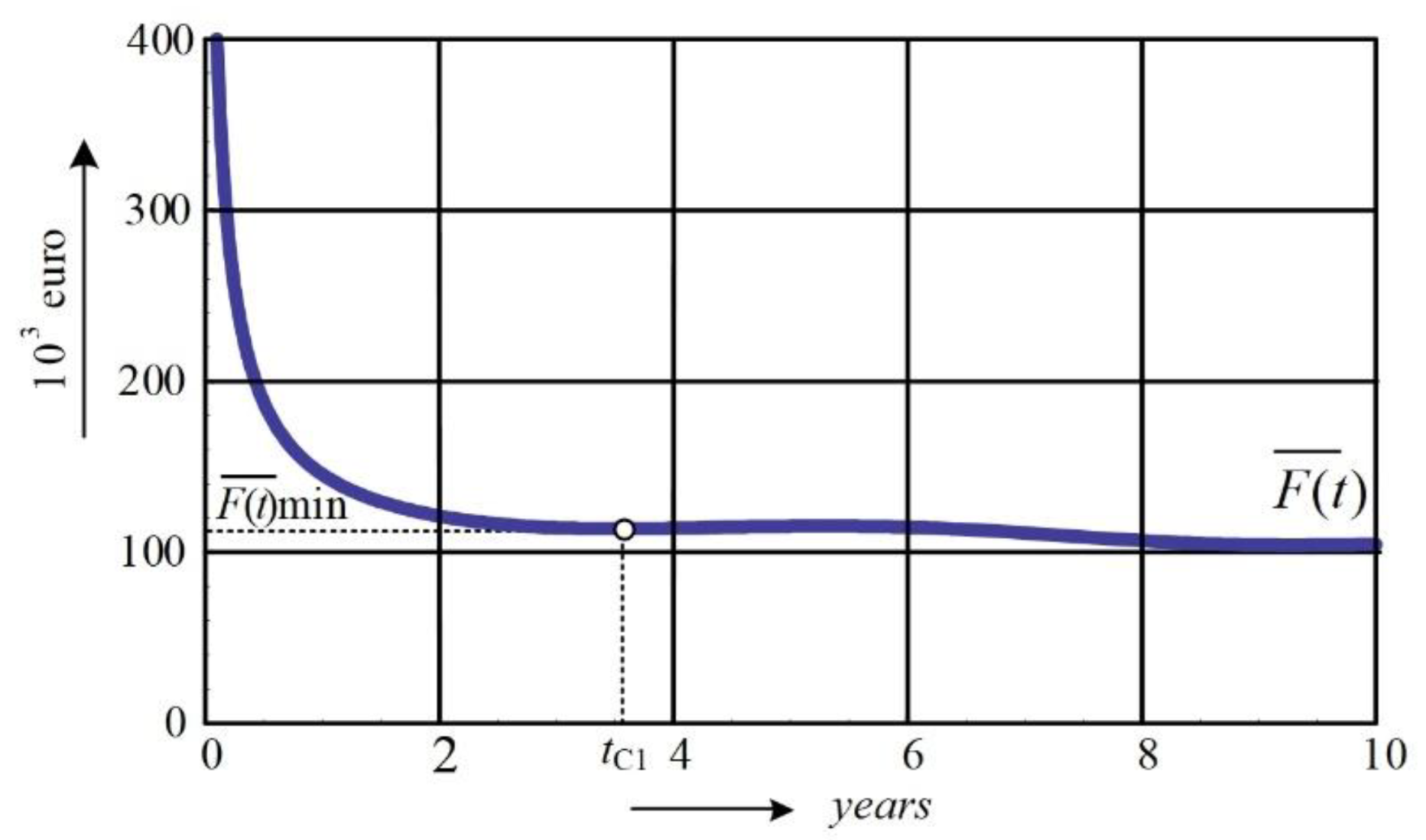
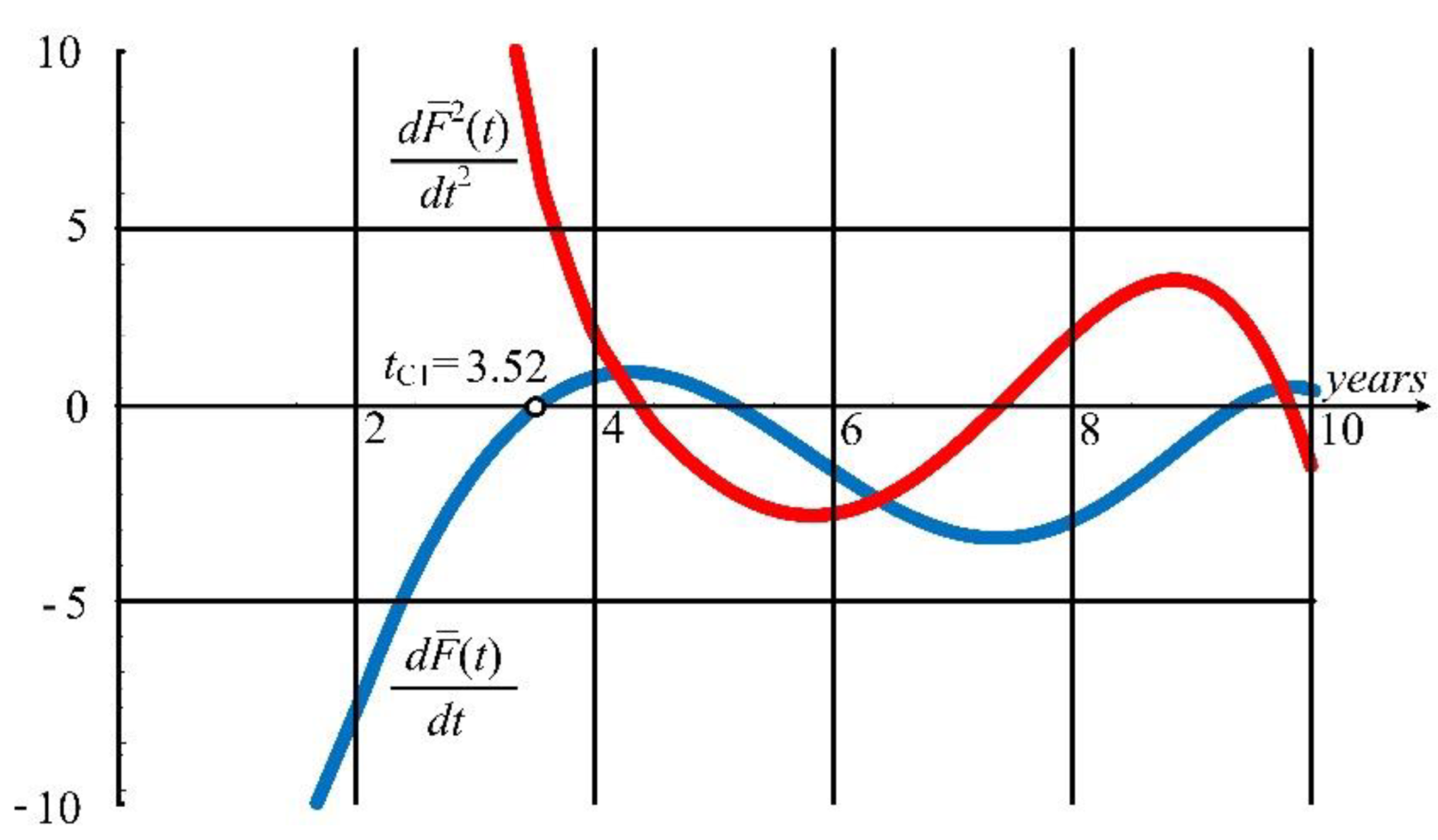
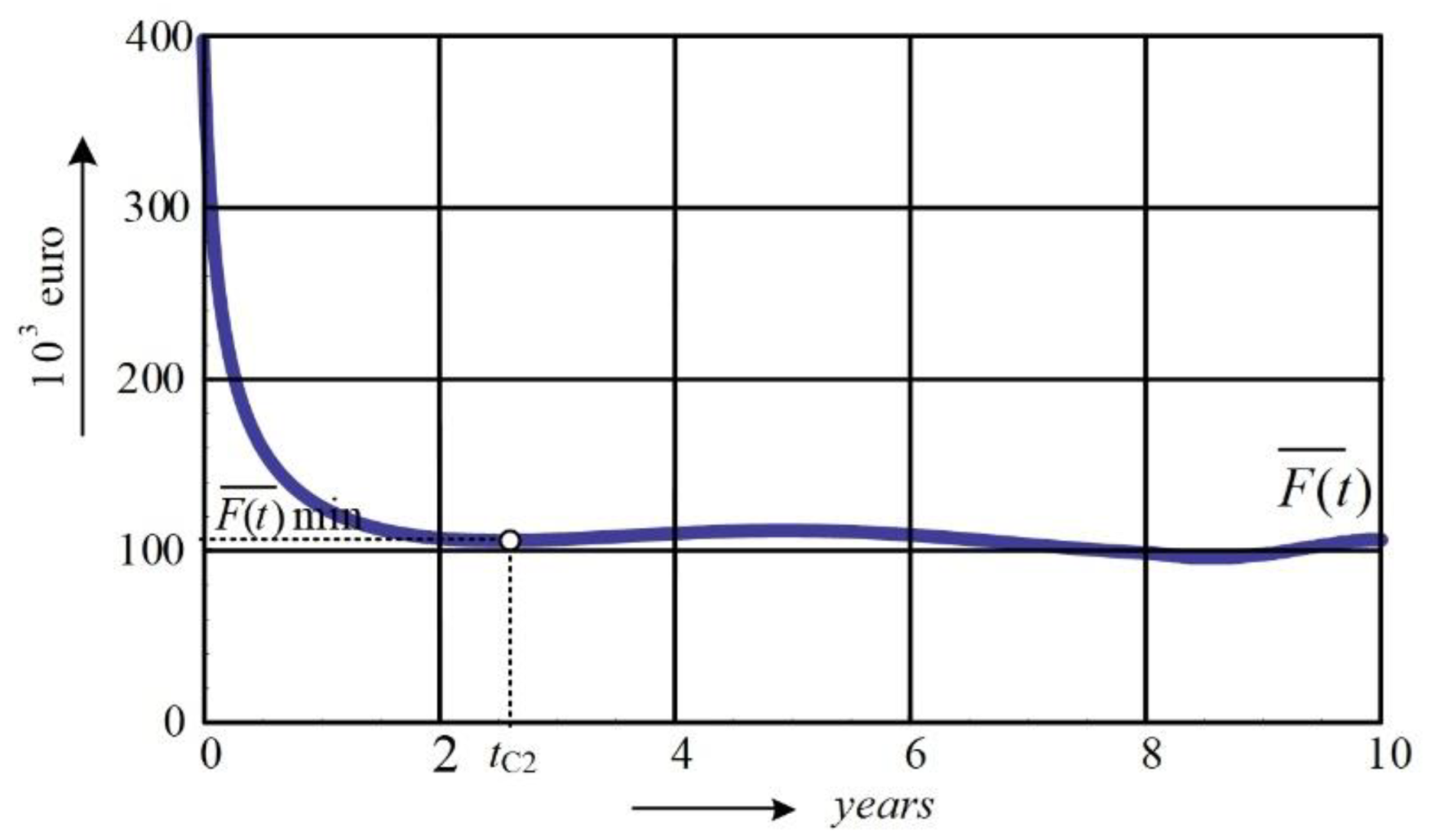
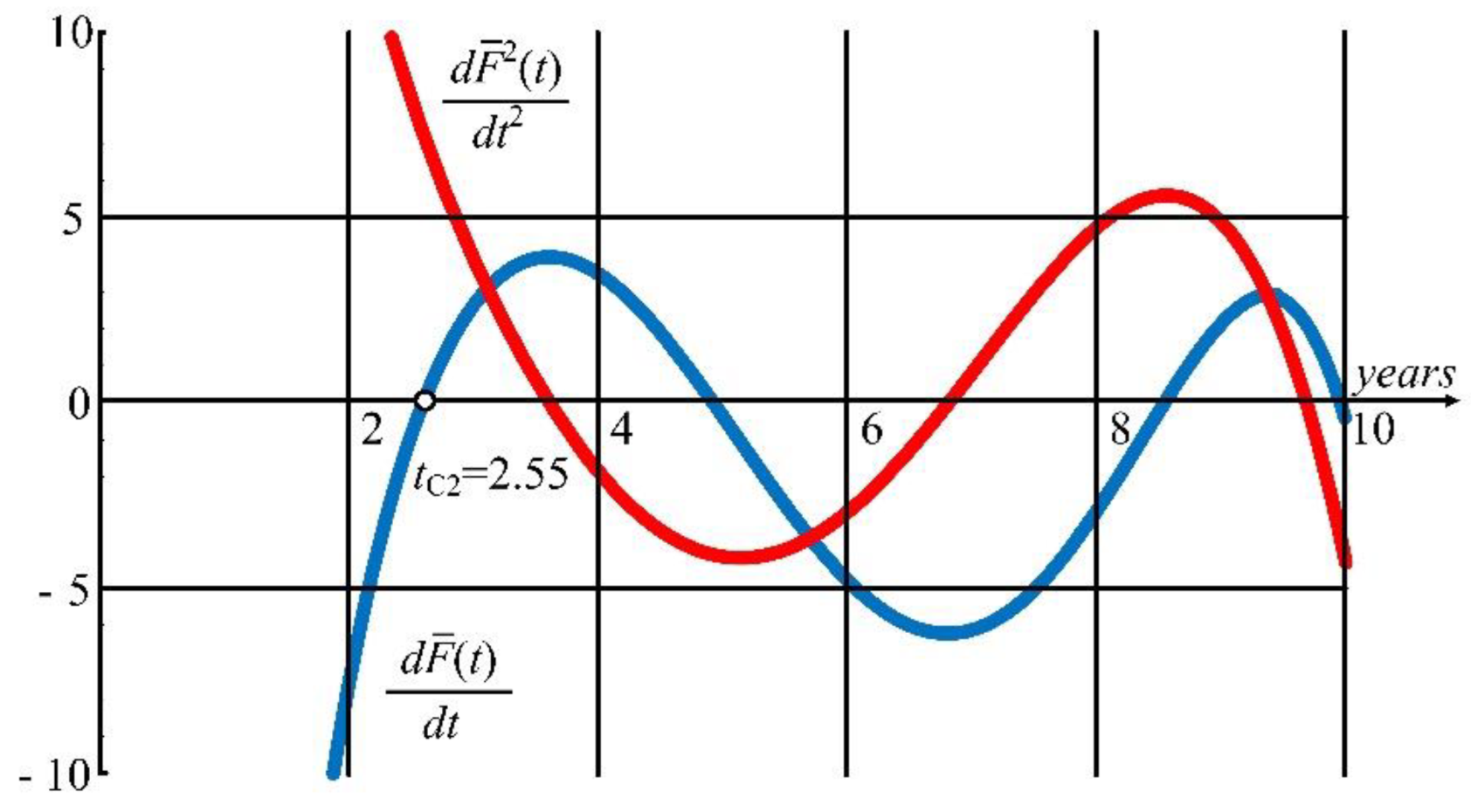
3.3. Reference Points of Minimal Costs Lifetime (tC)
- Machine type 1:
- Machine type 2:
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dhillon, B.S. Mining Equipment Reliability, Maintainability, and Safety; Springer: London, UK, 2008. [Google Scholar]
- Optimization of the organization, resources and costs of auxiliary mechanization in order to increase the degree of utilization of tailings and coal systems at the surface mines of electric power industry of serbia. In Study; Faculty of Mining and Geology Belgrade: Belgrade, Serbia, 2018. (In Serbian)
- Jagodic-Krunic, D.; Vujic, S.; Tanasijevic, M.; Dimitrijevic, B.; Subaranovic, T.; Ilic, S.; Maksimovic, S. Model Approaches to Life Cycle Assessment of Auxiliary Machines Based on an Example of a Coal Mine in Serbia. J. Min. Sci. 2018, 54, 404–413. [Google Scholar] [CrossRef]
- Al-Chalabi, H.; Lundberg, J.; Jonsson, A. Economic lifetime of a drilling machine: A case study on mining industry. Int. J. Strateg. Eng. Asset Manag. 2015, 2, 177–189. [Google Scholar] [CrossRef]
- IEC 60300-3-3:2017; Dependability Management—Part 3–3: Application Guide—Life Cycle Costing. The International Electrotechnical Commission: Geneva, Switzerland, 2009.
- Janković, I. Optimisation of the Life Cycle concept of Auxiliary Machinery at Lignite Open-pit Mines. Ph.D. Thesis, University of Belgrade, Belgrade, Serbia, 2020. Available online: https://uvidok.rcub.bg.ac.rs/handle/123456789/3788 (accessed on 13 May 2020). (In Serbian).
- Bugaric, U.; Tanasijevic, M.; Polovina, D.; Ignjatovic, D.; Jovancic, P. Lost production costs of the overburden excavation system caused by rubber belt failure. Eksploat. I Niezawodn. Maint. Reliab. 2012, 14, 333–341. [Google Scholar]
- Jankovic, I.; Djenadic, S.; Ignjatovic, D.; Jovancic, P.; Subaranovic, T.; Ristovic, I. Multi-criteria approach for selecting optimal dozer type in open-cast coal mining. Energies 2019, 12, 2245. [Google Scholar] [CrossRef]
- Pantelić, M.; Bošnjak, S.; Misita, M.; Gnjatović, N.; Stefanović, A. Service FMECA of a bucket wheel excavator. Eng. Fail. Anal. 2020, 108, 104289. [Google Scholar] [CrossRef]
- Djenadic, S.; Tanasijevic, M.; Jovancic, P.; Ignjatovic, D.; Petrovic, D.; Bugaric, U. Risk Evaluation: Brief Review and Innovation Model Based on Fuzzy Logic and MCDM. Mathematics 2022, 10, 811. [Google Scholar] [CrossRef]
- Gössling, S.; Kees, J.; Litman, T. The lifetime cost of driving a car. Ecol. Econ. 2022, 194, 107335. [Google Scholar] [CrossRef]
- Caterpillar Inc. Handbook, C.P., 42nd ed.; Caterpillar Inc.: Deerfield, IL, USA, 2012; pp. 1381–1422. [Google Scholar]
- Komatsu Ltd. Specifications & Application Handbook, 30th ed.; Komatsu Ltd.: Tokyo, Japan, 2009. [Google Scholar]
- Djenadic, S.; Ignjatovic, D.; Tanasijevic, M.; Bugaric, U.; Jankovic, I.; Subaranovic, T. Development of the Availability Concept by Using Fuzzy Theory with AHP Correction, a Case Study: Bulldozers in the Open-Pit Lignite Mine. Energies 2019, 12, 4044. [Google Scholar] [CrossRef]
- Vaughan, E.J. Risk Management; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Sazdanović, S. Elements of Operational Research; Naučna Knjiga: Belgrade, Serbia, 1980. (In Serbian) [Google Scholar]
- Hinkle, D.E.; Wiersma, W.; Jurs, S.G. Applied Statistics for the Behavioral Sciences; Houghton Mifflin Company: Boston, MA, USA, 2003. [Google Scholar]
- O’Connor, P.D.T.; Kleyner, A. Practical Reliability Engineering, 5th ed.; John Wiley & Sons Ltd.: West Sussex, UK, 2012. [Google Scholar]
- Wolfram research Inc. Mathematica for 386—Based MS-DOS Systems, User Guide; Wolfram research Inc.: Champaign, IL, USA, 1988. [Google Scholar]
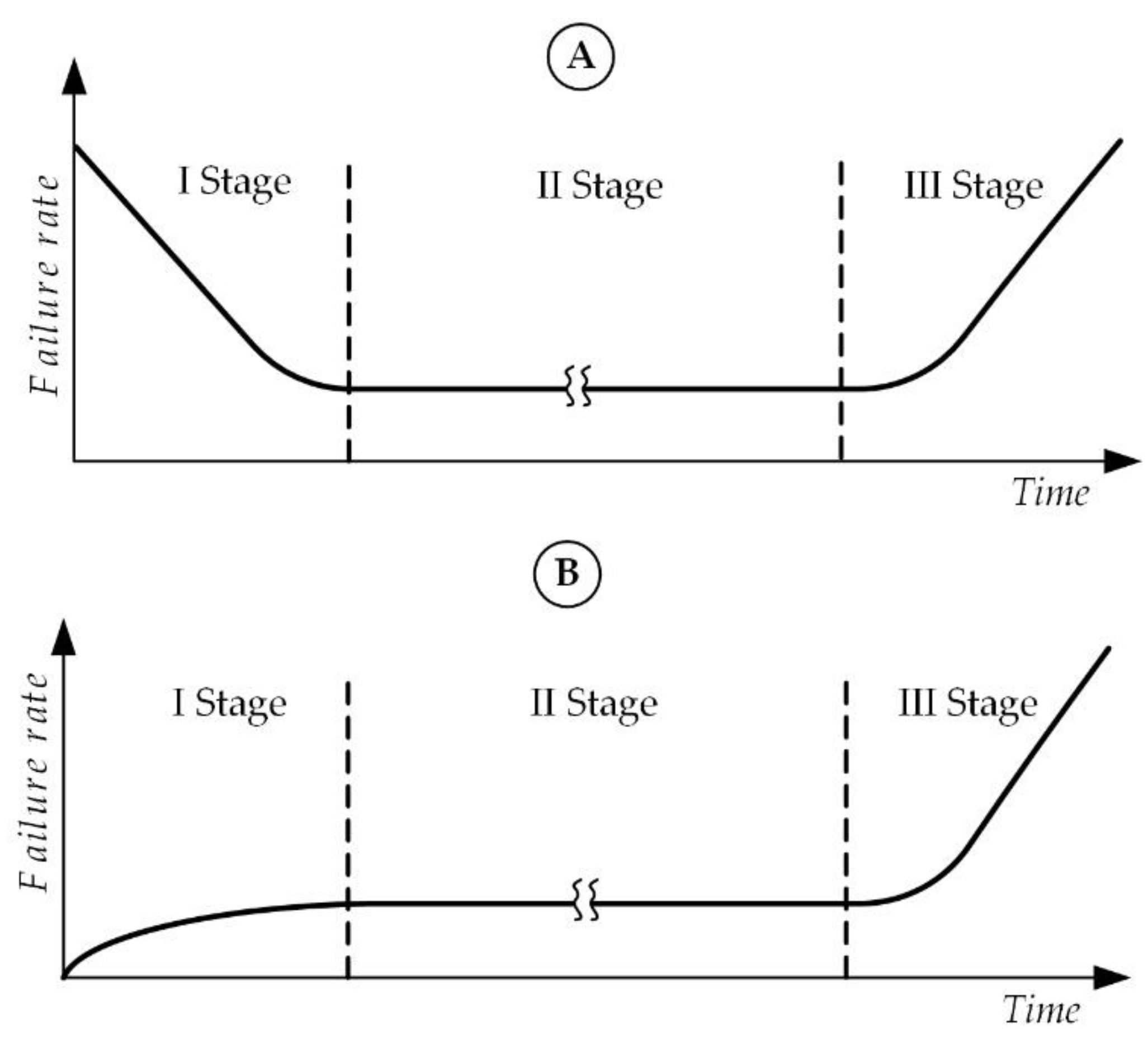
| Type of Machine | Stage | Failure Rate | Costs |
|---|---|---|---|
| A | I stage—Beginning of life | Decreasing failure rate | Additional costs |
| B | Increasing failure rate | Minimal costs | |
| A & B | II stage—Normal life | The low constant failure rate | Slight increase in costs |
| III stage—End of life | Increasing failure rate | Strong cost increase |
| Machine | Type 1—CAT | Type 2—LIE | ||||||
|---|---|---|---|---|---|---|---|---|
| Year | OWC, [EUR/wh] | OPC, [EUR/wh] | HRC, [EUR/wh] | TC, [EUR/wh] | OWC, [EUR/wh] | OPC, [EUR/wh] | HRC, [EUR/wh] | TC, [EUR/wh] |
| 1 | 14.62 | 26.74 | 18.43 | 57.79 | 18.04 | 18.02 | 18.43 | 54.49 |
| 2 | 26.49 | 59.54 | 23.02 | 59.49 | ||||
| 3 | 28.60 | 61.65 | 27.18 | 63.65 | ||||
| 4 | 37.05 | 68.10 | 26.96 | 63.43 | ||||
| 5 | 34.64 | 67.69 | 26.47 | 62.94 | ||||
| 6 | 32.99 | 66.04 | 32.00 | 68.47 | ||||
| 7 | 37.78 | 70.83 | 36.91 | 73.38 | ||||
| 8 | 26.89 | 66.42 | 36.39 | 72.86 | ||||
| 9 | 22.44 | 67.47 | 35.30 | 71.77 | ||||
| 10 | 38.85 | 78.37 | 41.40 | 77.87 | ||||
| Machine | Minimal Costs Lifetime | Economic Lifetime | ||
|---|---|---|---|---|
| tC, Years | EUR/wh | tE, Years | EUR/wh | |
| Type 1 | 3.52 | 63.6 | 7.70 | 70 |
| Type 2 | 2.55 | 60.1 | 6.88 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bugaric, U.; Tanasijevic, M.; Djenadic, S.; Ignjatovic, D.; Jankovic, I. Development of the Cost-Based Model for Monitoring the Lifetime of the Earth Moving Machines. Machines 2022, 10, 995. https://doi.org/10.3390/machines10110995
Bugaric U, Tanasijevic M, Djenadic S, Ignjatovic D, Jankovic I. Development of the Cost-Based Model for Monitoring the Lifetime of the Earth Moving Machines. Machines. 2022; 10(11):995. https://doi.org/10.3390/machines10110995
Chicago/Turabian StyleBugaric, Ugljesa, Milos Tanasijevic, Stevan Djenadic, Dragan Ignjatovic, and Ivan Jankovic. 2022. "Development of the Cost-Based Model for Monitoring the Lifetime of the Earth Moving Machines" Machines 10, no. 11: 995. https://doi.org/10.3390/machines10110995
APA StyleBugaric, U., Tanasijevic, M., Djenadic, S., Ignjatovic, D., & Jankovic, I. (2022). Development of the Cost-Based Model for Monitoring the Lifetime of the Earth Moving Machines. Machines, 10(11), 995. https://doi.org/10.3390/machines10110995






