Uniaxial Load Specification for Vehicle Knuckle Part Using Maximum Stress Similarity in Triaxial Load Case
Abstract
1. Introduction
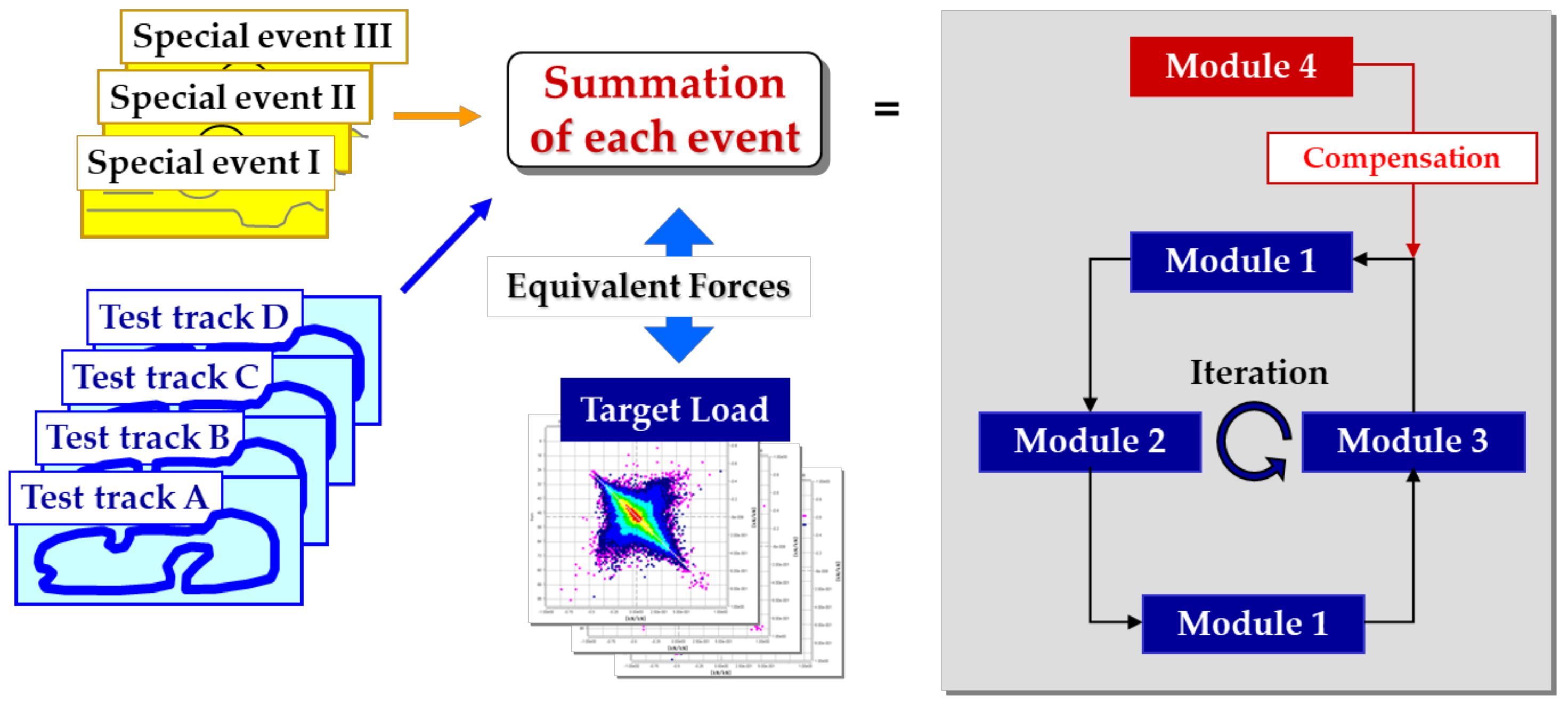
2. Theoretical Background
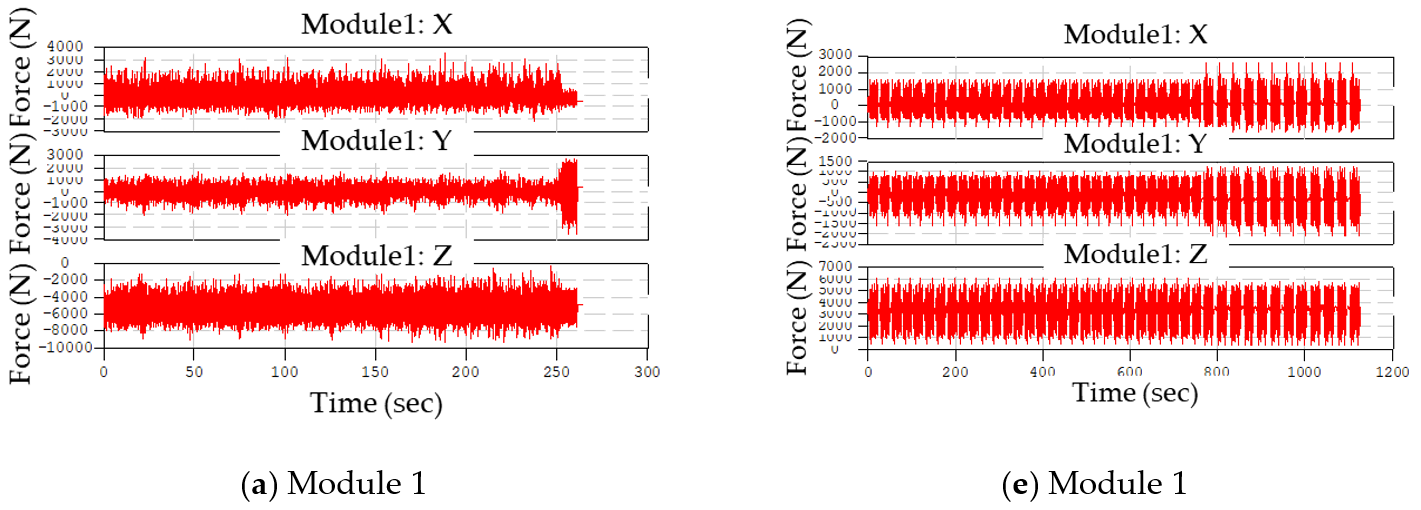
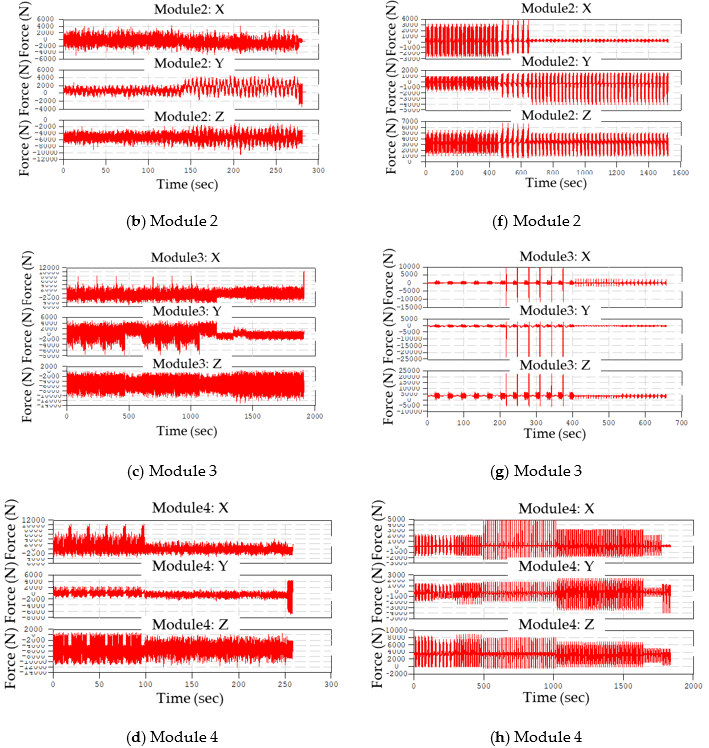
3. Accelerated Triaxial Load Events
4. Fatigue Analysis of Knuckle Parts
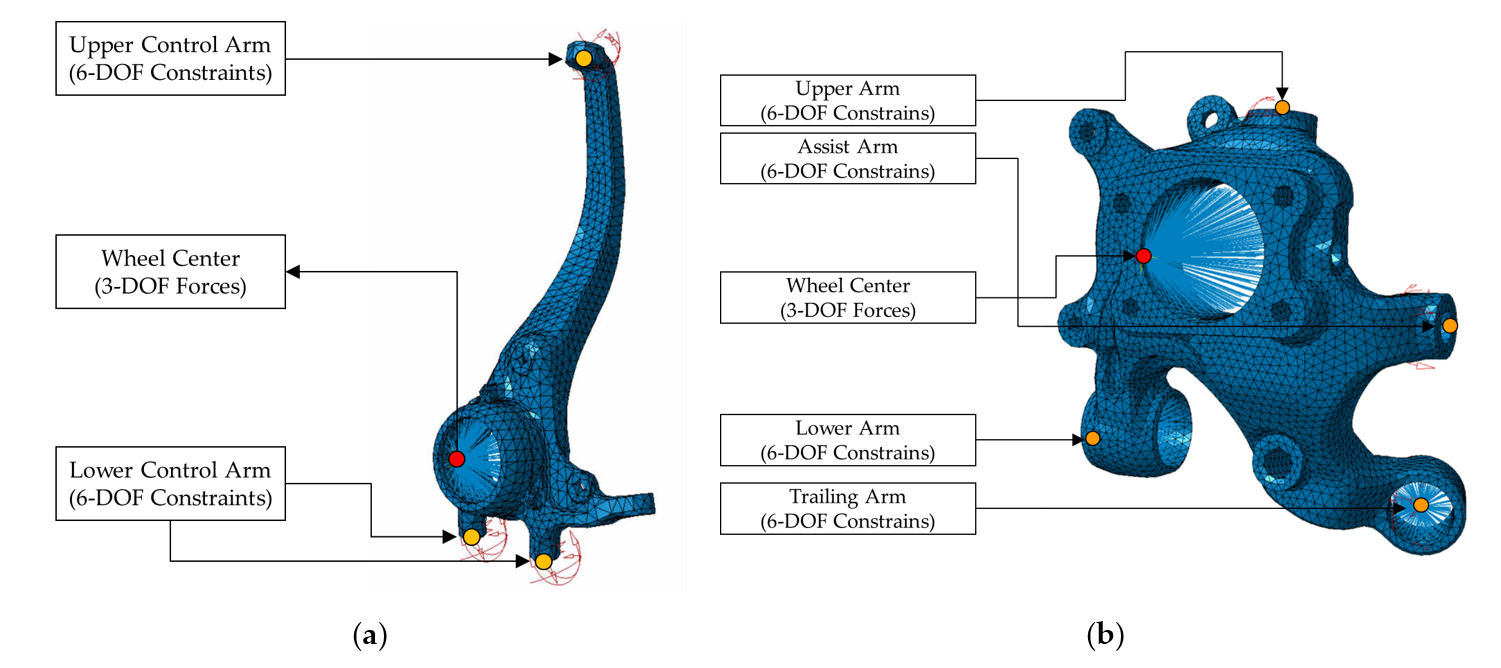
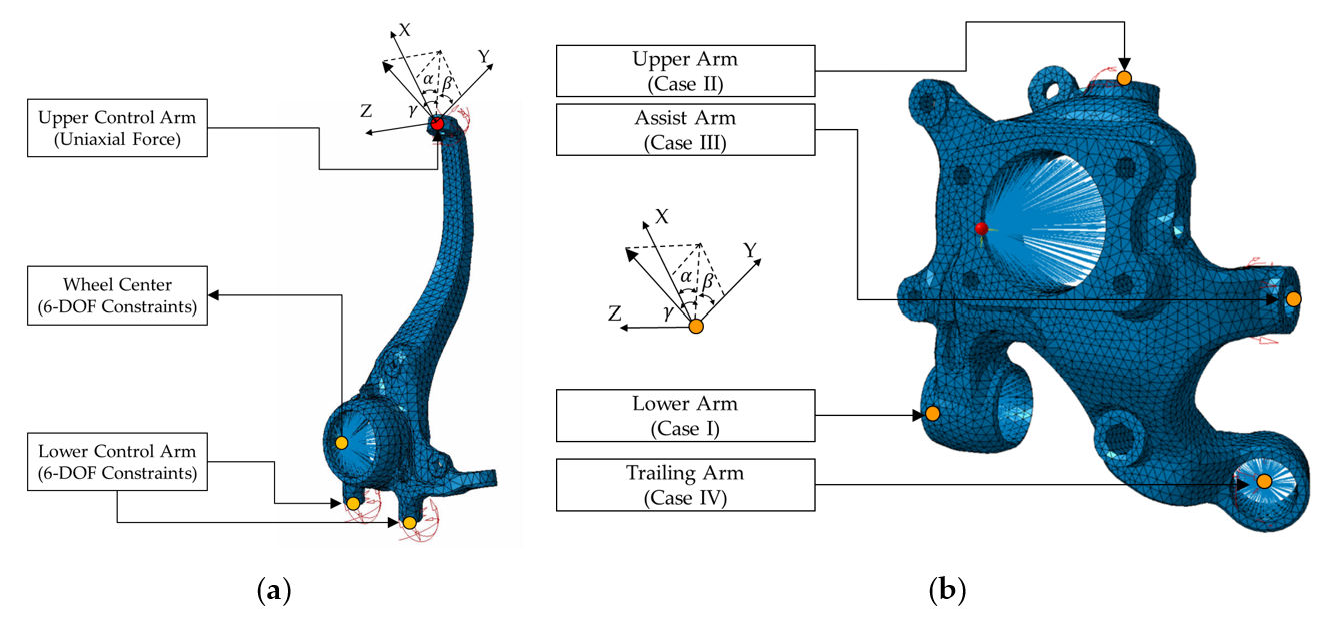
4.1. Analysis Setup
4.2. Analysis Results for Knuckle Parts
4.3. Uniaxial Load Conditions to Satisfy Severity Similarity
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nasada, M. Effect on compliance and alignment variation with respect to stiffness of knuckle and absorber in a McPherson struct suspension. Veh. Syst. Dyn. 2006, 44, 171–180. [Google Scholar] [CrossRef]
- D’Ippolito, R.; Hack, M.; Donders, S.; Hermans, L.; Tzannetakis, N.; Vandepitte, D. Improving the fatigue life of a vehicle knuckle with a reliability-based design optimization approach. J. Stat. Plan. Inference 2009, 139, 1619–1632. [Google Scholar] [CrossRef]
- Jeon, G.T.; Kim, K.Y.; Moon, J.H.; Lee, C.; Kim, W.J.; Kim, S.J. Effect of Al 6061 alloy compositions on mechanical properties of the automotive steering knuckle made by novel casting process. Metals 2018, 8, 857. [Google Scholar] [CrossRef]
- Kashyzadeh, K.R.; Souri, K.; Bayat, A.G.; Jabalbarez, R.S.; Ahmad, M. Fatigue life analysis of automotive cast iron knuckle under constant and variable amplitude loading conditions. Appl. Mech. 2022, 3, 517–532. [Google Scholar] [CrossRef]
- Wysocki, T.; Chahkar, J.; Gauterin, F. Small changes in vehicle suspension layouts could reduce interior road noise. Vehicles 2020, 2, 18–34. [Google Scholar] [CrossRef]
- Kim, J.; Kwon, S.; Ryu, S.; Lee, S.; Jeong, J.; Chung, J. Noise identification for an automotive wheel bearing. Appl. Sci. 2022, 12, 5515. [Google Scholar] [CrossRef]
- Reza Kashyzadeh, K.; Farrahi, G.H.; Shariyat, M.; Ahmadian, M.T. Experimental accuracy assessment of various high-cycle fatigue criterion for a critical component with a complicated geometry and multi-input random non-proportional 3D stress components. Eng. Fail. Anal. 2018, 90, 534–553. [Google Scholar] [CrossRef]
- Kim, C.J. Accelerated sine-on-random vibration test method of ground vehicle components over conventional single mode excitation. Appl. Sci. 2017, 7, 805. [Google Scholar] [CrossRef]
- Kim, C.J.; Kang, Y.J.; Lee, B.H. Generation of driving profile on a multiaxial vibration table for vibration fatigue damage. Mech. Syst. Signal Process. 2012, 26, 244–253. [Google Scholar] [CrossRef]
- Kim, C.J.; Kang, Y.J.; Lee, B.H. Experimental spectral damage prediction of a linear elastic system using acceleration response. Mech. Syst. Signal Process. 2011, 25, 2538–2548. [Google Scholar] [CrossRef]
- Pawliczek, R.; Rozumek, D. The effect of mean load for S355J0 steel with increased strength. Metals 2020, 10, 209. [Google Scholar] [CrossRef]
- Haug, E.J.; Choi, K.K.; Komkov, V. Design Sensitivity Analysis of Structural System; Academic Press: New York, NY, USA, 1986. [Google Scholar]
- Haftka, R.T.; Gurdal, Z. Elements of Structural Optimization, 3rd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Kim, C.J.; Lee, B.H.; Kang, Y.J.; Ahn, H.J. Accuracy enhancement of fatigue damage counting using design sensitivity analysis. J. Sound Vib. 2014, 333, 2971–2982. [Google Scholar] [CrossRef]
- Lee, Y.-L.; Barkey, M.; Kang, H.-T. Metal Fatigue Analysis Handbook; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering; Wiley Interscience: Singapore, 2001. [Google Scholar]
- Findley, W.M. Modified theories of fatigue failure under combined stress. Proc. Soc. Exp. Stress Anal. 1956, 14, 35–46. [Google Scholar]
- Shang, D.G.; Sun, G.Q.; Deng, J.; Yan, C.L. Multiaxial fatigue damage parameter and life prediction for medium-carbon steel based on the critical plane approach. Int. J. Fatigue 2006, 29, 2200–2207. [Google Scholar] [CrossRef]
- Choi, G.J.; Noh, K.H.; Yoo, Y.M. Real-time dynamic simulation using multibody vehicle model. Trans. Korean Soc. Mech. Eng. 2001, 25, 486–494. [Google Scholar]
- Kim, D.; Kim, G.; Chung, I.; Lim, H. Development of durability evaluation technique for semi-active suspension under Chines service condition. In Proceedings of the 2005 KSAE Fall Conference Proceedings, KSAE05-F0260. Anseong-si, Republic of Korea, 24–26 November 2008; pp. 1646–1652. [Google Scholar]
- Kim, K.; Kang, W.; Kim, D.; Ko, W.; Lim, J. The durability performance evaluation of automotive components in the virtual testing laboratory. Trans. KSAE 2006, 14, 68–74. [Google Scholar]
- Sonsino, C.M. Fatigue testing under variable amplitude loading. Int. J. Fatigue 2007, 29, 1080–1089. [Google Scholar] [CrossRef]
- Bellec, E.; Facchinetti, M.L.; Doudard, C.; Galloch, S.; Moyne, S.; Silverstri, M.P. Modelling and identification of fatigue load spectra: Application in the automotive industry. Int. J. Fatigue 2021, 149, 106222. [Google Scholar] [CrossRef]


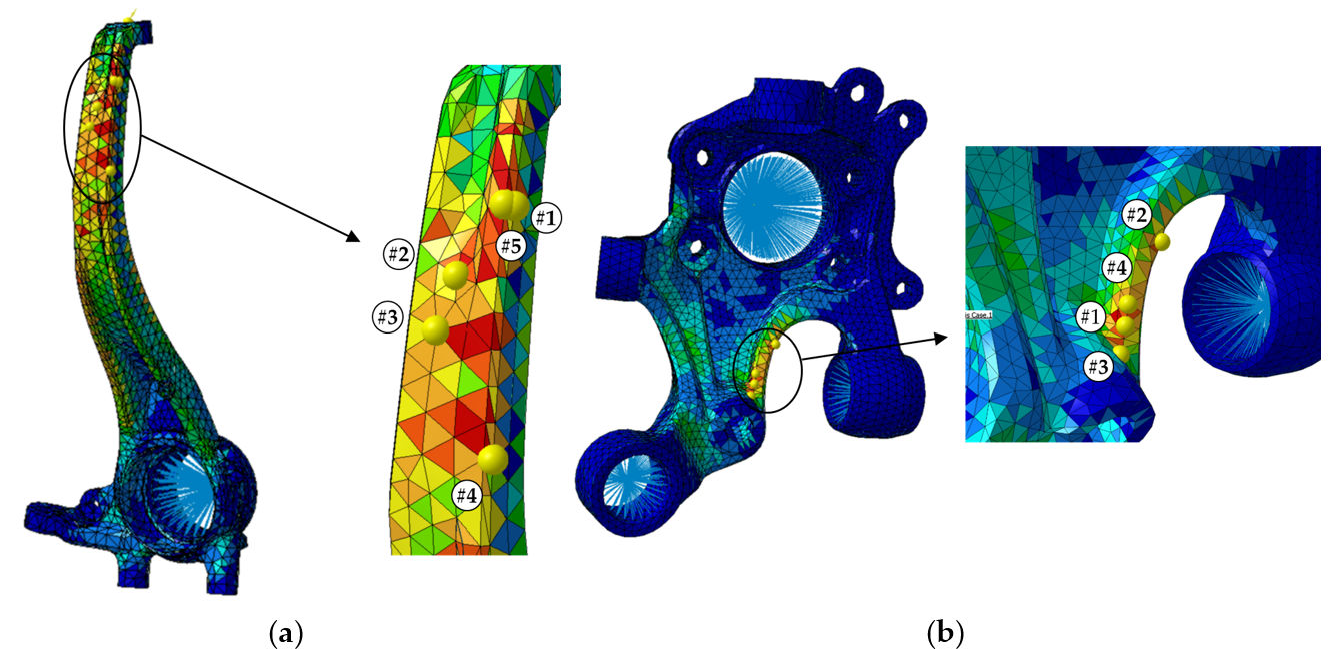
| Hot Point | Front Knuckle | Rear Knuckle |
|---|---|---|
| Inverse Safety Factor | Inverse Safety Factor | |
| #1 | 0.25 | 1.03 |
| #2 | 0.23 | 0.92 |
| #3 | 0.23 | 0.91 |
| #4 | 0.23 | 0.88 |
| Case (°) | Front Knuckle (°) | Rear Knuckle (°) | |||||
|---|---|---|---|---|---|---|---|
| Case I | Case II | Case III | Case IV | ||||
| 0 | 90 | 0 | −16.7 | 23.9 | −231.4 | 26.3 | 25.0 |
| 90 | 0 | 0 | 35.2 | 23.5 | 21.1 | 25.7 | 26.2 |
| 0 | 0 | 90 | 53.4 | 25.8 | 20.2 | 27.4 | 25.2 |
| 90 | 90 | 0 | −14.3 | 22.8 | 29.4 | 33.2 | 25.5 |
| 0 | 90 | 90 | 47.7 | 22.2 | 24.7 | 26.1 | 25.0 |
| 90 | 0 | 90 | −13.8 | 24.1 | 20.5 | 25.9 | 26.0 |
| Front Knuckle | Rear Knuckle | |||||||
|---|---|---|---|---|---|---|---|---|
| Target (Triaxial) | Proposed (Uniaxial) | Target | Proposed | |||||
| Hotspot | Inv. Safety Factor | Angle (°) | Inv. Safety Factor | Angle (°) | Inv. Safety Factor | Angle (°) | Inv. Safety Factor | Angle (°) |
| #1 | 0.25 | 6.4 | 0.23 | −4.4 | 1.03 | 33.3 | 1.07 | 32.5 |
| #2 | 0.24 | 0.21 | 0.92 | 1.03 | ||||
| #3 | 0.23 | 0.21 | 0.91 | 1.02 | ||||
| Part | Orientation | Magnitude (N) | ||
|---|---|---|---|---|
| front knuckle | 90 | 90 | 25 | 4598 |
| rear knuckle | 90 | 90 | 0 | 4498 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.-J. Uniaxial Load Specification for Vehicle Knuckle Part Using Maximum Stress Similarity in Triaxial Load Case. Machines 2022, 10, 1097. https://doi.org/10.3390/machines10111097
Kim C-J. Uniaxial Load Specification for Vehicle Knuckle Part Using Maximum Stress Similarity in Triaxial Load Case. Machines. 2022; 10(11):1097. https://doi.org/10.3390/machines10111097
Chicago/Turabian StyleKim, Chan-Jung. 2022. "Uniaxial Load Specification for Vehicle Knuckle Part Using Maximum Stress Similarity in Triaxial Load Case" Machines 10, no. 11: 1097. https://doi.org/10.3390/machines10111097
APA StyleKim, C.-J. (2022). Uniaxial Load Specification for Vehicle Knuckle Part Using Maximum Stress Similarity in Triaxial Load Case. Machines, 10(11), 1097. https://doi.org/10.3390/machines10111097






