Active Control Method for Rotor Eccentric Vibration of High-Speed Motor Based on Least Squares Support Vector Machine
Abstract
:1. Introduction
2. Active Control of Rotor Eccentric Vibration of High-Speed Motor Based on Least Squares Support Vector Machine
2.1. Structure and Composition Data of High-Speed Motor
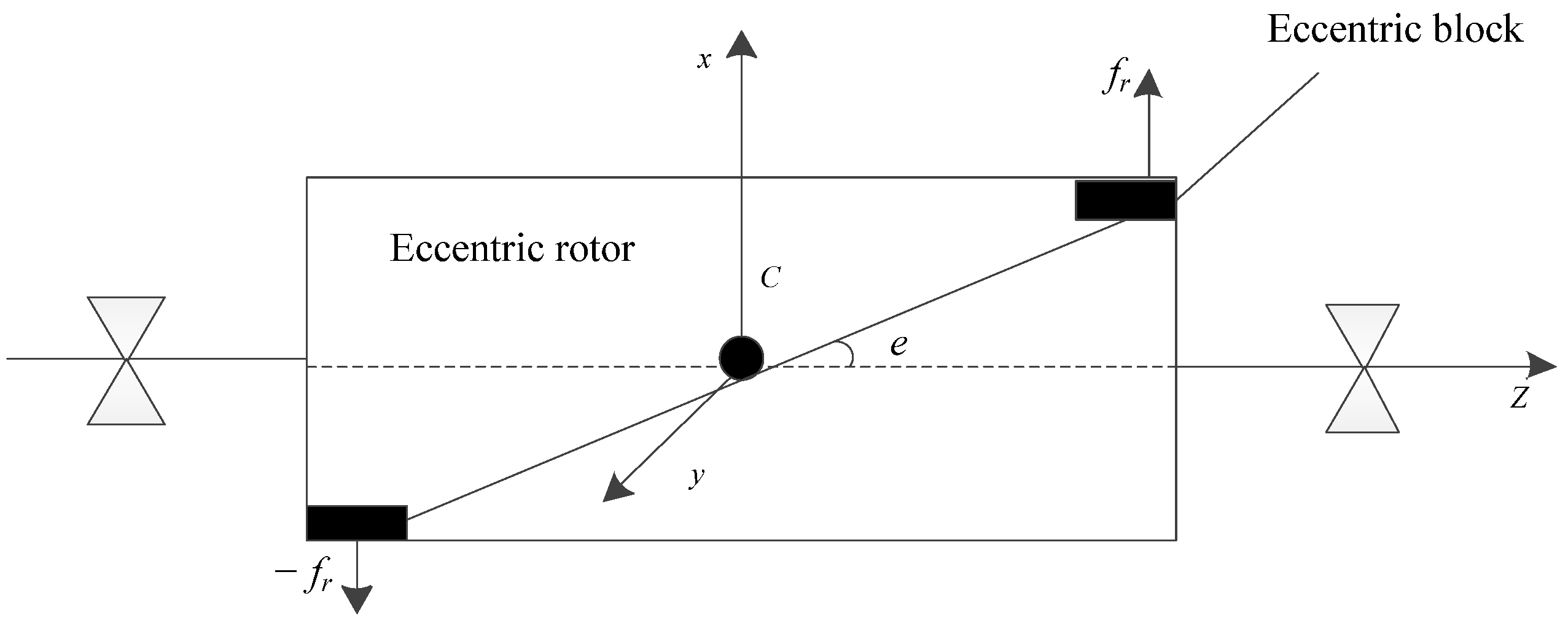
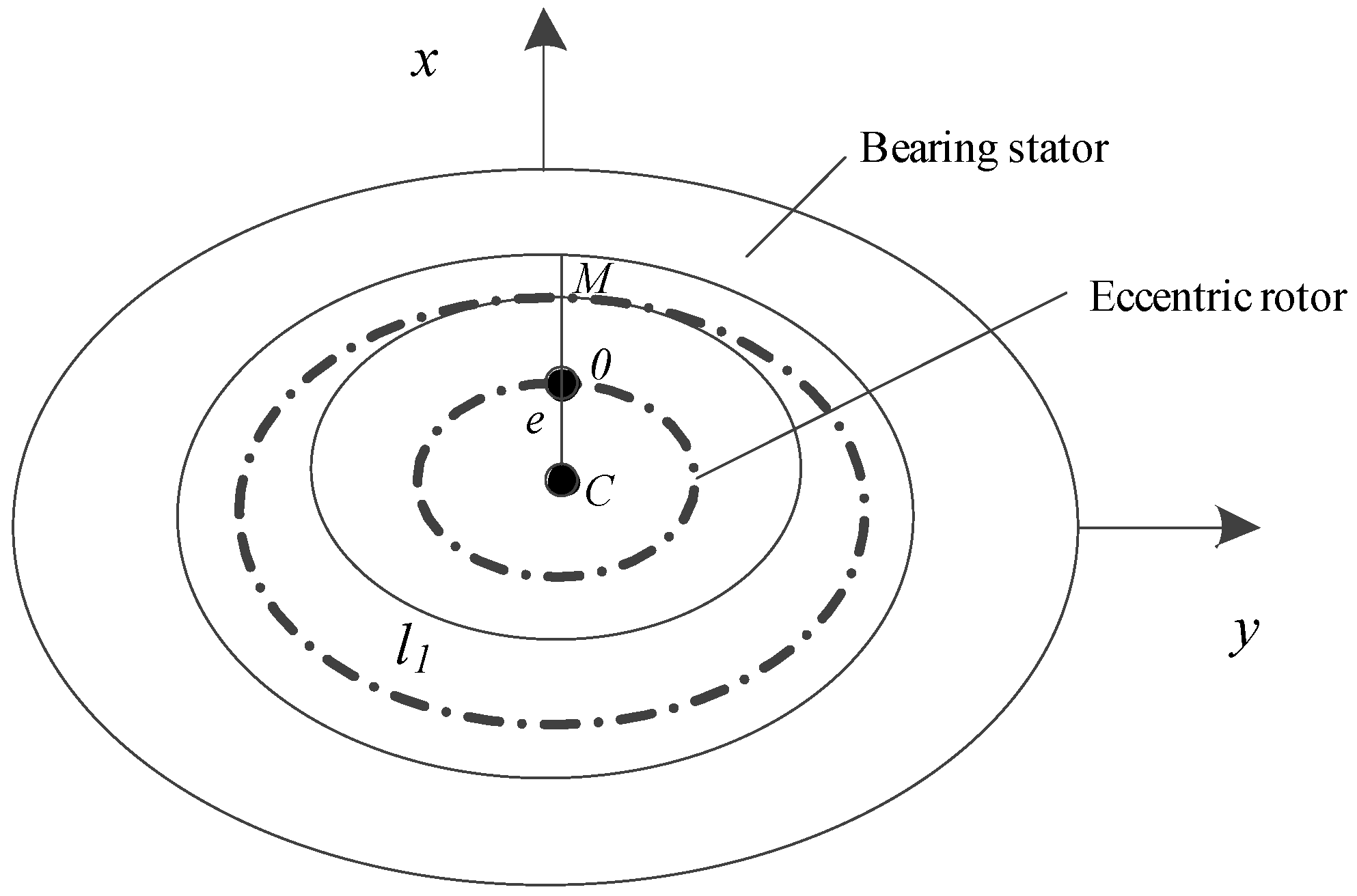
2.2. Mathematical Model of Rotor Eccentric Vibration of High-Speed Motor
2.3. Active Control of High-Speed Motor Based on Least Squares Support Vector Machine
3. Experimental Analysis
3.1. Design of Experimental Protocol
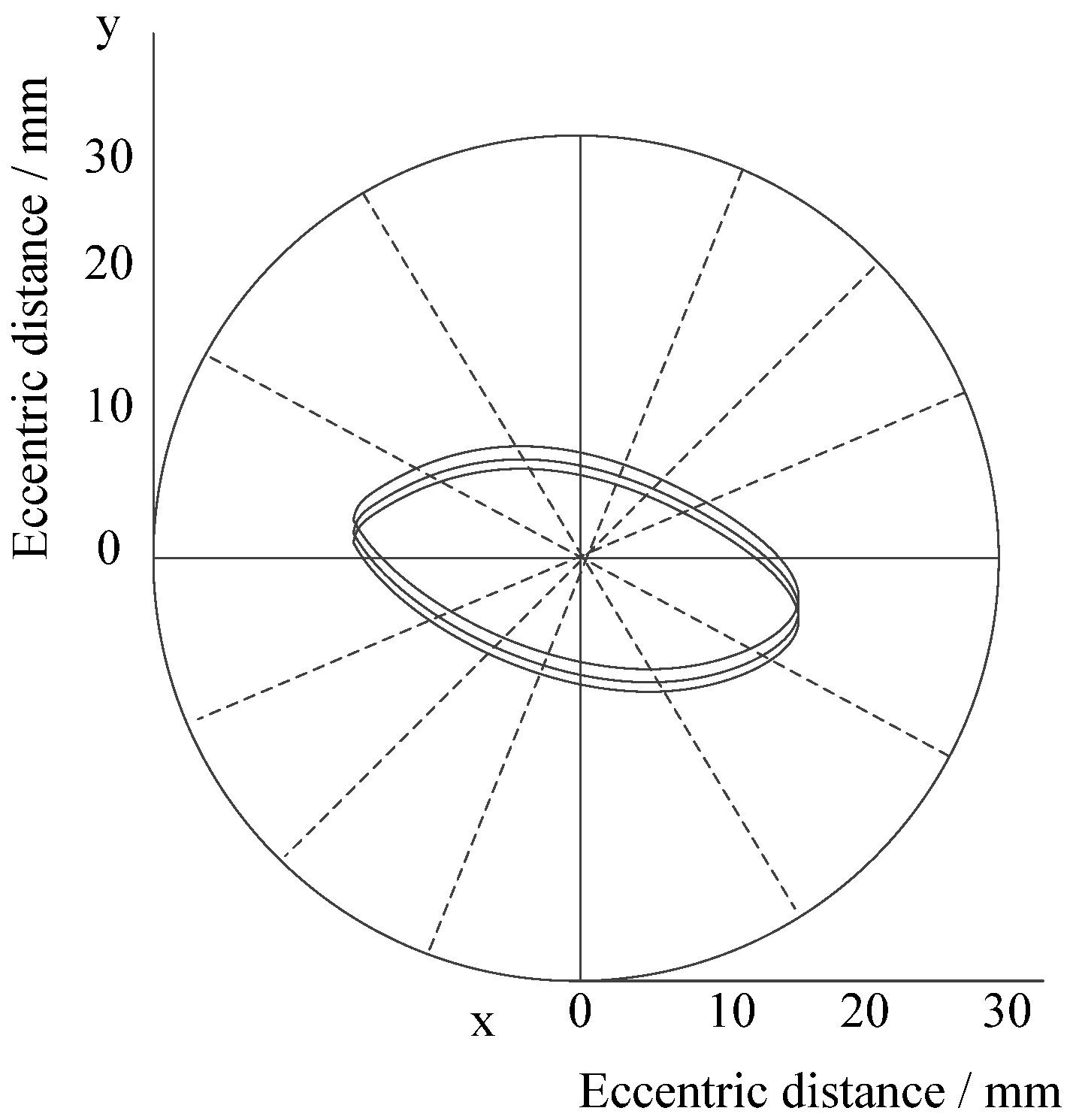
3.2. Experimental Result
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, J.K.; Zheng, G.F.; Liu, P.X.; Lin, D.Q. Overview for the Development and Key Technologies of High Speed Motors. Electr. Drive 2020, 50, 3–915. [Google Scholar]
- Bao, X.C.; Wang, X.L.; Peng, X.H.; Yan, T.X.; Gao, Q.X. Rerview of key technologies for high-speed motor drive. Chin. J. Electr. Eng. 2022, 42, 6856–6870. [Google Scholar]
- Qin, W.J.; Zhao, F.; Dong, J.F.; Zhuo, L. Research onapplication of amorphous materials in high-speed motors for high-altitude aircraft. Micromotor 2021, 54, 104–109. [Google Scholar]
- Wang, X.P.; Yang, C.H.; Qu, C.Y. Electromagnetic analysis and parameter optimization of auxiliary magnetic barrier permanent magnet synchronous motor. Micromotor 2022, 55, 28–36. [Google Scholar]
- Du, W.; Sun, Y.G.; Tian, D.Z.; Gui, L. Online monitoring method for rotor demagnetization fault of permanent magnet synchronous machine based on new type of search coil. Power Autom. Equip. 2020, 40, 218–222. [Google Scholar]
- Gong, L.; Zhu, C.S. Simultaneous vibration suppression of rigid rotor of maglev high-speed motor based on four factor variable polarity control. Chin. J. Electr. Eng. 2021, 41, 1515–1524. [Google Scholar]
- Li, Q.F.; Huang, H.J.; Huang, S.R.; Li, L.H. Research on fast diagnosis of rotor eccentricity fault for surface-mounted permanent magnet motor. Electr. Mach. Control 2019, 23, 48–58+67. [Google Scholar]
- Ren, J.; Wang, X.H.; Zhao, W.L.; Xing, Z.Z. Open circuit magnetic field prediction in permanent magnet synchronous machine with rotor eccentricity. Electr. Mach. Control 2020, 24, 26–32. [Google Scholar]
- Du, X.B.; Huang, K.S.; Cai, L.M. Reducing torque ripple of external rotor permanent magnet motor based on structure of stator tooth eccentricity. Small Spec. Electr. Mach. 2019, 47, 21–24, 28. [Google Scholar]
- Ji, Y.; Sun, L.; Li, Y.; Li, J.; Liu, S.; Xie, X.; Xu, Y. Non-destructive classification of defective potatoes based on hyperspectral imaging and support vector machine. Infrared Phys. Technol. 2019, 99, 71–79. [Google Scholar] [CrossRef]
- Ma, C.; Gao, Y.; Degano, M.; Wang, Y.; Fang, J.; Gerada, C.; Zhou, S.; Mu, Y. Eccentric position diagnosis of static eccentricity fault of external rotor permanent magnet synchronous motor as an in-wheel motor. IET Electr. Power Appl. 2020, 14, 2263–2272. [Google Scholar] [CrossRef]
- Jacobellis, G.; Gandhi, F.; Floros, M. Using control redundancy for power and vibration reduction on a coaxial rotor helicopter at high speeds. J. Am. Helicopter Soc. 2019, 64, 1–13. [Google Scholar] [CrossRef]
- Dong, H.M.; Zhang, A.S.; Shu, H.; Zhang, C. Simultaneous identification method of rotor distributed unbalance and bearing characteristic parameters. J. Harbin Inst. Technol. 2022, 54, 128–135. [Google Scholar]
- Li, B.; Bu, W.S.; Chen, Y.P. Simulation compensation of rotor unbalance vibration of bearingless asynchronous motor. Comput. Simul. 2020, 37, 243–247. [Google Scholar]
- Nair, R.; Gopalaratnam, N. Stator flux based model reference adaptive observers for sensorless vector control and direct voltage control of doubly-fed induction generator. IEEE Trans. Ind. Appl. 2020, 56, 3776–3789. [Google Scholar] [CrossRef]
- Ji, L.; Ma, X.Q.; Chen, Z.M. Low frequency vibration mechanism for amb high-speed motor rotor systems and its compensation strategy. China Mech. Eng. 2022, 17, 2053–2060. [Google Scholar]
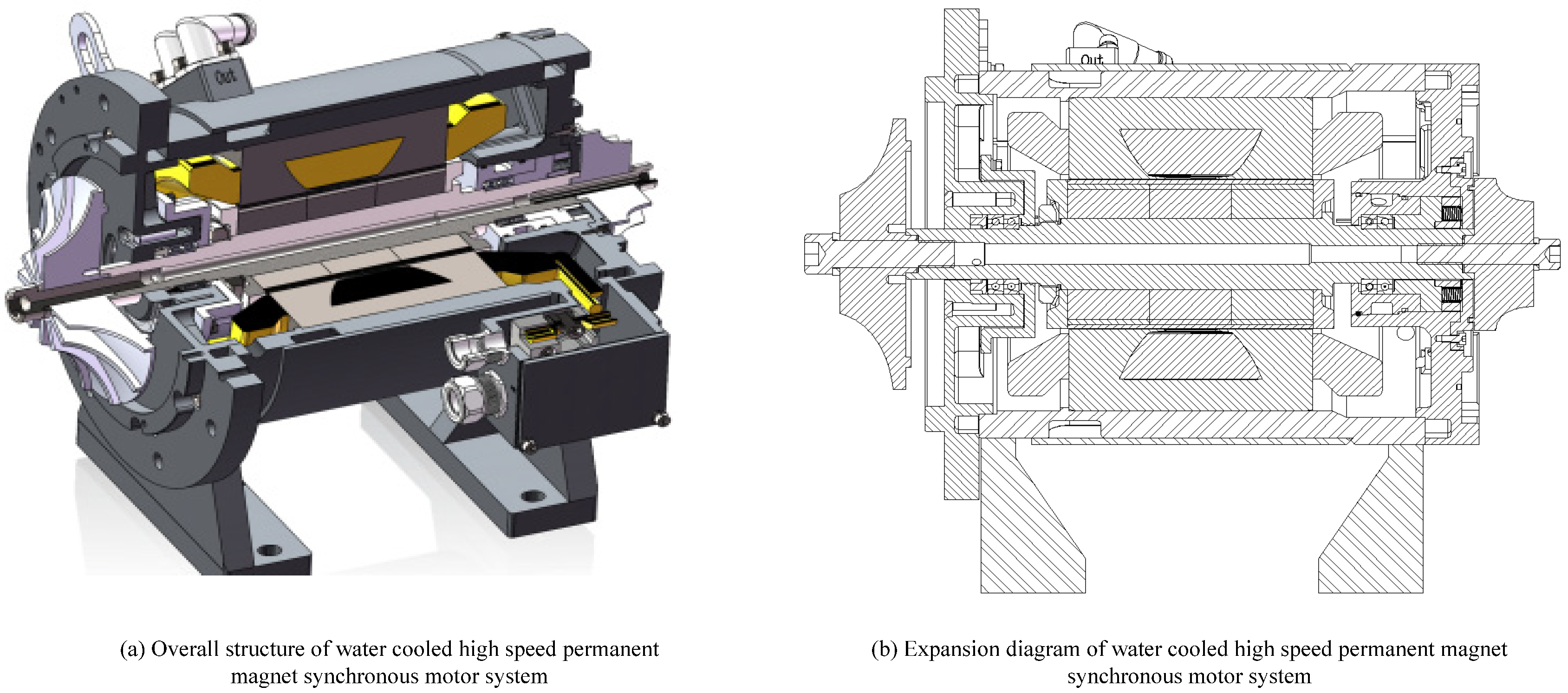
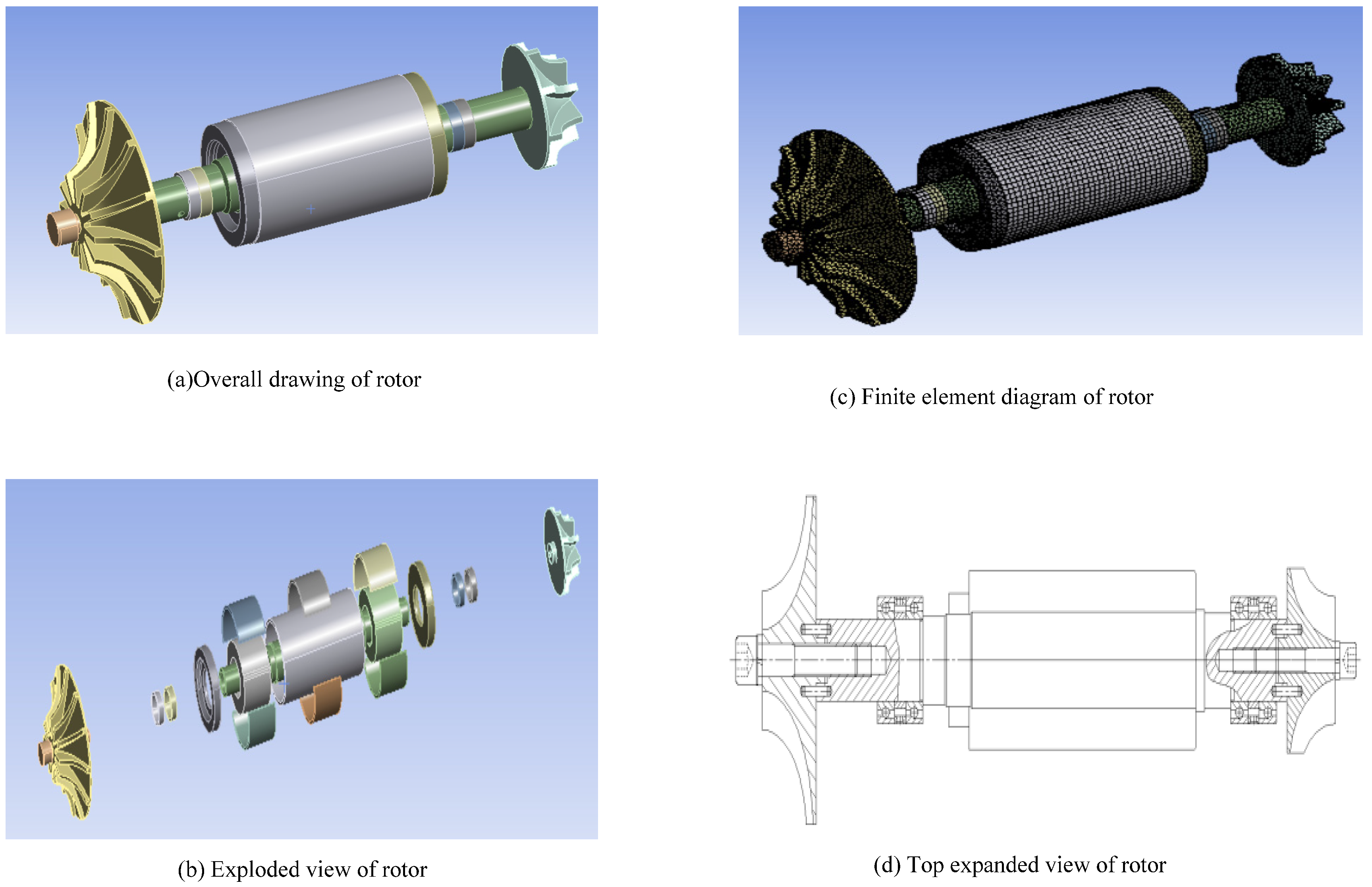



| Composition | Data |
|---|---|
| Category | Water-cooled high-speed permanent magnet synchronous motor |
| Rated value | 380 Vac, 96 Arms, 50 kW, 35,000 rpm |
| Rotor structure | External diameter, 87.4 mm; axial, 140 mm; 2-pole surface paste, the permanent magnet under monopole is magnetized in parallel in three sections and wound with high-strength carbon fiber sheath |
| Stator structure | External diameter, 185 mm; internal diameter, 89 mm; axial, 140 mm 24-slot, 3-phase, double-layer, short-distance laminated winding |
| Main materials | Core 0.2 mm silicon steel sheet Samarium cobalt permanent magnet Spindle material 42CrMo |
| Motor application | Refrigeration equipment with impeller at both ends |
| Project | Data |
|---|---|
| Entrance pressure at the booster end (bar) | 3.5 |
| Export pressure at the booster end (bar) | 5.873 |
| Supercharged end flow (g/s) | 1011 |
| Biocharged end inlet temperature (°C) | 30 |
| Charge outlet temperature (°C) | 100 |
| Expansion-end inlet pressure (bar) | 5.773 |
| Export pressure at the expansion end (bar) | 3.57 |
| Expansion end flow (g/s) | 1011 |
| Expansion-end inlet temperature (°C) | −55.12 |
| Export temperature at the expansion end (°C) | −80 |
| Project | Data |
|---|---|
| Work environment | Atmospheric environment |
| Specific application purpose | Hang the turbine for the cooling application |
| Air intake atmospheric pressure | 3.5 bar |
| Exhaust atmospheric pressure | 5.7 bar |
| Rate of flow | 1.1 kg/s |
| Internal atmospheric pressure inside the motor | 6 bars |
| Compressor air inlet temperature | 35 °C |
| Compressor exhaust temperature | 100 °C |
| Rotor Speed (rpm) | Eccentric Control Time Cost of this Paper Method(s) | Eccentric Control Time Cost of Document [7] Method(s) | Eccentric Control Time Cost of Document [8] Method(s) |
|---|---|---|---|
| 25,000 | 0.11 | 0.23 | 0.32 |
| 30,000 | 0.12 | 0.25 | 0.34 |
| 35,000 | 0.12 | 0.28 | 0.36 |
| 40,000 | 0.13 | 0.31 | 0.42 |
| 45,000 | 0.12 | 0.36 | 0.44 |
| 50,000 | 0.11 | 0.40 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhuang, M.; Yuan, K. Active Control Method for Rotor Eccentric Vibration of High-Speed Motor Based on Least Squares Support Vector Machine. Machines 2022, 10, 1094. https://doi.org/10.3390/machines10111094
Wang L, Zhuang M, Yuan K. Active Control Method for Rotor Eccentric Vibration of High-Speed Motor Based on Least Squares Support Vector Machine. Machines. 2022; 10(11):1094. https://doi.org/10.3390/machines10111094
Chicago/Turabian StyleWang, Liheng, Ming Zhuang, and Kai Yuan. 2022. "Active Control Method for Rotor Eccentric Vibration of High-Speed Motor Based on Least Squares Support Vector Machine" Machines 10, no. 11: 1094. https://doi.org/10.3390/machines10111094
APA StyleWang, L., Zhuang, M., & Yuan, K. (2022). Active Control Method for Rotor Eccentric Vibration of High-Speed Motor Based on Least Squares Support Vector Machine. Machines, 10(11), 1094. https://doi.org/10.3390/machines10111094





