An Investigation of the Performance and Internal Flow of Variable Nozzle Turbines with Split Sliding Guide Vanes
Abstract
1. Introduction
2. Research Model and Numerical Method
2.1. Base and SSGV Models
2.2. Numerical Method
2.3. Grid Independence Verification
2.4. Numerical Verification
3. Result Analysis
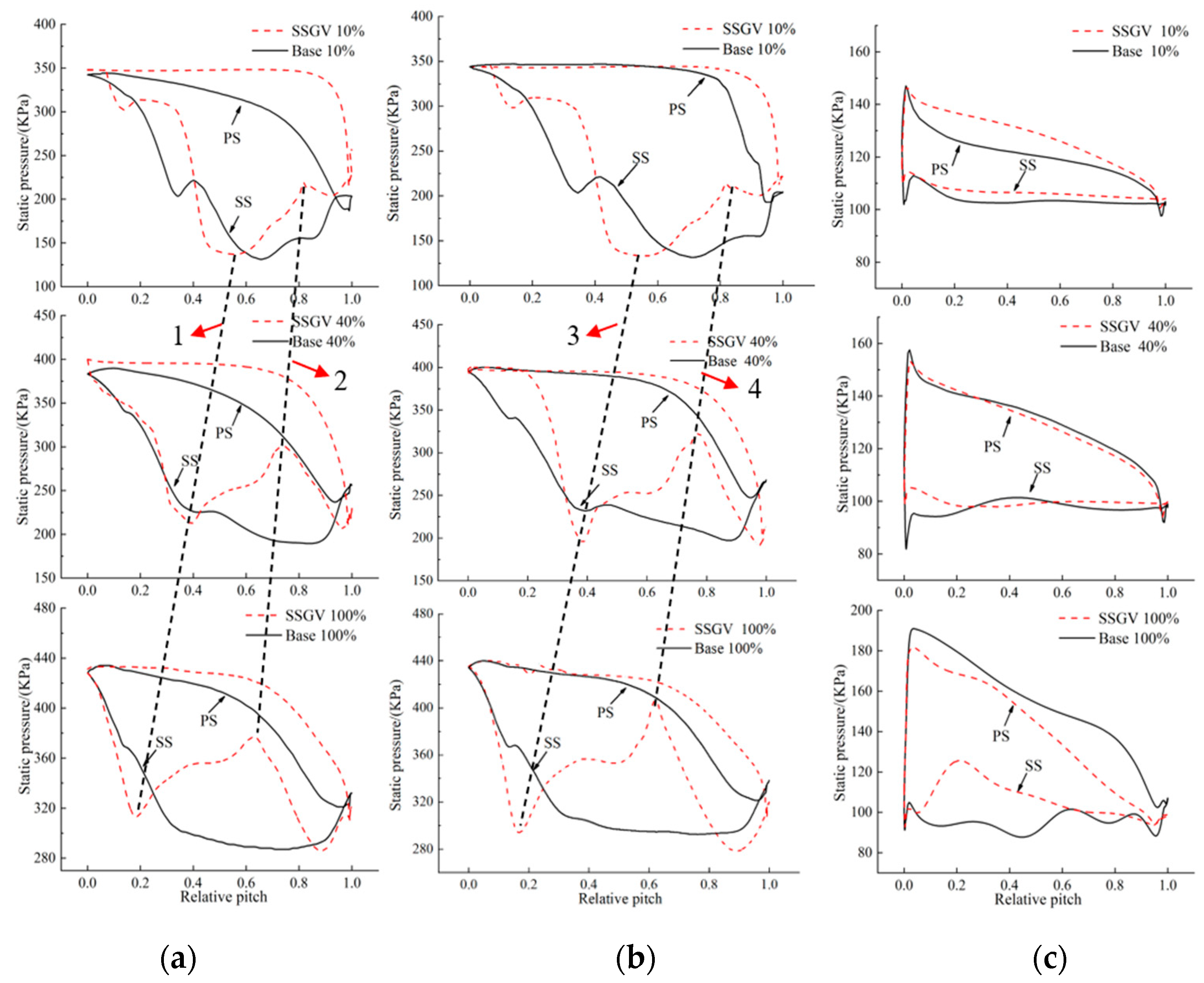
3.1. Performance Comparison
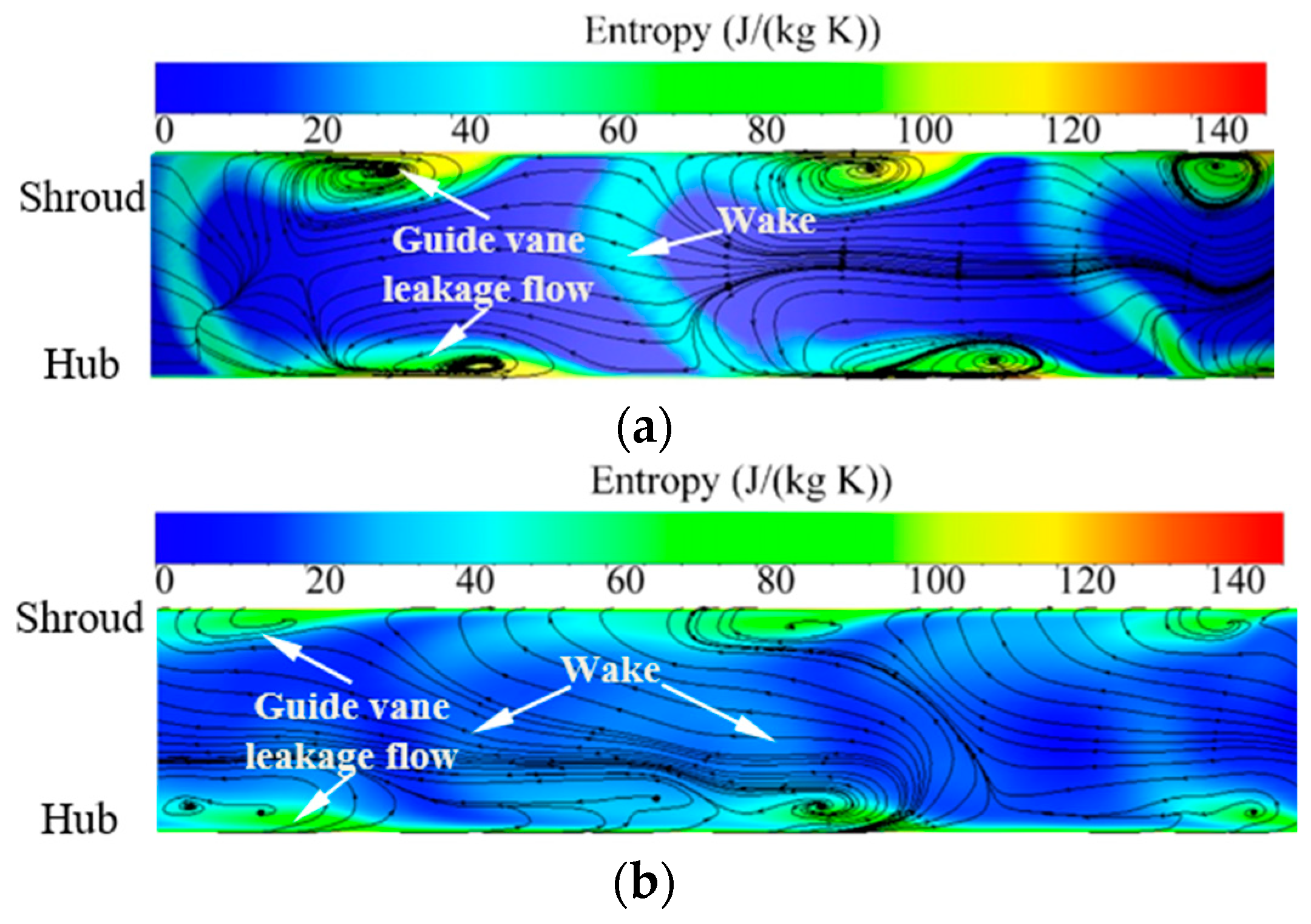
3.2. Leakage Flow Analysis
3.3. Flow and Loss in the Rotor
4. Shock and Rotor Blade Load Fluctuations
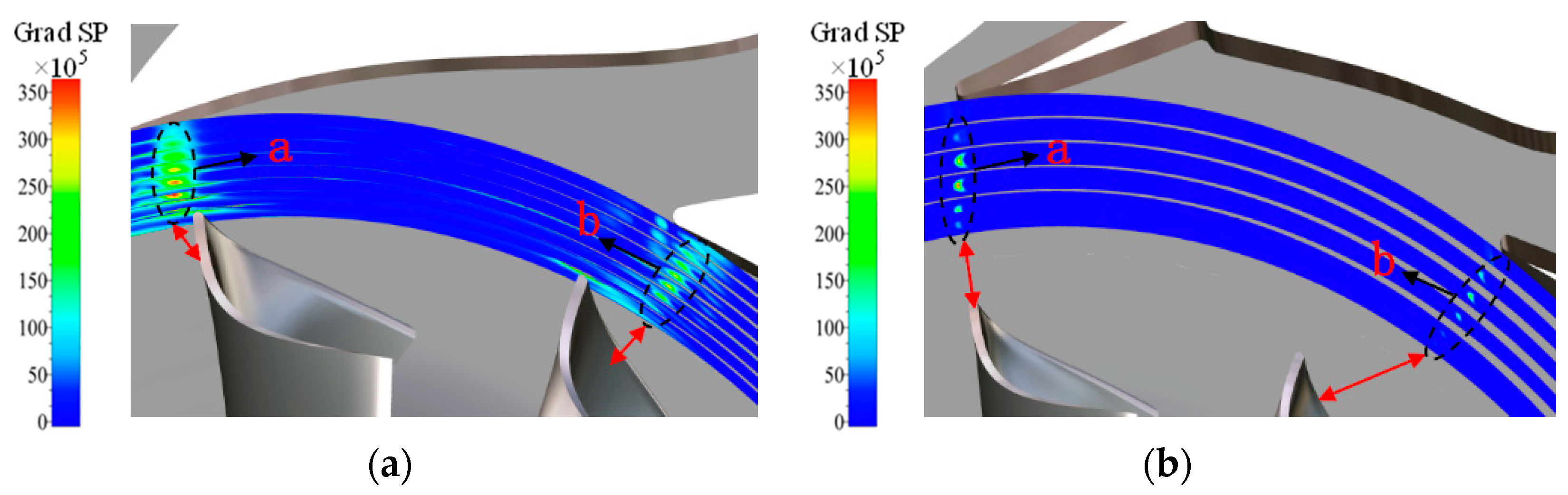
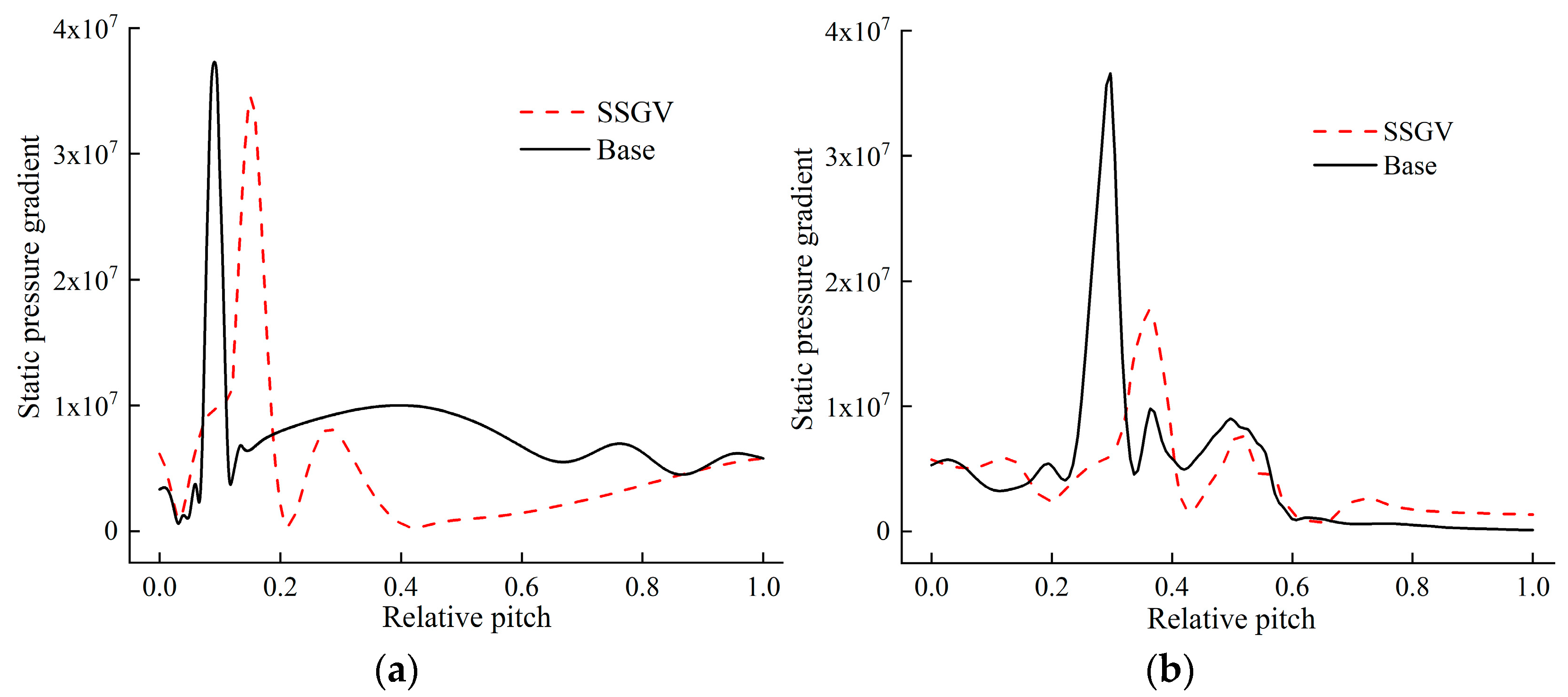
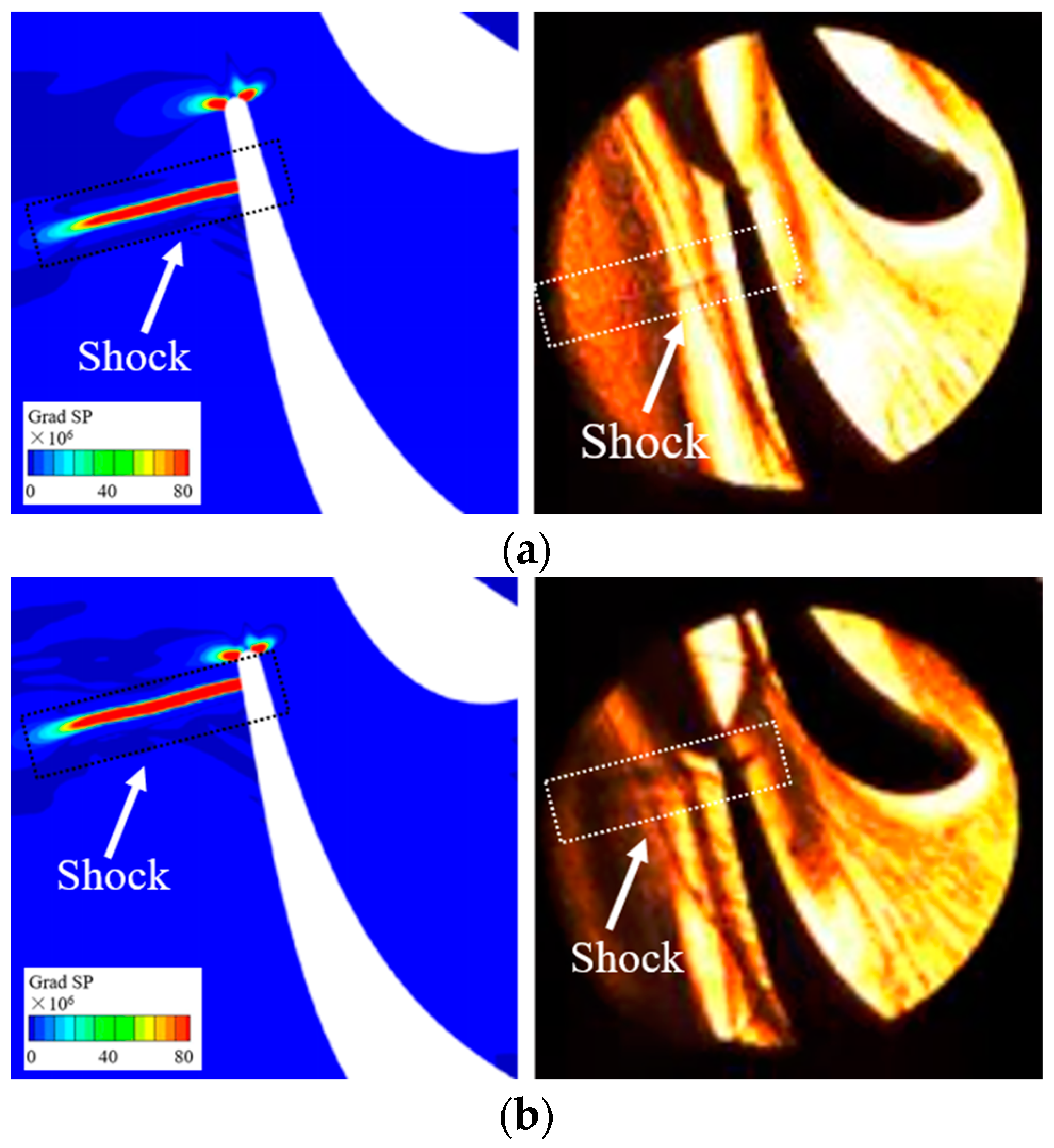
4.1. Shock Distribution at the Transition Region between the Rotor and Stator
4.2. Rotor Blade Load Fluctuations
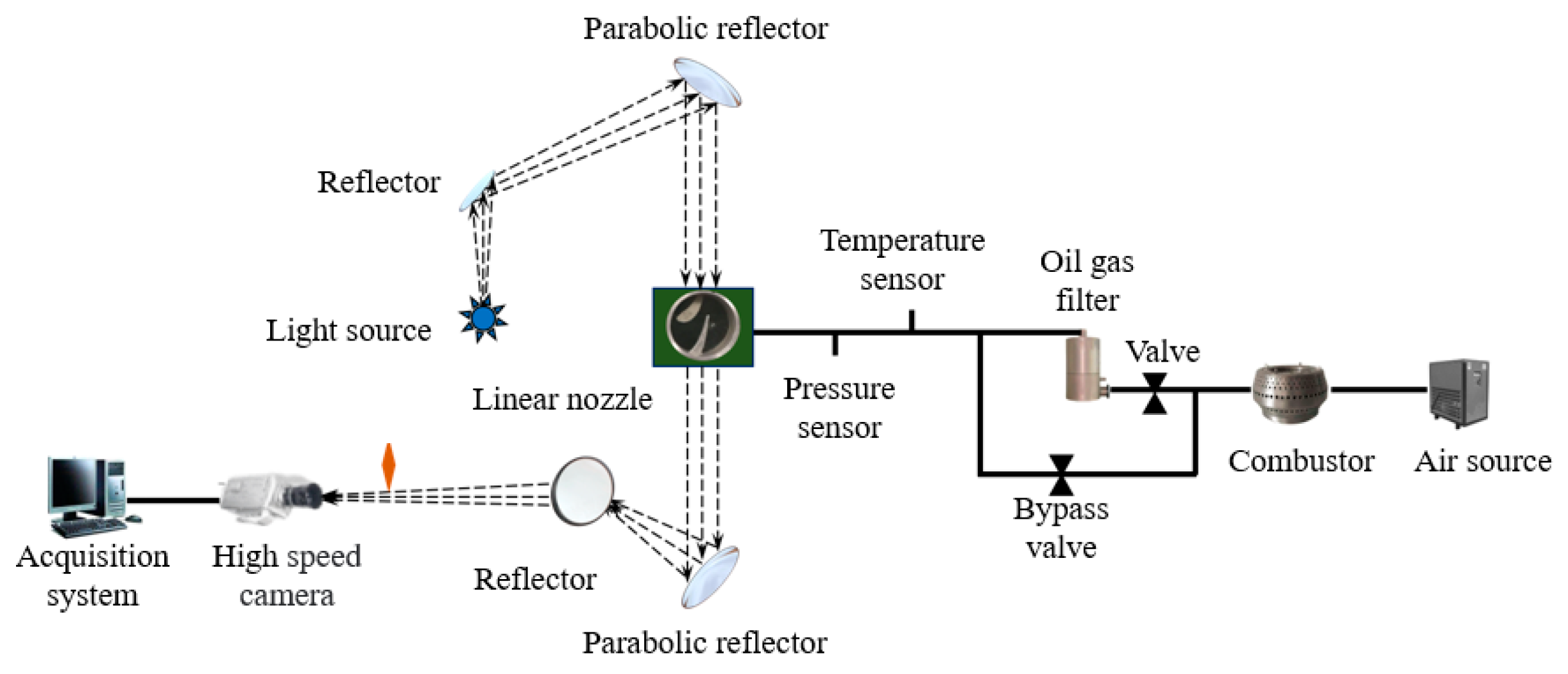
4.3. Shock Validation
5. Conclusions
- (1)
- The SSGV could better inhibit the guide vane and rotor clearance leakage flow, thus improving the global performance of VNTs, especially at small guide vane openings. In this work, the SSGV could increase the VNT performance by 12% at a 10% opening since the guide vane clearance leakage flow was decreased by 57%.
- (2)
- Due to the special vane shape of the SSGV, the angle of attack of the airflow at the rotor leading edge was greater than that of the base model, resulting in strong gas separation vortices and flow loss in the rotor. Therefore, reducing the flow loss caused by its own geometric factors is an important problem to be considered in the design of the SSGV.
- (3)
- In the rotor-stator transition region, when the shock gradually approached the rotor blade, its intensity also gradually increased. Otherwise, it gradually decreased. Since the distance between the rotor and stator was enlarged for the SSGV, its shock intensity was much weaker than that of the base model.
- (4)
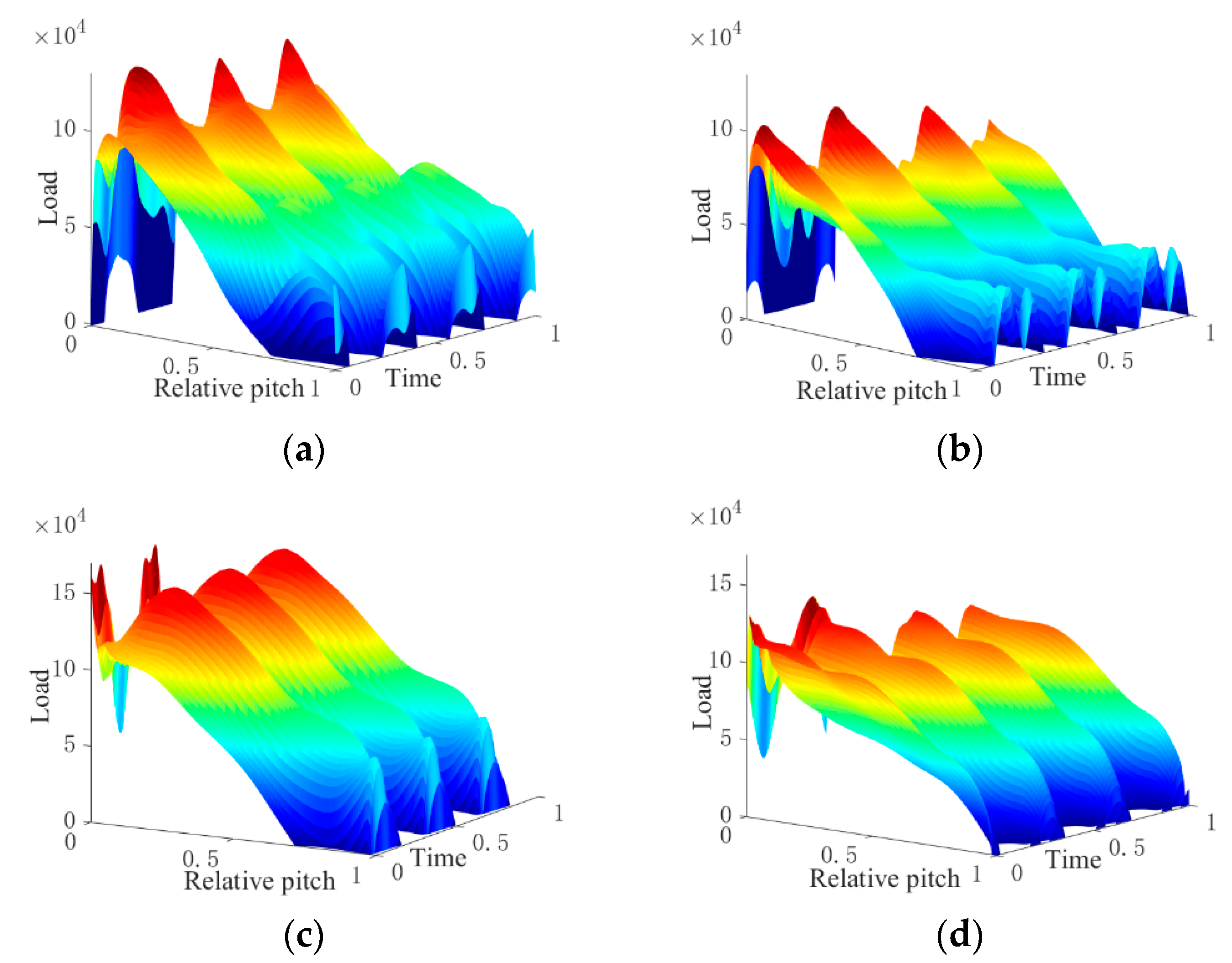
- By comparing the load distribution characteristics of the rotor blades of the two models in a rotation period, it was found that since the guide vane leakage flow and shock were weakened, the load amplitude, as well as the degree of load fluctuation, were both reduced to a certain extent for the SSGV model, indicating that using of an SSGV for a VNT could enhance the reliability of the rotor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| VNT | Variable nozzle turbine |
| VGT | Variable geometry turbine |
| S-A | Spalar-Allmaras |
| R/S | Rotor and Stator |
| SSGV | Split sliding guide vane |
| CFD | Computational Fluid Dynamics |
| u/c | Velocity ratio |
| m | Mass flow rate |
| π | Expansion ratio |
| η | Efficiency |
| PS | Pressure surface |
| SS | Suction surface |
| SP | Static pressure |
References
- Kagawa, J. Health effects of diesel exhaust emissions-a mixture of air pollutants of worldwide concern. Toxicology 2002, 181, 349–353. [Google Scholar] [CrossRef]
- Shi, M.; Wang, H.; Yang, C.; Wang, Y.; Niu, X. Experimental Research on the Matching Characteristics of the Compound VGT-STC System with a V-Type Diesel Engine. Machines 2022, 10, 788. [Google Scholar] [CrossRef]
- Effect of Nozzle Vane and Rotor Clearance on Performance of Variable Nozzle Turbine. J. Therm. Sci. 2022, 31, 1745–1758. [CrossRef]
- Zhao, B.; Yang, C.; Hu, L.; Sun, H.; Yi, J.; Eric, C.; Shi, X.; Engeda, A. Understanding of the interaction between tip leakage flow and main passage flow in a VGT turbine. Adv. Mech. Eng. 2015, 7, 652769. [Google Scholar] [CrossRef]
- Viskup, R.; Alberer, D.; Oppenauer, K.; del Re, L. Measurement of Transient PM Emissions in Diesel Engine; SAE Technical Paper; SAE: Detroit, MI, USA, 2011. [Google Scholar]
- Ishii, M.; Shimokawa, K.; Machida, K.; Nakajima, H. A Study on Improving Fuel Consumption of Heavy-Duty Diesel Engine Specifically Designed for Long-Haul Trucks on Highway; SAE 2015 World Congress and Exhibition; SAE: Detroit, MI, USA, 2015. [Google Scholar]
- Spence, S.W.T.; O’neill, J.W.; Cunningham, G. An investigation of the flowfield through a variable geometry turbine stator with vane endwall clearance. Proc. IMechE Part A J. Power Energy 2006, 220, 899–910. [Google Scholar] [CrossRef]
- Hu, L.; Sun, H.; Yi, J.; Curtis, E.; Zhang, J. Investigation of Nozzle Clearance Effects on a Radial Turbine: Aerodynamic Performance and Forced Response; SAE Technical Paper; SAE: Detroit, MI, USA, 2013. [Google Scholar]
- Chen, H. Turbine wheel design for Garrett advancd variable geometry turbines for commercial vehicle applications. In Proceedings of the 8th ICTT, London, UK, 17–18 May 2006; pp. 317–327. [Google Scholar]
- Kawakubo, T. Unsteady Rotor-Stator Interaction of a Radial-Inflow Turbine with Variable Nozzle Vanes. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; paper GT2010-23677; ASME: New York, NY, USA, 2010. [Google Scholar]
- Qi, M.; Lei, X.; Wang, Z.; Ma, C. Investigation on the flow characteristics of a VNT turbine under pulsating flow conditions. Proc. IMechE Part D J. Automob. Eng. 2018, 233, 396–412. [Google Scholar] [CrossRef]
- Yang, D.; Yang, C.; Lao, D.; Zeng, T. A detailed investigation of a variable nozzle turbine with novel forepart rotation guide vane. Proc. IMechE Part D J. Automob. Eng. 2019, 233, 994–1007. [Google Scholar] [CrossRef]
- Taghavi-Zenouz, R.; Behbahani MH, A. Improvement of aerodynamic performance of a low speed axial compressor rotor blade row through air injection. Aerosp. Sci. Technol. 2018, 72, 409–417. [Google Scholar] [CrossRef]
- Künzelmann, M.; Urban, R.; Mailach, R. Active flow control at a 1.5-stage low-speed research compressor with varying rotor tip clearance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 886–896. [Google Scholar] [CrossRef]
- Bindon, J.P. The Measurement and formation of tip clearance loss. J. Turbomach. 1989, 111, 257–263. [Google Scholar] [CrossRef]
- Masashi, F.; Masatoshi, W.; Tetsuo, U. Compressible Turlent Flow Analysis on Variable Nozzle Vane and Spacer in Turbocharger Turbine; SAE Paper; SAE: Detroit, MI, USA, 2000. [Google Scholar]
- Vemula, R. Turbocharger with Variable Turbine Geometry Having Grooved Guide Vanes. U.S. US10138744B2, 14 February 2018. [Google Scholar]
- Walkingshaw, J.; Spence, S.; Ehrhard, J.; Thornhill, D. An experimental assessment of the effects of stator vane tip clearance location and back swept blading on an automotive variable geometry turbocharger. J. Turbomach. 2014, 136, 927–937. [Google Scholar] [CrossRef]
- Ben ZH, A.O.; Leilei WA, N.G.; Hongjun HO, U. Numerical analysis for impacts of nozzle end-clearances on aerodynamic performance and forced response in a VNT turbine. Chin. J. Aeronaut. 2018, 31, 168–178. [Google Scholar]
- Zhang, H.; Lao, D.; Yang, C.; Yang, D.; Hou, X.; Wang, X. Internal flow characteristics of a variable mixed flow turbine with partially-rotating vane nozzle. J. Mech. Sci. Technol. 2017, 31, 4977–4987. [Google Scholar] [CrossRef]
- Chen, H.; Huang, L. Variable Geometry Turbine Nozzle Design for High Expansio Ratios. In Proceedings of the ASME Turbo Expo 2018: Power for Land, Sea, and Air, Oslo, Norway, 11–15 June 2018; paper GT2018-57013; ASME: New York, NY, USA, 2018. [Google Scholar]
- Yang, D.; Lao, D.; Yang, C.; Hu, L.; Sun, H. Investigations on the Generation and Weakening of Shock Wave in a Radial Turbine with Variable Guide Vanes. In Proceedings of the ASME Turbo Expo 2016: Power for Land, Sea, and Air, Seoul, South Korea, 13–17 June 2016; paper GT2016-57047; ASME: New York, NY, USA, 2016. [Google Scholar]
- Sonoda, T.; Arima, T.; Olhofer, M.; Sendhoff, B.; Kost, F.T.; Giess, P.A. A Study of Advanced High Loaded Transonic Turbine Airfoils. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; paper GT2004-53773; ASME: New York, NY, USA, 2004. [Google Scholar]
- Lei, X.; Qi, M.; Sun, H.; Hu, L. Investigation on the shock control using grooved surface in a linear turbine nozzle. J. Turbomach. 2017, 139, 121008. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, H.; Shi, X.; Qi, M.; Guo, S. Investigation of using multi-shockwave system instead of single normal shock for improving radial inflow turbine reliability. Int. J. Heat Fluid Flow 2018, 71, 170–178. [Google Scholar] [CrossRef]
- Liu, Y.; Lao, D.; Liu, Y.; Yang, C.; Qi, M. Investigation on the Effects of Nozzle Openings for a Radial Turbine with Variable Nozzle; SAE International: Detroit, MI, USA, 2014; No. 14PFL-0879. [Google Scholar]
- Denton, J.D.; Xu, L. The trailing edge loss of transonic turbine blades. J. Turbomach. 1990, 112, 277. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Qi, M.; Zhang, H.; Zhao, B. Shock, Leakage Flow and Wake Interactions in a Radial Turbine with Variable Guide Vanes. In Proceedings of the ASME Turbo Expo 2014: Power for Land, Sea, and Air, Düsseldorf, Germany, 16–20 June 2014; paper GT2014-25888; ASME: New York, NY, USA, 2014. [Google Scholar]
- Stephen, S.M.; Seiler, M.; Schaefer, O. Blade excitation in pulse-charged mixed-flow turbocharger turbines. J. Turbomach. 2011, 133, 021012. [Google Scholar]
- Kulkarni, A.; Tisserant, D.; Hosny, D.; Liang, E.; Krishnaraja, N. Turbine Wheel High Cycle Fatigue Reliability Prediction; ASME Paper; SAE: Detroit, MI, USA, 2010; pp. 171–181. [Google Scholar]
- Galindo, J.; Fajardo, P.; Navarro, R.; García-Cuevas, L.M. Characterization of a radial turbocharger turbine in pulsating flow by means of CFD and its application to engine modeling. Appl. Energy 2013, 103, 116–127. [Google Scholar] [CrossRef]
- Zhang, J.; Zhuge, W.; Hu, L.; Li, S. Design of Turbocharger Variable Nozzle. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; paper GT2007-27562. ASME: New York, NY, USA, 2007. [Google Scholar]
- Spraker, N. Contour Clearance Losses in Radial Inflow Turbines for Turbochargers; ASME Paper, No. 87-ICE-52; ASME: New York, NY, USA, 1987. [Google Scholar]

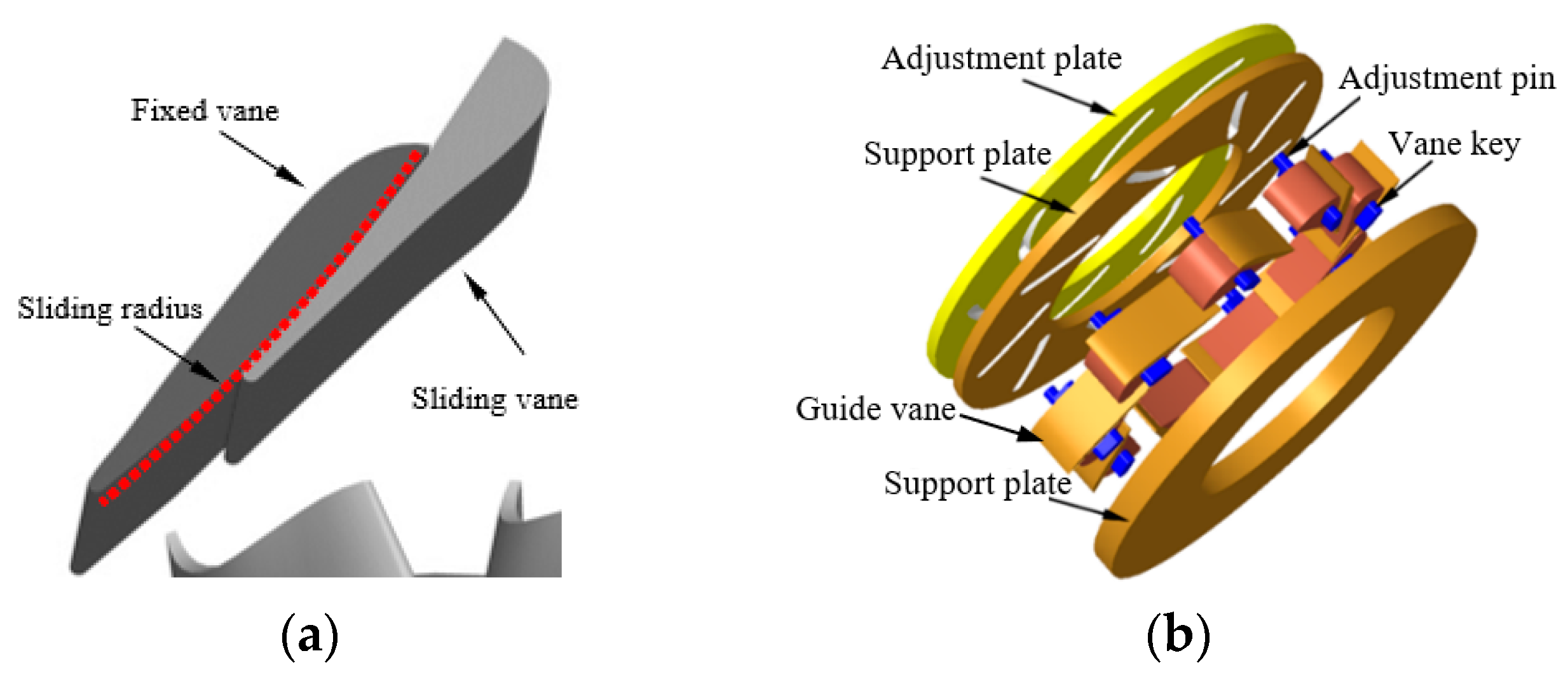
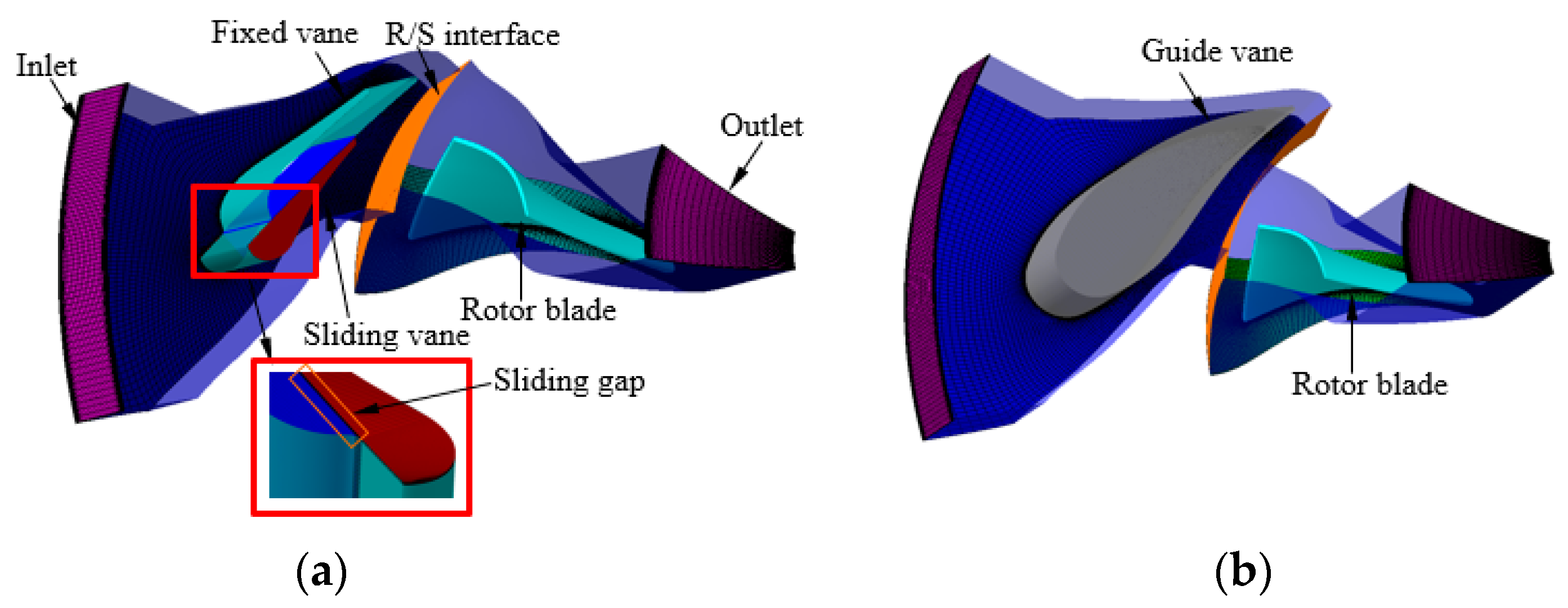

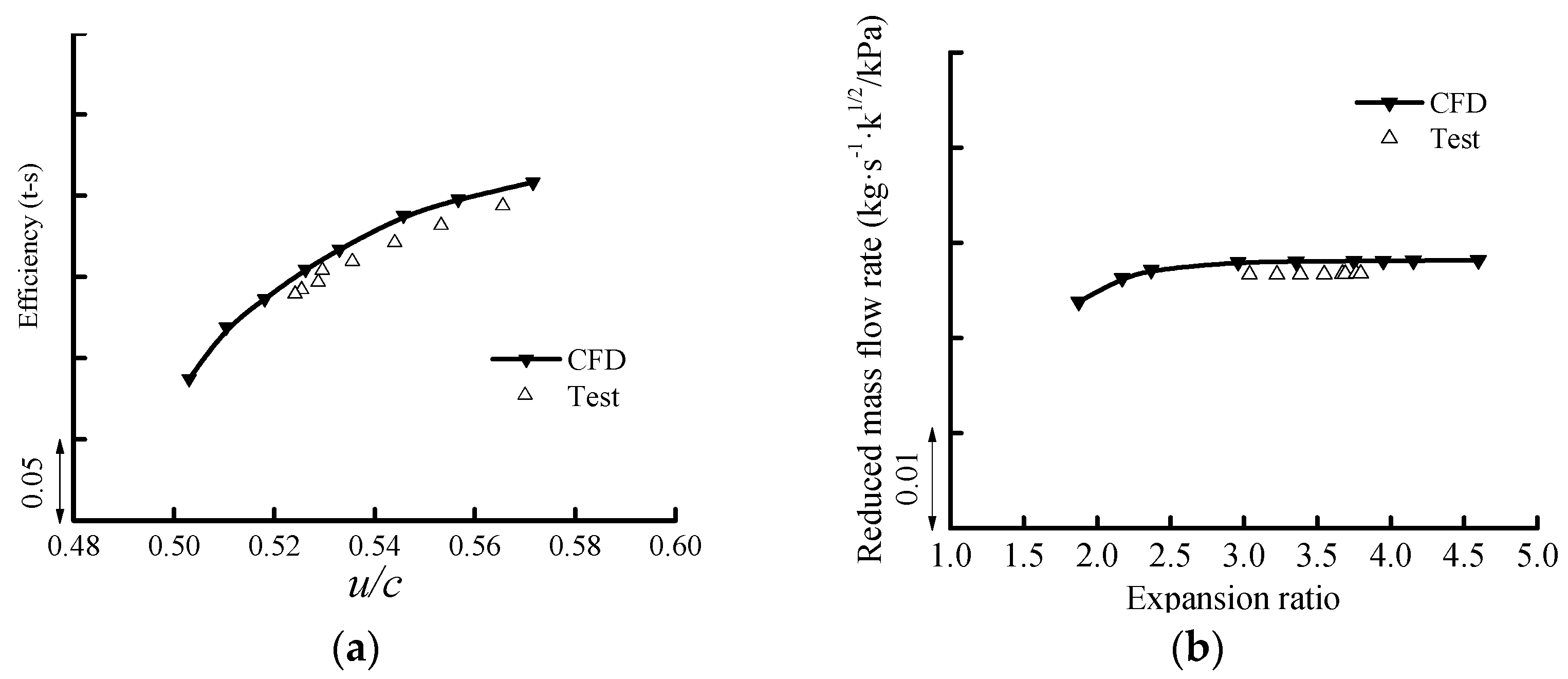
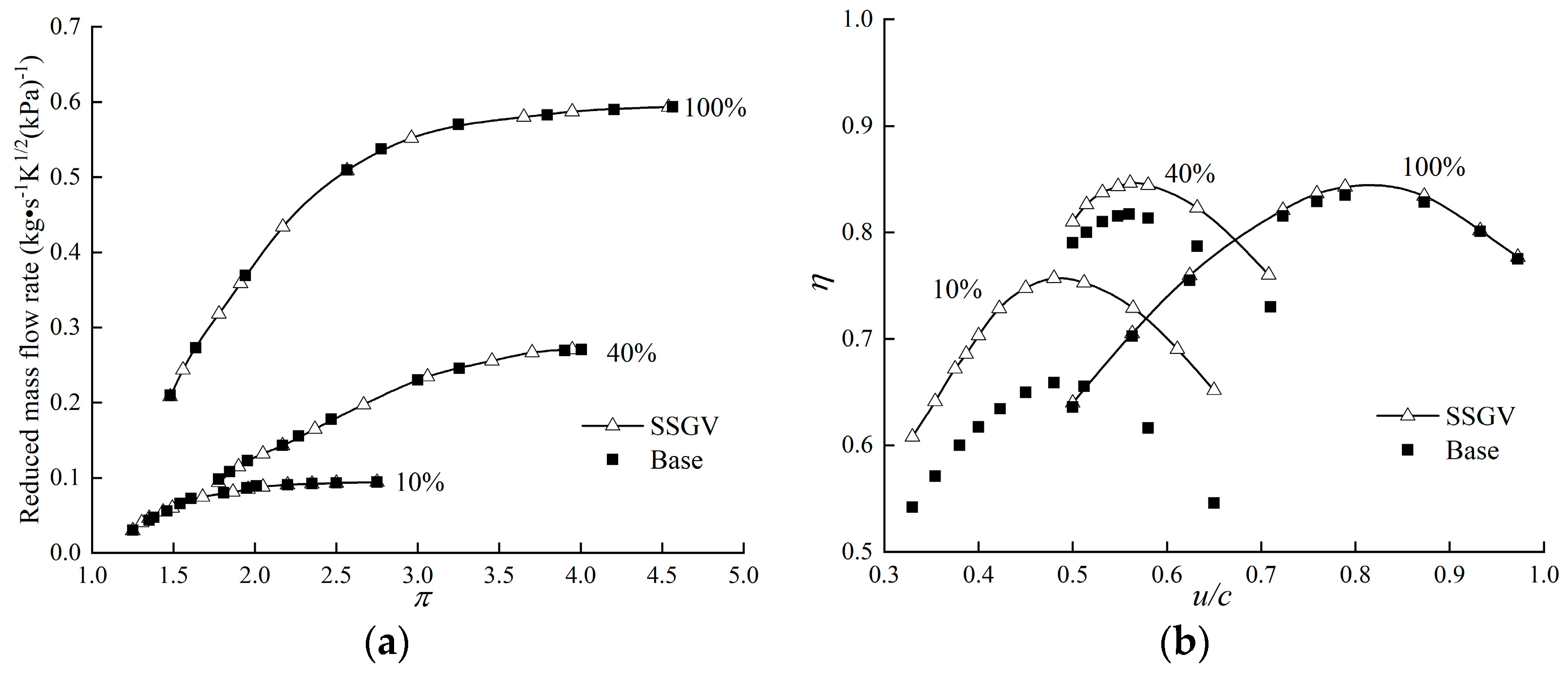



| Parameters | Guide Vane | Rotor |
|---|---|---|
| Number | 9 | 13 |
| Inlet diameter (mm) | 118 | 58 |
| Outlet diameter (mm) | 87 | 19 |
| Height (mm) | 11 | -- |
| Chord (mm) | 38 | -- |
| Thickness ratio | 0.3 | -- |
| Trailing edge diameter (mm) | 0.5 | -- |
| Endwall clearance (mm) | 0.15 | 0.3 |
| Parameters | Fixed Vane | Sliding Vane | ||
|---|---|---|---|---|
| 10% | 40% | 100% | ||
| Inlet diameter (mm) | 125 | 113.4 | 120.5 | 129.6 |
| Outlet diameter (mm) | 87.4 | 90.4 | 94.3 | 100.2 |
| Height (mm) | 11 | 10.7 | 10.7 | 10.7 |
| Chord (mm) | 35.7 | 23 | 23 | 23 |
| Incidence (°) | 77.2 | 86.9 | 79.8 | 73.4 |
| Trailing edge diameter (mm) | 0.7 | 0.7 | 0.7 | 0.7 |
| Endwall clearance (mm) | 0.2 | 0.2 | 0.2 | 0.2 |
| Sliding clearance (mm) | 0 | 0.15 | 0.15 | 0.15 |
| Sliding radius (mm) | 134.8 | 135 | 135 | 135 |
| Base | SSGV | ||||||
|---|---|---|---|---|---|---|---|
| Grids | m (kg/s) | π | η | Grids | m (kg/s) | π | η |
| 955,290 | 0.3882 | 3.0 | 0.5538 | 1,051,457 | 0.3880 | 3.0 | 0.5864 |
| 1,102,890 | 0.3880 | 3.0 | 0.5570 | 1,202,489 | 0.3879 | 3.0 | 0.5900 |
| 1,332,470 | 0.3881 | 3.0 | 0.5579 | 1,483,547 | 0.3881 | 3.0 | 0.5908 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Wang, K.; Wang, H.; Zhang, Q.; Lei, X.; Hu, L. An Investigation of the Performance and Internal Flow of Variable Nozzle Turbines with Split Sliding Guide Vanes. Machines 2022, 10, 1084. https://doi.org/10.3390/machines10111084
Yang D, Wang K, Wang H, Zhang Q, Lei X, Hu L. An Investigation of the Performance and Internal Flow of Variable Nozzle Turbines with Split Sliding Guide Vanes. Machines. 2022; 10(11):1084. https://doi.org/10.3390/machines10111084
Chicago/Turabian StyleYang, Dengfeng, Kai Wang, Huaiyu Wang, Qian Zhang, Xinguo Lei, and Leon Hu. 2022. "An Investigation of the Performance and Internal Flow of Variable Nozzle Turbines with Split Sliding Guide Vanes" Machines 10, no. 11: 1084. https://doi.org/10.3390/machines10111084
APA StyleYang, D., Wang, K., Wang, H., Zhang, Q., Lei, X., & Hu, L. (2022). An Investigation of the Performance and Internal Flow of Variable Nozzle Turbines with Split Sliding Guide Vanes. Machines, 10(11), 1084. https://doi.org/10.3390/machines10111084





