Abstract
This paper deals with the control development of a wind energy conversion system (WECS) interfaced to a utility grid by using a doubly fed induction generator (DFIG), a back-to-back (B2B) converter and an RL filter for optimal power extraction. The aim was to design a sensorless controller to improve the system reliability and to simultaneously achieve the regulation of the generator speed, reactive power and DC-link voltage. The proposed global control scheme combines: (i) a high-gain observer employed to estimate the generator speed and the mechanical torque, usually regarded as accessible, (ii) a sensorless MPPT block developed to provide optimal generator speed reference, which is designed on the basis of the mechanical observer and a polynomial wind-speed estimator and (iii) a finite-time controller (FTC) applied to the B2B converter to meet the output reference’s tracking objectives in a short predefined finite time by using the backstepping and Lyapunov approaches. The proposed controller performance is formally analysed, and its capabilities are verified by numerical simulations using a 2 MW DFIG wind turbine (WT) under different operating conditions.
1. Introduction
The demand for renewable energy is rapidly increasing as a result of the depletion of conventional energy sources, industrial expansion and huge human consumption of electrical power [1]. Accordingly, a particular focus is given to other inexhaustible and environment-friendly sources, in particular solar and wind energy generators [2]. Wind energy conversion systems have gained an undoubtedly distinguished place that will always be recognized in the history of renewable energies because wind energy is much more extensively available than other energy sources and is an essential mean of obtaining clean and cheap energy [3]. Wind turbines based on different wind generators can be distinguished into two main types: fixed-speed WTs and variable-speed WTs. The latter are more attractive than the former for the reason that the WT’s mechanical speed varies according to the fluctuation of the wind velocity, which allows maximum power extraction [2,4]. Among all existing variable-speed WT topologies, the DFIG is a widely used wind power generator [3]. Compared to the existing alternative technological solutions, DFIGs have a reduced power electronics rating, variable-speed operation capability, which leads to a maximum power extraction from the wind as well as a reduction in power losses [4]. Additionally, the DFIG stator is directly connected to the grid while a frequency converter (B2B converter) interfaces between the rotor and utility grid, permitting a decoupled control of the stator power and a reduced B2B converter size and making only 30% of the generator power flow through the power converters, which further reduces the cost and power losses [5].
To get the full benefits from variable-speed wind turbines (VSWT), an MPPT strategy is required to extract the maximum available power from the wind. For this purpose, several strategies are devoted to achieving this goal, such as, the optimal tip speed ratio (TSR), optimum speed–power curve MPPT, incremental conductance (INC), power signal feedback (PSF), optimal torque control (OTC) and perturb and observe (P&O) algorithm. Moreover, more sophisticated approaches have been proposed such as particle swarm optimization (PSO)-based methods, neural networks (NN), fuzzy logic (FL) and adaptive neuro-fuzzy inference systems (ANFIS) [2,6].
The optimum speed–power curve MPPT technique is efficient, has a fast response and is simple to apply [2]. However, it employs anemometers distributed over the WT in order to measure the exact effective wind speed, which reduces the reliability and increases the cost of the overall variable-speed WECS. Moreover, the measurement of the wind velocity interfacing the WT blades is inaccurate since the sensors are installed on the nacelle, which reduces the overall system efficiency. Recently, the desire to eliminate the wind speed sensors has attracted widespread interests and several algorithms have been suggested to improve MPPT strategies without the knowledge of the wind velocity [7,8,9,10,11]. In particular, the polynomial approximation equation can be used for MPPT because of its simple structure and high accuracy [12,13,14,15].
The improvement of the MPPT technique’s effectiveness for wind energy conversion systems through a variety of control strategies has been studied in several works. In fact, the most widely applied control method consists of a field-oriented control (FOC) technique incorporated with PI controllers that is a recognized scheme in the drive industry due to its simple implementation [16]. However, the controller structure cannot maintain a consistent control performance for the WECS in the presence of uncertainties and disturbances since the PI gains are related to the system parameters [17]. In this way, various optimal parameter tuning methods have been investigated in the literature to improve the PI control’s efficiency. A PSO method was developed in [18] for tuning the PI controller gains of a WT system. A DFIG currents control based on a self-tuning fuzzy PI algorithm was used in [19]. A direct power control (DPC) strategy is another possible alternative to the FOC-based PI regulators. It offers the advantage of minimizing computational efforts and improving system dynamics. Its principle is based on the calculation of stator powers and a voltage-vector lookup table [17]. The DPC can also be implemented on the grid side to control the power flow through the DFIG rotor [20]. Nevertheless, the hysteresis blocks used produce a variable switching frequency resulting in high-magnitude current ripples [21]. On the other hand, a variety of nonlinear control strategies have been developed in the literature to interface the WECS nonlinearity. In [22], a high-order sliding-mode control of the rotor side converter (RSC) under an unbalanced grid voltage was proposed. In [23], a nonlinear predictive controller to deal with the aeroturbine and the generator for power capture optimization was designed. In [24], an adaptive control for the generator speed of WT-based DFIG using some tools from Lyapunov’s theory was addressed. However, the proposed controller was applied on the approximated model of the DFIG where the system’s nonlinearity was not taken into account. In fact, the control performance with the previous controller had limitations, especially in the presence of large fluctuations in wind velocity. The finite-time controllers (FTCs) are an efficient solution for nonlinear systems subject to unmodelled dynamics, uncertainties and external disturbances. They offer fast responses with reduced tracking errors and finite-time convergence to the system’s steady-state. In FTCs, state trajectories converge to the desired reference values in a well-known finite time [25,26].
The limitations imposed by the need for mechanical variables sensors, e.g., wind speed, rotor position, generator speed and mechanical torque, in controller designs and MPPT strategies are the main drawbacks of the aforementioned methods, as long as one seeks to eliminate these sensors in electric drive systems, since they increase the maintenance costs and reduce the system reliability. Therefore, it is desirable to design a controller that is unrelated to physical sensors. The presence of mechanical observers for the mechanical variables would be useful since they can be used as an alternative solution to mechanical sensors to improve the reliability of the system and detect sensor failures. Several works have been devoted to nonlinear control strategies involving observers for mechanical variables and for different classes of plant-state models. The studies conducted in these works showed that the sensorless techniques demonstrated a superiority in terms of their tracking performance, handling disturbances and insensitivity against the lumped uncertainties. In [27], an extended Luenberger observer in a variable-speed stand-alone DFIG system application was proposed. The estimator involved two interconnected observers. The first one was a classical Luenberger observer used to estimate the stator flux and the second one was an adaptive Luenberger observer to deliver the needed rotor position desired to the stator flux estimation. The output feedback control of a DFIG machine based on a fictitious ohmic quantity observer was reported in [28]. This observer was developed to provide an online estimation of the rotor speed without using the stator and rotor resistance to improve the reliability and reduce the costs of the proposed controller. In [29], a classical adaptive backstepping observer to estimate the generator speed and the rotor position for a DFIG was proposed. A sensorless controller, a type of stator FOC, was applied to directly control the active and reactive power. In [30], a high-order sliding-mode output feedback control for a DFIG-WECS-based mechanical torque observer was proposed for the regulation of the power produced by the generator. A high-order sliding-mode observer and a high-order sliding-mode controller for the mechanical torque were separately discussed. A sensorless nonlinear controller based on a high-gain observer to estimate the mechanical torque was discussed in [31] and the validity of the observer design was demonstrated. In [32], the authors used a high-gain observer for a permanent magnet synchronous generator (PMSG) connected to the electrical grid to estimate the mechanical variables. Other works proposed high-gain observers to estimate the stator flux and the rotor speed for induction machine applications [33,34]. In [35], a high-gain observer application for a DFIG was proposed to provide the developed controller with online estimation of the mechanical variables. The proposed observer was designed based on the generator model represented in the stationary reference frame. However, the dq transformation of the used model was actually performed on the basis of the rotor position, which made it necessary to employ the rotor position sensor, thus reducing the reliability of the entire variable-speed WT. In addition, the DC-link voltage regulation, the grid-side reactive power control and the influence of the grid-side converter (GSC) on the overall control system were not included to illustrate the overall power transfer on both sides; the DFIG stator connected directly to the grid and the rotor connected to the B2B converter and then the grid.
In this paper, the proposed approach deals with the development of a sensorless control and stability analysis of a variable-speed grid-connected DFIG-based WT for optimal power extraction. This should allow us to achieve a maximum output power, which would improve overall system performance and eliminates mechanical sensors or allow the implementation of fault-tolerant control (FTC) approaches [36]. The studied system has standard components requiring a fixed investment cost depending on the nominal power (e.g., turbine, gearbox, generators, power converters, etc.). From a practical implementation point of view, advanced DSP cards should be required to implement the proposed approach, which may slightly increase the overall system cost. Moreover, the proposed sensorless MPPT control allows us to avoid the usage of anemometers and rotor position/speed sensors for the generator shaft, which allows us to reduce the overall system investment and maintenance costs. The contribution of this study can be summarized by the three following points:
- (i)
- A sensorless MPPT strategy is designed to provide the optimal generator speed reference for maximum power extraction. Wind speed is estimated using a high-order polynomial approximation of the WT power coefficient. This choice is motivated by the fact that the mechanical anemometers installed at the nacelle reduce the WT system’s efficiency and reliability.
- (ii)
- A high-gain observer is developed to provide an online estimation of the DFIG mechanical variables, i.e., the generator speed and the mechanical torque, by only measuring the stator and rotor voltages and currents. The observer is synthesized by using the DFIG model in the stationary reference frame (- frame) where the rotor position information is not required for the WT modelling and observer implementation. Furthermore, the designed observer is backed by a formal analysis according to Lyapunov’s stability theory to emphasize the required conditions for the achievement of the estimation objectives. The observer is used in the sensorless MPPT to estimate wind speed as well as in the controller design to improve the system’s efficiency and reliability.
- (iii)
- A robust finite-time feedback state controller is developed according to the backstepping approach and Lyapunov’s theory. The controller is designed based on the DFIG-based WT model connected to an AC/DC/AC converter in the synchronous reference frame (d-q frame). Additionally, the system requires a multiloop regulator for the generator speed, stator reactive power, DC-link voltage and grid-side reactive power control. The closed-loop stability is theoretically investigated using Lyapunov’s stability theory to prove the achievement of the control objectives. Furthermore, the system robustness against lumped uncertainties and external disturbances (e.g., modelling errors, parameters variations and mechanical vibrations) is illustrated.
This study deals with the problem of the high cost and unreliability of sensors in a WECS application. The proposed approaches are meant to replace physical sensors, which could experience a failure issue, with software ones via designing a sensorless controller to improve the system reliability and to simultaneously implement an MPPT algorithm and regulate the generator speed, reactive power and DC-link voltage.
The rest of this paper is organized as follows: Section 2 is devoted to the description and modelling of the overall DFIG based WECS. Section 3 develops the sensorless MPPT. Section 4 is dedicated to the control design of the RSC and GSC and the stability analysis of the closed-loop system. The high-gain observer is synthesized and analysed in Section 5. In Section 6, simulation results are provided and discussed. Finally, some concluding remarks are provided in the last section.
2. System Description and Modelling
The DFIG-based WEC system configuration is depicted in Figure 1. This figure shows the wind energy conversion system subassemblies: turbine, DFIG, back-to-back converter (generator-side and grid-side converters) and RL filter for the grid interface.
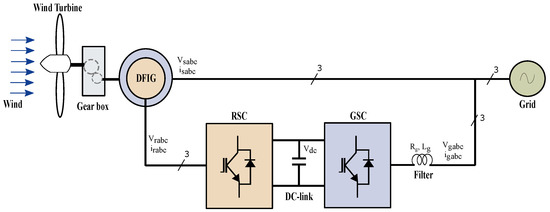
Figure 1.
A simplified scheme of a DFIG-based wind energy conversion system.
2.1. Wind Turbine Model
The power produced by a WT is based on the interaction between the turbine rotor and the wind. The latter has an unpredictable behaviour, which makes it difficult to model the amount of mechanical power available in the WT rotor. The momentum theory is used to model the power contained in the form of the kinetic energy in the wind. The WT can only capture a portion of that power, which is given by [2,5]:
where
The power coefficient equation is expressed as follows:
where corresponds to the aerodynamic efficiency of the wind turbine, which can be represented as a function of the tip speed ratio and the pitch angle as depicted in Figure 2. The captured power is represented by Figure 3 with
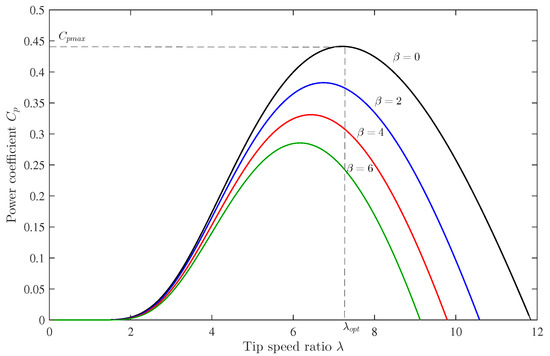
Figure 2.
Power coefficient as a function of tip speed ratio.
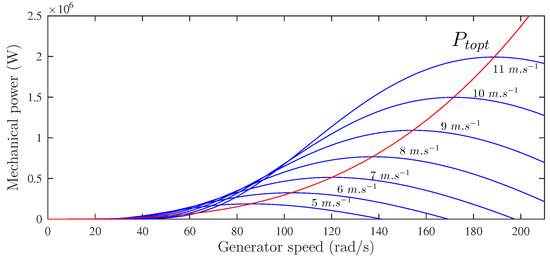
Figure 3.
Mechanical power as a function of the generator speed and wind speed.
2.2. DFIG Dynamic Model
Different variable-speed wind turbines are used in the literature. The DFIG coupled to a WT is common, robust and efficient. The state-space vector dynamics of the DFIG machine in the dq reference frame is widely used in the literature and detailed using Park’s transformation [4,23,30]:
where i and u are given by:
while A and B can be expressed as follows:
where
, , , , , , , , , , and .
The electromagnetic torque in the dq frame can be represented by the following equation:
The stator active and reactive powers in the dq frame are given by:
The generator speed dynamics of the WT is given by:
2.3. Grid-Side Converter Model
The system on the grid side consists of a DC-link capacitor associated with a three-phase voltage source inverter and an RL filter. The following differential equations describe the model of the GSC [16]:
The active and reactive power provided by the grid side are given by:
3. Sensorless Maximum Power Point Tracking
To extract the maximum available power, an MPPT algorithm is required. This algorithm requires the measurement, in real time, of the wind speed and mechanical variables of the DFIG generator using sensors that can be expensive and can make the overall control system fragile. To overcome these problems, a high-gain observer and an estimator were jointly used (Figure 4).
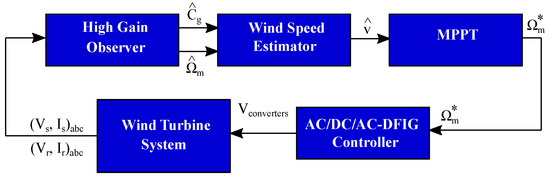
Figure 4.
Structure of the sensorless MPPT.
Under varying wind speeds, the WT can operate in four different regions as shown by Figure 5. In this work, only the MPPT zone was considered (zone II). In this zone, the pitch angle is maintained constant where the WECS controller implements the MPPT algorithm to extract the maximum available power [37]. Indeed, the MPPT mode is achieved only by adjusting the rotational speed of the generator and consequently the turbine rotational speed. The pitch angle is specifically used to limit the extracted power for a high wind speed (Zone III in Figure 5) or stop the turbine for dangerous and harmful wind speeds (zone IV in Figure 5). Figure 6 illustrates the power coefficient variations as a function of the tip speed ratio and the pitch angle of the WT presented in Table 2. This figure shows that for the power coefficient achieves its maximum value, which means capturing the peak power from the available wind power [38]. Thus, the pitch angle was considered to be . This fact implied that the power coefficient only depended on the tip speed ratio [39]. Under these considerations, a simplified expression of the power coefficient is:
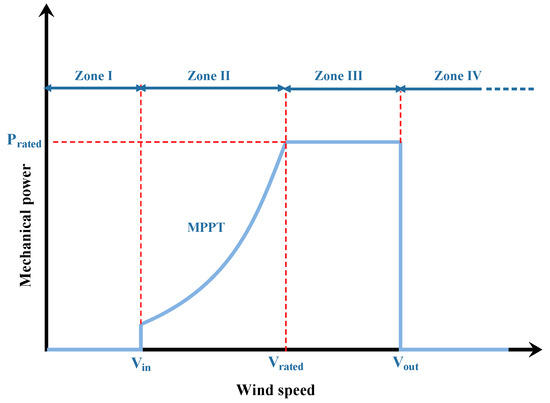
Figure 5.
The four different operating zones of a VSWT.
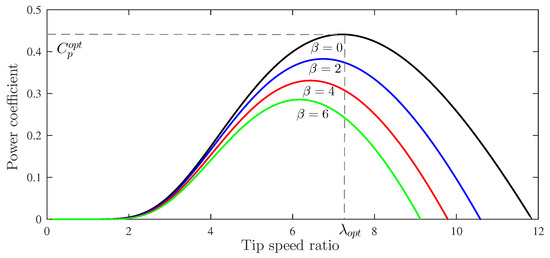
Figure 6.
Power coefficient as a function of tip speed ratio.
The optimal theoretical power can be derived as follows:
3.1. Wind Speed Estimation
In this section, the focus is on the implementation of a wind speed estimator. For this, the power coefficient given by equation (11) is represented by the following polynomial approximation [15]:
where the power coefficient constants , are given in Table 1.

Table 1.
MPPT parameters.
Replacing the expression of from (2) in (13) and using (1), the mechanical power expression can be rewritten as:
From (14), can be seen as a function of the estimated values and of the generator speed and the mechanical torque. The estimated quantities and are provided by the high-gain observer presented later in Section 5. In doing so, one has:
Solving polynomial equation (15) yields an estimated value of the wind speed.
3.2. MPPT Strategy
The mechanical power captured by the wind energy conversion system versus the generator speed for different values of the wind speed is illustrated in Figure 7. This figure shows that for each value of wind speed, there is a particular value of rotational velocity for which the mechanical power generated by the WT is maximum. To put it differently, the optimal operation of a DFIG corresponds to a special value of the tip speed ratio . To force the DFIG to operate at its optimal conditions, an appropriate MPPT algorithm must be used. It consists of regulating the WT rotational speed in a way that the tip speed ratio is maintained at its optimal value . In order to do so, the optimal reference speed is elaborated according to Figure 7. A graphical search of the intersection points between the curves of the optimal power and is conducted and the points are interpolated to construct a fourth-order polynomial function, which represents the generator reference speed [40]:
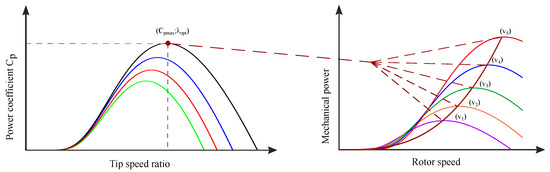
Figure 7.
WT power characteristics.
4. Controller Design and Stability Analysis
4.1. Reduced Model for the Rotor-Side and Grid-Side System
Based on the machine model defined in Section 2, Equations (5)–(8) can be simplified by using the well-known stator flux orientation. According to this technique, the reference frame is aligned with the stator flux, therefore, the electromagnetic torque and the stator reactive power can be controlled independently through the q-axis and d-axis currents, respectively. Moreover, by applying this strategy on the grid side, a decoupling control between the active and reactive powers is established. Then, the global system model formed by the DFIG and AC/DC/AC converter association are summarized as follows [30,41]:
where , , , , and are the average values over the switching period of the signals , , , , and , respectively, and .
, (respectively, ) denotes the input voltage vector of the RSC (respectively, GSC) in the dq frame. , (respectively, ) are the duty cycles in the dq reference frame corresponding to the 3-phase duty ratios of , (respectively, ), where , , , are the switching signals of the RSC and GSC, respectively, taking values in the discrete set and defined as follows:
4.2. Controller Design
The required control objectives are fourfold:
- (i)
- The generator speed must track the optimal reference value provided by the MPPT control.
- (ii)
- The stator reactive power should be regulated to its reference, which is usually considered to be zero in order to ensure a unity power factor correction at the stator level.
- (iii)
- The DC bus voltage must be adjusted to an appropriate level to guarantee the correct operation of the converter on the grid side.
- (iv)
- The reactive power at the output of the converter located on the grid side must be maintained at zero.
The above mathematical model shows that the considered topology allows the control of several variables, which means that through the control of RSC and GSC, one gets the control of the DFIG WT system. To meet these objectives, an accurate design of the control laws was developed by using an FTC.
4.2.1. RSC Controller
The rotor-side controller aims to regulate the generator speed to track the optimum value and control the stator reactive power exchange with the grid.
Generator speed control loop:
Define the following tracking errors:
where the reference is the optimal generator speed of (16), denotes the virtual control input and serves as a stabilizing function of (17b), which is developed hereafter. The speed control synthesis is designed by following the conventional backstepping design technique. As there is no real control law acting on , the speed controller is designed in two steps:
Step 1
By choosing the Lyapunov’s function candidate and its derivative , one gets the first stabilization function:
where , are the controller parameters.
The tracking error dynamical equation takes the following expression:
It can be observed that is not the actual input control but just a state variable. By introducing error given by (20), the time derivatives of and are rewritten as follows:
Step 2
Based on (17b), (20) and (22), the time derivative of is given by:
where is given by the following expression:
Let us consider the new Lyapunov function candidate given by:
Taking into account (25), the dynamics of can be expressed as follows:
If one chooses the time derivative of error according to the expression given by (30), then the derivative of the Lyapunov function becomes negative as shown by (31).
Using Equations (26) and (30), the generator speed control law takes the following form
where is a suitable coefficient.
Stator reactive power control loop:
To design a controller for the stator reactive power exchanged with the grid, error is introduced as follows:
where the reactive power equation is given by:
Let us consider the following Lyapunov function candidate:
In order to stabilize the stator reactive power control loop, the time derivative of (32) is chosen to be negative as:
where is a positive design parameter.
To achieve the above stabilization objective, the stator reactive power control law must be selected as:
Proposition 1.
Considering the RSC control laws in (32) and (38), and the rotor side model consisting of subsystem (17a), (17b), (17c) the resulting dynamic behaviour of the closed loop system is governed, in the (, , ) coordinates, by the following equation:
As a result, it is worth noting that the closed loop system is finite-time stable and its convergence time meets the following inequality, whatever the initial trajectory: .
Proof.
Replacing the control laws (22), (32) and (36) in (21), (26) and (35), respectively, one obtains directly given in Equation (39).
Let us consider (40) as the global Lyapunov function candidate of the rotor side
Its time derivative is:
Taking into account that the following inequality is satisfied, when and ,
It follows from (42) that for
In view of (44), the closed loop of the rotor-side system converges to the origin in finite time, which is computed by: . This completes the proof. □
4.2.2. GSC Controller
The grid-side controller aims to control the DC-link voltage and the grid-side reactive power, in order to inject the part of the wind power that passes through the DFIG’s rotor winding. Subsystem (17d), (17e), (17f) shows that the grid-side controller can be designed in the same way as the one presented in the previous subsection.
DC-link voltage control loop:
Let us define the tracking errors of the squared DC-link voltage and the virtual control input as follows:
is the squared DC-link voltage reference, denotes the virtual control input and serves as a stabilizing function, which is developed hereafter. The DC-link voltage control synthesis is designed in two steps since the relative degree of the system is two with respect to .
Step 1
By choosing the Lyapunov function candidate and its derivative , one gets the following stabilizing function:
where is a suitable controller parameter.
The tracking error is governed by the following expression:
It can be observed that is not the actual input control but just a state variable. By introducing error given by (20), the time derivatives of and become:
Step 2
Let us consider the augmented Lyapunov function candidate given by:
Taking into account (51), the derivative of can be expressed as follows:
If one chooses the time derivative of error according to the expression given by (56), then the derivative of the Lyapunov function becomes negative as shown by (57).
Using Equations (52) and (56), the control law for the DC-link voltage takes the following form:
where is a design constant.
Grid-side reactive power controller:
In order to guarantee a unitary power factor on the grid side, the reactive power must be zero. To meet this objective, indirect control is carried out through the zero-current regulation of the d-axis. To do this, error is introduced as follows:
Based on the alignment discussed before, one can calculate the reference of the d-axis current using (10b) such that .
Let us consider the following Lyapunov function candidate:
In order to stabilize the d-axis control loop, the time derivative of given in (61) is chosen to be negative as:
where is a positive design parameter.
To achieve the above stabilization objective, the d-axis control law must be selected as follows:
Proposition 2.
Considering the GSC control laws in (32) and (38), and the rotor-side model consisting of subsystem (17a), (17b), (17c) the resulting dynamic behaviour of the closed loop system is governed, in the (, , ) coordinates, by the following equation:
Consequently, the finite-time convergence of (64) of any initial trajectory satisfies the inequality
Proof.
Replacing the control laws (48), (58) and (63) in (47), (52) and (60), respectively, one obtains directly Equation (64).
Let us consider given in (65) as the global Lyapunov function candidate of the grid side.
Its derivative is
In view of (68), the closed-loop grid-side system converges to the origin in finite time, which fulfils the inequality . This completes the proof. □
Remark 1.
The design of the FTC-based control is mostly developed by adding a switching term to the control laws. Usually, the chattering phenomenon can take place due to the use of the signum function sgn(.). In this paper, we suggest modifying the control laws in (32), (36), (58) and (63) by using a sigmoid tanh(.) function instead of sgn(.) in order to avoid the chattering during the reaching mode.
5. High-Gain Observer
As presented in Section 4, the rotor-side and grid-side mathematical models are described in the dq reference frame to design the control laws so as to achieve the control objectives. In this section, the objective is to reduce the number of sensors needed in the control design. To this end the mechanical torque, generator speed and rotor position are not considered as measurable variables. Since the transformation of the rotor currents and voltages from the abc coordinates to dq coordinates and vice versa need the information about the rotor position as shown in Figure 8, a high-gain observer is designed based on the DFIG model described in the --coordinates to provide online estimations of the mechanical variables (Figure 8).
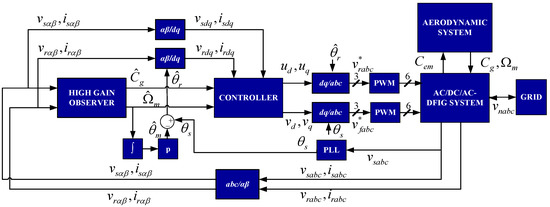
Figure 8.
Output feedback control block diagram.
The DFIG currents, in the -coordinates, can be represented as follows [32,42,43]:
with
; ;
;
The electromagnetic torque equation in the - frame can be represented by the following equation:
where
; ; .
Based on Equations (8), (69) and (70), the state-space model of the DFIG can be represented as follows:
where
- y is the output vector.
- D, and are given by:; ; .with;;; ; ;.
- The unknown signal is supposed to be bounded. This choice is justified by the fact that the mechanical torque does not vary so rapidly, and that the mechanical torque and its derivative are considered to be bounded.
Then, we design the following dynamical system, which represents a high-gain observer for system (71) [44,45,46]:
where
- is defined as follows:
- The block diagonal matrix is defined by:, is a positive constant design parameter.
- The gain matrix K is selected so that the matrix is Hurwitz, with . Then, there exists a unique positive definite matrix , which satisfies the following equality [44]:
Observer Analysis:
Consider the estimation error . Deriving with respect to time and using Equations (71) and (72), one gets:
Equation (75) may be written as:
The last formulation can be derived by considering the following modified error: .
Let us introduce the Lyapunov function candidate in the following form:
Its time derivative is given by:
In view of (74), one has:
Bounding the right terms of the above equation, we obtain:
where , and indicates the largest eigenvalue of the positive definite matrix P.
It is required that be a Lipschitz function and as mentioned before, the function is bounded, where is the upper bound. Then, one can write:
where and are positive constants.
Using the above inequalities leads to rewrite (82) as follows:
Knowing that is a bounded function that fulfils:
where denotes the smallest eigenvalue of the positive definite matrix P, one gets:
Using the following notation
Inequalities (86), can be written as follows:
In addition, for , we have:
Then, regardless of the initial condition , the observation error vector converges exponentially towards a neighbourhood that decreases when takes a large value, thus allowing us to have an observer that provides practical estimates of the suggested signals.
Remark 2.
The observer parameter is chosen high enough to guarantee that the dynamic behaviour of the observer is fast enough regarding the closed loop system dynamic behaviour. Therefore, confusion between the actual and estimated values occurs during the control law synthesis, and the mechanical signals are replaced by their estimated values. Moreover, in order to ensure a fast-tracking performance, the controller design parameters are chosen according to the closed-loop system’s eigenvalues and the fact that the inner loops require a much faster response than the outer loops.
6. Simulation Results
Figure 9 illustrates the global WECS. The controlled plant, having the parameters given in Table 2, was a WT based on a DFIG associated with a B2B converter and an RL filter. The overall controller was comprised of the wind speed estimator (15), the sensorless MPPT algorithm (16), the high-gain observer (72) and the control laws for the rotor-side and grid-side systems (32), (36), (58) and (63). The numerical values of the controller are represented in Table 1 and Table 3. The controller parameters were selected based on a trial-and-error search. The observer parameters had large enough values, which allowed the observer to converge faster than the controller to ensure a satisfactory controller/observer performance. The output feedback control strategy, based on the 2 MW DFIG WT, was constructed and tested using a MATLAB/Simulink/SimPowerSystems environment, that offers quite accurate models of power components. In this study, the Euler solver ODE1 was chosen with a fixed time step for the simulation process. The performance of the WECS was examined under variable wind speed and realistic wind speed profiles to confirm the reliability and validity of the control strategy.
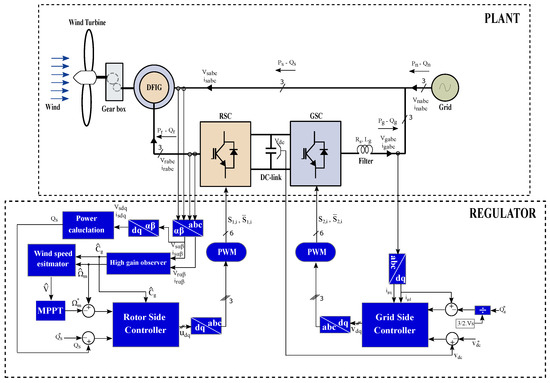
Figure 9.
Controller design of the global studied system.

Table 2.
DFIG-based wind energy conversion system parameters.

Table 3.
Sensorless finite-time controllers’ parameters.
6.1. Controller Performances under Variable Wind Speed Profile
In order to evaluate the system performances, the output feedback controller was carried out under the wind speed profile depicted in Figure 10a. This figure also shows the online estimated wind speed profile, which corresponds to actual wind speed as shown by Figure 10b. As a result, the MPPT block generated the optimum generator speed reference without the requirement of an anemometer (wind speed sensor).
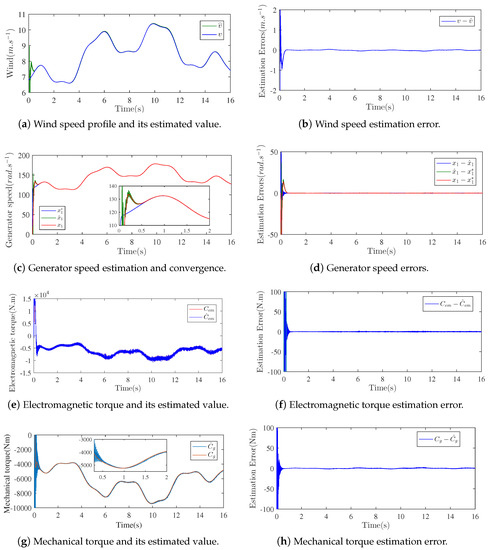
Figure 10.
Output feedback control-based sensorless MPPT convergence.
Figure 10c–h illustrate the performance of the high-gain observer. Figure 10,d show that the observed generator speed corresponded to the actual generator speed and both tracked the optimal reference provided by the sensorless MPPT algorithm. Figure 10g,h show that the online estimation of the mechanical torque met the measured value. Moreover, it can be noticed that the high-gain observer converged faster than the generator speed controller.
Figure 11 depicts the WT characteristics. Figure 11a shows that the power coefficient was maintained at the maximal value, which guaranteed the maximum extraction of the available power, and it can be seen in Figure 11b that the tip speed ratio was sustained at the optimal value despite the wind speed variations. Figure 11c illustrates the available and the extracted mechanical power, where it is clearly shown that the available power was totally extracted, which guaranteed the MPPT objective.
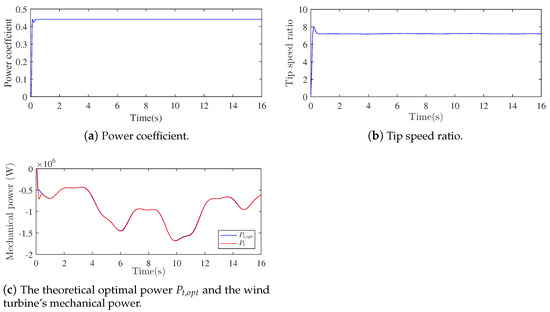
Figure 11.
The wind turbine characteristics.
Figure 12 represents the stator reactive power exchanged with the grid. The reactive power tended towards zero, which means that in the stator–grid association, only the stator active power was exchanged with the grid. This guaranteed the achievement of the unitary power factor objective.
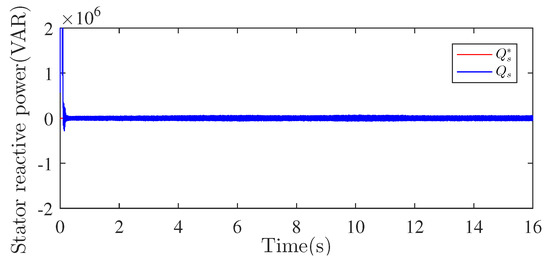
Figure 12.
Stator reactive power response.
Figure 13 confirms that the GSC controller gave a satisfactory performance, which improved the WECS’s resiliency and reliability. The tight regulation of the DC-link voltage is depicted in Figure 13a. Figure 13b shows that the grid-side d-axis filter current converged to its reference, which took the value 0, as initially fixed. This ensure a unitary power factor as shown in Figure 14a. Figure 14b shows one phase of the grid’s three-phase currents and voltages, where the current has a sinusoidal form and with a phase shift with the grid voltage. Figure 14b represents the three-phase rotor currents. Figure 14d illustrates the mechanical power captured by the WT blades and the global electrical active power exchanged with the grid. As we can see, the mechanical power was almost totally injected into the grid. This figure also represents the stator and the rotor active powers. It can be noticed that the stator active power varied according to the generator speed variation. Moreover, during these variations two operation modes can be distinguished for the rotor active power. In the subsynchronous operation mode, the rotor active power had negative values, which means that the active power was transferred from the grid to the DFIG rotor, and in the case of the supersynchronous operation mode, the rotor active power had positive values, which means that the DFIG rotor power was supplied to the grid.
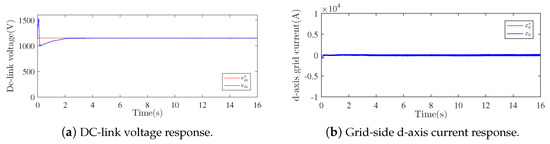
Figure 13.
Grid-side results.
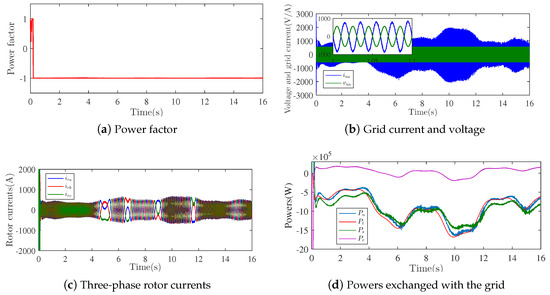
Figure 14.
WECS powers.
6.2. Controller Performance under Parametric Mismatch
In this case study, the plant model was subject to parameter uncertainties and variations, which reflected realistic problems such as skin effect phenomena, magnetic saturation problem and wear due to ageing. To this end, the parameter variations were undertaken as shown in Table 4. An uncertainty of and on the mechanical system parameters was applied at time s and 5 s, respectively. Furthermore, a variation of and on the stator and rotor resistances and the mutual inductance was applied at time s and 8 s, respectively.

Table 4.
Parameters’ variation.
Figure 15, Figure 16 and Figure 17 depict the obtained simulation results with the aforementioned WEC parameter variations. Figure 15 provide the generator speed control performance under a varying wind speed in the presence of electrical and mechanical parameters mismatch and Figure 16 shows the reactive power control performance under the same conditions. These figures show a satisfactory robustness of the proposed output feedback controller. In fact, the output reference tracking objectives were practically preserved despite the parameter uncertainties. Finally, the DC-bus voltage under parameter mismatch is given in Figure 17 and shows satisfactory results. All these results confirm the effectiveness of the proposed approach for external (wind speed fluctuations) and internal disturbances and parameter uncertainties rejection.
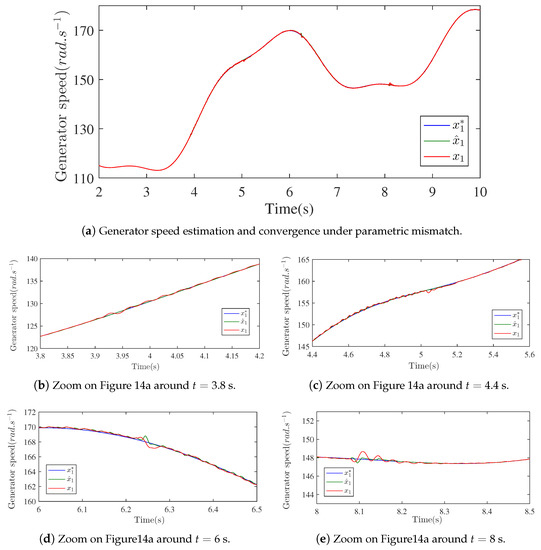
Figure 15.
Generator speed feedback control convergence under parametric mismatch.
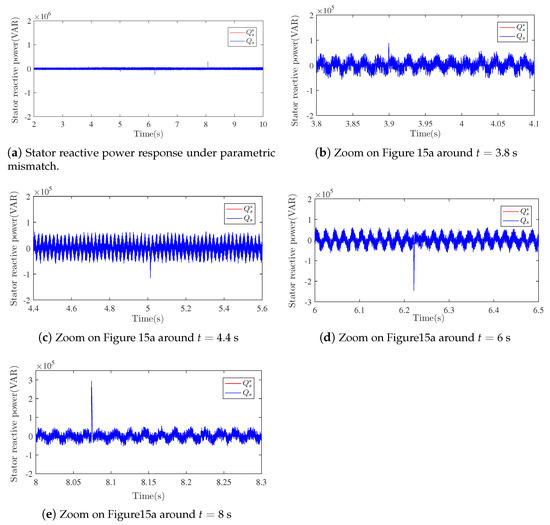
Figure 16.
Stator reactive control convergence under parametric mismatch.
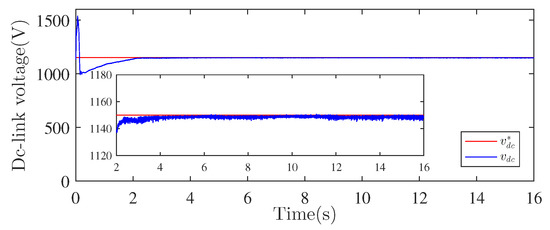
Figure 17.
DC-link voltage response under parametric mismatch.
The proposed solution is based on a nonlinear multiloop controller, which increases the controller’s complexity. However, its synthesis is systematic, and its mathematical development is rigorous. In addition, using an observer helps reduce the number of sensors used in the controller structure and offers backup software sensors, which allow the implementation of FTC algorithms. Actually, the developed observer replaces physical sensors that might be subjected to faults and failures, making the controlled system more reliable. Compared to conventional nonlinear controllers, the proposed one can be easily implemented in practice because it neither requires mechanical sensors nor wind speed sensors. Only current and voltage transducers are needed, which makes the implementation costs lower.
7. Conclusions
In this paper, the problem of controlling and improving the reliability of a grid-connected DFIG-based WT was studied using a sensorless nonlinear controller. A high-gain observer was synthesised to provide an online estimation of the mechanical variables. The MPPT implementation dealt with using the wind-speed-estimator-based optimum speed–power curve MPPT, in order to generate the optimal generator speed reference during wind speed variation without using anemometers. Indeed, of the available mechanical power was extracted using the proposed approach. The convergence stability of the mechanical variables’ observer and the finite-time controller of the closed-loop WECS was theoretically conducted. The theoretical results were confirmed by numerical simulations, which demonstrated that the proposed sensorless controller offered better performance in terms of output reference tracking and emphasized the extra robustness under different operation conditions, parameter uncertainties, and internal/external disturbances.
Author Contributions
Conceptualization, A.A., K.N., E.E., H.K., I.L. and A.E.A.; formal analysis, A.A.; funding acquisition, A.A. and A.E.A.; investigation, E.E., H.K., I.L. and A.E.A.; methodology, A.A., K.N., E.E. and H.K.; project administration, H.K.; supervision, A.A., E.E., I.L. and A.E.A.; validation, A.A., K.N., E.E. and H.K.; visualization, A.A., K.N. and I.L.; writing—original draft, A.A.; writing—review and editing, K.N., E.E., I.L. and A.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
M. Al-Numay and A. El Aroudi acknowledge financial support from the Researchers Supporting Project number (RSP-2021/150), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| List of Acronyms | Parameters |
| VS-WECS Variable-speed wind energy | v Wind speed |
| conversion system | Air density |
| WT Wind turbine | R Rotor radius |
| FTC Finite-time control | Mechanical power |
| MPPT Maximum power point tracking | Power coefficient |
| DFIG Doubly fed induction generator | Tip speed ratio |
| RSC Rotor-side converter | pitch angle |
| GSC Grid-side converter | Rotor speed (generator speed) |
| N Gearbox ratio | |
| Electromagnetic torque | |
| Mechanical torque | |
| p Pole pairs number | |
| Angular speed (synchronous speed) | |
| Stator (rotor) index | |
| Filter (DC-link) index | |
| Stationary reference frame index | |
| Synchronous reference frame index | |
| Voltage (current) | |
| Flux | |
| R Resistance | |
| L Inductance | |
| M Mutual inductance | |
| C Capacitor |
References
- Al-Shetwi, A.Q.; Hannan, M.; Jern, K.P.; Mansur, M.; Mahlia, T. Grid-connected renewable energy sources: Review of the recent integration requirements and control methods. J. Clean. Prod. 2020, 253, 119831. [Google Scholar] [CrossRef]
- Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970. [Google Scholar] [CrossRef]
- Mishra, A.; Tripathi, P.; Chatterjee, K. A review of harmonic elimination techniques in grid connected doubly fed induction generator based wind energy system. Renew. Sustain. Energy Rev. 2018, 89, 1–15. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Feld, G.; Amirat, Y.; Benbouzid, M.; Le Gall, F. Design and experimental implementation of a wind energy conversion platform with education and research capabilities. Comput. Electr. Eng. 2020, 85, 106661. [Google Scholar] [CrossRef]
- Puchalapalli, S.; Singh, B. A Novel Control Scheme for Wind Turbine Driven DFIG Interfaced to Utility Grid. IEEE Trans. Ind. Appl. 2020, 56, 2925–2937. [Google Scholar] [CrossRef]
- Mali, S.S.; Kushare, B. Mppt algorithms: Extracting maximum power from wind turbines. Int. J. Innov. Res. Electr. Electron. Instrum. Control Eng. 2013, 1, 199–202. [Google Scholar]
- Jena, D.; Rajendran, S. A review of estimation of effective wind speed based control of wind turbines. Renew. Sustain. Energy Rev. 2015, 43, 1046–1062. [Google Scholar] [CrossRef]
- Qiao, W.; Zhou, W.; Aller, J.M.; Harley, R.G. Wind speed estimation based sensorless output maximization control for a wind turbine driving a DFIG. IEEE Trans. Power Electron. 2008, 23, 1156–1169. [Google Scholar] [CrossRef]
- Lopez-Flores, D.R.; Duran-Gomez, J.L.; Chacon-Murguia, M.I. A Mechanical Sensorless MPPT Algorithm for a Wind Energy Conversion System based on a Modular Multilayer Perceptron and a Processor-in-the-Loop Approach. Electr. Power Syst. Res. 2020, 186, 106409. [Google Scholar] [CrossRef]
- Hussain, J.; Mishra, M.K. An efficient wind speed computation method using sliding mode observers in wind energy conversion system control applications. IEEE Trans. Ind. Appl. 2019, 56, 730–739. [Google Scholar] [CrossRef]
- Wang, J.; Bo, D. Adaptive fixed-time sensorless maximum power point tracking control scheme for DFIG wind energy conversion system. Int. J. Electr. Power Energy Syst. 2022, 135, 107424. [Google Scholar] [CrossRef]
- Østergaard, K.Z.; Brath, P.; Stoustrup, J. Estimation of effective wind speed. In Proceedings of the Journal of Physics: Conference Series. The Science of Making Torque from Wind Lyngby, Lyngby, Denmark, 28–31 August 2007; Volume 75, p. 012082. [Google Scholar]
- Abdellatif, W.S.; Hamada, A.; Abdelwahab, S.A.M. Wind speed estimation MPPT technique of DFIG-based wind turbines theoretical and experimental investigation. Electr. Eng. 2021, 103, 2769–2781. [Google Scholar] [CrossRef]
- González-Castaño, C.; Lorente-Leyva, L.L.; Muñoz, J.; Restrepo, C.; Peluffo-Ordóñez, D.H. An MPPT strategy based on a surface-based polynomial fitting for solar photovoltaic systems using real-time hardware. Electronics 2021, 10, 206. [Google Scholar] [CrossRef]
- Mousa, H.H.; Youssef, A.R.; Mohamed, E.E. Variable step size P&O MPPT algorithm for optimal power extraction of multi-phase PMSG based wind generation system. Int. J. Electr. Power Energy Syst. 2019, 108, 218–231. [Google Scholar]
- Merabet, A.; Eshaft, H.; Tanvir, A.A. Power-current controller based sliding mode control for DFIG-wind energy conversion system. IET Renew. Power Gener. 2018, 12, 1155–1163. [Google Scholar] [CrossRef]
- Mazouz, F.; Belkacem, S.; Colak, I.; Drid, S.; Harbouche, Y. Adaptive direct power control for double fed induction generator used in wind turbine. Int. J. Electr. Power Energy Syst. 2020, 114, 105395. [Google Scholar] [CrossRef]
- Aguilar, M.E.B.; Coury, D.V.; Reginatto, R.; Monaro, R.M. Multi-objective PSO applied to PI control of DFIG wind turbine under electrical fault conditions. Electr. Power Syst. Res. 2020, 180, 106081. [Google Scholar] [CrossRef]
- Demirbas, S. Self-tuning fuzzy-PI-based current control algorithm for doubly fed induction generator. IET Renew. Power Gener. 2017, 11, 1714–1722. [Google Scholar] [CrossRef]
- Lee, S.S.; Heng, Y.E. Table-based DPC for grid connected VSC under unbalanced and distorted grid voltages: Review and optimal method. Renew. Sustain. Energy Rev. 2017, 76, 51–61. [Google Scholar] [CrossRef]
- Karad, S.; Thakur, R. Recent trends of control strategies for doubly fed induction generator based wind turbine systems: A comparative review. Arch. Comput. Methods Eng. 2019, 28, 15–29. [Google Scholar] [CrossRef]
- Xiong, L.; Li, P.; Wang, J. High-order sliding mode control of DFIG under unbalanced grid voltage conditions. Int. J. Electr. Power Energy Syst. 2020, 117, 105608. [Google Scholar] [CrossRef]
- Phan, D.C.; Yamamoto, S. Rotor speed control of doubly fed induction generator wind turbines using adaptive maximum power point tracking. Energy 2016, 111, 377–388. [Google Scholar] [CrossRef]
- Bektache, A.; Boukhezzar, B. Nonlinear predictive control of a DFIG-based wind turbine for power capture optimization. Int. J. Electr. Power Energy Syst. 2018, 101, 92–102. [Google Scholar] [CrossRef]
- Shotorbani, A.M.; Mohammadi-Ivatloo, B.; Wang, L.; Marzband, M.; Sabahi, M. Application of finite-time control Lyapunov function in low-power PMSG wind energy conversion systems for sensorless MPPT. Int. J. Electr. Power Energy Syst. 2019, 106, 169–182. [Google Scholar] [CrossRef]
- Dhar, S.; Dash, P. A new backstepping finite time sliding mode control of grid connected PV system using multivariable dynamic VSC model. Int. J. Electr. Power Energy Syst. 2016, 82, 314–330. [Google Scholar] [CrossRef]
- Forchetti, D.G.; Garcia, G.O.; Valla, M.I. Adaptive observer for sensorless control of stand-alone doubly fed induction generator. IEEE Trans. Ind. Electron. 2009, 56, 4174–4180. [Google Scholar] [CrossRef]
- Kumar, R.; Das, S. MRAS-based speed estimation of grid-connected doubly fed induction machine drive. IET Power Electron. 2017, 10, 726–737. [Google Scholar] [CrossRef]
- Morawiec, M.; Blecharz, K.; Lewicki, A. Sensorless Rotor Position Estimation of Doubly Fed Induction Generator Based on Backstepping Technique. IEEE Trans. Ind. Electron. 2019, 67, 5889–5899. [Google Scholar] [CrossRef]
- Beltran, B.; Ahmed-Ali, T.; Benbouzid, M.E.H. High-order sliding-mode control of variable-speed wind turbines. IEEE Trans. Ind. Electron. 2008, 56, 3314–3321. [Google Scholar] [CrossRef]
- Adekanle, O.; Guisser, M.; Abdelmounim, E.; Aboulfatah, M. Robust Integral Backstepping Control of Doubly Fed Induction Generator Under Parameter Variation. Int. Rev. Autom. Control (IREACO) 2017, 10, 178–185. [Google Scholar] [CrossRef]
- Watil, A.; El Magri, A.; Raihani, A.; Lajouad, R.; Giri, F. Multi-objective output feedback control strategy for a variable speed wind energy conversion system. Int. J. Electr. Power Energy Syst. 2020, 121, 106081. [Google Scholar] [CrossRef]
- Dib, A.; Farza, M.; M’Saad, M.; Dorléans, P.; Massieu, J.F. High gain observer for sensorless induction motor. IFAC Proc. Vol. 2011, 44, 674–679. [Google Scholar] [CrossRef]
- Chakir, H.; Ouadi, H.; Giri, F. Output Feedback control of wind energy conversion system with hybrid excitation synchronous generator. IFAC-PapersOnLine 2015, 48, 622–627. [Google Scholar] [CrossRef]
- Barra, A.; Ouadi, H.; Giri, F.; Chakib, R. Sensorless nonlinear control of wind energy systems with doubly fed induction generator. J. Control. Autom. Electr. Syst. 2016, 27, 562–578. [Google Scholar] [CrossRef]
- Pham, H.T.; Bourgeot, J.M.; Benbouzid, M.E.H. Comparative investigations of sensor fault-tolerant control strategies performance for marine current turbine applications. IEEE J. Ocean. Eng. 2017, 43, 1024–1036. [Google Scholar] [CrossRef]
- Golnary, F.; Moradi, H. Dynamic modelling and design of various robust sliding mode controls for the wind turbine with estimation of wind speed. Appl. Math. Model. 2019, 65, 566–585. [Google Scholar] [CrossRef]
- Maher, R.A.; Abdelsalam, A.K.; Dessouky, Y.G.; Nouman, A. High performance state-flow based MPPT technique for micro WECS. IET Renew. Power Gener. 2019, 13, 3009–3021. [Google Scholar] [CrossRef]
- Chhipa, A.A.; Kumar, V.; Joshi, R.R.; Chakrabarti, P.; Jasinski, M.; Burgio, A.; Leonowicz, Z.; Jasinska, E.; Soni, R.; Chakrabarti, T. Adaptive neuro-fuzzy inference system-based maximum power tracking controller for variable speed WECS. Energies 2021, 14, 6275. [Google Scholar] [CrossRef]
- El Magri, A.; Giri, F.; Besancon, G.; El Fadili, A.; Dugard, L.; Chaoui, F.Z. Sensorless adaptive output feedback control of wind energy systems with PMS generators. Control Eng. Pract. 2013, 21, 530–543. [Google Scholar] [CrossRef]
- Taveiros, F.E.V.; Barros, L.S.; Costa, F.B. Back-to-back converter state-feedback control of DFIG (doubly-fed induction generator)-based wind turbines. Energy 2015, 89, 896–906. [Google Scholar] [CrossRef]
- Bornard, G.; Hammouri, H. A high gain observer for a class of uniformly observable systems. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991; pp. 1494–1496. [Google Scholar]
- Khalil, H.K. High-Gain Observers in Nonlinear Feedback Control; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar]
- Stitou, M.; El Fadili, A.; Chaoui, F.Z.; Giri, F. Adaptive High Gain Observer for Photovoltaic Systems. In Proceedings of the 2019 4th World Conference on Complex Systems (WCCS), Ouarzazate, Morocco, 22–25 April 2019; pp. 1–6. [Google Scholar]
- Boizot, N.; Busvelle, E.; Gauthier, J.P. An adaptive high-gain observer for nonlinear systems. Automatica 2010, 46, 1483–1488. [Google Scholar] [CrossRef]
- Schreier, G.; DeLeon, J.; Glumineau, A.; Boisliveau, R. Cascade nonlinear observers: Application to an experimental induction motor benchmark. IEE Proc.-Control Theory Appl. 2001, 148, 509–515. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).