Comparison of Two Sinusoidal Magnetization Modes of Bonded Magnetic Rings
Abstract
:1. Introduction
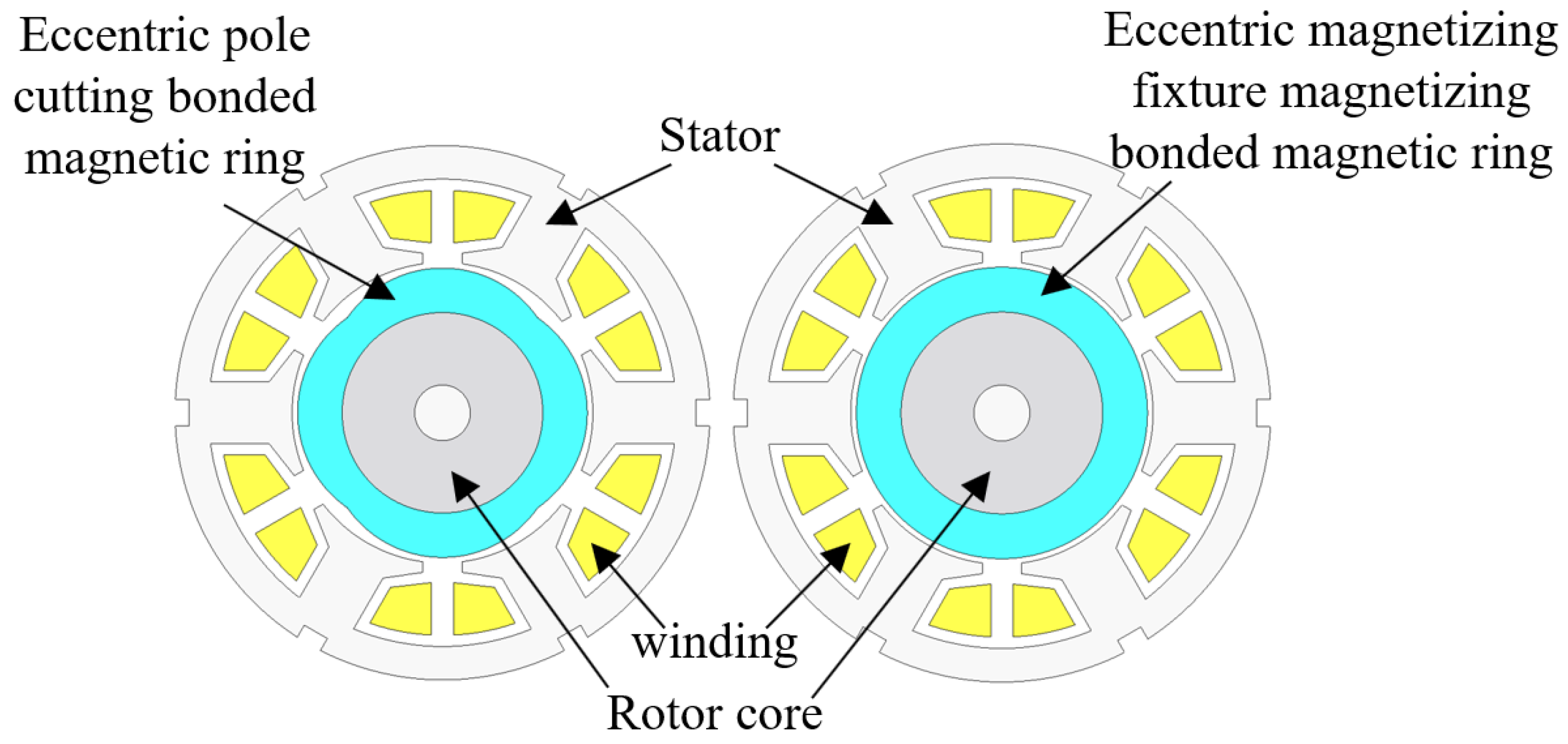
2. Finite Element Analysis
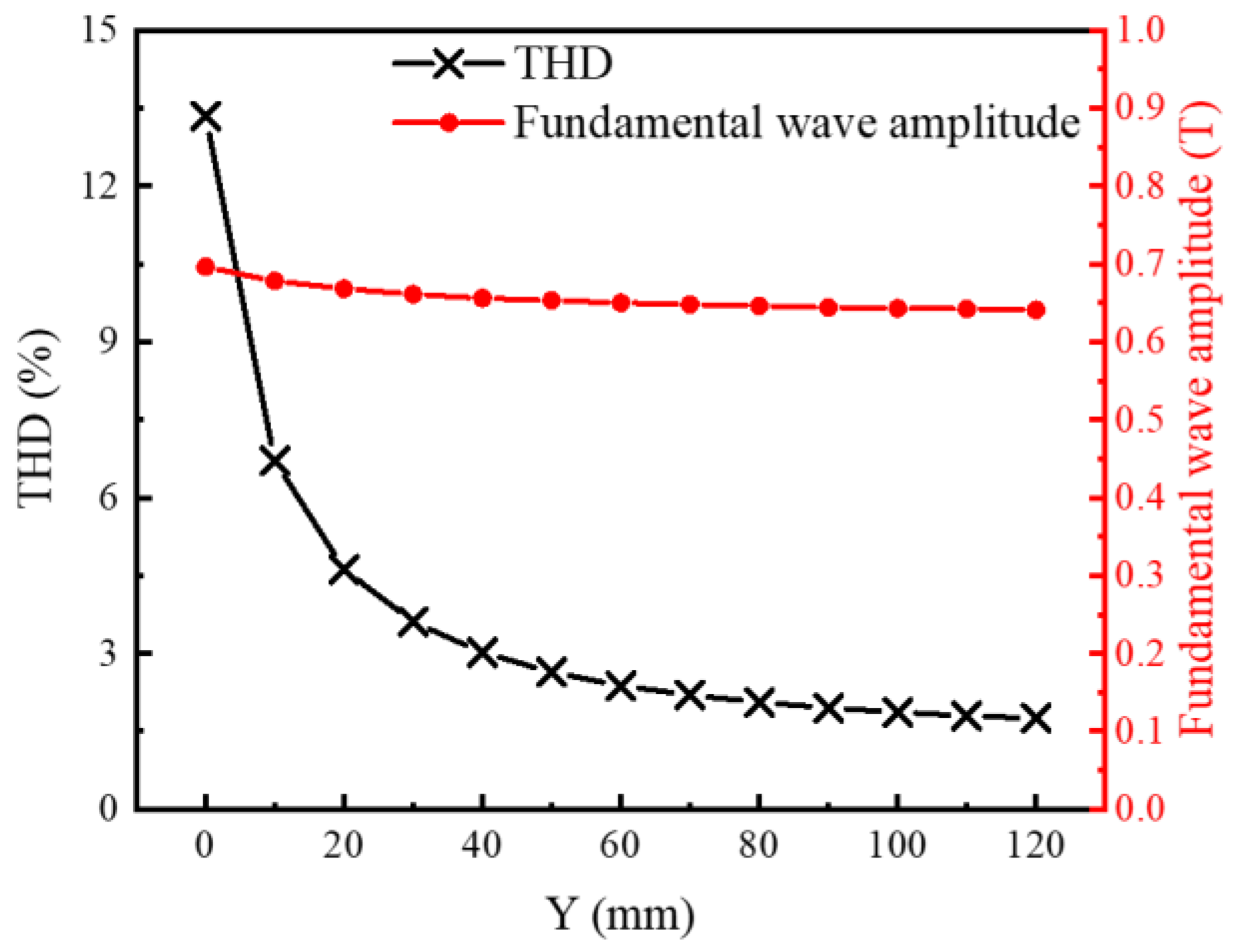
2.1. Eccentric Pole Cutting
2.2. Eccentric Magnetizing Fixture
3. Comparison in Motor Application
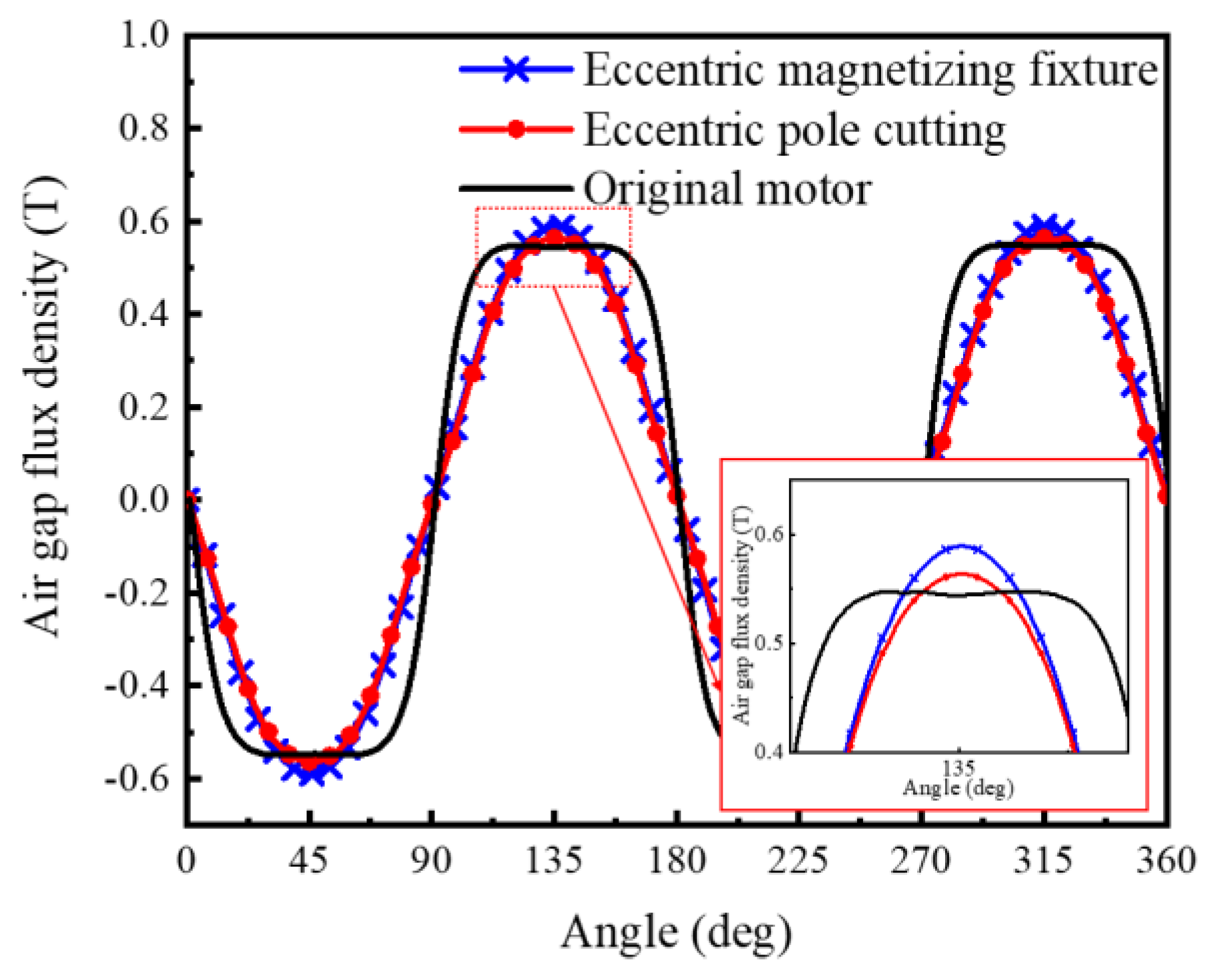
3.1. Comparison of No−Load Back−EMF
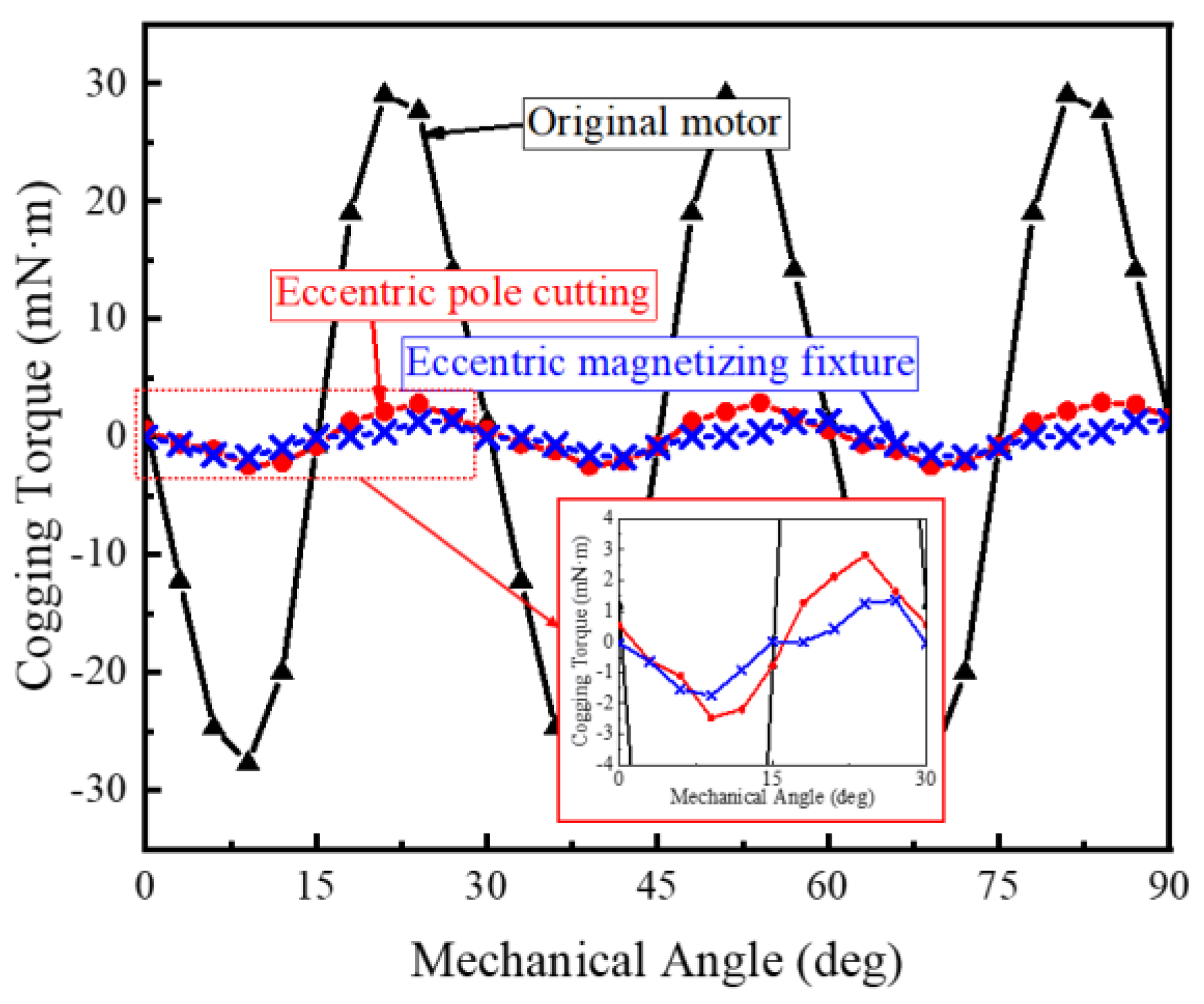
3.2. Cogging Torque Comparison
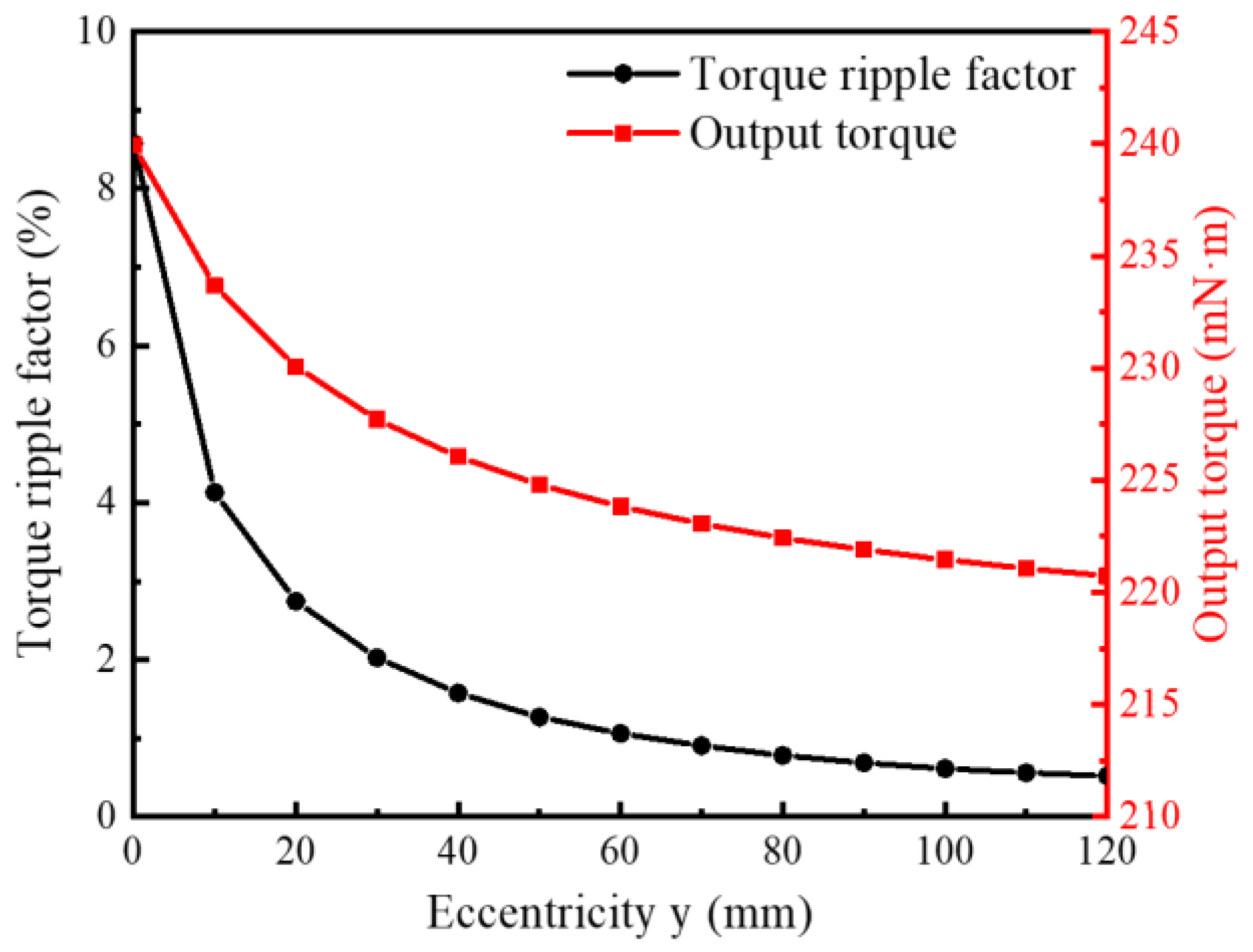
3.3. Comparison of Rated Output Torque
3.4. Comparison of Magnet Dosage
4. Prototype Comparison
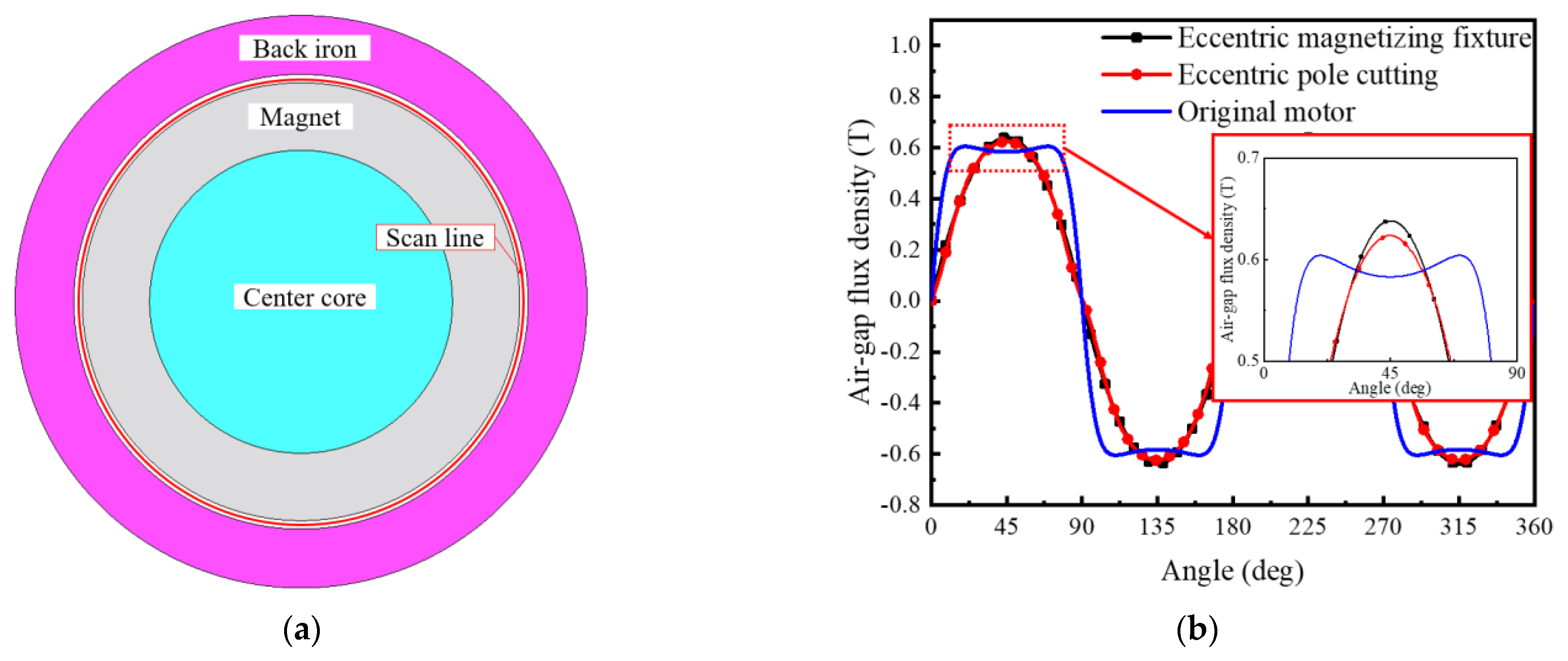
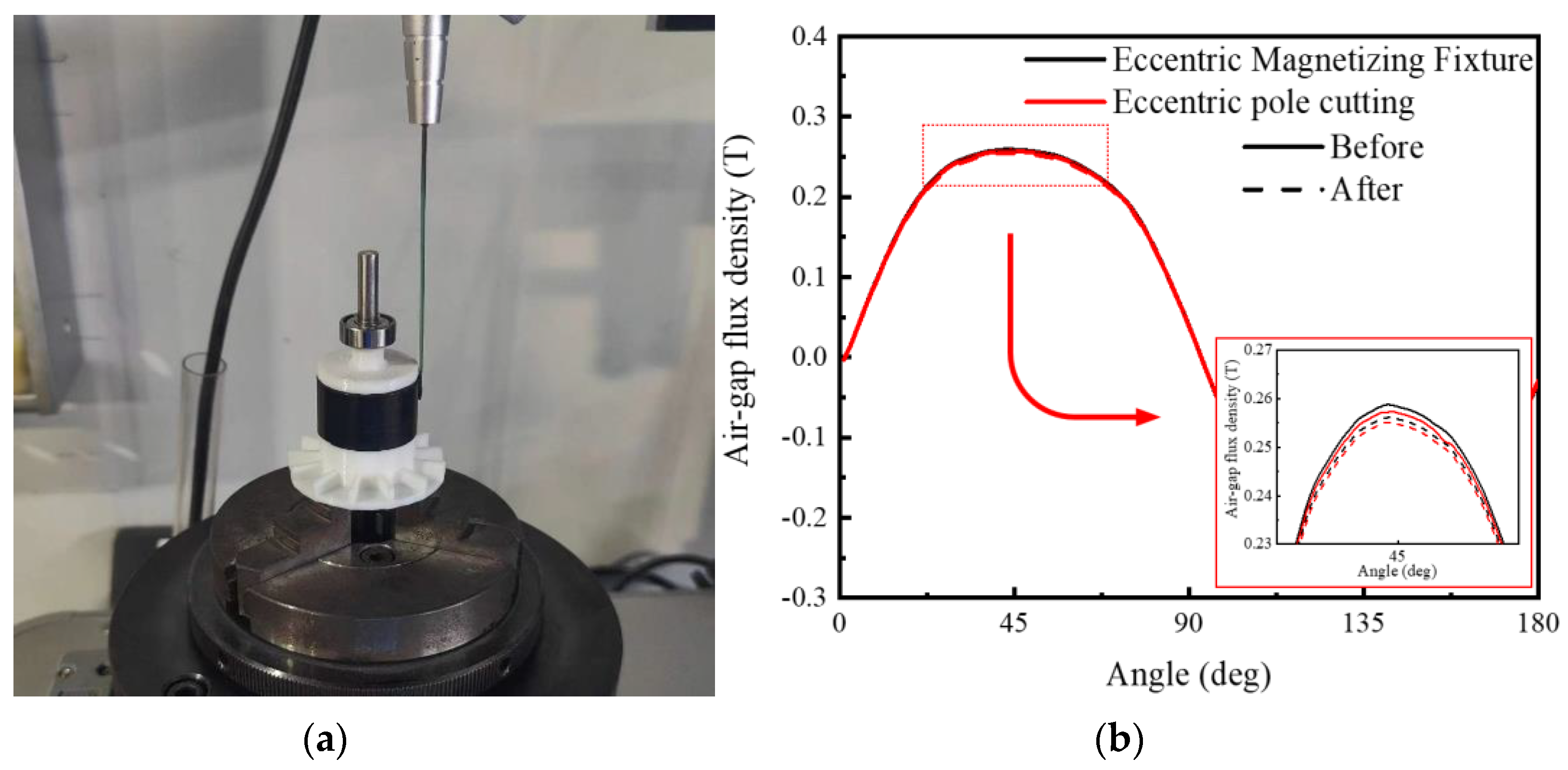
4.1. Air−Gap Flux Density Comparison
4.2. Cogging Torque Comparison
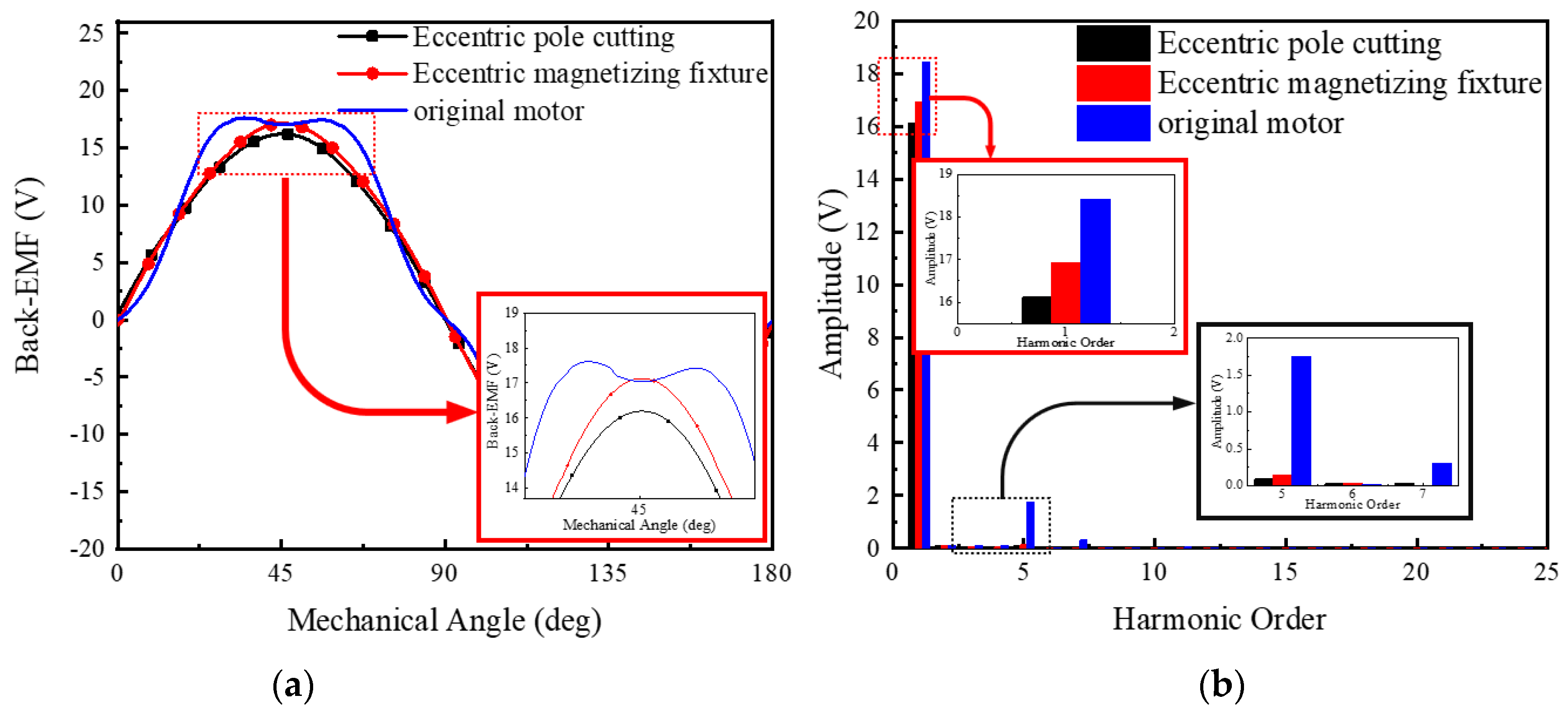
4.3. Comparison of No−Load Back−EMF
4.4. Demagnetization Test
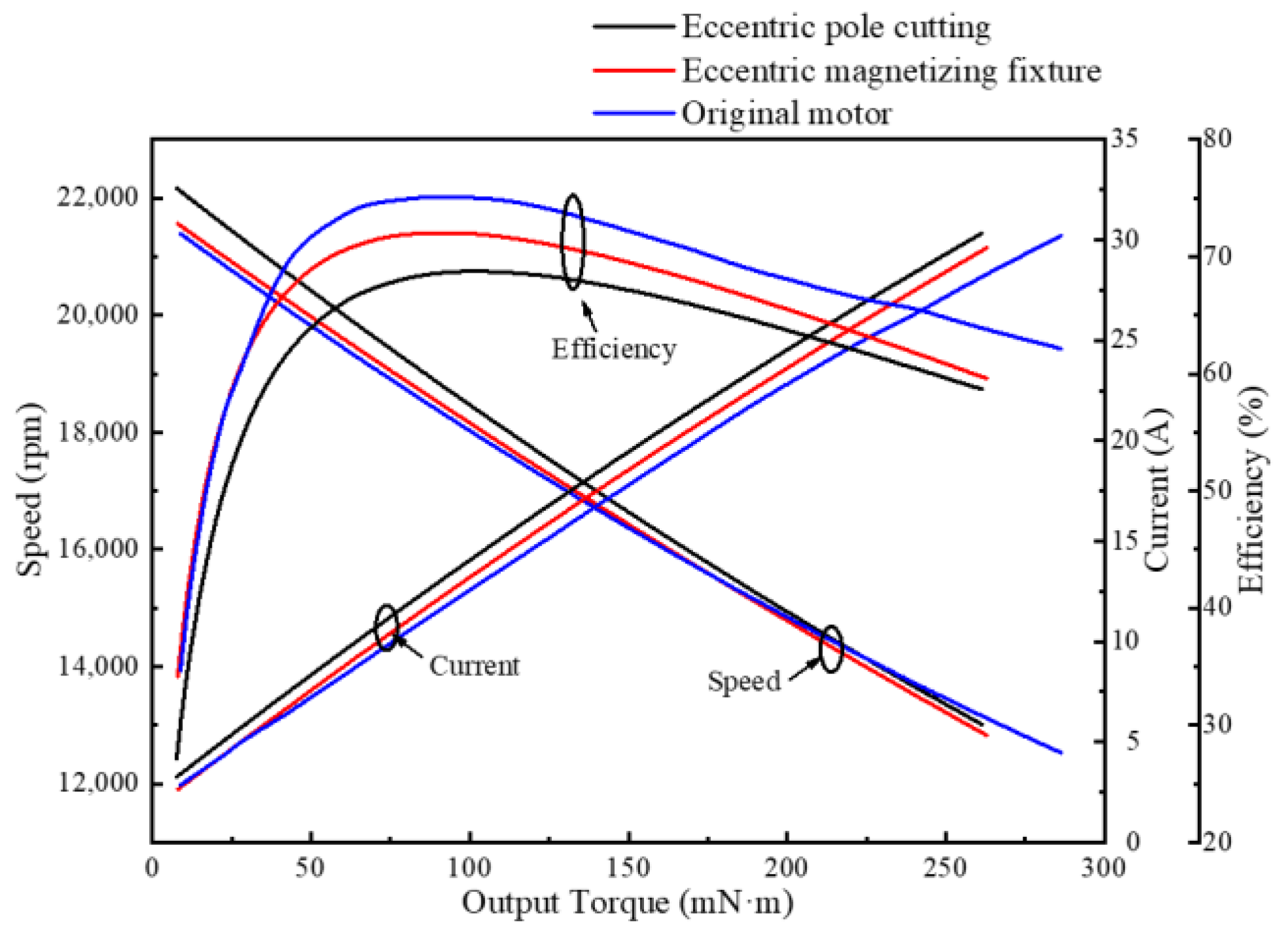
4.5. Motor Performance Test
5. Conclusions
- On the premise that the optimization effect reaches the standard, it is recommended to use the eccentric pole cutting method in the mass production process, which can reduce the amount of bonded magnetic powder and thus reduce the material cost.
- Since the eccentric pole cutting method has better optimization effect, it is recommended to use the eccentric magnetizing fixture in the scene pursuing higher optimization effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Fei, W.; Luk, P.C.K. A New Technique of Cogging Torque Suppression in Direct−Drive Permanent−Magnet Brushless Machines. IEEE Trans. Ind. Appl. 2010, 46, 1332–1340. [Google Scholar] [CrossRef] [Green Version]
- Dorrell, D.G.; Hsieh, M.F.; Popescu, M.; Evans, L.; Staton, D.A.; Grout, V. A Review of the Design Issues and Techniques for Radial−Flux Brushless Surface and Internal Rare−Earth Permanent−Magnet Motors. IEEE Trans. Ind. Electron. 2010, 58, 3741–3757. [Google Scholar] [CrossRef]
- Li, R.; Shi, C.; Qu, R.; Li, D.; Ren, X.; Fedida, V.; Zhou, Y. A Novel Modular Stator Fractional Pole−Pair Permanent−Magnet Vernier Machine with Low Torque Ripple for Servo Applications. IEEE Trans. Magn. 2020, 57, 1–6. [Google Scholar] [CrossRef]
- Jabbari, A. An Analytical Expression for Magnet Shape Optimization in Surface−Mounted Permanent Magnet Machines. Math. Comput. Appl. 2018, 23, 57. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Zhu, Z.Q. Analytical Modeling of Surface−Mounted PM Machines Accounting for Magnet Shaping and Varied Magnet Property Distribution. IEEE Trans. Magn. 2014, 50, 1–11. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Meng, G.; Zhou, S.; Cao, Q. Analytical Calculation of Magnetic Field and Cogging Torque in Surface−Mounted Permanent Magnet Machines Accounting for Any Eccentric Rotor Shape. IEEE Trans. Ind. Electron. 2014, 62, 3438–3447. [Google Scholar] [CrossRef]
- Chu, W.Q.; Zhu, Z.Q. Investigation of Torque Ripples in Permanent Magnet Synchronous Machines with Skewing. IEEE Trans. Magn. 2012, 49, 1211–1220. [Google Scholar] [CrossRef]
- Li, Y.; Xing, J.; Wang, T.; Lu, Y. Programmable Design of Magnet Shape for Permanent−Magnet Synchronous Motors with Sinusoidal Back−EMF Waveforms. IEEE Trans. Magn. 2008, 44, 2163–2167. [Google Scholar] [CrossRef]
- Zheng, P.; Zhao, J.; Han, J.; Wang, J.; Yao, Z.; Liu, R. Optimization of the Magnetic Pole Shape of a Permanent−Magnet Synchronous Motor. IEEE Trans. Magn. 2007, 43, 2531–2533. [Google Scholar] [CrossRef]
- Merkel, M.; Gangl, P.; Schöps, S. Shape Optimization of Rotating Electric Machines Using Isogeometric Analysis. IEEE Trans. Energy Convers. 2021, 36, 2683–2690. [Google Scholar] [CrossRef]
- Kong, X.; Hua, Y.; Zhang, Z.; Wang, C.; Liu, Y. Analytical Modeling of High−Torque−Density Spoke−Type Permanent Magnet In−Wheel Motor Accounting for Rotor Slot and Eccentric Magnetic Pole. IEEE Trans. Transp. Electrif. 2021, 7, 2683–2693. [Google Scholar] [CrossRef]
- Dhulipati, H.; Mukundan, S.; Li, Z.; Ghosh, E.; Tjong, J.; Kar, N.C. Torque Performance Enhancement in Consequent Pole PMSM Based on Magnet Pole Shape Optimization for Direct−Drive EV. IEEE Trans. Magn. 2020, 57, 1–7. [Google Scholar] [CrossRef]
- Hu, P.; Wang, D. Analytical Average Torque Optimization Method of Parallel Magnetized Surface−Mounted Permanent−Magnet Machine with Third−Order Harmonic Shaping Method. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1377–1383. [Google Scholar] [CrossRef]
- Du, Z.S.; Lipo, T.A. High Torque Density and Low Torque Ripple Shaped−Magnet Machines Using Sinusoidal Plus Third Harmonic Shaped Magnets. IEEE Trans. Ind. Appl. 2019, 55, 2601–2610. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, C.; Geng, Q.; Yan, Y. Modeling and Analyzing of Surface−Mounted Permanent−Magnet Synchronous Machines with Optimized Magnetic Pole Shape. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Tavana, N.R.; Shoulaie, A. Analysis and Design of Magnetic Pole Shape in Linear Permanent−Magnet Machine. IEEE Trans. Magn. 2009, 46, 1000–1006. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Z.Q.; Ombach, G. Torque Improvement of Five−Phase Surface−Mounted Permanent Magnet Machine Using Third−Order Harmonic. IEEE Trans. Energy Convers. 2014, 29, 735–747. [Google Scholar] [CrossRef]
- Scuiller, F. Magnet Shape Optimization to Reduce Pulsating Torque for a Five−Phase Permanent−Magnet Low−Speed Machine. IEEE Trans. Magn. 2013, 50, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Laskaris, K.I.; Kladas, A.G. Permanent−Magnet Shape Optimization Effects on Synchronous Motor Performance. IEEE Trans. Ind. Electron. 2011, 58, 3776–3783. [Google Scholar] [CrossRef]
- Lim, S.; Izui, K.; Nishiwaki, S.; Hong, J.P.; Min, S. Magnetising fixture design for optimal magnetisation orientation of ring-type magnet in surface-mounted permanent magnet motor. IET Electr. Power Appl. 2018, 12, 1344–1349. [Google Scholar] [CrossRef]
- Koh, C.S.; Seol, J.S. New cogging−torque reduction method for brushless permanent−magnet motors. IEEE Trans. Magn. 2003, 39, 3503–3506. [Google Scholar] [CrossRef]
- Shen, Y.; Hu, P.; Jin, S.; Wei, Y.; Lan, R.; Zhuang, S.; Liu, D. Design of Novel Shaftless Pump−Jet Propulsor for Multi−Purpose Long−Range and High−Speed Autonomous Underwater Vehicle. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Chen, J.W.; Zhang, B.; Ding, H. Design optimization of an arc−edged trapezoidal Halbach array in the linear permanent magnet actuator for precision engineering. Int. J. Appl. Electromagn. Mech. 2016, 51, 319–335. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, G.Y.; Xia, Z.P.; Zhu, Z.Q. Determination of Maximum Electromagnetic Torque in PM Brushless Machines Having Two−Segment Halbach Array. IEEE Trans. Ind. Electron. 2014, 61, 718–729. [Google Scholar] [CrossRef]
- Raich, H.; Blümler, P. Design and construction of a dipolar Halbach array with a homogeneous field from identical bar magnets: NMR Mandhalas. Concepts Magn. Reson. Part B 2004, 23, 16–25. [Google Scholar] [CrossRef]
- Kee, H.; Lee, H.; Park, S. Optimized Halbach array for focused magnetic drug targeting. J. Magn. Magn. Mater. 2020, 514, 167180. [Google Scholar] [CrossRef]
- Zhang, L.F.; Wang, K.; Sun, H.Y.; Zhu, S.S. Multiphase PM machines with Halbach array considering third harmonic flux density. IEEE Trans. Ind. Electron. 2018, 66, 9184–9193. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; Harris, N. Increasing output power of electromagnetic vibration energy harvesters using improved Halbach arrays. Sens. Actuator A Phys. 2013, 203, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Herchenroeder, J.; Miller, D.; Sheth, N.K.; Foo, M.C.; Nagarathnam, K. High performance bonded neo magnets using high density compaction. J. Appl. Phys. 2011, 109, 07A743. [Google Scholar] [CrossRef]
- Horikawa, T.; Yamazaki, M.; Matsuura, M.; Sugimoto, S. Recent progress in the development of high−performance bonded magnets using rare earth–Fe compounds. Sci. Technol. Adv. Mater. 2021, 22, 729–747. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.W.; Wang, Z.L.; Li, T.H.; Zhu, S.J.; Yu, D.B.; Yan, W.L.; Luo, Y. Effect of silane coupling agents on flowability and compressibility of compound for bonded NdFeB magnet. J. Rare Earths 2022, 40, 772–777. [Google Scholar] [CrossRef]
- Prakht, V.; Dmitrievskii, V.; Kazakbaev, V. Optimal Design of a High−Speed Flux Reversal Motor with Bonded Rare−Earth Permanent Magnets. Mathematics 2021, 9, 256. [Google Scholar] [CrossRef]
- Jewell, G.W.; Howe, D.; Riley, C.D. The design of radial−field multipole impulse magnetizing fixtures for isotropic NdFeB magnets. IEEE Trans. Magn. 1997, 33, 708–722. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, Y.; Wang, Z.L.; Yu, D.B.; Yang, Y.F.; Yan, W.L.; Peng, H.J.; Wu, K.W.; Yan, W.J. Research on influencing factors of magnetic property test of permanent magnetic ring. Electr. Eng. 2022, 1–10. [Google Scholar] [CrossRef]
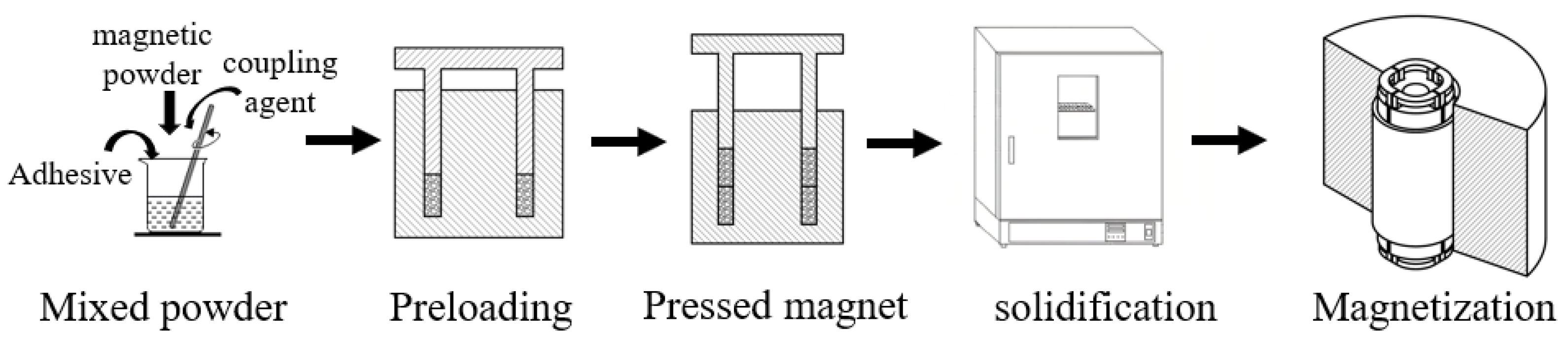
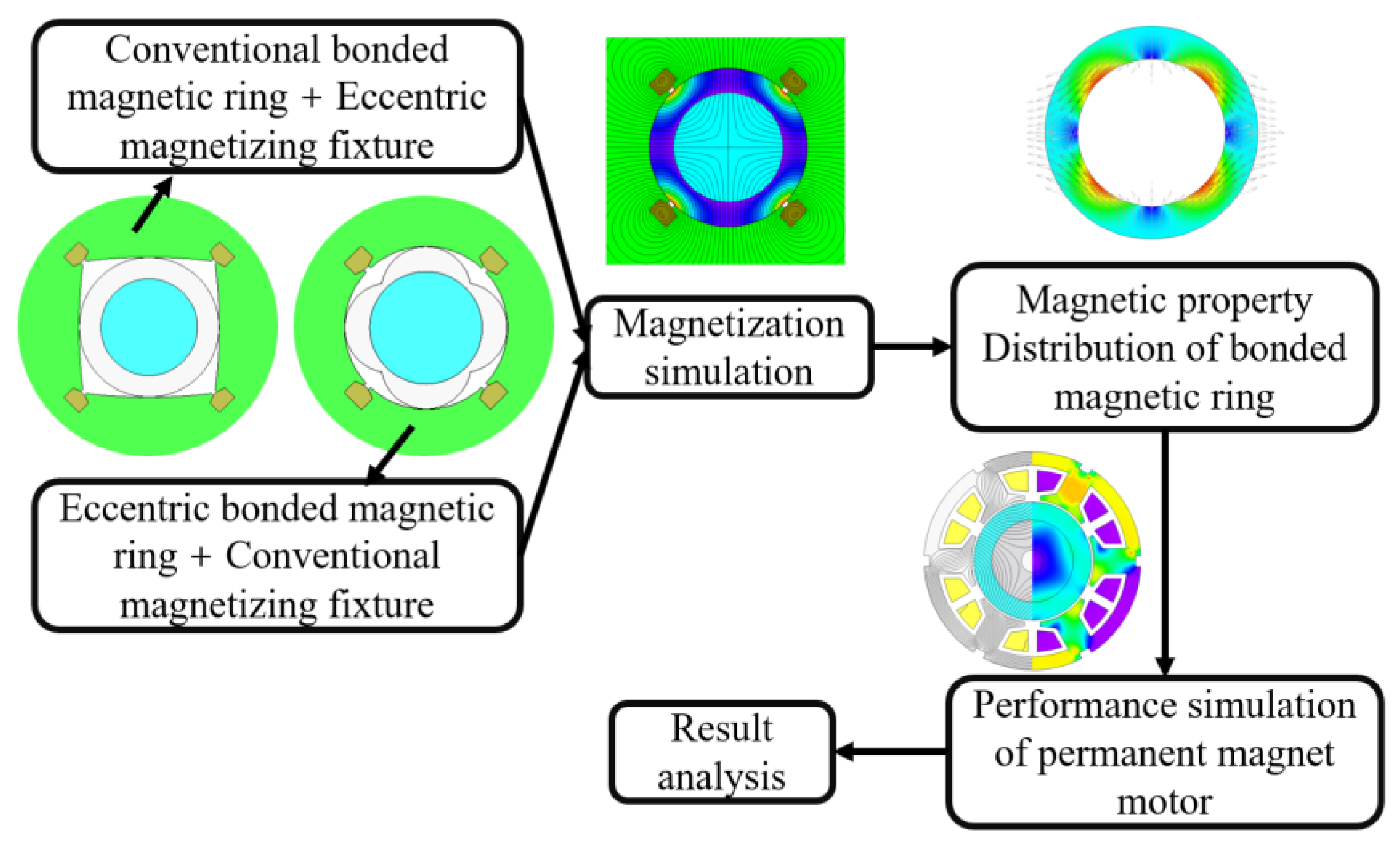
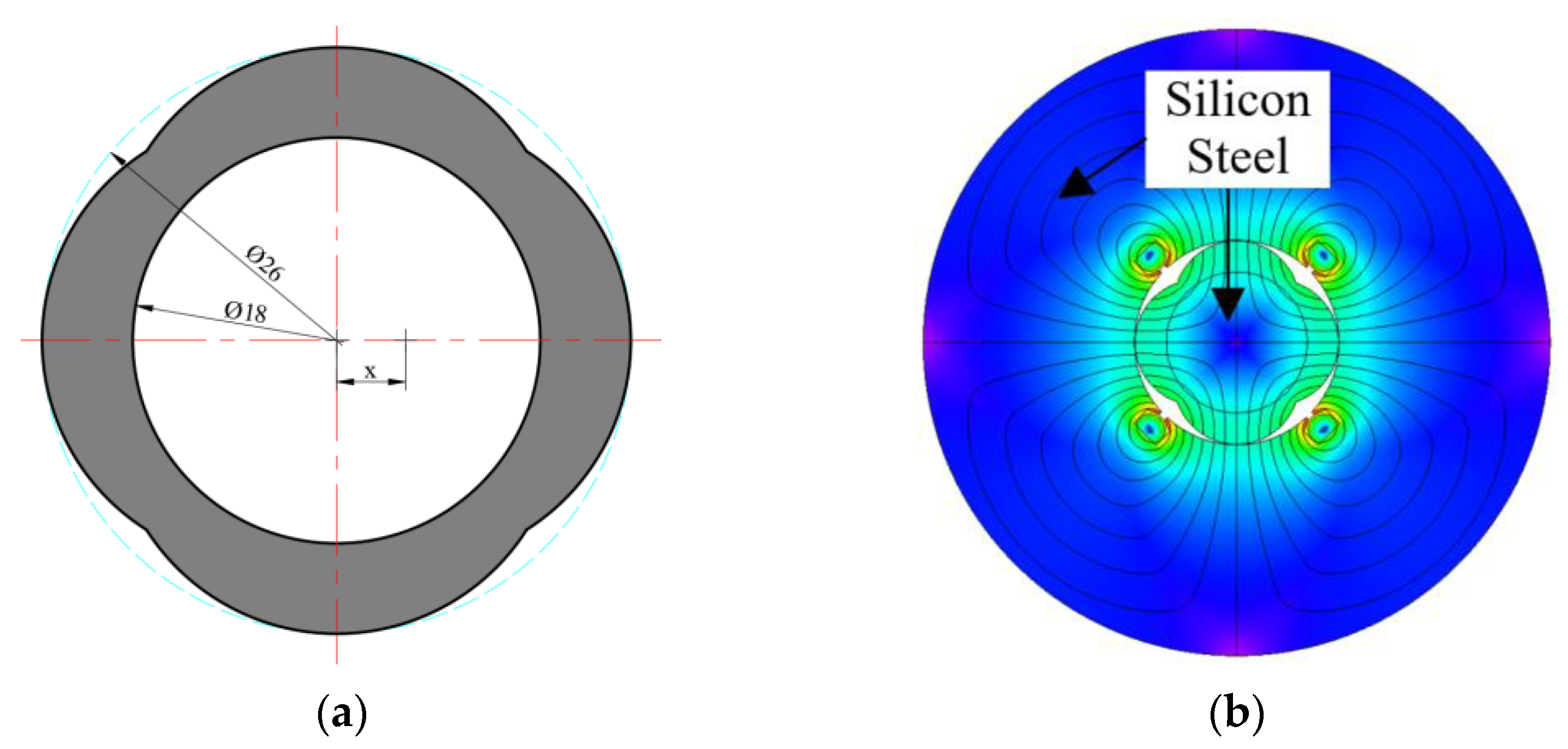

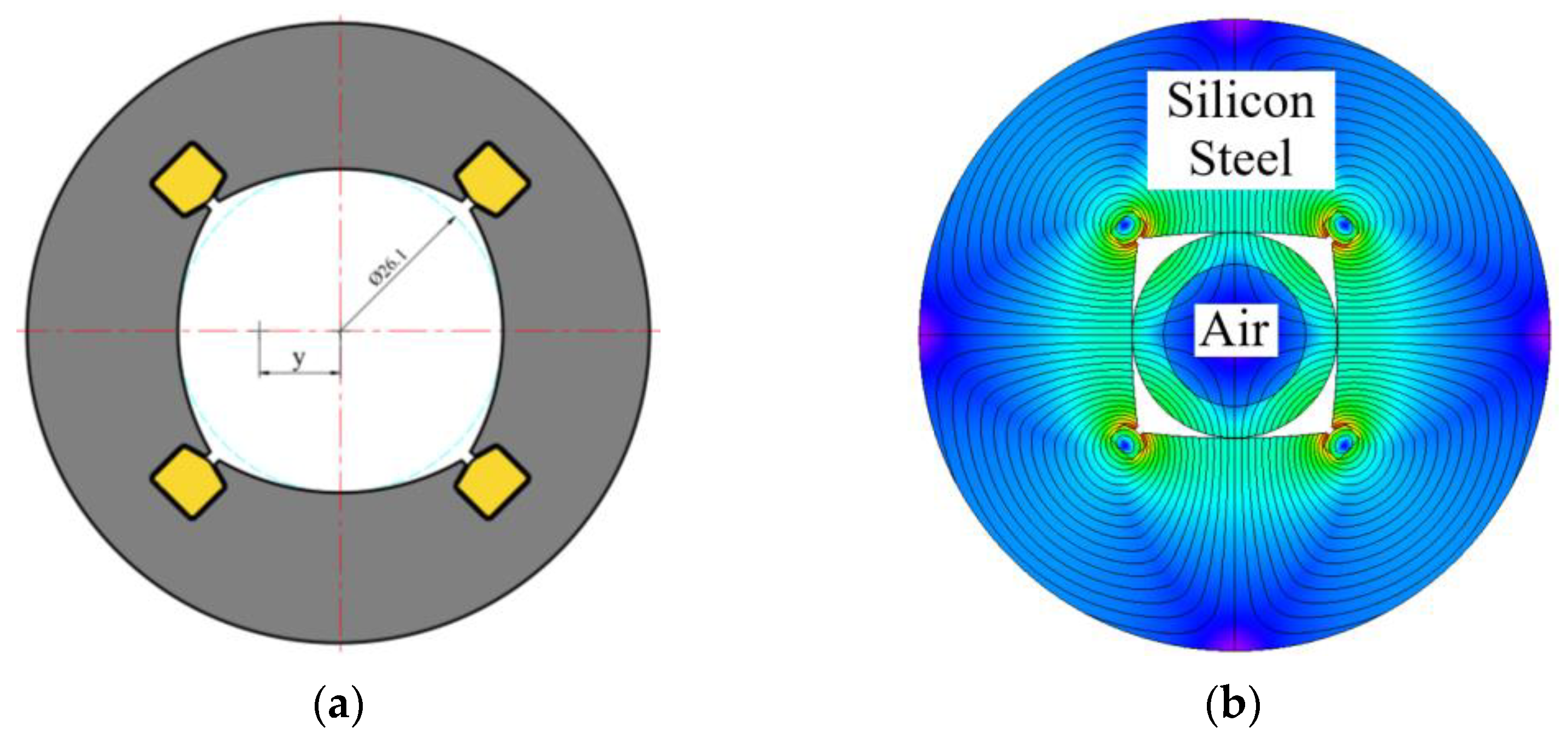





| Item | Unit | Value |
|---|---|---|
| Stator slots | - | 6 |
| Magnet poles | - | 4 |
| Rated speed | rpm | 15,000 |
| Stator outer diameter | mm | 48 |
| Stator inner diameter | mm | 27 |
| Rotor diameter | mm | 26 |
| Inside diameter of magnet | mm | 18 |
| Shaft diameter | mm | 5 |
| Motor axial length | mm | 15 |
| Number of turns | - | 20 |
| Diameter of wire | mm | 0.74 |
| Steel grade | - | 35CS300 |
| Stator steel mass | g | 76.62 |
| Copper mass | g | 23.56 |
| Br | Hcb | Hcj | BH (max) | Maximum Operating Temperature |
|---|---|---|---|---|
| 0.8 T | 475 kA/m | 750 kA/m | 95 kJ/m3 | 160 ℃ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, Z.; Yu, J.; Yu, D.; Luo, Y.; Yan, W.; Yang, Y.; Hu, T.; Wang, L. Comparison of Two Sinusoidal Magnetization Modes of Bonded Magnetic Rings. Machines 2022, 10, 911. https://doi.org/10.3390/machines10100911
Zhang Z, Wang Z, Yu J, Yu D, Luo Y, Yan W, Yang Y, Hu T, Wang L. Comparison of Two Sinusoidal Magnetization Modes of Bonded Magnetic Rings. Machines. 2022; 10(10):911. https://doi.org/10.3390/machines10100911
Chicago/Turabian StyleZhang, Ze, Zilong Wang, Juntao Yu, Dunbo Yu, Yang Luo, Wenlong Yan, Yuanfei Yang, Tengfei Hu, and Li Wang. 2022. "Comparison of Two Sinusoidal Magnetization Modes of Bonded Magnetic Rings" Machines 10, no. 10: 911. https://doi.org/10.3390/machines10100911
APA StyleZhang, Z., Wang, Z., Yu, J., Yu, D., Luo, Y., Yan, W., Yang, Y., Hu, T., & Wang, L. (2022). Comparison of Two Sinusoidal Magnetization Modes of Bonded Magnetic Rings. Machines, 10(10), 911. https://doi.org/10.3390/machines10100911







