Numerical Shape Planning Algorithm for Hyper-Redundant Robots Based on Discrete Bézier Curve Fitting
Abstract
:1. Introduction
2. Conceptual Description of Shape Planning Algorithm
- -
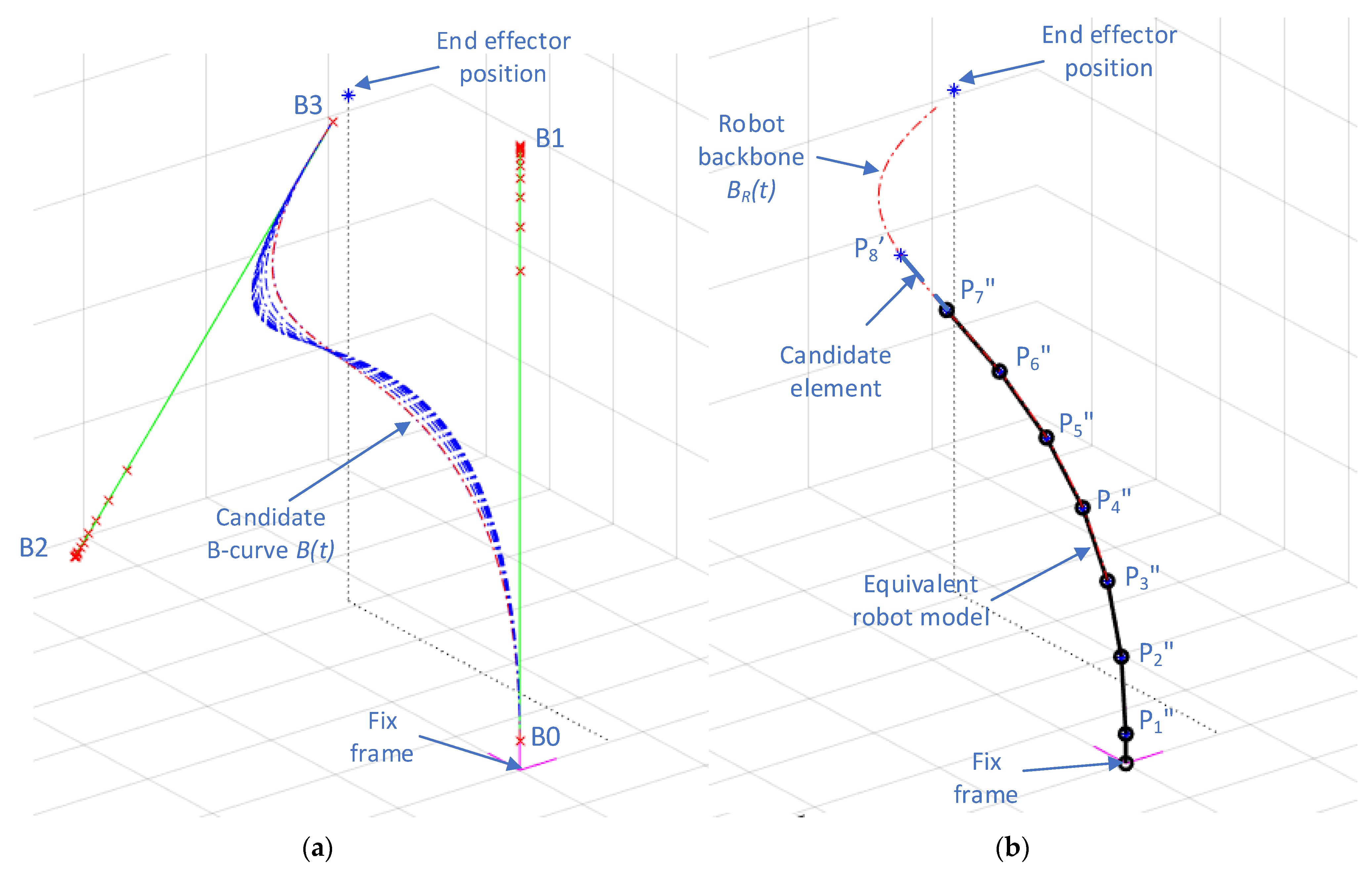
- The position of point Pj′ {j = 2…n−1} belonging to the backbone curve BR(t) is determine by finding a segment (candidate element) on the BR(t) curve that has the length ≈ lj−1. The length of the candidate element is measured between the point Pi′ ϵ BR(t) and the point Pj−1″ ϵ ERM that defines the end of the previous element.
- -
- For each obtained Pj′ the spherical coordinates are measured in respect to a coordinate system placed in Pj−1″ that has the orientation of the global coordinate system.
- -
- Using the angles and and the length lj, the elements j−1 from the ERM is constructed by finding the position of point ϵ ERM using Equation (9).
3. Numerical Results
3.1. Performance Assessment of the S-GUIDE Method
3.2. S-GUIDE Method Testing for the Python Robot
- -
- remain in a home position until a harvest command is received
- -
- determine the needed trajectory from the home position to the object to grasp
- -
- perform grasping
- -
- place the object in designated containers and return to the home position.
3.3. Discussions and Results Comparison
- -
- a comparative study between different algorithms for solving the IKP problem for a 10-DoF structure was presented in [36]. The authors used an exhaustive method and error optimization algorithms for this purpose. It was observed that the exhaustive methods gave good results on positioning errors, but the processing time was fairly high and not applicable for real-time applications (ex.:18 s for a 4 DoF structure). Using error optimization algorithms (Patternsearch, Genetic algorithms, Multistart and Simulannelbnd), the computation time for a 10-DoF robot varied from 0.5 s to 14 s with errors that ranged from 4 to 10 mm. Using S-GUIDE for a 24-DoF robot, the computational time was 0.001 s with an average positioning error of 0.0537 mm.
- -
- Another method proposed for calculating the inverse kinematics of HRRs called PASO is based on a particle swarm optimization algorithm and was presented in [35]. Using this method for a 30-DoF robot (ReMod3D) a processing time of 1.57 s with an average positioning error of 0.46 mm was obtained. Using S-GUIDE for a robot with 30 DoF the processing time was 0.001731 s with a similar positioning precision.
- -
- A good performance in relation to the computational time was obtained using the natural CCD algorithm presented in [39]. For a 20-DoF robot (integrates joints with 2 DoF) the processing time was around 0.05 s with a precision of 0.1. Using S-GUIDE for a 24-DoF robot the computational time was 0.001 s with a precision of 0.006%.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chirikjian, G.S.; Joel, W.B. An obstacle avoidance algorithm for hyper-redundant manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 625–631. [Google Scholar] [CrossRef] [Green Version]
- Chirikjian, G.S. Theory and Applications of Hyperredundant Robotic Mechanisms. Ph.D. Thesis, Department of Applied Mechanics, California Institute of Technology, Pasadena, CA, USA, 22 May 1992. Available online: https://thesis.library.caltech.edu/4458/1/Chirikjian_gs_1992.pdf (accessed on 21 July 2022).
- Rad, C.; Hancu, O.; Lapusan, C. Aspects regarding “soft” grasping in smart agricultural harvesting tasks. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2020, 63, 389–394. [Google Scholar]
- Martín-Barrio, A. Design, Modelling, Control and Teleoperation of Hyper-Redundant Robots. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2 November 2020. Available online: https://oa.upm.es/65161/1/ANDRES_MARTIN_BARRIO.pdf (accessed on 21 July 2022).
- Singh, I. Curve Based Approach for Shape Reconstruction of Continuum Manipulators. Ph.D. Thesis, Universite de Lille, Lille, France, 2018. Available online: https://hal.archives-ouvertes.fr/tel-01967054/document (accessed on 21 July 2022).
- Liu, J.; Tong, Y.; Liu, J. Review of snake robots in constrained environments. Robot. Auton. Syst. 2021, 101, 103785. [Google Scholar] [CrossRef]
- Lapusan, C.; Hancu, O.; Rad, C. Shape Sensing of Hyper-Redundant Robots Using an AHRS IMU Sensor Network. Sensors 2022, 22, 373. [Google Scholar] [CrossRef] [PubMed]
- Walker, I.D. Continuous backbone “continuum” robot manipulators. ISRN Robot. 2013, 2013, 726506. [Google Scholar] [CrossRef] [Green Version]
- Kolachalama, S.; Lakshmanan, S. Continuum robots for manipulation applications: A survey. J. Robot. 2020, 2020, 4187048. [Google Scholar] [CrossRef]
- Rad, C.; Hancu, O.; Lapusan, C. Data-Driven Kinematic Model of PneuNets Bending Actuators for Soft Grasping Tasks. Actuators 2022, 11, 58. [Google Scholar] [CrossRef]
- Yeshmukhametov, A.; Koganezawa, K.; Yamamoto, Y.; Buribayev, Z.; Mukhtar, Z.; Amirgaliyev, Y. Development of Continuum Robot Arm and Gripper for Harvesting Cherry Tomatoes. Appl. Sci. 2022, 12, 6922. [Google Scholar] [CrossRef]
- Canali, C.; Pistone, A.; Ludovico, D.; Guardiani, P.; Gagliardi, R.; De Mari Casareto Dal Verme, L.; Sofia, G.; Caldwell, D.G. Design of a Novel Long-Reach Cable-Driven Hyper-Redundant Snake-like Manipulator for Inspection and Maintenance. Appl. Sci. 2022, 12, 3348. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Y.; Huang, F.; Li, J.; Chen, Z.; Song, W.; Zhu, S.; Gu, J. Design and Kinematic Control of the Cable-Driven Hyper-Redundant Manipulator for Potential Underwater Applications. Appl. Sci. 2019, 9, 1142. [Google Scholar] [CrossRef] [Green Version]
- Lapusan, C.; Rad, C.; Hancu, O. Kinematic analysis of a hyper-redundant robot with application in vertical farming. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1190, 012014. [Google Scholar] [CrossRef]
- Martin, A.; Terrile, S.; Barrientos, A.; del Cerro, J. Hyper-redundant robots: Classification, state-of-the-art and issues. Rev. Iberoam. De Automática E Inf. Ind. 2018, 15, 351–362. [Google Scholar] [CrossRef]
- Lee, C.; An, D. AI-Based Posture Control Algorithm for a 7-DOF Robot Manipulator. Machines 2022, 10, 651. [Google Scholar] [CrossRef]
- Lapusan, C.; Hancu, O.; Rad, C. Quaternion-Based Approach for Solving the Direct Kinematics of a Modular Hyper Redundant Robot. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2020, 63, 363–366. [Google Scholar]
- Zhao, Y.; Jin, L.; Zhang, P.; Li, J. Inverse Displacement Analysis of a Hyper-redundant Elephant’s Trunk Robot. J. Bionic Eng. 2018, 15, 397–407. [Google Scholar] [CrossRef]
- Chibani, A.; Mahfoudi, C.; Chettibi, T.; Merzouk, R.; Zaatri, A. Generating optimal reference kinematic configurations for hyper-redundant parallel robots. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 867–882. [Google Scholar] [CrossRef]
- Bieze, T.M. Contribution to the Kinematic Modeling and Control of Soft Manipulators Using Computational Mechanics. Ph.D. Thesis, Universite de Lille, Lille, France, 24 October 2017. Available online: https://hal.archives-ouvertes.fr/tel-03516545/document (accessed on 21 July 2022).
- Qi, P.; Liu, C.; Zhang, L.; Wang, S.; Lam, H.-K.; Althoefer, K. Fuzzy logic control of a continuum manipulator for surgical applications. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Bali, Indonesia, 5–10 December 2014; pp. 413–418. [Google Scholar] [CrossRef]
- Runge, G.; Peters, J.; Raatz, A. Design optimization of soft pneumatic actuators using genetic algorithms. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, Macao, 26 March 2018; pp. 393–400. [Google Scholar] [CrossRef]
- Melingui, A.; Lakhal, O.; Daachi, B.; Mbede, J.B.; Merzouki, R. Adaptive Neural Network Control of a Compact Bionic Handling Arm. IEEE/ASME Trans. Mechatron. 2015, 20, 2862–2875. [Google Scholar] [CrossRef]
- Hannan, M.W.; Walker, I.D. Novel kinematics for continuum robots. In Advances in Robot Kinematics; Lenarčič, J., Stanišić, M.M., Eds.; Springer: Dordrecht, Netherlands, 2000; pp. 227–238. [Google Scholar]
- Chirikjian, G.S. Conformational Modeling of Continuum Structures in Robotics and Structural Biology: A Review. Adv. Robot. 2015, 29, 817–829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trivedi, D.; Lotfi, A.; Rahn, C.D. Geometrically Exact Models for Soft Robotic Manipulators. IEEE Trans. Robot. 2008, 24, 773–780. [Google Scholar] [CrossRef]
- Trivedi, D.; Rahn, C.D.; Kier, W.M.; Walker, I.D. Soft robotics: Biological inspiration, state of the art, and future research. Appl. Bionics Biomech. 2008, 5, 99–117. [Google Scholar] [CrossRef]
- Wang, T.; Lin, B.; Chong, B.; Whitman, J.; Travers, M.; Goldman, D.I.; Blekherman, G.; Choset, H. Reconstruction of backbone curves for snake robots. IEEE Robot. Autom. Lett. 2021, 6, 3264–3270. [Google Scholar] [CrossRef]
- Zeid, I. Mastering CAD/CAM, 1st ed.; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 2004. [Google Scholar]
- Sarcar, M.M. Computer Aided Design and Manufacturing, 1st ed.; Prentice-Hall of India Pvt. Ltd: Delhi, India, 2008. [Google Scholar]
- Pérez, L.H.; Aguilar, M.C.M.; Montés Sánchez, N.; Montesinos, A.F. Path Planning Based on Parametric Curves. In Advanced Path Planning for Mobile Entities; Róka, R., Ed.; IntechOpen: London, UK, 2017; pp. 125–143. [Google Scholar]
- Chirikjian, G.S.; Burdick, J.W. A modal approach to hyper-redundant manipulator kinematics. IEEE Trans. Robot. Autom. 1994, 10, 343–354. [Google Scholar] [CrossRef] [Green Version]
- Zanganeh, K.E.; Angeles, J. The inverse kinematics of hyper-redundant manipulators using splines. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 2797–2802. [Google Scholar] [CrossRef]
- Song, S.; Li, Z.; Yu, H.; Ren, H. Shape reconstruction for wire-driven flexible robots based on Bézier curve and electromagnetic positioning. Mechatronics 2015, 29, 28–35. [Google Scholar] [CrossRef]
- Collins, T.; Shen, W.M. PASO: An Integrated, Scalable PSO-Based Optimization Framework for Hyper-Redundant Manipulator Path Planning and Inverse Kinematics; Technical Report No. ISI-TR-697; Information Sciences Institute, University of Southern California (USC) Viterbi School of Engineering: Los Angeles, CA, USA, 2016. [Google Scholar]
- Espinoza, M.S.; Gonçalves, J.; Leitao, P.; Sánchez, J.L.G.; Herreros, A. Inverse kinematics of a 10 DoF modular hyper-redundant robot resorting to exhaustive and error-optimization methods: A comparative study. In Proceedings of the 2012 Brazilian Robotics Symposium and Latin American Robotics Symposium, Fortaleza, Brazil, 16–19 October 2012; pp. 125–130. [Google Scholar] [CrossRef] [Green Version]
- Gravagne, I.A.; Walker, I.D. Manipulability, force, and compliance analysis for planar continuum manipulators. IEEE Trans. Robot. Autom. 2002, 18, 263–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mochiyama, H.; Shimemura, E.; Kobayashi, H. Shape correspondence between a spatial curve and a manipulator with hyper degrees of freedom, In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Innovations in Theory, Practice and Applications, Victoria, BC, Canada, 17 October 1998; Volume 1, pp. 161–166. [Google Scholar] [CrossRef]
- Martin, A.; Barrientos, A.; Del Cerro, J. The natural-CCD algorithm, a novel method to solve the inverse kinematics of hyper-redundant and soft robots. Soft Robot. 2018, 5, 242–257. [Google Scholar] [CrossRef] [PubMed]

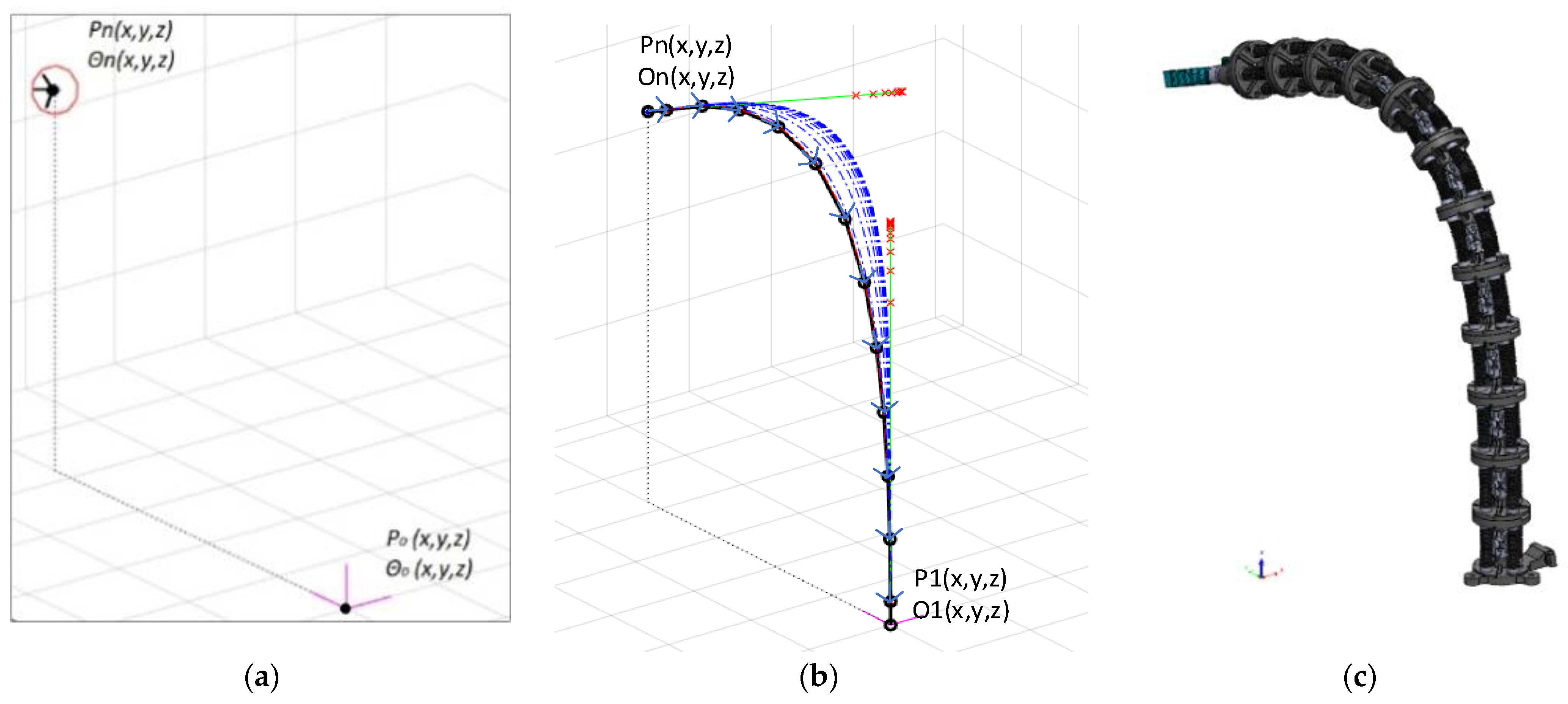









| I. Task Specifications | II. Robot Shape Planning | III. Shape Inverse Problem |
|---|---|---|
| Specifying the robot’s geometric characteristics, end-effector pose (position and orientation) and algorithm specific parameters. (See Figure 2a) | Based on the operational specifications, a candidate 3D Bézier parametric curve for modeling the shape of the robot is generated (A1). Further, the candidate curve is iteratively adjusted (BC of HRR) simultaneously with the reconstruction of an equivalent model of the robot (A2). (See Figure 2b) | For a particular robotic structure (here, a Python robot) and a planned 3D shape the joint displacements are determined (based on step 3 results). (See Figure 2c) |
| Experiment | (mm) | (mm) |
|---|---|---|
| Constant orientation for end −effector | 0.0012 | 0.00077 |
| Variable orientation for end −effector | 0.0019 | 0.00076 |
(mm) | Step 2 A1 Time (s) | Step 2 A2 Time (s) | Step 3.1 Time (s) | Step 3.2 Time (s) | Cycle Time (s) |
|---|---|---|---|---|---|
| 0.000384 | 0.000318 | 0.000054 | 0.000103 | 0.000859 | |
| 0.000403 | 0.000334 | 0.000055 | 0.000105 | 0.000897 | |
| 0.000391 | 0.000507 | 0.000055 | 0.000106 | 0.001059 | |
| 0.000441 | 0.0013 | 0.000060 | 0.000108 | 0.001909 | |
| 0.000490 | 0.0022 | 0.000062 | 0.000106 | 0.002858 | |
| 0.0011 | 0.0114 | 0.000061 | 0.000103 | 0.012664 | |
| 0.0022 | 0.0251 | 0.000062 | 0.000107 | 0.027469 |
(mm) | Cycle Time for HRR 18 DoF (s) | Cycle Time for HRR 24 DoF (s) | Cycle Time for HRR 30 DoF (s) | Cycle Time for HRR 36 DoF (s) |
|---|---|---|---|---|
| 0.000846 | 0.000859 | 0.001414 | 0.001414 | |
| 0.000867 | 0.000897 | 0.001649 | 0.001726 | |
| 0.001037 | 0.001059 | 0.001731 | 0.002053 | |
| 0.001665 | 0.001909 | 0.004247 | 0.004725 | |
| 0.002714 | 0.002858 | 0.006968 | 0.008511 | |
| 0.01012 | 0.012664 | 0.03328 | 0.041637 | |
| 0.02274 | 0.027469 | 0.064486 | 0.064486 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapusan, C.; Hancu, O.; Rad, C. Numerical Shape Planning Algorithm for Hyper-Redundant Robots Based on Discrete Bézier Curve Fitting. Machines 2022, 10, 894. https://doi.org/10.3390/machines10100894
Lapusan C, Hancu O, Rad C. Numerical Shape Planning Algorithm for Hyper-Redundant Robots Based on Discrete Bézier Curve Fitting. Machines. 2022; 10(10):894. https://doi.org/10.3390/machines10100894
Chicago/Turabian StyleLapusan, Ciprian, Olimpiu Hancu, and Ciprian Rad. 2022. "Numerical Shape Planning Algorithm for Hyper-Redundant Robots Based on Discrete Bézier Curve Fitting" Machines 10, no. 10: 894. https://doi.org/10.3390/machines10100894
APA StyleLapusan, C., Hancu, O., & Rad, C. (2022). Numerical Shape Planning Algorithm for Hyper-Redundant Robots Based on Discrete Bézier Curve Fitting. Machines, 10(10), 894. https://doi.org/10.3390/machines10100894







