Abstract
Pneumatic muscles have significant advantages over typical pneumatic cylinders, such as smooth speed adjustment, higher power-to-weight ratio and longer operating life. Applying a pneumatic artificial muscle is a way to considerably simplify manipulator mechanisms due to its physical properties. This paper deals with the development of positioning control principles of pneumatic artificial muscle drive and presents numerical and experimental investigations of different operation modes such as lifting and lowering a load under normal working conditions, operation in a case of a sudden load separation and position control by manual operator force. In this work, the mathematical model elaborated earlier was numerically and experimentally investigated. Experimental validation of static and dynamic characteristics confirmed the results of the theoretical studies, so the elaborated model can be used to design a PAM-based manipulator with required characteristics.
1. Introduction
In a general way, a pneumatic artificial muscle (PAM) is a linear single-acting actuator that consists of a rubber tube (bladder), surrounded [1] or reinforced [2] by a braided mesh shell with nonextensile threads and with two fittings on both sides. When a rubber tube is pressurized, its volume is increased. At the same time, the nonextensile threads prevent the volume increase, which leads to contraction of a rubber tube in the axial direction, and pneumatic muscle produces force.
Nowadays, there are many types of pneumatic artificial muscles. Commercial pneumatic muscles include FESTO fluidic muscles, Shadow Air Muscles and Rubbertuators; noncommercial pneumatic muscles include Yarlott and Kukolj [3]. Characteristics of commercial pneumatic muscles are presented in Table 1.

Table 1.
Characteristics of commercial PAMs.
It can be seen from Table 1 that FESTO fluidic muscle has the best characteristics for selection as an actuator of an industrial manipulator. FESTO fluidic muscle is a pneumatic artificial muscle that consists of a rubber tube reinforced by a braided mesh shell that is attached by fitting caps at the ends. If a FESTO fluidic muscle is used instead of a pneumatic cylinder, it is possible to exclude jerkiness at slow speeds and reduce the weight of the structure due to the high power-to-weight ratio (the mass of the FESTO fluidic muscle is lower than that of a pneumatic cylinder by 5–10 times with the same developed force). At the same time, both the pneumatic cylinder and the FESTO fluidic muscle are low-cost; can be used in dusty, humid, explosion-prone and radioactive environments; and have a wide range of working regimes and a high operating resource (up to 5 million cycles) [4]. In Table 2, a comparison between FESTO pneumatic cylinder DSBC and FESTO fluidic muscle DMSP-40 is presented. As can be seen from Table 2, the pneumatic muscle would produce 5 times more force than the pneumatic cylinder while having 5 times less mass at the same working pressure.

Table 2.
Comparison between pneumatic cylinder DBSC and FESTO fluidic muscle.
Due to the advantages of pneumatic muscle, many works deal with the design of the PAM-based systems and their implementation in industrial equipment. The main part of PAM-based system design is the elaboration of an exact mathematical model of pneumatic muscle.
There are many works dedicated to the elaboration of the static force of PAM. There are two main types of mathematical models of static force: the expressions obtained by geometric parametrization and the empirical expressions consisting of adjusting factors. The expressions obtained in the course of geometric parametrization [1,5,6,7] are discrepant with the experimental curves presented in the FESTO catalog [4], in some cases by up to 50%. Such expressions are not suitable for modeling FESTO fluidic muscles. The empirical expressions of the authors of [8,9,10,11] contain many correction factors (from 6 to 21) and are not universal for any length of the bladder and the operating mode of FESTO fluidic muscles. So, a new model of the static force of PAM was elaborated earlier in [12].
Developing a mathematical model of pneumatic muscle is a complex task due to the nonlinear working behavior of the pneumatic artificial muscle. Nonlinearities are caused by the properties of the bladder of pneumatic muscle and mesh shell and the compressibility of air. Many works deal with the modeling of hysteresis of pneumatic artificial muscle to eliminate its influence on the work of the system [13]. In order to obtain high positioning accuracy, many authors elaborated control systems of PAM-based drive with different control approaches [14,15,16,17,18,19]. For example, in [16], the authors developed a McKibben muscle manipulator with a new position control method with a hybrid (PID+MRAC) adaptive controller. In [17], the control system of agonist–antagonist pairs of pneumatic artificial muscles with an iterative linear quadratic regulator (iLQR) was presented. In [18,19], a position-tracking control system with nonlinear controllers was implemented in a pneumatic muscle system.
Experimental validation and numerical modeling confirm that the control methods presented in these studies help to improve the performance of the pneumatic muscle drive in industrial manipulators and robots. However, the realization of these methods can lead to the application of difficult mathematical modeling and implementation of electro-pneumatic equipment that would decrease the safety of the manipulator and make the control system more complex. Such control systems are not always required for many industrial tasks (for example, lifting or lowering a load). In the industry, manipulators with manual control are widespread. An operator can realize position control of the loading arm by the commands expressed by pressing relevant control buttons of the direct control valve and by applying the manual force on the load [20,21]. In this paper, the possibility of realization of positioning by operator manual force in PAM-based manipulators was proven.
In [22], the industrial manipulators based on FESTO fluidic muscles are analyzed and their drawbacks are identified: using expensive electro-pneumatic equipment [14,15], building a complex system for operation both in regular mode and in a mode with changing the external load [14,15] and not providing automatic leading or balancing of the loading arm at the set positioning point [23]. The kinematic and pneumatic schemes of PAM-based manipulators with FESTO fluidic muscle that eliminate these shortcomings were presented in [22].
Due to the actuator properties shown above, manipulators based on pneumatic artificial muscles have advantages such as lower weight and more safety for the operator and environment than manipulators based on pneumatic cylinders. The force of pneumatic muscle is decreased at the end of the stroke [4], so the loading arm of PAM-based manipulators does not need damping devices under normal working conditions. However, an emergency working mode such as a sudden load separation can lead to a high acceleration of the output link. Some works deal with this problem [15,24], but presented solutions make control systems more complex or lead to the application of hydraulic systems that are more expensive than pneumatic systems. In this paper, we propose the implementation of a hydraulic damper in PAM-based manipulators and show the effectiveness of this solution.
So, the main aims of this work are to investigate the position method using manual operator force and braking method with the hydraulic damper in the case of a load separation, to validate the mathematical model presented earlier [12,22] and to give recommendations for its further application in PAM-based manipulator design.
Section 2 presents the analytical dependence of the static force of the pneumatic artificial muscle elaborated earlier. It also describes the developed dynamic model of the pneumatic artificial muscle given the change in the geometry of the mesh shell and the diameter and rigidity of the shell in the process of contraction of the pneumatic artificial muscle. In addition, the mathematical model of pneumatic artificial muscle-actuated drive for an industrial manipulator that is based on the dynamic model of the pneumatic artificial muscle is given. ln Section 3 the results of mathematical modeling are discussed. The position control method by manual operator force and the braking method in the case of a sudden load separation are proposed and investigated. In addition, Section 4 discusses the experimental validation of the analytical model of static force and the dynamic model of the pneumatic artificial muscle. Section 5 presents conclusions.
2. Methods
2.1. Model of the Static Force of the PAM
Figure 1a shows that after compressed air is supplied, the cell of the pneumatic muscle mesh shell is affected by lateral force FLAT and longitudinal force FLONG. The action of these forces deforms the cell in the cross direction, straining the cell height r0 by value ΔyLAT, and in the longitudinal direction, reducing the cell length l0 by value ΔxLONG, and changes the mesh angle α0. The cell height becomes equal to rinf, and the cell length becomes equal to linf.
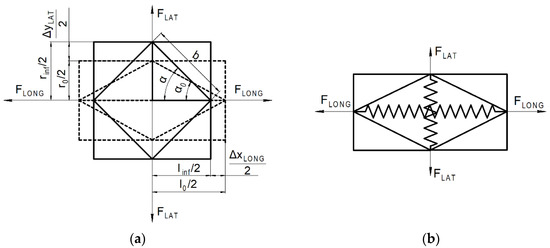
Figure 1.
The cell of the mesh shell of the pneumatic muscle: (a) changed geometrical dimensions before (dashed line) and after pressure supply (solid line); (b) cell with springs.
Differently from the existing models of the pneumatic muscle, in addition to the lateral and longitudinal forces, elastic deformation force considering the rigidity of the material of the bladder was taken into account. In order to consider the elastic deformation force, the cell was represented in the form of two springs located perpendicularly to each other (Figure 1b). The rigidities of the cell in the directions towards the perimeter and along the length were expressed through specific rigidity c0. A detailed description of the static force model is presented in [12].
When simulating the static force, the following assumptions were made: the pneumatic muscle was considered as a bladder having an ideal cylinder shape with zero thickness of the wall, and the threads of the mesh shell were defined as inextensible.
For better convergence with the results of the experiment obtained by FESTO company, the developed analytical dependence was adapted with some adjusting factors being introduced to the equation that describes the rigidity of the bladder as a function of pressure c(p). As a result, the following model for the static force of the pneumatic muscle was obtained [12]:
where T is the force exerted by the pneumatic muscle, x is the length contraction (load displacement) of the bladder, D0 is the initial diameter of the bladder, D is the diameter of the bladder after pressure is supplied, L0 is the initial length of the bladder, α0 is the initial mesh angle, α is the mesh angle after pressure is supplied, is the rigidity of the bladder, r and q are the adjusting factors, is the atmospheric pressure and is the supply line pressure.
The adjusting factors for all typical sizes of FESTO muscle are presented in Table 3. The factors were adjusted according to the experimental curves presented in the FESTO catalog [4].

Table 3.
Values of adjusting factors.
In order to verify model (1) for static force T, the curves showing the dependences of the exerted force on the relative contraction of the bladder were obtained and compared to the experimental curves presented in the catalog of FESTO company [4].
Figure 2a illustrates that the discrepancy between theoretical results obtained using the Tondu and Lopez model [5] and experimental curves of the static force of FESTO fluidic muscle is up to 50%. Figure 2b shows that the elaborated model (1) allows obtaining static characteristics with up to 10% for working pressure p = 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 MPa.

Figure 2.
Dependence of the pneumatic muscle force on the relative contraction for DMSP-10: black line at p = 0.1 MPa, violet line at p = 0.2 MPa, orange line at p = 0.3 MPa, brown line at p = 0.4 MPa, yellow line at p = 0.5 MPa, green line at p = 0.6 MPa, blue line at p = 0.7 MPa, red line at p = 0.8 MPa; (a) dashed curves represent the FESTO experiment, solid curves represent the calculation results for model presented in [5]; (b) dashed curves represent the FESTO experiment, solid curves represent the calculation results for elaborated model (1).
The obtained analytical expression of the pneumatic muscle force is different from those developed by other authors because:
- It considers the change in the mesh angle and diameter of the bladder after pressure is supplied;
- It considers the rigidity of the material of the bladder;
- It shows the divergence of the predicted curves with the experimental data of FESTO within 10%.
2.2. Dynamic Model of the PAM
The dynamic model of the pneumatic artificial muscle is based on the static model of the PAM (1). It represents a system of differential equations, which consists of:
- The equation of movement of the pneumatic muscle;
- The equation of pressure change in the bladder;
- The equations describing the change in the force, volume, diameter, mesh angle and rigidity of the bladder.
The equation of the pneumatic artificial muscle motion is as follows [12]:
where m is a load mass, T is the force generated by the pneumatic muscle, g is the acceleration of gravity (g = 9.8 m/s2) and h is the damping coefficient.
Modeling the dynamic behavior of the pneumatic actuators is a complex task [25,26,27], so the following assumptions were accepted:
- Gas dynamic processes in the bladder are quasi-stationary;
- Temperature and pressure of the gas in the supple line are constant;
- Gas leakage is neglected;
- The process of gas flow is isothermal;
- Heat transfer is neglected.
The dynamic behavior of the pneumatic muscle is based on the pressure change in the bladder. The pressure change was derived with the help of the gas conservation law (first law of thermodynamics) and the equation for ideal gases (Clapeyron–Mendeleev’s law) [25].
The equation of pressure change in the bladder when it is filled or emptied can be written as:
where is the air pressure in the supply line, p is the pressure in the bladder, k is the adiabatic coefficient for air (k = 1.4), f is the area of the pneumatic line (f = πd2/4, where d is the inlet port diameter), R is the gas constant (R = 287 J/(kg·K), TS is the air temperature in the supply line, ζ is the resistance factor of the line, V is the volume of the pneumatic muscle bladder after pressurization and a1 is the logical factor that determines the nature of the dynamic pneumatic process in the pneumatic muscle. When a1 = 1, the pneumatic muscle is filled; when a1 = 0, it is emptied.
The expression for the change in the volume V of the bladder is as follows:
The developed model (1)–(4) is used to investigate the mode of load positioning by the operator force, which is described in Section 3. Table 4 presents the initial parameters for numerical modeling. The resistance factor of the line is chosen from [25].

Table 4.
The initial parameters for numerical modeling of the operator force static characteristics.
2.3. Dynamic Model of the Pneumatic Artificial Muscle-Actuated Drive for an Industrial Manipulator
Figure 3a shows the working principle of the PAM-based drive during lifting and lowering a load. Initial parameters are D0, L0, α0 and V0; parameters after pressurization are D, L, α and V; x is the required coordinate. The compressed air delivered to a bladder and the PAM produces force T and overcomes FLOAD which consists of moving parts of the manipulator and a load mass.

Figure 3.
The schemes of the PAM-based drive: (a) principle of operation of the PAM-based drive; (b) the kinematic scheme of the PAM-based manipulator; (c) the calculation model for the mode of load positioning by the operator force.
In [22], the kinematic scheme of the manipulator was chosen (Figure 3b). The following designations are accepted in the scheme: 1—rigid support; 2—PAM actuator; 3, 4, 5, 6—links of the loading arm, A, B, C, D; 7—joints; 8—vertical guide; 9—horizontal guide; N—a load fixed on the point E; XM—required height. When pneumatic artificial muscle 2 is pressurized with compressed air and contracts, joint 7 in guide 8 moves down. Links 5 and 6 rotate around joint D, and point E moves up with load N to the required height XM. Link 4 moves up and displaces joint D to the right in guide 9.
The mathematical model of a pneumatic muscle-actuated system for a balanced manually operated PAM manipulator is based on the dynamical model (1)–(4) and is given as follows:
where mM is the mass of moving parts of the manipulator, m is a load mass, K is the transmission force coefficient, LBC is the length of the BC link and LCE is the length of the CE link.
The following expressions of the position coordinate XM of the manipulator arm and the velocity are obtained:
The dynamic model (5)–(7) was used to investigate the following operating modes:
- The mode of lifting and lowering a load;
- The emergency operating mode of the manipulator in the case of a sudden separation of a load.
Numerical investigation of dynamic characteristics was performed in the MATLAB/Simulink environment with the Dormand–Pride method (Ode45) with an adoptive integration step of 0.0001 s. Models of the PAM-based manipulator and the PAM-based drive in the MATLAB/Simulink environment are presented in [22]. Table 5 presents the initial parameters for numerical modeling.

Table 5.
Initial parameters for numerical modeling of dynamic characteristics of the manipulator.
3. Results and Discussion
3.1. Numerical Investigation of the Dynamic Characteristics of the PAM-Based Manipulator
Figure 4 and Figure 5 show the dynamic responses of the manipulator arm under normal working conditions. The initial parameters are presented below in Table 5. The input times for the lifting and lowering command values were 0 s and 4 s, respectively.

Figure 4.
Dynamic responses of the loading arm displacement during lifting and lowering a load.
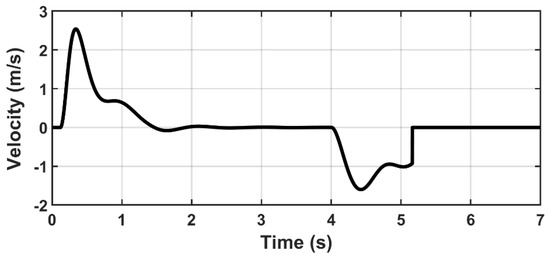
Figure 5.
Dynamic responses of the loading arm velocity during lifting and lowering a load.
From these diagrams, we can estimate the maximum displacement (1.25 m), maximum velocity of the loading arm (2.5 m/s) and time of lifting and lowering a load (1.4 s and 1.26 s).
3.2. Numerical Investigation of the PAM-Based Manipulator with Hydraulic Damper
As mentioned above, it is necessary to investigate the emergency work of a PAM-based manipulator in the case of a sudden load separation. The initial parameters of numerical modeling are presented in Section 2 in Table 5. The time of a sudden load separation is 3 s.
It can be seen from Figure 6 (red line) that a sudden load separation causes a high velocity of the loading arm (X’M = 5.7 m/s for m = 30 kg) and can involve damage to the operator and environment. So, the braking method of the manipulator arm was proposed and investigated.

Figure 6.
Dynamic response of the PAM manipulator arm velocity for the case without a hydraulic damper (red line) and the case with a hydraulic damper (blue line).
Hydraulic dampers are widely used in pneumatic drives for reducing oscillation and decreasing the velocity of the output link. As shown in Figure 7, the pneumatic artificial muscle can be rigidly fixed with the rod of the hydraulic damper filled with a medium of oil.

Figure 7.
The scheme of PAM-based drive with hydraulic damper.
When the pneumatic artificial muscle contracts, the rod of the hydraulic damper moves down, presses oil in the reservoir and produces damping force PD.
The equation of the damping force PD is as follows:
where k1 is the damping coefficient, which depends on the hydraulic damper construction. The value of the damping coefficient k1 was 1300 N·s2/m.
Equation (2) of the pneumatic artificial muscle motion according to Figure 7 is as follows:
The results of numerical modeling are also depicted in Figure 6 (blue line). As we can see, the application of a hydraulic damper shows effectiveness in decreasing the velocity of the loading arm of the PAM-based manipulator. The velocity is decreased from 5.7 m/s to 1.5 m/s.
3.3. The Mode of Load Positioning by Manual Operator’s Force
Aside from control by directional valves with manual or mechanical actuation, the position error, Δx, of the loading arm can be corrected by operator manual force as shown in Figure 3c. This type of position control is often applied in industrial pneumatic manipulators [20,21].
However, the realization of this control method in PAM-based manipulators can be difficult due to the relationship between the load position of the manipulator arm and the pressure in the pneumatic artificial muscle. The static characteristics of operator force were investigated for typical size DMSP-40, different working regimes (pressure in the bladder p), lengths of the bladder and load masses. The initial parameters are presented below in Table 4.
According to calculation model in Figure 3c, the operator applies manual force Q to the actuator, so the equation of pneumatic artificial muscle motion (2) can be written as follows:
Initial conditions for numerical modeling were presented earlier in Section 2. The maximum value of operator force according to the standard [28] is QMAX = 50 N. The results of modeling are presented in Figure 8, Figure 9 and Figure 10. Positive values of the position error correspond to the positive direction of the operator force (operator lifts the load up). Negative values of the position errors correspond to the negative direction of the operator force (operator lowers the load down).

Figure 8.
Diagram of correlation between the operator force and a load position error Δx: red line for L0 = 1.5 m; dashed line for L0 = 2.0 m; blue line for L0 = 3.0 m.

Figure 9.
Diagram of correlation between the operator force and relative position error: red line for p = 0.6 MPa, dashed line for p = 0.4 MPa, blue line for p = 0.2 MPa.

Figure 10.
Diagram of correlation between the operator force and relative position error: solid line for m = 200 kg, dashed line for m = 150 kg, dotted line for m = 100 kg.
Figure 8 shows the diagrams of the correlation between the operator force and position error for different lengths of the bladder for load position coordinate 0.2 m. The values of position error, Δx, were −10, −5, −1, 1, 5 and 10. As can be seen from Figure 8, the operator can correct position error in a wide range for the initial length of the bladder L0 = 3.0 m (from −20 mm to 20 mm) and for the initial length L0 = 2.0 m (from −12.0 mm to 12.0 mm).
It can be concluded that the value of operator force depends on the initial length of the PAM bladder. So, the dimensionless relative position error Δxrel is incorporated:
Figure 9 and Figure 10 illustrate the results of numerical modeling of the correlation of operator force and relative position error for different working pressures and different load masses. Figure 9 shows that the lowest pressure working regimes provide the highest positioning range. The maximum position range was obtained for p = 0.2 MPa (from −0.7% to 0.8%). Figure 10 shows that operator can correct position error for large load masses (from −0.5% to 0.5% for m = 100 kg, from −0.45% to 0.45% for m = 150 kg, from −0.3% to 0.3% for m = 200 kg). The numerical results are universal for any length of PAM bladder. So, the model helps estimate the length of a bladder for the required position error range that the operator can correct.
Similar results can be obtained for other typical sizes of FESTO fluidic muscle and parameters (lengths, working pressures and load masses). It can be concluded that the operator can correct the position error in a wide range with an operator manual force of up to 50 N.
4. Experimental Validation
Experiments were carried out to investigate the static and dynamic characteristics of the pneumatic artificial muscle and validate results obtained by the mathematical model (1)–(4) discussed above. Figure 11 shows the image of the experimental setup.

Figure 11.
Experimental setup for studying the static and dynamic characteristics of the pneumatic muscle: (1) pneumatic artificial muscle; (2) motion sensor; (3) load; (4) pneumatic control valve; (5) pressure sensor; (6) air preparation unit; (7) analog–digital converter; (8) PC.
The main part of the experimental setup is the pneumatic artificial muscle FESTO DMSP-10-400NPM-CM. The pneumatic artificial muscle has an initial diameter of 10 mm and an initial length of 400 mm. The range of working pressure is 0–0.9 MPa and the maximum relative contraction is 25%; the maximum force output is 1500 N. The pneumatic artificial muscle was oriented vertically with a load attached to the moving end. Compressed air was supplied to the system by a power unit JUN-AIR compressor, model 625. The level of pressure was adjusted by the air preparation unit FESTO LFR QS45M-MICRO. Pneumatic on/off valve with pushbutton FESTO D:S-PSV-3/2-S-3+S controlled the flow in the bladder of the pneumatic muscle. It has a maximum flow rate of 65 L/min. The experimental data of contraction of the pneumatic muscle were collected by the linear displacement transducer TWK D-40041 RP 12/300 with a measuring stroke of 300 mm and operating speed of 1.5 m/s. The lower end of the pneumatic artificial muscle was rigidly fixed with the rod of the linear displacement transducer. The pressure sensor FESTO SDE1-D10-G2-H18-C-PU-M8 measured the pressure in the bladder of the pneumatic artificial muscle. The measuring pressure range in the bladder was 0–0.7 MPa and corresponded to the analog output of 0–10 V. The data from the sensors were sent to the analog–digital converter HIOKI LRB431-20 that provided 10 ms sampling and a 10-channel logger, with operating environment Windows 10/8/7 (32 bit/64 bit), Vista (32 bit/64 bit), XP (with SP2 or later) (32 bit). The analog–digital converter was connected to a PC by USB cable. The PC communicated with the converter using a special HIOKI program as an interface. The initial parameters of pneumatic muscle were as follows: pressure inside the bladder was 0 MPa, contraction of the bladder was 0% and produced force was 0 N. The measurements were performed at a temperature of 23 °C. Figure 12 illustrates the crucial scheme of the experimental setup.

Figure 12.
The crucial pneumatic scheme of the experimental setup.
4.1. Experimental Validation of the Analytical Model of Static Force
These experimental studies were performed for the working pressures in the range of 0–0.7 MPa and for the load masses 2.5, 5.0 and 7.5 kg. Eight constant levels of pressure were set by the air preparation unit, so the experimental curves were sampled in eight points. One of the constant loads was attached at the lower end of the pneumatic artificial muscle. After the operator pushed the command button of a pneumatic valve, the PAM inflated and the bladder contracted and lifted the constant load. Then, after the operator released the button, the PAM deflated and lowered the load. The bladder contraction was measured by the linear displacement transducer. Data were sampled by the analog–digital converter.
Figure 13, Figure 14 and Figure 15 also show the comparison between experimental and predicted (theoretical) curves (dashed line).

Figure 13.
Diagram of correlation between the length contraction and working pressure for m = 2.5 kg: dashed line for theoretical modeling, blue line for experimental results of lifting a load, red line for experimental results of lowering a load.

Figure 14.
Diagram of correlation between the length contraction and working pressure for m = 5.0 kg: dashed line for theoretical modeling, blue line for experimental results of lifting a load, red line for experimental results of lowering a load.
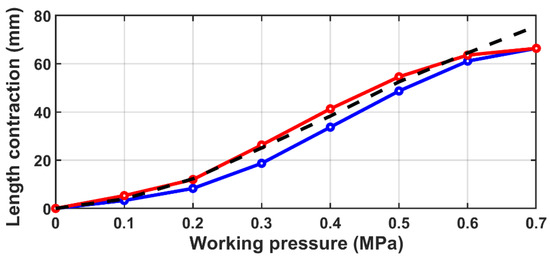
Figure 15.
Diagram of correlation between the length contraction and working pressure for m = 7.5 kg: dashed line for theoretical modeling, blue line for experimental results of lifting a load, red line for experimental results of lowering a load.
The experimental data and theoretical results of the length contraction–pressure relationship for three load masses are given in Table 6. In Table 6, the following designations are assumed: x—theoretical length contraction; xi—length contraction during inflation process; xd—length contraction during deflation process.

Table 6.
Experimental data and theoretical results of length contraction–pressure relationship.
Figure 13, Figure 14 and Figure 15 illustrate the hysteresis loop of the length contraction–pressure relationship. The blue line corresponds to the process of lifting a load (inflation of the bladder) and the red line corresponds to lowering a load (deflation of the bladder). The experimental results show that the hysteresis loop maximum height is about 12.7 mm and width is about 0.07 MPa for load mass 2.5 kg, maximum height is about 12.1 mm and width is about 0.07 MPa for load mass 5.0 kg, and maximum height is about 7.6 mm and width is about 0.04 MPa for load mass 7.5 kg.
From Figure 13 it can be seen that the theoretical results have satisfactory convergence at the working pressures 0.4, 0.5, 0.6 and 0.7 MPa for the inflation and deflation process (maximum discrepancy is 13.54% for the inflation process at the working pressure 0.4 MPa). The model has bad convergence for the inflation process at the low working pressures of 0.1, 0.2 and 0.3 MPa.
Similar to the previous results, the model has bad convergence for the inflation process at the low pressures of 0.1, 0.2 and 0.3 MPa for a load mass of 5.0 kg, as depicted in Figure 14. Results obtained from numerical modeling have satisfactory convergence with experimental results at the high working pressures of 0.4, 0.5, 0.6 and 0.7 MPa (maximum discrepancy is 14.72% at the working pressure of 0.7 MPa).
As shown in Figure 15, the theoretical results for the load mass of 7.5 kg have satisfactory convergence with experimental results for working pressures of 0.4, 0.5, 0.6 and 0.7 MPa (maximum convergence is 13.64% for the inflation process at the working pressure of 0.4 MPa) and bad convergence for inflation process at the low working pressures of 0.1, 0.2 and 0.3 MPa.
4.2. Experimental Validation of the Dynamic Model of Pneumatic Artificial Muscle
Experimental studies of dynamic characteristics were accomplished at the working pressure of 0.7 MPa and at load masses of 2.5, 5.0 and 7.5 kg. Load mass was attached at the lower end of the PAM. The desired level of pressure was adjusted by the air preparation unit. Dynamic responses for the contraction of the bladder were measured from the linear displacement transducer. The results are shown in Figure 16, Figure 17 and Figure 18.

Figure 16.
Dynamic responses of the actuator: black line—theoretical results; red line—experimental results for m = 2.5 kg.

Figure 17.
Dynamic responses of the actuator: red line—theoretical results; blue line—experimental results for m = 5.0 kg.

Figure 18.
Dynamic responses of the actuator: black line—theoretical results; red line—experimental results for m = 7.5 kg.
Figure 16, Figure 17 and Figure 18 show that discrepancies between predicted and experimental curves obtained by model (1)–(4) are 15.43% for the load mass of 2.5 kg, 14.47% for the load mass of 5.0 kg and 12.95% for the load mass of 7.5 kg.
Despite the discrepancy, the elaborated model shows the correct representation of the nature of the processes of length contraction of the bladder. The experimental curves of the dynamic response of a load displacement have the same slope as the calculated characteristic, which indicates that the model correctly takes into account both the processes in the pneumatic system and the processes occurring in the bladder.
The discrepancy with the experimental data of both static and dynamic characteristics is up to 14%. However, earlier the task was to simplify the mathematical model of the pneumatic muscle for its application in the design of industrial manipulators for operations that do not require high accuracy [23]. The model has a minimum number of correction coefficients and does not take into account such phenomena in the shell as hysteresis, which also affected its accuracy. However, in this work, the mode of positioning by the manual effort of the operator was studied, and it was found that the operator will be able to correct the load position error by applying a small force (within 50 N with correctly selected parameters of the PAM-based drive).
5. Conclusions
- The application of the elaborated pneumatic schemes and chosen kinematic scheme in a balanced PAM-type manipulator allows the operations of lifting, lowering, positioning, fixation and balancing of a load in vertical and horizontal planes at any point in the work zone.
- Mathematical investigations have shown that position control of the loading arm with manual operator force can be applied to the PAM-based industrial manipulator. The operator can correct the position of a loading arm without the implementation of a complex control system and expensive electro-pneumatic equipment;
- In addition, modeling of the proposed braking method shows that the implemented hydraulic damper would decrease the velocity of the loading arm in case of a sudden load separation.
- The elaborated model shows satisfactory convergence with experimental data (less than 14.0% for static curves of lifting and lowering a load at working pressures of 0.4, 0.5, 0.6 and 0.7 MPa, less than 16.0% for dynamic response of the load displacement). As discussed above, the discrepancy of measures appears due to the features of the bladder material. In future works, we will investigate the dependence of the damping coefficient and rigidity of the bladder material on various factors: load mass and working pressure. Despite the discrepancy, this model can be applied for designing industrial manipulators for operations that do not require high accuracy;
- The presented mathematical model allows estimating parameters of the actuator (length, diameter, working pressure) to design a PAM-based industrial manipulator with the required characteristics (displacement and velocity of the loading arm, load mass, positioning range).
Author Contributions
Conceptualization, A.D., L.K. and N.Z.; methodology, A.D.; software, N.Z. and L.K.; validation, L.K.; formal analysis, A.D. and L.K.; investigation, L.K.; resources, A.Z.; data curation, A.Z.; writing—original draft preparation, L.K.; writing—review and editing, N.Z. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Peter the Great St. Petersburg Polytechnic University and under the strategic academic leadership program ‘Priority 2030’ of the Russian Federation (Agreement 075-15-2021-1333 dated 30 September 2021).
Institutional Review Board Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chou, C.P.; Hannaford, B. Measurement and modelling of McKibben pneumatic artificial muscle. IEEE Trans. Robot. Autom. 1996, 6, 90–102. [Google Scholar] [CrossRef]
- Actuating Means. US Patent No. US63497476 B1, 2002.
- Daerden, F.; Lefeber, D. Pneumatic artificial muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 11–211. [Google Scholar]
- Festo. Corporation. Available online: http://www.festo.com (accessed on 4 August 2022).
- Tondu, B.; Lopez, P. Modelling and control of McKibben artificial muscle robot actuators. IEEE Control Syst. Mag. 2000, 20, 15–38. [Google Scholar]
- Kerscher, T.; Albiez, J.; Zollner, J.M.; Dillmann, R. Evaluation of the dynamic model of fluidic muscles using quick release. In Proceedings of the 2003 European Control Conference (ECC), Cambridge, UK, 1–4 September 2003. [Google Scholar]
- Sharovatov, V.T.; Loshitskiy, P.A. Mathematical model of a power roadless single acting shell-type pneumatic cylinder. Mechatron. Autom. Control 2011, 2, 30–36. [Google Scholar]
- Sarosi, J. New approximation algorithm for the force of fluidic muscles. In Proceedings of the 7th IEEE International Symposium on Applied Computational Intelligence and Informatics (SACI 2012), Timisoara, Romania, 22–24 May 2012. [Google Scholar]
- Joupilla, V.T.; Gadsden, S.A.; Ellman, A. Modelling and identification of a pneumatic muscle actuator system controlled by an ON/OFF solenoid valve. In Proceedings of the 7th International Fluid Power Conference, Aachen, Germany, 22–24 March 2010. [Google Scholar]
- Hildebrandt, A.; Sawodny, O.; Neumann, R.; Hartmann, A. Cascade control concept of a robot with two degrees of freedom driven by four artificial pneumatic muscle actuators. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005. [Google Scholar]
- Hosovsky, A.; Havran, M. Dynamic modelling of one degree of freedom pneumatic muscle actuator for industrial applications. Teh. Vjestn. 2012, 3, 673–681. [Google Scholar]
- Donskoj, A.; Kotkas, L.; Salova, T.; Barilovich, V.; Girshov, V.; Mertens, K.; Cherkesov, G.; Fokin, G.; Akhmetova, I. Modelling the static and dynamic characteristics of pneumatic muscle. In Proceedings of the IOP Conference Series: Earth and Environmental Science, St. Petersburg, Russia, 13–14 December 2018. [Google Scholar]
- Shin, T.; Lbayashi, T.; Kogiso, K. Detailed Dynamic Model of Antagonistic PAM System and its Experimental Validation: Sensor-less Angle and Torque Control with UKF. IEEE/ASME Trans. Mechatron. 2022, 27, 1715–1726. [Google Scholar] [CrossRef]
- Ahn, K.K.; Chau, N.U.T. Intelligent switching control of pneumatic muscle robot arm using learning vector quantization neural network. Mechatronics 2007, 17, 255–262. [Google Scholar] [CrossRef]
- Ahn, K.K.; Thahn, T.D.C. Performance improvement of pneumatic artificial muscle manipulators using magneto-rheological brake. J. Mech. Sci. Technol. (KSME Int. J.) 2005, 19, 778–791. [Google Scholar] [CrossRef]
- Bomfim, M.H.S.; Lima, I.I.E.J.; Monteiro, N.S.; Sena, V.A. A new approach for hybrid (PID + MRAC) adaptive controller applied to two-axes McKibben muscle manipulator: A mechanism for human robot collaboration. Ind. Robot 2021, 48, 836–845. [Google Scholar] [CrossRef]
- Kumari Hari Shankar Lal Das, G.; Tondu, B.; Forget, F.; Manhes, J.; Stasse, O.; Soueres, P. Controlling a multi-joint arm actuated by pneumatic muscles with quasi-DDP optimal control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Muller, D.; Raisch, A.; Hildebrandt, A.; Sawodny, O. Nonlinear Model based Dynamic Control of Pneumatic driven Quasi Continuum Manipulators. In Proceedings of IEEE/SICE International Symposium on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020. [Google Scholar]
- Ba, D.X.; Dihn, T.Q.; Ahn, K.K. An integrated intelligent nonlinear control method for a pneumatic artificial muscle. IEEE/ASME Trans. Mechatron. 2016, 21, 1835–1845. [Google Scholar]
- Adrianov, Y.D.; Bobrikov, E.P.; Goncharenko, V.I. Applying of the robots and manipulators for automatization and mechanization for handling material operations. In Robotic Technology; Popov, E.P., Yurevich, E.I., Eds.; Machinostroenie: Moscow, Russia, 1984; pp. 166–209. [Google Scholar]
- Romanov, P.I. Current state of development of balanced manipulators. In Development of Scientific Foundations of General Assembly Mechanization of Forestry Machines Technological Equipment; SPbLTA: St. Petersburg, Russia, 2001; pp. 25–43. [Google Scholar]
- Kotkas, L.; Zhurkin, N.; Donskoj, A.; Zharkovskij, A. Mathematical modelling of balanced manually operated pneumatic artificial muscle manipulator in Matlab/Simulink environment. In Proceedings of the International Conference on Dynamics and Vibroacoustics of Machines (DVM), Samara, Russia, 16–18 September 2020. [Google Scholar]
- Dolgih, E.V. Manipulator for Operations Related to Changing the Position of the Workpiece or Item in Space. RU 118 578 U1. Russian Federation, 20212. Bull. No. 21. Available online: https://patents.s3.yandex.net/RU118578U1_20120727.pdf (accessed on 4 August 2022).
- Feng, Y.; Ide, T.; Nabae, H.; Endo, G.; Sakura, R.; Ohno, S.; Suzumori, K. Safety-enhanced control strategy of a power soft robot driven by hydraulic artificial muscles. Robomech J. 2021, 8, 10. [Google Scholar] [CrossRef]
- Donskoj, A.S. Mathematical Modelling of Processes in Pneumatic Drives; SPbPU: St. Petersburg, Russia, 2009; pp. 31–41. [Google Scholar]
- Shcherba, V.E.; Blinov, V.N.; Paramonov, A.M.; Rybak, A.T.; Grigor’ev, A.V.; Lobov, I.E. Analysis of the influence of volumes of receivers and diameters of connecting fluid pipelines on piston hybrid power machine working processes based on use of gas pressure fluctuations in discharge line. Chem. Pet. Eng. 2018, 54, 425–430. [Google Scholar] [CrossRef]
- Shcherba, V.E.; Zanin, A.V.; Nosov, E.Y.; Paramonov, A.M.; Blinov, V.N. Calculation of compression and discharge processes in a two-stage hybrid piston power machine with liquid piston. Chem. Pet. Eng. 2019, 55, 632–641. [Google Scholar] [CrossRef]
- GOST EN 1005-3-2005; Safety of Machinery. Human Physical Performance. Part 3. Recommended Force Limits for Machinery Operation. CRC Press: Boca Raton, FL, USA, 2005.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).