Safety Control Architecture for Ventricular Assist Devices

Abstract

In patients with severe heart disease, the implantation of a ventricular assist device (VAD) may be necessary, especially in patients with an indication for heart transplantation. For this, the Institute Dante Pazzanese of Cardiology (IDPC) has developed an implantable centrifugal blood pump that will be able to help a diseased human heart to maintain physiological blood flow and pressure. This device will be used as a totally or partially implantable VAD. Therefore, performance assurance and correct specification of the VAD are important factors in achieving a safe interaction between the device and the patient’s behavior or condition. Even with reliable devices, some failures may occur if the pumping control does not keep up with changes in the patient’s behavior or condition. If the VAD control system has no fault tolerance and no system dynamic adaptation that occurs according to changes in the patient’s cardiovascular system, a number of limitations can be observed in the results and effectiveness of these devices, especially in patients with acute comorbidities. This work proposes the application of a mechatronic approach to this class of devices based on advanced control, instrumentation, and automation techniques to define a method to develop a hierarchical supervisory control system capable of dynamically, automatically, and safely VAD control. For this methodology, concepts based on Bayesian networks (BN) were used to diagnose the patient’s cardiovascular system conditions, Petri nets (PN) to generate the VAD control algorithm, and safety instrumented systems to ensure the safety of the VAD system.

1. Introduction

A ventricular assist device (VAD) has the main function of helping the patient with heart failure to lead a relatively normal life, despite the disease. This blood pump can be used in several cases: during the period the patient is waiting for a heart transplant; during a pre- or postoperative recovery period, or as a destination therapy when the patient has no indication for heart transplantation due to immunological incompatibility, chronic infections, or advanced age [1,2]. VAD projects involve several research areas, such as: mechanical and electromechanical engineering, biomaterials, medicine, and computer technologies for data collection, processing, and decision making. Therefore, sensors are needed to indicate blood pressure, blood flow, body temperature, and heart rate [3]. Two aspects should be taken into account:

• First: the device must perform effectively and accurately; otherwise, if the pump fails during operation and there is no control system capable of interpreting and autonomously handling failures, serious risks to the patient are inevitable [4]. Medical equipment should provide personalized care to reduce such risks [5];
• Second: many VADs keep the blood flow constant regardless of the patient’s daily needs, they assist the blood circulation, and do not react adequately to changes in the patient’s behavior [6]. If the patient is at rest and needs to perform physical activity, the patient’s heart automatically changes its behavior, pumping more blood, but some VADs do not follow the need of the patient’s circulatory system by keeping the rotation speed of the VAD fixed.

1.1. Evolution of VADs

With the technological evolution that can be applied in the design of VADs, the use of electric motors to drive blood pumps is highlighted. During the initial phase of the use of these actuators, the rotation control system was focused only on maintaining a reference rotation. Later, control algorithms were developed that could be reconfigured in terms of set-point variation [3,7,8,9]. Although this evolution was very interesting for the patient to be assisted by the medical team in the postoperative period, the great challenge was to establish the correct time for specialist intervention to reprogram the set point: the patient’s return to be reevaluated could be ineffective, if any adverse event occurred that implied an immediate correction of the pump’s behavior.

To overcome this limitation, there was the advancement of sensing resources, that is, VADs became automatic devices as it became possible through sensors to monitor the physiological behavior of their patients. This had an impact on the design of control architectures for VADs and on the performance of these devices [10]. In this context, automation has a fundamental characteristic in the development of autonomous devices. Thus, in this work, a methodology is proposed for the development of a VAD rotation control system in a dynamic way, considering: monitoring the rotor speed to act upon the occurrence of failures in the device; reconfiguration of the control system according to the need to supply cardiac output according to the physical activities that the patient is performing at all times and; the possibility of dynamic change in the behavior of the pump, depending on the patient’s global status, upon the occurrence of adverse events. For the development of this control solution, not only physical sensors are considered, but also virtual sensors based on specific algorithms to calculate the desired parameters, for example, indicating that the blood flow increased.

1.2. Research Motivation

Therefore, with a VAD with no fault tolerance and no dynamic behavior that adapts to the performance conditions of the cardiovascular system, serious limitations are observed in the results of this application [6]. Thus, this work proposes the application of a mechatronic approach to this class of devices based on advanced control, instrumentation, and automation techniques [11]. These techniques allow in a systematic way to consider in the control architecture the limitations of the current solutions. This methodology has been applied to other medical equipment [12]. In this context, a method is proposed for a VAD supervisory control system that:

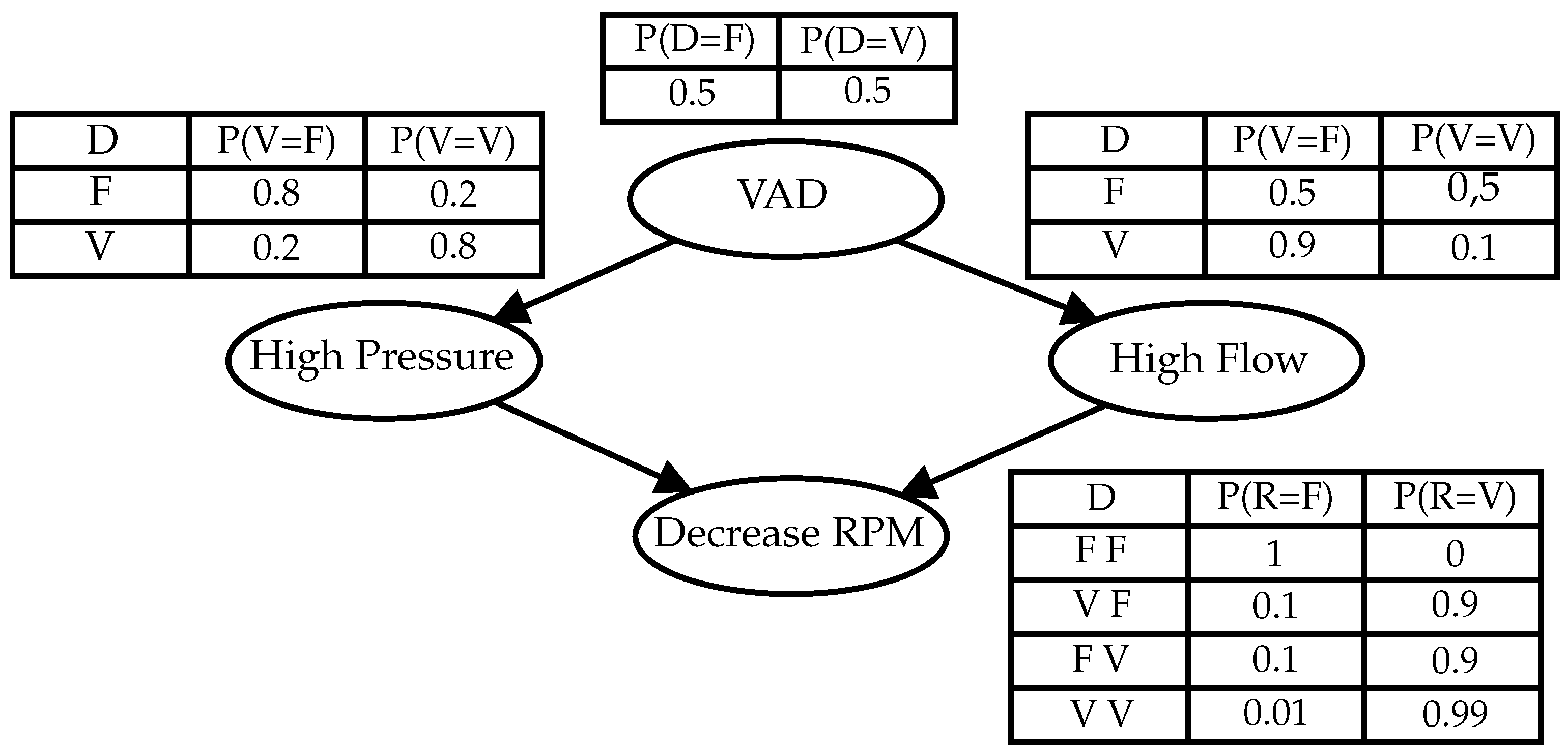
• Specifies a logic for the pump speed control, according to the dynamic behavior of the patient. Models based on Bayesian network (BN) [13] should be applied to diagnose the dynamic state of the patient at each moment and to act in controlling the VAD;
• Specifies a safety interlocking logic to prevent failures in the VAD that could generate risks to the patient’s life. To do this, the critical states will be diagnosed by means of BN and, from these, implement a real-time diagnostic control system by means of Petri nets (PN).
• Once the diagnostic control system is implemented in parallel, fault handling should be implemented according to the specification of the instrumented functions of security (SIFs) [14,15]. These functions are modeled in PN [16] for generating the control algorithm for fault-handling.
• Check the supervisory model observing the human cardiovascular electronical model, considering the proposed model [17]. Making the supervisory control system validation, the next step is the “in vitro” and “in vivo” validation.

These items are relevant and essential to make the control system of a DAV autonomous and intelligent. However, approaching all these subjects in a single article is a difficult task. Thus, this work approaches the development of a VAD rotation control system in a dynamic way that will solve the local rotation control considering physical sensors. Thus, as a result, an automatic system will be obtained that will allow the speed control to become dynamic. The part of security control with adverse and unknown situations will be the subject of another work.

Thereby, the paper is structured starting with the introduction and research motivation. Section 2 describes some basic concepts: 1. Product Flow Schema (PFS); 2. Hybrid PN (HPN); 3. The PFS/HPN Top-Down approach, and 4. The safety instrumented systems (SIS) and BN/HPN approach. The first approach is used to represent the controller, and the second approach is used to connect the sensors and the treatment modeling to the controller. Section 3 has the proposed VAD supervisory control system design methodology. Section 4 has the results and Section 6 has the conclusions and future works.

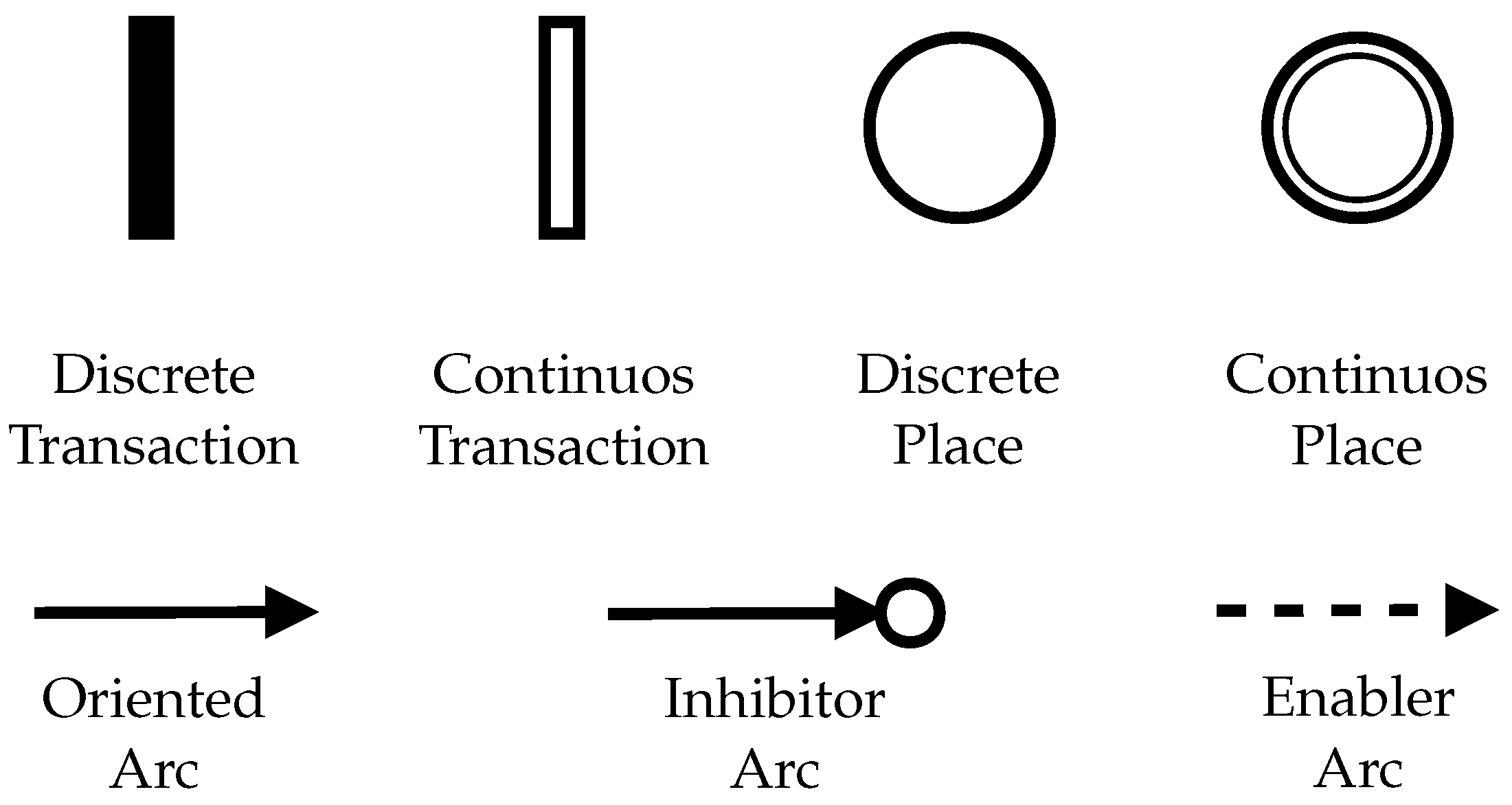
2. Basic Concepts

This section is divided into four parts. The first part explains the PFS representation. The PFS is a bipartite graph used to represent a sequence of operations for different situations. The second part explains the HPN used to create formal representations. It also includes the manipulation of continuous variables. The third part explains the top-down PFS/PN approach. The PFS is refined using PN, the dynamics of the logic operations are described using PN. This approach will create the VAD control. The fourth part explains the BN/PN approach where the treatment and sensor information are connected to the controller.

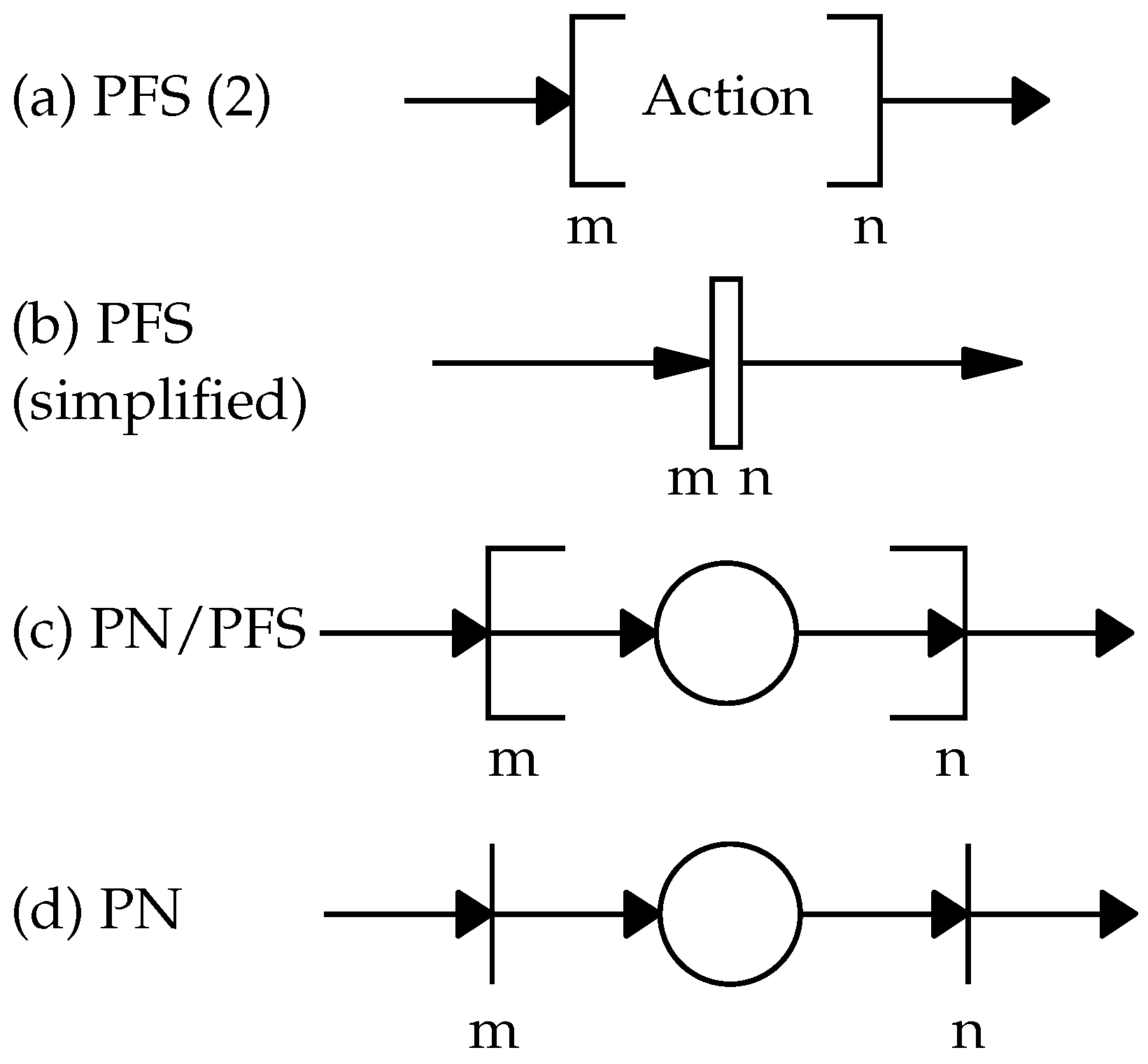
2.1. Product Flow Schema (PFS)

The PFS is a bipartite graph composed of activity elements (action, execution), distribution elements (collect, accumulate, and/or store information or items), and oriented arcs to connect the elements. Figure 1 shows the graphical representation of these elements. It is capable of modeling the specific control functionalities and operations that will be performed by the VAD. Functionality depends on circumstances: normal device behavior, behavior in the face of failure situations, or behavior in the face of adverse events that are associated with the patient’s physiology. In this context, the PFS model is descriptive. It is able to represent the sequence of operations for each situation. It also allows representing the causality associated with the occurrence of events. It is represented in terms of oriented arcs that establish a sequential logic for carrying out the operations.

2.2. Hybrid Petri Net (HPN)

Murata [18] presents the PN as a promising tool to describe and study systems with concurrency, parallelism, asynchronous, non-deterministic, and/or stochastic. According to Li and Zhao [19], the PN is a suitable mathematical tool to model and analyze discrete event systems that have behaviors such as concurrency, conflict, and casual dependence between events (parallelism). Thus, considering the requirement that VAD needs to perform control functions to adjust pump speed according to changes in cardiac frequency and needs to react against the occurrence of critical faults, a PN is a useful tool to model, analyze, and validate the VAD control. Figure 2 shows the PN elements graphical notation: discrete transaction, discrete place, oriented arc, inhibitor arc, and enabler arc [16]. The continuous transaction and continuous place will be described in the following with the HPN.

According to Li and Zhao [19] a general N PN is a 4-tuple $(P,T,F,W)$. Where P and T are disjoint sets, finite, not empty. P is a set of places, and T is a set of transitions. $F\subseteq (P\times T)\cup (T\times P)$ is called the flow relationship or the set of directed arcs. $W:F\to N^{+}$ is a mapping that assigns a weight to an arc, that is, it is a weighting function, where $N^{+}=\left\{1,2,\dots \right\}$. The precondition of a node $x\in (P\cup T)$ is defined as ${}^{o}x=\left\{y\in P\cup T\left|\right(y,x)\in F\right\}$. The postcondition of a node $x\in (P\cup T)$ is defined as $x^o=\left\{y\in P\cup T\left|\right(x,y)\in F\right\}$.

The precondition/postcondition of a set is defined as the union of the preconditions and postconditions of its elements. $N=(P,T,F,W)$ is called an ordinary net, and its notation is $N=(P,T,F)$, if $\forall f\in F,W\left(f\right)=1$. A token M of $N=(P,T,F)$ is a mapping of $M:P\to N$, where $N=N^{+}\cup 0$ and $M\left(p\right)$ indicates the number of tokens M in p. Token M is denoted by ${\sum }_{p\in P}M\left(p\right)$.

The HPN model was introduced as an extension of the discrete PN model, allowing the manipulation of real numbers in a continuous form, thus allowing to express explicitly the relation between continuous values and discrete values, keeping good modeling characteristics of discrete systems consented in a consecrated way by PN. The HPN is a bipartite graph that is represented with places and transitions. The components of the HPN are classified into discrete/continuous places and discrete/continuous transitions. A nonnegative real number is represented by a continuous place and the firing rate of the continuous transition is given as a function of the places in the HPN model. Figure 2 shows graphical notations of HPN elements [16]. The HPN has inhibitor and enabler arcs; these arcs enable/disable specific activities. The refinement of a model generated using PFS to a model in HPN is done based on the procedure adopted in Villani et al. [20].

A system where there are different kinds of variables and that simultaneously presents the evolution of continuous variables and discrete events should be considered a Hybrid System and could be modeled by HPN theory [20]. This behavior, considering the Discrete Event System (DES), unifies with the behavior of the Continuous Variable System (CVS) [21]. Considering the need for the VAD to perform control functions to adjust the pump speed according to changes in heart rate and the need to react to the occurrence of critical failures, a hybrid supervisory control system has been proposed [20].

2.3. The Top-Down PFS/HPN Approach

Details of each activity modeled in the PFS can be refined using PN. The activity element can be refined into another PFS model or a PN using top-down methodology. Figure 3 shows the graphical representation of top-down methodology. Figure 3a shows the initial PFS activity, which will be transformed into the PN representation shown in Figure 3d. It is even possible to create a combined PFS/PN representation as shown in Figure 3c. In turn, after establishing the operation logic using PFS, it is necessary to describe how the operations should be performed dynamically. This description is refined using PN. It is based on the concept of local states associated with structural element markings. Therefore, applying the systematic to generate a PN model from a PFS model, it will be possible to obtain the association between the semantics of PFS and PN. This association will model the execution of each functionality/operation and the local control, according to the state in which the VAD system is at any given time.

The Product Flow Schema (PFS) tool [20] can be used to systematically model the set of activities that a VAD can perform in a top-down approach. The activity element can be refined into another PFS model or a HPN using top-down methodology. Considering the VAD, some components are the treatment of diagnosed problems, patient diagnosis, control algorithm, validation of the control algorithm, and others. The control algorithm is represented by a new set of activities. The HPN is the lowest level and it represents the control implementation. This approach has been widely used in industrial applications [22]. Therefore, with the mathematical formalism of the HPN, it is possible to create a control algorithm that can be modeled and that complies with the requirements of reachability, liveliness, limitability, conservativeness, and reversibility. This characteristic can be analyzed mathematically in the HPN, qualifying the control to be fault-free, providing adequate security to critical systems such as a VAD control. The HPN generated by PFS model is able to represent the dynamic behavior of VAD system. Since the VAD introduces continuous variables, than HPN is required.

2.4. SIS and BN/PN Approach

To develop the fault diagnosis and treatment model, the concepts of SIS and BN are used. According to Squillante Jr et al. [14] the SIS is a control layer with the objective of mitigating risk or bringing the process to a safe state. The definition of each failure is made from the identification of Safety Instrumented Functions (SIF). In this way, a SIF describes a system failure that must be diagnosed and treated by the SIS. A SIS implements its SIFs by means of sensors and system devices, and performs control by actuators. For each SIF, a parameter called the safety integrity level (SIL) is defined. This parameter is a measure of safety for each component and/or system. BNs provide a formalism for the system to reason about conditions of uncertainty and process failures. In this formalism, propositions are given as numerical parameters that signify the degree of belief according to some evidence or knowledge. Thus, formally, BN $B=(G;Pr)$ are composed of a topological structure G and a set of parameters $Pr$ that represents the probabilistic relationship between its variables [14].

The human body can assume different states depending on the heart disease of each patient. Some states are known and others are unknown, which may vary from patient to patient. Some states can be detected by sensors. Other states, no less important, do not have sensors, which can generate uncertainty in relation to the real state of the variable. However, there are tools that allow the deduction of these states, indirectly, performing an analysis of the global state of the system. Thus, to deal with the uncertainties inherent to this class of systems, the use of BN is proposed. With the BN formalism, it is possible to work with states that are not monitored by sensors and/or unknown states, and with that it is possible to abduct the information and make decisions that would not be possible without the BN analysis.

Thus, in Figure 4 a BN is presented, where two situations are defined: (a) high blood pressure and (b) high blood flow, with their respective probabilities. Depending on the patient’s global status, the occurrence of these events can lead to a decrease in VAD rotation. Thus, initially, the probability of $50\%$ of occurring or not the alteration in the rotation of the VAD was considered. If the occurrence of high blood pressure is detected (V), a chance of $20\%$ of this information not influencing the rotation P(V=F) and $80\%$ that the rotation will be decreased to solve this event P(V=V) is defined. Respectively, this analysis can be considered for other combinations of states that the system can assume, following the BN formalism.

As BN is an analysis tool, it is necessary to use HPN to generate dynamic control models. Therefore, with the analysis of the incidence of events related to the possible states that the VAD can assume, the refinement of BN into HPN is proposed and, in this way, diagnostic and control models are generated. In Figure 5 the HPN referring to the BN obtained in Figure 4 is represented. In order for the control algorithm to meet the security conditions of a critical system, this activity must be performed, observing the following situations:

• Obtain the causal dependency relationships from the BN for each failure;
• Obtain the logical relationships between external variables (sensors) from the causal relationship;
• Build the HPN from the diagnostic reasoning, obtain an effect versus cause structure to represent the BN diagnostic model in HPN, so that it is possible to carry out the control;
• Consider in the HPN design that it must allow its restart to meet the required restartability property and consider the possibility of the failure being spurious, that is, the possibility of the diagnosis not being carried out considering the calculated uncertainties in the BN;
• Represent in the model the events associated with the transitions and how to represent them, indicating, in particular, the events that require an interaction with the external environment (for example, sensors and actuators).

By following these procedures, it is possible to obtain the PN represented in Figure 5.

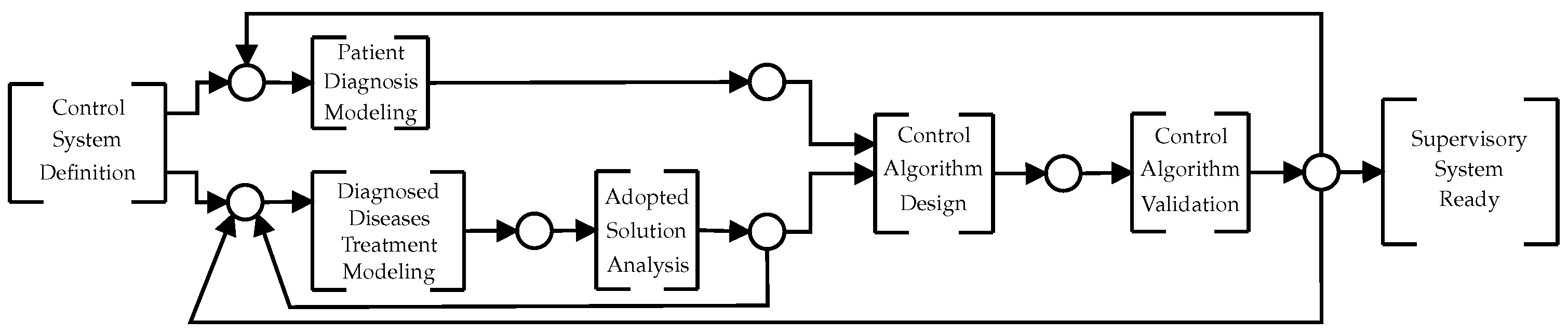
3. Proposed VAD Supervisory Control System Design Methodology

To design the VAD supervisory control system systematically according to the techniques presented [23], a set of procedures are proposed below:

• Control System Definition—physicians, engineers, and specialist teams are defined to define the VAD autonomy. This is the team that is responsible for developing the control system. They need to select ideas that can be implemented taking into consideration: available sensors, performance characteristics of the VAD, and technological limitations. The VAD control functions are specified in this phase.
• Patient Diagnosis Modeling—The cause and effect matrix is created considering the definitions made in the last step. Every effect considered is converted to a node of a BN. Then, following the procedures proposed in [24] this fault diagnosis network can be converted into a PN control model.
• Diagnosed Diseases Treatment Modeling—To obtain the HAZOP (hazard and operability) study [15] for VAD, a risk analysis report can be used for the IEC 31010 standard. Thus, the SIL and events (from sensors) and actions (for actuators) for each SIF are obtained. Then, to obtain the safety instrumented systems (SIS), each SIFs are modeled in PN.
• Adopted Solution Analysis—To validate the obtained PN models, first a structural analysis is performed. Then, it is verified by PN deadlock (markings where no transition is enabled). For this, the Visual Object Net simulator [25] can be used.
• Control Algorithm Design—To generate the control algorithm, the validated PN models are translated to a Programmable Controller language following the rules proposed in [24] to generate the control program according to IEC 61131-3 [26] standard.
• Control Algorithm Validation—To make “in vitro” tests, a mathematical model can be used to simulate the human cardiovascular system [17]. Once the control system is validated, the next step is to implement the prototype physically to confirm the functionality of the cardiovascular simulator system. At the Institute Dante Pazzanese of Cardiology (IDPC), there is a programmable mechanical simulator to perform in vitro tests. This equipment allows to simulate a real patient cardiovascular system [27].
• Supervisory System Ready—This step amounts the in vivo validation of the control algorithm. Once the in vitro simulation is validated, the VAD control algorithm is ready for in vivo testing [2].

By defining the design of the supervisory control system method and applying the set of procedures proposed above, it is possible to provide security to the system and enable control of the VAD rotational speed according to changes in the patient’s heart rate, which can improve the quality of life and safety of patients, increasing the patient’s life and providing time before a heart transplant. The proposed methodology is shown in Figure 6 according to the PFS formalism.

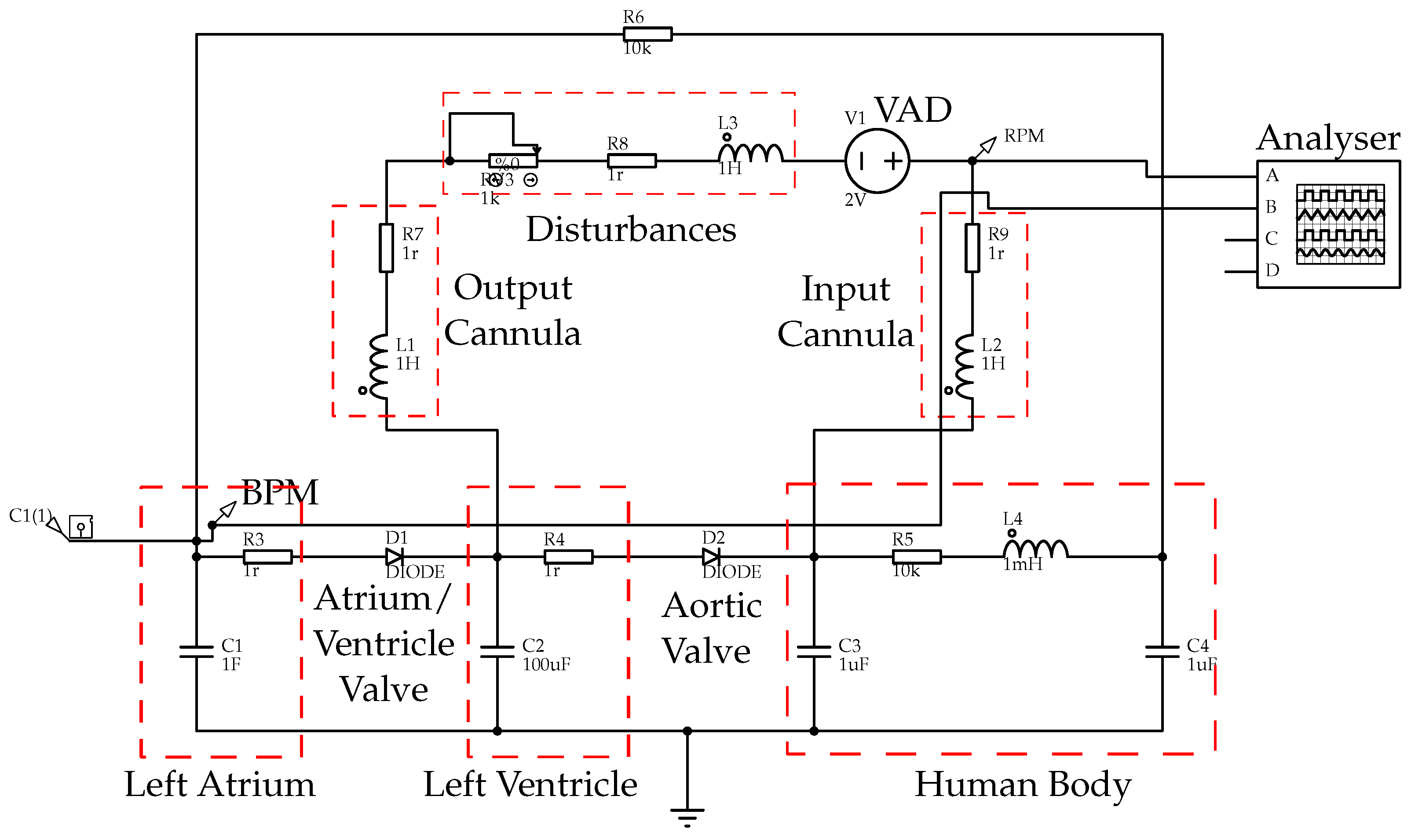
4. Results

By applying the proposed procedure, a method is defined and some characteristics are accomplished: (i) the HAZOP study is applied and considers critical failures to VAD control system, (ii) BN is used to diagnose and decide, (iii) Safety Instrumented Functions (SIF) are used to model HPN and (iv) Supervisory control system modeling is made considering the discrete and continuous variables of VAD.

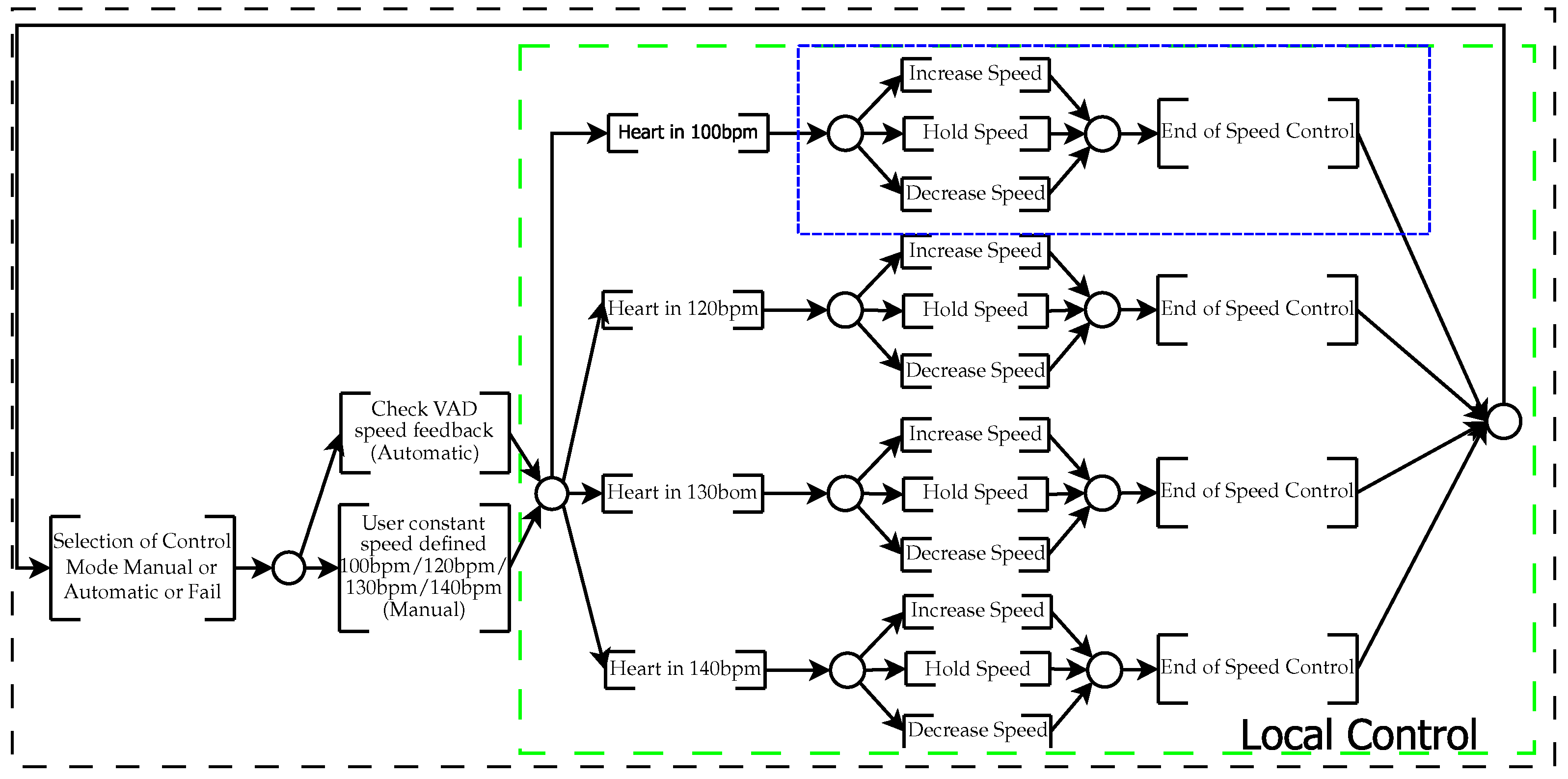
4.1. Supervisory Design

Tests using a physical prototype are made to confirm the functionality by using a IDPC programmable mechanical simulator to validate the control performance. The local control model is shown in Figure 7. The supervisory modeled in PFS shows four possible heart beating ranges. The sensor information switches the HPN flow to activate the proper range. After switching, the proper control happens.

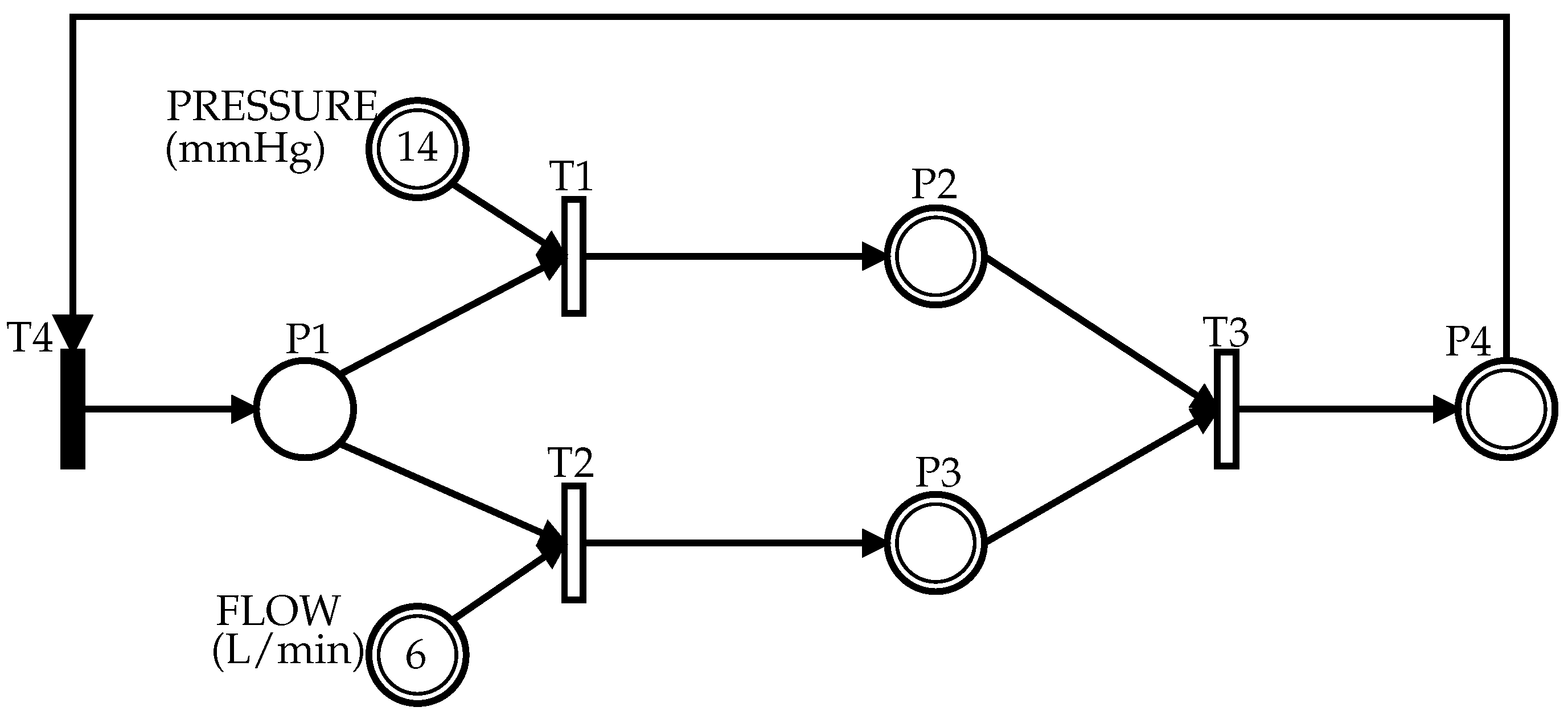
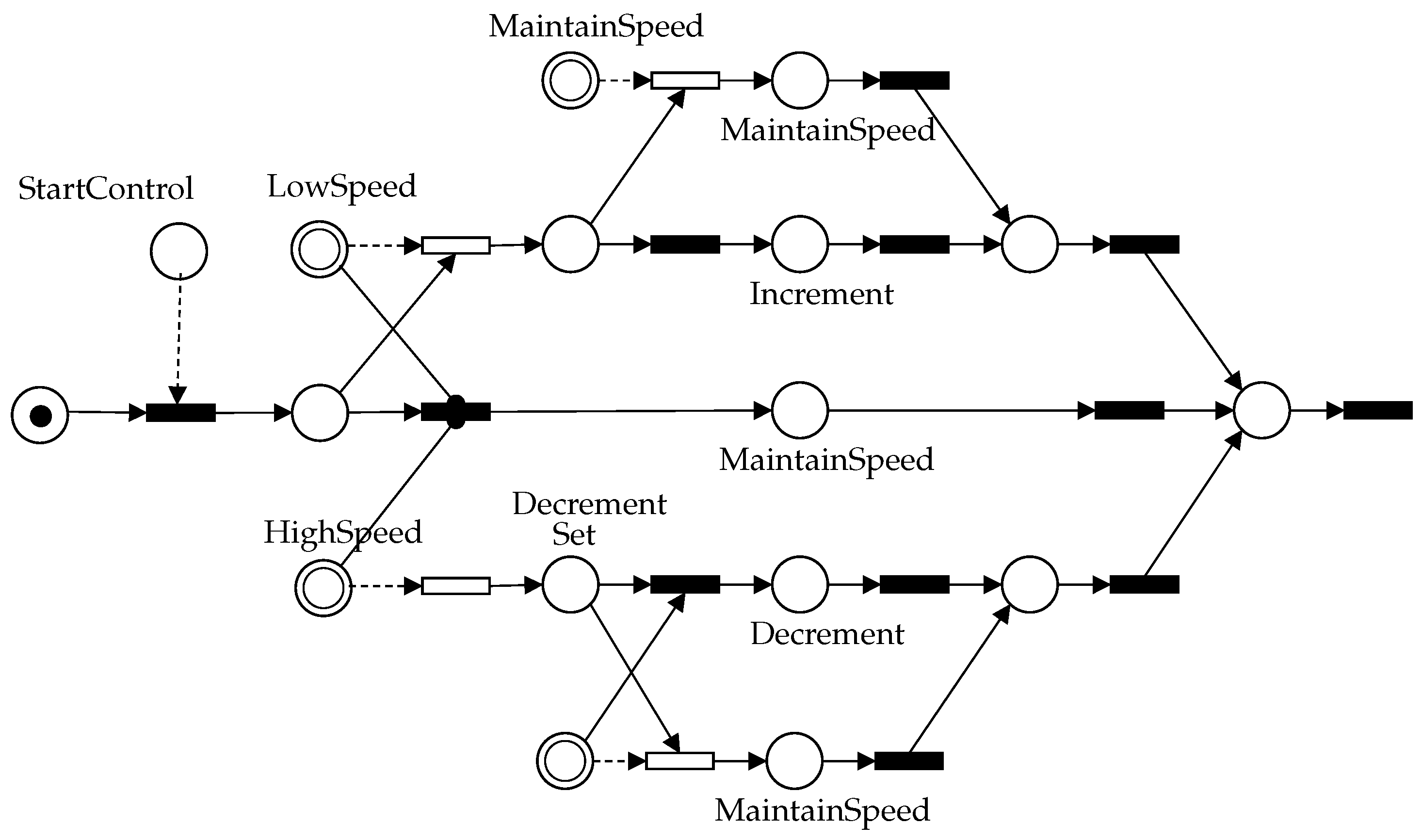
4.2. Control Design

The PFS shown in Figure 7 is refined into a HPN. Figure 8 shows the detailed control of the blue box represented in Figure 7. It has the following dynamics. When the “StartControl” place receives a token, the Speed Control HPN starts and the “LowSpeed” and “HighSpeed” places are monitored. The DAV rotation has a target rotation, considering the specific heart beat. If the speed is not low or high, then the DAV rotation shows the error equals 0, and the speed output remains constant. If the error is different from 0 appears, one of the signals “LowSpeed” or “HighSpeed” has a token. If “LowSpeed” has a token, the speed control token is directed through the enabling arc to the “IncrementSet” place, which has the function of incrementing the controller output to perform the speed adjustment in the driver (local pump control of the DAV) and continues increasing the output until the value is controlled, i.e., the error becomes zero.

The range of the desired speed value is represented by “LowSpeed” and “HighSpeed” without a token, which enables the token control to the “MaintainSpeed” place, by enabling both inhibiting arcs, keeping the speed value sent to the driver. Another situation expected by the HPN is when the speed increment value reaches the maximum signal value that can be generated by the pump driver, i.e., full rotation or 100% of the activation signal or maximum speed request. This state is represented by the “MaxSpeed” place, which indicates that the signal has reached saturation. In this way, the token is shifted to the “MaintainSpeed” place. This state is implemented to avoid the control’s windup problem. The reciprocal situation happens for the state of “HighSpeed”, causing the activation of the control of “DecrementSet”.

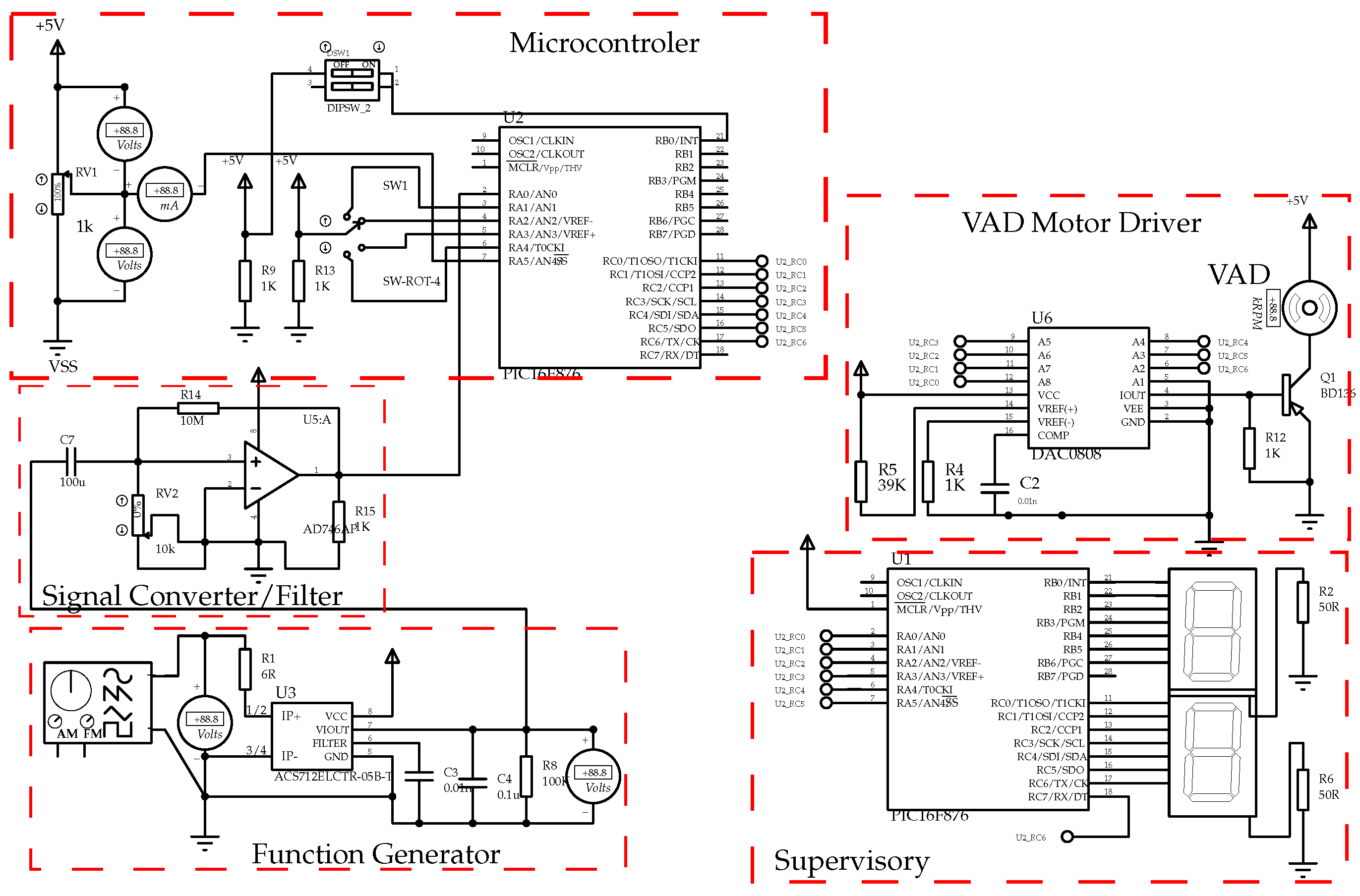
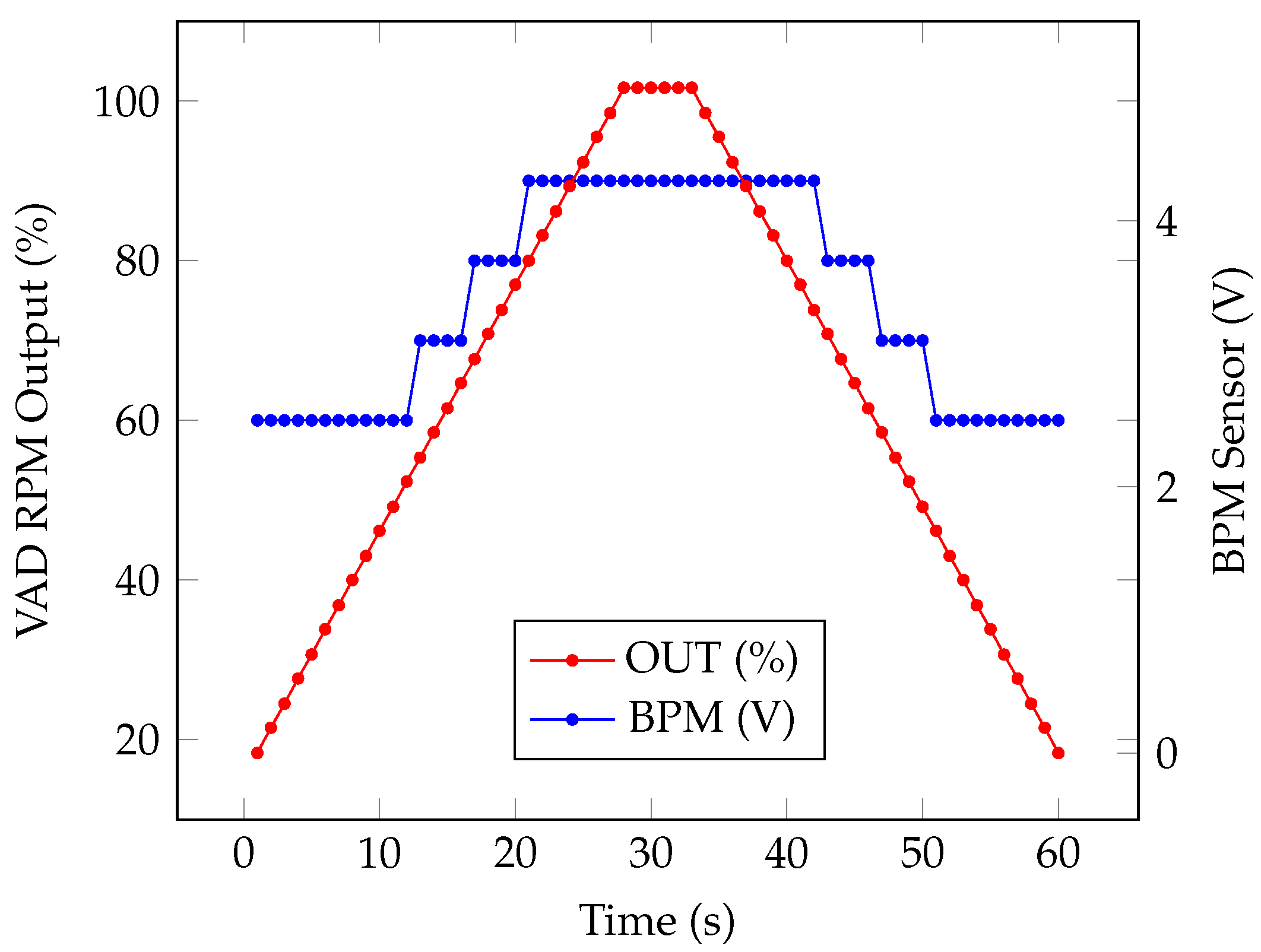
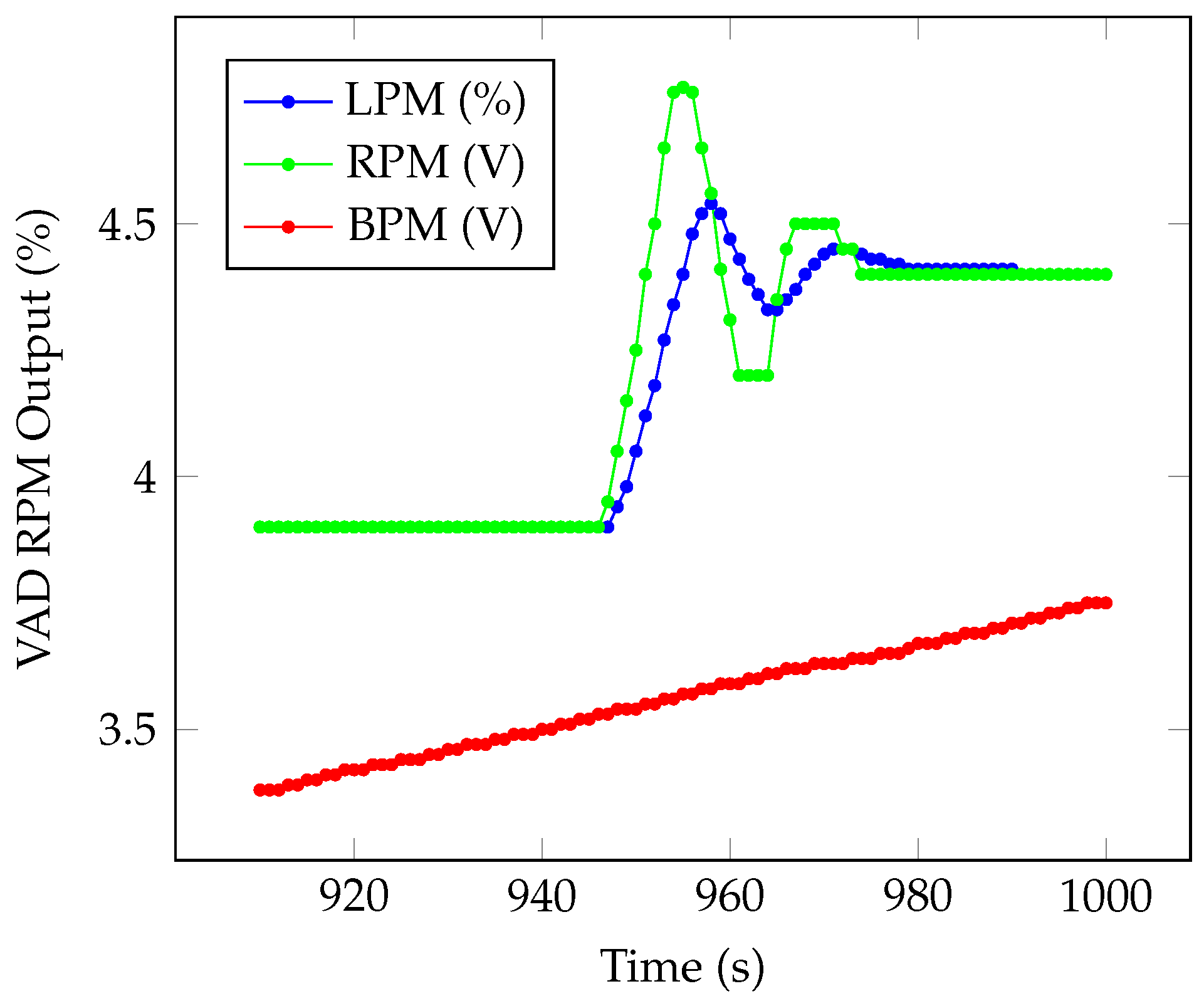
4.3. Numerical Simulation

Numerical results of physical VAD supervisory control system simulation were obtained. Once the modeling and validation of the VAD’s control algorithm is performed using HPN and the model is converted to the microcontroller programming language using the procedure of replacing each element of the HPN by elements of the Ladder diagram [24], it enables the implementation of the system and in vitro computational validation, providing an implementation of the device control within a cardiac simulator to validate the computational model. To this end, this algorithm is implemented in the hardware architecture proposed in Figure 9, modeled using the Proteus Design Suite^® software. The proposed hardware architecture is composed of the following components:

• Microcontroller: device responsible for executing the security control;
• VAD Motor Driver: device responsible for driving the VAD motor;
• Supervisory: device responsible for the human-machine interface;
• Function Generator: equipment used to simulate the signals coming from the sensors and generate disturbances to carry out analysis of the control system;
• Signal Converter/Filter: device responsible for conditioning the signals generated by the function generator.

In this way, disturbance signals are generated by the Function Generator and sent to the controller through the signal conditioning system. These signals are processed by the VAD control algorithm, which sends, depending on the control model, the appropriate command for the VAD Motor Driver. The VAD Motor Driver is responsible for performing the electrical power interface and activating the VAD motor. In this experiment, the signal range generated by the VAD Motor Driver is from 0 to 5 V DC, where 0 V means 0 RPM and 5 V means the maximum speed, which in the case of this application is 3000 RPM.

To validate the architecture and the control algorithm, a model of the human cardiovascular system [17] was considered, enabling a virtual simulation of the human cardiovascular system (see Figure 10). It is an electrical equivalent model where the signal generated by the pump rotation control is represented in Figure 10 by the positive and negative poles of the VAD. The electronic parameters are correlated with their mechanical parameters as follows: voltage (V) to pressure (mmHg), capacitance (mF) to elasticity (mL/Pa), electrical resistance (kΩ) to resistance to passage of blood (Pa·s/mL), and inductance ($\mathsf{\mu }$H) to inertia (Pa·s${}^2$/mL). The elements of each artery are represented, including one or two resistors, an inductor, and a capacitor.

The model of the human cardiovascular system (see Figure 10) is connected to the supervisory control (see Figure 9). This simulation environment is proposed to analyze the control algorithm. This signal will introduce the voltage relative to the blood flow into the simulation circuit. This increase in voltage together with the characteristics of the human body simulated by the electronic components will produce the reaction curve shown in Figure 11 and Figure 12 as a function of the control model response and the disturbance generated in the simulation.

Simulations of heart failure and heart rate oscillations are performed to verify that the control algorithm works correctly, changing the blood pump speed appropriately for each simulated case. The reaction curve of the pump implanted in the human body was used to verify the stability of the control system as a function of the conditions of the cardiovascular system in which the pump will be implanted.

With this, it is possible to validate the states that the system can reach computationally. Consequently, to validate the physical control using the real VAD driver, the designed electronic circuit was prototyped, as shown in Figure 10. Thus, it was possible to test the system in a physical simulator of the cardiovascular system [27].

With the physical test, it is possible to confirm whether the VAD will effectively help a weakened heart to regain its function as a heart pump in a physical way. This physical simulator serves mainly to verify if there is a tendency of the VAD to make a speed correction if there is a load change in the cardiovascular system, that is, if the VAD system controls a rotation rate to maintain the physiological functions independent of the pump rotation working in a synchronized demand with the natural heart. Using a tachograph and the proper instruments, the VAD state and its respective velocity measurements were performed as presented in Figure 11. Therefore, different reaction curves were generated for the different situations required by the control system. Thus, heart rate variation is applied to analyze how the VAD control system must operate in automatic control mode considering the PN model presented in Figure 8. As show in Figure 11, the system responded according to the proposed control model. The red line shows the simulated heart rate starting at zero beats per minute (bpm) and increasing the value to the maximum bpm value that a patient may present (in this case, 200 bpm was considered), then maintaining stability at the upper level and after decreasing the value again until 0 bpm. With this simulation, it is possible to observe how the control should react considering the whole range of flow control considering the bpm patient range. The blue line shows the pump rotation output sent from the supervisory system to the local control, where the change in speed (0–3000 RPM) as a function of heartbeat (bpm) is observed by the control. The green line indicates the blood flow (0–5 LPM), considering the local control of the pump as shown in Figure 12.

These characteristics are confirmed at the time of testing with the physical simulator to validate the model, which will prepare it for the next phase of the proposed method, which is the in vivo test system.

5. VAD Validation

The research project “Electromagnetic Propulsion Systems for Circulatory Support, Implantable Ventricle Assist Device, and Artificial Heart”, supported by FAPESP, is currently in the execution phase. This project aims to integrate engineering and medicine to develop solutions for mechanical circulatory support systems. For this, a methodology with the development of 11 subprojects based on applied engineering and medicine was used.

This research work presented is part of the subproject responsible for developing proposals for Safety Supervisory Control Systems for Implantable Blood Pumps. In turn, for the validation of a VAD that has a coupled control system, a test protocol is required to be implemented in human beings [28]. In this context, as an engineering project, a VAD must undergo all verification and validation tests with the help of specialized benches so that in vitro tests are carried out, applying a deductive method based on the formal analysis of appropriate mathematical models to represent the dynamic behavior that is desired [29]. In turn, after this technological validation of the device, it is necessary to carry out the in vivo test steps. Initially, the tests are carried out on animals through procedures established by teams of veterinarians and in accordance with the current code of ethics [30].

Once approved in animals, the last stage of in vivo tests is to carry out the evaluation in human beings. In this context, there is a subproject focused solely on the clinical evaluation study of VAD, which involves the Instituto Dante Pazzanese de Cardiologia [31]. The initial step was to submit a Clinical Assessment Protocol to the National Research Ethics Council and the National Health Surveillance Agency, receiving authorization from both bodies to implant devices in 10 patients. The procedure adopted for analyzing the patient’s behavior consists of: (i) performing biochemical studies, tests of the patient’s hemodynamic performance; (ii) detailed definition of the surgical procedure; (iii) detailed definition of the postoperative procedure to specify monitoring of physiological signs and administration of compatible medication; (iv) specification of laboratory data to be monitored; (v) planning the indication of heart transplantation and removal of the device in an emergency and; (vi) provision for device removal after satisfactory circulatory assistance tests.

Thus, the procedure for validating a VAD from its technological design to its implantation in patients is explained.

6. Conclusions and Future Works

Currently, the usual VAD control has difficulty to adjust the blood flow according to the patient’s condition: there is no supervisory control of the device that adjusts the rotation speed according to the patient’s needs, and there is no treatment of VAD failure that helps patient safety. The presented study contributed to a great evolution of the VAD control system, proposing a suppository control layer that identifies and recognizes the adverse event, providing a better quality of life for the patient and increased survival. Thereby, the supervisory system can also assist in diagnosis and interventions to maintain the functions of the VAD. With this study, we can have personalized VAD considering the patient’s disease and metabolism. In addition, the concept of SIS is essential to provide a reduction of risks that may interfere with the function of the VAD and the patient’s life.