Functors among Relational Variants of Categories Related to L-Fuzzy Partitions, L-Fuzzy Pretopological Spaces and L-Fuzzy Closure Spaces
Abstract
1. Introduction
2. Preliminaries
- 1.
- is a bounded lattice with the least element 0 and the greatest element 1;
- 2.
- is a commutative monoid, and
- 3.
- , .
- 1.
- ,
- 2.
- ,
- 3.
- .
- 1.
- ,
- 2.
- ,
- 3.
- .
- 1.
- ,
- 2.
- ,
- 3.
- .
- 1.
- ,
- 2.
- ,
- 3.
- .
- 1.
- The corresponding set of ordinary subsets is a partition of X, and
- 2.
- implies .
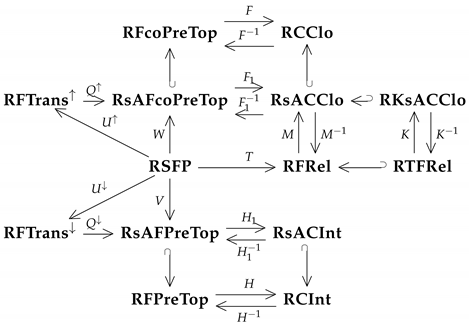
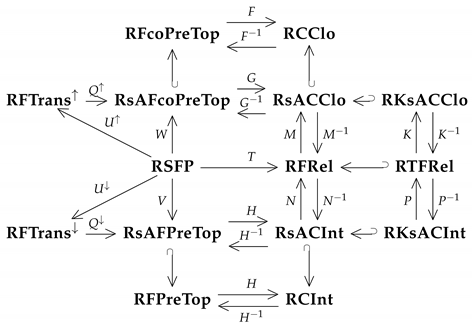
3. Relational Categories of -Valued Topological Objects and Functors among Them
- 1.
- The category is defined by:
- (a)
- Objects are pairs , where is a Čech L-fuzzy interior operator (Definition 2),
- (b)
- is a morphism, if is an L-fuzzy relation and
- 2.
- The category is defined by:
- (a)
- Objects are pairs , where is a Čech L-fuzzy closure operator (Definition 3),
- (b)
- is a morphism, if is an L-fuzzy relation, and
- 3.
- The category is defined by:
- (a)
- Objects are L-fuzzy pretopological spaces (Definition 4),
- (b)
- is a morphism, where , , if is an L-fuzzy relation, and for all ,
- 4.
- The category is defined by:
- (a)
- Objects are L-fuzzy co-pretopological spaces (Definition 5),
- (b)
- is a morphism, where , , if is an L-fuzzy relation, and for all ,
- 5.
- The category is defined by:
- (a)
- Objects are pairs , where r is a reflexive L-fuzzy relation on X,
- (b)
- is a morphism, if is an L-fuzzy relation, andwhere ∘ is the composition of L-fuzzy relations.
- 6.
- The category is defined by:
- (a)
- Objects are sets with an L-fuzzy partition , (Definition 6),
- (b)
- is a morphism if and are L-fuzzy relations such that
- i.
- For each ,
- ii.
- For each ,
- 7.
- The category is defined by:
- (a)
- Objects are upper F-transforms , where are sets with L-fuzzy partitions and , where ,
- (b)
- is a morphism if and are L-fuzzy relations and for each ,hold.
- 8.
- The category is defined by:
- (a)
- Objects are lower F-transforms , where are sets with L-fuzzy partitions, where , for , ,
- (b)
- is a morphism if and are L-fuzzy relations and and for each ,hold.
- 1.
- The full subcategory of with transitive L-fuzzy relations as objects,
- 2.
- The full subcategory of with strong Čech–Alexandroff L-fuzzy closure operators as objects,
- 3.
- The full subcategory of with Kuratowski strong Čech–Alexandroff L-fuzzy closure operators,
- 4.
- The full subcategory of with strong Čech–Alexandroff L-fuzzy interior operators as objects,
- 5.
- The full subcategory of with Kuratowski strong Čech–Alexandroff L-fuzzy interior operators,
- 6.
- The full subcategory of with strong Čech–Alexandroff L-fuzzy pretopological spaces as objects,
- 7.
- The full subcategory of with strong Čech–Alexandroff L-fuzzy co-pretopological spaces.
 |
 |
4. Conclusions
Funding
Conflicts of Interest
References
- Bělohlávek, R. Fuzzy closure operators. J. Math. Anal. Appl. 2001, 262, 473–489. [Google Scholar] [CrossRef]
- Bělohlávek, R. Fuzzy closure operators II. Soft Comput. 2002, 7, 53–64. [Google Scholar] [CrossRef]
- Biacino, V.; Gerla, G. Closure systems and L-subalgebras. Inf. Sci. 1984, 33, 181–195. [Google Scholar] [CrossRef]
- Elkins, A.; Šostak, A.; Uljane, I. On a category of extensional fuzzy rough approximation operators. In Communication in Computer and Information Science; Springer: Berlin, Germany, 2016. [Google Scholar]
- Perfilieva, I.; Singh, A.P.; Tiwari, S.P. On the relationship among F-transform, fuzzy rough set and fuzzy topology. Soft Comput. 2017, 21, 3513–3523. [Google Scholar] [CrossRef]
- Ramadan, A.A.; Li, L. Categories of lattice-valued closure (interior) operators and Alexandroff L-fuzzy topologies. Iran. J. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Perfilieva, I.; Singh, A.P.; Tiwari, S.P. On F-transform, L-fuzzy partitions and l-fuzzy pretopological spaces. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Zhang, D. Fuzzy pretopological spaces, an extensional topological extension of FTS. Chin. Ann. Math. 1999, 3, 309–316. [Google Scholar] [CrossRef]
- Močkoř, J.; Perfiljeva, I. Functors among categories of L-fuzzy partitions, L-fuzzy pretopological spaces and L-fuzzy closure spaces. In IFSA World Congress and NAFIPS Annual Conference: Fuzzy Techniques: Theory and Applications. IFSA/NAFIPS Louisiana, USA; Springer: Cham, Switzerland, 2019; pp. 382–393. [Google Scholar]
- Goguen, J.A. L-fuzzy sets. J. Math. Anal. Appl. 1967, 18, 145–174. [Google Scholar] [CrossRef]
- Dikranjan, D.; Šostak, A. On two categories of many-valued fuzzy relations. In IFSA-EUSFLAT Proceedings; Atlantis Press: Paris, France, 2015; pp. 933–938. [Google Scholar]
- Wang, C.Y. Fuzzy rough sets based on generalized residuated lattices. Inf. Sci. 2013, 248, 31–49. [Google Scholar] [CrossRef]
- Wu, W.Z.; Leung, Y.; Mi, J.S. On characterization of (, )-fuzzy rough approximation operators. Fuzzy Sets Syst. 2005, 154, 76–102. [Google Scholar] [CrossRef]
- Höhle, U. Fuzzy sets and sheaves. Part I, Basic concepts. Fuzzy Sets Syst. 2007, 158, 1143–1174. [Google Scholar] [CrossRef]
- Novák, V.; Perfilijeva, I.; Močkoř, J. Mathematical Principles of Fuzzy Logic; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Bandler, W.; Kohout, L. Special properties, closures and interiors of crisp and fuzzy relations. Fuzzy Sets Syst. 1988, 26, 317–331. [Google Scholar] [CrossRef]
- Bodenhofer, U.; De Cock, M.; Kerre, E.E. Openings and closures of fuzzy preorderings: Theoretical basics and applications to fuzzy rule-based systems. Int. J. Gen. Syst. 2003, 32, 343–360. [Google Scholar] [CrossRef]
- Močkoř, J. Spaces with fuzzy partitions and fuzzy transform. Soft Comput. 2017, 13, 3479–3492. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Rodabaugh, S.E. Powerset operator foundation for poslat fuzzy sst theories and topologies. In Mathematics of Fuzzy Sets: Logic, Topology and Measure Theory, The Handbook of Fuzzy Sets Series; Höhle, U., Rodabaugh, S.E., Eds.; Kluwer Academic Publishers: Boston, MA, USA, 1999; Volume 3, pp. 91–116. [Google Scholar]
- Močkoř, J. Axiomatic of lattice-valued F-transform. Fuzzy Sets Syst. 2018, 342, 53–66. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Močkoř, J. Functors among Relational Variants of Categories Related to L-Fuzzy Partitions, L-Fuzzy Pretopological Spaces and L-Fuzzy Closure Spaces. Axioms 2020, 9, 63. https://doi.org/10.3390/axioms9020063
Močkoř J. Functors among Relational Variants of Categories Related to L-Fuzzy Partitions, L-Fuzzy Pretopological Spaces and L-Fuzzy Closure Spaces. Axioms. 2020; 9(2):63. https://doi.org/10.3390/axioms9020063
Chicago/Turabian StyleMočkoř, Jiří. 2020. "Functors among Relational Variants of Categories Related to L-Fuzzy Partitions, L-Fuzzy Pretopological Spaces and L-Fuzzy Closure Spaces" Axioms 9, no. 2: 63. https://doi.org/10.3390/axioms9020063
APA StyleMočkoř, J. (2020). Functors among Relational Variants of Categories Related to L-Fuzzy Partitions, L-Fuzzy Pretopological Spaces and L-Fuzzy Closure Spaces. Axioms, 9(2), 63. https://doi.org/10.3390/axioms9020063



