Complex Dynamics in a Minimal Model of Protection-Based Mutualism

Abstract

This paper presents the first five variable model of mutualism motivated by the interaction between ants and homopterans. In this mutualism, homopterans benefit both directly through increased feeding rates and indirectly through predator protection. Results of our analyses show oscillatory, complex, and chaotic dynamic behavior. In addition, we show that intraspecies interactions are crucial for closing trophic levels and stabilizing the dynamic system from potential “chaotic” behavior.

1. Introduction

Despite calls throughout the past half-century for a more general perspective on the importance of mutualism in ecological systems [1], relatively few studies have explored the effects of mutualism on the dynamics of ecological systems. While modeling efforts have been a dominant focus of studies on predator–prey or competitive interactions [2], recent studies of mutualism have focused on understanding the context-dependency of outcomes [3] or on expanding the scope of participants to include multiple partners [4]. In this paper, we consider the population dynamic consequences of a protection-based mutualism that includes multiple mechanisms of benefit. In protection mutualism, a protector species helps a host species in return for a resource reward. This assistance by the protector species can take several forms, such as removal of the host species’ predator, tending the young of the host species, or protection against parasites. Protection mutualism is both geographically widespread and considers a diverse range of taxa, including interactions between cleaner fish and their hosts [5], ants and plants that produce extrafloral nectar [6], and ants and herbivores [7,8].

The interaction between ants and homopterans has become a model system for studies of protection mutualism. In this interaction, ants protect homopterans by removing their predators (e.g., lady beetles and spiders) in exchange for honeydew, a sugary waste-product excreted by homopterans [7,8]. Because ants remove accumulated honeydew, many homopterans benefit from ant-tending both directly, via enhanced feeding efficiency [9,10,11,12], as well as indirectly, via predator removal [11,13].

The interaction between ants and homopterans is considered conditional [14] in part because the degree to which treehoppers benefit depends on the level of ant-tending, which depends itself on the density of homopterans [11,13,15]. This density-dependent effect of mutualism follows from the consumer-resource basis of the interaction—in this system ants are consuming honeydew and provide by-product benefits to homopterans in return [16]. Recent modeling approaches have leveraged the consumer-resource basis of this interaction by using modified consumer-resource models that incorporate saturating functional “responses” by consumers to characterize patterns of density-dependent benefit resulting from consumer “satiation” [17]. We follow this approach here.

The structure of this paper is as follows: Section 2 introduces the model’s mechanism, constructs the mathematical foundation for the model, and analyzes the model utilizing linear stability analysis of a system of ordinary differential equations (ODEs). Section 3 looks at time series and phase plane diagrams for different combinations of variables. Section 4 examines Poincare sections of maxima as bifurcation diagrams. We conclude in Section 5 with a discussion of the implications of our results, mainly the importance of intraspecies interaction terms and mathematical chaos in ecological models.

2. Minimal Model of Protection-Based Mutualism

The analysis of population dynamics in ecological systems is credited to Alfred Lotka’s work on autocatalytic steps in chemical oscillations [18]. Independently, Vito Volterra utilized similar differential equations in studying the relationship between fish and shark in the Adriatic Sea [19]. The model later became known as the Lotka–Volterra Model (LVM) and has remained the basis for much of population dynamics analysis for the past century. However, the LVM is a highly restricted model that, while still used greatly today, has been replaced by several other models that better model ecological reality.

In this section, we propose a mechanism for some of the interactions between homopterans and ants on a single plant. We consider five variables in this model: Plant quality (G), Untended homopterans (I), Tended homopterans ($I_m$), Ants (A), and uncollected honeydew, or Waste (W), which interact according to the following set of interactions:

$$\begin{array}{cc}\hfill G\stackrel{k_o}{\to }& G+G\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill G+I\stackrel{k_{n1}}{\to }& I+I\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill I\stackrel{k_w}{\to }& I+W\hfill \end{array}$$

(1c)

$$\begin{array}{cc}\hfill A+W\stackrel{k_r}{\to }& A+A\hfill \end{array}$$

(1d)

$$\begin{array}{cc}\hfill A+I\stackrel{k_m^{+}{k}_m^{-}}{\rightleftharpoons }& I_m\hfill \end{array}$$

(1e)

$$\begin{array}{cc}\hfill G+I_m\stackrel{k_{n2}}{\to }& I_m+I\hfill \end{array}$$

(1f)

$$\begin{array}{cc}\hfill I+I\stackrel{k_f}{\to }& I\hfill \end{array}$$

(1g)

$$\begin{array}{cc}\hfill I_m+I_m\stackrel{k_{fm}}{\to }& I_m\hfill \end{array}$$

(1h)

$$\begin{array}{cc}\hfill I\stackrel{k_d}{\to }& \varphi \hfill \end{array}$$

(1i)

$$\begin{array}{cc}\hfill I_m\stackrel{k_{dm}}{\to }& \varphi \hfill \end{array}$$

(1j)

$$\begin{array}{cc}\hfill W\stackrel{k_q}{\to }& \varphi \hfill \end{array}$$

(1k)

Notice that, for each mechanistic step, the actual functional form of interaction requires an ecological interpretation, like in the MacArthur–Rosenweig [20] model, which used Holling-type functional responses to describe satiation of the predators.

In contrast with chemical reaction, our set of interactions does not follow the Mass Action Laws. Consequently, for each interaction, we need to propose a phenomenological expression for the rate of each process. We start with Equation (1a), which represents plant growth and considers a logistic growth, where the rate is a function of the plant density G, a rate constant $k_{\circ }$, and the carrying capacity, $G_{\circ }$, yielding the following rate:

$$r_{1a}=k_{\circ }\left(1-{\displaystyle \frac{G}{G_{\circ }}}\right)G$$

(2)

In Equation (1b), we represent the interaction between the insects (I) and the plants (G). In this case, it is known that the insects produce waste (W) that interfere with their development. To model the rate, we consider a Holling-type function for the interaction between the insect and the plant, which shows saturation or satiation, represented by $K_G$. To consider the negative effect of the waste (W), we include a term $(K_z+W)$ in the denominator, yielding the following expression for the rate:

$$r_{1b}={\displaystyle \frac{k_{1m}{K}_{Z}GI}{(K_z+W)(K_G+G)}}$$

(3)

where the term $\alpha r_{1b}$ represents the rate of plant consumption. The next step, Equation (1c), considers the production of waste by the insect, which is proportional to the insect population. Thus, we use a simple term for the rate, $k_{w}I$. Equation (1d) models the consumption of waste by the ants, which represents an additional source of food for the ants. For this process, we consider a simple Holling-type function that shows satiation, $K_r$, with the following rate:

$${\displaystyle \frac{k_{r}WA}{K_r+W}}$$

(4)

Additional parameters, $\gamma$ and $\delta$, are associated with the net effect on ant population, $\left(A\right)$, and waste (W).

The interaction of ants and insects yields the so-called tended insects. Here, we consider a simple one to one reversible interaction, represented by the rates $k_m^{+}AI$, and $K_m^{-}{I}_m$. The next step, Equation (1f), represents the growth of the tended insects $\left(I_m\right)$, with a rate that follows a Holling-type function,

$${\displaystyle \frac{k_{n2}G{I}_m}{K_G+G}}$$

(5)

This rate, if multiplied by $\alpha$ or $\beta$, determines the effects on the plants (G) and the insect populations (I). Notice that there is no negative effect due to the accumulation of waste, because the ants remove the waste around the tended insects. Next, Equations (1g) and (1h) represent the intraspecies interaction, which can be interpreted as a “fighting” term or a “cannibalistic” interaction, found when the populations reach large values. This interaction has a simple rate proportional to the square of the population. In contrast, insect death rate, represented by Equation (1i), is proportional to its population. For the waste degradation, Equation (1k), however, the process reaches a maximum rate for large values of the waste. Therefore, we propose a simple waste degradation rate,

$${\displaystyle \frac{k_{q}W}{K_q+W}}$$

(6)

Finally, we consider a logistic growth for the ants, independent of the waste, in which the rate is characterized by a carrying capacity of $A_{\circ }$ and a rate constant $r_A$.

In this new model, we, in particular, consider plant quality which increases at a rate of $k_o$, and reflects the primary food source for both Untended and Tended homopterans. Thus, homopterans reproduction is inherently dependent on $k_o$. As the homopterans feed on plants, they produce waste (honeydew) at a rate of $k_w$ that is both proportional to the number of homopterans present in the system and also serves to attract ants. In the presence of ants, the population of untended homopterans decreases as the two species enter into a mutualistic relationship to form a paired species, $I_m$, at a rate of $k_m^{+}$. Dissociation of the paired species ($k_m^{-}$) is possible, albeit at a significantly lower rate than $k_m^{+}$. The waste the tended homopterans produce is not accumulated in the system, as the tending ants consume any waste produced as a secondary food source. The homopterans reproduce unimpeded by their waste and the next generation of nymphal homopterans are eventually tended by the ants. As the population of untended and tended homopterans increase, intraspecies interactions reduce the population size at rates of $k_f$ and $k_{fm}$, respectively. These intraspecies interactions can be understood as intraspecific competition for resources [21]. Untended homopterans die at a rate of $k_d$ and tended homopterans die at a rate of $k_{dm}$. Honeydew, (W), that is not consumed is degraded at a rate of $k_q$.

From this mechanism, we construct the following system of ordinary differential equations (ODEs) to express the system’s dynamics. Below we provide the dimensional ODEs characterizing the mechanism described above. This model can be considered a modified mechanism based upon the MacArthur–Rosenweig model, which includes the effect of waste on the growth of untended homopterans, as well the relevance of the intraspecies interactions.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dG}{dt}}=k_o\left(1-{\displaystyle \frac{G}{G_o}}\right)G-{\displaystyle \frac{\alpha k_{n1}{K}_{z}GI}{(K_z+W)(K_G+G)}}-{\displaystyle \frac{\alpha k_{n2}G{I}_m}{(K_G+G)}}\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dI}{dt}}={\displaystyle \frac{\beta k_{n1}{K}_{z}GI}{(K_z+W)(K_G+G)}}-k_{d}I-k_f{I}^2+{\displaystyle \frac{\beta k_{n2}G{I}_m}{(K_G+G)}}-k_m^{+}AI+k_m^{-}{I}_m\hfill \end{array}$$

(7b)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d{I}_m}{dt}}=k_m^{+}AI-k_m^{-}{I}_m-k_{dm}{I}_m-k_{fm}{I}_m^2\hfill \end{array}$$

(7c)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dA}{dt}}=r_A\left(1-{\displaystyle \frac{A}{A_o}}\right)A+{\displaystyle \frac{\gamma k_{r}WA}{K_r+W}}-k_m^{+}AI+k_m^{-}{I}_m\hfill \end{array}$$

(7d)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dW}{dt}}=k_{w}I-{\displaystyle \frac{k_{q}W}{K_q+W}}-{\displaystyle \frac{\delta k_{r}WA}{K_r+W}}\hfill \end{array}$$

(7e)

For a thorough “translation” from a mechanism to a system of ODEs, we recommend our previous work [21].

In our set of ODES, we define $\alpha ,\beta ,\delta ,$ and $\gamma$ as the turnover constants, $G_o$ and $A_o$ are carrying capacities for plant quality and ants (respectively), and $K_G$, $K_z$, $K_r$, and $K_q$ are satiation constants for plant quality and waste. The inclusion of logistic growth terms for both plant quality and ants is due to their nonuniform reliance on variables within the system as necessary for growth or death. That is, their rates of reproduction and death are not dependent on variables within the mutualistic system; even if the homopterans stop producing waste to attract and feed the ants, the waste is a secondary food source for the ants (i.e., they have a primary food source that has greater control on their growth and death rates).

As is common practice, to reduce the number of parameters, we scale Equations (8a)–(8e) by using the following definitions: $\tau \equiv t{k}_d,s\equiv K_G,X\equiv G/s,Y\equiv I/s,Y_m\equiv I_m/s,M\equiv A/s,Z\equiv W/s,r\equiv k_o/k_d,r_m\equiv r_A/k_d,X_o\equiv G_o/s,M_o\equiv A_o/s,k_1\equiv \alpha k_{n1}/k_d=\alpha k_{n2}/k_d,k_2\equiv \beta k_{n1}/k_d=\beta k_{n2}/k_d,k_r^{\prime }\equiv \gamma k_r/k_d,k_{rr}\equiv \delta k_r/k_d,K_r^{\prime }\equiv K_r/s,K_z^{\prime }\equiv K_z/s,K_q^{\prime }\equiv K_q/s,k_q^{\prime }\equiv k_q/k_{d}s,k_{mp}\equiv k_m^{+}{K}_G/k_d,k_{mm}\equiv k_m^{-}/k_d,k_f^{\prime }\equiv k_f{K}_G/k_d,k_{fm}^{\prime }\equiv k_{fm}{K}_G/k_d,k_{dm}^{\prime }\equiv k_{dm}/k_d,k_w^{\prime }\equiv k_w/k_d$. This scaling yields the following dimensionless set of ODEs:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dX}{d\tau }}& =r\left(1-{\displaystyle \frac{X}{X_o}}\right)X-{\displaystyle \frac{k_1{K}_{z}XY}{(K_z+Z)(1+X)}}-{\displaystyle \frac{k_{1}X{Y}_m}{(1+X)}}\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill {\displaystyle \frac{dY}{d\tau }}& ={\displaystyle \frac{k_2{K}_{z}XY}{(K_z+Z)(1+X)}}-Y-k_f{Y}^2+{\displaystyle \frac{k_{2}X{Y}_m}{(1+X)}}-k_{mp}MY+k_{mm}{Y}_m\hfill \end{array}$$

(8b)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{Y}_m}{d\tau }}& =k_{mp}MY-k_{mm}{Y}_m-k_{dm}{Y}_m-k_{fm}{Y}_m^2\hfill \end{array}$$

(8c)

$$\begin{array}{cc}\hfill {\displaystyle \frac{dM}{d\tau }}& =r_m\left(1-{\displaystyle \frac{M}{M_o}}\right)M+{\displaystyle \frac{k_{r}ZM}{K_r+Z}}-k_{mp}MY+k_{mm}{Y}_m\hfill \end{array}$$

(8d)

$$\begin{array}{cc}\hfill {\displaystyle \frac{dZ}{d\tau }}& =k_{w}Y-{\displaystyle \frac{k_{q}Z}{K_q+Z}}-{\displaystyle \frac{k_{rr}ZM}{K_r+Z}}\hfill \end{array}$$

(8e)

where we have dropped the primes for simplicity. Notice that all terms that take the form $K_{\alpha }+Z$ are production terms that, per the MacArthur–Rosenweig model, take into account satiation of waste, whereas all terms that take the form 1 + X are production terms that take into account satiation of plant quality.

In order to perform analytic and numerical analyses, we use linear stability analysis to understand what happens to the system when it is slightly perturbed [22]. In the first step of linear stability analysis we set the right-hand side of the differential equations equal to zero and solve for the steady state values, $X^{SS},Y^{SS},Y_m^{SS},M^{SS}$, and $Z^{SS}$. Once these steady-state solutions are obtained, we study what would happen to the dynamic variables when the solutions are slightly perturbed, as to see if the perturbations would grow or die out. In this approach we calculate the relaxation matrix associated with the set of ODEs in Equation (8a):

For our analysis we consider parameter values, in

Table 1. Dimensionless parameter values.

$r=4.8$	$X_o=8.0$	$M_o=2,0$	$k_{mp}=6.0$
$k_f=0.001$	$k_{fm}=0.001$	$k_w=12.0$	$K_q=0.2$
$k_{mm}=1.0$	$k_{dm}=1.0$	$K_r=0.2$	$r_m=2.0$
$k_r^{\prime }=k_{rr}=5.0$	$k_q=10.0$	$k_1=k_2=1.3$	$K_z=5.0$

, used in our previous work [21,23] (Table 1):

The steady state solutions of the ODEs yield multiple solutions, and we consider only the physically relevant ones, which are real and positive. Of these six physical solutions, only one is consistent with the coexistence of all the five species. The other five steady solutions imply the extinction of one, or several of the species, including total extinction. If we consider a notation $(X,Y,Y_m,M,Z)$ for the steady solutions of (Plants, Untended, Tended, Ants, and Waste), the steady state solutions for the parameters in Table 1, are: (0,0,0,0,0), (8,0,0,0,0), (8,0,0,2,0), (0,0,0,2,0), (7.86,0.66,0,0,0.76), and (3.82,1.37,8.14,1.99,0.93).

For the coexistence steady state: (3.82,1.37,8.14,1.99,0.93), the determinant is $-88.7421$ and of the five eigenvalues associated with the relaxation matrix, one is real negative and four are complex with negative real part: $-21.360,-0.959752\pm i2.98211$, $-0.170365\pm i0.627922i$. Therefore, for this particular set of parameters the coexistence steady state is stable.

Since our main goal is to show that our model can sustain simple and complex dynamics, we select a reduced set of parameters and initial conditions that we have used before [21,23]. By no means is our analysis extensive, because our model is the first to address the conditions for protection-based mutualism, and we want to show that its dynamic properties are worth analyzing.

3. Time Series and Phase Plane Diagrams

In this section we consider time series as well as phase planes diagrams of different combinations of the five variables. For the numerical integration we use XXPAUT [24] with adaptive Runge–Kutta, Gear, stiff integrators, and an error tolerance of $1\times {10}^{-8}$. We consider the effect of the rate constants $k_w$ (the rate of production of waste by untended homopterans), $k_{mp}$ (the rate of conversion of untended homopterans and ants into tended homopterans), $k_f$ (the intraspecies interaction rate for untended homopterans), and $k_{fm}$ (the intraspecies interaction rate for tended homopterans). In particular, we focus on the effect of these rate constants on Y (untended homopterans), $Y_m$ (tended homopterans), and M (ants). Using the integration software AUTO [24] and the parameters in Table 1, we observe three separate bifurcations for $k_w$ occurring in this system: a transcritical bifurcation at $k_w=3.974$, a period doubling Poincare–Andronov–Hopf (PAH) bifurcation between $k_w=8.653$, and a period doubling bifurcation at $k_w=8.845$. These values are of particular interest, and as such subsequent analysis of the time series and phase planes diagrams is based upon and around these values.

3.1. Time Series for Different Values of the Rate Constant of Waste Production, $k_w$

For different values of $k_w$, we set the following initial conditions for the five variables, as in our previous work [21]: $X=4.7$, $Y=0.6$, $Y_m=0$, $M=2$, $Z=0$. For simplicity and as the first analysis of a new five variable model of protection-based mutualism, all integrations utilize the same initial conditions, as well as the parameter values specified in Table 1, unless noted otherwise. Definitely, other initial conditions should be considered, but given our goals, the novelty of the model, and length of the analysis, we defer such analysis to future publications. As we mentioned before, we want to show some of the complex dynamics of the model that are relevant and comparable to the dynamics of other ecological models.

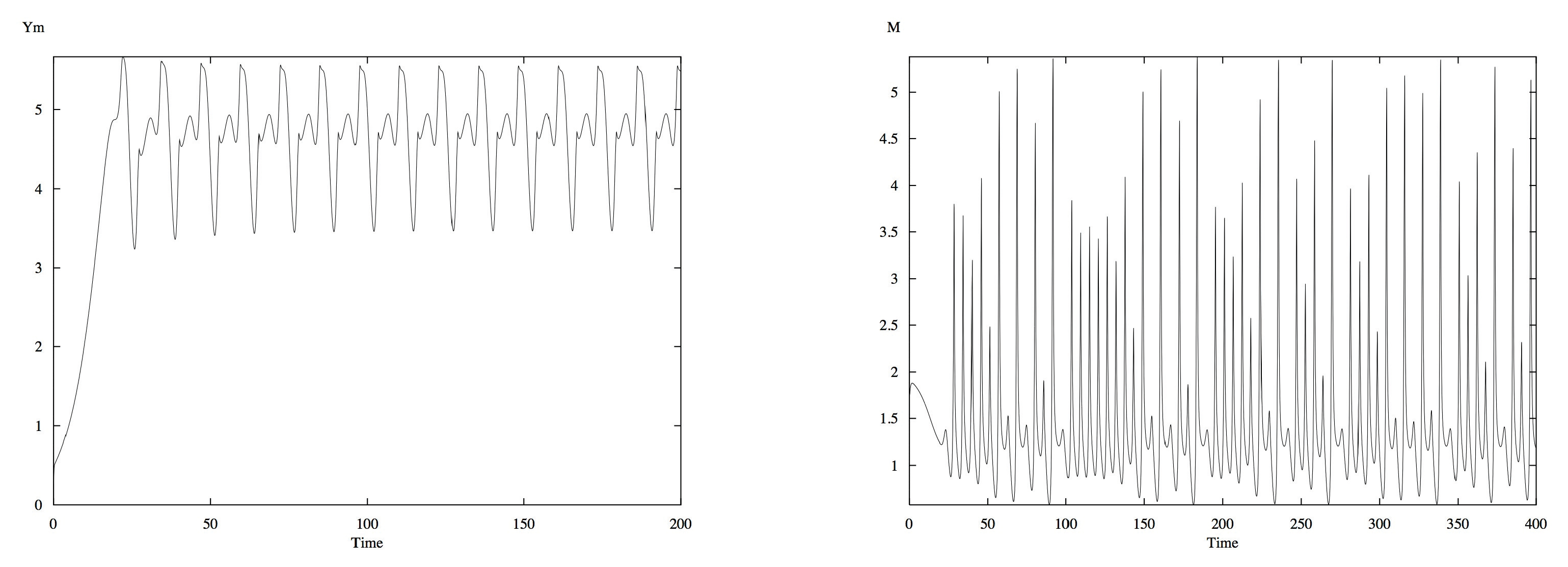
First, we vary $k_w$. For low rates of waste production ($0<k_w<4.7$), the concentration of all variables reach and stay at their steady states. As $k_w$ increases from 4.7, oscillations quickly begin to occur. While the oscillations are both periodic and stable, as $k_w$ approaches 6.12, the oscillations become more complex. Period doubling occurs at $k_w=7.288$, and a variety of complex oscillations are displayed, along with additional period doubling, in Figure 1a. The time series exhibit the most complex and aperiodic oscillations around $k_w=8.76$, seen in Figure 1b, but subsequently decrease in complexity and return to stable periodic behavior as $k_w$ increases to 9.658. As $k_w$ increases further, the oscillations decrease in amplitude size, increase in frequency, and, by $k_w=11$, all of the oscillations had died out and all the variables returned to their corresponding steady state values.

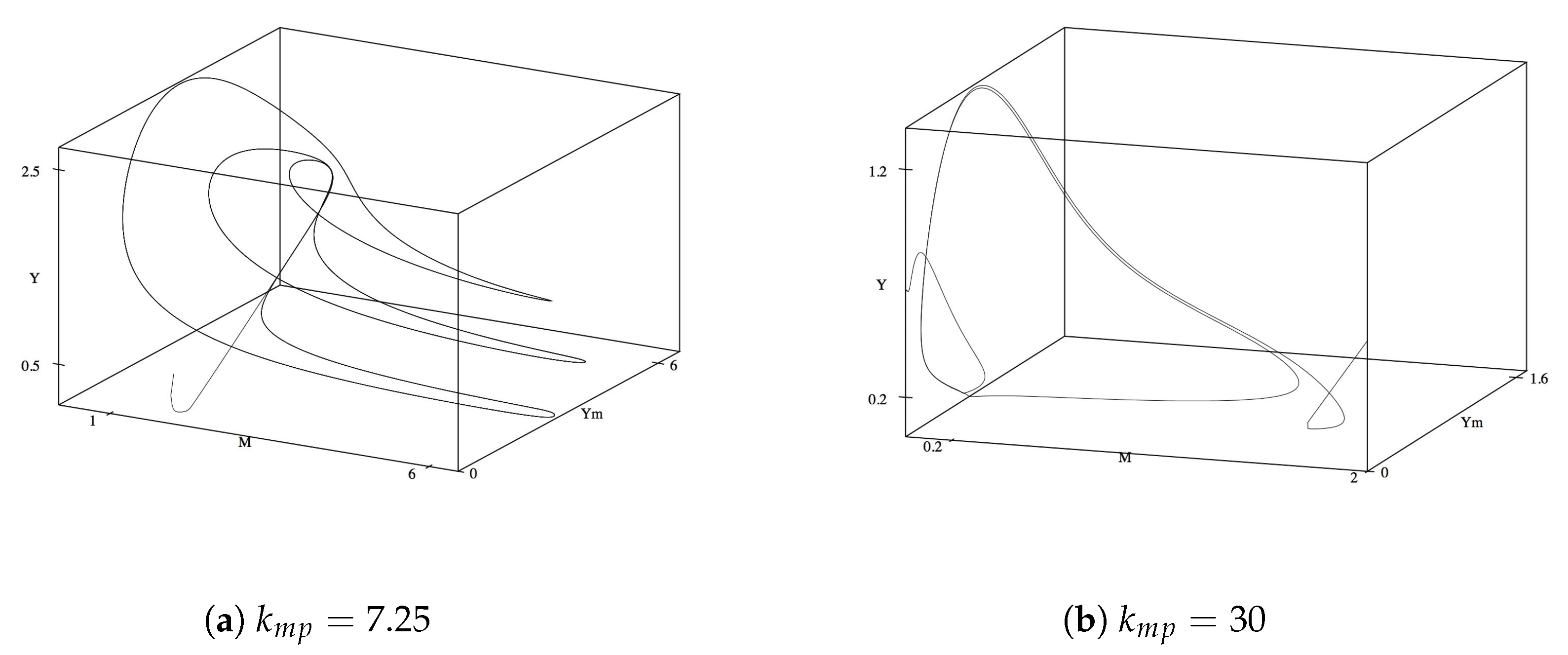
3.2. Phase Planes for $k_w$

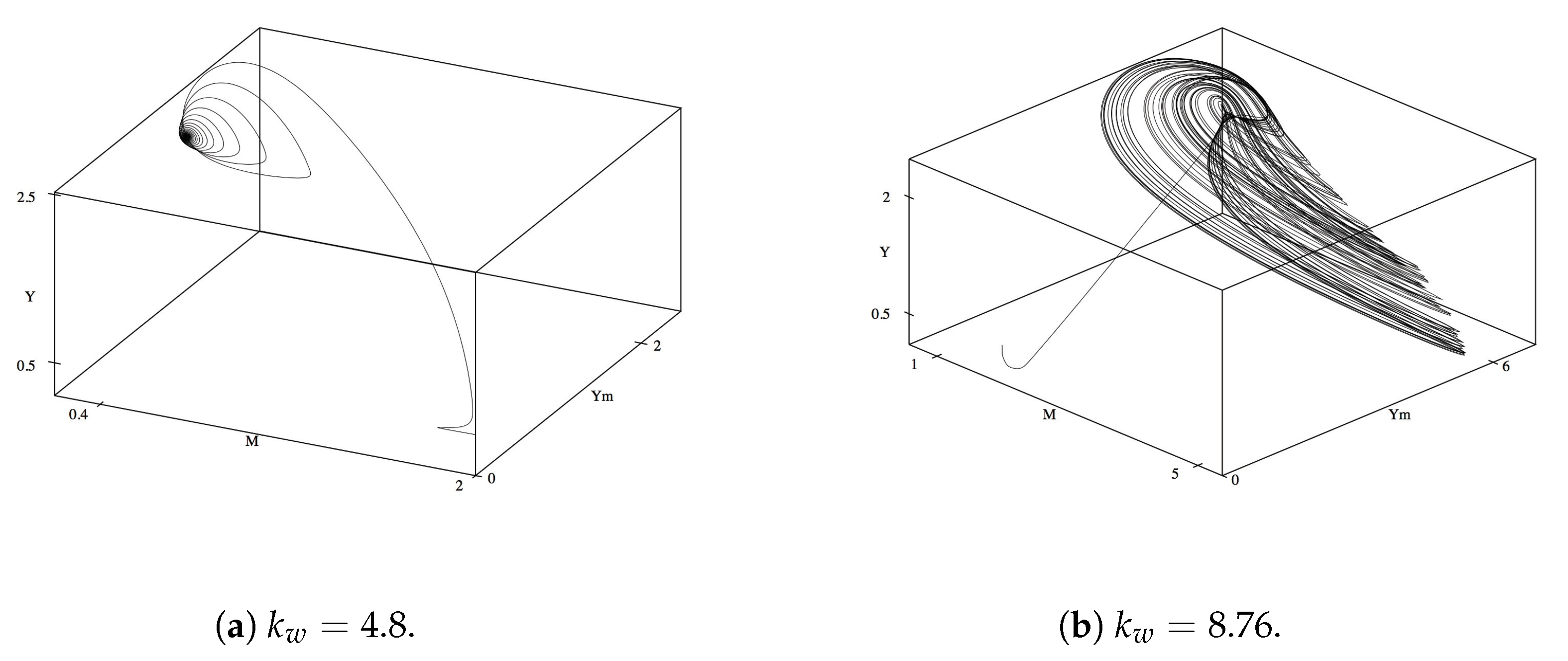
To understand the interdependence of the variables on one another, we look at the phase plane diagrams of different combinations of variables. We first consider M, $Y_m$ and Y as to understand the central variables for the mutualistic relationship. For the initial and reference value, $k_w=0$, all three variables reach their corresponding steady state levels and maintained steady values until $k_w$ reaches approximately 4. As $k_w$ increases to 4.8, oscillations begin to occur, as seen in Figure 2a. The oscillations become more complex as $k_w$ reaches 6.8. We also observe multiple period doubling incidents in Figure 2b. As with the time series, after $k_w=9.7$, the complexity of the oscillations decrease, followed by spiraling into a stable steady state around $k_w=11$.

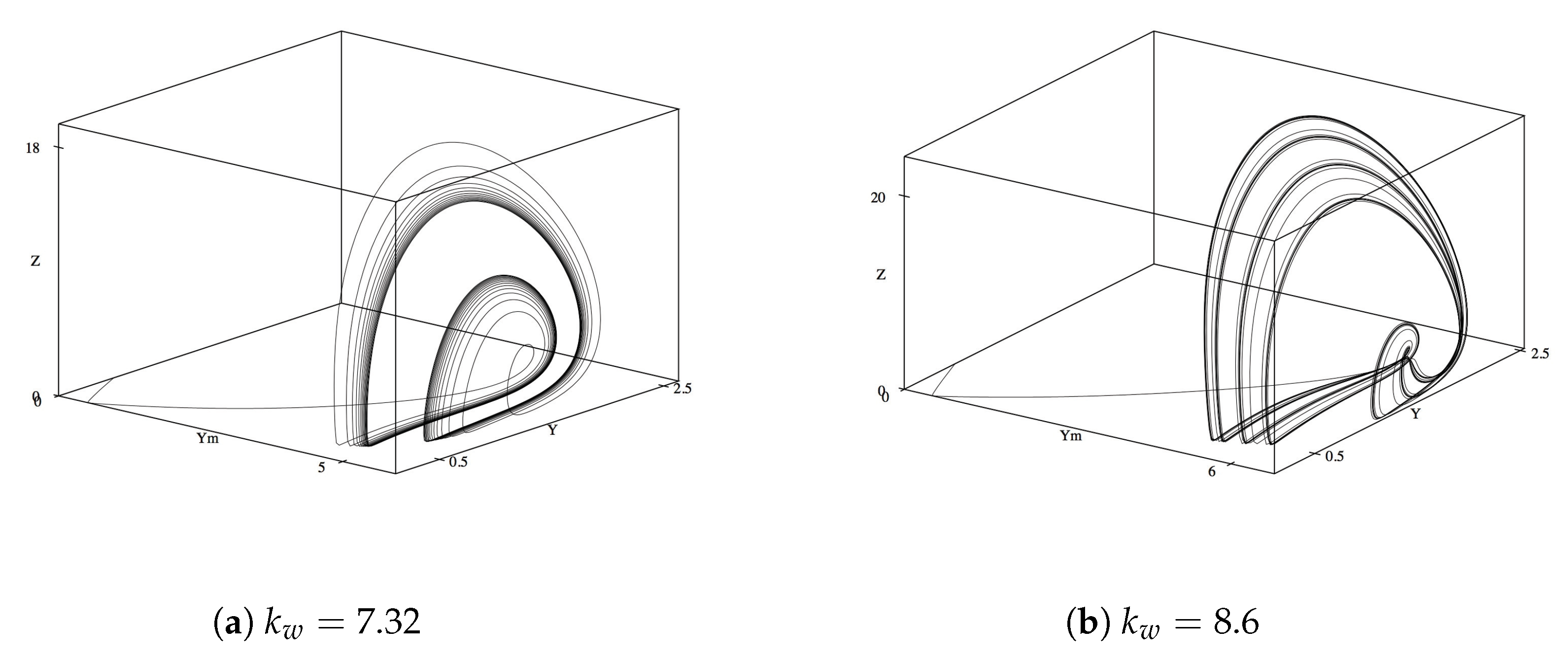
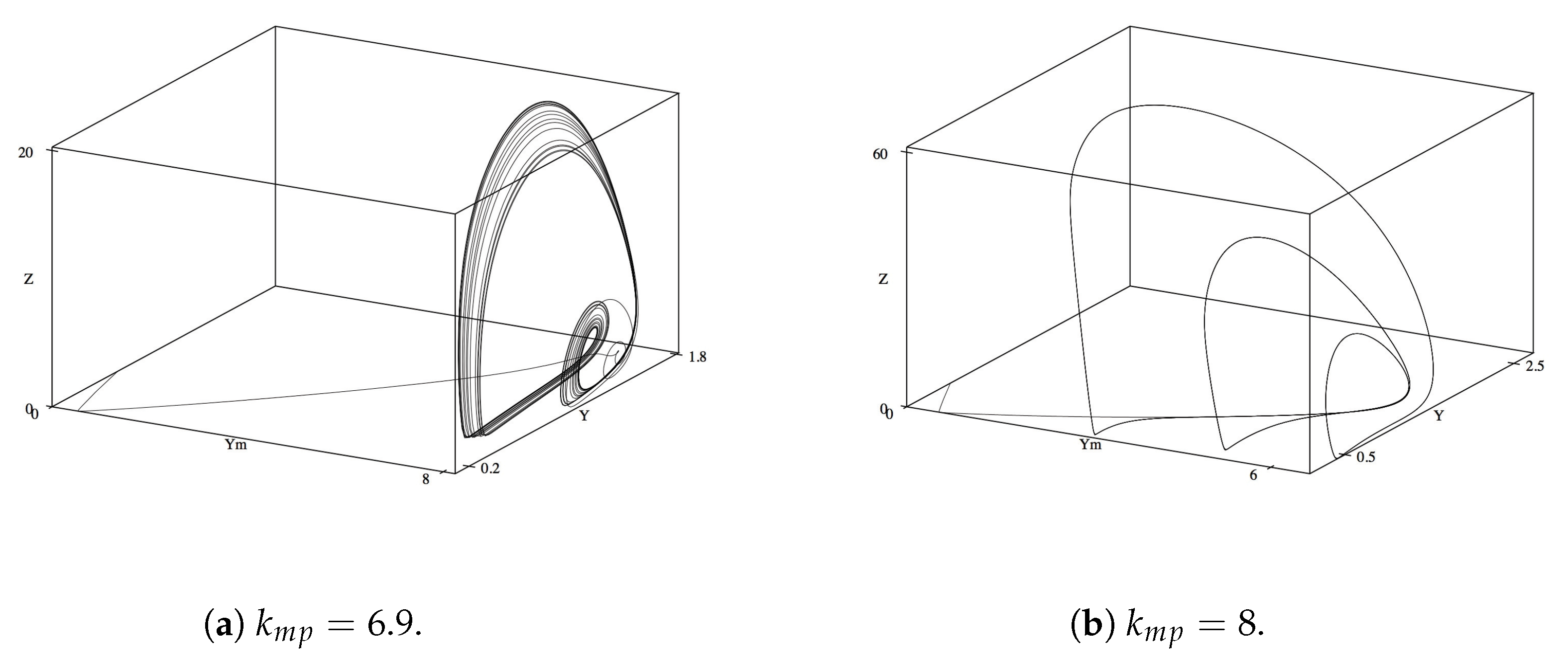
Next we look at phase diagrams for M, $Y_m$, and Z, so as to look at the dynamics of waste in relation to its ability to entice the ants to enter the mutualistic relationship and tend the homopterans. Compared to the previous phase diagram of Y, $Y_m$, and M, the relationship between M, $Y_m$, and Z exhibits less qualitatively complex oscillations and limit cycles. While the increases in $k_w$ varied the diagram at similar values as with the previous phase diagram, the variations and topological changes are less drastic (Figure 3a,b). Of note, the oscillatory behavior dies out at slightly lower $k_w$ values as compared with the phase diagrams in Figure 4 ($k_w=7.32$ instead of $k_w=8.4$). This might hint at the necessity of a stabilized production of waste as a precedent from which the untended homopterans can return to their steady state.

Finally, we consider the phase diagrams for Y, $Y_m$, and Z as to investigate the indirect relationship of waste in its conversion of untended homopterans into tended homopterans. Interestingly, these phase diagrams (Figure 5a,b) show that Y is more sensitive to Z compared to $Y_m$. Even as $k_w$ increases to values that exhibited complex and chaotic behavior and oscillations, unlike Y, $Y_m$ do not dramatically crash but rather remain at relatively stable values (between 4 and 7) throughout the entire range of $k_w$ values. This may point to an initial dependence of $Y_m$ on Z as M increases but, after reaching a high enough value, $Y_m$ might switch its main dependence from the waste production to other parameters.

3.3. The Ant Tending Rate Constant $k_{mp}$

Another parameter of great effect on the dynamic behavior of the system is $k_{mp}$, the rate at which untended homopterans and ants are, through the mutualistic relationship, converted into a paired species. We set $k_w$ back to its initial steady state value of 12 and subsequently vary $k_{mp}$. For $0<k_{mp}<6.6$ the concentration of all variables quickly reaches and remains at their steady state values. As $k_{mp}$ increases from 6.6, oscillations immediately begin to occur. These stable oscillations become complex at $k_{mp}=6.9$ (Figure 6a), but restabilize back to simple, periodic oscillations at $k_{mp}=8.0$ (Figure 6b). These stable oscillations continue until $k_{mp}=7.7$ where they become complex again until $k_{mp}=8.3$, whereafter the limit cycle decreases in size and complexity until $k_{mp}=30$, where $Y_m$ and M approaches zero and ($X,Y,Z$) reach their final steady state values. These results point to an upper limit on the systems capacity to have ants and tended homopterans as the mutualistic system collapses and/or the results become nonphysical.

Surprisingly, and unlike the previous variation for $k_w$, very small changes in $k_{mp}$ result in swift qualitative changes in the complexity of the oscillations (Figure 7a,b). Additionally, while for $k_w$ there is a continuous range of values that produce complex oscillations, there are two distinct ranges for $k_{mp}$ with an inner range where stable oscillations are observed ($6.9<k_{mp}<8.0$) (Figure 8).

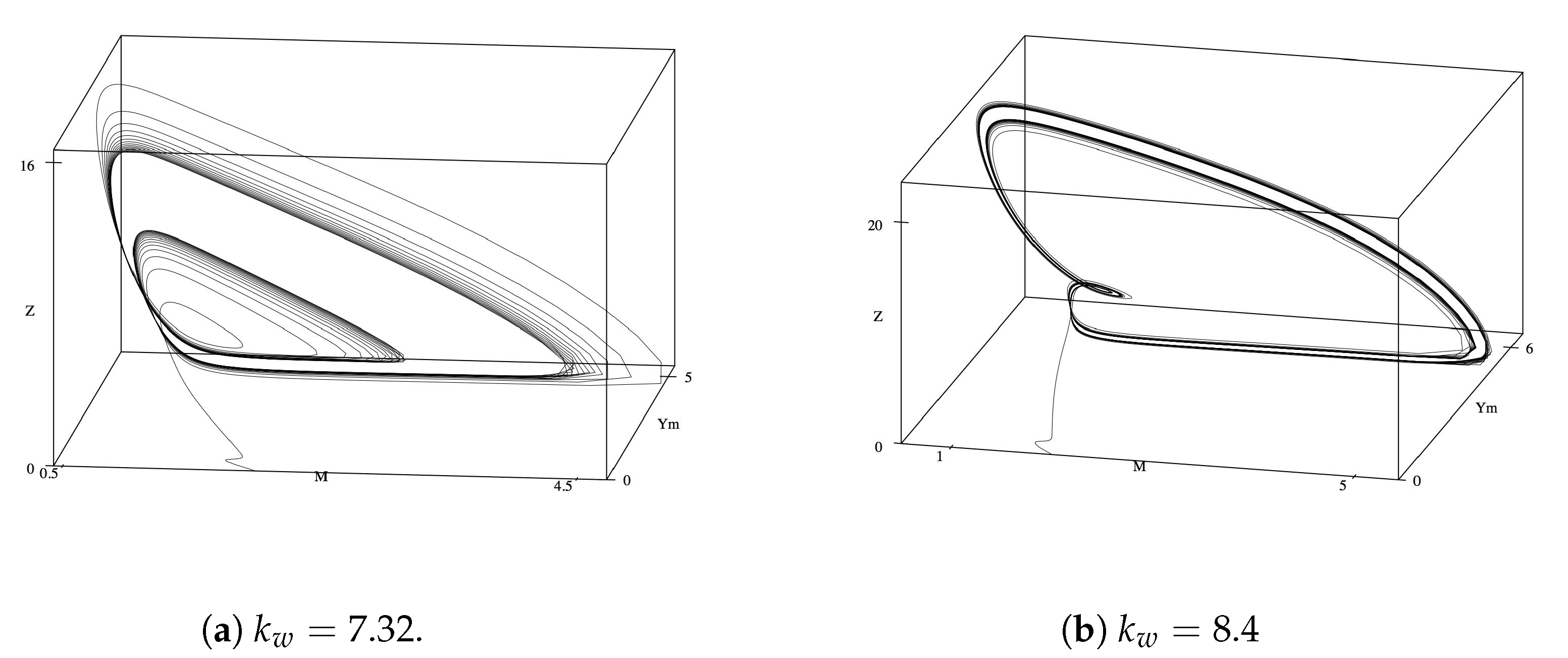
As with the phase plane analysis above, we first examine the phase plane of M, $Y_m$, and Y. From $0<k_{mp}<6.6$ all three variables remain in a stable steady state. Oscillations are exhibited as $k_{mp}$ increases from 6.6 and quickly become complex by $k_{mp}=6.9$ (Figure 8a). While the oscillations appeared to begin to stabilize and the limit cycles decrease as $k_{mp}=7.25$, we observe additional limit cycles and complex oscillations, when $k_{mp}$ reached 8.0 (Figure 8b). Curiously, these oscillations retain their general shape as $k_{mp}$ increases up to 30, thereafter the limit cycle brake and the variables return to their final steady state values.

The phase plane for M, $Y_m$, and Z, and Y, $Y_m$ and Z are similar in their general topology and limit cycle shape with the phase plane of M, $Y_m$, and Y with varying values of $k_{mp}$. We observe that the system reaches steady states from the initial values, $k_{mp}=0$, until approximately 6.9, complex oscillations until $k_{mp}=7.3$, a small period of stabilization until $k_{mp}=7.7$, a small period of additional complex oscillations until $k_{mp}=8.3$, and finally restabilization and decreasing size of limit cycle until the final steady state values are reached around $k_{mp}=30$ (Figure 7a,b).

The variations in $k_{mp}$, compared to $k_w$, have a smaller range of complex oscillatory behavior despite a larger range of values after such oscillations until the final steady state is reached. This points to a narrow but important sensitivity of the system on $k_{mp}$ for both tended and untended homopterans, as well as for ants. While complex limit cycles are present for a large range of $k_{mp}$ values, the swiftness in which the complex oscillations and crashing of certain variables to low levels occurs indicates that shocks to the system (e.g., weather patterns or depletion of a food source) that could increase or decrease the rate of $k_{mp}$ to this narrow range might have drastic ecological effects that, while mathematically would be recuperable, might be otherwise in reality.

3.4. The Rate Constants of Intraspecies Interactions, $k_f$ and $k_{fm}$

Another set of parameters that we investigate are $k_f$ and $k_{fm}$, the intraspecies interaction rates for untended and tended homopterans, respectively. These interactions are most easily interpreted in this system as intraspecific competition for resources. As described in previous work, Peacock–López [21] introduces the intraspecies interaction terms that can close trophic levels for a multi variable system. As such, we want to explore if similar effects are present for our five variable mutualism system.

All of the previous analysis of variations of the value of $k_w$ and $k_{mp}$ are for $k_f$ and $k_{fm}$ both equal to 0.001. Setting $k_f$ and $k_{fm}$ both equal to zero (open trophic levels) and setting all other parameters to their initial values, produce marginal changes in the steady state behavior of Y and $Y_m$ in comparison to $k_f$ and $k_{fm}$ both equal to 0.001. Next, we change $k_w$ and $k_{mp}$ to their respective complex oscillatory ranges, so as to see what would happen when $k_f$ and $k_{fm}$ are increased or decreased. In periods of complex behavior for varying $k_w$ ($7.2<k_w<9.7$), changing $k_f$ and $k_{fm}$ from 0.001 to 0 produced virtually the exact same time series and phase diagrams as when one or both of the values are equal to 0.001. Surprisingly, setting $k_{fm}$ equal to 0.001 and varying $k_f$ from 0 to 0.01 only slightly narrowed the range of complex oscillations for the time series of Y and $Y_m$. However, when setting $k_f$ equal to 0.001 and varying $k_{fm}$ from 0.001 to 0.005 to 0.007 to 0.01, we observe noticeable changes, as the increase in $k_{fm}$ reduces the range of complex behavior as well as the oscillatory range in general.

In accordance with the time series, the phase diagram displays similar topological changes in both the types of limit cycles as well as the existence of limit cycles in general when compared to the initial parameter values. As $k_{fm}$ increases from 0.001 up to 0.007, the limit cycle reduces in size and collapses into itself, eventually resulting in a new steady state at a lower $k_w$ value. Conversely, $k_f$ has to increase to approximately 0.1 for the complex limit cycles to collapse. These differing sensitivities of the system on $k_f$ and $k_{fm}$ highlight the homopterans’ interactions, both internal and external to the population, as fundamental for the system’s stability as a whole.

In this section we have shown examples of complex dynamics, and we have centered our parameter selection around the waste production, the tending, and the intraspecies interactions. These are relevant to understand the mutualistic relation between the ants and the insects. The interspecies parameter represents the closing of the trophic levels, which in many models is ignored yielding open trophic system, showing chaotic dynamics.

4. Bifurcation Diagrams

In this section we consider and examine the Poincare section of maxima. We plot only the maximum values of the time series using the software package INSITE [25] and evaluate such sections with an error tolerance of ${10}^{-12}$ and a stiff integrator. Given an initial condition, we fix $k_w$ and increase and decrease parameter values to get both forward and backward direction sections. These sections enable us to look at more specific and narrowly defined areas of complex or chaotic behavior, so as to further evaluate how changes in parameter values, mainly $k_f$ and $k_{fm}$, change the range of complex maxima behavior.

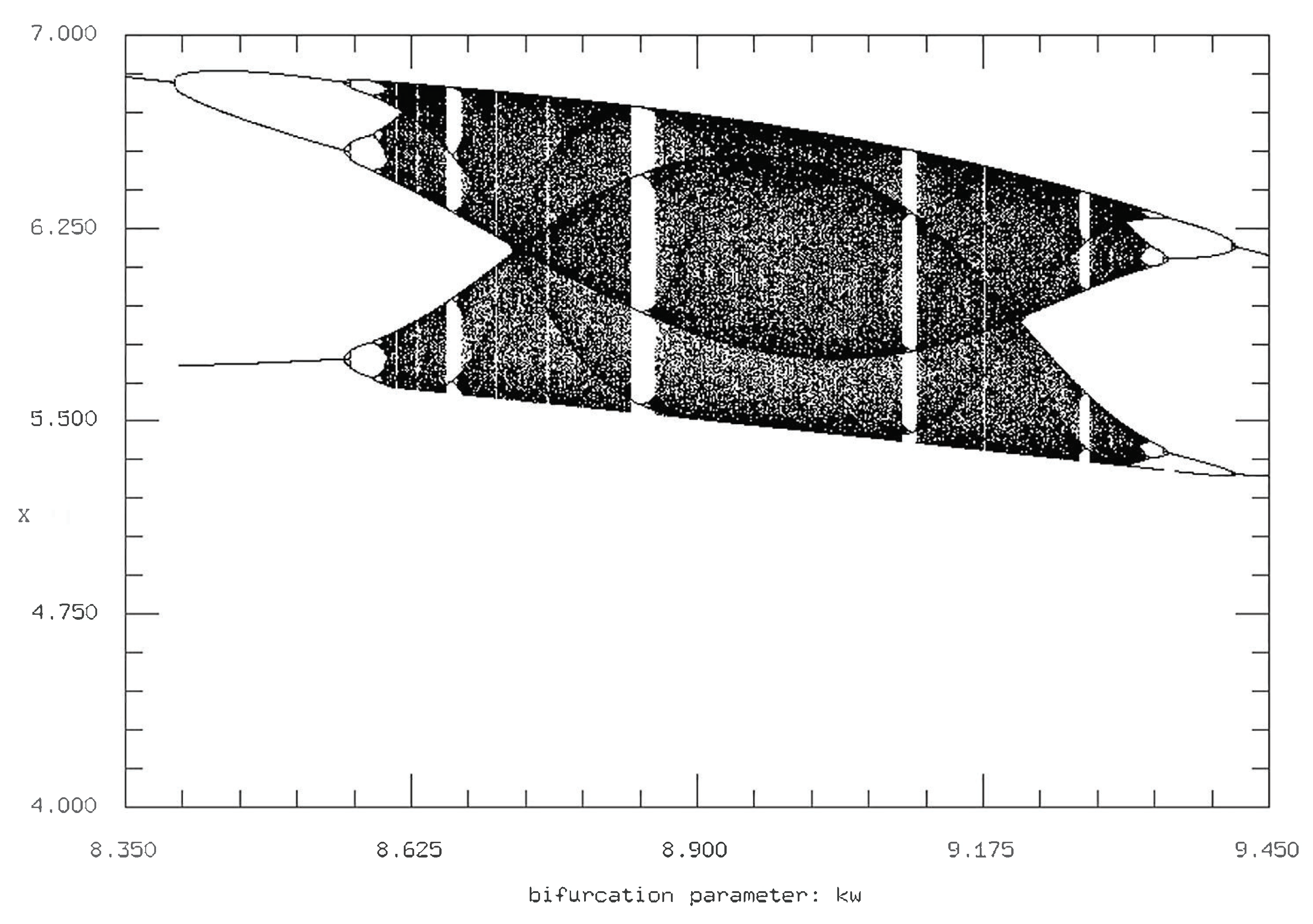
We first examine the Poincare sections of each of the variables plotted against $k_w$ to gain a baseline through which to compare other sections against in regards to the variables’ complexity at different values. We utilize $k_w$ as the main bifurcation parameter throughout due to its large range of complex behavior in comparison to other parameters such as $k_{mp}$ (Figure 9). This allow for easier comparison of qualitative differences in the bifurcations diagrams.

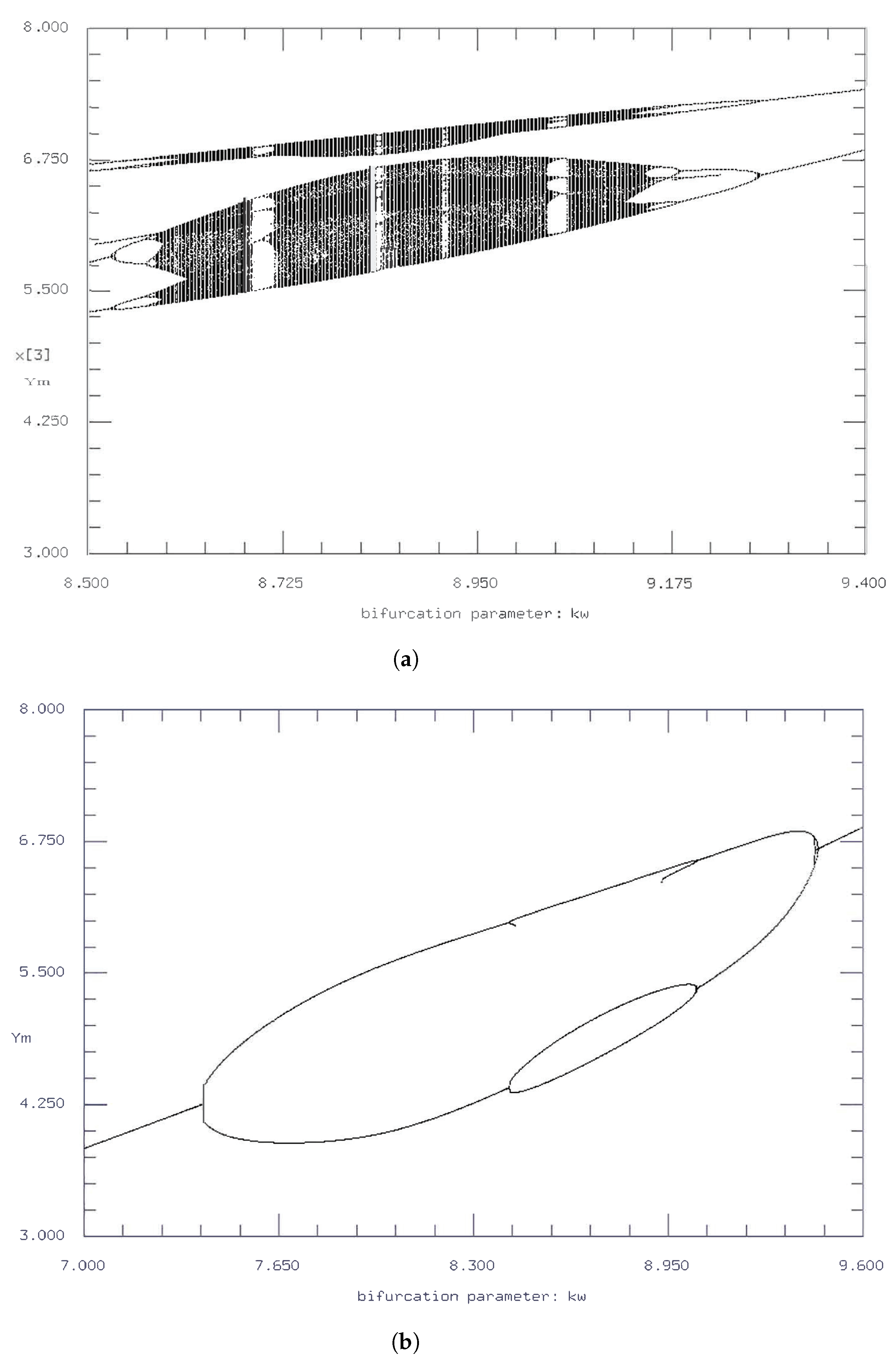
The bifurcation diagrams for the initial parameter values are in accordance with the time series and phase plane diagrams described above, where there are, for $k_w$ values between 7.2 and 9.8, a variety of complex behavior including multiple period doubling and cascading events. However, such complex oscillatory behavior is fundamentally temporary, as steady state values occurred both before and after the period doubling (Figure 10).

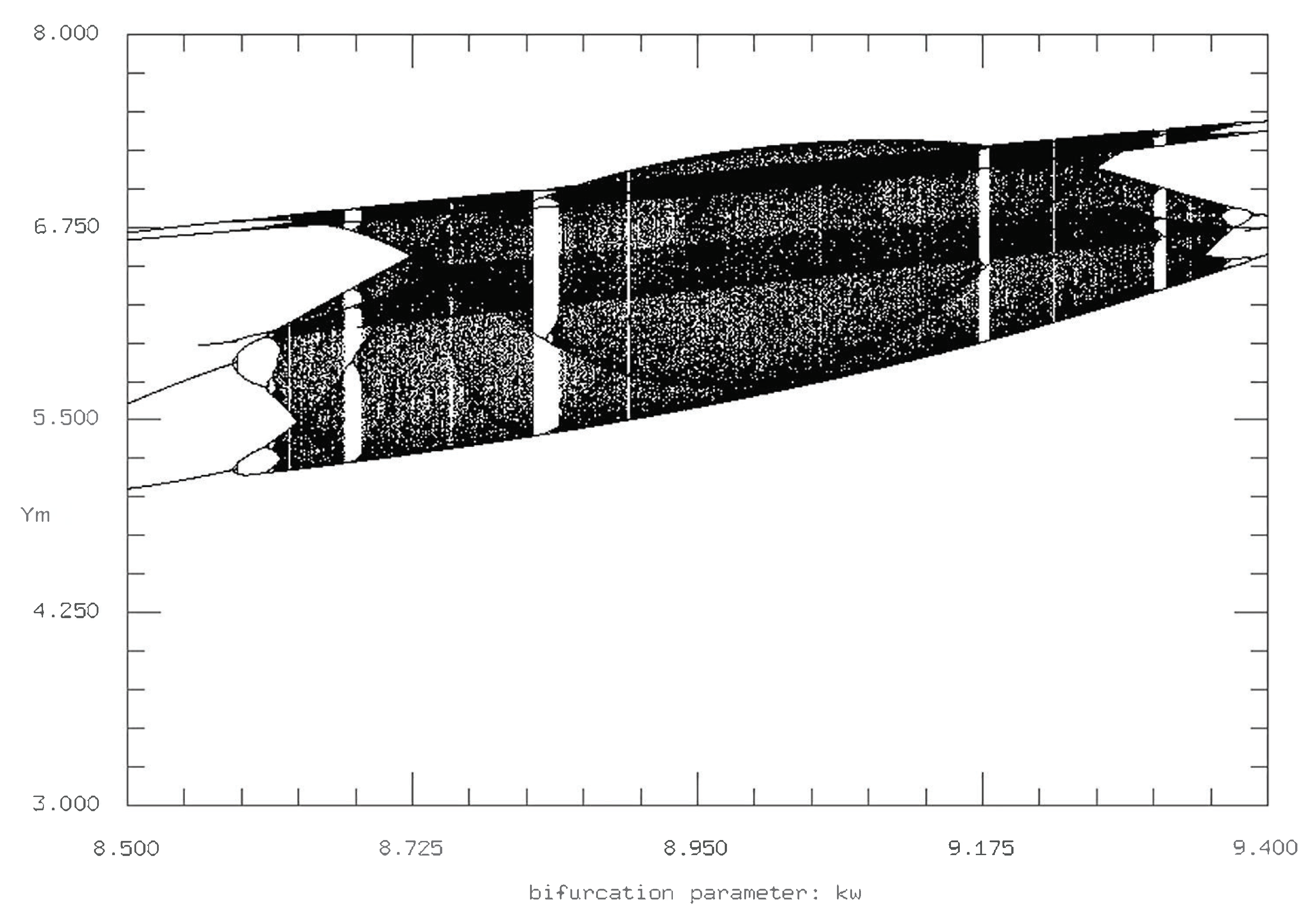
While in the time series, changing $k_f$ and $k_{fm}$ from 0.001 to 0 has little observable effect, the Poincare sections for $k_f$ and $k_{fm}$ both equal to 0 display interesting changes in complex behavior, where for all five variables, the boundaries of period doubling and complex behavior change (Figure 11). Furthermore, the uniformity of the complexity, that is the general structure of the period doubling and cascading, is more sporadic and complex as $k_f$ and $k_{fm}$ both equaled zero.

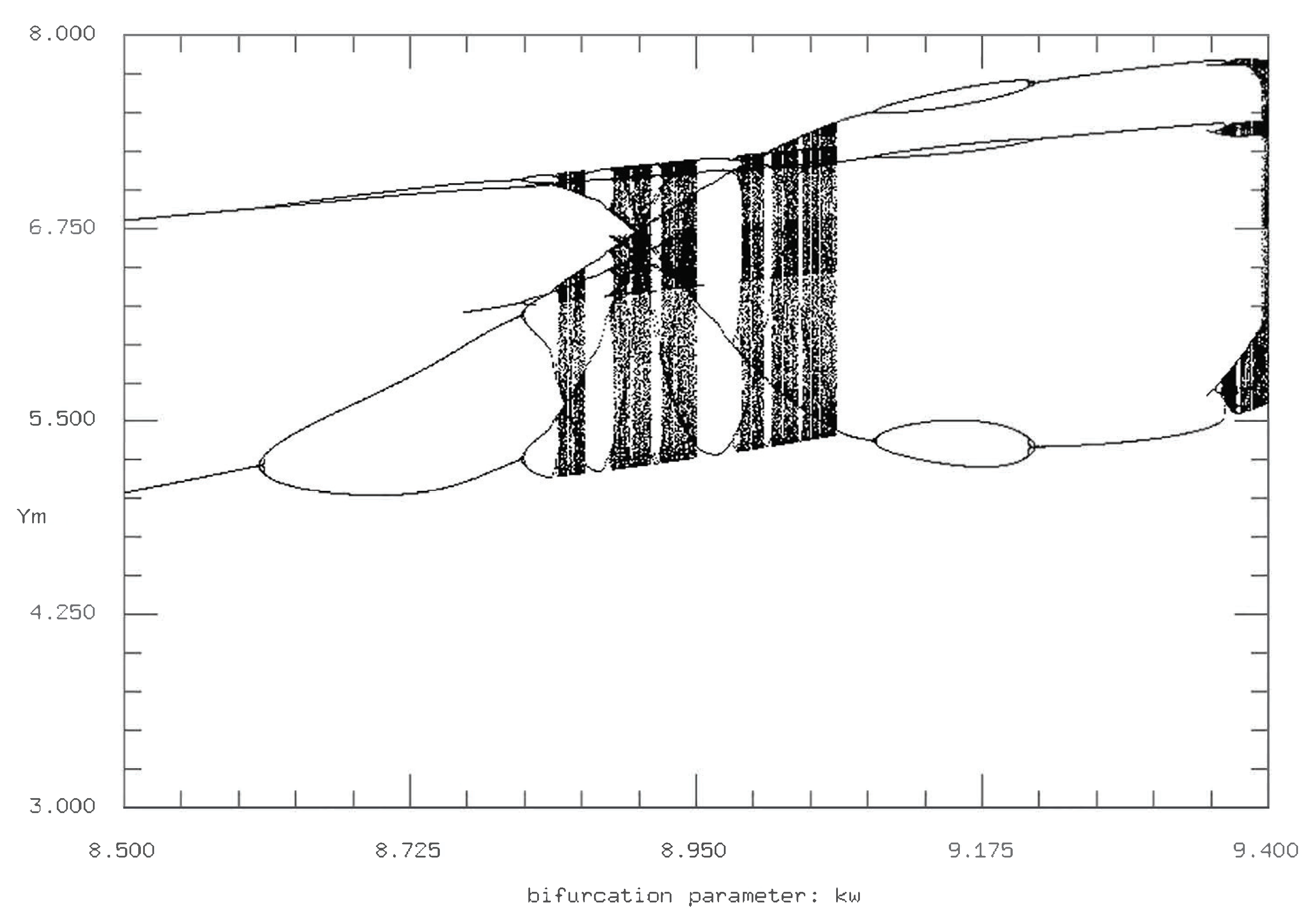
As with the time series, we fix either $k_f$ or $k_{fm}$ back at its initial parameter value of 0.001 and vary the other value. First, we fix $k_{fm}$ and vary $k_f$. The resulting Poincare sections are similar to those in Figure 11, where the difference between setting the intraspecies interaction rates at 0 and 0.001 is negligible, whereas setting them to a value above 0.005 produces measurable and important differences. However, of note, the Poincare sections for $k_f$ and $k_{fm}$ both equal to zero display a different period doubling cascade in comparison with $k_f$ and $k_{fm}$ both equal to 0.001 (Figure 10 and Figure 11). In particular, for the initial conditions of $k_f$ and $k_{fm}$ both equal to 0.001, the chaotic region is more consistent but also more structured; the two primary curves for the bifurcation both reach their maxima at the same $k_w$ value and then reverse period double back to the steady state.

In contrast, there is little (if any) uniformity to the structure of the period doubling and cascading for $k_f$ and $k_{fm}$ both equal to zero. As shown in Figure 11, while the initial period doubling is similar to that of the initial conditions, there is an abrupt return to stable/fixed points, followed by multiple period doubling and cascading, followed by additional chaos before the reverse period doubling back to the steady state. We can interpret this observation as a period of nonchaotic oscillations in between two periods of chaotic oscillations. Interestingly, this is similar to the oscillation regions for the time series with $k_{mp}$ as the varying parameter. The reason is that despite the visual lack of chaos in certain regions that would be predicted to exhibit chaos otherwise, the additional period doubling cascade and reverse doubling cascade adds additional layers of complexity to the system and the simulation that compensate for strictly defined chaotic oscillations.

While it appears that $k_f$ has to be increased tenfold to 0.01 to have qualitative changes in the phase plane diagram and time series, the period doubling boundaries slightly increase for $k_f=0$ and decrease as $k_f$ subsequently increases, where no complex behavior is observed for $k_f=0.01$ (Figure 12 and Figure 13).

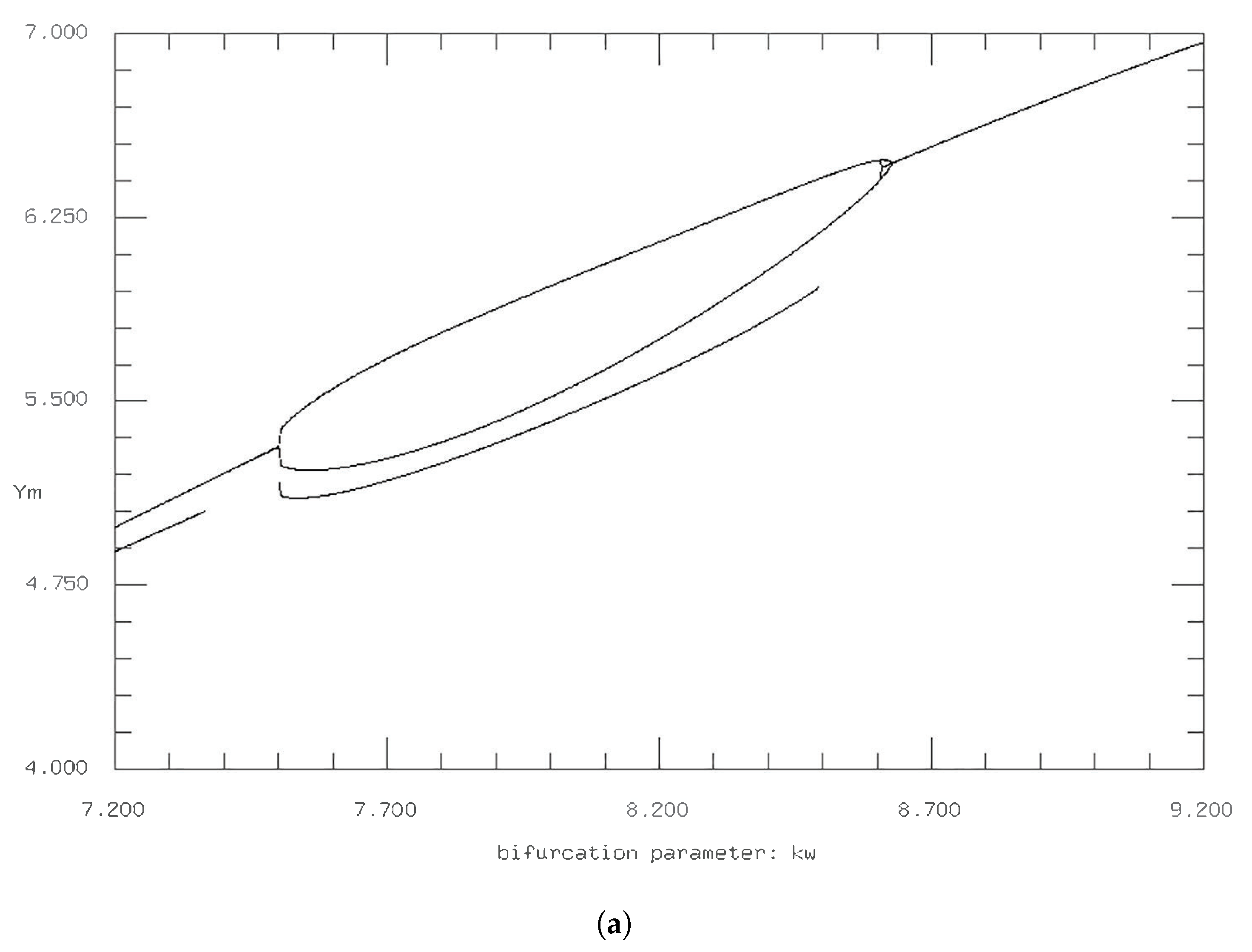
Next we fix $k_f$ back to 0.001 and vary $k_{fm}$. Similar to the time series and phase plane diagrams analyzed above, $k_{fm}$ has a greater effect on the system and thus is more sensitive to variation in regards to the production of both stable and complex oscillations. This increased sensitivity is evident for $k_{fm}=0.005$, where only stable period doubling is observed without any complex oscillations or additional period redoubling. Furthermore, for $k_{fm}=0.01$, we do not observe any period doubling whatsoever; only steady states and fixed points are exhibited (Figure 14a,b).

5. Discussion

Of the seventeen scaled parameter values, we chose $k_w$ and $k_{mp}$ as our main bifurcation parameters and $k_f$ and $k_{fm}$ as our secondary bifurcation parameters. Another potential candidate considered was $k_r$, the rate at which the ants eat the homopterans’ waste and reproduce. Ecologically, an interpretation of $k_r$ is the quality of the waste, as higher quality waste is proportional to increases in tending of homopterans, as more ants migrate from the nest to engage in the mutualistic encounter. However, as the waste is only a secondary source of food for the ants and the presence of waste is more important than the quality of waste for the creation of tended ants (i.e., little amounts of waste will attract ants, whereas no waste produces no tended homopterans), $k_w$ and $k_{mp}$ were considered more ecologically significant in the model. While $k_w$ is only mathematically present in the waste’s rate term, its ecological implication, that of determining how fast untended homopterans produce waste, is much greater than just the single term, as the rate at which waste, the ecological-catalyst for this mutualistic relationship, is produced determines how fast the ants converge to the homopterans, how many ants converge, and, thus, to a certain extent, how quickly the conversion of untended homopterans to tended homopterans occurs. Broadly speaking, this rate most likely has implications and effects on $k_{mp}$, and the comparatively wide range of values that can produce both stable and complex oscillations makes $k_w$ an important parameter to vary and analyze.

Similarly, while $k_{mp}$, the rate at which untended homopterans become tended by the ants (thus enter into the mutualistic relationship) is both more difficult to precisely measure than $k_w$ and produces a narrower range of oscillatory and complex behavior, coupled with $k_w$, $k_{mp}$ broadly governs the rate at which the system’s mutualistic behavior occurs. While $k_w$ deals with the quantity of waste the homopterans produce, $k_{mp}$ deals more with the quality of that waste. The higher quality waste produced, the more ants are attracted to the homopterans’ host plants, thus increasing the likelihood that the ants would tend the homopterans.

A key difference between this model in comparison to previous models [26,27] is that we incorporate separate terms for intraspecies interaction ($k_f$ and $k_{fm}$) within the system, whereas previous models that have studied dynamic ecological system either have not included intraspecies interaction terms [26,27] or have only included it on one trophic level [28]. These nontrivial intraspecies interaction terms can be understood in a variety of ways, such as inner population fighting or cannibalism [29,30,31]. Regardless of the ecological interpretation, the overarching effect is uniform: the trophic levels of the system becomes closed, that is, the populations cannot grow to infinite levels. In ecological terms, this could occur when the population reaches a point where it is overconsuming the resources available to it (plant quality declines) and either part of the population dies off due to disadvantages in fitness.

Many of the models that do not have an intraspecies interaction term or set it equal to zero subsequently predict that the overarching system will both become complex but moreover remain complex and become, in essence, chaotic. We believe that these results are not because the systems, in reality, become chaotic but because the mathematical foundation of the model itself lends itself to producing sustained complex behavior that is consequently interpreted as chaotic. Our model suggests that having a very small rate of intraspecies interactions can have qualitative and quantitative differences on the system and its ability to both sustain complex behavior as well as become or not become chaotic. Furthermore, our results indicate that substantially smaller rates, compared to other parameters ($k_{fm}=0.005$ vs. $k_w=12$) can dramatically change both the oscillatory time scale of the system but moreover eliminate complex behavior all together. These results are ecologically significant in that they provide a reason as to why biological systems, while potentially predicted by models to become chaotic, rarely, if ever, do so in reality. Moreover, these results are mathematically significant because they give a basis (negative, quadratic terms) for which to stabilize nonlinear, dynamic systems from potential complex or mathematically chaotic behavior.

Our work is in accordance with previous studies analyzing chaos in dynamic systems [32,33,34] in that there is a very narrow parameter range when complex behavior is both present and can be labeled as “chaotic”. As Hastings [35] astutely notes, it is within these narrow parameter ranges that the “biology” of the system becomes crucial and empirical studies are necessary to corroborate the accuracy of the model and its behavior. We believe that many of the issues surrounding “chaos” within labeling systems, both physical and natural, lie within the differing usages of chaos in the two fields of ecology and mathematics. While mathematics understands chaos as a sensitivity depending on initial conditions [35] or as containing a positive Lyapunov exponent, nontheoretically oriented ecologists may understand or interpret chaos in a less technical manner, such as a general state of disorder or stochasticity. As we have shown with parameters such as $k_{mp}$ and $k_{fm}$, small changes in the parameter value can lead to important qualitative changes in the systems behavior, leading towards or away from both stable and strange attractors, limit cycles, and oscillations. However, we caution interpreting these strange attractors and chaotic behavior as implicating the system’s dynamics as chaotic; no empirical evidence to date in the ant–homopterans system has shown such chaotic behavior in reality.

In regards to mutualism as a method through which to understand our reality, this model provides a foundation through which to construct multivariate, nonlinear systems without needlessly sacrificing the necessary complexities to make the model ecologically feasible. Nevertheless, there are limitations to this model, since we did not include all of the known interactions between ants and homopterans. For instance, the tended homopterans are treated as the combination of two separate species through mutualism. There are separate methods through which to understand mutualism and the differences between the two species in a mutualistic relationship and the process through which such relationship is brought about. Different understandings of the mutualistic process will inherently produce different mathematical and theoretical models, in which different dynamics and behaviors are inevitable. As such, we encourage using our model as a basis through which to explore more complex mutualistic systems utilizing, in particular, intraspecies interaction terms, satiation terms, and logistic growth terms.

6. Conclusions

While predator–prey and competitive models still dominate both field and theoretical investigations in ecology, mutualism and its corresponding models are important both in their elucidation of understudied ecological relationships but also in their ability to display the mathematical effects of different parameters on the model itself. In our analysis, we consider an ecosystem with five different interacting species and find a wide variety of complex dynamics. While periods of complex oscillations were observed, the preceding and resulting stable oscillations, as well as steady states, indicate that the presence of complex behavior in ecological systems is, if anything, fundamentally temporary in nature and is more due to the class of ecological models used rather than this model in particular [36]. Furthermore, we have shown that certain terms that close trophic levels are crucial to both understanding complex behavior in a system as well as stabilizing the system as a whole.

As with other similar and less representative models of mutualistic systems, our model can be interpreted as displaying chaotic solutions. However, in contrast to other studies, we emphasize the importance of mutualism in the switch from chaotic trajectories towards simpler and more stable oscillations. While period doubling and doubling cascades do occur and the system seems to go to chaos, the occurrence of inverse period doubling and the system’s return simple oscillations (and eventually back to steady state values) gives us serious pause as to label our system as wholly or even partially chaotic. We believe that our model mirrors reality in that there are the correct stabilizing terms through which the system safeguards against such chaos but moreover they will not display chaotic or complex behavior whatsoever if the system is stabilized to begin with. While chaotic behavior in ecological systems has not been readily observed [35], chaos and chaotic attractors in ecological models have and will continue to be contentious points of debate that require scholarly research, both mathematically and ecologically.