Abstract
This document introduces a method to solve linear optimization problems. The method’s strategy is based on the bounding condition that each constraint exerts over the dimensions of the problem. The solution of a linear optimization problem is at the intersection of the constraints defining the extreme vertex. The method decomposes the n-dimensional linear problem into n-1 two-dimensional problems. After studying the role of constraints in these two-dimensional problems, we identify the constraints intersecting at the extreme vertex. We then formulate a linear equation system that directly leads to the solution of the optimization problem. The algorithm is remarkably different from previously existing linear programming algorithms in the sense that it does not iterate; it is deterministic. A fully c-sharp-coded algorithm is made available. We believe this algorithm and the methods applied for classifying constraints according to their role open up a useful framework for studying complex linear problems through feasible-space and constraint analysis.
1. Introduction
Since the apparition of Dantzig’s simplex algorithm in 1947, linear optimization has become a widely used method to model multidimensional decision problems. Appearing even before the establishment of digital computers, the first version of the simplex algorithm has remained for long time as the most effective way to solve large scale linear problems. This fact was perhaps explained by Dantzig in a report written for Stanford University in 1987 [], where he indicated that even though most large scale problems are formulated with sparse matrices, the inverse of these matrixes are generally dense, thus producing a burden to record and track these matrices as the algorithm advances towards the problem solution. Dantzig’s simplex algorithm, on the other hand, does not need to register the partial results of inverting these matrices.
Other algorithms have implemented radically different strategies from the simplex method. Some of them deserve mentioning. In 1965 J. Nelder and R. Mead [] introduced an algorithm that evaluates the coordinates of the vertexes of a growing simplex to find the optimal value of minimization problems. This algorithm disregards derivatives of the objective function and thus is effected when the problem’s dimension grows. During the 1970s, Shamos and Hoey [,], as well as Shamos [] explored options for building efficient linear optimization algorithms based on the geometrical properties of convex spaces. Their proposal is mostly applicable to problems of two and three dimensions.
The first polynomial-time algorithm for solving linear programs was announced by Khanchian [] in 1979. The algorithm is based on building a hyper-ellipsis which volume and shape evolve to contain an extreme feasible point. Under specific configurations of the constraints, the ellipsoidal methods’ convergence-process may become exponential, which probably one of the few weaknesses of these methods.
The next class of algorithms for solving LPs are called “interior point” methods. As the name suggests, these algorithms start by finding an interior point of the feasible space and then proceed to the optimal solution by moving the evaluated point inside the feasible space. The first interior point method was presented by Karmarkar [] in 1984. This work unchained an essential debate about the patentability of math formulas and software. Karmarkar was granted a patent for his algorithm, but patenting software and ideas is not allowed anymore in the United States. Karmarkar’s patent expired in 2006, and now his algorithm is in the public domain.
A growing set of algorithms named “exterior point” algorithms that allow for the pivoting process to go beyond the feasible region appeared during the 90s. Some works, with details of the initial versions and later improvements of these algorithms, can be found are K. Paparrizos [], K. Anstreicher and T. Terlaky [], J. F. Andrus 1 and M. R. Schaferkotter [], A. S. O. Hassan, H. L. Abdel-Male and I. M. Sharaf [], Paparrizos K, Samaras N, and Sifaleras A [] and T. Glavelis, N. Ploskas, and N. Samaras [].
Besides the methods for solving linear optimization problems, some techniques have been developed to improve their performance. We mention first the scaling of linear problems used before the optimization process itself. This technique deals with the coefficients of the constraints to reduce the number of iterations required to reach the problem’s solution. However, their effectiveness is a matter of discussion because they often add more computational costs than the effects related to the reduction of complexity they offer. See Elble J. M. and Sahinidis N. V. [] for a discussion on this point. Improving the phases of the simplex algorithm by limiting the complexity of dealing with a large number of constraints continues to be a subject of study.
Developing more effective pivoting rules has been a way to improve the performance of the simplex method. An interesting method introduced by J. Gondzio [] uses the projections of the objective function gradient onto the current set of active constraints. Another strategy to improve the complexity of the algorithms is the randomization of the pivoting rules applied. This technique is mostly used with the simplex and the interior point algorithms. In this regard, it is worthwhile to mention the works of G. Kalai [] and T. D. Hansen and U. Zwick [], and Kelner and Spielman [] who presented, in 2006, an algorithm they claim runs in polynomial time for all inputs. The complexity of analyzing this facet of the problem increases, since the algorithms vary upon the type of processing unit used for its implementation. N. Ploskas and N. Samaras [] presented an interesting comparison among some of the most well-known pivoting rules. In this work, Ploskas and Samaras evaluate and compare the sensibility of the pivoting rules’ performance to the introduction of elements of parallel processing by using a graphical process unit as compared to as the conventional central process unit.
A different branch of development started with the so-named Las Vegas algorithm introduced by K. L. Clarkson []. Clarkson’s algorithm recursively identifies redundant constraints and afterward determines the optimal point by intersecting the remaining non-redundant constraints. Due to the recursive process, the algorithm is useful for problems with a small number of dimensions—later modifications by Y. Brise, B. Gartner, and K. L. Clarkson [] improved the algorithm’s performance.
The study of linear optimization problems exhibits positive progress. It has been especially fruitful in the sense of understanding the essence of the problem and in producing new ways to tackle different algorithmic situations. However, despite the advantages the more recent studies and algorithms may offer, the simplex method remains among the fastest and the most widely used linear programming algorithm. It seems we are approaching an algorithmic complexity limit for non-parallel computer processing. There is an aspect we may still be far from the limit: The iterative condition of all known linear programming algorithms. Back in 1992, G. Kalai [] mentioned, as an element of his list of open problems, “Find a deterministic subexponential pivoting rule.” This paper presents a deterministic method for solving linear optimization problems. The method’s strategy is based on some characteristics of the boundary on any convex multidimensional polytope and its two-dimensional projections over the principal planes of the space where the polytope exists. An algorithm is devised and presented.
2. The Method
The method’s strategy is to deal with the complexity of an n-dimensional optimization problem by inspecting the objective function’s bounding conditions in the sense of every single orthogonal dimension. All constraints are classified according to their role in limiting the growth of the objective function’s value. After geometrical analysis, we can recognize the active constraints—the constraints intersecting at the extreme-vertex. The coordinates of the extreme-vertex are determined by solving a system of linear equations formulated with the identified active constraints. An example is included in Appendix A, where the rationale of the method is applied to small multidimensional problems.
2.1. General Approach and Definitions
Consider the classical linear optimization problem:
where and represent finite real numbers, while and are positive integers with . Notice the non-negativity constraints have been relaxed to allow non-zero right-hand values. The approach is to solve the linear maximization problem (Equation (1)) by identifying the constraints defining the extreme vertex. This would be rather easy had it not been for the redundant constraints that may be present in the problem formulation. Detecting redundant constraints is a difficult task. It is intuitively easy to understand that redundant constraints cause great confusion in most algorithms because they intersect other constraints, forming unfeasible vertexes, which, when not being properly dealt with, bring the extreme vertex search to a long and fruitless process. Proving or disproving constraint redundancy is computationally equivalent to a linear program []. Previous works related to this issue were presented by M. I. Shamos and D. Hoey [,]. They classified some optimization problems and created categories they named closest point problems and geometric intersection problems, but in these studies, the authors do not present problems of more than two dimensions (in the geometrical sense). Later, in his Ph.D. Thesis, Shamos [] deals with multidimensional spaces, though his treatment focuses on geometric problems and does not directly connect to optimization problems, as he had done previously with two dimensions. Some definitions need to be exposed to present a non-iterative algorithm to tackle higher-dimensional problems.
2.2. The Dominant Dimension
Simplifying the identification of the constraints intersecting at the extreme vertex is done by noting that this vertex should be located near the direction of the axis that, according to the objective function’s vector and the constraints’ angles, represents the dominant growth dimension. Loosely said, the dominant dimension is the one that “offers,” by itself, the highest profitability. Therefore, searching for the optimal point implies ”pressuring” along this most profitable direction until the best location is reached. Dimension g is the dominant growing dimension if the relationship of constraint’s coefficient , and the corresponding objective function’s coefficient in dimension g is maximized. Then, the dominant growth dimension is identified using the following criterion:
where i and g are dimensions the problem, and are objective function coefficients, and and the constraints coefficients for dimensions i and g, respectively. Being able to identify the dominant growth dimension allows one to focus on the dominant dimension and relieves us from directly dealing with the complexity of an n-dimensional problem. This convenience is set in the form of the following Conjecture.
Conjecture 1.
Linear optimization problem bounding condition. A linear optimization problem is bounded if and only if its dominant growth dimension is bounded.
Proof.
If a solution for any linear optimization problem is optimal, then no movement in another dimension may produce a net benefit at the expense of the position on the dominant dimension; otherwise it would not be the optimal solution. Therefore, by limiting the solution’s position in the dominant dimension, the problem’s optimal solution is also limited. Additionally, if the problem’s optimal solution is bounded, then the dominant dimension must not have an unbounded value. □
2.3. Problem Decomposition
In a linear space of dimensions, properly oriented constraints are necessary to limit the growth of the objective function in the direction of the dominant dimension . For two-dimensional problems, this seems trivial, since, otherwise, having only one constraint, the solution-point may indefinitely “slide” varying the other dimension, limitlessly increasing the objective value. For problems with more than two dimensions, we can think of the same idea. However, it is not an obvious situation, since as the number of dimensions increases, we lose track of the interaction effects among multidimensional constraints. Nevertheless, we can apply the idea to the two-dimensional projections of the problem; one projection onto each principal plane containing the dominant-dimension axis g, and each other axes of the problem’s dimensions. The surface of any principal plane not containing axis g is orthogonal to the direction implied in dimension g. For that reason, the projections over principal planes not containing the dominant dimension axis g can be disregarded; they “see” the -dimensional problem from an irrelevant perspective. Therefore, the problem can be decomposed and thus represented by n − 1 2D-projected problems. This artifice breaks down the combinatorial nature of the number of principal planes to be considered. More formally, the relationship between the bound condition of a problem and the bound condition of the 2D-projections of the problem can be established by the following conjecture.
Conjecture 2.
All projections of a bounded linear optimization problem are bounded in the sense of the dominant dimension. Any projection over a space with n − 1 or less dimensions of an n-dimensional linear optimization problem which is bounded in the sense of the dominant dimension is also bounded in the sense of the dominant dimension.
Proof.
If an n-dimensional linear optimization problem is bounded in the sense of the dominant dimension, then the possibility of indefinitely increasing the dominant dimension’s value from a point located within the feasible region is null, and it is also null for any projection of the problem on a space with a lower number of dimensions. Since any of these projections is a subspace of the original problem’s feasible-space, all projections of the original problem must be bounded. □
Finally, if the -dimensional problem is bounded, then, we can obtain as many as n − 1 two-dimensional situations, each one bounded by the projections of two constraints—an upper and a lower constraint. There will also be projections of other non-active or even redundant constraints, but their irrelevant condition will be evident by looking at each of the projected problems. This reasoning leads us to state that an n-dimensional problem is bounded if the n − 1 two-dimensional projections over the principal planes are bounded.
2.4. Constraint Closest Point
Since the objective function’s direction is the most relevant direction for a linear problem, we consider the constraint’s distance to the origin measured by the objective function’s direction. This criterion does not consider constraints with a normal vector forming an angle of more than radians respects to the objective function’s vector. Constraints oriented within this range of angles do not bound linear maximization problems. Thus, they can be neglected.
Figure 1 illustrates the closest point coordinates for several constraints. There is a coordinate value for each constraint on each dimension of the problem. For example, the closest point of constraint has coordinates and in the axes of dimensions i and g, respectively. As is shown below, computing the closest point coordinates for some constraints is key to identify the active constraints intersecting at the extreme vertex.
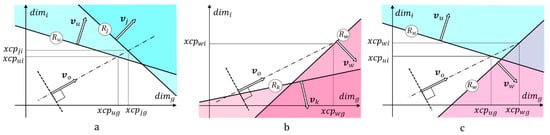
Figure 1.
Possibilities for two constraints combined to limit the objective function of two-dimensional problems. (a): Two constraints blocking the objective from their upper regions (blue areas). The objective function is not bounded. (b): Two constraints blocking the objective from their lower regions (red areas). The objective function is not bounded. (c): A constraint blocks the objective from entering its upper region (blue area), and another constraint blocks the objective from entering its lower region (red area). The objective function is bounded. The figure also shows the closest points for several constraints and their corresponding coordinates and over the axes i and g.
2.5. Upper and Lower Constraints
By inspecting the two-dimensional projections, we notice that the combined effect of two constraints comprising the boundary of the feasible space can be reduced to the three cases illustrated in Figure 1: (a) Two constraints blocking the solution point from entering into the upper sub-spaces, corresponding to each constraint; (b) two constraints blocking the solution point from entering into the lower sub-spaces corresponding to each constraint; and (c) a constraint preventing the solution point from entering into the upper sub-space and another constraint blocking the solution point from entering into the lower sub-space, therefore effectively limiting the two-dimensional problem.
The words “upper” and “lower” differentiate the role a constraint plays in relation to the dominant dimension g and the objective function. Whether or not a constraint is type upper or lower depends on the angles formed by the constraint’s normal vector and the objective function’s vector. Figure 2 shows the angle-ranges and the corresponding type of constraint. Figure 2a shows a criterion to recognize constraints that may “work” as upper-constraints. Each upper-constraint identified has its lower-constraint counterpart from those constraints complying with the criterion shown in Figure 2b. Thus, once an upper-constraint has been identified, the constraints’ projections forming the appropriate angle with the upper-constraint are in the set of lower-constraints associated with the upper-constraint.
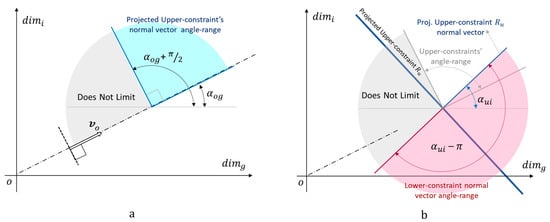
Figure 2.
Identifying upper and lower-constraints for the 2D-projected problems. (a): A constraint projected of on the principal plane ig is a 2D-upper-constraint if it is in the range of angles between zero and radians with respect to the objective-function’s vector. (b): For each 2D-upper-constraint identified, the projection on the principal plane ig is a 2D-lower-constraint if the projected angle is within the range from zero to −π radians respect to 2D-upper-constraint’s normal vector.
Expressions (3) and (4) present these criteria in the form of angular ranges.
2.6. Inward and Outward Constraints
We use the terms “inward” and “outward” to characterize constraints according to the following criterion based on the angle formed by the normal vector of constraint and the objective function’s normal vector . The following criterion is used:
Figure 3 illustrates the role of inward and outward constraints in defining the problem’s extreme vertex. With the help of Figure 3, we can follow the changes in the constraints’ classes that are produced by rotating the orientation of the objective function. This leads us to state the following conjecture:
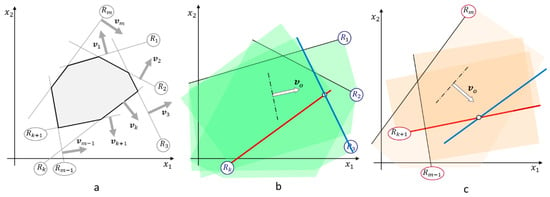
Figure 3.
Graphic representation of the elements of a generic two-dimensional linear optimization problem. The shaded areas indicate the feasible region for each constraint. (a) m constraints defining a multidimensional feasible space (b) constraints 1 to k representing inward constraints. (c) constraints k + 1 to m representing outward constraints.
Conjecture 3.
The extreme vertex is defined by at least an inward constraint. For any bounded system of constraints and an objective function, the extreme vertex is defined by the intersection of constraints from which at least one must an inward constraint.
Proof.
The objective function’s angle in Figure 3b determines the extreme point located at the intersection of inward constraints and . Rotating an objective function’s angle clockwise, as shown in Figure 3c, eventually the extreme point “jumps” to the intersection of inward constraint and outward constraint . Rotating the objective function even more will make the extreme point jump again, this time to the intersection of constraints and . The constraint becomes inward while constraint remains outward. □
Following the consequences of Conjecture 3, we can imagine an optimal solution point laying over the intersection of exclusively inward constraints or over a combination of inward and outward constraints. This type of “visualization” might be helpful when interpreting the final results after solving any optimization problem. The inward–outward classification is also useful within the code. It allows for the assignment of proper signs to computed coordinates and distances.
We consider important to highlight the fact inward–outward classification applies to constraints “living” in the n-dimensional space where the problem is defined. Whereas the upper–lower classification applies to each projection of a constraint over the two-dimensional principal projection plane. Thus, they are very different ways of looking at the same constraints.
2.7. Principal Planes and Constraint Projections
We know that in a linear space the maximum value of a linear objective function is located over the surface of the fastest-growing constraints in the sense of the objective function. Additionally, as previously stated, the problem “pressures” the search for better objective-function’s values in the direction of the dominant dimension. Thus, if focusing on the effect of varying a dimension, say dim i, the problem’s maximum value search should also vary the dominant dimension value while keeping over the constraint’s surface. With these conditions, the search for a better objective function’s value moves the evaluated coordinates along a line that is parallel to the plane formed by axes representing dimensions i and g. We refer to this specific hypothetical trajectory of the point being evaluated, as the “extreme-vertex-movement”. The extreme-point-movement is shown in Figure 4a as a blue double arrow. Of course, these coordinate’s value variations in the search for a “better” point should occur not only for dimensions i and g, but simultaneously in all dimensions, and for all constraints passing ‘near’ the extreme vertex that represents the problem’s optimum point. We do not know yet where the extreme vertex is, neither do we know what the exact meaning of the word “near” in this context, is. Here we introduce a method to work it around and to determine the constraints intersecting at the extreme vertex without iterating.
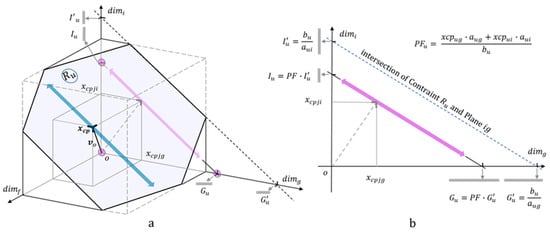
Figure 4.
Moving the extreme point in the vicinity of the intersection of the objective function vector and constraint . (a) Shows a perspective of the constraint , and the direction of the closest point . The direction of movements, represented by the blue arrow, are limited to the surface of generic constraint and only varying values for dimension i and the dominant dimension g. Thus, these movements are parallel to plane ig. The violet arrow represents these movements projected on the plane ig. (b) Shows these movements’ projections and the projection factor .
Figure 4a shows a constraint oriented to work as an upper constraint for the 2D-problem formed by the projection over the principal plane ig. There are other principal planes containing the dominant dimension g, i.e., the plane fg, as illustrated in Figure 4a. For our purposes here, this explanation focuses on the 2D-problem formed over the plane ig. The blue arrow in Figure 4a runs over the surface of constraint and around the point where the objective function’s vector crosses the constraint’s surface. Deliberately, the blue arrow is also placed parallel to the principal plane ig, therefore, it represents the possible variations of values of dimensions i and g exclusively while just complying with constraint . The violet arrows shown in Figure 3a,b correspond to the projection of the blue arrow over the surface of plane ig. Additionally, the constraint intersects the principal plane ig where the segmented lines indicate in Figure 3a,b. The points where the intersection of constraint and the principal plane ig cut axes dim i and dim g, together with the origin, form a rectangle–triangle. Similarly, the points where the projected extreme-point-movement (the violet arrow) cut axes of dimensions i and g, also form a triangle. These two triangles are important because they let us to determine the projection factor , a number that relates the actual constraint in the 2D-problem with the intersection of constraint with the plane ig. This is done by using the line where constraint intersects the principal plane ig as a reference. The points where this reference line cuts axes i and g are easily obtained setting to zero all dimensions except for i and g in the expression describing the constraint . Thus, the cutting coordinates are:
Using Figure 3a,b and some algebra, the projection factor that allows us to scale the similar triangles is obtained. From this analysis:
and are the values of the coordinates where the constraint and the extreme point movement projected line cut axes of dims i and g, is the projection factor that relates the size of both triangles, and the coordinates on dimensions i and g of the point where the objective function’s vector cuts the constraint , and and the coefficients used to describe constraint . There is then a way to determine the projection of the extreme-point-movement over the principal plane ig for variations of the values of a dimension and the dominant dimension g. Considering the projections of these extreme-point-movements, it is possible, as we will see in the next sections, to identify the upper-constraints intersecting at the extreme vertex. To identify the lower-constraints intersecting at the extreme vertex, a two-dimensional geometrical analysis is performed based on the knowledge about each prospective active upper-constraint already identified.
The analysis shown is illustrated with representations of three dimensions. Nevertheless, since it is based on geometrical computations of two-dimensional orthogonal projections, it is valid for any Cartesian space of more than three dimensions.
2.7.1. Identifying the 2D Projected Problem Active Upper-Constraints
The analysis to determine whether or not an upper-constraint can be the active one is based on geometrical considerations. Figure 5 shows the plane formed by dominant dimension’s axis g and axis representing any other of the n − 1 remaining dimensions complying . The extreme-point-movements over the surface of the upper-constraints and , projected on the plane ig, are shown as straight lines tagged with the corresponding constraints’ names. These projected lines form triangles with the axes of dim i and dim g. The constraint with the shortest triangle’s hypotenuse is referenced using the sub-index , and constraint will be used as a reference to compare to other upper-constraints and to discard those who, according to the relative position of their hypotenuses, cannot be active. As illustrated in Figure 5, is a redundant upper constraint —one that does not limit the indefinite growth of dominant dimension g since it does not share any boundary with the feasible region.
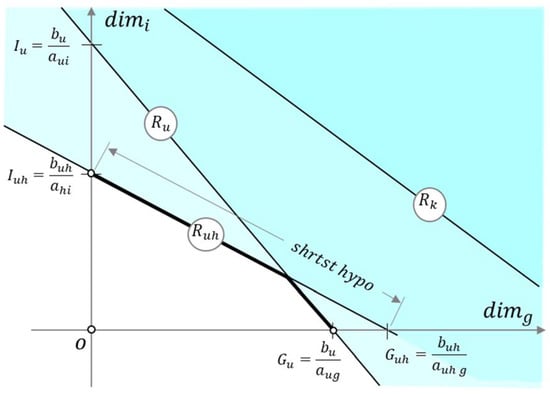
Figure 5.
Identifying possibly active upper-constraints. Shaded (upper-constraints) areas indicate unfeasible regions. The white area represents the region not restricted by upper-constraints. Constraints and both can be the active upper-constraint because they cut within the quadrant > 0 and > 0. Constraint is a redundant constraint in this context, since it does not cut the shortest-hypotenuse constraint within the quadrant > 0 and > 0.
Identifying the constraint with the shortest hypotenuse is straight forward. However, some special cases deserve mention. A first situation occurs when more than one constraint with infinite hypotenuses are competing for the shortest-hypotenuse constraint. This happens when constraints are either parallel to axis dim i, parallel to axis dim g, or parallel to both axes (parallel to the plane ig). The shortest hypotenuse constraint shall be considered the constraint parallel to axis dim i which is closest to the origin. A second situation occurs when more than one constraint cuts the plane formed by dimensions i and g in the same places, thus having overlapping hypotenuses. Notice this does not necessarily mean the constraints are overlapping. It means these constraints are equally sensitive to variations on dimensions i and g but not necessarily in other dimensions. This situation is solved by considering the smallest-hypotenuse constraint is the one with the smallest hypotenuse in other planes formed with axis g. The code included in www.figsshare.com [] shows explicit details about how to deal with these cases. Indeed, this issue adds line-commands to the algorithm. However, this procedure recognizes redundant and overlapping constraints while adding minimal additional computational burden, and it certainly does not change the code’s complexity class.
Figure 5 also indicates that any upper-constraint may be active if, and only if, its extreme-point-movement-projection intersects within the shown positive quadrant, the extreme- point -movement’s projection of the minimal-hypotenuse constraint . The extreme-point-movement-projections intersect in the referred quadrant if the following expression holds:
The intersection of these hypotenuses within the positive quadrant, provides a way of recognition for the possibly active upper-constraints. There is, however, a case in which a constraint not actually intersecting the shortest hypotenuse within the positive quadrant may perform as an active constraint. This special case occurs when = , that is when constraints and cut axis g precisely at the same point (see Figure 5). Nevertheless, at this extreme condition, constraint , even not intersecting the shortest hypotenuse, could participate in defining the extreme point that may result optimal at the end of the problem’s solution. To incorporate this case into the discriminating expression, the logical condition “or ” is added as part of the conditional expression. This logical condition sets as possibly active any constraint that cuts the dominant axis g at the same point where the constraint with the shortest-hypotenuse does. Therefore, a rule to dismiss an upper-constraint that cannot be active is written in the form of the conditional probability for constraint being active, provided that dimension g is dominant and dimensions g and i are different. The resulting expression is:
After applying Expression (7), a ranked stack is formed by the upper-constraints which still can be active (in the sense of the plane defined by dimensions i and g. The top of the stack is for constraints with larger values of , which corresponds to higher slope values. This gives priority to the selection of the constraints “better” aligned with the sense of the objective function.
2.7.2. Identifying the 2D Projected Problem Active Lower-Constraints
Lower-constraints may be associated with upper-constraints to shrink the feasible region, creating a sort of “pocket” that limits the indefinite growth for each principal plane. Once an upper-constraint has been identified, the lower-constraint cutting the upper-constraint at the shortest distance measured over the dominant dimension g is the lower-constraint that determines the extreme position for dimensions i and g. This distance is used as a criterion to assess the active lower-constraint, and we refer to it as wCritDist. Figure 6a shows a straight forward trigonometrical computation of wCritDist based on the coordinates of the lower-constraint closest point . However, when the lower-constraint passes over the origin, this computation is not defined. Then, for this case (Figure 6b), we use the value where the upper-constraint cut axis g as the value of wCritDist. This decision assumes that if another lower-constraint cut axis g within a shorter distance, then it becomes the active one, relegating the constraint being evaluated to an inactive role.
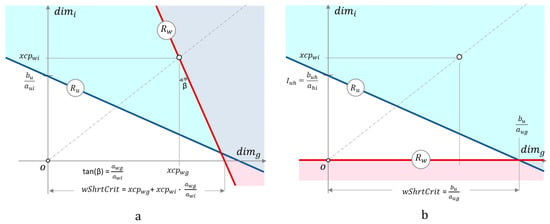
Figure 6.
Identifying the active lower-constraint. (a) The criterion to identify the active lower-constraint is the value of dim g at the intersection of the projected point-movement around the lower-constraint closest point and axis g. The smallest value is an indication of the constraint to be selected as active. (b) For lower-constraint passing over the origin, the value is considered equal to the value of dim g at the intersection of the upper-constraint and axis g.
2.8. Selecting Active Constraints and Solving the Problem
Problem 1’s solution is found by solving a linear set of equations formed with the active constraints for each dimension. This stage may not be as simple as it sounds. When two prospective active-constraints intersect a principal plane at the same line, the matrix formed to solve the problem becomes not positive definite. Thus, at least one of these constraints must not be selected. More details about this are included in the next section.
3. The Algorithm
The algorithm’s major sections are listed below. A fully extended copy of the algorithm’s code is available at https://fishare.com []. The algorithm has been implemented in C Sharp. A working version of the algorithm is included in the complex experiment platform MoNet. Details about MoNet’s structures and criteria are available at []. For reference purposes, the numbers leading each section in the following list are kept within the code comments.
3.1. Define and Dimension set Variables and Arrays
This section reviews the problem’s dimensional coherence and builds some arrays needed afterwards.
- 3.1.1.
- Check dimensional coherence. Define variables and arrays. Allocating values for matrixes and vectors describing the problem takes + . This includes allocating values for the objective function’s coefficients , the constraints’ coefficients , the resources and the vector of constraint operator-comparators (greater than or equal, lower or than or equal).
- 3.1.2.
- Determine dominant dimension g. Fastest growing dimension g. Identifying the fastest growing dimension g is performed by applying Criterion (2) to each dimensional component of each constraints. Thus, Criterion (2) is evaluated times.
- 3.1.3.
- Determine the coordinate for each dimension of the closest point for all constraints . In this segment, the code first computes the shortest distance from the origin to each constraint. Then the coordinate value for each dimension is determined. This process requires steps.
- 3.1.4.
- Determine the objective-function’s angles and the on-principal-planes-projected-constraint angles .
This computation is needed for all constraints and dimensions except for the dominant dimension g. Thus, the process requires steps. The function Math.Atan is needed for this segment of the code, and, therefore, these steps may be time consuming as compared as to other equally complex computation stages.
3.2. Study the 2D-Projected Problem’s Upper-Constraints
Three segments comprise this code section. In this section, the code scans all principal planes formed with the dominant dimension g and each other dimension i with . The result is stored in the two-indexed array RankedUpperConstrJndx[i][rnk], which returns the constraint identification index in the original n-dimensional problem. The array’s first index i refers to the dimension or axis , which, together with dimension g, forms the principal plane where each 2D-projection is considered. The second index refers to the ranked position the constraint holds, as a likely active upper-constraint, in this projected 2D-problem. For every cycle in this code loop, if a constraint’s projection exhibits the highest slope , it is located at the top of the array, therefore keeping the array ranked. At the end of the loop, the constraint located at the top of the array is the one that works as the active upper-constraint for each 2D-projection problem.
- 3.2.1.
- Recognize upper-constraints for all projections over the principal planes. Apply Equation (3). The variable UpperBoundsDIMg[j, i] is set to true or false for each constraint and for each dimension except for the dominant dimension g. The computational complexity of this segment is .
- 3.2.2.
- Identify the upper-constraint with the shortest hypotenuse for each principal plane projection. Apply Equation (7). 3.2.2.a. Compute the projection-factor for upper-constraints. Equation (6). In this segment the hypotenuse length is determined for all constraint-projections on having a value UpperBoundsDIMg[j, i] = true. There are n − 1 constraint-projections for each constraint, then the worst case scenario leads to steps.
- 3.2.3.
- Build array with the possible active upper-constraints in each projections over the principal planes. Rank upper constraints according to the constraint gradient criterion.
Here, the process builds an array identifying the constraints with possibilities for upper-constraining each projected 2D-problem. This is done by recognizing all the constraints intersecting the shortest hypotenuse. Scanning all constraints and the n − 1 constraint-projections requires steps. The method also ranks projections for each constraint with possibilities for being active. In the worst-case scenario, the number of constraints with possibilities for being active is m. However, this looks like an extremely unlikely situation. If u represents the average number of possibly active constraints per projection, an estimation of the computational complexity for this segment would be steps.
3.3. Study the 2D-Projected Problem’s Lower-Constraints
Two segments comprise this code section. For each decomposition 2D-projection i, the constraint located at the top of the array (RankedUpperConstrJndx[i][0]) is taken as the active upper-constraint. The code determines the corresponding lower-constraint using as a criterion, the distance measured in the sense of axis g, from the origin to the intersection of the lower and the upper projected 2D-constraints. The result is stored in the two-indexed array RankedLowerConstrJndx[i][rnk]. The array’s first index refers to the dimension or axis i, which, together with dimension g, forms the principal plane where each 2D-projection is considered. The second index refers to the ranked position the constraint holds, as a likely active lower-constraint, in this projected 2D-problem. When a constraint’s projection exhibits the smallest cut coordinate on the dim g axis, it goes to the top of the array, therefore keeping the array ranked upon this criterion.
Recognize prospective lower-constraints for all projections over the principal planes. Apply Equation (4). The variable LowerBoundsDIMg[j, i] is set to true or false for each constraint and for each dimension except for the dominant dimension g.
For each projected 2D-problem, this code segment identifies the constraint that works as the most restrictive lower-constraint, corresponding to the upper-constraint located at the top of the array built in the segment Section 3.2 list 3.2.3. In the worst-case scenario, this requires visiting m constraints and n − 1 dimensions. Thus, the computational complexity of this segment is . However, since the number of constraints oriented as to work as a lower-constraint is expected to be considerably lower than , the actual complexity of this stage may be significantly lower.
3.4. Select Active Constraints
This segment scans the arrays RankedUpperConstrJndx[i][0] and RankedLowerConstrJndx[i][0] to select the set of constraints actually limiting dimension in the -dimensional space of the original problem. Notice the total number of top elements that arrays RankedUpperConstrJndx and RankedLowerConstrJndx add up is customarily greater than , the number of dimensions of the original problem. Additionally, while some of these array-top elements indicate that a constraint works to limit more than one 2D projected problem, others may intersect a principal plane at the same place. Therefore, the algorithm must carefully account for the constraints being selected and excluded to form the final set of equations. This code section takes this behavior into account and identifies the indexes of exactly n active constraints intersecting at the sought extreme vertex. Despite the increase in the code’s number of instructions caused in dealing with these issues, the complexity of this segment remains .
3.5. Find the Extreme Vertex’s Coordinates by Intersecting Active Constraints
In this stage, the method solves a system of linear equations. These equations are obtained from the constraints selected on Stage 3.4. In this stage, the method can use any matrix-inversion algorithm. While this matrix-inversion algorithm does not belong to the proposed method, its computational burden must be included as part of the computational process. Most matrix inversion algorithms run with complexity . There are cases which lower down this account to , as referred to in [].
4. Computational Study
All linear programming algorithms we know about perform a process of successive iterations until reaching the optimal point. Being essentially constant the computational burden for each iteration, it makes sense to qualify the performance of linear programming algorithms by considering the number of iterations required to solve the problem.
The case here studied is radically different. As explained above, the proposed algorithm consists of a sequence of stages devoted to identifying the active constraints intersecting at the problem’s optimal point. As a result, this algorithm executes only two iterations-like operations. One iteration is used to determine the active constraints defining the optimal vertex. The other iteration is to solve a system of linear equations. Following the estimate of the number of operations for each stage presented in the previous section, the overall complexity of this algorithm is + . For a large number of dimensions , this approximates to .
An algorithm that applies the method has been coded and implemented in the computer simulation platform named MoNet. MoNet is capable of representing complex structures as arrays, trees, and even meshes in single cells of a data-grid. MoNet is particularly suitable for large-scale testing of problem-solving methods. Information about MoNet is offered in []. Dozens of problems of a different number of constraints and dimensionalities were tested. The interested reader may see the results of applying this algorithm by visiting the author’s site https://gfebres.net [] and inspecting the menu “Descargas” (Downloads). Click on MoNet.4.Optim to download the system Monet and load these examples.
5. Discussion
The classical simplex method strategy is to traverse from a first feasible vertex towards the optimal vertex. The sequence of vertexes visited results from conveniently choosing an adjacent vertex each time the algorithm goes to a new vertex. The number of vertexes may rapidly increase with the number of dimensions and constraints, situating the worst cases of the simplex algorithm within the category of exponentially complex problems. The simplex algorithm, in the worst case, indeed visits all vertices, and this turns out to be true for any known deterministic pivot rule []. Nevertheless, despite the number of vertexes visited, the relatively simple calculations required to update the data of neighbor-vertexes at each step keep the simplex method computationally effective for most practical situations and the most popular linear optimization algorithm.
Ellipsoidal methods base their strategy on the behavior of convex polytopes. These methods substitute the traverse of vertexes with a convergence process that “directly” builds a hyper-ellipse containing the extreme vertex. This convergence process is polynomial but may present the problems of stability typical of convergence processes.
The method here proposed is based on characteristics of convex bodies and general geometric properties. We present a way to identify the constraints defining the optimal vertex. By inspecting two-dimensional optimization problems created with the projections of the original problem, we simplify the overall computation complexity. The idea of reducing the original problem’s complexity by detecting the constraints not intersecting at the extreme vertex has been formerly used. In 1995 Clarkson [] presented the Las Vegas algorithm, which relies on a random process to reject redundant or non-relevant constraints. Our algorithm, as well, is based on the reduction of the number of constraints it needs to consider. However, the strategy of decoupling the original n-dimensional linear optimization problem into n-1 two-dimensional logical-geometrical problems—as opposed to optimization problems—allows for the construction of a non-iterative method for the problem’s solution.
The scope of the method proposed goes beyond the numerical computation of the optimal coordinates. The actual worth of the method resides in classifying the constraints according to their role within the feasible region. This aspect is regarded as very useful for the feasible-space analysis in highly complex linear problems. In addition to the typical results regarding the optimal solution, the method offers possibilities for
- A better understanding of the effect each constraint exerts over the problem’s feasible region by classifying the role of each constraint.
- Returning lists of active, non-active and redundant constraints.
- Ranking non-active constraints according to their distance to the feasible extreme vertex found. This ranking provides a useful scope of the sequence of conditions bounding a real situation beyond the found extreme point.
6. Conclusions
An algorithm to solve optimization linear-problems has been introduced. The representation of any linear problem as a convex object in an n-dimensional space provides the rational basis for this algorithm. The algorithm’s complexity is the same as the complexity of inverting a matrix; or depending on the matrix-inversion algorithm used []. In this regard, the algorithm does not offer dramatic advantages if compared to the traditional simplex algorithm. However, it does offer the advantage of being a non-iterative method towards the optimal result; therefore, it is easier to follow and implemented in a wide range of computational environments.
The method is especially suited for linear optimization problems, but modifications to treat nonlinear-monotonic objective functions and constraints, are foreseeable. The method relies on the geometrical properties of multidimensional Cartesian spaces, as well as the intrinsic behavior of convex spaces. We think this approach proves to be powerful in dealing with complex and higher-dimensional linear problems, thus opening up a promising perspective in the field of studying the feasible-spaces of complex-problem descriptions.
In 1992 G. Kalai [] considered in his list of open problems, to “find a deterministic subexponential pivot rule” to improve the simplex algorithm. I believe here it is.
Funding
No external founding was received for this research.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Appendix A.1. Example 1: Problem A.1: 3 Dims, 8 Constraints. Cradle
The following is a three-dimensional linear maximization problem. The objective function’s normal vector is represented by the green arrow shown in Figure A1 left and right. The eight constraints are illustrated in Figure A1 right. Following, this example is solved applying the method and showing the major steps of the process.
| max z = | , | ||||
| subject to: | R1 | ≤ | 4.0 | , | |
| R2 | ≤ | 8.0 | , | ||
| R3 | ≤ | 5.2 | , | ||
| R4 | ≤ | 8.0 | , | ||
| R5 | ≤ | 10.0 | , | ||
| R6 | ≤ | 0 | , | ||
| R7 | ≤ | 0 | , | ||
| R8 | ≤ | 0 | . |
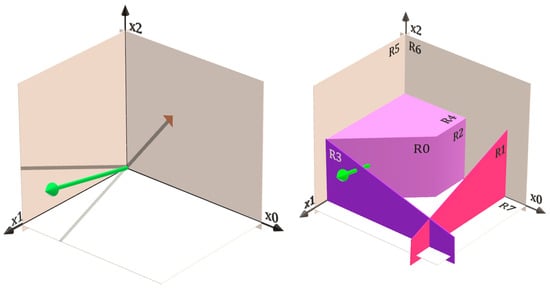
Figure A1.
Spatial representation of Problem A.1. (Left) Objective function’s normal vector. (Right) Represents the eight constraint boundaries. The planes representing these constraint boundaries are infinite. They are shown truncated to allow the viewing of hidden objects.
Appendix A.1.1. Define and Dimension Set Variables and Arrays
- A.1.1.1. Check dimensional coherence. Define variables and arrays.
- A.1.1.2. Determine dominant dimension g. Fastest growing g dimension g. Applying Equation (2) the dominant dimension is , thus g = 2.
- A.1.1.3. and A.1.1.4. Determine the coordinate xcpi for each dimension of the closest point for all constraints j. Determine the objective-function’s angles , and the on-principal-planes-projected-constraint angles .

Table A1.
Closest point coordinates and projection angles.
Table A1.
Closest point coordinates and projection angles.
| Closest Point Coordinates | Projection Angles to Axes (Rad) | ||||||
|---|---|---|---|---|---|---|---|
| Constraint | Dimension i | Dimension i | |||||
| Rj | By Objective Function Direction Distance to Origin | xcp0 | xcp1 | xcp2 | |||
| R0 | 6.5652 | 2.296 | 5.714 | 2.296 | π/4 | 0 | 0 |
| R1 | 22.9783 | 8 | 20 | 8 | π/2 | 0 | ∞ |
| R2 | 14.9359 | 5.2 | 13 | 5.2 | π/2 | 0 | ∞ |
| R3 | 9.1913 | 3.2 | 8 | 3.2 | 0 | 0 | 0 |
| R4 | 28.7228 | 10 | 25 | 10 | ∞ | 0 | π/2 |
| R5 | NR | NR | NR | NR | −π/2 | 0 | ∞ |
| R6 | NR | NR | NR | NR | −π | 0 | −π |
| R7 | NR | NR | NR | NR | ∞ | 0 | −π/2 |
NR = Not Relevant.
Appendix A.1.2. Study the 2D-Projected Problem’s Upper-Constraints and Lower-Constraints
Figure A2 shows the projections of relevant constraints over principal planes X1x2 and x2x3. The following tables resume the results of the method as it goes over the study of the 2D-projected upper and lower constraints.

Table A2.
Hypotenuse for projected upper-constraints and possibilities for being the active upper-constraint.
Table A2.
Hypotenuse for projected upper-constraints and possibilities for being the active upper-constraint.
| Over Principal Planes Projected Extreme-Point-Movement Hypotenuse Length | True if Projected Upper-Constraint Limits Dim i. Stack Position (1 = Top) Indicates Higher Probability | |||||
|---|---|---|---|---|---|---|
| Constraint | Dimension i | Dimension i | ||||
| Rj | 0 | 1 (*) | 2 | 0 | 1 (*) | 2 |
| R0 | 11.3137 | NR | DNUC | true (1) | NR | false |
| R1 | ∞ | NR | DNUC | false | NR | false |
| R2 | ∞ | NR | DNUC | true (2) | NR | false |
| R3 | DNUC | NR | DNUC | false | NR | false |
| R4 | DNUC | NR | ∞ | false | NR | true (1) |
| R5 | DNUC | NR | DNUC | false | NR | false |
| R6 | DNUC | NR | DNUC | false | NR | false |
| R7 | DNUC | NR | DNUC | false | NR | false |
* Dominant dimension; DNUC = Does not upper constraint, NR = Not relevant because i = g.
Appendix A.1.3. Study the 2D-Projected Problem’s Lower-Constraints

Table A3.
Values of the wCritDistG criterion for projected lower-constraints and possibilities for being the active lower-constraint.
Table A3.
Values of the wCritDistG criterion for projected lower-constraints and possibilities for being the active lower-constraint.
| Over Principal Planes Criterion Distance wCritDistG | True if Projected Lower-Constraint Limits Dim i | |||||
|---|---|---|---|---|---|---|
| Constraint | Dimension i | Dimension i | ||||
| Rj | 0 | 1 (*) | 2 | 0 | 1 (*) | 2 |
| R0 | DNWC | NR | 5.174 | false | NR | true |
| R1 | DNWC | NR | DNWC | false | NR | false |
| R2 | DNWC | NR | DNWC | false | NR | false |
| R3 | 8 | NR | 8 | true | NR | true |
| R4 | DNWC | NR | DNWC | false | NR | false |
| R5 | 8 | NR | DNWC | true | NR | false |
| R6 | DNWC | NR | DNWC | false | NR | false |
| R7 | DNWC | NR | DNWC | false | NR | false |
* Dominant dimension; DNWC = Does not lower constraint, NR = Not relevant because i = g.
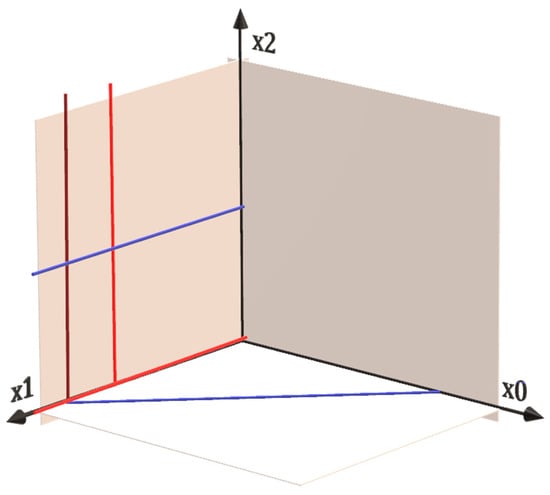
Figure A2.
Constraints R0, R3, R4 and R5 projected over the principal planes to work as upper and lower constraints for two-dimensional problems. Projected upper-constraints are blue, and projected lower-constraints are red. Bright red is used for constraint R0 projected (wCritDistG = 5.174) over plane to indicate it has priority over projected constraint R3 projected (wCritDistG = 8) shown with dark red.
Appendix A.1.4. Select Active Constraints
From steps A.1.2 and A.1.3, it can be seen that non-dominant dimension is upper-limited by Constraint R0 and lower-limited by Constraint R3 and R5, while non-dominant dimension is upper-limited by Constraint R4 and lower-limited by Constraint R0 and R3. Notice Constraint R0 appears twice; once upper-limiting dimension and another lower-limiting dimension . Thus, joining all detected active constraints gets us R0, R5, R4, and R3. A total of four constraints, (one more than the number needed for n = 3) reflect the fact in this example, the extreme is over-defined because four constraints define this vertex. Considering Constraints R0 and R3 intersect principal plane at exactly the same place, we take R0 and disregard R3. Finally, there are three different constraints R0, R4, and R5 defining a point in a three-dimensional space, which makes sense according to the dimensionality of the problem.
Appendix A.1.5. Find the Extreme Vertex’s Coordinates by Intersecting Active Constraints
Solving for the intersection of Constraints R1, R5 and R6 the coordinates of the optimal point are determined as and , and the optimal objective function’s value z = 30.
References
- Dantzig, G.B. Origins of The Simplex Method; Technical Report SOL 87-5; Stanford University: Stanford, CA, USA, 1987. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Shamos, M.I.; Hoey, D. CLOSEST-POINT PROBLEMS. 1975. Available online: https://pdfs.semanticscholar.org/dfba/35c318f0fc244c6d6cad98c1ad33f82d16ad.pdf (accessed on 15 October 2018).
- Shamos, M.I.; Hoey, D. Geometric Intersection Problems. 1976. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.366.9983&rep=rep1&type=pdf (accessed on 15 October 2018).
- Shamos, M.I. Computational Geometry [Internet]. Yale Universiy. 1978. Available online: http://euro.ecom.cmu.edu/people/faculty/mshamos/1978ShamosThesis.pdf (accessed on 15 October 2018).
- Khachiyan, L. Polynomial algorithm in linear programming. Sov. Math. Dokl. 1979, 20, 191–194. [Google Scholar] [CrossRef]
- Karmarkar, N. A new polynomial-time algorithm for linear programming. Combinatorica 1984, 4, 373–395. [Google Scholar] [CrossRef]
- Paparrizos, K. An infeasible (exterior point) simplex algorithm for assignment problems. Math. Program. 1991, 51, 45–54. [Google Scholar] [CrossRef]
- Anstreicher, K.M.; Terlaky, T. A Monotonic Build-Up Simplex Algorithm for Linear Programming. Oper. Res. 1994, 42, 556–561. [Google Scholar] [CrossRef][Green Version]
- Andrus, J.F.; Schaferkotter, M.R. An exterior-point method for linear programming problems. J. Optim. Theory Appl. 1996, 91, 561–583. [Google Scholar] [CrossRef]
- Hassan, A.S.O.; Abdel-Malek, H.L.; Sharaf, I.M. An exterior point algorithm for some linear complementarity problems with applications. Eng. Optim. 2007, 39, 661–677. [Google Scholar] [CrossRef]
- Paparrizos, K.; Samaras, N.; Sifaleras, A. Exterior point simplex-type algorithms for linear and network optimization problems. Ann. Oper. Res. 2015, 229, 607–633. [Google Scholar] [CrossRef]
- Glavelis, T.; Ploskas, N.; Samaras, N. Improving a primal–dual simplex-type algorithm using interior point methods. Optimization 2018, 67, 2259–2274. [Google Scholar] [CrossRef]
- Elble, J.M.; Sahinidis, N.V. Scaling linear optimization problems prior to application of the simplex method. Comput. Optim. Appl. 2012, 52, 345–371. [Google Scholar] [CrossRef]
- Gondzio, J. Another Simplex-type Method for Large Scale 1 Introduction; Technical Report ZTSW-1-G244/94; Systems Research Institute, Polish Academy of Sciences: Warsaw, Poland, 1996. [Google Scholar]
- Kalai, G.A. Subexponential randomized simplex algorithm. In Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing, STOC’92, Victoria, BC, Canada, 4–6 May 1992; pp. 475–482. [Google Scholar]
- Hansen, T.D.; Zwick, U. An Improved Version of the Random-Facet Pivoting Rule for the Simplex Algorithm Categories and Subject Descriptors. In Proceedings of the 47th ACM Symposium of Theory Compution, Portland, OR, USA, 14–17 June 2015; pp. 209–218. [Google Scholar] [CrossRef]
- Kelner, J.A.; Spielman, D.A. A randomized polynomial-time simplex algorithm for linear programming. In Proceedings of the Thirty-Eighth Annual ACM Symposium on Theory of Computing—STOC’06, Seattle, WA, USA, 21–23 May 2006; Volume 51. [Google Scholar] [CrossRef]
- Ploskas, N.; Samaras, N. GPU accelerated pivoting rules for the simplex algorithm. J. Syst. Softw. 2014, 96, 1–9. [Google Scholar] [CrossRef]
- Clarkson, K.L. Las Vegas algorithms for linear and integer programming when the dimension is small. J. ACM 1995, 42, 488–499. [Google Scholar] [CrossRef]
- Brise, Y.; Gartner, B. Clarkson’s Algorithm for Violator Spaces. In Proceedings of the 21st Annual Canadian Conference on Computational Geometry, Vancouver, BC, Canada, 30 June 2009. [Google Scholar]
- RinnooyKan, A.H.G.; Telgen, J. The Complexity of Linear Programming. Stat. Neerl. 1981, 35, 91–107. [Google Scholar] [CrossRef]
- Febres, G.L. Non-Iterative Linear Maximization Algorithm [Internet]. figshare.com. 2019. Available online: https://figshare.com/articles/Non-Iterative_Linear_Maximization_Algorithm/7928948 (accessed on 20 May 2019).
- Febres, G.L. Basis to Develop a Platform for Multiple-Scale Complex Systems Modeling and Visualization: MoNet v3. arXiv 2017, arXiv:1701.04064. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; Available online: http://www.jstor.org/stable/1269484?origin=crossref (accessed on 15 May 2019).
- Febres, G.L. Gerardo Luis Febres’s Homepage. 2019. Available online: Gfebres.net (accessed on 20 May 2019).
- Klee, V.; Minty, G.J. How Good Is the Simplex Method. In Inequalities III; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1972; pp. 159–175. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).