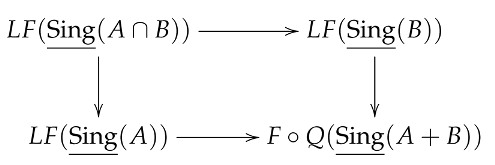2. Topological Groups and Modules
We work in
, the category of compactly generated, weakly Hausdorff spaces, enriched with a modification of the compact-open topology on spaces of maps. This makes
into a cartesian closed category; see [
8] for a good general reference on this. We will write
for the space of maps
in
equipped with this topology. More generally, for a category
enriched over a category
, we will write
for the enriched hom-object, or
when there is no ambiguity.
Please note that the definitions in this section also make sense for spaces in , the category of compactly generated spaces, which is also cartesian closed; we restrict to for compatibility with later sections, where a model structure is only constructed on .
We can define internal group objects in
: these are groups
G with a topology on their underlying set making multiplication
and inversion
continuous. Please note that the product
here is the internal product in
. For ease of use we will refer to such group objects as topological groups, although they are not topological groups in general: in particular, writing
for the product in the category of topological spaces, the map
may not be continuous. Indeed, ([
3] Example 2.14) shows that group objects
G in
for which
is not continuous do arise in nature.
As for these topological groups, we can define a category of ring objects in
, which we will call topological rings. Similarly, for a topological ring
R, we write
R-
for the category of left
R-module objects in
. All this includes as a special case
, the category of abelian group objects in
, which is
-
where
is given the discrete topology. Indeed, results that apply analogously to
R-
will mostly be stated in this paper as results about
, with the generalisation being left to the reader. For details on this module category, see [
4] (Sections 7–8). In the rest of this section we summarise the results we will need, without further reference.
Given -, write for the set of morphisms : this naturally has the structure of an abelian group, and the restriction of the topology on makes into an abelian topological group, so that R- becomes an additive category enriched over .
One generalisation of abelian categories is the concept of quasi-abelian categories. A quasi-abelian category is an additive category with all kernels and cokernels, satisfying two additional properties:
- (i)
in any pull-back square
if f is the cokernel of some map then so is ;
- (ii)
in any push-out square
if f is the kernel of some map then so is .
It turns out that R- is a complete and cocomplete quasi-abelian category. R- also has free modules. That is, the forgetful functor R- has a left adjoint, which we will write as F.
See ([
9] Section 1) for a complete account of homological algebra over quasi-abelian categories. For
a quasi-abelian category, there is an abelian category
called the left heart of
whose objects consist of monomorphisms in
. There is a fully faithful, exact embedding
which induces an equivalence on the derived categories of chain complexes in the two categories. Thus for a chain complex in
we can think of it as a chain complex in
and take homology there: the resulting
nth homology functor sends
to the map
in the left heart. Since the embedding
is exact, the family
of functors takes a short exact sequence of chain complexes in
and gives a long exact sequence in the left heart.
Please note that all this can be dualised to give a right heart and a right homology functor, which we will not use in this paper.
The class of all kernel-cokernel pairs in R- thus makes it into an exact category, in the sense of Quillen. We will refer to this as the quasi-abelian structure, or the regular structure, by analogy to the non-additive case below.
However, with this exact structure R- does not have enough projectives, which is a serious drawback in doing homological algebra. Since R- has free modules (that is, the forgetful functor to has a left adjoint), we have various other structures available, which make R- into a left exact category (a generalisation of an exact category which requires a well-behaved class of deflations but not inflations) with enough projectives. We are interested here in the case where the projectives are summands of free modules on disjoint unions of compact Hausdorff spaces, and the deflations are the epimorphisms such that the induced map is surjective for all projectives P. We will refer to this as the compact Hausdorff exact structure.
4. Model Structures
As for abstract groups, to construct spaces with some chosen topological homotopy group
G, we must develop some tools to allow the calculation of the homotopy groups of interesting spaces. In our context the most important tools are the model structures defined in [
4].
We recall here the pieces of machinery we will need. We use the definitions of model structures and model categories given in ([
10] Section 1.1). That is, a model category is a complete and cocomplete category together with a model structure, and we require factorisations to be functorial.
Given two model categories and and an adjoint pair of functors with , suppose F preserves cofibrations and trivial cofibrations, or equivalently G preserves fibrations and trivial fibrations. We say that such a pair of functors forms a Quillen adjunction. Then we can define the left derived functor of F and dually the right derived functor of G, such that these derived functors preserve weak equivalences and hence induce functors on the associated homotopy categories. Explicitly, can be constructed as the composite of F with the cofibrant replacement functor on , and dually for .
An important example of this idea is that of homotopy colimits (or dually homotopy limits): given a small category , the colimit functor is left adjoint to the diagonal functor . We would like to put a model structure on that makes these functors into a Quillen adjunction.
Theorem 6. If is class-cofibrantly generated in the sense of [4], the projective model structure defined in ([5] Section A.2.8) exists on , is class-cofibrantly generated, and makes a Quillen adjunction. Proof. The proof of ([
5] Proposition A.2.8.2) proves the existence of the projective model structure on
when
is cofibrantly generated: the hypothesis of combinatoriality is not used in this part of the proof. However, in fact a careful reading shows that exactly the same proof works in our situation, and shows that
is class-cofibrantly generated. Then the final statement follows exactly as in ([
5] Proposition A.2.8.7(1)). ☐
We now define homotopy colimits (of shape ) to be the left derived functor of colim.
Remark 1. The question of the existence of homotopy limits is more delicate here; the usual requirement for the existence of an injective model structure is that be combinatorial. It may be possible to pursue a definition of class-combinatorial, analogously to the definition of class-cofibrantly generated, and construct homotopy limits in that way. However, we will not need this here.
We can now define the model structures we will need in this paper. First on : a weak equivalence (respectively, fibration) is a map such that the induced map is a weak homotopy equivalence (respectively, Serre fibration) for all compact, Hausdorff spaces K. A cofibration is a retract of a composition of pushouts by maps of the form , where is the n-ball.
Next we consider the category of simplicial spaces
. Here
is the simplex category—see ([
10] Chapter 3) for details on
and simplicial sets. This category is also cartesian closed by ([
4] Proposition 3.2), so in particular it is enriched, via a forgetful functor, over simplicial sets
and over
. We get for free a projective model structure induced from the compact Hausdorff model structure on
, but here we consider a different one. See [
4] for more details.
Let
,
and
be the standard simplicial
-horn,
n-sphere and
n-simplex, respectively. Let
I be the class of maps in
of the form
K compact Hausdorff, and let
J be the class of maps of the form
K compact Hausdorff, where
are the inclusion maps. Then a map
f in
is a cofibration if it is a retract of a composition of pushouts by maps in
I, a fibration if it has the right lifting property with respect to
J, and a weak equivalence if
is a weak equivalence in
for all compact Hausdorff
K. Here disc is the constant simplicial space functor.
Finally, we also consider the categories of simplicial objects in
R-
and chain complexes in non-negative degrees in
R-
. We write
-
for the former category and
-
for the latter. By ([
11] Theorem 1.2.3.7), these two categories are equivalent, and correspondingly we get equivalent model structures on them. We give an explicit description of the structure on
-
: a map is a weak equivalence if its mapping cone is exact in the compact Hausdorff exact structure, a cofibration if it is a levelwise split monomorphism, and a fibration if it is a levelwise deflation in the compact Hausdorff exact structure.
Theorem 7. These data define model structures on , and -, which we call the compact Hausdorff model structures. All three are class-cofibrantly generated.
Proof. ([
4] Theorem 2.4, Theorem 4.19, Theorem 8.2) ☐
These categories have various Quillen functors between them, as shown in the following diagram:
here Sing is the singular simplicial space functor,
is geometric realisation,
F is the free
R-module functor and
U is the forgetful functor;
is left adjoint to
and
F is left adjoint to
U. See [
4] for details.
We also need the standard Quillen model structures on
and
as defined in [
10], where the weak equivalences are weak homotopy equivalences.
Finally, we need one more homotopical structure on
, which we call the regular structure. In [
4] the regular structure is referred to as
. The regular structure is defined on internal Kan complexes in
, i.e., objects
X such that
is a regular epimorphism (that is, a quotient map) for all
. On these objects
X we can define homotopy group objects
in the exact completion of
, for a choice of basepoint
x. Here we say a map
is a weak equivalence if it induces isomorphisms of all homotopy groups, a fibration if
is a regular epimorphism for all
and a trivial fibration if
is a regular epimorphism for all
n.
We would like to extend some of this structure to all of
. Certainly the definition of fibrations and trivial fibrations makes sense. As for abstract simplicial sets, there is a functor
(see [
12]).
It is stated in ([
12] Theorem 2.8) that in a regular category, if finite limits commute with colimits of sequences indexed by
, then
preserves fibrations and trivial fibrations,
is an internal Kan complex for all
X in
, and if
X is an internal Kan complex, the canonical map
is a weak equivalence.
This does not hold in . However, we do have the following.
Lemma 1. Suppose D is a finite category and we have a sequence of functors and natural transformations . Suppose that for all and all n the maps are closed inclusions. Then the induced maps are closed inclusions and .
Proof. The induced maps of limits are closed inclusions because closed inclusions are equalisers in and limits commute.
When
D is a pullback diagram
and all the maps
and
are identities, the commuting of limit and colimit is a special case of ([
13] Corollary 10.4). The general case where
D is a pullback diagram follows easily from this. Finite products commute with all colimits because
is cartesian closed.
When
D is an equaliser diagram
, the equaliser of
is the pullback of
So
All finite limits can be constructed as equalisers of maps between finite products, so a similar argument shows that the lemma holds for these too. ☐
All the colimits indexed by
in the argument for ([
12] Theorem 2.8) are colimits of closed inclusions, because
is a split monomorphism, and hence a regular monomorphism. So its conclusions hold here too, and we get:
Proposition 1. preserves fibrations and trivial fibrations, is an internal Kan complex for all X in , and if X is an internal Kan complex, the canonical map is a weak equivalence.
Then we can define regular weak equivalences in
to be maps
such that
is a regular weak equivalence. It follows easily that weak equivalences in
in the compact Hausdorff structure are weak equivalences in the regular structure: see ([
4] Lemma 5.16).
Just as we can define homotopy group objects for , we can now define homology group objects too. To ensure that these are invariant under weak equivalence in the compact-Hausdorff structure, we define to be – where is the left derived functor of the free group functor F, calculated in the compact Hausdorff structure. This works because weak equivalences in in the compact Hausdorff structure are weak equivalences in the regular structure.
5. and
Write Sing for the usual singular simplicial set functor. As for
, it has a geometric realisation functor
as a left adjoint. It is a standard result of homotopical algebra that the two compositions
and
are weakly equivalent to the identity. In fact the same is true of
, by ([
4] Proposition 4.29). However, it is easy to find counter-examples showing the same is not true of the other composition. Much of the rest of the paper will go into showing a partial result in this direction, Theorem 13. In fact the construction of Eilenberg–Mac Lane spaces for totally path-disconnected groups follows quite easily from this result.
We can now state the main technical result of the paper. This can be thought of as a continuous version of the Seifert–van Kampen Theorem.
Theorem 8. If C is an open cover of , write for the poset of finite intersections of sets in C, ordered by inclusion. Then is weakly equivalent (in the regular structure on ) to the homotopy colimit (in the compact Hausdorff structure on ) of .
Remark 2. This mixture of the two homotopical structures is not beautiful, but it is a necessary evil. We will see later in Example 1 that in general the homotopy colimit of is not weakly equivalent to in the compact Hausdorff structure; on the other hand, without a well-behaved notion of cofibrations in the regular structure, we have no way of defining homotopy colimits there—but see Section 6. This may be thought of as a `continuous version’ of ([
11] Proposition A.3.2), and we will start by reproving the intermediate result ([
11] Lemma A.3.3), using an approach that carries across better to the current situation.
Lemma 2. ([11] Lemma A.3.3) Let , and let C be an open cover of X. Let be the simplicial subset of spanned by those n-simplices which factor through some . Then the inclusion is a weak equivalence of simplicial sets. Proof. Via the adjunction between Sing and
, we see that
is naturally isomorphic to the subset of
which maps each simplex of
into some
. In this way we think of
as a simplicial subset of
. Iterating this reasoning, we can identify the limit
as the simplicial subset of
consisting of all maps
for which there is some
such that each simplex of
is mapped into some
. By standard arguments, e.g., ([
14] Proof of Proposition 2.21), this is all of them. That is,
.
There is a subtlety here. There is a canonical map
for a simplicial set
S, but that is not the inclusion map we are using here. It is well-known that
e is a trivial cofibration, and hence
is too – we want to show our inclusion maps are all trivial cofibrations, and the result will follow. Since all our inclusion maps are injective and hence cofibrations of simplicial sets, it suffices to show each inclusion, which we will write (by abuse of notation) as
is a weak equivalence. We do this by showing
i is homotopic to the weak equivalence
after which the result follows by standard model category theory.
This homotopy comes simply from understanding what the maps i and e are doing: i is induced by the identity map , while e is induced by the map which identifies one of the n-simplices of with , and retracts all the other simplices onto faces of . These two maps are clearly homotopic, and a choice of homotopy induces a homotopy between i and e. ☐
We can immediately prove a continuous version:
Lemma 3. Let , and let C be an open cover of X. Let be the simplicial subspace of spanned by those n-simplices which factor through some . Then the inclusion is a weak equivalence of simplicial spaces in the compact Hausdorff structure.
Proof. It is an easy exercise to check that each
has
as its underlying set, and that its topology is the subspace topology from its inclusion map into
, defined as in the previous lemma. Hence
as before and we have to show the resulting map
is a weak equivalence. This works in exactly the same way as in ([
4] Theorem 4.19 (ii)): first, for any
and
, we have
, because
Please note that each
is open in
via the inclusion
i, by definition of the compact-open topology: it is the subset consisting of the finite intersection (over simplices
K of
) of the unions (over open sets
U in the cover
C) of the open sets
. So the maps
are open inclusions. Since every compact Hausdorff space
K is small with respect to open inclusions (that is, any compact Hausdorff subspace of
must be contained in one of the sequence
of open subspaces), we get
for all
K. By the previous lemma,
is a weak equivalence for all
K, so the result follows. ☐
We want a concrete model for the homotopy colimit of (in the compact Hausdorff structure). The model structure on gives a cofibrant replacement functor Q: explicitly, for Y in , is the disjoint union of the compact subspaces of and is the disjoint union of the compact subspaces of the pullback . This gives each a canonical decomposition as a disjoint union of compact subspaces which we want to fix for later: call these compact subspaces `fat cells’. The intuition is that fat n-cells should be treated like single n-cells of simplicial sets which have been fattened up.
Lemma 4. is a homotopy colimit for .
Proof. Let
be the poset of all intersections of open sets in
C. We will show
is cofibrant in the projective model structure induced from the compact Hausdorff model structure on
; the colimit of
is the colimit of
by cofinality, and the result follows. The argument echoes the second part of the proof of ([
11] Proposition A.3.2).
Write
as a transfinite colimit
of pushouts by maps of the form
with
compact Hausdorff (that is, the generating cofibrations of the model structure), ordered by dimension. Identify each
with its image as a simplicial subspace of
, consisting of a subset of the fat cells. Then the result follows by showing that for each
the induced map
is a cofibration in the projective model structure, since these are closed under transfinite composition. Let
be the intersection of sets in
C which contain the image of
: then this map is a pushout by the projective cofibration
, where
☐
It remains to show that is weakly equivalent in the regular structure to . However, first we will give an example to show that it is not a weak equivalence in general in the compact Hausdorff structure.
Factor the canonical map
using the functorial factorisation into a trivial cofibration followed by a fibration
Example 1. Let X be the pseudo-arc, as defined in [15]. This is a compact Hausdorff space (so in ) which is connected and totally path-disconnected. Let C be any open cover of X which does not contain X itself. To show the fibration is not a trivial fibration it is enough to show that is not -split, in the terminology of [4]: that is, not every map from a compact Hausdorff space to lifts to a map to . More specifically, since is itself compact Hausdorff, it is enough to show does not split. Indeed, in the functorial factorisation, Z is the colimit of a sequence where new 0-cells in are attached via spaces of 1-cells in (or equivalently via spaces of paths in X) with one end in , and . Since all paths in X are constant, and all spaces of 0-cells in are disjoint unions of spaces whose image is contained in some , the same is true of Z. So is a disjoint union of spaces whose image is not the whole of X. Therefore any splitting would disconnect X, giving a contradiction.
We will prove the theorem by showing that is a trivial fibration in the regular structure. To do this we must first understand Z better. We set . Given , for all , for all , for every compact subspace K of , we attach K-cells and Kn-cells filling in this space of n-horns, and call the resulting space . Then Z is the colimit of the sequence with the obvious inclusion maps.
The strategy is to show that the map
is a
-epimorphism for all
n, in the terminology of [
8]: that is, that for every compact subspace of the pullback there is a compact subspace of
mapping onto it. The theorem will follow since
-epimorphisms are regular epimorphisms by ([
8] Proposition 3.12).
We do this by proving a slightly stronger result. Instead of just considering the standard
n-simplex
, we wish to consider every finite triangulation
of the
n-ball. Just as for
, we may consider its boundary
, which is a finite triangulation of the
n-sphere. Just as we may speak of spaces of
n-boundaries
in a simplicial space
Z, we may define
, the weighted limit of
Z over
; for more detail on weighted limits see [
16].
Theorem 8 will follow once we prove:
Proposition 2. For all such Σ, the mapis a β-epimorphism. We prove this in several steps.
By Lemma 1, for each finite triangulation , is a finite limit, so it is the union of the closed subspaces , so any compact subspace of is contained in some . Similarly using . This allows us to use an inductive argument; we start with the base case.
Suppose we have a compact subspace
K of
. Label the canonical maps from the pullback
We can assume that each simplex of
(that is, the image of
under the map
induced by a simplex inclusion
) is contained in a single fat cell, since
K is the disjoint union of finitely many spaces of this form.
Proposition 3. If is contained in the subspace , there is a compact cover of K such that the inclusion map of each into lifts to a map .
Proof. We will start by replacing K with an associated subspace of . For each m-cell D of , K has a space of m-cells in , which by hypothesis is contained in a single fat cell, i.e., some compact subspace of some . The image of in is compact, so it corresponds to some fat cell in . Replacing with is functorial in the cells of , so together these spaces of cells give a subspace of , homeomorphic to whose image in is the same. Then let be the pullback of . This is canonically homeomorphic to K, and it is not hard to see that there is a series of simplicial homotopies in between and K.
Now consider
. We use the same compactness argument as Lemma 3: applying barycentric subdivision
k times to
, each
is an open subspace of
and
. Since
is compact there must be some
containing it. In the compact-open topology, the space
maps from
to
X such that each simplex maps into some
has an open cover by sets of the form
. This gives an open cover of
which pulls back to an open cover of
; pick a finite subcover
. By the Shrinking Lemma of ([
17] Exercise 4.36.4), we can find a cover of
by compact subspaces
such that
for each
i. For each simplex
D in
, there is some
such that every element of
maps
D into
U. Therefore the inclusion
lifts to a map
. Because
is a fibration, we can stick all these spaces of cells together to get a lift
.
Because is a fibration in the compact Hausdorff structure, we may now use the series of simplicial homotopies between and K to get a compact cover of K whose inclusion maps into lift to maps . ☐
Proof of Proposition 2. Now suppose we have a compact subspace K of : is contained in some , . Suppose we have shown, for every compact subspace of such that is contained in , that there is a compact cover of such that the inclusion map of each into the pullback lifts to a map .
Suppose is a triangulation of the -ball. In the process of constructing Z, there are two possibilities: a fat k-cell in can be added by a -horn and have all its faces in , or it can be added by a k-horn and have one face in , and all other faces in . Therefore can only have fat n-cells and fat -cells in ; moreover, any of its fat -cells in is only the face of one fat n-cell in , but it is the face of two fat n-cells in , so these two fat cells must be the same. So there are two situations to deal with:
- (i)
a fat n-cell in with all its faces in ;
- (ii)
two copies of the same fat n-cell in stuck together at one face in .
- (i)
For each fat n-cell D in case (i), we have a fat -cell that has D as one face and all other faces in . Write for the triangulation of the -ball obtained by attaching a new -cell to at the face corresponding to D. Consider the new compact subspace of : for each element of K, change its image in by attaching a new -cell via the map attaching at D, and change its image in by replacing the image of with an -horn via the map attaching at D. Please note that has fewer fat n-cells in than . Note too that, if we can find a compact cover of such that the inclusion map of each into the pullback lifts to a map , we can use the fact that is a fibration in the compact Hausdorff structure to get a compact cover of K such that the inclusion map of each into lifts to a map .
So by applying this procedure finitely many times we reduce to the case where has no fat n-cells of this type in .
- (ii)
For each fat n-cell D in case (ii), the approach is similar. Let be the triangulation given by attaching a new -cell to at the two faces corresponding to D. Consider the new compact subspace of : for each element of K, change its image in by attaching a new degenerate -cell coming from the degeneracy maps on D to the faces corresponding to and , and change its image in by replacing the images of and with the other faces of the new -cell. These other faces are the degeneracies of -cells in , so they are in ; so, as before, we reduce the number of fat cells in . As before, if we can find a compact cover of such that the inclusion map of each into the pullback lifts to a map , we can use the fact that is a fibration in the compact Hausdorff structure to get a compact cover of K such that the inclusion map of each into lifts to a map .
So by applying this procedure finitely many times we reduce to the case where has no fat n-cells in , and we are done.
☐
6. Excision
If the weak equivalence in the regular structure proved in Theorem 8 were a weak equivalence the CH structure, an excision theorem for homology would be an easy corollary: since left derived functors preserve homotopy colimits, we could apply
to get a result analogous to ([
14] Proposition 2.21), and deduce excision from there exactly as in [
14]. As it is not, we have to work a bit harder.
As before, let C be an open cover of , and write for the poset of finite intersections of sets in C, ordered by inclusion. The idea here is that the map looks a lot like a trivial cofibration, even though it is not one in general. We can produce from by attaching collections of cells which are close enough to trivial cofibrations that they behave nicely under F.
Let . We will create , for ordinals , by adding spaces of cells to when is a successor, and by taking for a limit. At each step will be a simplicial subspace of consisting of a subset of the fat cells.
We need two new operations: filling empty horns and gluing fat cells together.
An empty n-horn in is a fat n-cell K of which is not in , such that all but one of its face maps factors through but there is some k such that its kth face map does not. We can attach K-cells and Kn-cells to via these maps, and refer to this as filling an empty horn in .
Suppose we have a fat n-cell K of which is not in , but all of its face maps factor through . Suppose there is a finite cover of K by compact subspaces , such that there are fat n-cells in for each i and and have the same image in the pullback for each i. We want to glue the s together to get K, but it is not yet clear whether this can be done without changing homotopically `too much’, in a sense which will become clear later. For now, call this a 1-valid opportunity.
If, for each non-empty intersection , has a fat cell of -cells filling the space of -boundaries created by the subspaces of cells of and , we say the opportunity is 2-valid.
Similarly, we inductively say an -valid opportunity is r-valid if, for each non-empty intersection , has a fat cell of -cells filling the space of -boundaries created by the subspaces of cells of for . If an opportunity is r-valid for all r (equivalently, if it is j-valid), we say it is valid, and call n its dimension.
Given a valid opportunity, we can glue fat cells together. Attach D to . For each i, attach a fat cell of -cells to the space of -boundaries created by and the subspace of cells of D. Continue inductively: for each non-empty intersection , attach a fat cell of -cells to the space of -boundaries created by and the subspaces of cells of for . Please note that this process terminates after at most j steps.
Now we can define inductively: for a successor, if has any empty horns, pick one, fill it, and call the result . If it has no empty horns, but has valid opportunities to glue fat cells together, pick one of minimal dimension, take it, and call the result . For a limit we let .
Please note that when is a simplicial subspace of consisting of a subset of the fat cells, is too, so we can see inductively that this is true for all . So this process must terminate: there is some ordinal such that has no empty horns and no valid opportunities.
As we are building , we can label each fat cell K with a finite compact cover of the space of cells. For fat cells in , take , and assume we have labelled all the fat cells in for all . Assume that all the labels for have the following two properties. First, any face map of a fat cell K in sends any into some element of the label of the face. Second, for any fat cell K in and , the image of the subspace in is contained in some .
For
a limit there is no more to do; suppose it is a successor. When we create
from
by filling an empty
k-horn, each face map except the
kth on the new fat cell pulls back to a finite compact cover of
K; pick a common refinement of all of these: that is, a finite compact cover
such that the image of every
under every face map except the
kth is contained in one of the compact spaces in the finite cover labelling that space. For each
, we get an open cover by sets of the form
the image of
in
is contained in
. Pick a finite subcover of this, and then a compact refinement
, which exists by the Shrinking Lemma, ([
17] Exercise 4.36.4). The compact cover of
K given by
has the required properties, showing such a cover exists. Now take a compact cover of
K of minimal size satisfying these properties to be the labels of
K and its
kth face.
If comes from by gluing cells, we are attaching finitely many fat cells by filling spaces of boundaries. For each of these fat cells K, we pick some finite compact cover which is a common refinement of all the finite compact covers induced by the face maps. We refine it further, as above, to show a label satisfying the required properties exists; then we label K with a label of minimal size satisfying these properties.
Proposition 4. Consider a fat cell K in whose image in is contained in some , whose image under each face map is in some , and each such image is contained in a single element of the label of a single fat cell. Then K is in some , , obtained from just by filling empty horns.
Proof. This is proved by induction on ; thanks to our hypotheses on the labels, everything works when we imitate the proof of Proposition 2. ☐
Proposition 5. .
Proof. Suppose not. Let n be the minimal dimension of a fat cell of which is not in , and let K be such a fat cell. For simplicity we can assume that every simplex of K (that is, the image of K under any sequence of face maps) is contained in a single fat cell, since K is the disjoint union of finitely many spaces of cells of this form.
By hypothesis, all the faces of K are in , and already labelled. We can label as above, so that any face map of K sends any into some element of the label of the face, and the image of each in is contained in some . We will show that K can be added to by gluing cells together, giving a contradiction.
For every , the corresponding fat cell such that and have the same image in the pullback has a single element in its label, since we have chosen the labels to have minimal size. So by the previous proposition, is in . Moreover, we see inductively that for every non-empty intersection , every has a single element in its label, and the subspaces of the cells of each form the boundary in of a space of degenerate -cells whose image in is contained in the image of . By the previous proposition again, is in . Since this holds for all non-empty , we have a valid opportunity to add K to by gluing fat cells, giving a contradiction. ☐
Lemma 5. Colimits of sequences of closed inclusions are exact in in the regular structure; that is, given short exact sequences in the regular structure on , and commutative diagrams
the induced sequence is exact.
Proof. Given any diagram of groups in , the colimit in with the colimit topology (if this is in ) becomes an object in . Indeed, the only non-trivial thing to check is that multiplication is continuous: is continuous because finite products commute with colimits in . It follows immediately that this is the colimit in .
Clearly in the current situation the colimit topologies on the s, s and s are in , so the sequence is an exact sequence of the underlying groups. We know colim is right exact because it is a left adjoint, so we only need to check is a closed inclusion of spaces. Each is a closed inclusion, which is an equaliser in , so the result follows because finite limits commute with colimits of sequences of closed inclusions in by Lemma 1. ☐
Theorem 9. is weakly equivalent (in the regular structure on ) to the homotopy colimit of (in the compact Hausdorff structure on ).
Proof. We already know that
is weakly equivalent (in the compact Hausdorff structure) to
. We also have that the homotopy colimit of
is
by Lemma 4. We will show inductively that
is weakly equivalent to
, in the regular structure, for all
; the result follows.
When
is a limit ordinal this follows immediately from Lemma 5. When
is a successor and
is a trivial cofibration, it is trivial. When
is a successor and
comes from an
n-dimensional opportunity to glue cells together in the notation used at the beginning of the section, use the Dold-Kan correspondence of ([
11] Theorem 1.2.3.7) and think of the
as chain complexes in
. The mapping cone of
is homotopic to the complex
M with
with maps induced by the face maps between the
, so we just need to show this is exact in the regular structure. It is not hard to check on the elements that the homology groups of the underlying abstract chain complex are trivial; it follows as in ([
3] Proposition 2.32) (using free abelian groups instead of free groups) that the induced maps
are isomorphisms in
, as required. ☐
Remark 3. Pushing out by these collections of cells, which look provocatively like finite length exact sequences of projectives, ought to be a trivial cofibration in some nice homotopical structure on , but I do not know what that structure should be.
From Theorem 9 we may deduce the usual form of the Excision Theorem as in ([
14] p.124), using mapping cones (i.e., homotopy cokernels) instead of quotient complexes.
Theorem 10 (Excision Theorem). Given subspaces in with A closed and B open, the inclusion induces isomorphisms of the homology group objects for all n. Equivalently, for open subspaces covering X, the inclusion induces isomorphisms of homology group objects for all n.
Proof. We prove the second formulation. Write for the pushout of . The square
is a pushout, so the cokernels of the two rows are isomorphic, so the maps induced on their homology group objects are isomorphisms. By Theorem 9, the canonical map
is a weak equivalence in the regular structure, so the maps induced on their homology group objects are isomorphisms too. Now we can use the long exact sequence in homology to see that the maps of homology group objects induced by
are isomorphisms, and the result follows. ☐
Much of the rest of Chapter 2 of Hatcher’s textbook [
14] can be carried across to our topological homology theory fairly painlessly from this point; we give a few highlights.
Theorem 11 (Mayer–Vietoris sequence).
For open subspaces covering X there is a long exact sequence of homology group objects Proof. Think of the rows of the commutative square in the proof of Theorem 10 as a chain complex of chain complexes; the vertical maps give a map between these chain complexes of chain complexes. This square is a pushout and a pullback; it is a standard result of commutative alebra in quasi-abelian categories that the mapping cone of this square is then a short exact sequence of chain complexes
in the regular structure. Taking homology and applying Theorem 9 gives the result. ☐
In constructing a homology theory on , we would like certain axioms to be satisfied: those of a generalised homology theory. These axioms are usually listed for homology theories from spaces to abelian groups, but they make sense in our context. A generalised homology theory is here taken to be a functor E from pairs of spaces in to chain complexes in R-, with the regular structure, satisfying:
- (i)
homotopy invariance: homotopies in induce homotopies in R-;
- (ii)
exactness: associated naturally to a pair is an exact triangle ;
- (iii)
additivity: if is a disjoint union of pairs , then the canonical map is a weak equivalence;
- (iv)
dimension: is exact in non-zero dimensions;
- (v)
excision: for with A closed and B open, the canonical map is a weak equivalence.
Given our definitions, the excision axiom was the only non-trivial thing to check, and this is provided by Theorem 10. So we have:
Theorem 12. Singular homology is a generalised homology theory.
7. Eilenberg–Mac Lane Spaces
Finally, we may use Theorem 8 to construct certain Eilenberg–Mac Lane spaces for topological groups.
Lemma 6. For all n, is weakly equivalent to in the compact Hausdorff structure.
Proof. Any map is a trivial cofibration; is homotopy equivalent to a point, so is homotopy equivalent to . ☐
Suppose . As usual, each comes with a canonical decomposition as a disjoint union of compact fat cells: write S for the set of fat cells. For each fat n-cell , consider the diagram in given by objects indexed by the m-cells of and maps indexed by the face and degeneracy maps of . Write as the colimit of a sequence of pushouts attaching fat cells in order of dimension: these attaching maps induce maps from the copies of in to copies of in wherever an m-face of K is attached to an m-face of . The set of diagrams , , together with these maps between objects of the diagrams, give a bigger diagram D.
Proposition 6. is the homotopy colimit of D.
Proof. The colimit of D is the colimit of the , since we can get each as the colimit (and in fact the homotopy colimit) of all the objects of except itself, and then the maps between the s induce the map from the pushout. And we know the colimit of the is .
Since we are adding fat cells in order of dimension, for each
n there is some
such that
is the
n-skeleton of
Y. Then
is the homotopy colimit of the pushout
because all three objects are cofibrant and the second map is a cofibration, by ([
5] Proposition A.2.4.4). Then
Y is the colimit of a sequence
of cofibrant objects with cofibrations between them, so it is the homotopy colimit by ([
16] Example 11.5.11). It follows that colimit
is the homotopy colimit of
D. ☐
Since we can change a diagram by a weak equivalence without changing the homotopy colimit, we can change D to a diagram of the same shape where we replace each with ; the maps in are the obvious ones induced by those of D. We conclude that is the homotopy colimit of .
We denote the points of by the coordinates , where parametrises the closed unit ball in spherical coordinates and . For each n, we have a map from to the n-skeleton of which restricts to a homeomorphism from to , in the same way as for CW-complexes.
Theorem 13. Suppose with totally path-disconnected for all n. Then is weakly equivalent to X in the regular structure.
Proof. By replacing X with (which gives a weak equivalence in the compact Hausdorff structure), if necessary, we may assume for simplicity that for any fat cell in the images of its face maps are pairwise disjoint.
is weakly equivalent to X in the compact Hausdorff structure, and if the are totally path-disconnected, so are the .
is then a KW-complex, as defined in ([
4]
Section 2), and we construct an open cover inductively on the skeleta: on the 0-skeleton we take an open cover whose open sets are the fat cells of
. Suppose we have an open cover
of the
-skeleton. For each fat cell
K of
, we have the open space
of open
n-cells
. Also, for every open
, think of
as an open subset of
; in spherical coordinates as before, define
for some small
. Take
to be the the open cover of the
n-skeleton given by the
s and the
s. Taking limits over
n, we get a cover
C of
.
Let be the set of finite intersections of open sets in C. We can see directly that any non-empty element of is homotopic to some fat cell K of . Since K is totally path-disconnected, all singular maps into K are constant and is just the constant simplicial space on K. By Theorem 8, is weakly equivalent (in the regular structure on ) to the homotopy colimit of , which is the homotopy colimit of . However, this diagram is easily seen to be isomorphic to , so its homotopy colimit is X. ☐
Given a group object
G in
, a construction is given in ([
4]
Section 6) for
such that
for
, and
. In this construction
.
Now if G is a topological group in , is a group object in , and is G for and trivial otherwise. Note too that if G is totally path-disconnected, every is too. So we can apply Theorem 13.
Theorem 14. If G is totally path-disconnected, is an Eilenberg–Mac Lane space for G.
Similarly, when G is totally path-disconnected and abelian, is a .
Please note that totally disconnected spaces are totally path-disconnected, so totally disconnected groups are included as a special case. Here is a totally path-disconnected topological group in which is not totally disconnected.
Example 2. Let X be the pseudo-arc, as in Example 1. Let be the free group object (in ) on X: see ([3] Notation 2.10) for the construction. is not totally disconnected because X is connected and the canonical map is a closed embedding by ([3] Theorem 2.12). Suppose there is a non-constant map . In the notation of [3], topologically is the colimit of the closed subspaces by ([3] Proposition 2.16). So by compactness, there is some n such that the image of p is contained in but not ; in particular there is some open subspaceof on which p is not constant, or else for we would have , implying and p is not constant on by hypothesis. Then pick a closed interval on which p is not constant. From the construction, is the disjoint union of spaces of the formwhere S ranges over subsets of . Observe that if we restrict to the subspaceswe haveSo must be contained in some . It follows from ([3] Proposition 2.16), by the same argument as ([3] Corollary 2.18), that is an embedding. So lifts to a non-constant map , but is totally path-disconnected as a subspace of a product of copies of X, giving a contradiction, and implying that is totally path-disconnected. As a final application, we return to singular homology. Generalise the definition of
-complexes given in ([
14] p.103) to allow totally path-disconnected spaces of cells: as in the classical case, the definition ensures that such a
-complex
is the geometric realisation of some
such that every
is totally path-disconnected. Call such spaces generalised simplicial complexes. As in the classical case, we define the simplicial homology
of
to be the singular homology of
X.
Proposition 7. The singular and simplicial homology theories for generalised Δ-complexes are naturally isomorphic.
Proof. We showed in the proof of Theorem 13 that X is weakly equivalent, in the compact Hausdorff structure, to , where is the open cover of described there. So is weakly equivalent in the compact Hausdorff structure to , which is weakly equivalent to in the regular structure by Theorem 9. So all three have the same homology. ☐