Abstract
The purpose of this note is to provide an expository introduction to some more curious integral formulas and transformations involving generating functions. We seek to generalize these results and integral representations which effectively provide a mechanism for converting between a sequence’s ordinary and exponential generating function (OGF and EGF, respectively) and vice versa. The Laplace transform provides an integral formula for the EGF-to-OGF transformation, where the reverse OGF-to-EGF operation requires more careful integration techniques. We prove two variants of the OGF-to-EGF transformation integrals from the Hankel loop contour for the reciprocal gamma function and from Fourier series expansions of integral representations for the Hadamard product of two generating functions, respectively. We also suggest several generalizations of these integral formulas and provide new examples along the way.
MSC:
05A15; 30E20; 31B10; 11B73
1. Introduction
1.1. Definitions
Given a sequence , we adopt the notation for the respective ordinary generating function (OGF), , and exponential generating function (EGF), , of the sequence in some formal indeterminate parameter :
Notice that we can always construct these functions over any sequence and formally perform operations on these functions within the ring of formal power series in z without any considerations on the constraints imposed by the convergence of the underlying series as a complex function of z. If we assume that the respective series for or is analytic, or converges absolutely, for all with , then we can apply complex function theory to these sequence generating functions and treat them as analytic functions of z on this region.
We can precisely define the form of an integral transformation (in one variable) as [1] (§ 1.4)
for and where the function is called the kernel of the transformation. When the function f which we operate on in the formula given by the last equation corresponds to an OGF or EGF of a sequence with which we are concerned in applications, we consider integrals of the form in (2) to be so-called generating function transformations. Such generating function transformations are employed to transform the ordinary power series of the target generating function for one sequence into the form of a generating function which enumerates another sequence we are interested in studying.
Generating function transformations form a useful combinatorial and analytic method (depending on perspective) which can be combined and employed to study new sequences of many forms. Our focus in this article is to motivate the constructions of generating function transformations as meaningful and indispensable tools in enumerative combinatorics, combinatorial number theory, and in the theory of partitions, among other fields where such applications live. The particular modus operandi within this article shows the evolution of integral transforms for the reciprocal gamma function, and its multi-factorial integer sequence special cases, as a motivating method for enumerating several types of special sequences and series which we will consider in the next sections.
The references [2,3,4] provide a much broader sense of the applications of generating function techniques in general to those readers who are not familiar with this topic as a means for sequence enumeration. A comprehensive array of analytic and experimental techniques in the theory of integral transformations is also treated in the references [1,5]. We focus on only a comparatively few concrete examples of integral and sequence transformations in the next subsections with hopes to motivate our primary results proved in this article from this perspective. We hope that the discussion of these techniques in this short note provide motivation and useful applications to readers in a broader range of mathematical areas.
1.2. From Hobby To Short Note: OGF-to-EGF Conversion Formulas
A time consuming hobby that the author assumes from time to time is rediscovering old and unusual identities in mathematics textbooks– particularly in the areas of combinatorics and discrete mathematics. Favorite books to search include Comtet’s Advanced Combinatorics and the exercises and their solutions found in Concrete Mathematics by Graham, Knuth and Patashnik. One curious and interesting conversion operation discussed in the exercises to Chapter 7 of the latter book involves a pair of integral formulas for converting an arbitrary sequence OGF into its EGF and vice versa provided the resulting integral is suitably convergent. The exercise listed in Concrete Mathematics suggests the second form of the operation. Namely, that of converting a sequence EGF into its OGF.
In this direction, we have an easy conversion integral for converting from the EGF of a sequence , denoted by , and its corresponding OGF, denoted by , given by the Laplace–Borel transform [6] (§ B.14):
Other integral formulas for conversions between specified generating function “types” can be constructed similarly as well (see Section 1.3). The key facets in constructing these semi-standard, or at least known, conversion integrals is in applying a termwise series operation which generates a factor, or reciprocal factor, of the gamma function when . The corresponding “reversion” operation of converting from a sequence’s OGF to its EGF requires a more careful treatment of the properties of the reciprocal gamma function, , and the construction of integral formulas which generate it for involving the Hankel loop contour described in Section 2.
That being said, Graham, Knuth and Patshnik already suggest a curious “known” integral formula for performing this corresponding OGF-to-EGF conversion operation of the following form [3] (p. 566):
The statement of this result is given without proof in the identity-full appendix section of the textbook. When first (re)-discovered many years back, the author assumed that the motivation for this integral transformation must correspond to the non-zero paths of a complex contour integral for the reciprocal gamma function. For many years the precise formulation of a proof of this termwise integral formula and its generalization to enumerating terms of reciprocal generalized multi-factorial functions, such as , remained a mystery and curiosity of periodic interest to the author. In the summer of 2017, the author finally decided to formally inquire about the proof and possible generalizations in an online mathematics forum. The question went unanswered for over a year until by chance the author stumbled onto a Fourier series identity which finally motivated a rigorous proof of the formula in (3). This note explains this proof and derives another integral formula for this operation of OGF-to-EGF inversion based on the Hankel loop contour. The preparation of this article is intended to be expository in nature in the hope of inspiring the creativity of more researchers towards developing related integral transformations of sequence generating functions.
1.3. Examples: Integral transformations of a Sequence Generating Function
Integral transformations are a powerful and convenient formal and analytic tool which are used to study sequences and their properties. Moreover, they are easy to parse and apply in many contexts with only basic knowledge of infinitesimal calculus making them easy-to-understand operations which we can apply to sequence generating functions. The author is an enthusiast for particularly pretty or interesting integral representations (cf. [5,7]) and has taken a special research interest in finding integral formulas of the ordinary generating function of sequence which transform the series into another generating function enumerating a modified special sequence.
One notable example of such an integral transformation given in [8] (§ 2) allows us to construct generalized polylogarithm-like and Dirichlet-like series over any prescribed sequence in the following forms for integers :
Another source of generating function transformation identities correspond to the bilateral series given by Lindelöf in [9] (§ 2) of the form
where is any closed contour in which contains all of the singular points of f in its interior. In this note, we will focus on integral formulas for generating function transformations of an arbitrary sequence, .
Additional series transformations involving a sequence generating function into the form of for and non-zero sequences are proved in [10,11]. Note that the harmonic-number-related coefficients implicit to these series transformations satisfy summation formulas which are readily expressed by Nörlund-Rice contour integral formulas as well. The author has proved in [12] so-called square series transformations providing that
Applications of these square series integral representations include many new integral formulas for theta functions and classical q-series identities such as the Jacobi triple product and the partition function generating function, , expanded by Euler’s pentagonal number theorem.
There are more general Meinardus methods for computing asymptotics of the coefficients of classes of partition number generating functions of the form [13]
where denotes the number of weighted partitions of n corresponding to the parameter weights for . Generating functions enumerating partition function sequences of this type are related to a known Euler transform of a sequence given by [14]
where and are the respective OGFs of the component sequences. In this case the right-hand-side generating function in the last equation is generated succinctly by a q-integral for the q-beta function of the form [15]
where inputting the modified generating function, for fixed z, into this integral formula generates the second to last series result.
1.4. Results Proved in This Note
In this short note we provide proofs of known integral formulas providing an ordinary-to-exponential generating function operation. We prove the following theorem using the Hankel loop contour for the reciprocal gamma function in Section 2.
Theorem 1 (OGF-to-EGF Integral Formula I).
For any real , provided that is analytic for , we have that
We also give a rigorous proof of the next integral formula relating and .
Theorem 2 (OGF-to-EGF Integral Formula II).
If is analytic for , we have that (3) holds. Namely, we have that
The proof of Theorem 2 is given in Section 3.
2. Integral Representations of the Reciprocal Gamma Function
Since is a meromorphic function of z with poles at the non-positive integers, it follows that the reciprocal gamma function, , is an entire function (of order one) with zeros at [16] (§ 5.1). Indeed, as at a constant , we can expand
which can be computed via the infinite products
where is Euler’s gamma constant. Classically, Karl Weierstrass called the function the “factorielle” function, and used its representation to prove his famous Weierstrass factorization theorem in complex analysis [17] (§ 2).
For such that we have a known series expansion for the reciprocal gamma function given by
The coefficients in this expansion satisfy many known recurrence relations and expansions by the Riemann zeta function. In [18] an exact integral formula for these coefficients is given by
This integral formula is obtained in the reference using Euler’s reflection formula for the gamma function given by
and then applying a standard known real integral to express the gamma function on the right-hand-side of the previous equation. Equivalently, the reflection formula can be stated as
2.1. The Hankel Loop Contour for the Reciprocal Gamma Function
We seek an exact integral representation for the reciprocal gamma function, not just an integral formula defining the coefficients of its Taylor series expansion about zero in this case. To find such a formula we must use the Hankel loop contour shown in Figure 1 and consider the contributions of each component section of the contour in the limiting cases for increasingly small . We prove Theorem 1 using the next lemma derived from this contour below.
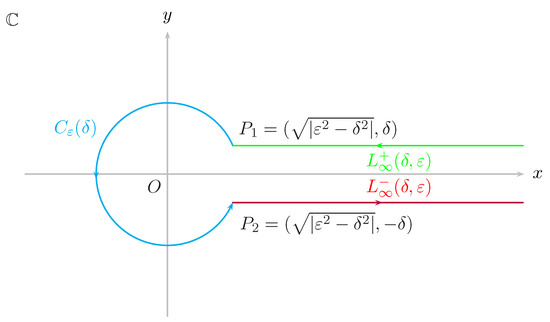
Figure 1.
The Hankel loop contour providing an integral representation of the reciprocal gamma function when . This contour starts positively from the right, traverses the horizontal line at distance from the x-axis from , then enters the semi-circular loop about the origin of radius denoted by at the point , and then at the point traverses the last horizontal line back to infinity parallel to the x-axis.
Lemma 1.
For any real and such that ,
Proof.
Working from the figure, we have that [16] (§5.9)
We will first approach the contribution of the section of the contour given by which is a path enclosing the origin along the circle of radius centered at . This portion of the contour is oriented in the positive direction and begins at the point and ends at the point . By parameterizing t along this circle, we obtain the real integral giving
since as independently tend to zero. Now we can easily parameterize each of the sections of the contour on the horizontal lines each at distance from the x-axis. In particular, let’s define our integrand in the complex parameters as . Then we consider the limiting cases of the following parameterizations of the two line segments on and , respectively, by evaluating the limit of and then letting T tend to :
When we take the first small-order limits we obtain
which by substitution provides us with the symmetric bounds of integration given by
We then finally arrive at the stated known integral formula for the reciprocal gamma function which holds for any fixed real . □
Proof of Theorem 1.
Since we are initially motivated by finding a general conversion integral from a sequence OGF into its EGF, we notice that we require an application of (11) termwise to the Taylor series expansions of our prescribed generating function by setting . For example, if we assume that our sequence OGF at hand is well enough behaved when its argument satisfies for some fixed choice of the real in the integral formula from above, we can sum the integrand of (11) termwise to obtain
□
2.2. Examples: Applications of the Integral Formula on the Real Line
We can perform the same “trick” of the generating function trades to sum a “doubly exponential” sequence generating function when we replace the sequence OGF by its EGF in the previous equation:
Perhaps at first glance this iterated integral formula is somewhat unsatisfying since we have really just repeated the procedure for constructing the first integral twice, but in fact there are notable special case applications which we can derive from this method of summation which provide new integral representations for otherwise hard-to-sum hypergeometric series.
For example, if we take the geometric series sequence case where for all , then we can arrive at a new integral formula for the doubly exponential series expansion of the incomplete Bessel function, [3] (§ 5.5). In particular, we easily obtain that
There is an integral representation for this function which is simpler to evaluate in the general case given in (3). We elaborate more on this identity, its proof, and the corresponding series involving Stirling numbers which it implies in the next section.
3. An Integral Formula from Fourier Analysis
One curious identity that the author has come across relating the OGF of a sequence to its EGF is found in the appendices of the Concrete Mathematics reference [3] (p. 566). It states (3) without proof, again providing that
Finding a precise method of verifying this unproven identity is the initial motivation for this note. Given the discussion and lead up to an integral for the reciprocal gamma function taken over the real line via the Hankel loop contour in the last section, the author initially assumed—and asked with no replies in online math forums—that this computationally correct integral representation must correspond to the non-zero components of some complex contour integral. It turns out that this formula follows from the basic theory and constructions of Fourier analysis.
Proof of Theorem 2.
Given a sequence, , its (mostly convergent) Fourier series is given by . The terms of this sequence are then generated by this Fourier series according to the standard integral formula [1,19]
for natural numbers . If we can assume that the Fourier series, , or equivalently the OGF, , is absolutely convergent for all then we can sum over the integral formula in the previous equation to obtain the first key component to this proof:
The change of variables for fixed z shows that this formula is equivalent to the integral formula in (3) directly by a change of variables. Also, by expanding the integrand in powers of where
it is apparent that these two formulas in fact generate the same power series representation for . □
Alternate Proof of Theorem 2.
Another satisfyingly less analytical and more formally motivated explanation for this behavior can be given by considering known integral formulas for the Hadamard product of two series given in terms of the orthogonal set for x on the symmetric interval [2] (§ 1.12(V); Ex. 1.30, p. 85) [4] (cf. §6.3). This perspective on the formulations of these two series allows us to swap the series variables from the input of one function in the product to another and similarly in the reverse direction. Thus we can effectively pick and choose where we would like to position the generating function parameter z in each component of the integrand—whether it be situated more naturally as an argument to F as in (3), or whether we choose to keep it nested in the corresponding multiplier function as in the previous equation. We shall see other examples of these integral formula variants in the next remark and following examples. □
Remark 1 (Generalizations of series expansions from Fourier series).
This technique of using a convergent Fourier series and the corresponding integral operation for extracting its coefficients can be generalized to generate many other series variants. For example, there are many zeta function and polylogarithm-related series which are summed by modifying a polylogarithmic series of the form expanded in Section 1.2 by the reciprocal of the central binomial coefficients, . In particular, in the exponential-series-based generating function cases we have that
and in the geometric-series-based OGF cases we recover the exponential error function by
There are many other possibilities for constructing integral transformations for modified generating function types. All one needs to do is be creative and consult a detailed reference of compendia such as [5,7].
Examples: Generalizations and Solutions to a Long-Standing Forum Post
The primary goal of the first post [20] mentioned in the introduction was to eventually generalize the integral formula in (3) to enumerate the modified EGF sequences of the form
for integers and , or over factors of the generalized integer multifactorials defined in [21] as
In the spirit of our realization that the integral representation in (3) is derived from a Fourier series coefficient formula, we may similarly complete our initial goal to sum the second forms of these series in the special cases where . In particular, we can sum these cases of the modified EGFs defined above in closed-form as explicit integral formulas in the forms
The modified exponential series of the first type identified above are primarily summed in closed-form using expansions of the Mittag–Leffler functions, , and powers of primitive roots of unity [16] (§ 10.46). For example, let’s take and observe that
Then we arrive at a corresponding explicit integral representation for the modified EGF of any sequence of the form
4. Concluding Remarks
We have proved two key new forms of integral representations for the reciprocal gamma function on the real line. By composition and the uniform convergence of power series for functions defined on some disc , these results effectively provide us with OGF-to-EGF conversion formulas between the generating functions for some . These integral formulas for OGF-to-EGF conversion can be applied termwise, or in analytic estimates of the asymptotic growth of the coefficients in the power series expansions of the functions defined by the corresponding integral transformation.
We have provided several examples of motivating cases of our so-termed generating function transformations by integral-based methods in Section 1.3. The broader applications of these transformation methods to other fields and phrasings of problems is certainly possible given a suitable context waiting for a new method from which to be approached. We hope that readers come away from this article with a new understanding of how useful and sometimes indispensable integral transformation methods are in sequence analysis.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Debnath, L.; Bhatta, D. Integral Transforms And Their Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics, Volume 2; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Boros, G.; Moll, V.H. Irresistible Integrals: Symbolics, Analysis and Experiements in the Evaluation of Integrals; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gradshetyn, I.S.; Rhyzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Borwein, D.; Borwein, J.M.; Girgensohn, R. Explicit evaluation of Euler sums. Proc. Edinb. Math. Soc. 1995, 38, 277–294. [Google Scholar] [CrossRef]
- Milgram, M.S. Integral and Series Representations of Riemann’s Zeta Function, Dirichlet’s eta Function and A Medley of Related Results. arXiv 2012, arXiv:1208.3429. [Google Scholar] [CrossRef]
- Schmidt, M.D. Zeta Series Generating Function Transformations Related to Generalized Stirling Numbers and Partial Sums of the Hurwitz Zeta Function. Online J. Anal. Comb. 2018, 13, 1–31. [Google Scholar]
- Schmidt, M.D. Zeta series generating function transformztions related to polylogarithm functions and the k–order harmonic numbers. Online J. Anal. Comb. 2017, 12, 1–22. [Google Scholar]
- Schmidt, M.D. Square series generating function transformations. Inequalities Spec. Funct. 2017, arXiv:1609.02803. [Google Scholar]
- Granovskya, B.L.; Starkb, D.; Erlihson, M. Meinardus’ theorem on weighted partitions: Extensions and a probabilistic proof. Adv. Appl. Math. 2008, 41, 307–328. [Google Scholar] [CrossRef]
- Bernstein, M.; Sloane, N.J.A. Some Cannonical Sequences of Integers. arXiv 2002, arXiv:math/0205301. [Google Scholar]
- Andrews, G.E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Remmert, R. Classical Topics in Complex Function Theory; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Fekih-Ahmed, L. On the power series expansions of the reciprocal gamma function. arXiv 2017, arXiv:abs/1407.5983. [Google Scholar]
- Tolstov, G.P. Fourier Series; Dover Publications: Mineola, NY, USA, 2014. [Google Scholar]
- An Integral Formula For The Reciprocal Gamma Function. Available online: https://math.stackexchange.com/questions/2274972/an-integral-formula-for-the-reciprocal-gamma-function (accessed on 22 May 2018).
- Schmidt, M.D. Generalized j–factorial functions, polynomials, and applications. J. Integer Seq. 2010, 13, 1–54. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).