A Short Note on Integral Transformations and Conversion Formulas for Sequence Generating Functions
Abstract
1. Introduction
1.1. Definitions
1.2. From Hobby To Short Note: OGF-to-EGF Conversion Formulas
1.3. Examples: Integral transformations of a Sequence Generating Function
1.4. Results Proved in This Note
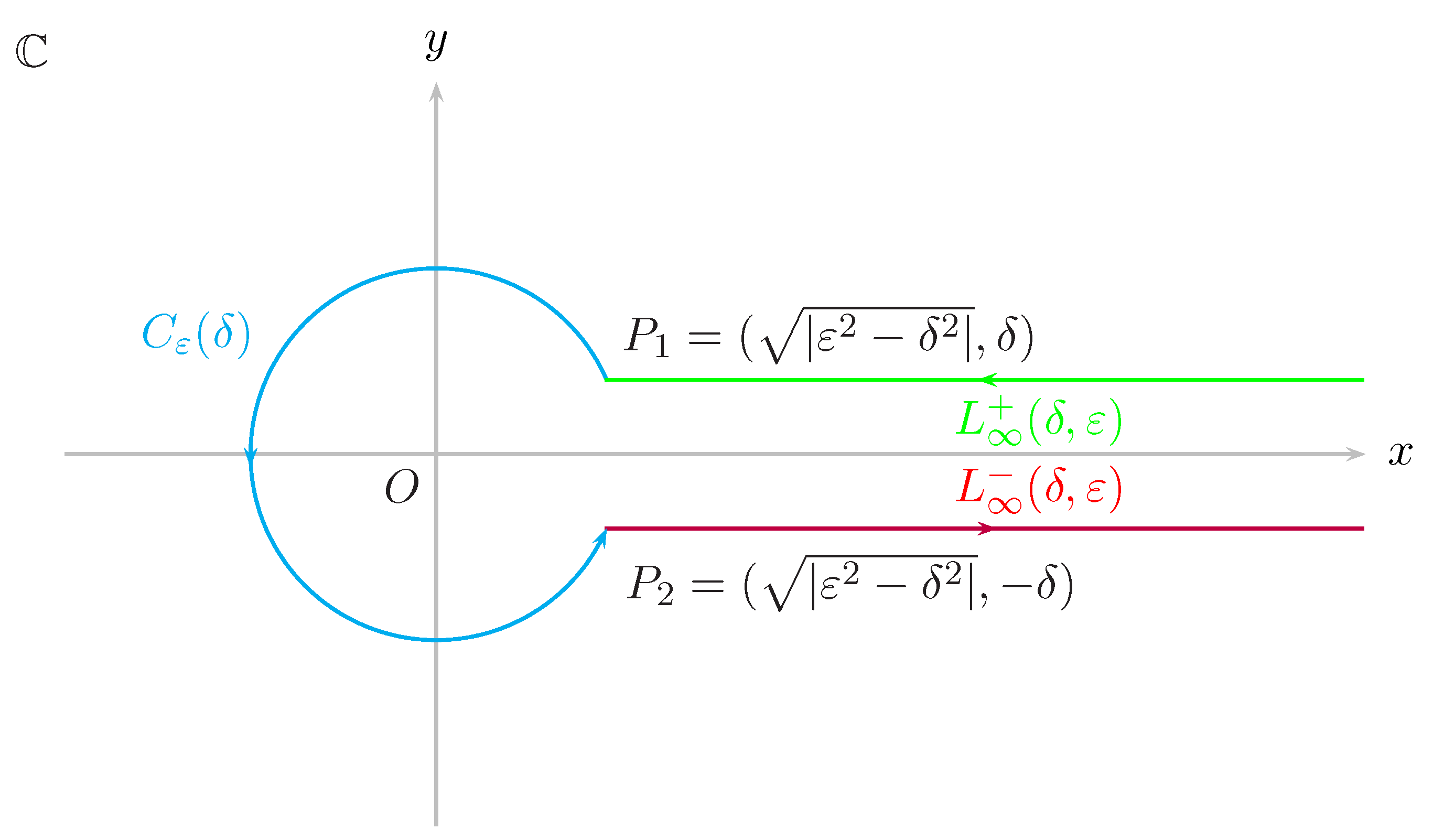
2. Integral Representations of the Reciprocal Gamma Function
2.1. The Hankel Loop Contour for the Reciprocal Gamma Function
2.2. Examples: Applications of the Integral Formula on the Real Line
3. An Integral Formula from Fourier Analysis
Examples: Generalizations and Solutions to a Long-Standing Forum Post
4. Concluding Remarks
Funding
Conflicts of Interest
References
- Debnath, L.; Bhatta, D. Integral Transforms And Their Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics, Volume 2; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Boros, G.; Moll, V.H. Irresistible Integrals: Symbolics, Analysis and Experiements in the Evaluation of Integrals; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gradshetyn, I.S.; Rhyzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Borwein, D.; Borwein, J.M.; Girgensohn, R. Explicit evaluation of Euler sums. Proc. Edinb. Math. Soc. 1995, 38, 277–294. [Google Scholar] [CrossRef]
- Milgram, M.S. Integral and Series Representations of Riemann’s Zeta Function, Dirichlet’s eta Function and A Medley of Related Results. arXiv 2012, arXiv:1208.3429. [Google Scholar] [CrossRef]
- Schmidt, M.D. Zeta Series Generating Function Transformations Related to Generalized Stirling Numbers and Partial Sums of the Hurwitz Zeta Function. Online J. Anal. Comb. 2018, 13, 1–31. [Google Scholar]
- Schmidt, M.D. Zeta series generating function transformztions related to polylogarithm functions and the k–order harmonic numbers. Online J. Anal. Comb. 2017, 12, 1–22. [Google Scholar]
- Schmidt, M.D. Square series generating function transformations. Inequalities Spec. Funct. 2017, arXiv:1609.02803. [Google Scholar]
- Granovskya, B.L.; Starkb, D.; Erlihson, M. Meinardus’ theorem on weighted partitions: Extensions and a probabilistic proof. Adv. Appl. Math. 2008, 41, 307–328. [Google Scholar] [CrossRef]
- Bernstein, M.; Sloane, N.J.A. Some Cannonical Sequences of Integers. arXiv 2002, arXiv:math/0205301. [Google Scholar]
- Andrews, G.E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Remmert, R. Classical Topics in Complex Function Theory; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Fekih-Ahmed, L. On the power series expansions of the reciprocal gamma function. arXiv 2017, arXiv:abs/1407.5983. [Google Scholar]
- Tolstov, G.P. Fourier Series; Dover Publications: Mineola, NY, USA, 2014. [Google Scholar]
- An Integral Formula For The Reciprocal Gamma Function. Available online: https://math.stackexchange.com/questions/2274972/an-integral-formula-for-the-reciprocal-gamma-function (accessed on 22 May 2018).
- Schmidt, M.D. Generalized j–factorial functions, polynomials, and applications. J. Integer Seq. 2010, 13, 1–54. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, M.D. A Short Note on Integral Transformations and Conversion Formulas for Sequence Generating Functions. Axioms 2019, 8, 62. https://doi.org/10.3390/axioms8020062
Schmidt MD. A Short Note on Integral Transformations and Conversion Formulas for Sequence Generating Functions. Axioms. 2019; 8(2):62. https://doi.org/10.3390/axioms8020062
Chicago/Turabian StyleSchmidt, Maxie D. 2019. "A Short Note on Integral Transformations and Conversion Formulas for Sequence Generating Functions" Axioms 8, no. 2: 62. https://doi.org/10.3390/axioms8020062
APA StyleSchmidt, M. D. (2019). A Short Note on Integral Transformations and Conversion Formulas for Sequence Generating Functions. Axioms, 8(2), 62. https://doi.org/10.3390/axioms8020062




