1. Introduction
In recent years, autonomous mobile robots have been used to perform a wide variety of important activities and specific functions. These robots are used to perform exploration tasks on other planets, monitor volcanic activities, study deep-water behavior, assemble cars, and support people’s surgeries, among many other activities. All these activities are carried out in conjunction with other disciplines and using new emerging technologies including the Internet of Things (IoT), as a tool or complement for the acquisition and transmission of data. From the place where the robot is located, the information obtained must be processed by an intelligent model (artificial intelligence) to give an answer or instructions to the autonomous robot.
There are several methods that are used in system control. The classic ones include proportional control (P), which determines the relation of the current error [
1]; proportional integral control (PI), which generates a proportional correction of the errors as observed in [
2,
3,
4,
5]; and proportional integral derivative (PID), which determines the reaction time in which the error occurs. There are two types of forms in a control algorithm that decide on a particular control action—the open loop system, in which the parameters of the algorithms are preset and do not change while the system is running, and the closed loop system, in which there are sensors that measure the error between the desired state of the system and its real state. This error is used to decide on the action to take; thus, closed circuit control systems are used.
These controllers can be used to solve a problem when there is no knowledge of the process, when its objective is to obtain greater precision in the control of the system, and when related works in the literature can be observed [
6,
7,
8].
In the literature, we can find works where the authors propose the use of other devices. For example, in [
9,
10,
11,
12], some works are presented, using
raspberry pi to solve different problems, such as to track and monitor animal activities, to control a robotic arm, to classify and recognize animals, and to detect and classify arrhythmias. It is also recommended to read [
13,
14], where the authors propose the use of other devices in their work.
An alternative method is to use fuzzy logic control (FLC) algorithms based on fuzzy rules, and these systems have been widely used, as shown in [
15,
16,
17,
18,
19,
20]. A fuzzy control system contains rules, and these rules are expressed in terms of linguistic variables. FLC is now also widely used to solve any problem that contains the concept of knowledge-based fuzzy inference proposed by Zadeh in 1965 [
21]. Unlike classical logic, where we have only true or false, a fuzzy inference system handles simple linguistic variables that adapt better to the real world, for example, minimum, maximum, etc. [
22]. Fuzzy logic has been widely used, as shown in [
23,
24,
25,
26,
27,
28,
29].
The era of robots has been very successful in recent years [
30], with various types of robots in existence. In this case, the Lego Mindstorms EV3 is considered, which is the third generation of the set of robotics belonging to the Lego company. These robots have been used to solve certain problems, as shown in [
31,
32,
33].
Today, it is difficult to make the decision about using a PID controller or an FLC system. In this paper, the three types of controls, called PI, PID, and FLC, are applied to the speed control of the Lego Mindstorms EV3, with the main objective being to achieve good speed control of the robot. Recently, these robots have been widely used, as shown in [
34,
35,
36,
37].
Different methods and techniques are used to find the best parameters for PI and PID controllers, such as the Ziegler Nichols method [
38,
39,
40]. On the other hand, for FLC, there are evolutionary computation techniques to find the best parameters by means of a genetic algorithm [
41,
42,
43,
44,
45]. However, in this case the values of the parameters of these controllers were found through trial and error.
The metrics used in this study are the integral of the squared error (ISE), the integral of the absolute value of error (IAE), the integral of the time-weighted squared error (ITSE), the integral of the time multiplied by the absolute value of error (ITAE), and the root mean square error (RMSE).
This paper is comprised of the following sections:
Section 2, in which the mathematical model of the Lego Mindstorms EV3 is presented;
Section 3, in which the case study is shown;
Section 4, in which the simulations and results are shown; and, finally,
Section 5, in which the conclusions are presented.
2. The Mathematical Model of the Lego Mindstorms EV3
The Lego Mindstorms team is the most popular educational platform, since it has a relatively accessible cost; it is reusable, robust, and reconfigurable; and its modules are easy to use by students of all educational levels. In addition, the EV3 team contains all the elements or parts necessary to build a functional robot. It is widely used for educational purposes, as well as for research experiments in robotics. In this work we are using the Matlab language programming framework, this language facilitates the interaction with the motors for readings of the positions with respect to the reference.
This model has an operating system based on LINUX, with an ARM9 processor of 300 MHz, a RAM memory of 64 MB, a Flash memory of 16 MB, RJ12 connectors ports for sensors and motors, and USB 2.0 communication (in this case, we used this port for the connection of a USB wireless module for synchronization with the developed block model).
In this paper, a Lego Mindstorms EV3 robot has been used for the experiment. This robot has several characteristics including two large motors, a medium motor, and a programmable brick EV3, which is the control center and the power source of the robot, as well as a wireless card for the experiment and therefore could be assembled in different ways. The particular robot configuration in this case is shown in
Figure 1.
The mathematical model for modeling the motor of the robot uses two fundamental laws of physics [
46]: the first is Kirchhoff’s law based on the energy conservation and load of the electrical circuits, as shown in Equation (1); and the second is Newton’s law based on the mechanical equation, as shown in Equation (2).
where,
Table 1 shows the description of each variable.
3. Case Study Used in This Work
Three different control methods to achieve the speed control of a Lego Mindstorms EV3 are used, and a closed circuit control systems is used [
47,
48,
49,
50].
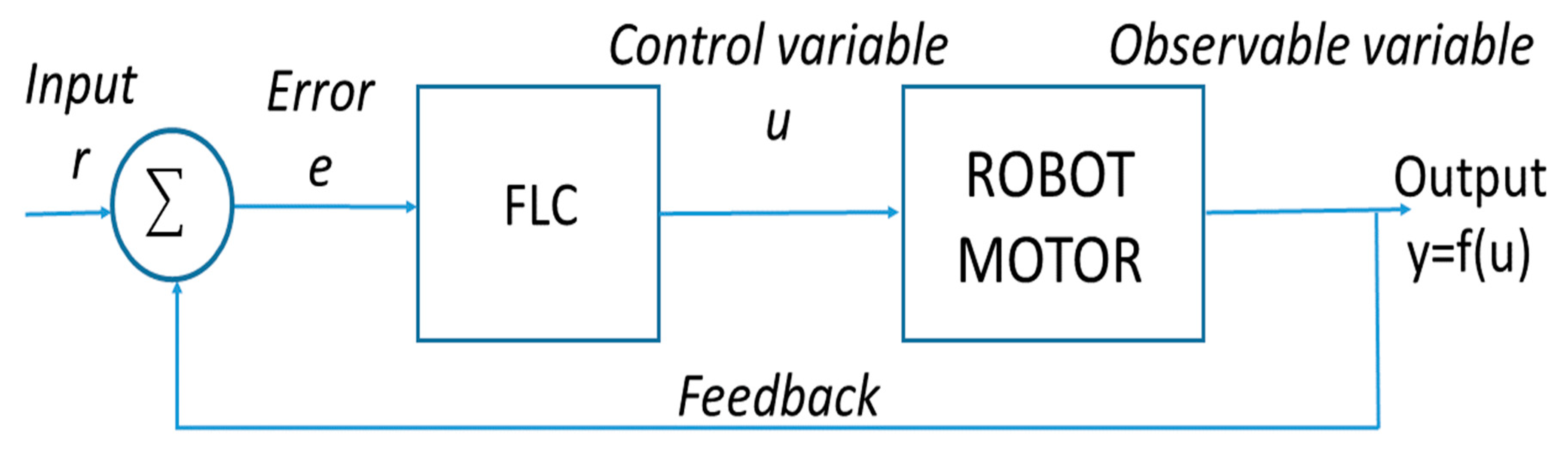
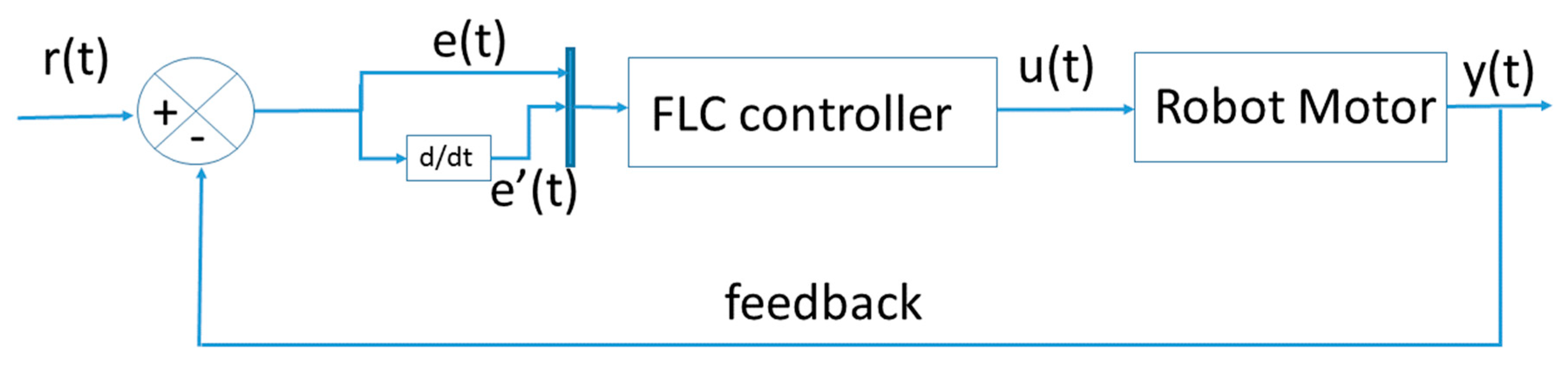
Figure 2 shows the general scheme of a closed loop control system.
The parameter denoted by r represents the reference value; the variable transformed into a control value is represented by u, and the y variable represents the output, which is calculated with the equation e = r − y.
The first is a PI controller based on the Equation (3), the second is a PID controller based on the Equation (4), and the third is a fuzzy controller that is based on the theory of fuzzy sets with which the FLC control systems can be created. The general diagram of an FLC is shown in
Figure 3.
where
r is the controller output,
t is the time,
is the proportional gain,
e is the error between the reference value and the system output, and
is the time derivative.
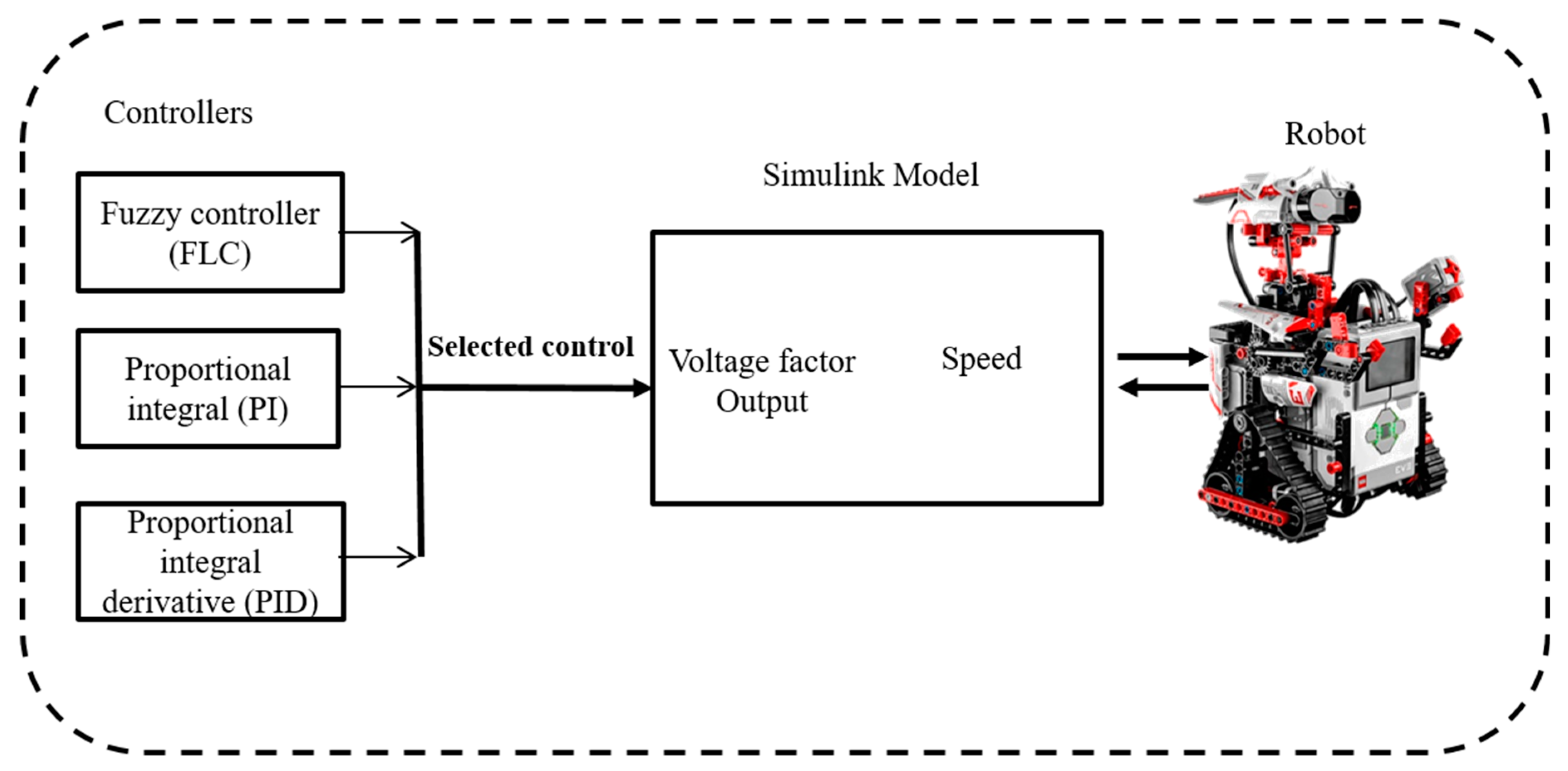
The Lego Mindstorms EV3 robot is shown in
Figure 1, and a general illustration of the proposal is presented in
Figure 4. The main challenge of this work was the synchronization between the controller and the robot in real time, and the methodology is as follows: a block model is developed with the help of Simulink, and the mathematical model of the Lego is codified. Afterwards, wireless synchronization is done with the Lego robot using an USB adapter; the values of the variables for the proposed controllers (FLC, PI, and PID) are added to perform the tests and observe the behavior of the robot.
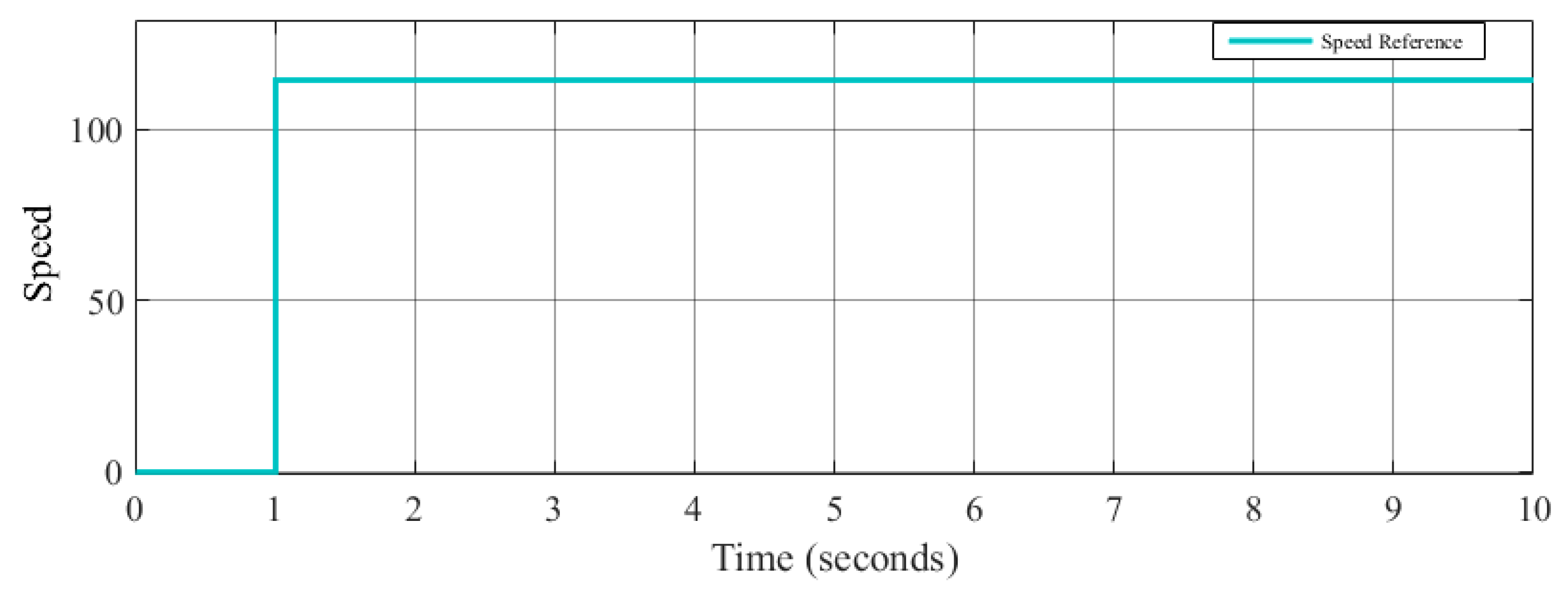
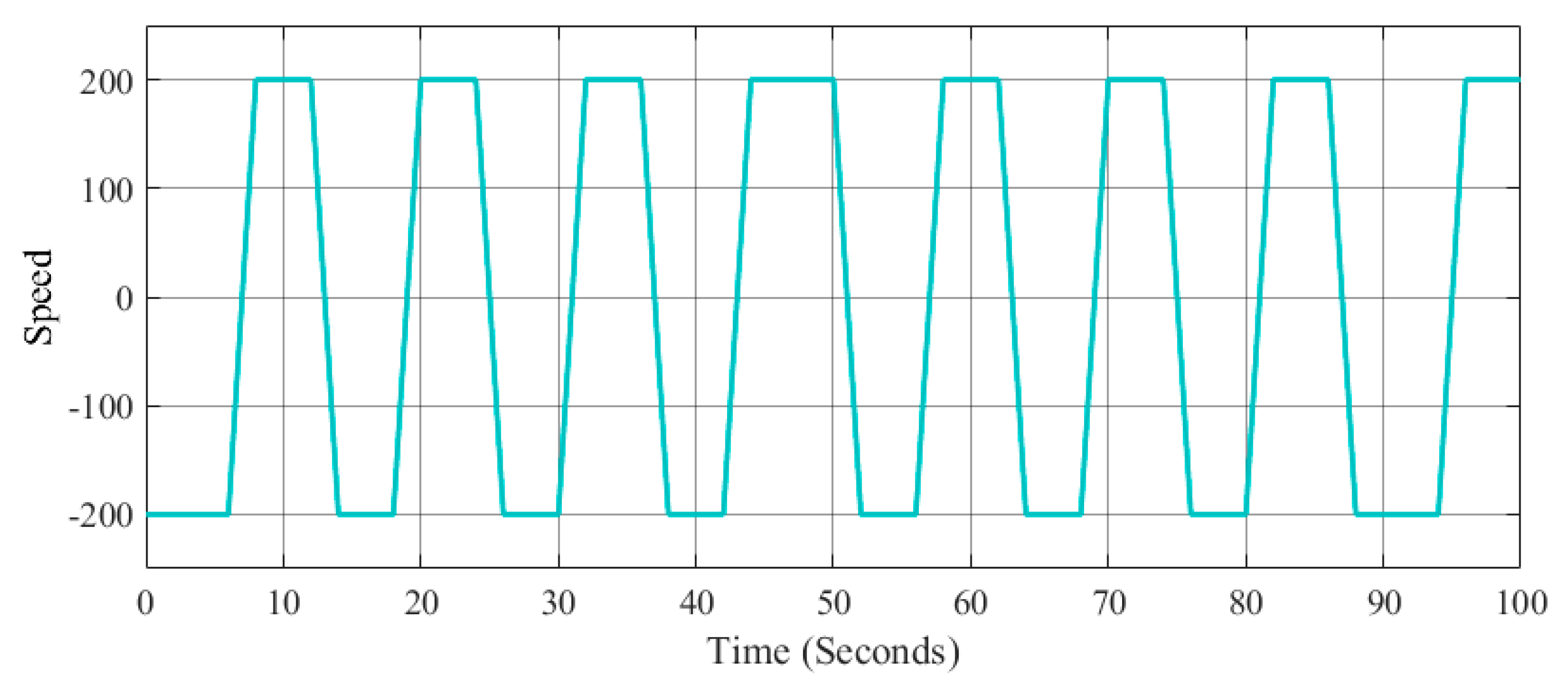
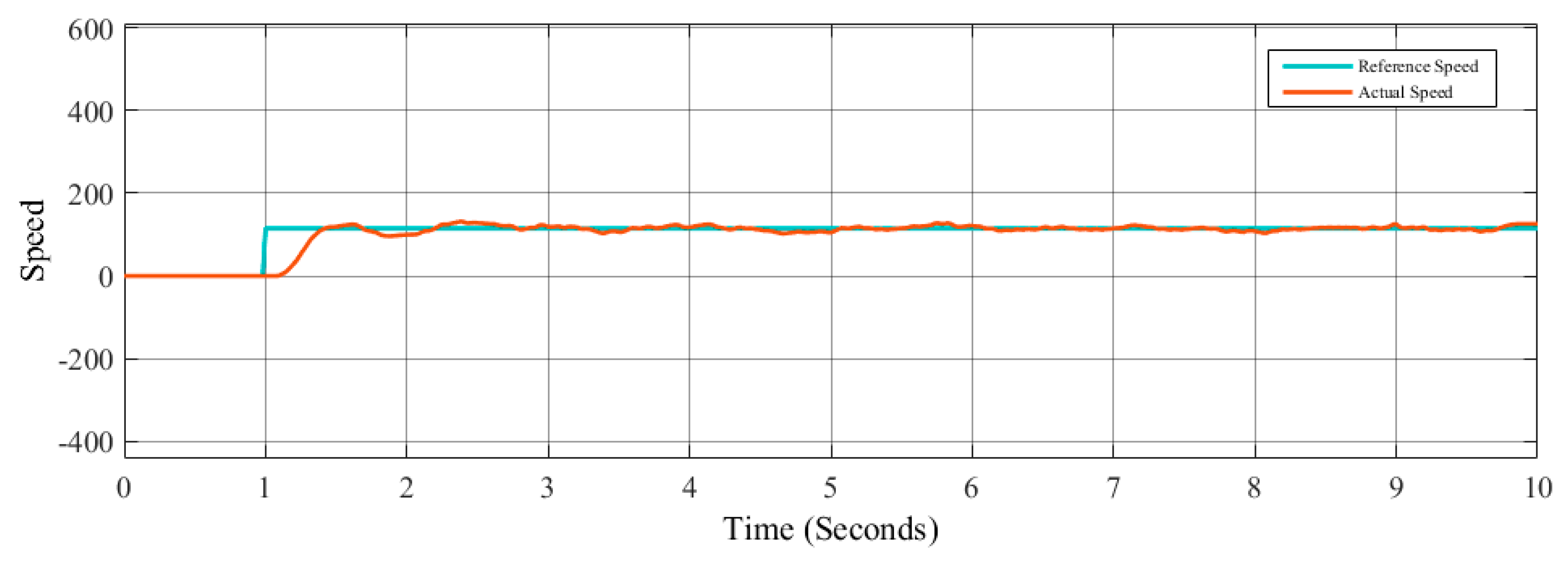
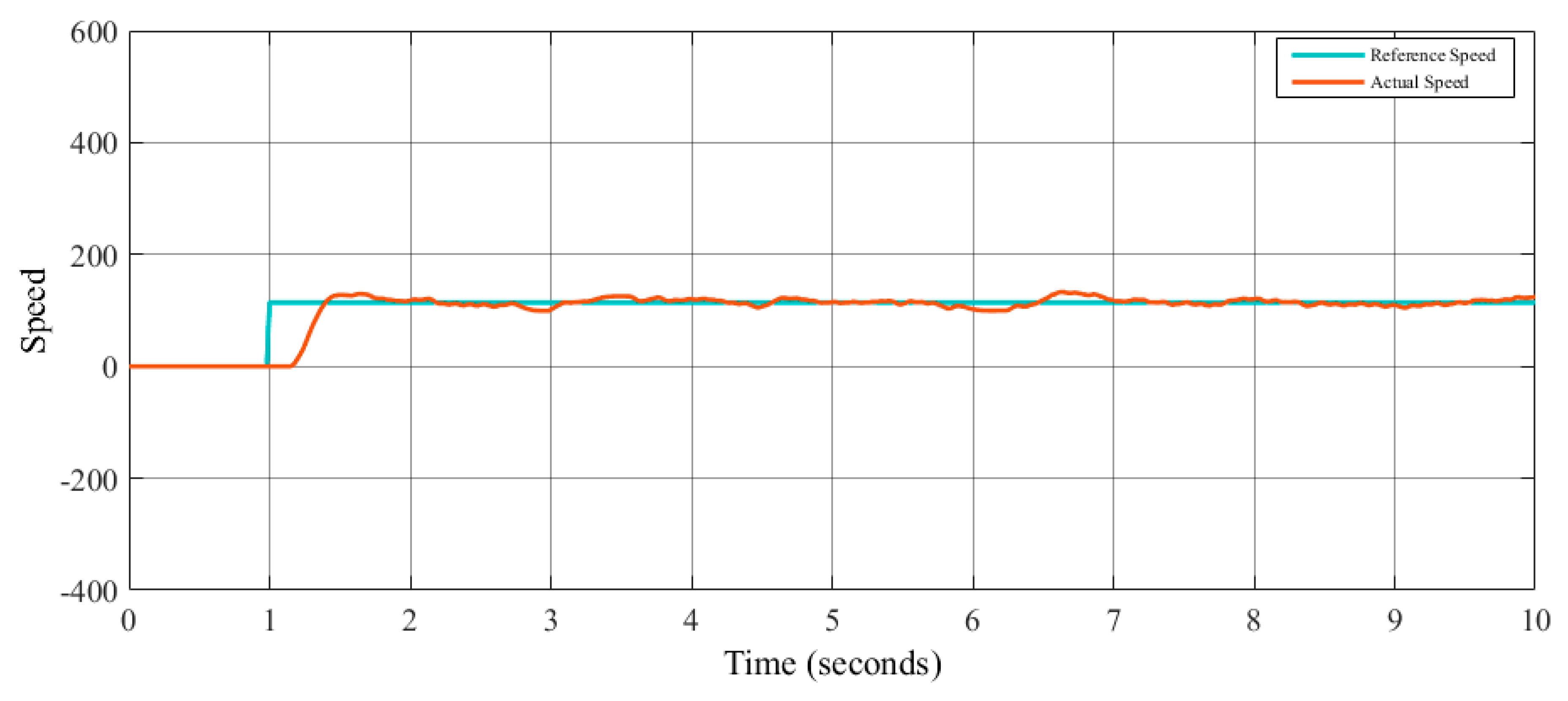
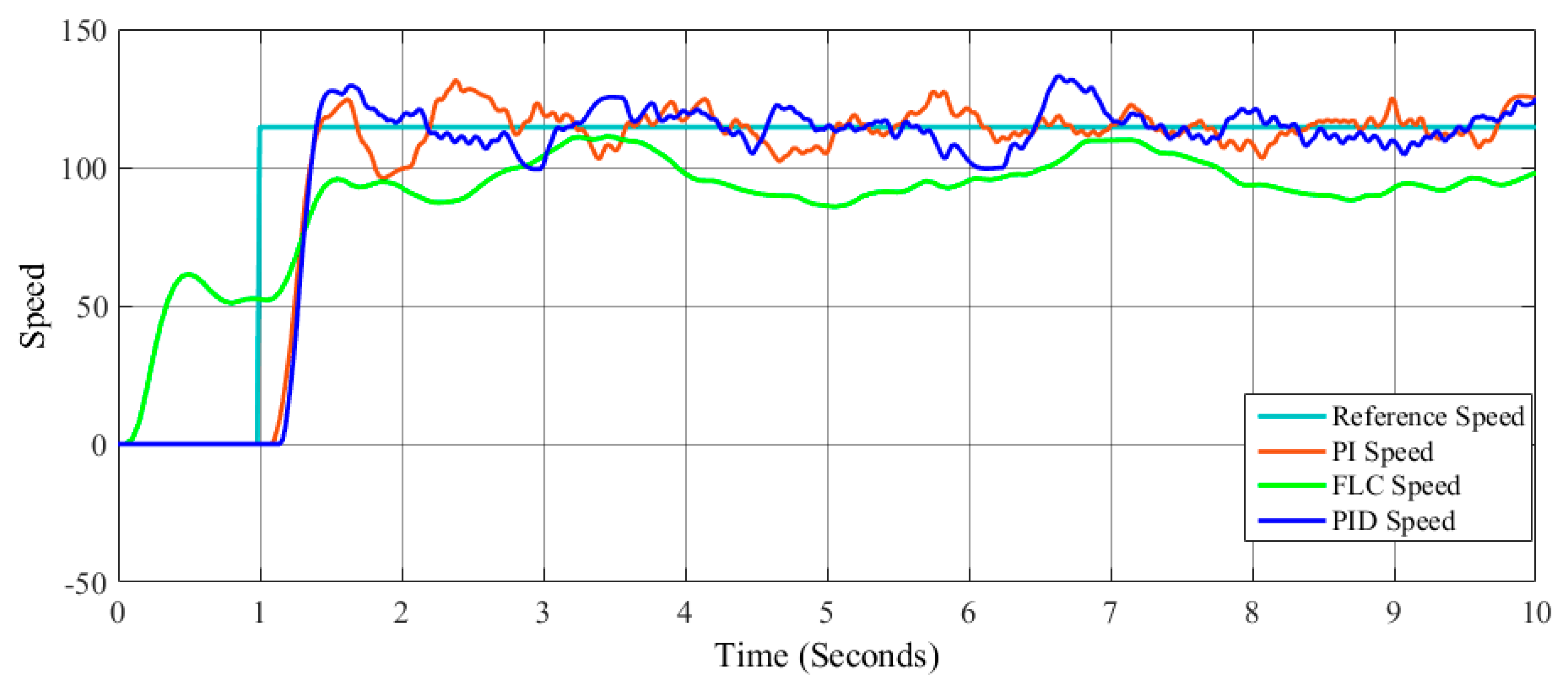
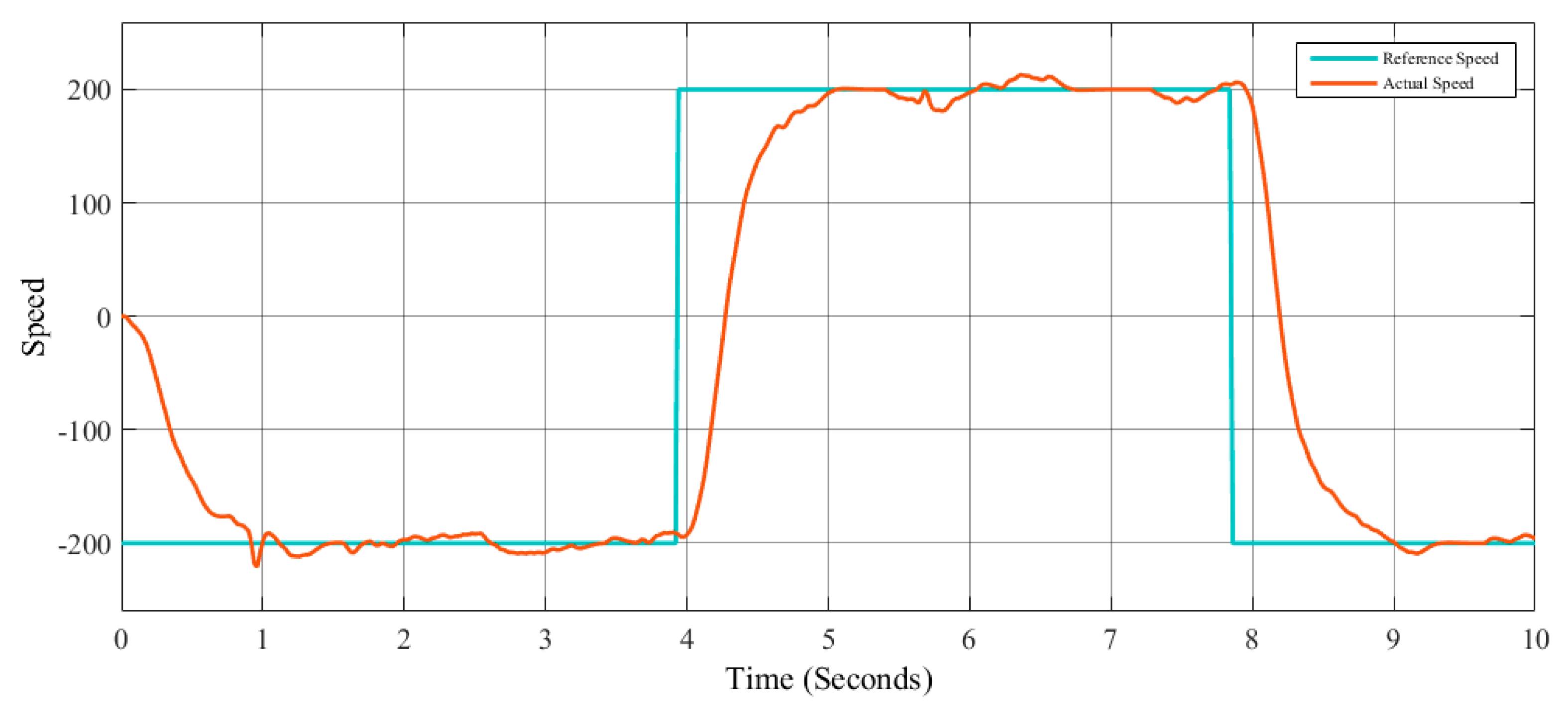
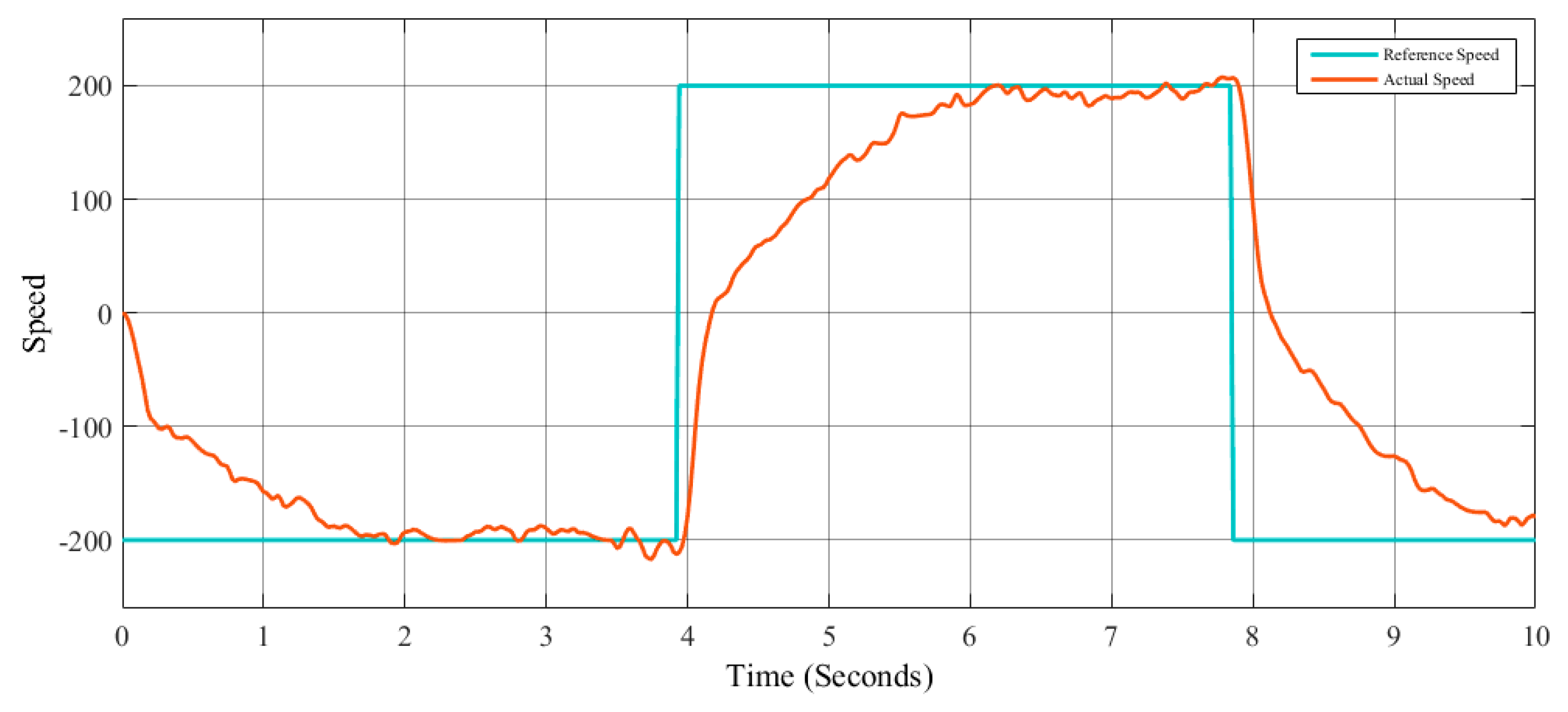
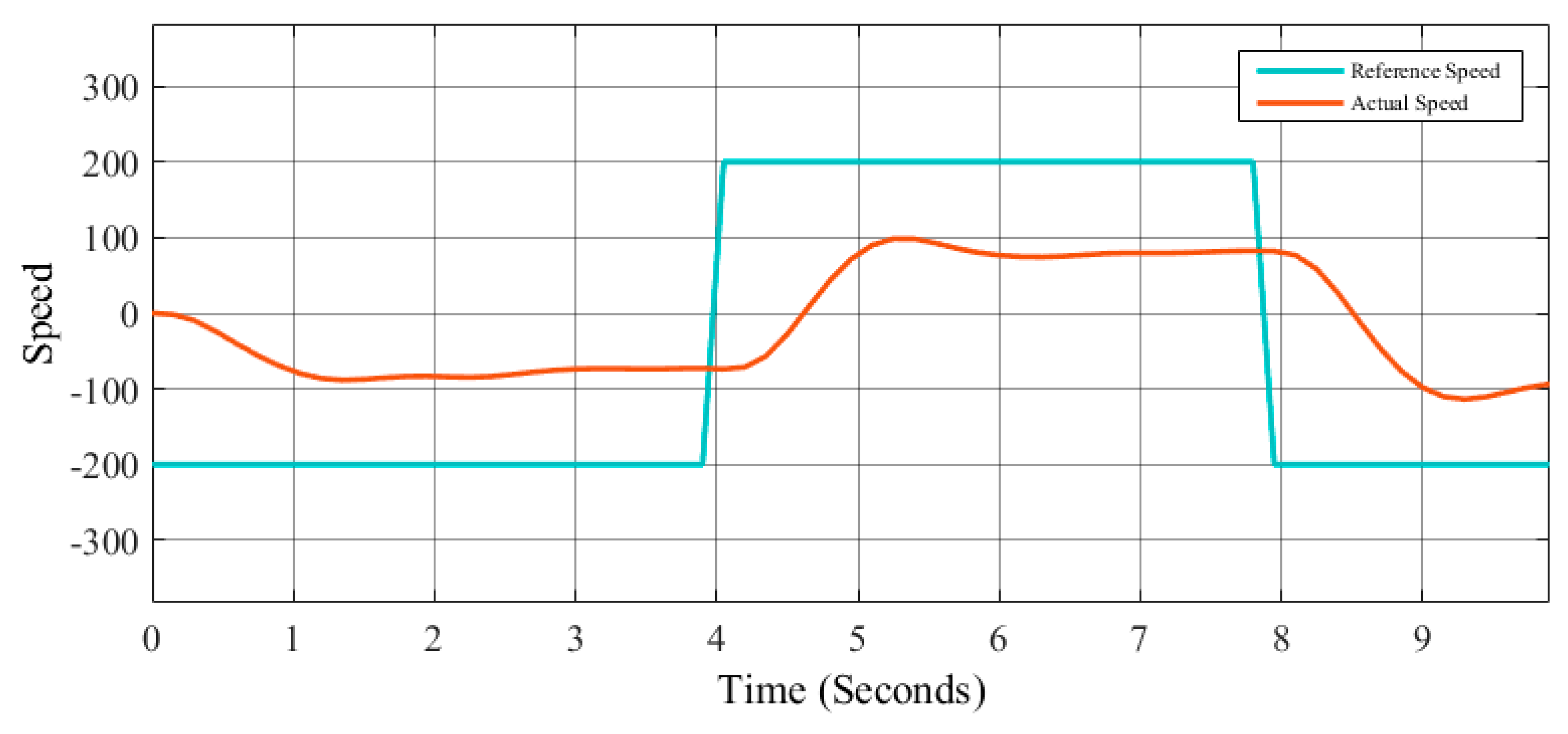
The main objective is to maintain control of the speed in the robot, and the tests are realized using one type of control (PI, PID, and FLC) for each test. The design of the controllers in this case was done by trial and error. The speed control was tested with two different speed signal references: a step and a signal generator for each method (PI, PID, and FLC). The step reference signal
r(
t) is given by Equation (5), where
t is the sampling time; the signal generator is given by Equation (6), where the amplitude is 200; the frequency is 0.8; the waveform is square; and
t is the simulation time.
The objective function for FLC is the root mean square error (RMSE) that is represented in Equation (7), and the objective function for PI and PID controller is the Settling Time, although there are other control metrics that are also used, as follows: ISE (Integral of Squared error), IAE (Integral of the Absolute value of the Error), ITSE (Integral of Time-weighted Squared Error), and ITAE (Integral of the Time multiplied by the Absolute value of the Error), respectively, presented in Equations (8)–(11). The metrics used to measure the error in this work were selected based on works published in the literature; most of the authors and experts in the area recommend some of them in works related to control [
17,
34,
36,
37].
3.1. Proportional Integral Controller for the Lego Mindstorms EV3
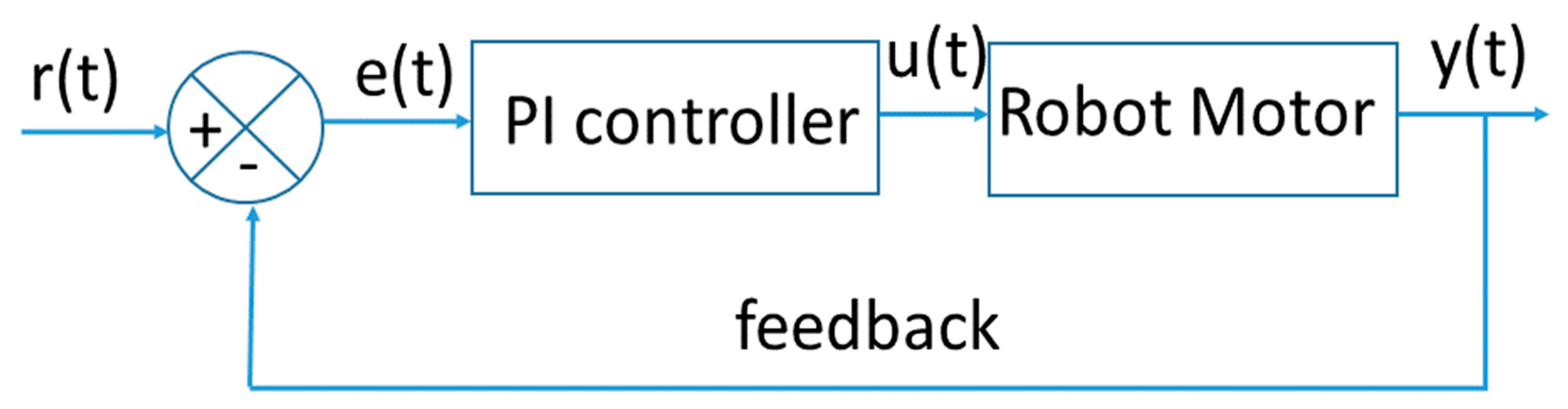
The two aforementioned speed reference signals are applied to a PI controller model in order to achieve the speed control in the Lego Mindstorms EV3 robot.
Figure 5 shows the diagram of this controller.
Where
r(
t) is the reference signal (step and signal generator);
e(
t) is the difference between the reference signal and the actual output signal
y(
t);
u(
t) is the controller output; and
y(
t) is the output, in this case the speed of the robot. The parameters used for speed control with the step reference signal are shown in
Table 2, and the parameters used for speed control with the signal generator reference signal are shown in
Table 3; the initial ranges for these cases are from −1 to 1, and in the tables the best parameters obtained for each reference are shown.
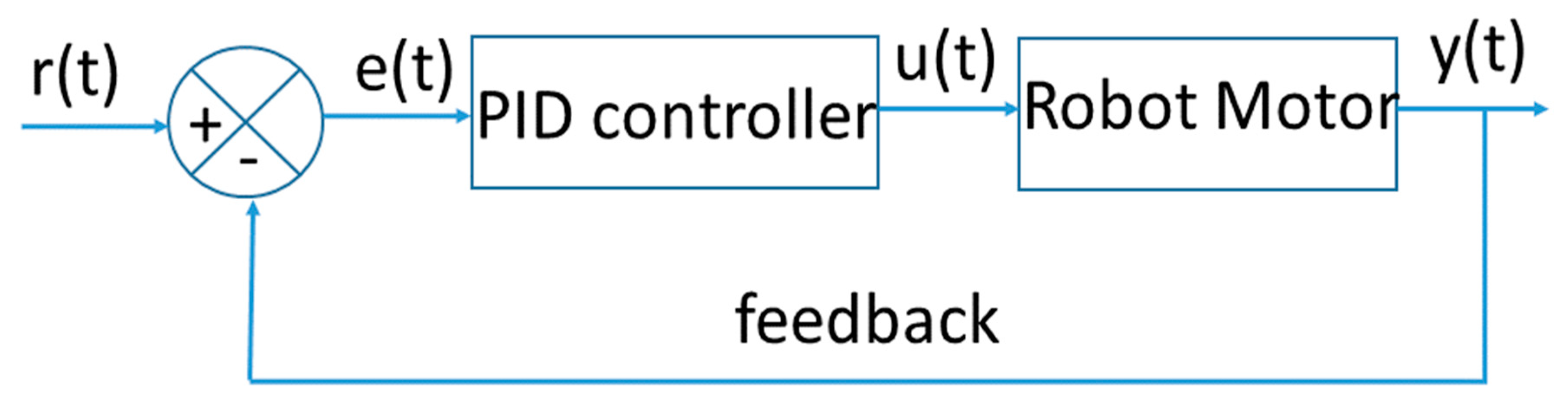
3.2. Proportional Integral Derivative Controller for Lego Mindstorms EV3
The PID controller model used to achieve the speed control of the Lego Mindstorms EV3 robot is illustrated in
Figure 6.
In this case, the same speed reference signals mentioned above were used. The parameters used for speed control with the step reference signal are shown in
Table 4, and the parameters used for speed control with the signal generator reference signal are shown in
Table 5. The initial ranges for these cases are from −1 to 1, and in the tables the best parameters obtained for each reference are shown.
3.3. Fuzzy Logic Controller for the Lego Mindstorms EV3
A fuzzy logic controller is used in order to control the speed of the robot; also, the two speed reference signals were used in the above Equations (5) and (6). The FLC control model can be found in
Figure 7.
The fuzzy system controller contains two inputs (the error
e(
t) and the error change
e’(
t)) and one output (the control signal (Voltage)
y(
t), see
Figure 8); the error and the error change are calculated using Equations (12) and (13).
The inputs and output are granulated into trapezoidal and triangular membership functions, which were created with Equations (14) and (15), respectively. These membership functions of this type were used for the ease of integration in this control problem.
The parameters of the membership functions for speed control with the step reference signal are presented in
Table 6. The parameters of the membership functions for speed control with the signal generator reference signal are shown in
Table 7. The FLC contains 15 rules, which are shown in
Table 8.
Table 6 shows the parameters of the triangular and trapezoidal membership functions used to achieve speed control with the step reference; it is important to mention that the values are obtained via the observations and experiences of experts in the area.
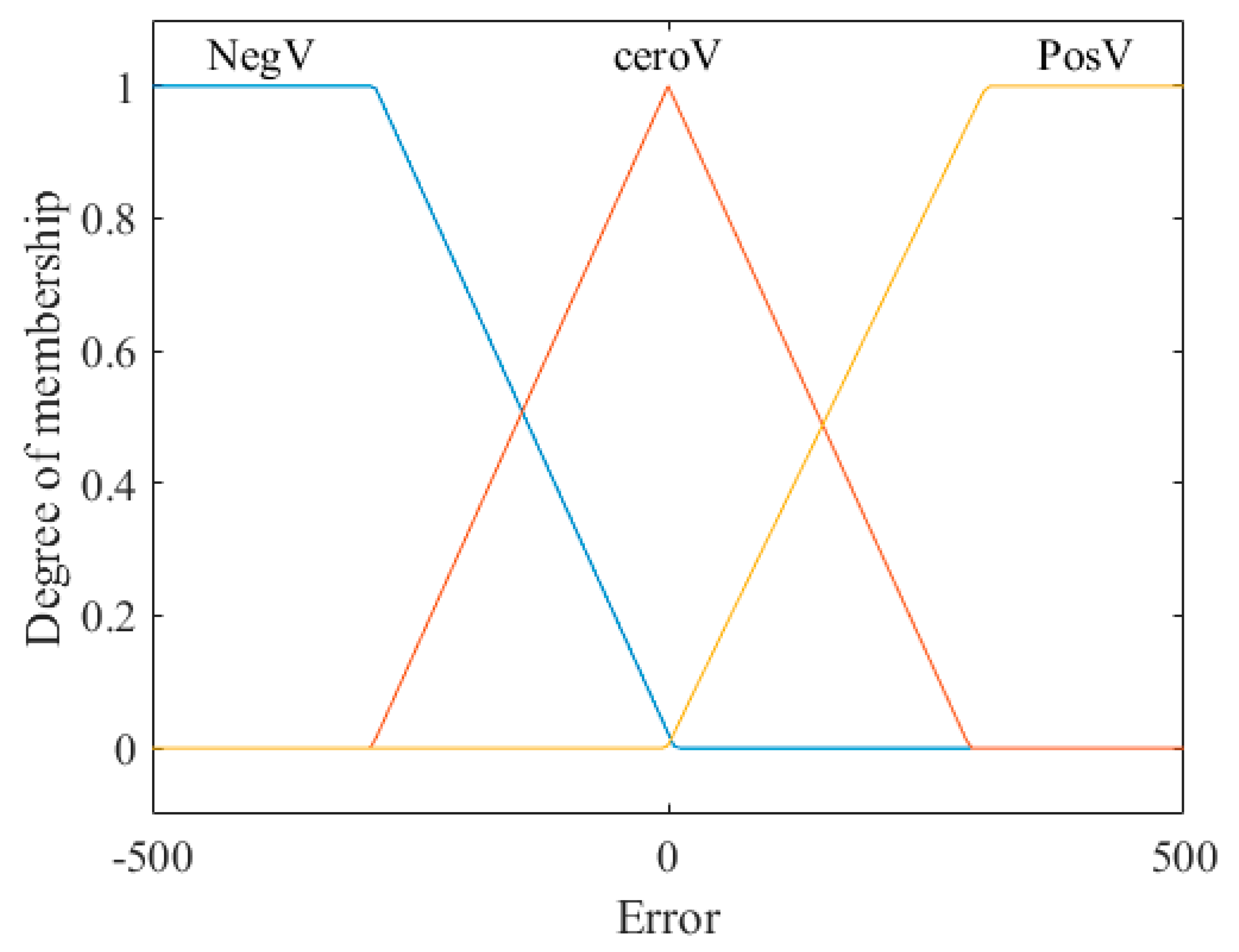
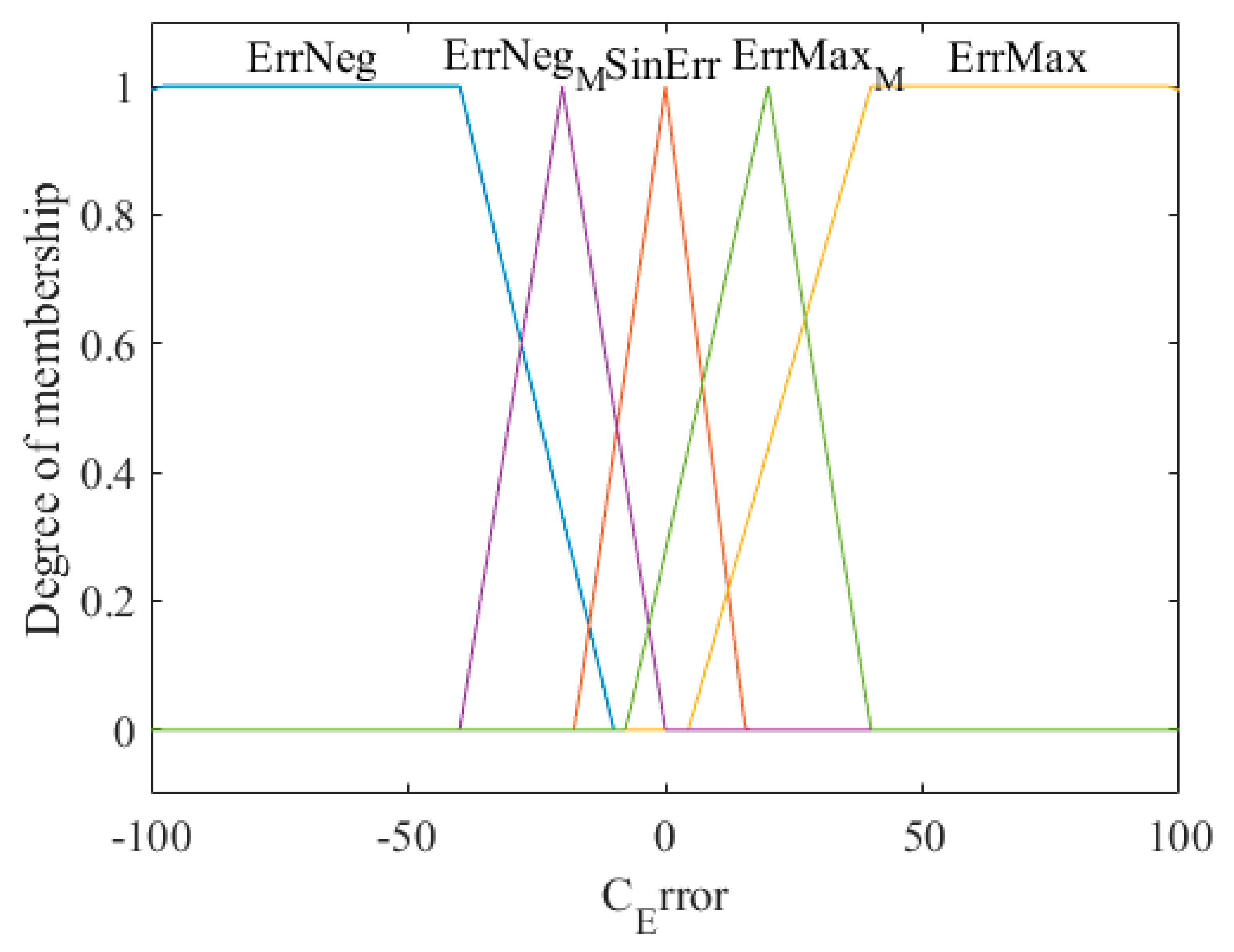
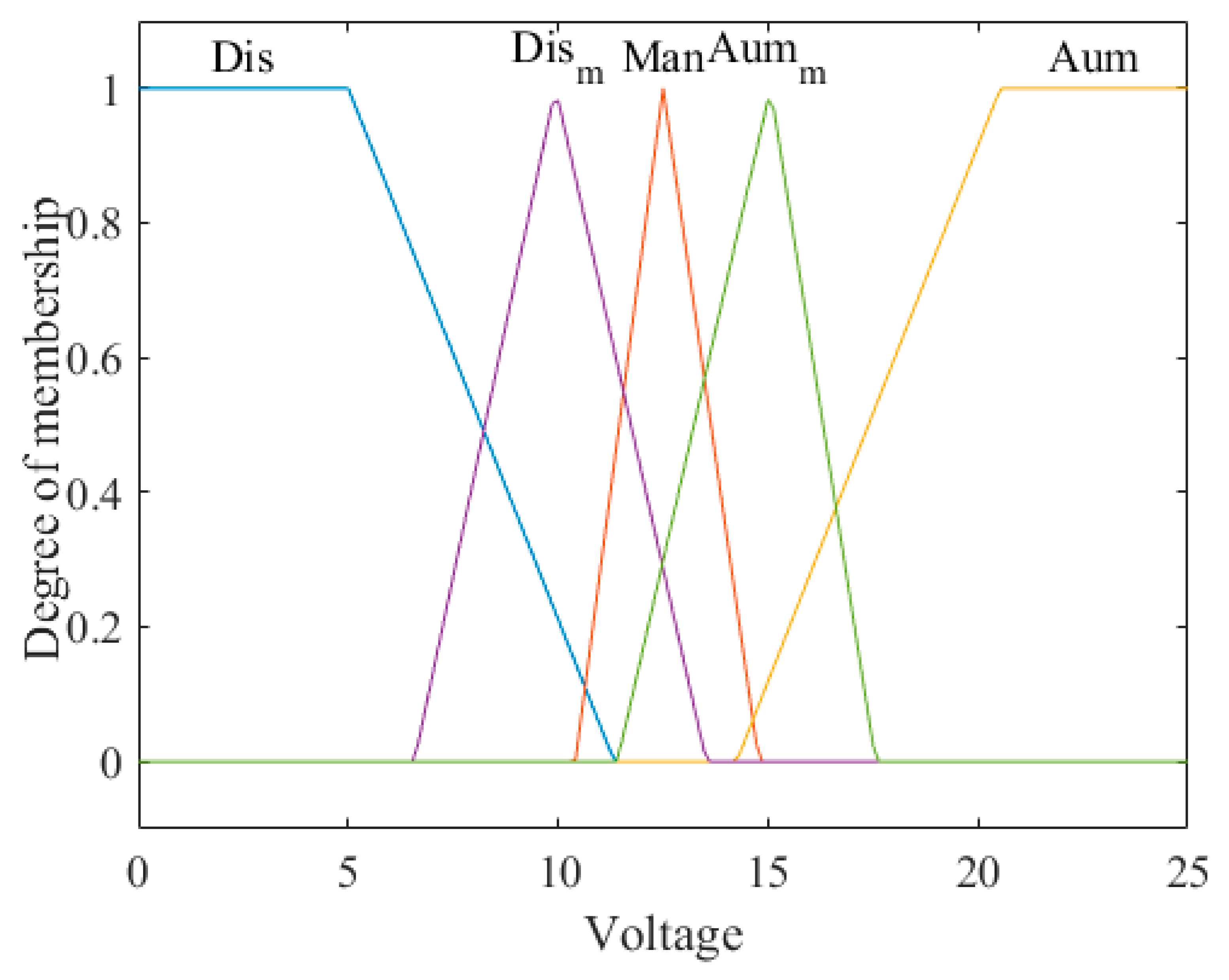
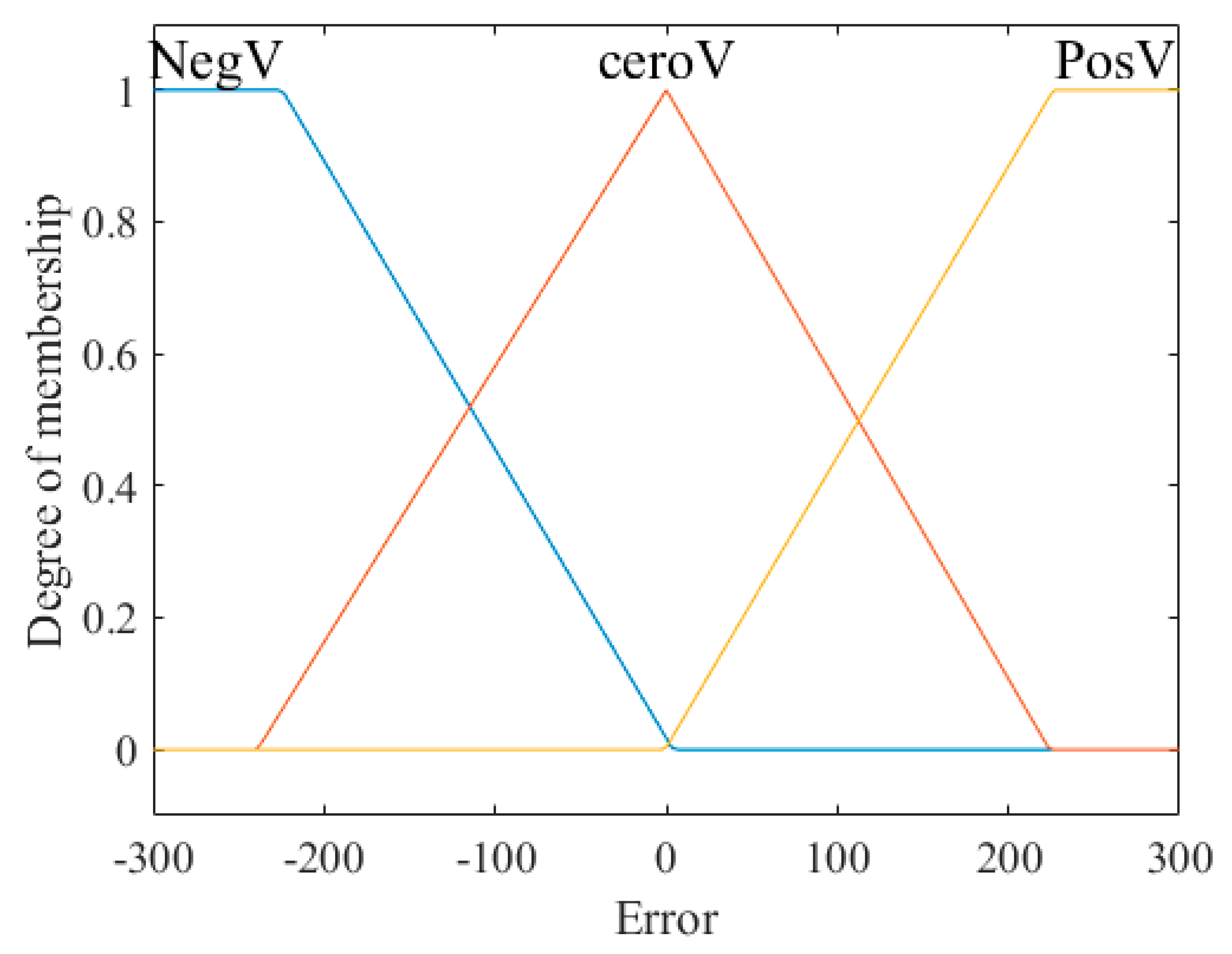
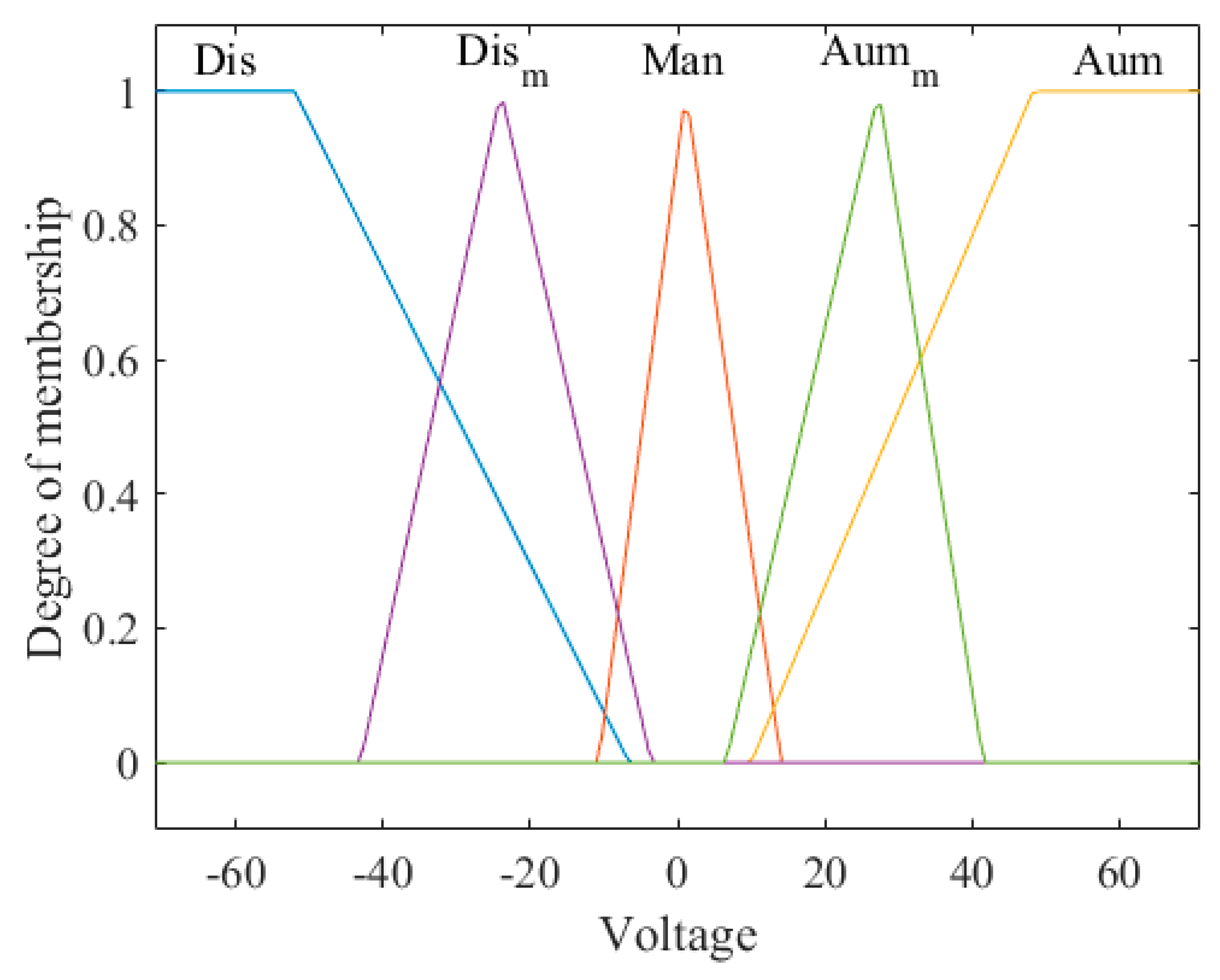
Figure 8,
Figure 9 and
Figure 10 show the inputs and output of the fuzzy system for the step speed reference, where input 1 is the error, input 2 is the change of the error, and the output is the voltage and its linguistic values.
Table 7 shows the parameters of the triangular and trapezoidal membership functions used to achieve speed control with the signal generator reference; it is important to mention that the values are obtained via the observations and experiences of experts in the area.
Figure 11,
Figure 12 and
Figure 13 show the inputs and outputs of the fuzzy system for the signal generator speed reference, where input 1 is the error, input 2 is the change of the error, and the output is the voltage and its linguistic values.
Table 8 shows the combination of if-then fuzzy rules for the proposed controller used to control the motor speed of the Lego Mindstorms EV3.
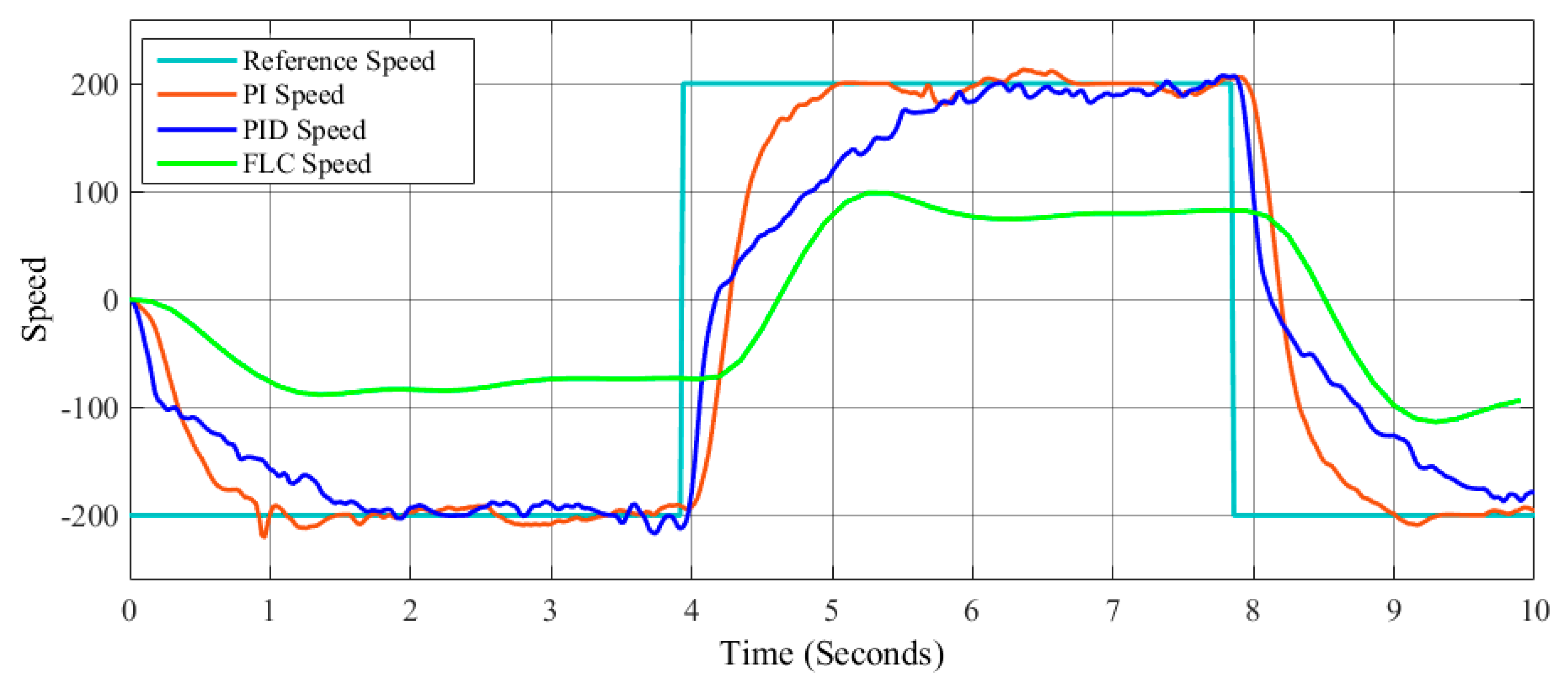
The speed step reference signal is illustrated in
Figure 14, and the speed signal generator reference is illustrated in
Figure 15, where the objective is to follow as close as possible the desired speed reference.