First Order Coupled Systems With Functional and Periodic Boundary Conditions: Existence Results and Application to an SIRS Model
Abstract
1. Introduction
2. Definitions and Assumptions
- (i)
- for each,are measurable onfor
- (ii)
- for almost everyare continuous onfor
- (iii)
- for each, there exists a positive functionsuch that, for,
3. Main Result for Functional Problems
4. Existence and Localization Result for the Periodic Case
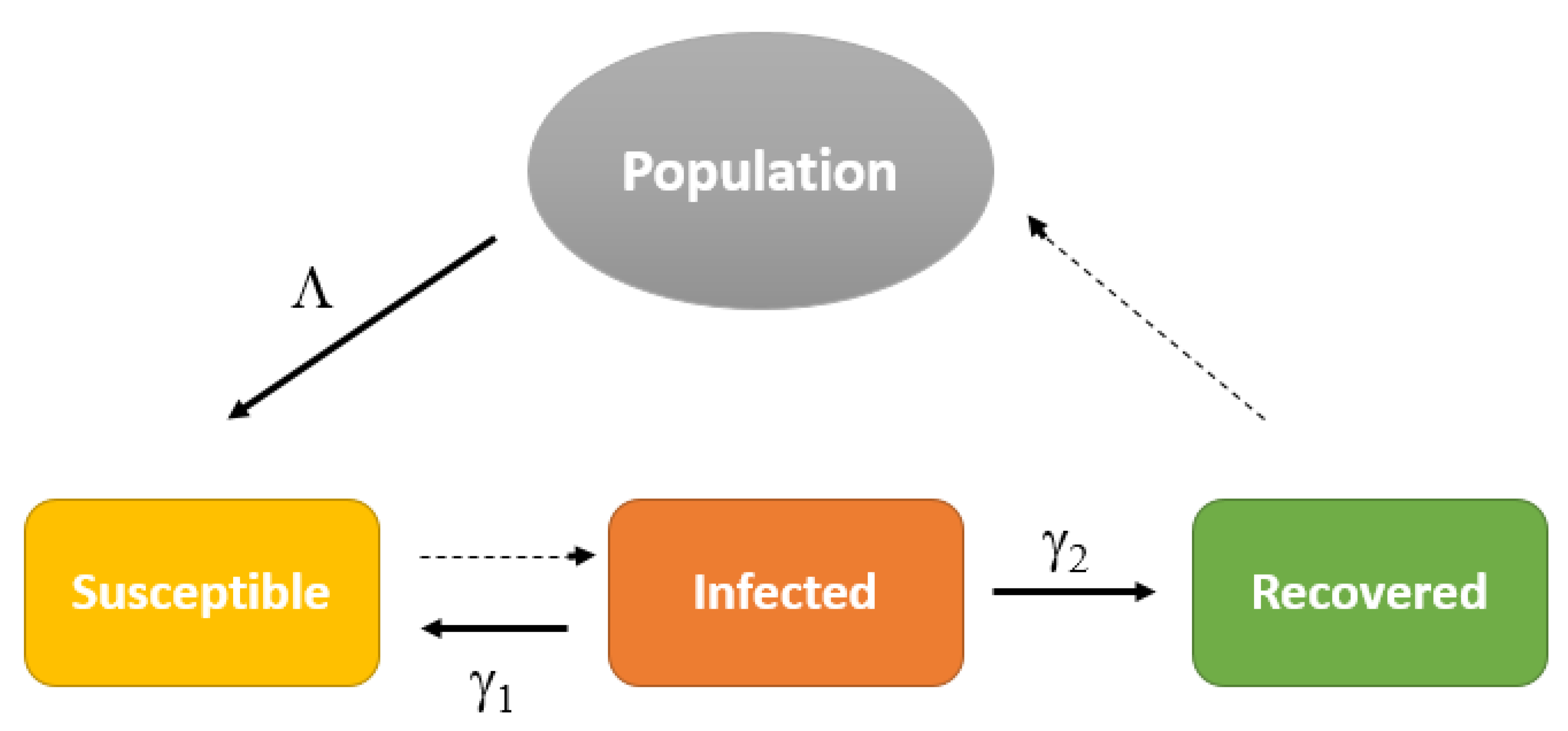
5. An Epidemic Model of an SIRS System With Nonlinear Incidence Rate and Interaction from Infectious to Susceptible Subjects
- represents the recruitment rate of susceptible individuals;
- is the natural death rate;
- is the transfer rate from the infected class to the susceptible class;
- is the transfer rate from the infected class to the recovered class;
- is the disease-induced death rate;
- the immunity loss rate.
- and for
- is continuous and monotonously increasing for and exists as
- , the initial number of susceptible subjects, is equal to the maximum of the infected subjects;
- the initial number of infected subjects, is a weighted average of the susceptible individuals, weighted by the final value of the susceptible S, at time
- the initial number of individuals who recovered, is equal to a weighted average of the infected individuals, weighted by the final value of the susceptible, S, at time T.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al-Moqbali, M.K.A.; Al-Salti, N.S.; Elmojtaba, I.M. Prey–Predator Models with Variable Carrying Capacity. Mathematics 2018, 6, 102. [Google Scholar] [CrossRef]
- Gumus, O.A.; Kose, H. On the Stability of Delay Population Dynamics Related with Allee Effects. Math. Comput. Appl. 2012, 17, 56–67. [Google Scholar] [CrossRef]
- Song, H.S.; Cannon, W.R.; Beliaev, A.S.; Konopka, A. Mathematical Modeling of Microbial Community Dynamics: A Methodological Review. Processes 2014, 2, 711–752. [Google Scholar] [CrossRef]
- Osakwe, C.J.U. Incentive Compatible Decision Making: Real Options with Adverse Incentives. Axioms 2018, 7, 9. [Google Scholar] [CrossRef]
- Deuflhard, P. Differential equations in technology and medicine: Computational concepts, adaptive algorithms, and virtual labs. In Computational Mathematics Driven by Industrial Problems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 69–125. [Google Scholar]
- Jang, S.S.; de la Hoz, H.; Ben-zvi, A.; McCaffrey, W.C.; Gopaluni, R.B. Parameter estimation in models with hidden variables: An application to a biotech process. Can. J. Chem. Eng. 2012, 90, 690–702. [Google Scholar] [CrossRef]
- Akarsu, M.; Özbaş, Ö. Monte Carlo Simulation for Electron Dynamics in Semiconductor Devices. Math. Comput. Appl. 2005, 10, 19–26. [Google Scholar] [CrossRef]
- Malinzi, J.; Quaye, P.A. Exact Solutions of Non-Linear Evolution Models in Physics and Biosciences Using the Hyperbolic Tangent Method. Math. Comput. Appl. 2018, 23, 35. [Google Scholar] [CrossRef]
- Nieto, J.J. Periodic boundary value problems for first-order impulsive ordinary differential equations. Nonlinear Anal. 2002, 51, 1223–1232. [Google Scholar] [CrossRef]
- Zhang, W.; Fan, M. Periodicity in a generalized ecological competition system governed by impulsive differential equations with delays. Math. Comput. Model. 2004, 39, 479–493. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Reagan, D. A coupled system of boundary value problems. Appl. Anal. 1998, 69, 381–385. [Google Scholar] [CrossRef]
- Asif, N.A.; Talib, I.; Tunc, C. Existence of solutions for first-order coupled system with nonlinear coupled boundary conditions. Bound. Val. Prob. 2015, 2015, 134. [Google Scholar] [CrossRef]
- Asif, N.A.; Khan, R.A. Positive solutions to singular system with four-point coupled boundary conditions. J. Math. Anal. Appl. 2012, 386, 848–861. [Google Scholar] [CrossRef]
- Cabada, A.; Fialho, J.; Minhós, F. Extremal solutions to fourth order discontinuous functional boundary value problems. Math. Nachr. 2013, 286, 1744–1751. [Google Scholar] [CrossRef]
- Cabada, A.; Pouso, R.; Minhós, F. Extremal solutions to fourth-order functional boundary value problems including multipoint condition. Nonlinear Anal. Real World Appl. 2009, 10, 2157–2170. [Google Scholar] [CrossRef]
- Fialho, J.; Minhós, F. Higher order functional boundary value problems without monotone assumptions. Bound. Val. Prob. 2013, 2013, 81. [Google Scholar] [CrossRef]
- Fialho, J.; Minhós, F. Multiplicity and location results for second order functional boundary value problems. Dyn. Syst. Appl. 2014, 23, 453–464. [Google Scholar]
- Graef, J.; Kong, L.; Minhós, F. Higher order boundary value problems with ϕ -Laplacian and functional boundary conditions. Comput. Math. Appl. 2011, 61, 236–249. [Google Scholar] [CrossRef]
- Graef, J.; Kong, L.; Minhós, F.; Fialho, J. On the lower and upper solution method for higher order functional boundary value problems. Appl. Anal. Discret. Math. 2011, 5, 133–146. [Google Scholar] [CrossRef]
- Zeidler, E. Nonlinear Functional Analysis and Its Applications, I: Fixed-Point Theorems; Springer: New York, NY, USA, 1986. [Google Scholar]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A Fractional-Order Infectivity and Recovery SIR Model. Fract. Fract. 2017, 1, 11. [Google Scholar] [CrossRef]
- Cui, Q.; Qiu, Z.; Liu, W.; Hu, Z. Complex Dynamics of an SIR Epidemic Model with Nonlinear Saturate Incidence and Recovery Rate. Entropy 2017, 19, 305. [Google Scholar] [CrossRef]
- Secer, A.; Ozdemir, N.; Bayram, M. A Hermite Polynomial Approach for Solving the SIR Model of Epidemics. Mathematics 2018, 6, 305. [Google Scholar] [CrossRef]
- Alexander, M.E.; Moghadas, S.M. Bifurcation analysis of an SIRS epidemic model with generalized incidence. SIAM J. Appl. Math. 2005, 65, 1794–1816. [Google Scholar] [CrossRef]
- Chen, J. An SIRS epidemic model. Appl. Math. J. Chin. Univ. 2004, 19, 101–108. [Google Scholar] [CrossRef]
- Hu, Z.; Bi, P.; Ma, W.; Ruan, S. Bifurcations of an SIRS epidemic model with nonlinear incidence rate. Discret. Contin. Dyn. Syst. Ser. B 2011, 15, 93–112. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Y. Global stability of an SIRS epidemic model with transport-related infection. Chaos Solitons Fract. 2009, 40, 145–158. [Google Scholar] [CrossRef]
- Teng, Z.; Liu, Y.; Zhang, L. Persistence and extinction of disease in non-autonomous SIRS epidemic models with disease-induced mortality. Nonlinear Anal. Theory Methods Appl. 2008, 69, 2599–2614. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, W.; Xiao, S. An SIRS model with a nonlinear incidence rate. Chaos Solitons Fract. 2007, 34, 1482–1497. [Google Scholar] [CrossRef]
- Li, T.; Zhang, F.; Liu, H.; Chen, Y. Threshold dynamics of an SIRS model with nonlinear incidence rate and transfer from infectious to susceptible. Appl. Math. Lett. 2017, 70, 52–57. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Xiao, Y.; Liu, S. A class of Lyapunov functions and the global stability of some epidemic models with nonlinear incidence. J. Appl. Anal. Comput. 2016, 6, 38–46. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fialho, J.; Minhós, F. First Order Coupled Systems With Functional and Periodic Boundary Conditions: Existence Results and Application to an SIRS Model. Axioms 2019, 8, 23. https://doi.org/10.3390/axioms8010023
Fialho J, Minhós F. First Order Coupled Systems With Functional and Periodic Boundary Conditions: Existence Results and Application to an SIRS Model. Axioms. 2019; 8(1):23. https://doi.org/10.3390/axioms8010023
Chicago/Turabian StyleFialho, João, and Feliz Minhós. 2019. "First Order Coupled Systems With Functional and Periodic Boundary Conditions: Existence Results and Application to an SIRS Model" Axioms 8, no. 1: 23. https://doi.org/10.3390/axioms8010023
APA StyleFialho, J., & Minhós, F. (2019). First Order Coupled Systems With Functional and Periodic Boundary Conditions: Existence Results and Application to an SIRS Model. Axioms, 8(1), 23. https://doi.org/10.3390/axioms8010023





