Sub-Optimal Control in the Zika Virus Epidemic Model Using Differential Evolution
Abstract
1. Introduction
2. Dynamical Control Model for ZIKV Infection
3. Differential Evolution
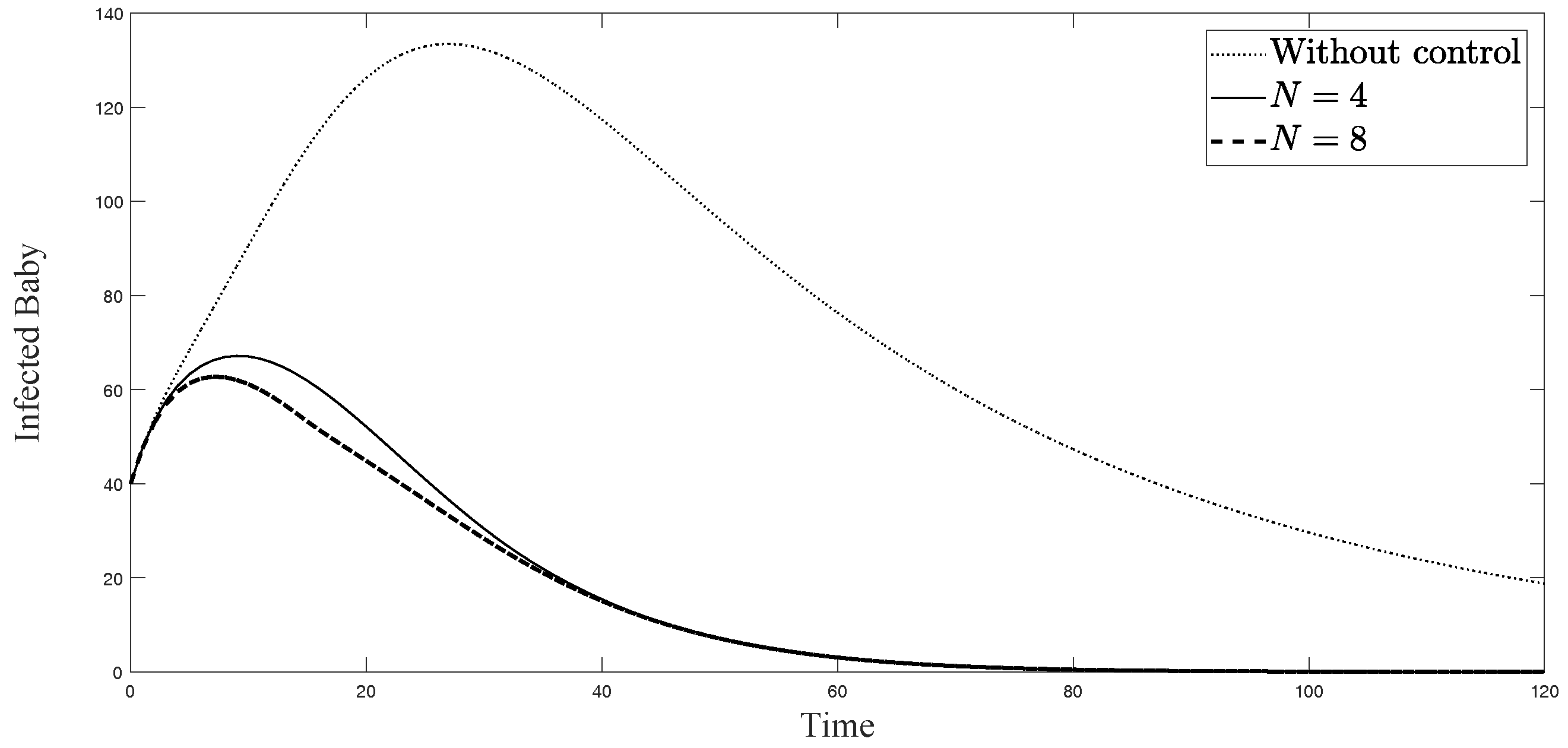
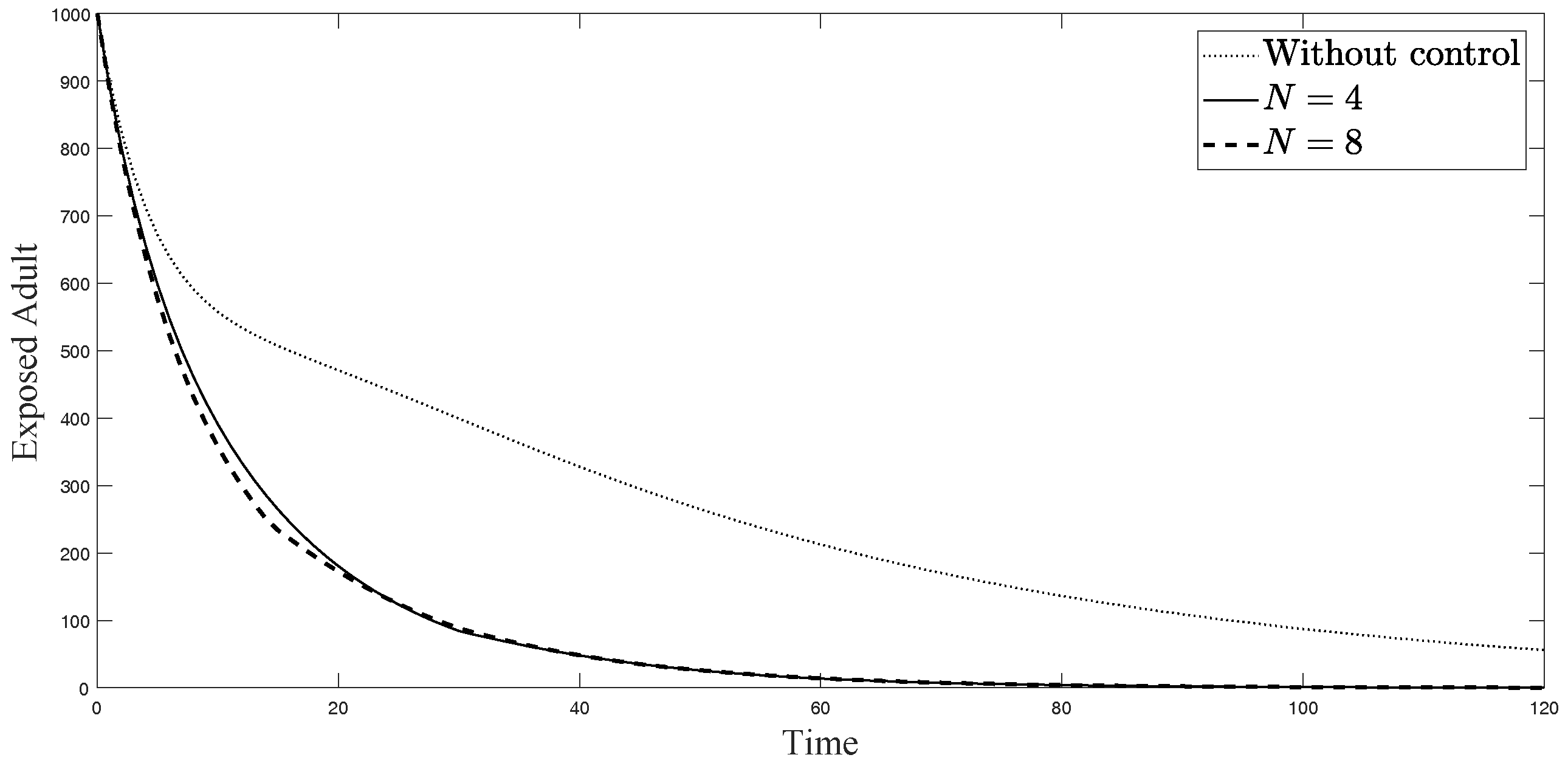
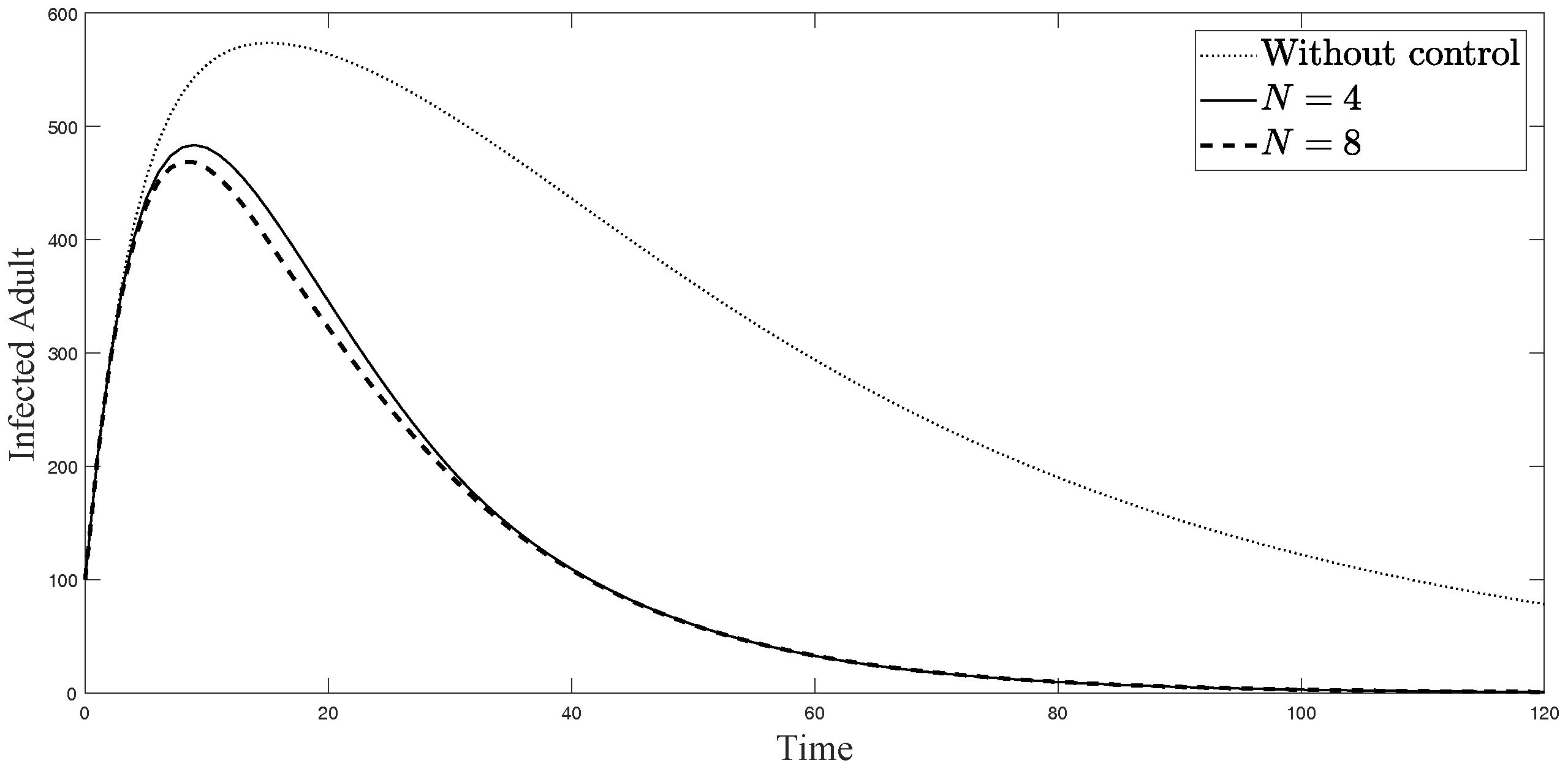
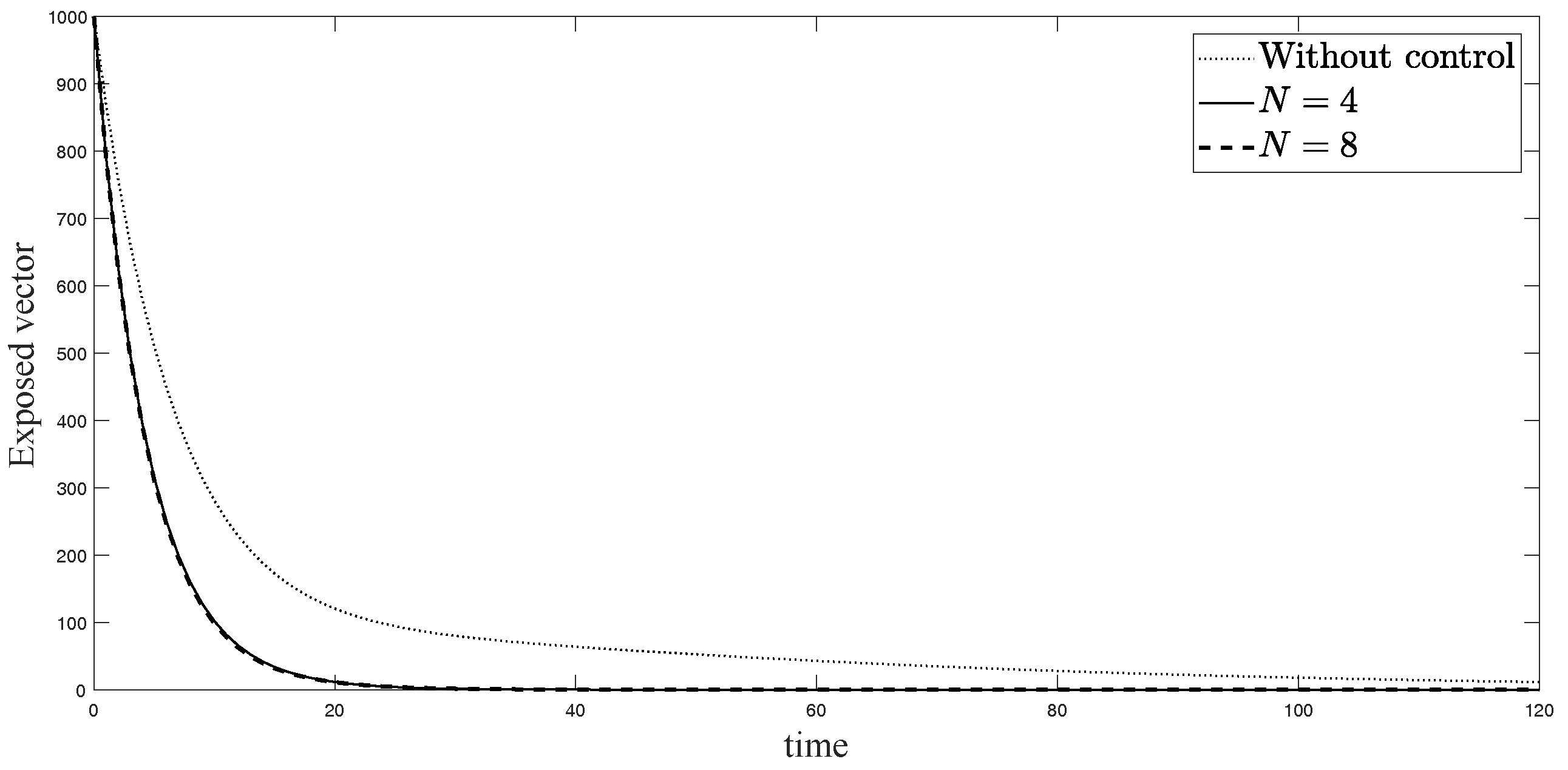
4. Numerical Simulations for Sub-Optimal Control Problem
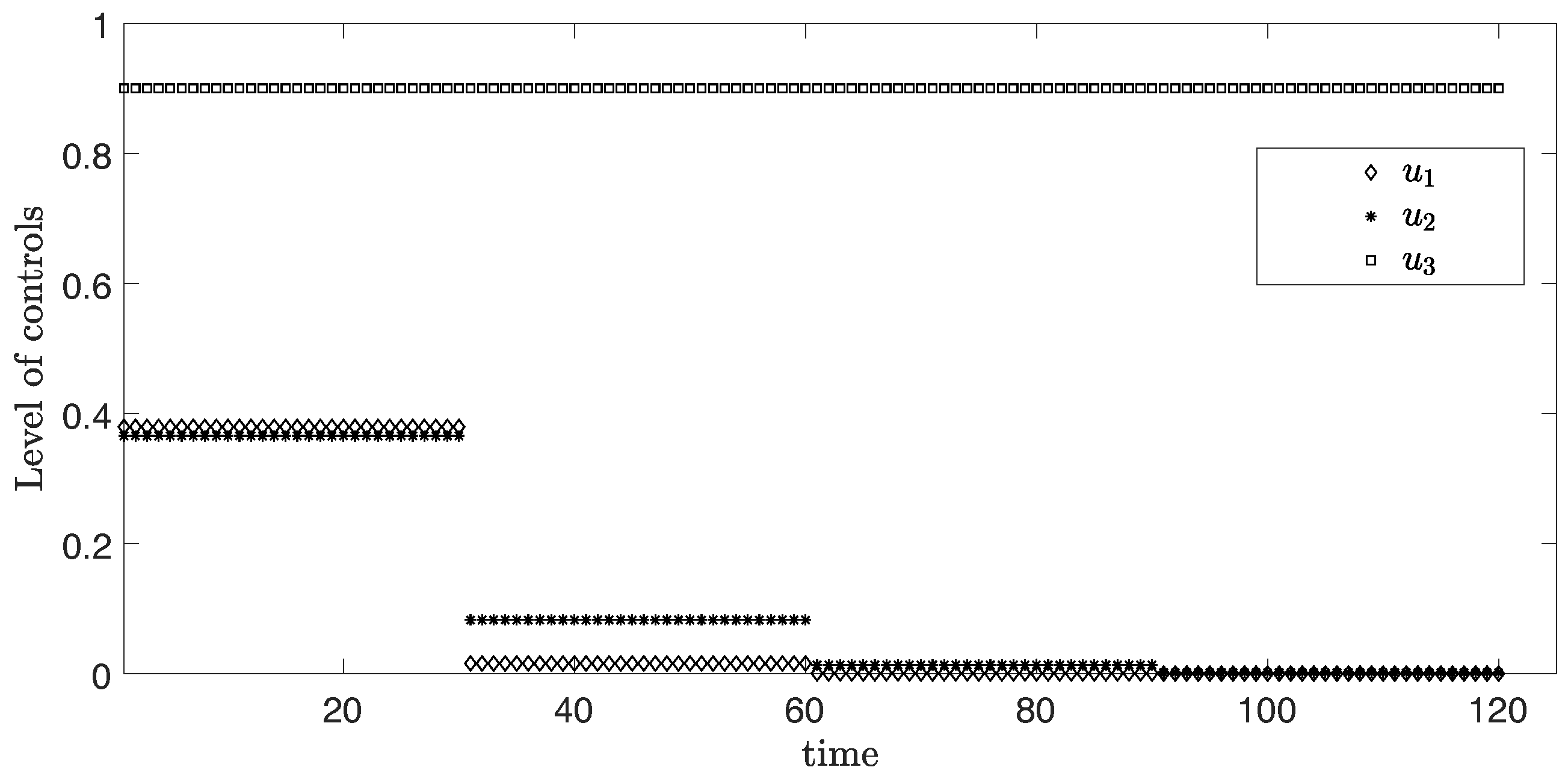
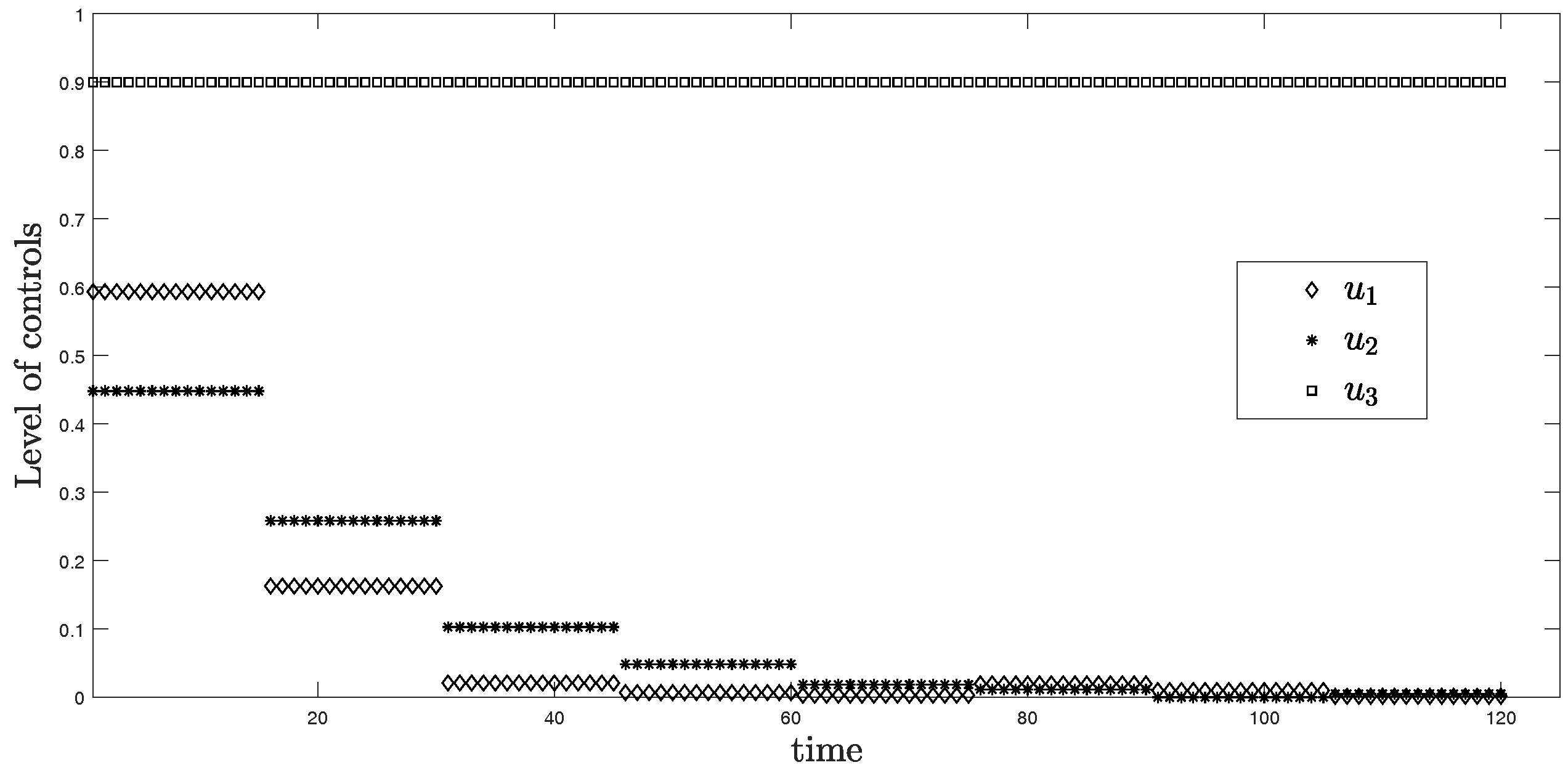
4.1. Sub-Optimal Control Problem
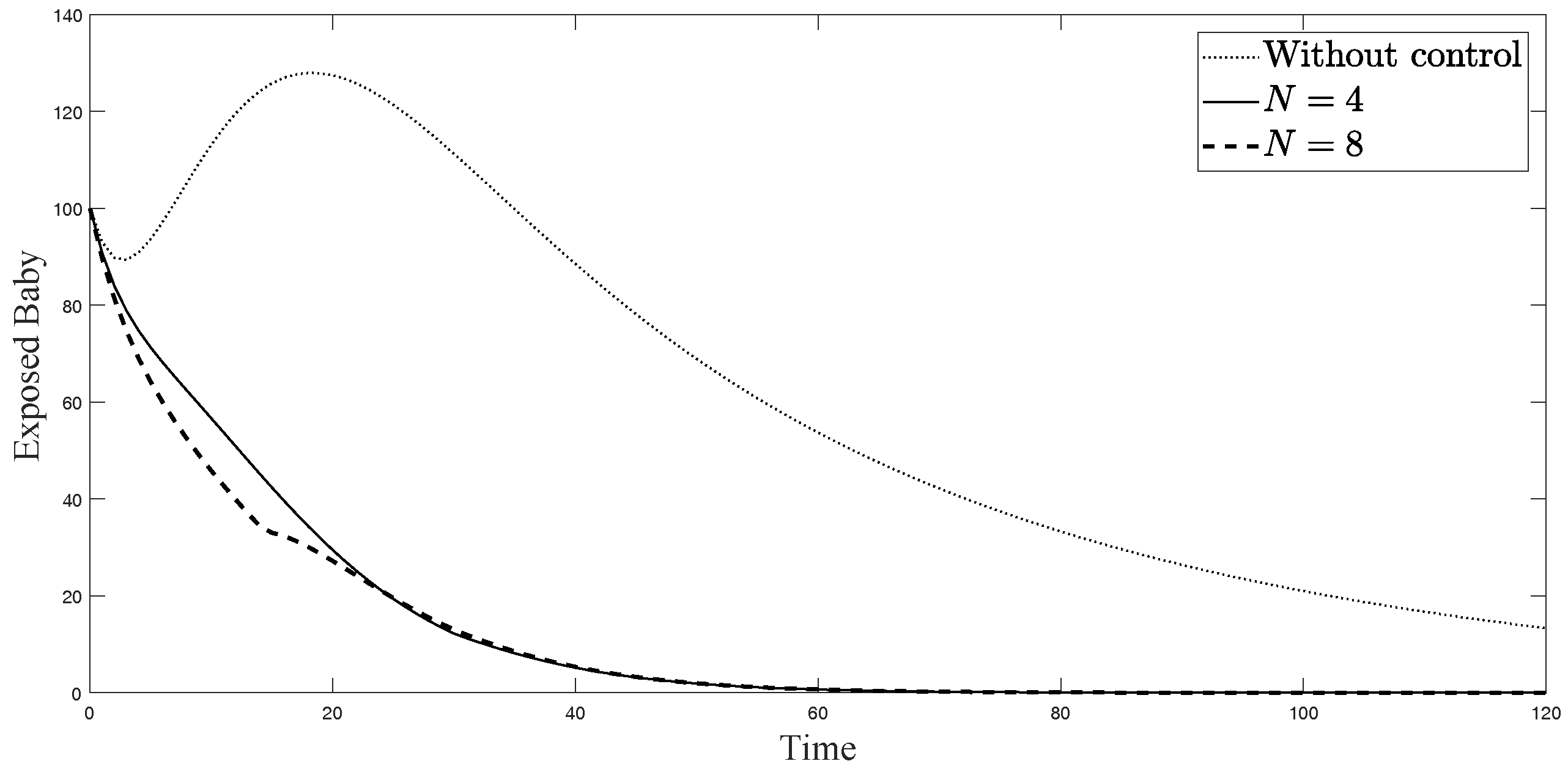
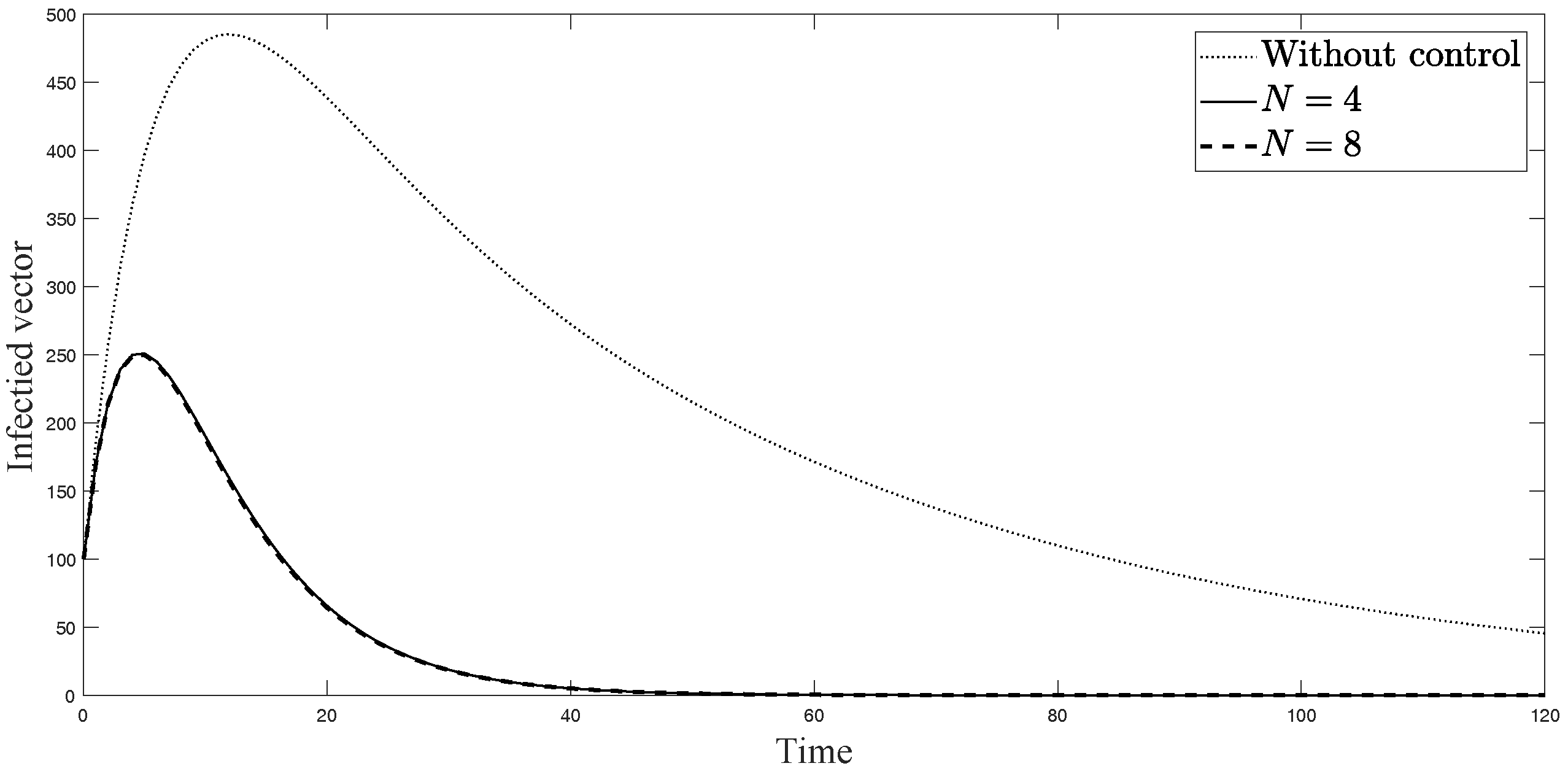
4.2. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WHO | World Health Organization |
| GA | Genetic Algorithm |
| DE | Differential Evolution |
References
- Dasti, J.I. Zika virus infections: An overview of current scenario. Asian Pac. J. Trop. Med. 2016, 7, 621–625. [Google Scholar] [CrossRef] [PubMed]
- European Centre for Disease Prevention and Control. Zika Virus Epidemic in the Americas: Potential Association with Microcephaly and Guillain-Barre Syndrome. Available online: https://ecdc.europa.eu/sites/portal/files/media/en/publications/Publications/zika-virus-americas-association-with-microcephaly-rapid-risk-assessment.pdf (accessed on 12 February 2017).
- World Health Organization. Microcephaly-Brazil: Disease Outbreak News. Available online: http://www.who.int/csr/don/archive/disease/microcephaly/en/ (accessed on 12 February 2017).
- World Health Organization. Zika Situation Report. Available online: http://www.who.int/emergencies/zika-virus/situation-report/12-february-2016/en/ (accessed on 12 February 2017).
- Coelho, F.C.; Durovni, B.; Saraceni, V.; Lemos, C.; Codeco, C.T.; Camargo, S.; de Carvalho, L.M.; Bastos, L.; Arduini, D.; Villela, D.A.; et al. Higher incidence of Zika in adult women than adult men in Rio de Janeiro suggests a significant contribution of sexual transmission from men to women. Int. J. Infect. Dis. 2016, 51, 128–132. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, B.; Hearn, P.; Afrough, B.; Lumley, S.; Carter, D.; Aarons, E.J.; Simpson, A.J.; Brooks, T.J.; Hewson, R. Detection of Zika virus in semen. Emerg. Infect. Dis. 2016, 22, 940. [Google Scholar] [CrossRef] [PubMed]
- Musso, D.; Roche, C.; Robin, E.; Nhan, T.; Teissier, A.; Cao-Lormeau, V.-M. Potential sexual transmission of Zika virus. Emerg. Infect. Dis. 2015, 21, 359–361. [Google Scholar] [CrossRef] [PubMed]
- Foy, B.D.; Kobylinski, K.C.; Foy, J.L.; Blitvich, B.J.; da Rosa, A.T.; Haddow, A.D.; Lanciotti, R.S.; Tesh, R.B. Probable non-vector-borne transmission of Zika virus. Emerg. Infect. Dis. 2011, 17, 880–882. [Google Scholar] [CrossRef] [PubMed]
- Chalishajar, D. Mathematical Analysis of Insulin-glucose feedback system of Diabetes. J. Eng. Appl. Sci. 2014, 5, 36–58. [Google Scholar]
- Chalishajar, D.; Geary, D.; Cox, G. Review Study of Detection of Diabetes Models through Delay Differential Equations. Appl. Math. 2016, 7, 1087–1102. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Funk, S.; Eggo, R.M.; Mallet, H.-P.; Edmunds, W.J.; Nilles, E.J. Transmission dynamics of Zika virus in island populations: A modelling analysis of the 2013-14 French Polynesia outbreak. PLoS Negl. Trop. Dis. 2016, 10, 0004726. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Lou, Y.; He, D.; Porco, T.C.; Kuang, Y.; Chowell, G.; Ruan, S. Prevention and control of Zika as a mosquito-borne and sexually transmitted disease: a mathematical modeling analysis. Sci. Rep. 2016, 6, 28070. [Google Scholar] [CrossRef] [PubMed]
- Agusto, F.B.; Bewick, S.; Fagan, W.F. Mathematical model of Zika virus with vertical transmission. Infect. Dis. Model. 2017, 2, 244–267. [Google Scholar] [CrossRef] [PubMed]
- Lashari, A.A.; Zaman, G. Optimal control of a vector borne disease with horizontal transmission. Nonlinear Anal. 2012, 13, 203–212. [Google Scholar] [CrossRef]
- Yan, X.; Zou, Y.; Li, J. Optimal quarantine and isolation strategies in epidemics control. World J. Model. Simul. 2007, 3, 202–211. [Google Scholar]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Moulay, D.; Aziz-Alaoui, M.; Kwon, H.-D. Optimal control of chikungunya disease: Larvae reduction, treatment and prevention. Math. Biosci. Eng. 2012, 9, 369–392. [Google Scholar] [CrossRef] [PubMed]
- Chaikham, N.; Sawangtong, W. Optimal control of Zika virus infection by vector elimination, vector-to-human and human-to-human contact reduction. Adv. Differ. Equ. 2017, 2017, 177. [Google Scholar] [CrossRef]
- World Health Organization. Mosquito Control: Can It Stop Zika at Source? Available online: http://www.who.int/emergencies/zika-virus/articles/mosquito-control/en/ (accessed on 12 February 2017).
- Centers for Disease Control and Prevention (CDC), Update: Interim Guidelines for Prevention of Sexual Transmission of Zika Virus-United States. 2016. Available online: https://emergency.cdc.gov/han/han00388.asp (accessed on 5 July 2017).
- Lenhart, S.; Workman, J.T. Basic Optimal Control Problems. In Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007; pp. 1–18. [Google Scholar]
- Camacho, E.F.; Alba, C.B. Introduction to Model Predictive Control. In Model Predictive Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; pp. 1–30. [Google Scholar]
- Grüne, L. Analysis and design of unconstrained nonlinear MPC schemes for finite and infinite dimensional systems. SIAM J. Control Optim. 2009, 48, 1206–1228. [Google Scholar] [CrossRef]
- Herty, M.; Zanella, M. Performance bounds for the mean-field limit of constrained dynamics. arXiv, 2015; arXiv:1511.08364. [Google Scholar]
- Caetano, M.A.L.; Yoneyama, T. Optimal and sub-optimal control in Dengue epidemics. Optim. Control Appl. Methods 2011, 22, 63–73. [Google Scholar] [CrossRef]
- Yan, X.; Zou, Y. Optimal and sub-optimal quarantine and isolation control in SARS epidemics. Math. Comput. Model. 2008, 47, 235–245. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.; Lampinen, J. The Differential Evolution Algorithm. In Differential Evolution: A Practical Approach to Global Optimization; Springer: New York, NY, USA, 2005; pp. 37–134. ISBN 978-3-540-31306-9. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hills, S.L. Transmission of Zika virus through sexual contact with travelers to areas of ongoing transmission-continental United States, 2016. Morb. Mortal. Wkly. Rep. 2016, 65, 215–216. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.A.; Staples, J.E.; Dobyns, W.B.; Pessoa, A.; Ventura, C.V.; Fonseca, E.B.D.; Ribeiro, E.M.; Ventura, L.O.; Neto, N.N.; Arena, J.E.; et al. Characterizing the Pattern of Anomalies in Congenital Zika Syndrome for Pediatric Clinicians. JAMA Pediatr. 2017, 171, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Schuler-Faccini, L.; Ribeiro, E.M.; Feitosa, I.M.; Horovitz, D.D.; Cavalcanti, D.P.; Pessoa, A.; Doriqui, M.J.; Neri, J.I.; Neto, J.M.; Wanderley, H.Y.; et al. Possible Association Between Zika Virus Infection and Microcephaly—Brazil, 2015. Morb. Mortal. Wkly. Rep. 2016, 65, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Besnard, M.; Lastere, S.; Teissier, A.; Cao-Lormeau, V.M.; Musso, D. Evidence of perinatal transmission of Zika virus, French Polynesia, December 2013 and February 2014. Euro Surveill. 2014, 19, 20751. [Google Scholar] [CrossRef] [PubMed]
- Carter, M.T.; Mirzaa, G.; McDonell, L.M.; Boycott, K.M. Microcephaly-Capillary Malformation Syndrome. 2013 December 12. GeneReviews®, Seattle (WA): University of Washington, Seattle, 1993–2018. Available online: https://www.ncbi.nlm.nih.gov/books/NBK174452/ (accessed on 5 July 2017).
- Wikipedia. List of Sovereign States and Dependent Territories by Birth Rate. Available online: https://en.wikipedia.org/wiki/List_of_sovereign_states_and_dependencies_by_total_fertility_rate (accessed on 1 February 2017).
- Manore, C.; Hickmann, J.; Xu, S.; Wearing, H.; Hyman, J. Comparing dengue and chikungunya emergence and endemic transmission in a. aegypti and a. albopictus. J. Theor. Biol. 2014, 356, 174–191. [Google Scholar] [CrossRef] [PubMed]
- Bewick, S.; Fagan, W.; Calabrese, J.; Agusto, F. Zika virus: Endemic versus epidemic dynamics and implications for disease spread in the Americas. bioRxiv 2016. [Google Scholar] [CrossRef]
- Andraud, M.; Hens, N.; Marais, C.; Beutels, P. Dynamic epidemiological models for dengue transmission: A systematic review of structural approaches. PLoS ONE 2012, 7, 49085. [Google Scholar] [CrossRef] [PubMed]
- Trpis, M.; Haussermann, W. Dispersal and other population parameters of aedes aegypti in an african village and their possible significance in epidemiology of vector-borne diseases. Am. J. Trop. Med. Hyg. 1986, 35, 1263–1279. [Google Scholar] [CrossRef] [PubMed]
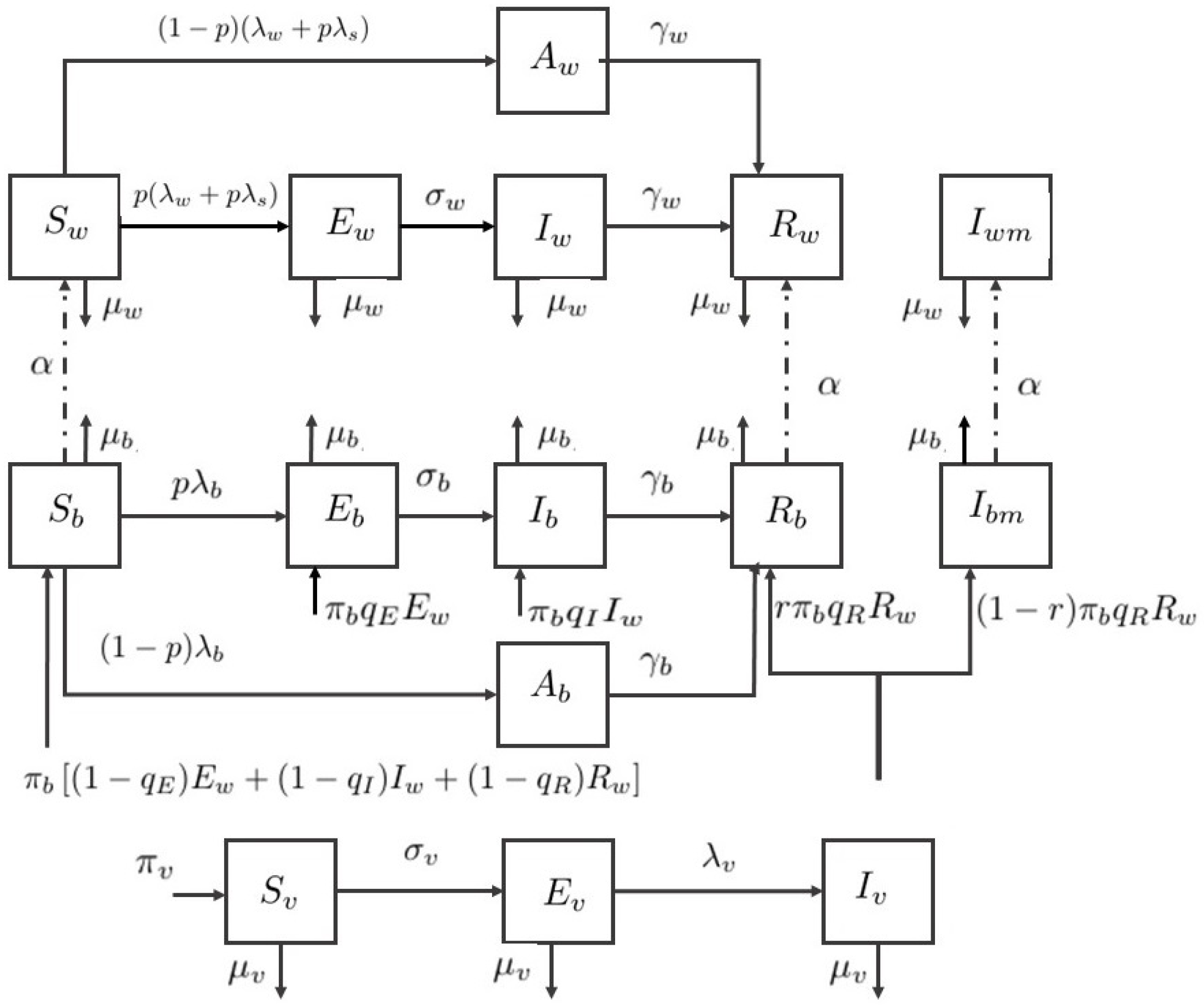
| Variable | Definition |
| Susceptible newborn babies and adults | |
| Exposed newborn babies and adults | |
| Asymptomatically infected newborn babies and adults | |
| Symptomatically infected newborn babies without microcephaly and symptomatically | |
| infected adults | |
| Newborn babies and adults with microcephaly | |
| Recovered newborn babies and adults | |
| Susceptible vectors | |
| Exposed vectors | |
| Infected vectors | |
| Parameter | Definition |
| Birth rate of newborn babies | |
| Maturity rate of babies | |
| p | Fraction of symptomatic infection |
| Remaining fraction of symptomatic infection | |
| Fraction of newborn babies who are infected from pregnant adult of each class | |
| Fraction of newborn babies who are infected with microcephaly | |
| Transmission probability per contact from infected vectors to susceptible newborn babies | |
| and adults | |
| Transmission probability per contact from infected humans to susceptible vectors | |
| Transmission probability per sexual contact from infected humans to susceptible humans | |
| Exposure modification parameter in babies | |
| Infectivity modification parameters in exposed babies and adults | |
| Sexual infectivity modification parameters in exposed adults | |
| Progression rate of exposed newborn babies and adults | |
| Recovery rate of newborn babies and adults | |
| Natural death rate of newborn babies and adults | |
| Recruitment rate of mosquitoes | |
| b | Biting rate of mosquitoes |
| Progression rate of exposed mosquitoes | |
| Mortality rate of mosquitoes |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaikham, N.; Sawangtong, W. Sub-Optimal Control in the Zika Virus Epidemic Model Using Differential Evolution. Axioms 2018, 7, 61. https://doi.org/10.3390/axioms7030061
Chaikham N, Sawangtong W. Sub-Optimal Control in the Zika Virus Epidemic Model Using Differential Evolution. Axioms. 2018; 7(3):61. https://doi.org/10.3390/axioms7030061
Chicago/Turabian StyleChaikham, Nonthamon, and Wannika Sawangtong. 2018. "Sub-Optimal Control in the Zika Virus Epidemic Model Using Differential Evolution" Axioms 7, no. 3: 61. https://doi.org/10.3390/axioms7030061
APA StyleChaikham, N., & Sawangtong, W. (2018). Sub-Optimal Control in the Zika Virus Epidemic Model Using Differential Evolution. Axioms, 7(3), 61. https://doi.org/10.3390/axioms7030061





