Decision-Making with Bipolar Neutrosophic TOPSIS and Bipolar Neutrosophic ELECTRE-I
Abstract
:1. Introduction
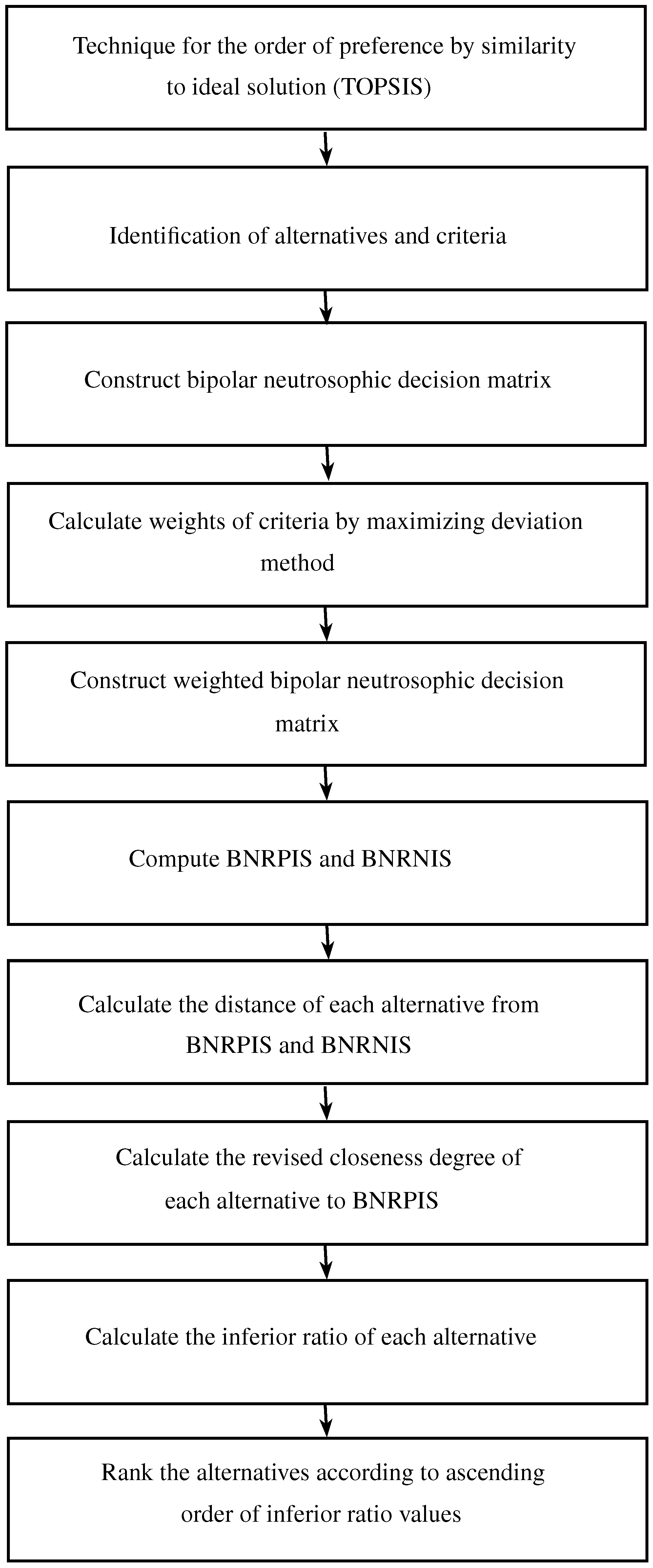
2. Bipolar Neutrosophic TOPSIS Method
- (i)
- Each value of alternative is estimated with respect to n criteria. The value of each alternative under each criterion is given in the form of BNSs and they can be expressed in the decision matrix asEach entry , where, and represent the degree of positive truth, indeterminacy and falsity membership, respectively, whereas, and represent the degree of negative truth, indeterminacy and falsity membership, respectively, such that , and , ; .
- (ii)
- Suppose that the weights of the criteria are not equally assigned and they are totally unknown to the decision maker. We use the maximizing deviation method [30] to determine the unknown weights of the criteria. Therefore, the weight of the attribute is given asand the normalized weight of the attribute is given as
- (iii)
- The accumulated weighted bipolar neutrosophic decision matrix is computed by multiplying the weights of the attributes to aggregated decision matrix as follows:where
- (iv)
- Two types of attributes, benefit type attributes and cost type attributes, are mostly applicable in real life decision making. The bipolar neutrosophic relative positive ideal solution (BNRPIS) and bipolar neutrosophic relative negative ideal solution (BNRNIS) for both type of attributes are defined as follows:such that, for benefit type criteria,Similarly, for cost type criteria,
- (v)
- The normalized Euclidean distance of each alternative from the BNRPIS can be calculated asand the normalized Euclidean distance of each alternative from the BNRNIS can be calculated as
- (vi)
- Revised closeness degree of each alternative to BNRPIS represented as and it is calculated using formula
- (vii)
- By using the revised closeness degrees, the inferior ratio to each alternative is determined as follows:It is clear that each value of lies in the closed unit interval [0,1].
- (viii)
- The alternatives are ranked according to the ascending order of inferior ratio values and the best alternative with minimum choice value is chosen.
3. Applications
3.1. Electronic Commerce Web Site
- Step 1.
- The decision matrix in the form of bipolar neutrosophic information is given as in Table 1:
- Step 2.
- The normalized weights of the criteria are calculated by using maximizing deviation method as given below:
- Step 3.
- The weighted bipolar neutrosophic decision matrix is constructed by multiplying the weights to decision matrix as given in Table 2:
- Step 4.
- The BNRPIS and BNRNIS are given by
- Step 5.
- The normalized Euclidean distances of each alternative from the BNRPISs and the BNRNISs are given as follows:
- Step 6.
- The revised closeness degree of each alternative is given as
- Step 7.
- The inferior ratio to each alternative is given as
- Step 8.
- Ordering the web stores according to ascending order of alternatives, we obtain: . Therefore, the person will choose the BigCommerce for opening a web store.
3.2. Heart Surgeon
- Step 1.
- The decision matrix in the form of bipolar neutrosophic information is given as in Table 3:
- Step 2.
- The normalized weights of the criteria are calculated by using maximizing deviation method as given below:
- Step 3.
- The weighted bipolar neutrosophic decision matrix is constructed by multiplying the weights to decision matrix as given in Table 4:
- Step 4.
- The BNRPIS and BNRNIS are given by
- Step 5.
- The normalized Euclidean distances of each alternative from the BNRPISs and the BNRNISs are given as follows:
- Step 6.
- The revised closeness degree of each alternative is given as
- Step 7.
- The inferior ratio to each alternative is given as
- Step 8.
- Ordering the alternatives in ascending order, we obtain: . Therefore, is best among all other alternatives.
3.3. Employee (Marketing Manager)
- Step 1.
- The decision matrix in the form of bipolar neutrosophic information is given as in Table 5:
- Step 2.
- The normalized weights of the criteria are calculated by using maximizing deviation method as given below:
- Step 3.
- The weighted bipolar neutrosophic decision matrix is constructed by multiplying the weights to decision matrix as given in Table 6:
- Step 4.
- The BNRPIS and BNRNIS are given by
- Step 5.
- The normalized Euclidean distances of each alternative from the BNRPISs and the BNRNISs are given as follows:
- Step 6.
- The revised closeness degree of each alternative is given as
- Step 7.
- The inferior ratio to each alternative is given as
- Step 8.
- Ordering the alternatives in ascending order, we obtain: . Therefore, the company will select the candidate for this post.
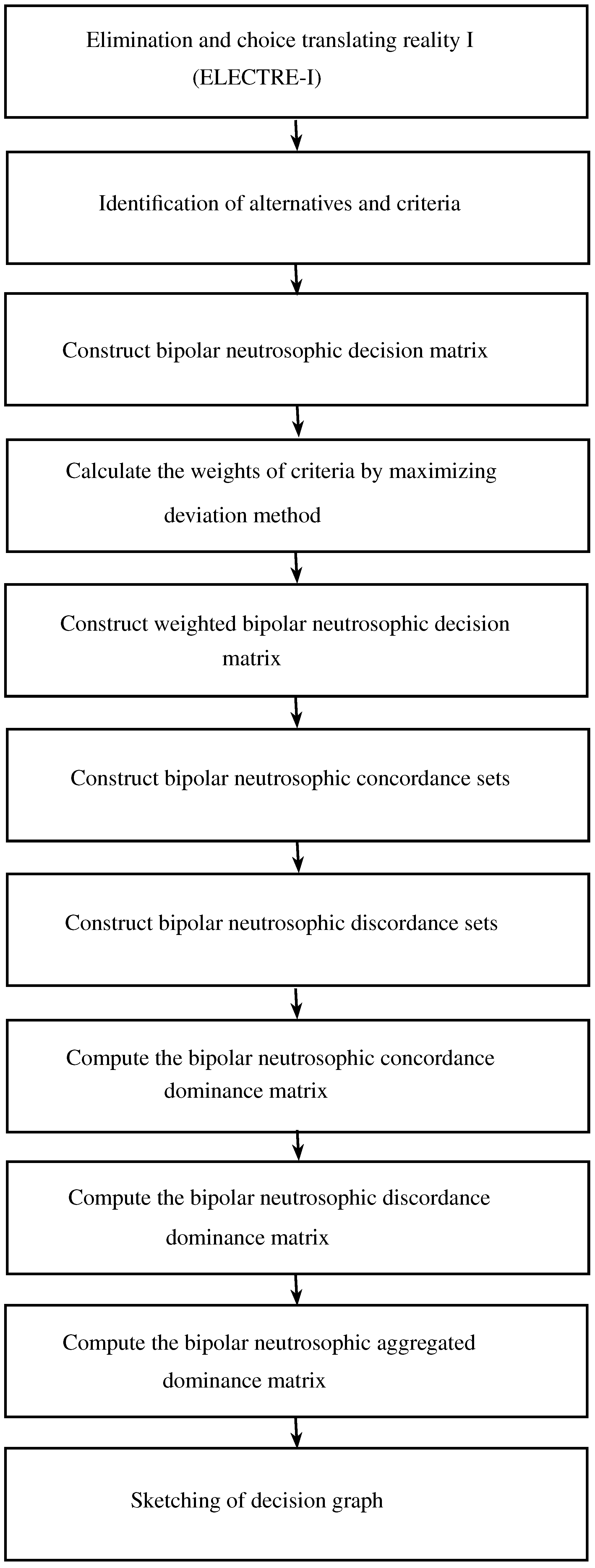
4. Bipolar Neutrosophic ELECTRE-I Method
- (i–iii)
- As in the section of bipolar neutrosophic TOPSIS, the rating values of alternatives with respect to the criteria are expressed in the form of matrix . The weights of the criteria are evaluated by maximizing deviation method and the weighted bipolar neutrosophic decision matrix is constructed.
- (iv)
- The bipolar neutrosophic concordance sets and bipolar neutrosophic discordance sets are defined as follows:where, .
- (v)
- The bipolar neutrosophic concordance matrix E is constructed as follows:where, the bipolar neutrosophic concordance indices are determined as
- (vi)
- The bipolar neutrosophic discordance matrix F is constructed as follows:where, the bipolar neutrosophic discordance indices are determined as
- (vii)
- Concordance and discordance levels are computed to rank the alternatives. The bipolar neutrosophic concordance level is defined as the average value of the bipolar neutrosophic concordance indices assimilarly, the bipolar neutrosophic discordance level is defined as the average value of the bipolar neutrosophic discordance indices as
- (viii)
- The bipolar neutrosophic concordance dominance matrix on the basis of is determined as follows:where, is defined as
- (ix)
- The bipolar neutrosophic discordance dominance matrix on the basis of is determined as follows:where, is defined as
- (x)
- Consequently, the bipolar neutrosophic aggregated dominance matrix is evaluated by multiplying the corresponding entries of and , that iswhere, is defined as
- (xi)
- Finally, the alternatives are ranked according to the outranking values . That is, for each pair of alternatives and , an arrow from to exists if and only if . As a result, we have three possible cases:
- (a)
- There exits a unique arrow from into .
- (b)
- There exist two possible arrows between and .
- (c)
- There is no arrow between and .
For case a, we decide that is preferred to . For the second case, and are indifferent, whereas, and are incomparable in case c.
Numerical Example
- Step 4.
- The bipolar neutrosophic concordance sets are given as in Table 7:
- Step 5.
- The bipolar neutrosophic discordance sets are given as in Table 8.
- Step 6.
- The bipolar neutrosophic concordance matrix E is computed as follows
- Step 7.
- The bipolar neutrosophic discordance matrix F is computed as follows
- Step 8.
- The bipolar neutrosophic concordance level is and bipolar neutrosophic discordance level is . The bipolar neutrosophic concordance dominance matrix and bipolar neutrosophic discordance dominance matrix are as follows
- Step 9.
- The bipolar neutrosophic aggregated dominance matrix is computed as
5. Comparison of Bipolar Neutrosophic TOPSIS and Bipolar Neutrosophic ELECTRE-I
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field of Logics, Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. In Multi-Space and Multi-Structure; Infinite Study: New Delhi, India, 2010; Volume 4, pp. 410–413. [Google Scholar]
- Deli, M.; Ali, F. Smarandache, Bipolar neutrosophic sets and their application based on multi-criteria decision making problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beiging, China, 20–24 August 2015; pp. 249–254. [Google Scholar]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis. Processings of the IEEE Conference, Fuzzy Information Processing Society Biannual Conference, San Antonio, TX, USA, 81–21 December 1994; pp. 305–309. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multi Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Chen, C.-T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Chu, T.C. Facility location selection using fuzzy TOPSIS under group decisions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 687–701. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Mirjaberi, M. Fuzzy inferior ratio method for multiple attribute decision making problems. Inf. Sci. 2014, 277, 263–272. [Google Scholar] [CrossRef]
- Joshi, D.; Kumar, S. Intuitionistic fuzzy entropy and distance measure based TOPSIS method for multi-criteria decision making. Egypt. Inform. J. 2014, 15, 97–104. [Google Scholar] [CrossRef]
- Kolios, A.; Mytilinou, V.; Lozano-Minguez, E.; Salonitis, K. A comparative study of multiple-criteria decision-making methods under stochastic inputs. Energies 2016, 9, 566. [Google Scholar] [CrossRef]
- Akram, M.; Alshehri, N.O.; Davvaz, B.; Ashraf, A. Bipolar fuzzy digraphs in decision support systems. J. Multiple-Valued Log. Soft Comput. 2016, 27, 531–551. [Google Scholar]
- Akram, M.; Feng, F.; Saeid, A.B.; Fotea, V. A new multiple criteria decision-making method based on bipolar fuzzy soft graphs. Iran. J. Fuzzy Syst. 2017. [Google Scholar] [CrossRef]
- Akram, M.; Waseem, N. Novel applications of bipolar fuzzy graphs to decision making problems. J. Appl. Math. Comput. 2018, 56, 73–91. [Google Scholar] [CrossRef]
- Sarwar, M.; Akram, M. Certain algorithms for computing strength of competition in bipolar fuzzy graphs. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2017, 25, 877–896. [Google Scholar] [CrossRef]
- Sarwar, M.; Akram, M. Novel concepts of bipolar fuzzy competition graphs. J. Appl. Math. Comput. 2017, 54, 511–547. [Google Scholar] [CrossRef]
- Faizi, S.; Salabun, W.; Rashid, T.; Watróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Alshehri, N.O.; Akram, M. Multi-criteria decision-making methods in bipolar fuzzy environment. Int. J. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Dey, P.P.; Pramanik, S.; Giri, B.C. TOPSIS for solving multi-attribute decision making problems under bipolar neutrosophic environment. In New Trends in Neutrosophic Theory and Applications; Pons Editions: Brussels, Belgium, 2016; pp. 65–77. [Google Scholar]
- Benayoun, R.; Roy, B.; Sussman, N. Manual de Reference du Programme Electre; Note de Synthese et Formation, No. 25; Direction Scientific SEMA: Paris, France, 1966. [Google Scholar]
- Hatami-Marbini, A.; Tavana, M. An extension of the ELECTRE method for group decision making under a fuzzy environment. Omega 2011, 39, 373–386. [Google Scholar] [CrossRef]
- Aytaç, E.; Isiķ, A.T.; Kundaki, N. Fuzzy ELECTRE I method for evaluating catering firm alternatives. Ege Acad. Rev. 2011, 11, 125–134. [Google Scholar]
- Wu, M.-C.; Chen, T.-Y. The ELECTRE multicriteria analysis approach based on Attanssov’s intuitionistic fuzzy sets. Expert Syst. Appl. 2011, 38, 12318–12327. [Google Scholar] [CrossRef]
- Chu, T.-C. Selecting plant location via a fuzzy TOPSIS approach. Int. J. Adv. Manuf. Technol. 2002, 20, 859–864. [Google Scholar]
- Guarini, M.R.; Battisti, F.; Chiovitti, A. A Methodology for the selection of multi-criteria decision analysis methods in real estate and land management processes. Sustainability 2018, 10, 507. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Tamošaitiene, J. Construction projects assessment based on the sustainable development criteria by an integrated fuzzy AHP and improved GRA model. Sustainability 2018, 10, 991. [Google Scholar] [CrossRef]
- Huang, Y.P.; Basanta, H.; Kuo, H.C.; Huang, A. Health symptom checking system for elderly people using fuzzy analytic hierarchy process. Appl. Syst. Innov. 2018, 1, 10. [Google Scholar] [CrossRef]
- Salabun, W.; Piegat, A. Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artif. Intell. Rev. 2017, 48, 557–571. [Google Scholar] [CrossRef]
- Triantaphyllou, E. Multi-Criteria Decision Making Methods, Multi-Criteria Decision Making Methods: A Comparative Study; Springer: Boston, MA, USA, 2000; pp. 5–21. [Google Scholar]
- Yang, Y.M. Using the method of maximizing deviations to make decision for multi-indices. Syst. Eng. Electron. 1998, 7, 24–31. [Google Scholar]
| ( | ( | ( | ( | |
| ) | ) | ) | ) | |
| ( | ( | ( | ( | |
| ) | ) | ) | ) | |
| ( | ( | ( | ( | |
| ) | ) | ) | ) | |
| ( | ( | ( | ( | |
| ) | ) | ) | ) |
| , | ||||
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| - | {1, 2, 3} | {1, 2} | { } | |
| {4} | - | {4} | { } | |
| {3, 4} | {1, 2, 3} | - | {3} | |
| {1, 2, 3, 4} | {1, 2, 3, 4} | {1, 2, 4} | - |
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| - | {4} | {3, 4} | {1, 2, 3, 4} | |
| {1, 2, 3} | - | {1, 2, 3} | {1, 2, 3, 4} | |
| {1, 2} | {4} | - | {1, 2, 4} | |
| { } | { } | {3} | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akram, M.; Shumaiza; Smarandache, F. Decision-Making with Bipolar Neutrosophic TOPSIS and Bipolar Neutrosophic ELECTRE-I. Axioms 2018, 7, 33. https://doi.org/10.3390/axioms7020033
Akram M, Shumaiza, Smarandache F. Decision-Making with Bipolar Neutrosophic TOPSIS and Bipolar Neutrosophic ELECTRE-I. Axioms. 2018; 7(2):33. https://doi.org/10.3390/axioms7020033
Chicago/Turabian StyleAkram, Muhammad, Shumaiza, and Florentin Smarandache. 2018. "Decision-Making with Bipolar Neutrosophic TOPSIS and Bipolar Neutrosophic ELECTRE-I" Axioms 7, no. 2: 33. https://doi.org/10.3390/axioms7020033
APA StyleAkram, M., Shumaiza, & Smarandache, F. (2018). Decision-Making with Bipolar Neutrosophic TOPSIS and Bipolar Neutrosophic ELECTRE-I. Axioms, 7(2), 33. https://doi.org/10.3390/axioms7020033






