A Dynamic Ticket Pricing Approach for Soccer Games
Abstract
1. Introduction
2. Materials and Methods
2.1. Dynamic Ticket Pricing Model
2.1.1. Methodology
Mean Season Ticket Price
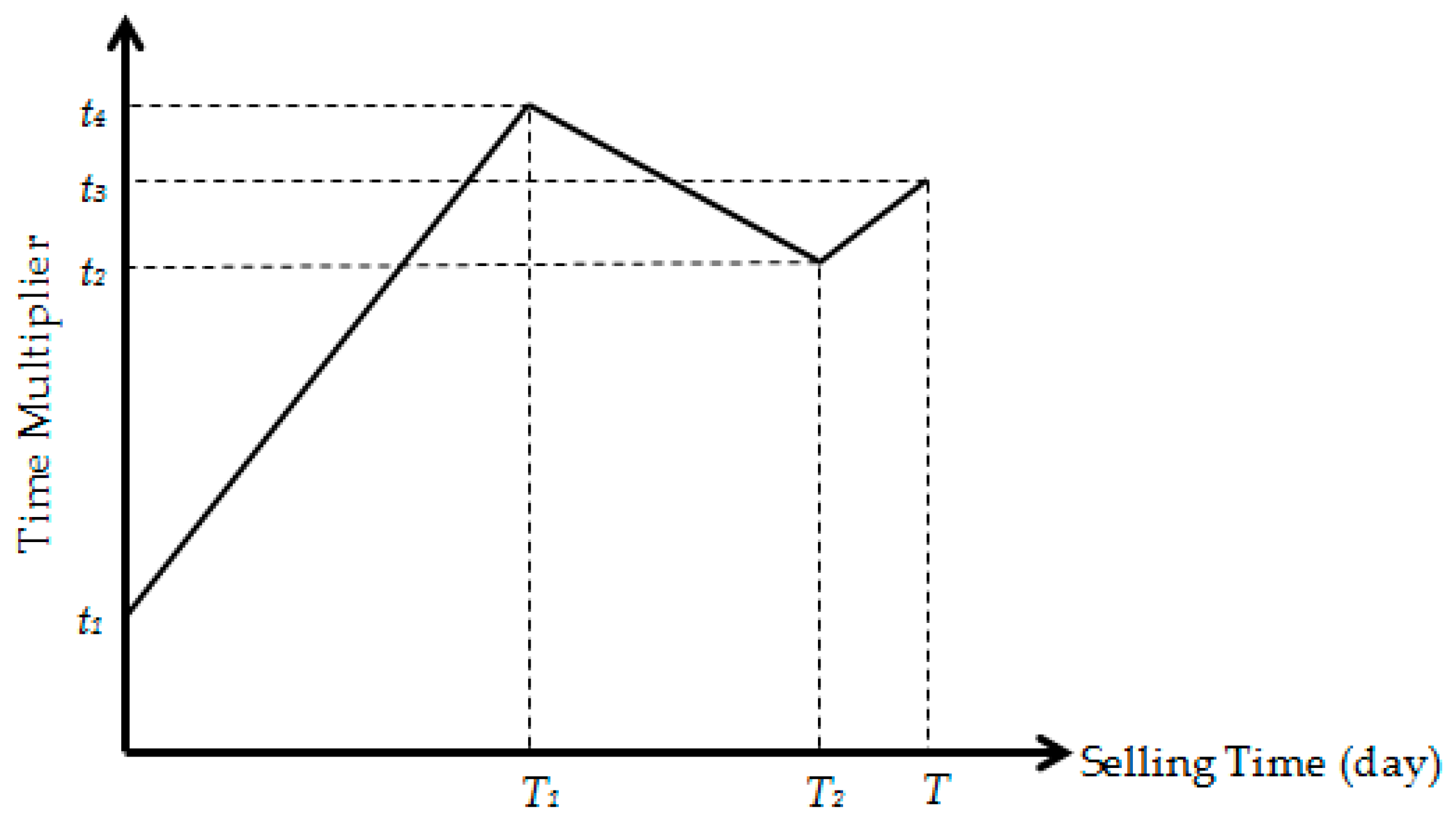
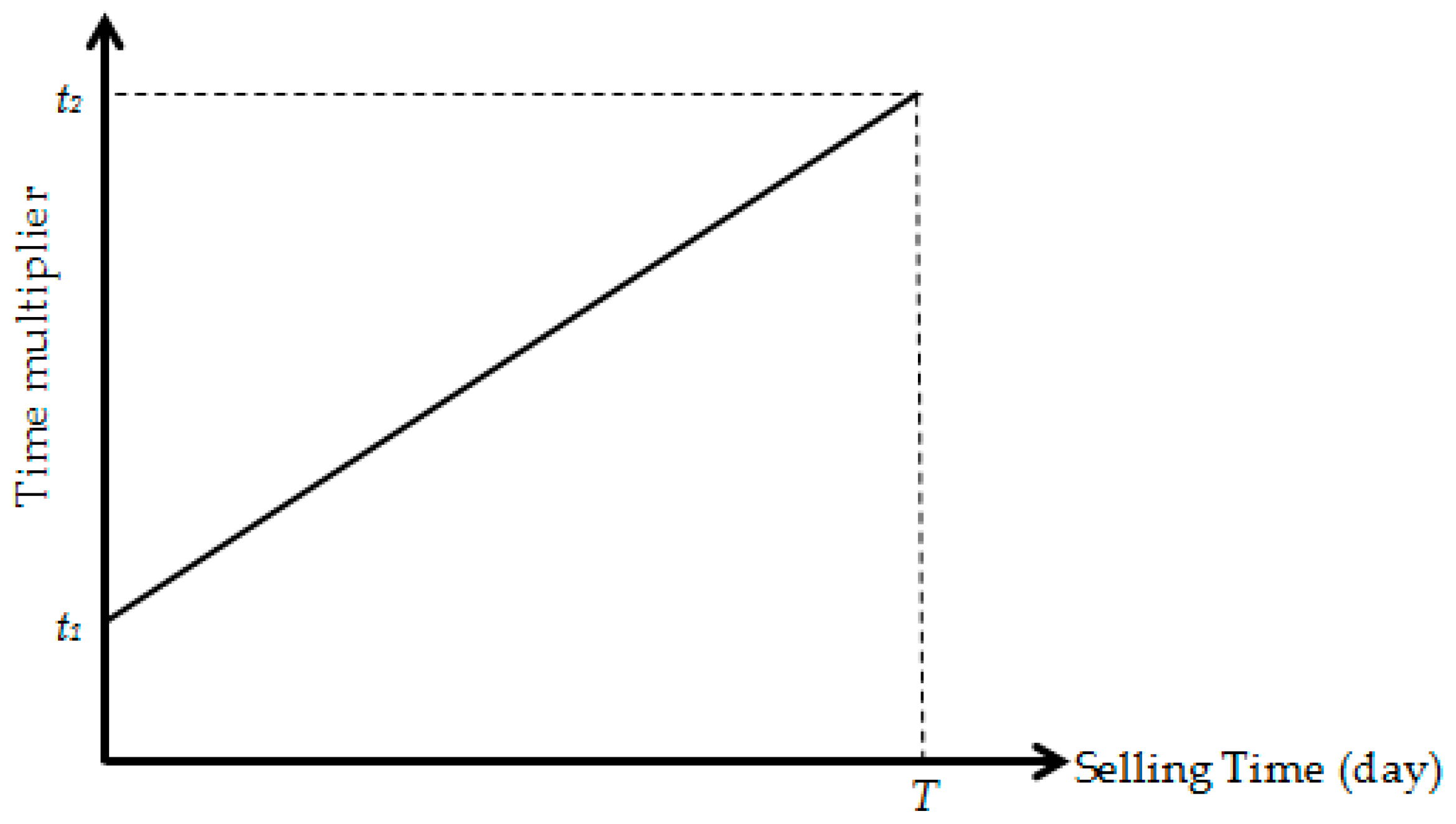
Time Multiplier
- In the first form, the time multiplier begins at its lowest level (t1) to sell as many tickets as possible by offering the lowest prices initially. As time passes, the time multiplier increases to its highest level (t4) at T1. If there are many tickets available, the time multiplier decreases to (t2) at T2. Towards the end of the selling period, it is assumed that customers are not concerned about the price, so the time multiplier increases to (t3). “T” represents the end of the selling period.
- In the second case, the time multiplier begins at its lowest level (t1) and, as time passes, it increases to (t2). This case is often stated in the sports literature [19,31]. The logic behind this scenario is offering low prices at the beginning to sell as many tickets as possible. Then, the multiplier increases continually towards end of selling period based on the assumption that last-minute spectators are not very concerned about prices.
Inventory Multiplier
2.1.2. Formulation
- t1, t2, t3, T1 and T2 are the optimization variables and t4 is the dependent variable.
- t1 is the optimization variable and t2 is the dependent variable.
- There is only one case for the inventory multiplier, as follows:
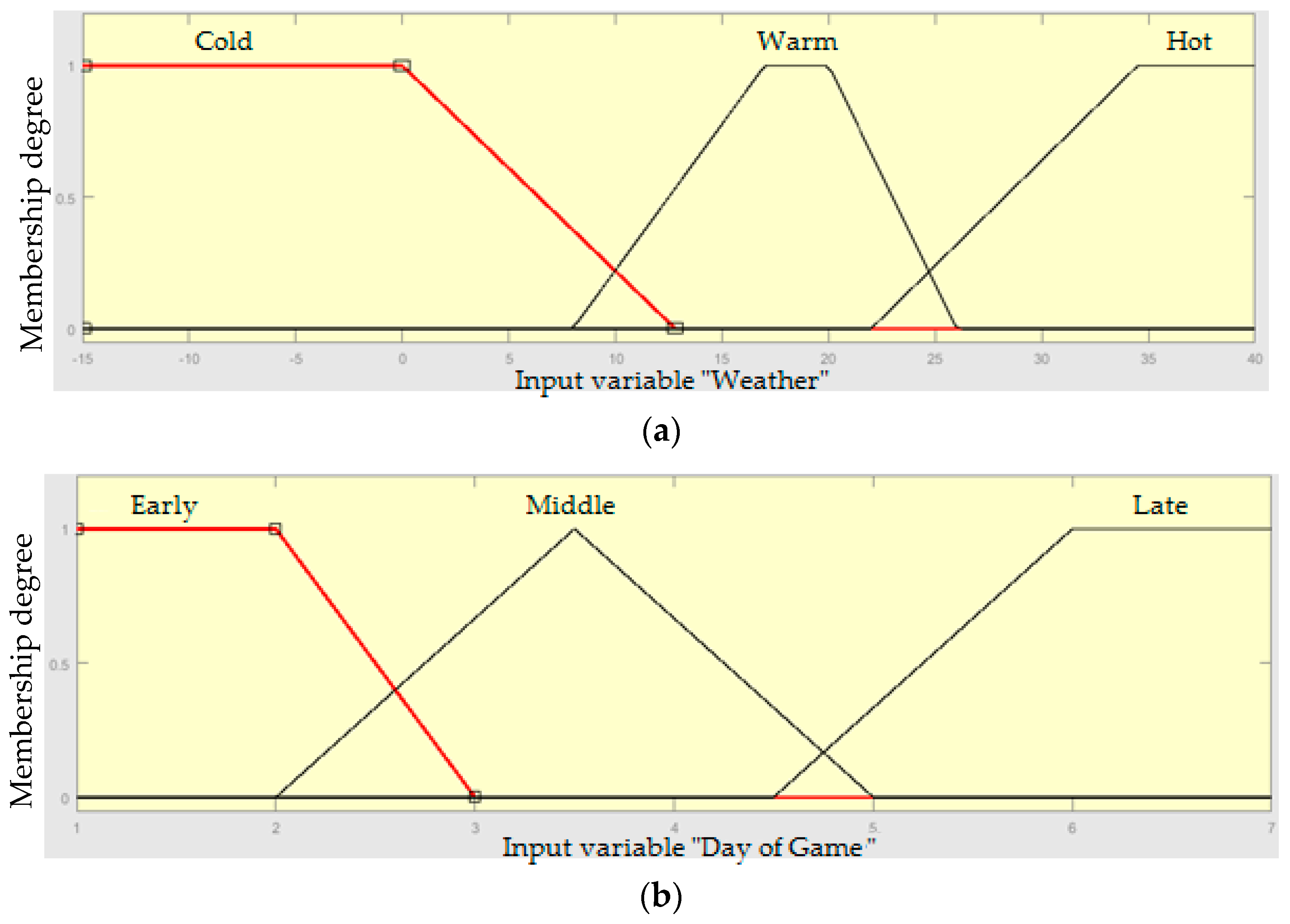
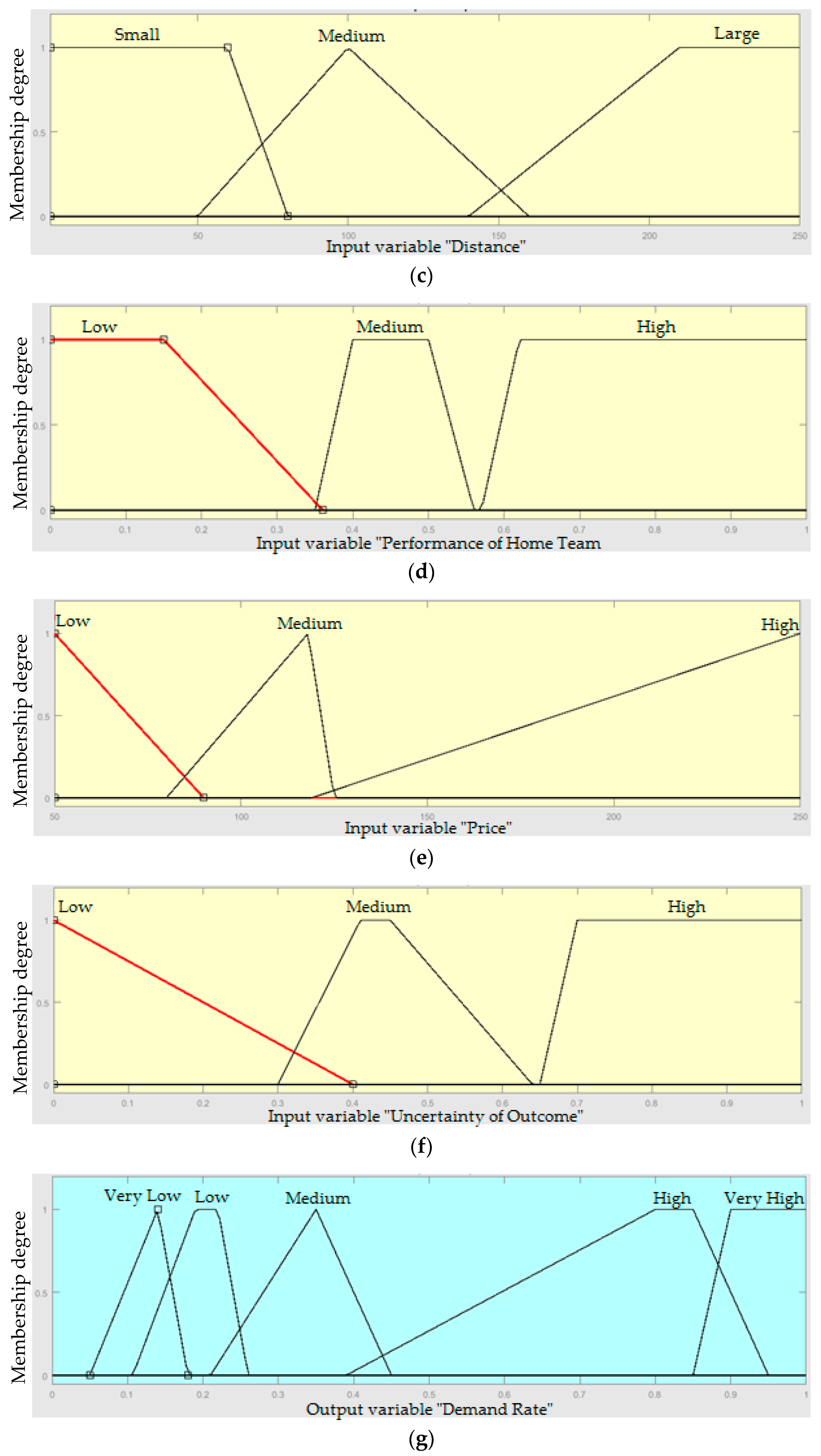
2.2. Demand Forecasting by a Fuzzy Logic System
If (Weather is not Cold) and (DayofGame is Late) and (Distance is Large) and (PerformanceofHomeTeam is High) and (Price is High) and (UncertaintyofOutcome is High) then (DemandRate is High) (1).
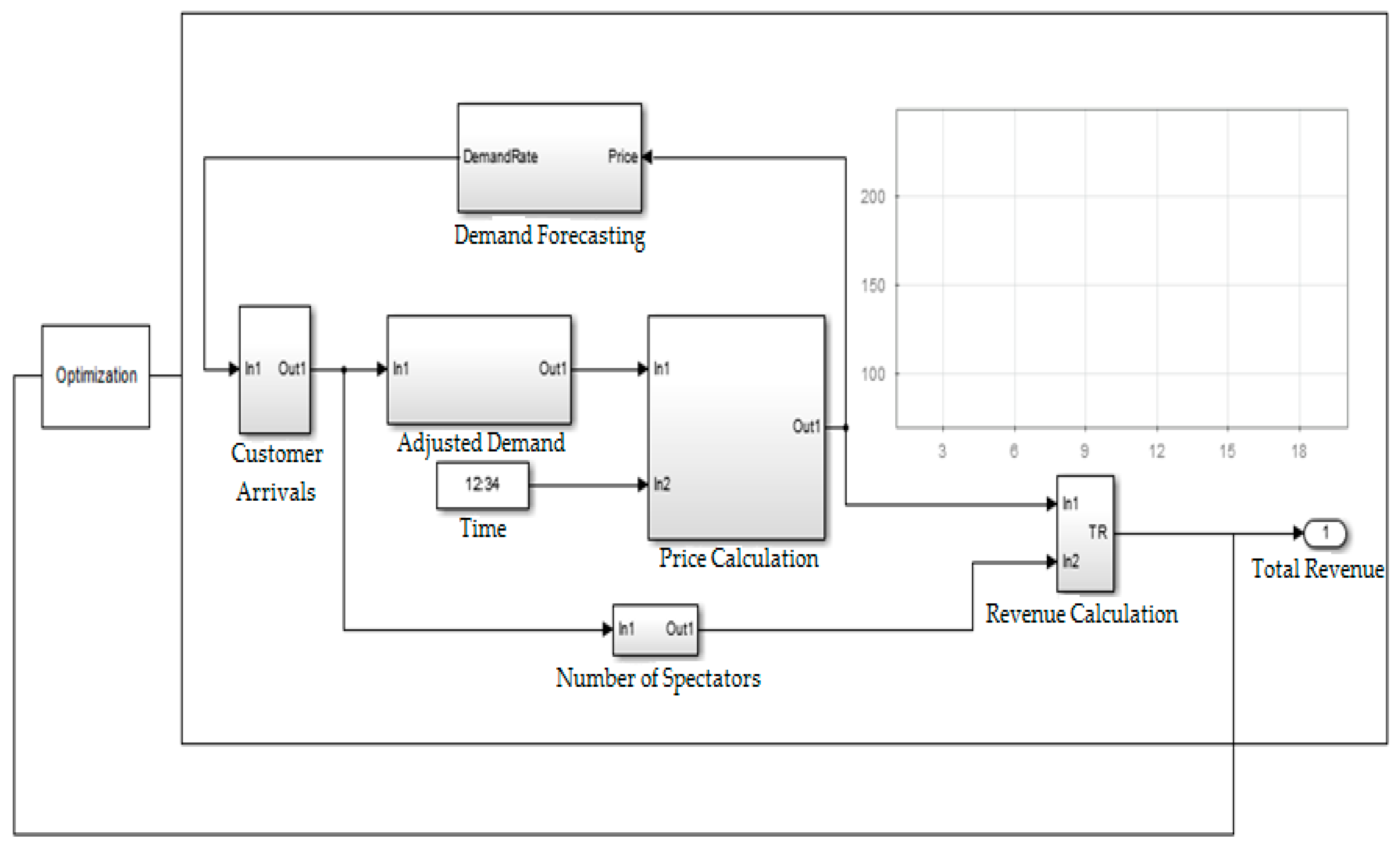
2.3. Application
3. Results and Discussion
3.1. Results of Demand Forecasting
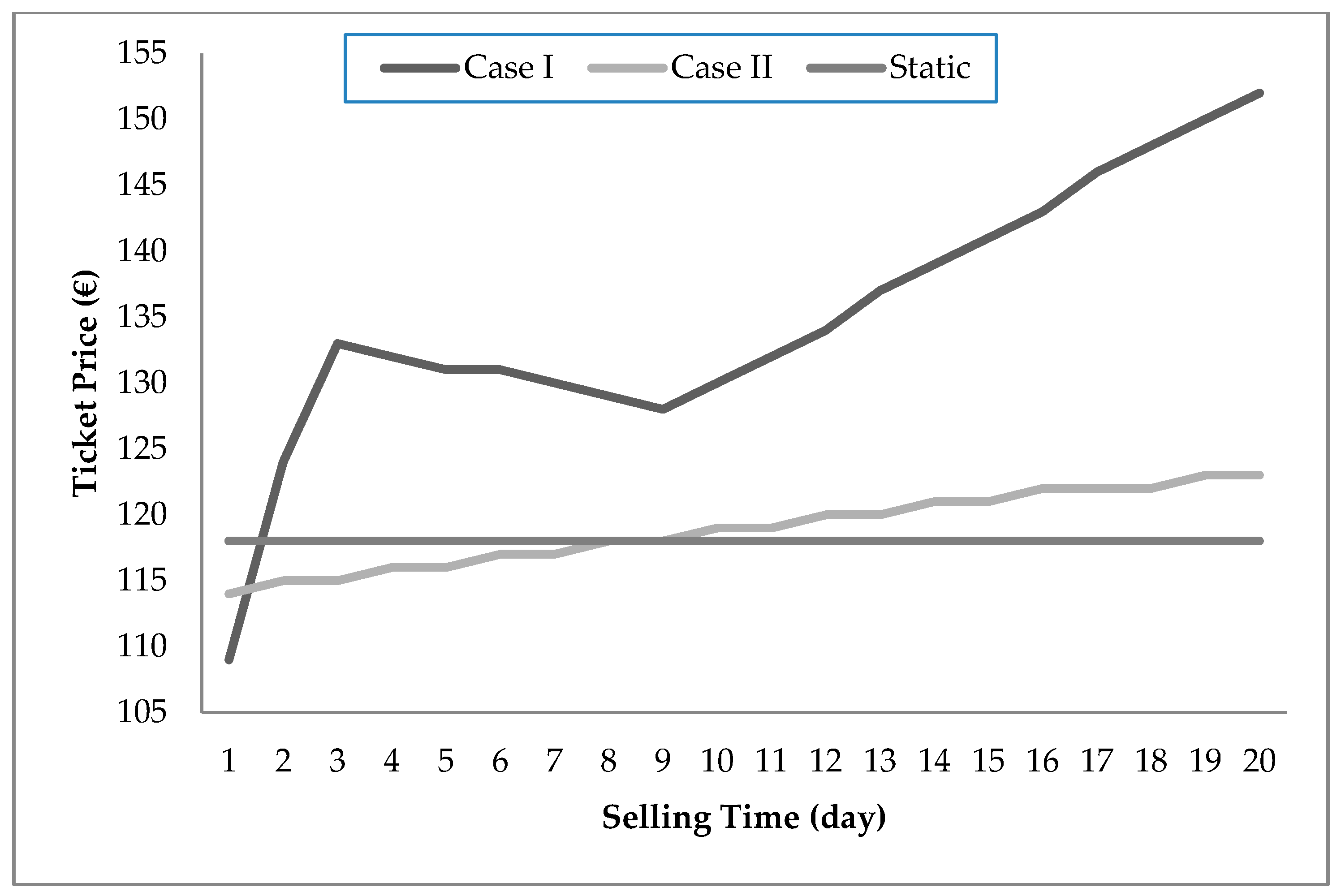
3.2. Results of Dynamic Ticket Pricing
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Boor, S.; Bosshardt, A.; Green, M.; Hanson, C.; Savage, J.; Shaffer, A.; Winn, C. Top of the Table—Football Money League; Jones, D., Ed.; Deloitte: New York, NY, USA, 2016. [Google Scholar]
- Drayer, J.; Shapiro, S.L.; Lee, S. Dynamic ticket pricing in sport: An agenda for research and practice. Sports Mark. Q. 2012, 21, 184–194. [Google Scholar]
- Nufer, G.; Fischer, J. Ticket pricing in European football—Analysis and implications. Int. J. Hum. Mov. Sports Sci. 2013, 1, 49–60. [Google Scholar]
- Rascher, D.A.; McEvoy, C.D.; Nagel, M.S.; Brown, M.T. Variable ticket pricing in major league baseball. J. Sport Manag. 2007, 21, 407–437. [Google Scholar] [CrossRef]
- Parris, D.L.; Drayer, J.; Shapiro, S.L. Developing a pricing strategy for the Los Angeles Dodgers. Sports Mark. Q. 2012, 21, 256–264. [Google Scholar]
- Shapiro, S.L.; Drayer, J. A new age of demand-based pricing: An examination of dynamic ticket pricing and secondary market prices in Major League Baseball. J. Sport Manag. 2012, 26, 532–546. [Google Scholar] [CrossRef]
- Van Ryzin, G.J.; Talluri, K.T. Emerging Theory, Methods, and Applications. In An Introduction to Revenue Management; INFORMS: Catonsville, MD, USA, 2005; pp. 142–194. [Google Scholar]
- Bitran, G.R.; Mondschein, S.V. An application of yield management to the hotel industry considering multiple day stays. Oper. Res. 1995, 43, 427–443. [Google Scholar] [CrossRef]
- Otero, D.F.; Akhavan-Tabatabaei, R. A stochastic dynamic pricing model for the multiclass problems in the airline industry. Eur. J. Oper. Res. 2015, 242, 188–200. [Google Scholar] [CrossRef]
- Zhang, D.; Weatherford, L. Dynamic pricing for network revenue management: A new approach and application in the hotel industry. INFORMS J. Comput. 2016, 29, 18–35. [Google Scholar] [CrossRef]
- Kimes, S.E. Yield management: A tool for capacity-considered service firms. J. Oper. Manag. 1989, 8, 348–363. [Google Scholar] [CrossRef]
- Kimes, S.E.; Chase, R.B.; Choi, S.; Lee, P.Y.; Ngonzi, E.N. Restaurant revenue management. Cornell Hotel Restaur. Adm. Q. 1998, 39, 32–39. [Google Scholar] [CrossRef]
- Phumchusri, N.; Swann, J.L. Scaling the house: Optimal seating zones for entertainment venues when location of seats affects demand. Int. J. Rev. Manag. 2014, 8, 56–98. [Google Scholar] [CrossRef]
- Davenport, T.H. Analytics in Sports: The New Science of Winning; International Institute for Analytics: Portlang, OR, USA, 2014. [Google Scholar]
- PwC. At the Gate and Beyond—Outlook for the Sports Market in North America through 2019. In PwC Sports Outlook; Jones, A.W., Ed.; PwC: London, UK, 2015. [Google Scholar]
- Kemper, C.; Breuer, C. How efficient is dynamic pricing for sport events? Designing a dynamic pricing model for Bayern Munich. Int. J. Sport Financ. 2016, 11, 4. [Google Scholar]
- Marburger, D.R. Optimal ticket pricing for performance goods. Manag. Decis. Econ. 1997, 18, 375–381. [Google Scholar] [CrossRef]
- Kemper, C.; Breuer, C. What factors determine the fans’ willingness to pay for Bundesliga tickets? An analysis of ticket sales in the secondary market using data from ebay.de. Sport Mark. Q. 2015, 24, 142. [Google Scholar]
- Kemper, C.; Breuer, C. Dynamic ticket pricing and the impact of time—An analysis of price paths of the English soccer club Derby County. Eur. Sport Manag. Q. 2016, 16, 233–253. [Google Scholar] [CrossRef]
- Hart, R.; Hutton, J.; Sharot, T. A statistical analysis of association football attendances. Appl. Stat. 1975, 24, 17–27. [Google Scholar] [CrossRef]
- Pawlowski, T.; Anders, C. Stadium attendance in German professional football—The (un)importance of uncertainty of outcome reconsidered. Appl. Econ. Lett. 2012, 19, 1553–1556. [Google Scholar] [CrossRef]
- Martins, A.M.; Cró, S. The Demand for Football in Portugal: New Insights on Outcome Uncertainty. J. Sports Econ. 2016. [Google Scholar] [CrossRef]
- Reilly, B. The demand for league of Ireland football. Econ. Soc. Rev. 2015, 46, 485–509. [Google Scholar]
- Dobson, S.; Goddard, J. The Economics of Football; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- García, J.; Rodríguez, P. The determinants of football match attendance revisited: Empirical evidence from the Spanish football league. J. Sports Econ. 2002, 3, 18–38. [Google Scholar] [CrossRef]
- Baranzini, A.; Ramirez, J.V.; Weber, S. The demand for football in Switzerland: An empirical estimation. SSRN Electron. J. 2008. [Google Scholar] [CrossRef]
- DeSchriver, T.D.; Rascher, D.A.; Shapiro, S.L. If we build it, will they come? Examining the effect of expansion teams and soccer-specific stadiums on Major League Soccer attendance. Sport Bus. Manag. Int. J. 2016, 6, 205–227. [Google Scholar] [CrossRef]
- Bayoumi, A.E.-M.; Saleh, M.; Atiya, A.F.; Aziz, H.A. Dynamic pricing for hotel revenue management using price multipliers. J. Rev. Pricing Manag. 2013, 12, 271–285. [Google Scholar] [CrossRef]
- Dorgham, K.; Saleh, M.; Atiya, A.F. A Novel Dynamic Pricing Model for the Telecommunications Industry. In Modelling, Computation and Optimization in Information Systems and Management Sciences; Springer: Berlin, Germany, 2015; pp. 129–140. [Google Scholar]
- Coşgun, Ö.; Ekinci, Y.; Yanık, S. Fuzzy rule-based demand forecasting for dynamic pricing of a maritime company. Knowl. Based Syst. 2014, 70, 88–96. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Drayer, J. An examination of dynamic ticket pricing and secondary market price determinants in Major League Baseball. Sport Manag. Rev. 2014, 17, 145–159. [Google Scholar] [CrossRef]
- Zadeh, L.A. A new direction in AI: Toward a computational theory of perceptions. AI Mag. 2001, 22, 73. [Google Scholar]
- Drever, P.; McDonald, J. Attendances at South Australian football games. Int. Rev. Sport Sociol. 1981, 16, 103–113. [Google Scholar] [CrossRef]
- Welki, A.M.; Zlatoper, T.J. US professional football game-day attendance. Atl. Econ. J. 1999, 27, 285–298. [Google Scholar] [CrossRef]
- Butler, M.R. Interleague play and baseball attendance. J. Sports Econ. 2002, 3, 320–334. [Google Scholar] [CrossRef]
- Borland, J.; MacDonald, R. Demand for sport. Oxf. Rev. Econ. Policy 2003, 19, 478–502. [Google Scholar] [CrossRef]
- Peel, D.A.; Thomas, D.A. The demand for football: Some evidence on outcome uncertainty. Empir. Econ. 1992, 17, 323–331. [Google Scholar] [CrossRef]
- Forrest, D.; Simmons, R. Outcome uncertainty and attendance demand in sport: The case of English soccer. J. R. Stat. Soc. Ser. D 2002, 51, 229–241. [Google Scholar] [CrossRef]
- Buraimo, B.; Simmons, R. Do sports fans really value uncertainty of outcome? Evidence from the English Premier League. Int. J. Sport Financ. 2008, 3, 146. [Google Scholar]
- Cox, A. Spectator demand, uncertainty of results, and public interest: Evidence from the English Premier League. J. Sports Econ. 2015. [Google Scholar] [CrossRef]
- Rascher, D.A. A test of the optimal positive production network externality in Major League Baseball. Sports, Economics: Current Research, 1999. Available online: https://ssrn.com/abstract=81914 (accessed on 1 October 2017).
- Bruggink, T.H.; Eaton, J.W. Rebuilding attendance in Major League Baseball: The demand for individual games. In Baseball Economics: Current Research; Praeger: Westport, NY, USA, 1996; pp. 9–31. [Google Scholar]
- Will, D.H. The Federation’s viewpoint on the new transfer rules. In Competition Policy and Professional Sports: Europe after the Bosman Case; ELS Belgium: Brussels, Belgium, 1999. [Google Scholar]
- Boyd, D.W.; Boyd, L.A. The home field advantage: Implications for the pricing of tickets to professional team sporting events. J. Econ. Financ. 1998, 22, 169–179. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy Set Theory—And Its Applications; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. Proc. Inst. Electr. Eng. 1974, 121, 1585–1588. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier Science Inc.: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Negnevitsky, M. Artificial Intelligence: A Guide to Intelligent Systems; Pearson Education: London, UK, 2005. [Google Scholar]




| Inventory Multipliers | Time Multiplier (Case I) | Time Multiplier (Case II) |
|---|---|---|
| Fuzzy Sets of Input Variables | Fuzzy Sets of Output Variable | |||||
|---|---|---|---|---|---|---|
| Weather (°C) | Day of Game | Distance (m) | Performance of Home Team | Price | Uncertainty of Outcome | Demand Rate |
| Cold | Early | Small | Low | Low | Low | Very Low |
| Warm | Middle | Medium | Medium | Medium | Medium | Low |
| Hot | Late | Large | High | High | High | Medium |
| - | - | - | - | - | - | High |
| - | - | - | - | - | - | Very High |
| Game No. | Temperature (°C) | Day of Game | Distance (m) | Performance of Home Team | Price | Uncertainty of Outcome | Demand Rate (Actual) | Demand Rate (Fuzzy Logic) |
|---|---|---|---|---|---|---|---|---|
| 1 | 24 | 7 | 241 | 0.50 | 118 | 0.33 | 0.186 | 0.192 |
| 2 | 19 | 2 | 364 | 0.50 | 118 | 0.63 | 0.158 | 0.123 |
| 3 | 10 | 6 | 85 | 0.67 | 118 | 0.40 | 0.934 | 0.937 |
| 4 | 12 | 7 | 376 | 0.63 | 118 | 0.18 | 0.316 | 0.337 |
| 5 | 8 | 7 | 0 | 0.69 | 118 | 0.93 | 0.966 | 0.935 |
| 6 | 6 | 7 | 739 | 0.69 | 118 | 0.13 | 0.338 | 0.335 |
| 7 | 2 | 6 | 37 | 0.67 | 118 | 0.50 | 0.301 | 0.336 |
| 8 | 4 | 7 | 205 | 0.57 | 118 | 0.61 | 0.256 | 0.214 |
| 9 | 11 | 6 | 95 | 0.60 | 118 | 0.34 | 0.289 | 0.313 |
| 10 | 14 | 7 | 925 | 0.60 | 118 | 0.10 | 0.320 | 0.287 |
| 11 | 16 | 7 | 140 | 0.56 | 118 | 0.16 | 0.387 | 0.337 |
| 12 | 27 | 6 | 206 | 0.00 | 118 | 0.21 | 0.245 | 0.209 |
| 13 | 20 | 6 | 925 | 0.33 | 118 | 0.35 | 0.234 | 0.192 |
| 14 | 12 | 7 | 103 | 0.42 | 118 | 0.35 | 0.298 | 0.327 |
| 15 | 2 | 6 | 95 | 0.51 | 118 | 0.26 | 0.212 | 0.231 |
| 16 | 6 | 3 | 140 | 0.55 | 118 | 0.21 | 0.196 | 0.189 |
| 17 | 8 | 7 | 0 | 0.52 | 118 | 0.72 | 0.951 | 0.935 |
| 18 | 6 | 7 | 241 | 0.57 | 118 | 0.22 | 0.134 | 0.189 |
| 19 | 5 | 6 | 98 | 0.56 | 118 | 0.35 | 0.235 | 0.265 |
| 20 | 11 | 7 | 364 | 0.55 | 118 | 0.50 | 0.231 | 0.191 |
| 21 | 16 | 6 | 85 | 0.53 | 118 | 0.51 | 0.924 | 0.939 |
| 22 | 17 | 4 | 118 | 0.53 | 118 | 0.19 | 0.153 | 0.192 |
| 23 | 20 | 7 | 85 | 1 | 118 | 0.70 | 0.978 | 0.939 |
| 24 | 11 | 7 | 205 | 0.67 | 118 | 0.57 | 0.311 | 0.336 |
| 25 | 7 | 7 | 0 | 0.52 | 118 | 0.97 | 0.986 | 0.934 |
| 26 | 11 | 7 | 560 | 0.43 | 118 | 0.42 | 0.184 | 0.191 |
| Pricing Strategy | Revenue (€) | Difference (%) | |
|---|---|---|---|
| Dynamic Pricing | Case I | 84,849 | 8.95 |
| Case II | 78,474 | 0.76 | |
| Static Pricing | - | 77,880 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şahin, M.; Erol, R. A Dynamic Ticket Pricing Approach for Soccer Games. Axioms 2017, 6, 31. https://doi.org/10.3390/axioms6040031
Şahin M, Erol R. A Dynamic Ticket Pricing Approach for Soccer Games. Axioms. 2017; 6(4):31. https://doi.org/10.3390/axioms6040031
Chicago/Turabian StyleŞahin, Mehmet, and Rızvan Erol. 2017. "A Dynamic Ticket Pricing Approach for Soccer Games" Axioms 6, no. 4: 31. https://doi.org/10.3390/axioms6040031
APA StyleŞahin, M., & Erol, R. (2017). A Dynamic Ticket Pricing Approach for Soccer Games. Axioms, 6(4), 31. https://doi.org/10.3390/axioms6040031





