Forman-Ricci Flow for Change Detection in Large Dynamic Data Sets
Abstract
:1. Introduction
2. Methods
2.1. Forman-Ricci Curvature on Networks
- e denotes the edge under consideration that connects the nodes and ;
- denotes the (positive) weight on the edge e;
- denote the (positive) weights associated with the nodes and , respectively;
- denote the set of edges connected to nodes and , respectively.
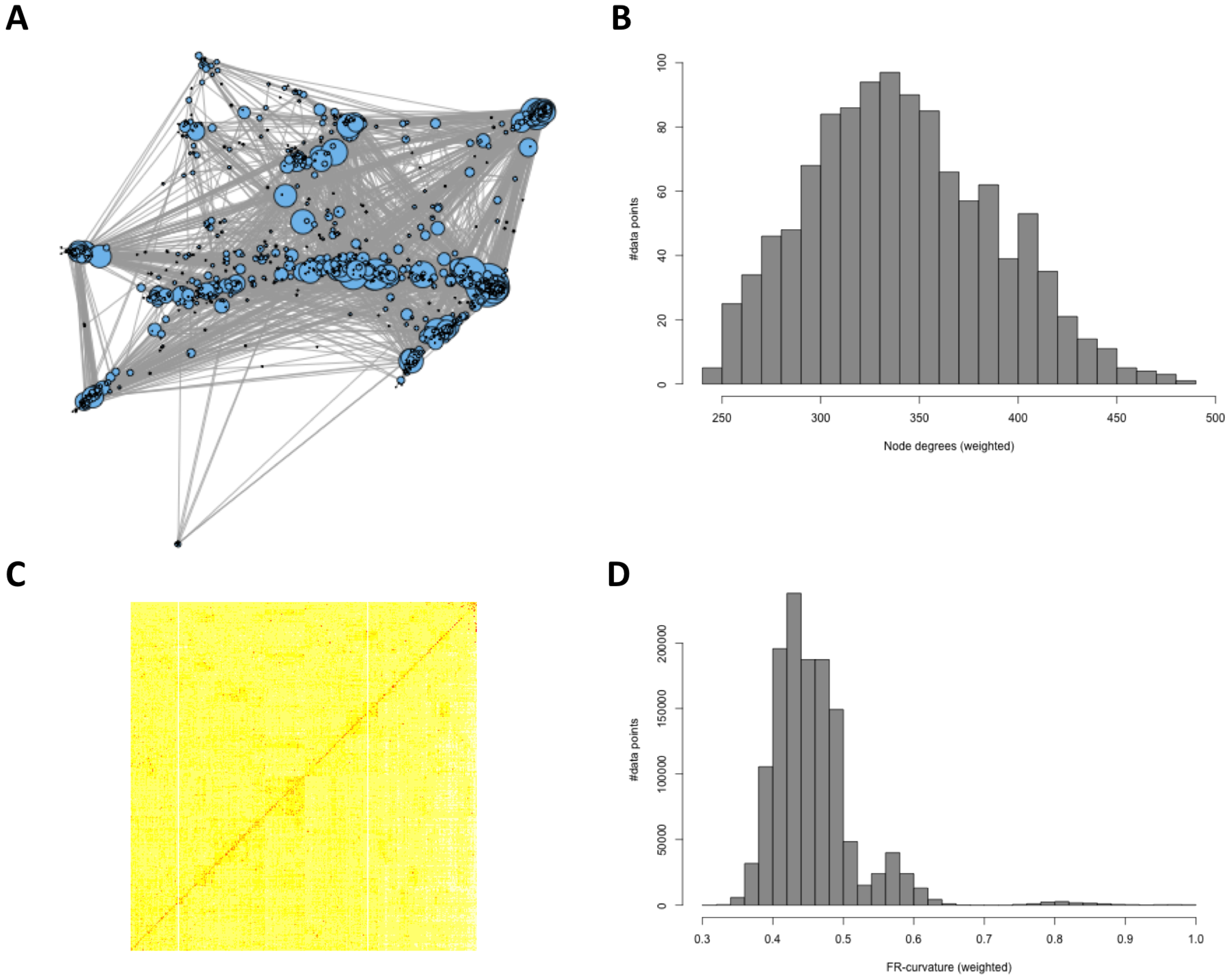
2.2. Characterizing Large Data Sets with Ricci Curvature
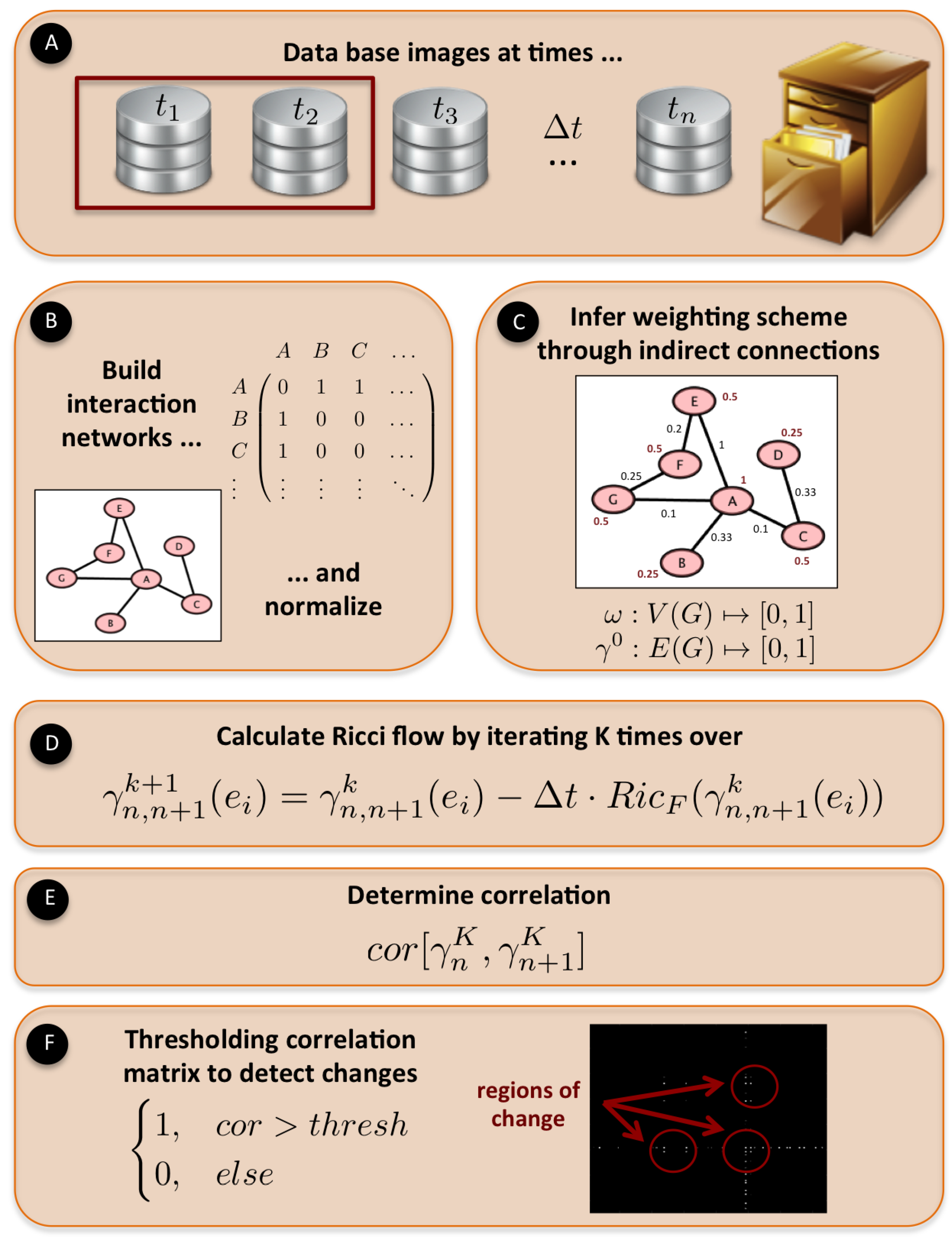
2.3. Ricci-Flow with Forman Curvature
- At each iteration step (i.e., in the process of updating to ), the Forman curvature has to be recomputed for each edge e, since it depends on its respective weight . This clearly increases the computational effort on magnitudes, however, the computation task is less formidable than it might appear at first.
- As already stressed, we consider a discrete time model. Since for smoothing (denoising) a short time flow has to be applied (because, by the theory for the smooth case, a long time flow will produce a limiting state of the network), only a small number of iterations needs be considered. The precise number of necessary iterations is to be determined experimentally. Even though a typical number can be found easily, best results may be obtained for slightly different numbers—depending on the network, and the type and level of the noise, of course.
- Ollivier also devised a continuous flow [11,22]. In the context of the present article, a continuous setting is not required, but for other types of networks, where the evolution is continuous in time, it might be preferable to implement the continuous variant, suitably adapted to the Forman curvature, rather than to Ollivier’s one.
2.4. Characterizing Dynamic Data with Ricci Flow
3. Application
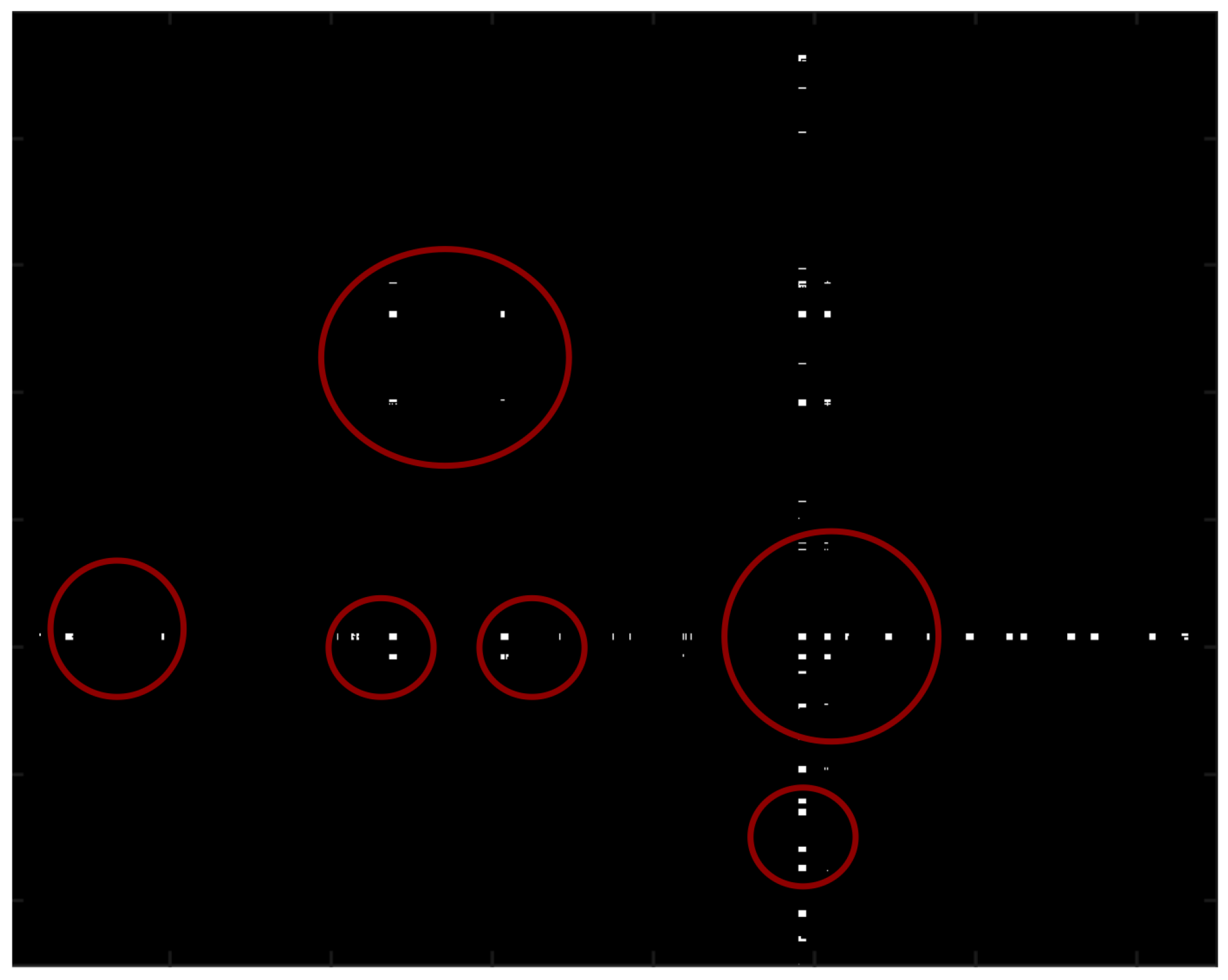
3.1. Change Detection with Ricci Flow
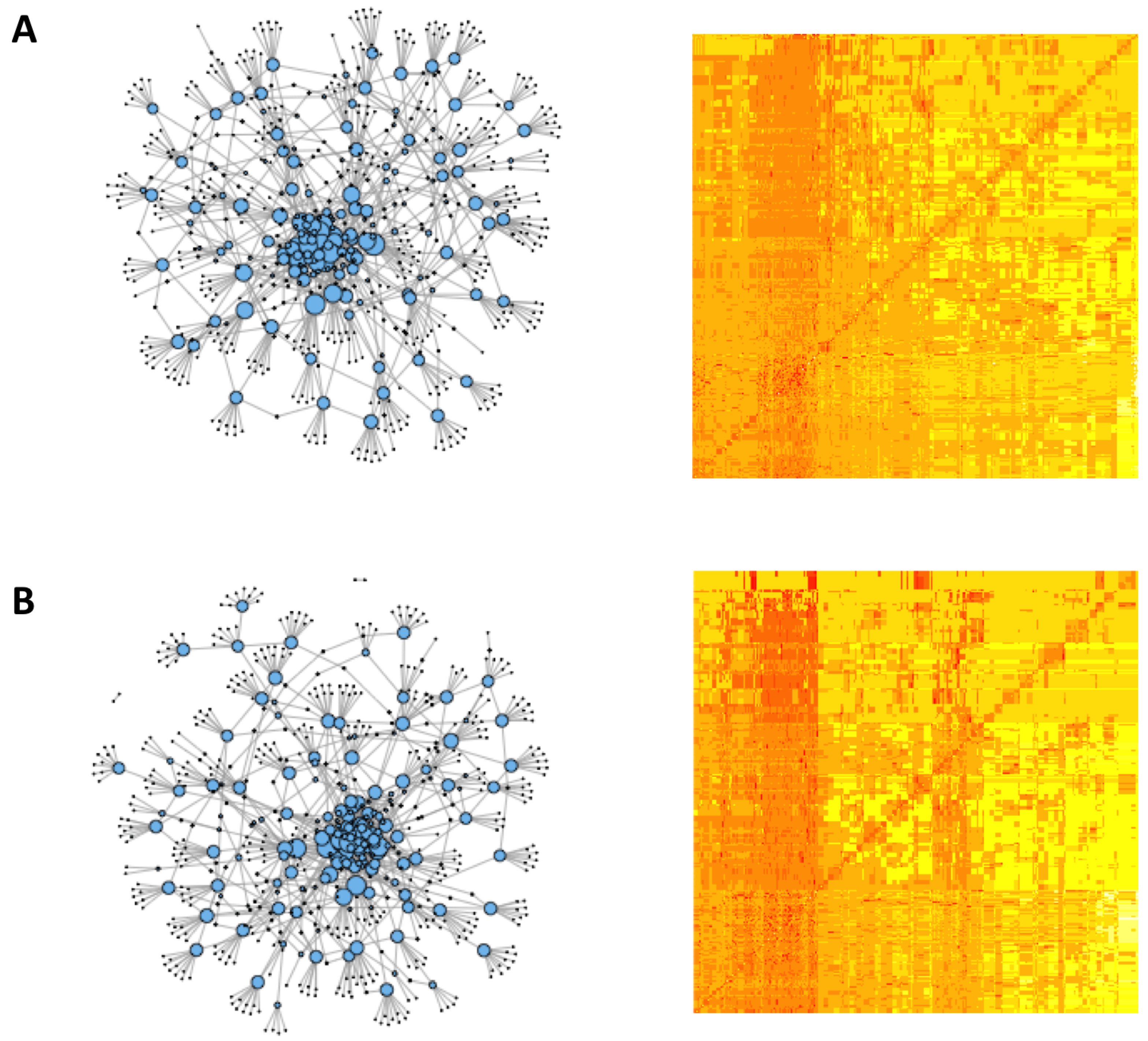
3.2. Analysis of Gnutella Peer-To-Peer Network
4. Discussion and Future Work
- A task that is almost self evident, is to further experiment with very large data sets (numbers of data points in the order of ten thousand and more);
- Another natural target is the use of our method on different types of networks, with special emphasis on Biological Networks;
- A statistical analysis regarding the Ricci flow, similar to the one presented here and in [31], should also be performed on various standard types of networks in order to confirm and calibrate the characterization and classifying capabilities of the Ricci curvature and flow.
- The Forman curvature versions of the scalar and Laplace–Beltrami flows. Especially the last one seems to be promising for network denoising, as applications of the analogous flow in image processing showed [44]. Moreover, the Forman-Ricci curvature comes naturally coupled with a fitting version of the so called Bochner Laplacian (and yet with another, intrinsically connected, rough Laplacian). This aspect is subject to ongoing work and will be covered in a forthcoming paper by the authors.
- As for the short time Ricci flow, a statistical analysis should be undertaken to validate the classification potential of the long term Ricci flow. A more ambitious, yet still feasible, future direction would be to explore network stability by considering the long time Forman-Ricci flow (as opposed to the short time one employed for denoising). This approach would exploit, in analogy with the smooth case [19,20], the propensity of the Ricci flow to preserve and quantify the overall, global Geometry (i.e., curvature) and essential topology of the network. This would allow us to study the evolution of a network “under its own pressure” and to detect and examine such catastrophic events as virus attacks and denial of service attempts. Given the basic numerical simplicity of our method, this approach might prove to be an effective alternative to the Persistent Homology method (see, e.g., [6]) for the 1-dimensional case of networks. Moreover, the Ricci flow does not need to make appeal to higher dimensional structures (namely simplicial complexes) that are necessary for the Persistent Homology based applications, with clear computational advantages (see, e.g., the code described in [45]), but also theoretically rigor. Furthermore, the here defined Ricci flow can be applied on weighted networks, whereas Persistant Homology requires unweighted complexes.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Barabasi, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Barabási, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Petri, G.; Expert, P.; Turkheimer, F.; Carhart-Harris, R.; Nutt, D.; Hellyer, P.J.; Vaccarino, F. Homological scaffolds of brain functional networks. J. R. Soc. Interface 2014, 11, 20140873. [Google Scholar] [CrossRef] [PubMed]
- Šubelj, L.; Bajec, M. Robust network community detection using balanced propagation. Eur. Phys. J. B 2011, 81, 353–362. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Ellison, N.B.; Steinfield, C.; Lampe, C. The benefits of Facebook friends: Social capital and college students’ use of online social network sites. J. Comput.-Mediat. Commun. 2007, 12, 1143–1168. [Google Scholar] [CrossRef]
- Banerjee, A.; Jost, J. Spectral plot properties: Towards a qualitative classification of networks. Netw. Heterog. Media 2008, 3, 395–411. [Google Scholar] [CrossRef]
- Ollivier, Y. Ricci curvature of Markov chains on metric spaces. J. Funct. Anal. 2009, 256, 810–864. [Google Scholar] [CrossRef]
- Jost, J.; Liu, S. Ollivierís Ricci curvature, local clustering and curvature-dimension inequalities on graphs. Discret. Comput. Geom. 2014, 51, 300–322. [Google Scholar] [CrossRef]
- Wu, Z.; Menichetti, G.; Rahmede, C.; Bianconi, G. Emergent complex network geometry. Sci. Rep. 2015, 5, 10073. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, R.; Georgiou, T.; Reznik, E.; Zhu, L.; Kolesov, I.; Senbabaoglu, Y.; Tannenbaum, A. Graph curvature for differentiating cancer networks. Sci. Rep. 2015, 5, 12323. [Google Scholar] [CrossRef] [PubMed]
- Eckmann, J.; Moses, E. Curvature of co-links uncovers hidden thematic layers in the world wide web. Proc. Natl. Acad. Sci. USA 2002, 99, 5825–5829. [Google Scholar] [CrossRef] [PubMed]
- Shavitt, Y.; Tankel, T. On the curvature of the Internet and its usage for overlay construction and distance estimation. In Proceedings of the NFOCOM 2004 Twenty-Third AnnualJoint Conference of the IEEE Computer and Communications Societies, Hong Kong, China, 7–11 March 2004; Volume 1.
- Saucan, E.; Appleboim, E. Curvature based clustering for DNA microarray data analysis. In Pattern Recognition and Image Analysis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 405–412. [Google Scholar]
- Narayan, O.; Saniee, I. Large-scale curvature of networks. Phys. Rev. E 2011, 84, 066108. [Google Scholar] [CrossRef] [PubMed]
- Perelman, G.J. The entropy formula for the Ricci flow and its geometric applications. arXiv, 2002; arXiv:math/0211159. [Google Scholar]
- Perelman, G.J. Ricci flow with surgery on three-manifolds. arXiv, 2003; arXiv:math/0303109. [Google Scholar]
- Hamilton, R.S. The Ricci flow on surfaces. In Mathematics and General Relativity; Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 1988; Volume 71, pp. 237–262. [Google Scholar]
- Ollivier, Y. A survey of Ricci curvature for metric spaces and Markov chains. Adv. Stud. Pure Math. 2010, 57, 343–381. [Google Scholar]
- Ollivier, Y. A Visual introduction to Riemannian Curvatures and Some Discrete Generalizations. Avaliable online: http://www.yann-ollivier.org/rech/publs/visualcurvature.pdf (accessed on 8 November 2016).
- Bauer, F.; Jost, J.; Liu, S. Ollivier-Ricci curvature and the spectrum of the normalized graph Laplace operator. Math. Res. Lett. 2012, 19, 1185–1205. [Google Scholar] [CrossRef]
- Ni, C.-C.; Lin, Y.-Y.; Gao, J. Ricci curvature of the Internet topology. In Proceedings of the IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 2758–2766.
- Sandhu, R.; Georgiou, T.; Tannenbaum, A. Market Fragility, Systemic Risk, and Ricci Curvature. arXiv, 2015; arXiv:1505.05182. [Google Scholar]
- Forman, R. Bochner’s method for cell complexes and combinatorial Ricci curvature. Discret. Comput. Geom. 2003, 29, 323–374. [Google Scholar] [CrossRef]
- Saucan, E.; Wolansky, G.; Appleboim, E. Combinatorial Ricci Curvature and Laplacians for Image Processing. In Proceedings of the 2nd International Congress on Image and Signal Processing (CISP’09), Tianjing, China, 17–19 October 2009; Volume 2, pp. 992–997.
- Appleboim, E.; Saucan, E.; Zeevi, Y.Y. Ricci Curvature and Flow for Image Denoising and Superesolution. In Proceedings of the the 20th Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 2743–2747.
- Sonn, E.; Saucan, E.; Appelboim, E. Ricci Flow for Image Processing. In Proceedings of the 28th Convention of Electrical & Electronics Engineers in Israel (IEEEI), Eylat, Israel, 3–5 December 2014.
- Sreejith, R.P.; Mohanraj, K.; Jost, J.; Saucan, E.; Samal, A. Forman curvature for complex networks. J. Stat. Mech. 2016, 063206. [Google Scholar] [CrossRef]
- Weber, M.; Saucan, E.; Jost, J. Characterizing Complex Networks with Forman-Ricci curvature and associated geometric flows. arXiv, 2016; arXiv:1607.08654. [Google Scholar]
- Kunegis, J. KONECT-The Koblenz Network Collection. In Proceedings of the International Conference on World Wide Web Companion, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1343–1350.
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph Evolution: Densification and Shrinking Diameters. In ACM Transactions on Knowledge Discovery from Data (ACM TKDD); ACM: New York, NY, USA, 2007; Volume 1. [Google Scholar]
- Ripeanu, M.; Foster, I.; Iamnitchi, A. Mapping the Gnutella Network: Properties of Large-Scale Peer-to-Peer Systems and Implications for System Design. IEEE Int. Comput. 2002, 6, 50–57. [Google Scholar]
- Weber, M.; Saucan, E.; Jost, J. Can one see the shape of a network? arXiv, 2016; arXiv:1608.07838v2. [Google Scholar]
- De Sola Pool, I.; Kochen, M. Contacts and influence. Soc. Net. 1978, 1, 5–51. [Google Scholar] [CrossRef]
- Michalski, R.; Palus, S.P. Matching Organizational Structure and Social Network Extracted from Email Communication. In Lecture Notes in Business Information Processing; Springer: Berlin/Heidelberg, Germany, 2011; Volume 87, pp. 197–206. [Google Scholar]
- Sarkar, R.; Yin, X.; Gao, J. Greedy Routing with Guaranteed Delivery Using Ricci Flows. In Proceedings of the 8th International Symposium on Information Processing in Sensor Networks (IPSN’09), San Francisco, CA, USA, 13–16 April 2009; pp. 121–132.
- Chow, B.; Luo, F. Combinatorial Ricci flows on surfaces. J. Differ. Geom. 2003, 63, 97–129. [Google Scholar]
- Saucan, E. A Metric Ricci Flow for Surfaces and its Applications. Geom. Imag. Comput. 2014, 1, 259–301. [Google Scholar] [CrossRef]
- Xu, G. Discrete Laplace–Beltrami operators and their convergence. Comput. Aided Geom. Des. 2004, 21, 767–784. [Google Scholar] [CrossRef]
- Jost, J. Riemannian Geometry and Geometric Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Saucan, E.; Appleboim, E.; Wolanski, G.; Zeevi, Y.Y. Combinatorial ricci curvature for image processing. MICCAI 2008 Workshop Manifolds in Medical Imaging: Metrics, Learning and Beyond. arXiv, 2008; arXiv:0903.3676. [Google Scholar]
- Mischaikow, K.; Nanda, V. Morse Theory for Filtrations and Efficient Computation of Persistent Homology. Discret. Comput. Geom. 2013, 50, 330–353. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, M.; Jost, J.; Saucan, E. Forman-Ricci Flow for Change Detection in Large Dynamic Data Sets. Axioms 2016, 5, 26. https://doi.org/10.3390/axioms5040026
Weber M, Jost J, Saucan E. Forman-Ricci Flow for Change Detection in Large Dynamic Data Sets. Axioms. 2016; 5(4):26. https://doi.org/10.3390/axioms5040026
Chicago/Turabian StyleWeber, Melanie, Jürgen Jost, and Emil Saucan. 2016. "Forman-Ricci Flow for Change Detection in Large Dynamic Data Sets" Axioms 5, no. 4: 26. https://doi.org/10.3390/axioms5040026
APA StyleWeber, M., Jost, J., & Saucan, E. (2016). Forman-Ricci Flow for Change Detection in Large Dynamic Data Sets. Axioms, 5(4), 26. https://doi.org/10.3390/axioms5040026





