Approach of Complexity in Nature: Entropic Nonuniqueness
Abstract
:1. Introduction
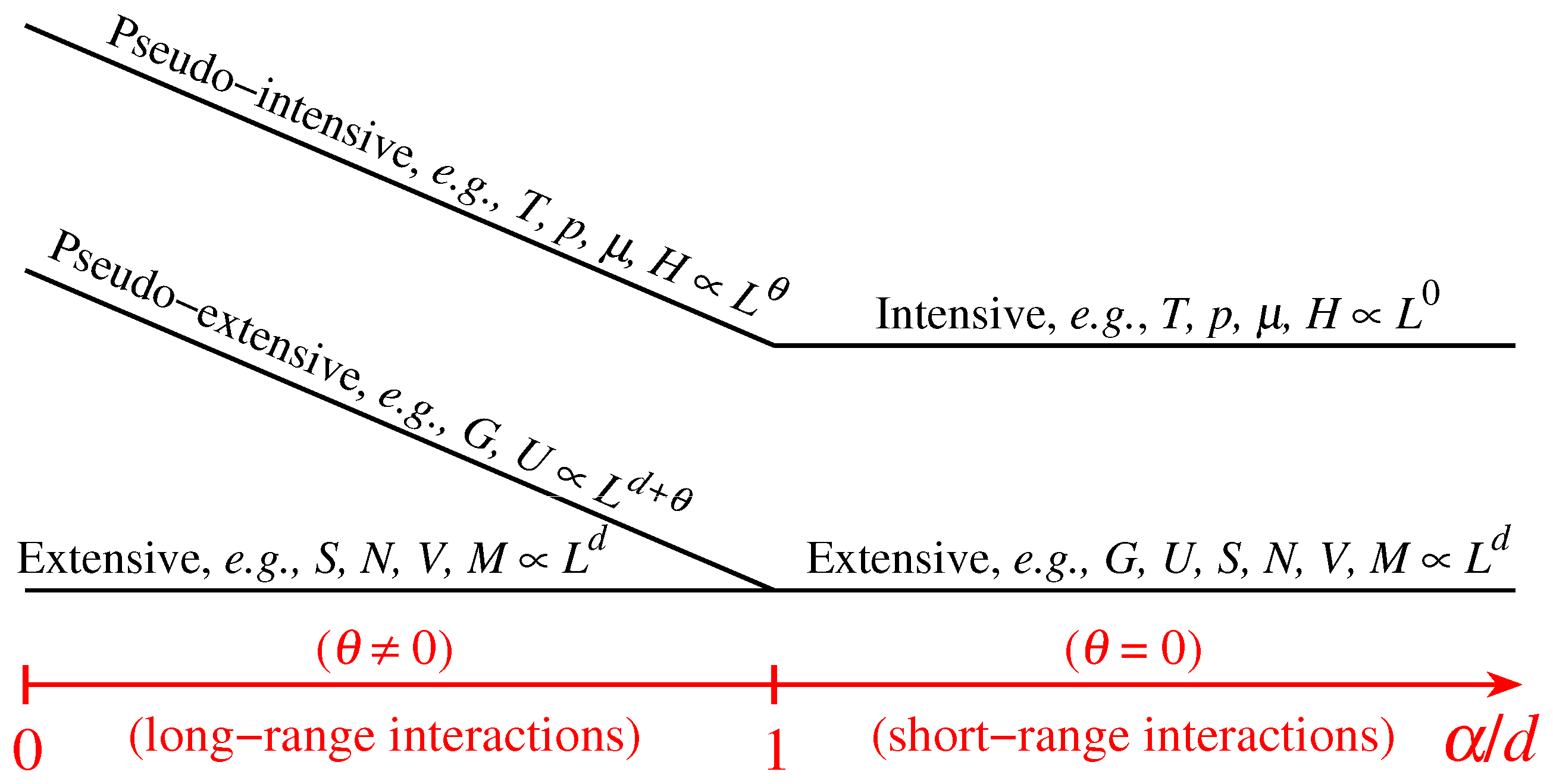
2. Additive Entropy versus Extensive Entropy
2.1. Definitions
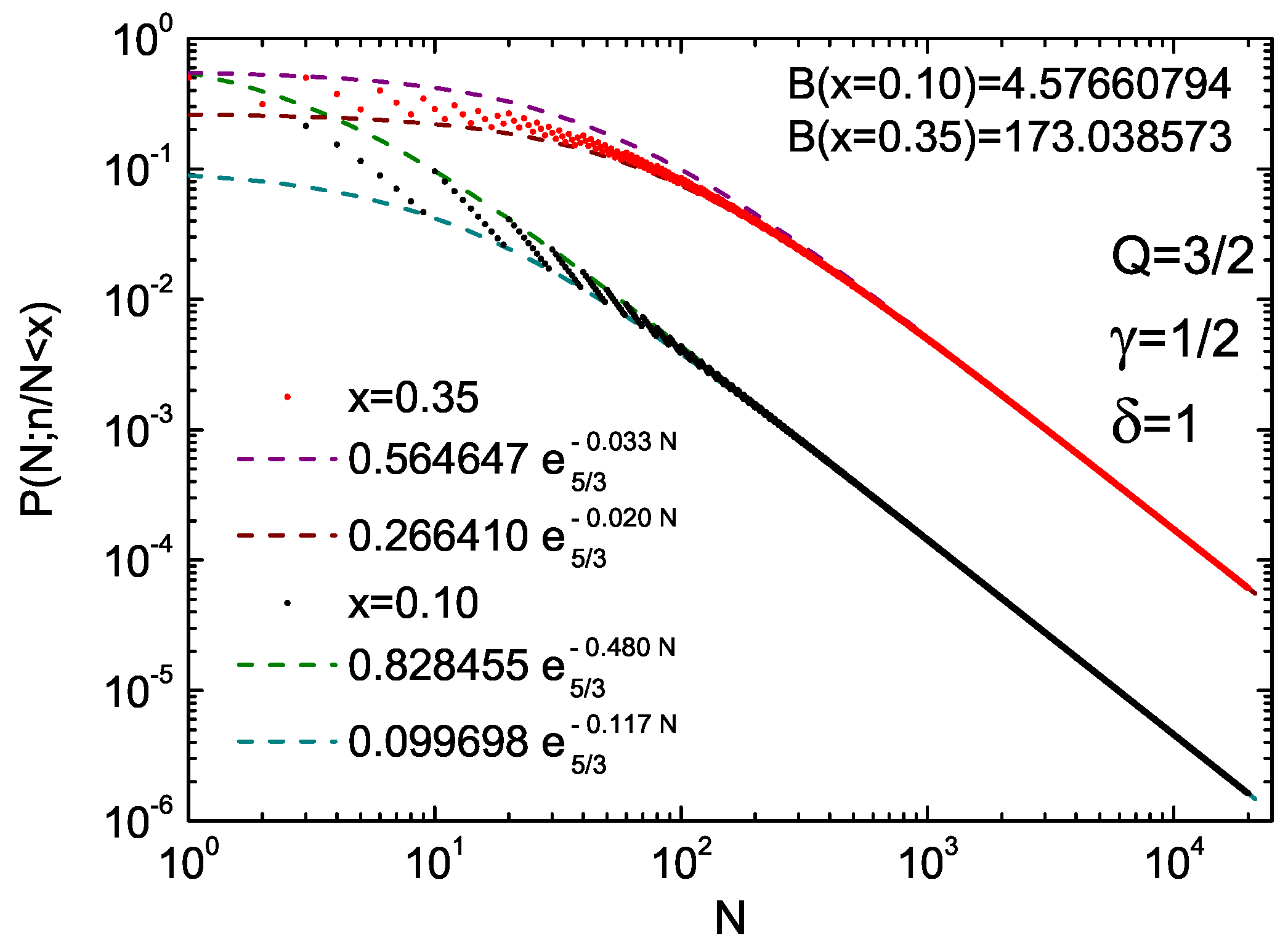
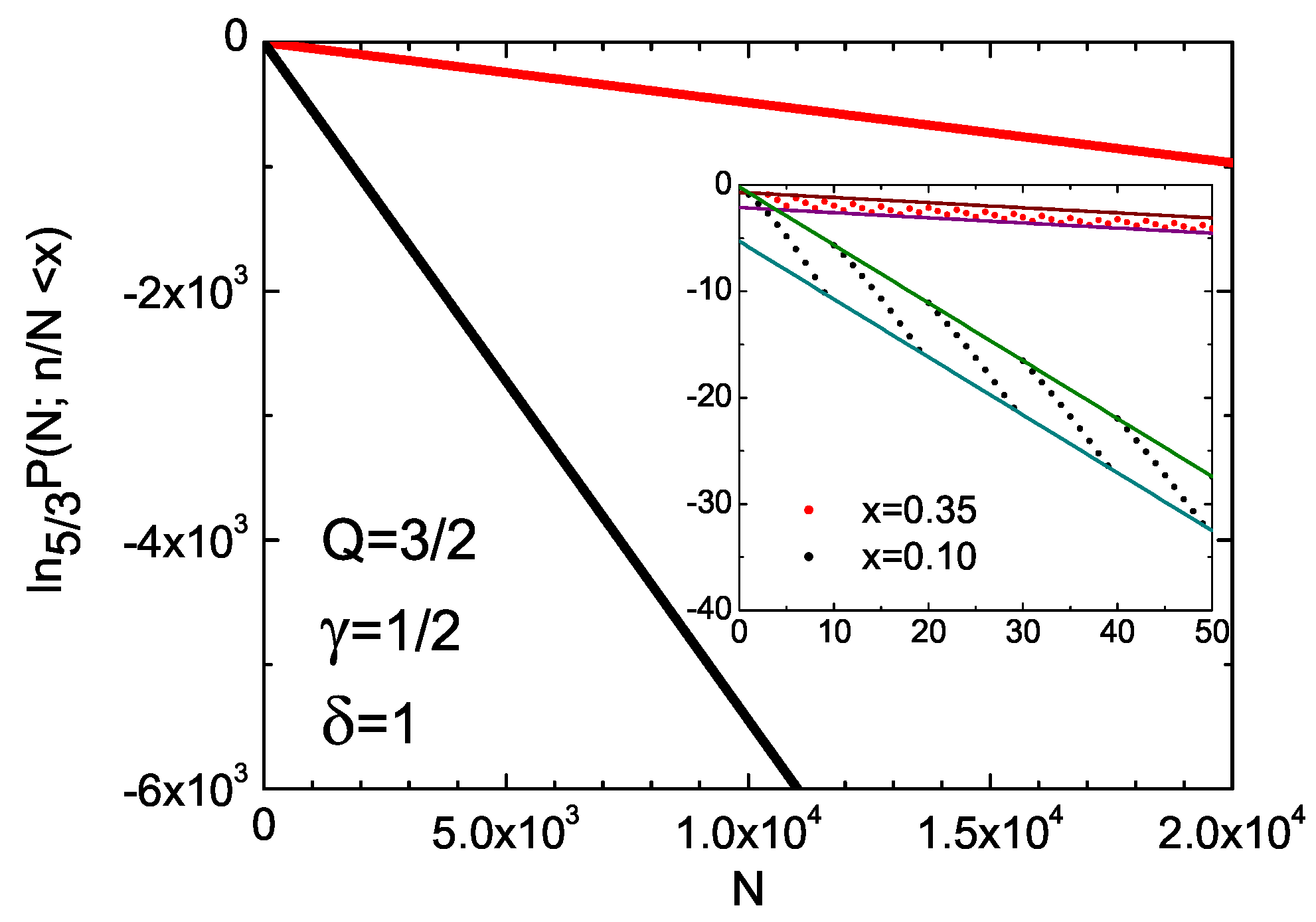
2.2. Probabilistic Illustrations
2.3. Physical Illustrations
- The logistic map at its Feigenbaum point;
- The entropy of a subsystem of a -dimensional system characterized by a central charge c at its quantum critical point;
- The entropy of a subsystem of a -dimensional generalized isotropic Lipkin–Meshkov–Glick model at its quantum critical point.
2.4. Renyi Entropy versus q-Entropy
- (i)
- Additivity: If A and B are two arbitrary probabilistically-independent systems, is additive, , whereas satisfies the non-additive property in Equation (4).
- (ii)
- Concavity: is concave for all , whereas is concave only for . Both and are convex for . These properties have consequences for characterizing the thermodynamic stability of the system.
- (iii)
- Lesche stability: is Lesche-stable , whereas is Lesche-stable only for . Lesche stability characterizes the experimental reproducibility of the entropy of a system.
- (iv)
- Pesin-like identity: For many physically important low-dimensional conservative or dissipative nonlinear dynamical systems with zero Lyapunov exponent, it is verified that, in the limit, for a unique special value of . This linearity property for is lost for ; indeed, for those systems, it can be easily verified that . No dynamical systems are yet known for which is linear for . This linearity enables, , a natural connection with the coefficient (Lyapunov exponent for the systems), which characterizes the dynamically meaningful sensitivity to the initial conditions.
- (v)
- Thermodynamical extensivity: For various N-sized quantum systems, it can be shown that a fixed value of exists, such that, in the limit, , thus satisfying the necessary thermodynamic extensivity for the entropy. For those systems, , which violates thermodynamics. For this statement, we have of course assumed that a (physically meaningful) limit exists in the limit. Various papers exist in the literature that focus on situations such that a phenomenological index q can be defined, which depends on N (see, for instance, [37,38] and the references therein), but they remain out of the present scope, since their limit yields .
- (vi)
- The likelihood function that satisfies Einstein’s requirement of factorizability coincides with the function, which extremizes the entropic functional of the system (currently, the inverse function of the generalized logarithm, which characterizes that precise entropic functional: For systems, the factorizable likelihood function is well known to be , the exponential function being the inverse of (for equal probabilities), and for appropriate constraints, it maximizes the entropy . For , we have [39] , where the q-exponential function precisely is the inverse of (for equal probabilities), and for appropriate constraints, it extremizes the entropy . In contrast with this property, the factorizable likelihood function for the Renyi entropy is , where the exponential function is the inverse of (for equal probabilities), but it differs from the q-exponential function, which is the one that extremizes . These properties plausibly have consequences for the large deviation theory of these systems (see the discussion about this theory below).
3. Why Must the Entropic Extensivity Be Preserved in All Circumstances?
3.1. Thermodynamics
3.2. Large Deviation Theory
4. Further Applications and Final Words
Acknowledgments
Conflicts of Interest
References
- Clausius, R. Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Ann. Phys. 1865, 125, 353. [Google Scholar] [CrossRef]
- Boltzmann, L. Weitere Studien über das Wärmegleichgewicht unter Gas molekülen. Wien Ber. 1872, 66, 275. [Google Scholar]
- Boltzmann, L. Über die Beziehung eines Allgemeine Mechanischen Satzes zum Zweiten Haupsatze der Wärmetheorie; Sitzungsberichte, K., Ed.; Akademie der Wissenschaften in Wien, Math.-Naturwissenschaften: Wien, Austria, 1877; Volume 75, pp. 67–73. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics—Developed with Especial Reference to the Rational Foundation of Thermodynamics; C. Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423; 623–656. [Google Scholar] [CrossRef]
- Cohen, E.G.D. Boltzmann and Einstein: Statistics and dynamics—An unsolved problem, Boltzmann Award Lecture at Statphys-Bangalore-2004. Pramana 2005, 64, 635–643. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Tsallis, C. Generalized statistical mechanics: Connection with thermodynamics. J. Phys. A Math. Gen. 1991, 24, L69–L72. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. A 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Penrose, O. Foundations of Statistical Mechanics: A Deductive Treatment; Pergamon: Oxford, UK, 1970; p. 167. [Google Scholar]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc. Natl. Acad. Sci. USA 2005, 102, 15377–15382. [Google Scholar] [CrossRef] [PubMed]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy—Interdisciplinary Applications; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Tsallis, C.; Cirto, L.J.L. Black hole thermodynamical entropy. Eur. Phys. J. C 2013, 73, 2487. [Google Scholar] [CrossRef]
- Renyi, A. On measures of information and entropy. In Proceedings of the Fourth Berkeley Symposium, Los Angeles, CA, USA, 20 June–30 July 1961; Volume 1, p. 547.
- Varma, R.S. Generalizations of Renyi’s entropy of order α. J. Math. Sci. 1966, 1, 34–48. [Google Scholar]
- Aczel, J.; Daroczy, Z. Mathematics in Science and Engineering; Bellman, R., Ed.; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Sharma, B.D.; Mittal, D.P. New non-additive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28–40. [Google Scholar]
- Sharma, B.D.; Taneja, I.J. Entropy of type (α, β) and other generalized measures in information theory. Metrika 1975, 22, 205–215. [Google Scholar] [CrossRef]
- Sharma, B.D.; Taneja, I.J. Three generalized additive measures of entropy. Elect. Infor. Kybern. 1977, 13, 419–433. [Google Scholar]
- Landsberg, P.T.; Vedral, V. Distributions and channel capacities in generalized statistical mechanics. Phys. Lett. A 1998, 247, 211–217. [Google Scholar] [CrossRef]
- Landsberg, P.T. Entropies galore! Nonextensive Statistical Mechanics and Thermodynamics. Braz. J. Phys. 1999, 29, 46–49. [Google Scholar] [CrossRef]
- Curado, E.M.F. General aspects of the thermodynamical formalism. Braz. J. Phys. 1999, 29, 36–45. [Google Scholar] [CrossRef]
- Anteneodo, C.; Plastino, A.R. Maximum entropy approach to stretched exponential probability distributions. J. Phys. A 1999, 32, 1089–1097. [Google Scholar] [CrossRef]
- Curado, E.M.F.; Nobre, F.D. On the stability of analytic entropic forms. Phys. A 2004, 335, 94–106. [Google Scholar] [CrossRef]
- Zaripov, R.G. Geometric representation of the group of entropy vectors in non extensive statistical mechanics. Russ. Phys. J. 2014, 57, 861–869. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. EPL 2011, 93, 20006. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. When do generalised entropies apply? How phase space volume determines entropy. EPL 2011, 96, 50003. [Google Scholar] [CrossRef]
- Lyra, M.L.; Tsallis, C. Nonextensivity and multifractality in low-dimensional dissipative systems. Phys. Rev. Lett. 1998, 80, 53–56. [Google Scholar] [CrossRef]
- Baldovin, F.; Robledo, A. Universal renormalization-group dynamics at the onset of chaos in logistic maps and nonextensive statistical mechanics. Phys. Rev. E 2002, 66, R045104. [Google Scholar] [CrossRef] [PubMed]
- Broadhurst, D. Available online: http://pi.lacim.uqam.ca/piDATA/feigenbaum.txt (accessed on 8 July 2016).
- Caruso, F.; Tsallis, C. Non-additive entropy reconciles the area law in quantum systems with classical thermodynamics. Phys. Rev. E 2008, 78, 021102. [Google Scholar] [CrossRef]
- Carrasco, J.A.; Finkel, F.; Gonzalez-Lopez, A.; Rodriguez, M.A.; Tempesta, P. Generalized isotropic Lipkin-Meshkov-Glick models: Ground state entanglement and quantum entropies. J. Stat. Mech. 2016, 3, 033114. [Google Scholar] [CrossRef]
- Saguia, A.; Sarandy, M.S. Nonadditive entropy for random quantum spin-S chains. Phys. Lett. A 2010, 374, 3384–3388. [Google Scholar] [CrossRef]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Extensivity and entropy production. Europhys. News Spec. Europhys. News 2005, 36, 186–189. [Google Scholar] [CrossRef]
- Parvan, A.S.; Biro, T.S. Extensive Renyi statistics from non-extensive entropy. Phys. Lett. A 2005, 340, 375–387. [Google Scholar] [CrossRef]
- Parvan, A.S.; Biro, T.S. Renyi statistics in equilibrium statistical mechanics. Phys. Lett. A 2010, 374, 1951–1957. [Google Scholar] [CrossRef]
- Tsallis, C.; Haubold, H.J. Boltzmann-Gibbs entropy is sufficient but not necessary for the likelihood factorization required by Einstein. EPL 2015, 110, 30005. [Google Scholar] [CrossRef]
- Tamarit, F.; Anteneodo, C. Long-range interacting rotators: Connection with the mean-field approximation. Phys. Rev. Lett. 2000, 84, 208–211. [Google Scholar] [CrossRef] [PubMed]
- Sicuro, G.; Tempesta, P. Groups, information theory and Einstein’ s likelihood principle. Phys. Rev. E 2016, 93, 040101. [Google Scholar] [CrossRef] [PubMed]
- Touchette, H. The large deviation approach to statistical mechanics. Phys. Rep. 2009, 478, 1–69. [Google Scholar] [CrossRef]
- Ruiz, G.; Tsallis, C. Towards a large deviation theory for strongly correlated systems. Phys. Lett. A 2012, 376, 2451–2454. [Google Scholar] [CrossRef]
- Touchette, H. Comment on “Towards a large deviation theory for strongly correlated systems”. Phys. Lett. A 2013, 377, 436–438. [Google Scholar] [CrossRef]
- Ruiz, G.; Tsallis, C. Reply to Comment on “Towards a large deviation theory for strongly correlated systems". Phys. Lett. A 2013, 377, 491–495. [Google Scholar] [CrossRef]
- Ruiz, G.; Tsallis, C. Emergence of q-statistical functions in a generalized binomial distribution with strong correlations. J. Math. Phys. 2015, 56, 053301. [Google Scholar] [CrossRef]
- Tsallis, C. Nonextensive Statistical Mechanics and Thermodynamics. Available online: http://tsallis.cat.cbpf.br/biblio.htm (accessed on 8 July 2016).
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, 2197–2200. [Google Scholar] [CrossRef]
- Combe, G.; Richefeu, V.; Stasiak, M.; Atman, A.P.F. Experimental validation of nonextensive scaling law in confined granular media. Phys. Rev. Lett. 2015, 115, 238301. [Google Scholar] [CrossRef] [PubMed]
- Malacarne, L.C.; Mendes, R.S.; Pedron, I.T.; Lenzi, E.K. Nonlinear equation for anomalous diffusion: Unified power-law and stretched exponential exact solution. Phys. Rev. E 2001, 63, R030101. [Google Scholar] [CrossRef] [PubMed]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann-Gibbs statistics to Tsallis statistics. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef] [PubMed]
- Moyano, L.G.; Tsallis, C.; Gell-Mann, M. Numerical indications of a q-generalised central limit theorem. Europhys. Lett. 2006, 73, 813–819. [Google Scholar] [CrossRef]
- Hilhorst, H.J.; Schehr, G. A note on q-Gaussians and non-Gaussians in statistical mechanics. J. Stat. Mech. 2007, 6, P06003. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C.; Steinberg, S. On a q-central limit theorem consistent with nonextensive statistical mechanics. Milan J. Math. 2008, 76, 307–328. [Google Scholar] [CrossRef]
- Umarov, S.; Tsallis, C.; Gell-Mann, M.; Steinberg, S. Generalization of symmetric α-stable Lévy distributions for q > 1. J. Math. Phys. 2010, 51, 033502. [Google Scholar] [CrossRef] [PubMed]
- Hilhorst, H.J. Note on a q-modified central limit theorem. J. Stat. Mech. 2010, 10, P10023. [Google Scholar] [CrossRef]
- Jauregui, M.; Tsallis, C. q-generalization of the inverse Fourier transform. Phys. Lett. A 2011, 375, 2085–2088. [Google Scholar] [CrossRef]
- Jauregui, M.; Tsallis, C.; Curado, E.M.F. q-moments remove the degeneracy associated with the inversion of the q-Fourier transform. J. Stat. Mech. 2011, 10, P10016. [Google Scholar] [CrossRef]
- Hahn, M.G.; Jiang, X.X.; Umarov, S. On q-Gaussians and exchangeability. J. Phys. A 2010, 43, 165208. [Google Scholar] [CrossRef]
- Jiang, X.X.; Hahn, M.G.; Umarov, S. On generalized Leibniz triangles and q-Gaussians. Phys. Lett. A 2012, 376, 2447–2450. [Google Scholar] [CrossRef]
- Plastino, A.; Rocca, M.C. Inversion of Umarov-Tsallis-Steinberg q-Fourier Transform and the complex-plane generalization. Phys. A 2012, 391, 4740–4747. [Google Scholar] [CrossRef]
- Plastino, A.; Rocca, M.C. q-Fourier Transform and its inversion-problem. Milan J. Math. 2012, 80, 243–249. [Google Scholar] [CrossRef]
- Budini, A.A. Central limit theorem for a class of globally correlated random variables. Phys. Rev. E 2016, 93, 062114. [Google Scholar] [CrossRef] [PubMed]
- Soares, D.J.B.; Tsallis, C.; Mariz, A.M.; da Silva, L.R. Preferential attachment growth model and nonextensive statistical mechanics. Europhys. Lett. 2005, 70, 70–76. [Google Scholar] [CrossRef]
- Thurner, S.; Tsallis, C. Nonextensive aspects of self-organized scale-free gas-like networks. Europhys. Lett. 2005, 72, 197–203. [Google Scholar] [CrossRef]
- Brito, S.G.A.; da Silva, L.R.; Tsallis, C. Role of dimensionality in complex networks. Sci. Rep. 2016, 6, 27992. [Google Scholar] [CrossRef] [PubMed]
- Kullmann, L.; Kertesz, J. Preferential growth: Exact solution of the time-dependent distributions. Phys. Rev. E 2001, 63, 051112. [Google Scholar] [CrossRef] [PubMed]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Mathai, A.M. A pathway to matrix-variate gamma and normal densities. Linear Algebra Its Appl. 2005, 396, 317–328. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Pathway model, superstatistics, Tsallis statistics, and a generalized measure of entropy. Phys. A 2007, 375, 110–122. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On generalized entropy measures and pathways. Phys. A 2007, 385, 493–500. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Pathway parameter and thermonuclear functions. Phys. A 2008, 387, 2462–2470. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On generalized distributions and pathways. Phys. Lett. A 2008, 372, 2109–2113. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Lavagno, A.; Quarati, P. Generalized statistics and solar neutrinos. Phys. Lett. B 1996, 369, 308–312. [Google Scholar] [CrossRef]
- Quarati, P.; Carbone, A.; Gervino, G.; Kaniadakis, G.; Lavagno, A.; Miraldi, E. Constraints for solar neutrinos fluxes. Nucl. Phys. A 1997, 621, 345c–348c. [Google Scholar] [CrossRef]
- Kaniadakis, G.; Lavagno, A.; Quarati, P. Non-extensive statistics and solar neutrinos. Astrophys. Space Sci. 1998, 258, 145–155. [Google Scholar] [CrossRef]
- Coraddu, M.; Kaniadakis, G.; Lavagno, A.; Lissia, M.; Mezzorani, G.; Quarati, P. Thermal distributions in stellar plasmas, nuclear reactions and solar neutrinos. Braz. J. Phys. 1999, 29, 153–168. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On a generalized entropy measure leading to the pathway model with a preliminary application to solar neutrino data. Entropy 2013, 15, 4011–4025. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Analysis of solar neutrino data from Super-Kamiokande I and II. Entropy 2014, 16, 1414–1425. [Google Scholar] [CrossRef]
- Biro, T.S.; Purcsel, G.; Urmossy, K. Non-extensive approach to quark matter. Statistical Power-Law Tails in High Energy Phenomena. Eur. Phys. J. A 2009, 40, 325–340. [Google Scholar] [CrossRef]
- Cleymans, J.; Hamar, G.; Levai, P.; Wheaton, S. Near-thermal equilibrium with Tsallis distributions in heavy ion collisions. J. Phys. G 2009, 36, 064018. [Google Scholar]
- Cleymans, J. Recent developments around chemical equilibrium. J. Phys. G 2010, 37, 094015. [Google Scholar] [CrossRef]
- Biro, T.S. Is there a temperature?—Conceptual challenges at high energy, acceleration and complexity. In Fundamental Theories in Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 171. [Google Scholar]
- Biro, T.S.; Van, P. Zeroth law compatibility of non-additive thermodynamics. Phys. Rev. E 2011, 83, 061147. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.Y.; Wilk, G. Tsallis fits to pt spectra for pp collisions at LHC. Acta Phys. Pol. B 2012, 43, 2047–2054. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra and relativistic hard scattering in pp collisions at LHC. Phys. Rev. D 2013, 87, 114007. [Google Scholar] [CrossRef]
- Marques, L.; Andrade, E., II; Deppman, A. Nonextensivity of hadronic systems. Phys. Rev. D 2013, 87, 114022. [Google Scholar] [CrossRef]
- Biro, T.S.; Van, P.; Barnafoldi, G.G.; Urmossy, K. Statistical power law due to reservoir fluctuations and the universal thermostat independence principle. Entropy 2014, 16, 6497–6514. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Tsallis distribution with complex nonextensivity parameter q. Phys. A 2014, 413, 53–58. [Google Scholar] [CrossRef]
- Deppman, A. Properties of hadronic systems according to the nonextensive self-consistent thermodynamics. J. Phys. G Nucl. Part. Phys. 2014, 41, 055108. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Quasi-power laws in multiparticle production processes. Chaos Solitons Fractals 2015, 81, 487–496. [Google Scholar] [CrossRef]
- Rybczynski, M.; Wilk, G.; Wlodarczyk, Z. System size dependence of the log-periodic oscillations of transverse momentum spectra. EPJ Web Conf. 2015, 90, 01002. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Tsallis distribution decorated with log-periodic oscillation. Entropy 2015, 17, 384–400. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. Possible implication of a single nonextensive pT distribution for hadron production in high-energy pp collisions. EPJ Web Conf. 2015, 90, 04002. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. From QCD-based hard-scattering to nonextensive statistical mechanical descriptions of transverse momentum spectra in high-energy pp and p collisions. Phys. Rev. D 2015, 91, 114027. [Google Scholar] [CrossRef]
- Marques, L.; Cleymans, J.; Deppman, A. Description of high-energy pp collisions using Tsallis thermodynamics: Transverse momentum and rapidity distributions. Phys. Rev. D 2015, 91, 054025. [Google Scholar] [CrossRef]
- Deppman, A.; Marques, L.; Cleymans, J. Longitudinal properties of high energy collisions. J. Phys. Conf. Ser. 2015, 623, 012009. [Google Scholar] [CrossRef]
- Deppman, A. Thermodynamics with fractal structure, Tsallis statistics, and hadrons. Phys. Rev. D 2016, 93, 054001. [Google Scholar] [CrossRef]
- Ferri, G.L.; Martinez, S.; Plastino, A. Equivalence of the four versions of Tsallis’ statistics. JSTAT J. Stat. Mech. Theory Exp. 2005, 4, PO4009. [Google Scholar] [CrossRef]
- Thistleton, W.; Marsh, J.A.; Nelson, K.; Tsallis, C. Generalized Box-Muller method for generating q-Gaussian random deviates. IEEE Trans. Inf. Theory 2007, 53, 4805–4810. [Google Scholar] [CrossRef]
- Abe, S. Generalized molecular chaos hypothesis and H-theorem: Problem of constraints and amendment of nonextensive statistical mechanics. Phys. Rev. E 2009, 79, 041116. [Google Scholar] [CrossRef] [PubMed]
- Caride, A.O.; Tsallis, C.; Zanette, S.I. Criticality of the anisotropic quantum Heisenberg-model on a self-dual hierarchical lattice. Phys. Rev. Lett. 1983, 51, 145–147. [Google Scholar] [CrossRef]
- Tirnakli, U.; Tsallis, C.; Lyra, M.L. Circular-like maps: Sensitivity to the initial conditions, multifractality and nonextensivity. Eur. Phys. J. B 1999, 11, 309–314. [Google Scholar] [CrossRef]
- Tsallis, C.; Lenzi, E.K. Anomalous diffusion: Nonlinear fractional Fokker-Planck equation. Chem. Phys. 2002, 84, 341–347. [Google Scholar] [CrossRef]
- Tsallis, C. Non-additive entropy: The concept and its use. Eur. Phys. J. A 2009, 40, 257–266. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsallis, C. Approach of Complexity in Nature: Entropic Nonuniqueness. Axioms 2016, 5, 20. https://doi.org/10.3390/axioms5030020
Tsallis C. Approach of Complexity in Nature: Entropic Nonuniqueness. Axioms. 2016; 5(3):20. https://doi.org/10.3390/axioms5030020
Chicago/Turabian StyleTsallis, Constantino. 2016. "Approach of Complexity in Nature: Entropic Nonuniqueness" Axioms 5, no. 3: 20. https://doi.org/10.3390/axioms5030020
APA StyleTsallis, C. (2016). Approach of Complexity in Nature: Entropic Nonuniqueness. Axioms, 5(3), 20. https://doi.org/10.3390/axioms5030020




