An Overview of the Fuzzy Axiomatic Systems and Characterizations Proposed at Ghent University

Abstract

During the past 40 years of fuzzy research at the Fuzziness and Uncertainty Modeling research unit of Ghent University several axiomatic systems and characterizations have been introduced. In this paper we highlight some of them. The main purpose of this paper consists of an invitation to continue research on these first attempts to axiomatize important concepts and systems in fuzzy set theory. Currently, these attempts are spread over many journals; with this paper they are now collected in a neat overview. In the literature, many axiom systems have been introduced, but as far as we know the axiomatic system of Huntington concerning a Boolean algebra has been the only one where the axioms have been proven independent. Another line of further research could be with respect to the simplification of these systems, in discovering redundancies between the axioms.

1. Overview

We start with the characterization of a Chang fuzzy topology by means of a preassigned operation such as an interior operator. In Section 3 we dwell upon the separation axioms in Chang fuzzy topological spaces and refer to dependencies between the different fuzzy separation axioms. In Section 4 a fuzzy extension of the well-known Armstrong axioms in a fuzzy relational database is given. A lot of work has been done on the characterization of a fuzzy preference structure. Some results are repeated in Section 5. In the next section a characterization is given of lattices that are needed to establish the equivalence between Goguen’s L-fuzzy sets and Gentilhomme’s L-flou sets, leading to the introduction of the kite-tail lattices. We also dwell upon the modifications of the condition that sometimes appear in the literature. Section 7 summarizes the work on the axiomatization of the ordering of fuzzy quantities, in particular fuzzy numbers. In the next section some axioms are introduced for a defuzzification technique in order to transform a fuzzy set into a single element of the underlying universe. The concept of a fuzzy implication is important from a theoretical as well as a practical point of view. In Section 9 we describe the extension of Smets-Magrez axioms for a fuzzy implication. Finally Section 10 treats the axiomatization of a triangle algebra.

2. On the Characterization of a Chang Fuzzy Topology by Means of Preassigned Operations

Perhaps general topology has been the first mathematical structure that has been fuzzified. Already in 1968, three years after the publication of Zadeh’s seminal paper “Fuzzy Sets” [1], Chang’s paper “Fuzzy Topological Spaces” [2] appeared in JMAA. A fuzzy topology on a set X was defined as a class T of fuzzy sets satisfying the straightforward fuzzifications of the classical axioms for a fuzzy topology:

• (O.1) $\varnothing \in T$ and $X\in T$
• (O.2) $(O_1\in T\mathrm{and}{O}_2\in T)\Rightarrow O_1\cap O_2\in T$
• (O.3) $(\forall i\in I)(O_i\in T)\Rightarrow {\bigcup }_{i\in I}{O}_i\in T$

where fuzzy intersection and arbitrary fuzzy union were modeled by means of the minimum and supremum in the unit interval $[0,1]$. The elements of T were called open fuzzy sets. In [3] the characterization of a fuzzy topology by means of preassigned operations has been studied. As an example, we repeat the characterization by means of the interior operator. Let $(X,T)$ be a fuzzy topological space and A a fuzzy set on X. The interior of A in $(X,T)$ is defined as the greatest open fuzzy set contained in A, i.e., $\mathrm{Int}A=\bigcup \left\{O\right|O\in T\mathrm{and}O\subseteq A\}$. In [4] it was proven that the interior operator Int satisfies the following properties:

• (I.1) $\mathrm{Int}X=X$
• (I.2) $\mathrm{Int}A\subseteq A$
• (I.3) $\mathrm{Int}(\mathrm{Int}A)=\mathrm{Int}A$
• (I.4) $\mathrm{Int}(A\cap B)=\mathrm{Int}A\cap \mathrm{Int}B$

and hence Int is a kernel operator [5] on the class $\mathcal{F}(X)$ of all fuzzy sets on X.

Conversely let X be a non-empty set and i a $\mathcal{F}(X)\to \mathcal{F}(X)$ mapping satisfying the following axioms:

• (i.1) $i(X)=X$
• (i.2) $i(A)\subseteq A$
• (i.3) $i(i(A))=i(A)$
• (i.4) $i(A\cap B)=i(A)\cap i(B)$.

Then the class $T=\left\{O\right|O\in \mathcal{F}(X)\mathrm{and}i(O)=O\}$ is a fuzzy topology on X such that $\mathrm{Int}A=i(A)$ for every $A\in \mathcal{F}(X)$. See [2] for a proof.

In [2] similar characterizations have been given in terms of closed fuzzy sets and the Kuratowski closure operator. The characterization in terms of neighborhoods is much more complicated (for example a straightforward fuzzification of the neighborhood characterization of a classical topology does not lead to a characterization as in the crisp case) and has been treated by many authors, leading to the introduction of different definitions of a fuzzy neighbourhood and dito properties. Our research group has made a complete unifying study of this research. For more details we refer to [6,7,8,9].

3. On the Separation Axioms in Chang Fuzzy Topological Spaces

Separation axioms of fuzzy topological spaces have been widely studied. In [10] all different separation axioms have been discussed in detail. In [4] a characterization of normality in fuzzy topology has been given as well as a full study of the normality of a fuzzy Sierpinski space [11]. During an attempt to fuzzify upper semi-continuity of multivalued mappings [12] some missing links were detected in the class of separated, regular and normal fuzzy topological spaces. In the classical binary case upper semi-continuity is related to the closedness of a mapping. Most of the links between upper semi-continuity and closed multivalued mappings in the crisp case are with respect to separated topological spaces. It was observed that in the fuzzy case separated fuzzy topological spaces are not sufficient to keep these links. To repair these shortcomings the separation axioms were further studied in [13]. More concretely a Hasse diagram was constructed establishing the relationship between different separation concepts in fuzzy topological spaces. This diagram is shown in Figure 1. Three more equivalences hold as well:

• regular ⇔ locally closed,
• compact ⇔ every closed crisp set is compact,
• quasi-separated ⇔ every crisp singleton is closed.

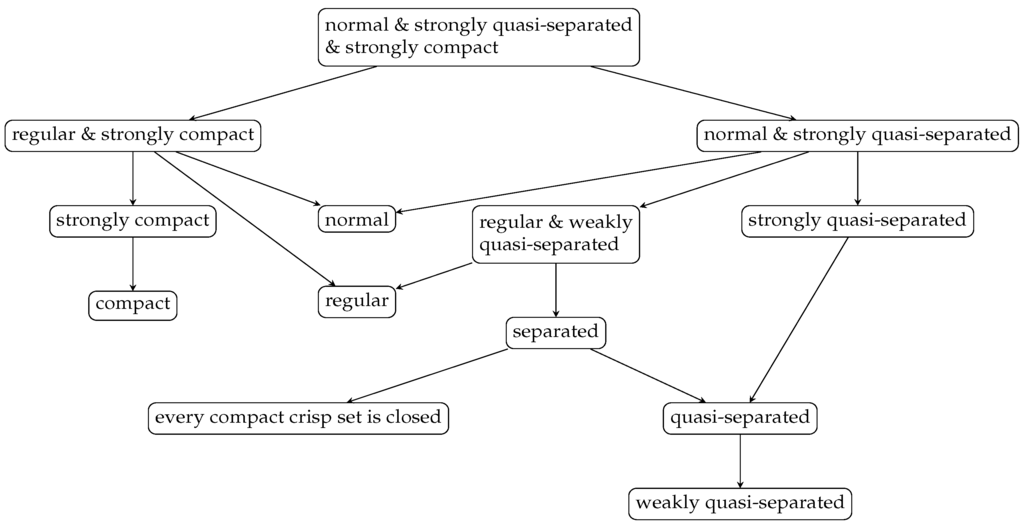
Figure 1. Relationships between the separation axioms in fuzzy topological spaces.

4. Axiomatics in Fuzzy Relational Databases

In a series of papers [14,15,16,17,18] our team focused on the axiomatization of fuzzy functional dependencies in a fuzzy relational data model, which is considered as a fundamental issue towards building a theory of fuzzy relational database design. Fuzzy functional dependencies result from reflections about the real world, they express relationships among the attributes of the objects in a database.

Let U be a set of attributes, R a relation, I a fuzzy implicator such as Kleene-Dienes or Łukasiewicz and X, Y, Z subsets of U. Then X functionally determines Y to the degree α ($\alpha \in [0,1]$) (or Y is functionally dependent on X to a degree α), denoted by $X\underset{\alpha }{\to }Y$ if and only if $\min I(c(t(X),t^{\prime }(X)),c(t(Y),t^{\prime }(Y)))\ge \alpha$, where c is a closeness relation (i.e., c is reflexive and symmetric) and $t(X)$, $t^{\prime }(X)$, $t(Y)$ and $t^{\prime }(Y)$ are the values of tuples t and $t^{\prime }$ corresponding to the attribute sets X and Y. The fuzzy implicator I must possess some properties if the fuzzy functional dependency is restricted to the inference rules known as the fuzzy extension of Armstrong’s axioms:

(A1)

if $Y\subseteq X$, then $X\underset{\alpha }{\to }Y$ for all α

(A2)

if $X\underset{\alpha }{\to }Y$, then $XZ\underset{\alpha }{\to }YZ$

(A3)

if $X\underset{\alpha }{\to }Y$ and $Y\underset{\beta }{\to }Z$, then $X\underset{min(\alpha ,\beta )}{\to }Z$

(A4)

if $X\underset{\alpha }{\to }Y$, then $X\underset{\beta }{\to }Y$ for all $\beta \le \alpha$.

For more details and consequences w.r.t. soundness and completeness, we refer to the references mentioned above.

5. On the Characterization of a Fuzzy Preference Structure

Classical preference structures are very important for the modeling of decision making problems. A classical preference structure consists of three binary relations on a set of alternatives A: a strict preference relation P, an indifference relation I and an incomparability relation J that satisfy the following axioms:

(P1)

I is reflexive, J is irreflexive

(P2)

P is asymmetrical: $P\cap P^t=\varnothing$

(P3)

I and J are symmetrical: $I=I^t$, $J=J^t$

(P4)

$P\cap I=\varnothing$, $P\cap J=\varnothing$, $I\cap J=\varnothing$

(P5)

$P\cup I\cup J$ is complete: $(P\cup I\cup J)\cup {(P\cup I\cup J)}^t=A^2$

where $P^t$ denotes the converse or transpose of the relation P, i.e., $(x,y)\in P^t\iff (y,x)\in P$ [19]. The relation $R=P\cup I$ is called the large preference relation. Roubens and Vincke [19] have proved that a classical preference structure $\Pi =(P,I,J)$ on A can be characterized by means of the large preference relation $R=P\cup I$ in the following way:

(1)

$P=R\cap R^d$

(2)

$I=R\cap R^t$

(3)

$J=R^c\cap R^d$

where $R^c$ is the complement of R (i.e., $(x,y)\in R^c\iff (x,y)\notin R$) and $R^d$ is the dual of R (i.e., $(x,y)\in R^d\iff (y,x)\notin R$). Conversely a triplet $(P,I,J)$ defined from a binary relation R by (1)–(3) is a preference structure on A.

Classical preference structures do not allow to express degrees of strict preference and indifference. Hence, that is why fuzzy set theory has been introduced very soon. In various contributions our research team has tackled the fuzzification of a preference structure and its characterization. Let us first introduce some preliminary concepts. A binary fuzzy relation on a set of alternatives A is an $A\times A\to [0,1]$ mapping, i.e., a fuzzy set on $A^2$. The set-theoretic operations (union, intersection, complementation) on fuzzy sets can be applied to fuzzy relations. Let $R_1$ and $R_2$ be two fuzzy relations on A. Then we define for $(x,y)\in A^2$:

$$\begin{array}{cc}\hfill (R_1\cup R_2)(x,y)& =max(R_1(x,y),R_2(x,y))\hfill \\ \hfill (R_1{\cup }_S{R}_2)(x,y)& =S(R_1(x,y),R_2(x,y))\hfill \\ \hfill (R_1\cap R_2)(x,y)& =min(R_1(x,y),R_2(x,y))\hfill \\ \hfill (R_1{\cap }_T{R}_2)(x,y)& =T(R_1(x,y),R_2(x,y))\hfill \\ \hfill (co{R}_1)(x,y)& =1-R_1(x,y)\hfill \\ \hfill ({co}_N{R}_1)(x,y)& =N(R_1(x,y))\hfill \end{array}$$

where S is a triangular conorm, T is a triangular norm and N a negator (i.e., a strictly decreasing involution on $[0,1]$).

The N-dual of $R_1$ is defined as:

$${(R_1)}_N^d(x,y)=N(R_1(y,x))$$

and the transpose or converse of $R_1$ is given by:

$$R_1^t(x,y)=R_1(y,x).$$

A crucial role in the definition of a fuzzy preference structure is played by the Łukasiewicz triangular norm to model fuzzy intersection:

$$W(x,y)=max(x+y-1,0),\forall (x,y)\in {[0,1]}^2.$$

For an extensive motivation for this choice we refer to [20] and [21]. To end the preliminaries, we introduce the Φ-transform of a mapping, where Φ denotes an order-preserving permutation of $[0,1]$. For example, the Φ-transform of the Łukasiewicz intersection operator W is:

$$\begin{array}{cc}\hfill W_{\Phi }(x,y)& ={\Phi }^{-1}(W(\Phi (x),\Phi (y)))\hfill \\ & ={\Phi }^{-1}(max(\Phi (x)+\Phi (y)-1,0))\hfill \end{array}$$

The $N_{\Phi }$-triangular conorm corresponding to the Φ-transform $W_{\Phi }$ of W is given by:

$$W_{\Phi }^{N_{\Phi }}(x,y)={\Phi }^{-1}(min(\Phi (x)+\Phi (y),1)).$$

Now we are ready to introduce the axiomatic definition of a fuzzy preference structure. A Φ-fuzzy preference structure – with Φ a $[0,1]$-automorphism – on a set A of alternatives is a triplet $(P,I,J)$ of binary fuzzy relations on A satisfying the following axioms:

(FP1)

I is reflexive, J is irreflexive

(FP2)

P is $W_{\Phi }$-asymmetrical: $P{\cap }_{W_{\Phi }}{P}^t=\varnothing$

(FP3)

I and J are symmetrical: $I=I^t$, $J=J^t$

(FP4)

$P{\cap }_{W_{\Phi }}I=\varnothing$, $P{\cap }_{W_{\Phi }}J=\varnothing$, $I{\cap }_{W_{\Phi }}J=\varnothing$

(FP5)

$({co}_{N_{\Phi }}P){\cap }_{W_{\Phi }}(P_{N_{\Phi }}^d){\cap }_{W_{\Phi }}({co}_{N_{\Phi }}I)=J$

In [22] it was proved that the condition (FP5) reduces to the classical completeness condition (P5) for crisp relations P, I and J. Similarly as in the crisp case it can be shown [22] that a Φ-fuzzy preference structure $(P,I,J)$ can be characterized by means of a fuzzy large preference relation R given by:

$$R=P{\cup }_{W_{\Phi }^{N_{\Phi }}}I$$

in the following way:

(1)

$P=R{\cap }_{W_{\Phi }}{R}_{N_{\Phi }}^d$

(2)

$I=R\cap R^t$

(3)

$J=({co}_{N_{\Phi }}R)\cap R_{N_{\Phi }}^d$

or explicitly for every $(x,y)\in A^2$:

(1)

$P(x,y)={\Phi }^{-1}(max(\Phi (R(x,y))-\Phi (R(y,x)),0))$

(2)

$I(x,y)=min(R(x,y),R(y,x))$

(3)

$J(x,y)={\Phi }^{-1}(min(1-\Phi (R(x,y)),1-\Phi (R(y,x))))$

Conversely a triplet $(P,I,J)$ defined from a binary fuzzy relation R on A by the above expressions is a Φ-fuzzy preference structure on A.

6. On the Equivalency between L-fuzzy Sets and L-flou Sets

Already in 1967, J. Goguen [23] extended Zadeh’s fuzzy set theory to L-fuzzy set theory, where L denotes a complete lattice. A fuzzy set takes its degrees of membership in the totally ordered evaluation set $[0,1]$. However, in some applications it may not be possible to compare every two degrees of membership. To model these situations Goguen introduced the concept of an L-fuzzy set, i.e., a mapping from a universal set into L.

In 1968, Y. Gentilhomme [24] introduced the concept of a flou set as an alternative to model uncertainty. A flou set in a universe X is an ordered pair $(E,F)$ of crisp subsets of X satisfying $E\subseteq F$, where E is called the certain region, F the region of maximal extension and $F\backslash E$ the flou region.

In 1975 Negoita and Ralescu [25] extended this notion to L-flou sets where L is a complete lattice. In order to compare L-fuzzy sets with L-flou sets, Negoita and Ralescu introduced a supplementary condition for the underlying lattice $(L,\le )$:

$$(\mathcal{L})(\forall A\subseteq L)(\forall a\in L)(a<supA\Rightarrow (\exists b\in A)(a\le b))$$

They proved a famous representation theorem stating that for $(L,\le )$ a complete lattice satisfying condition $(\mathcal{L})$ the complete lattice of Goguen’s L-fuzzy sets being dual isomorphic to “Gentilhomme’s” L-flou sets.

Now we want to dwell upon condition $(\mathcal{L})$ since in the literature one often finds some modification of condition $(\mathcal{L})$ in which other combinations of the involved inequalities appear:

$$\begin{array}{cc}\hfill ({\mathcal{L}}_1)& (\forall A\subseteq L)(\forall a\in L)(a\le supA\Rightarrow (\exists b\in A)(a<b))\hfill \\ \hfill ({\mathcal{L}}_2)& (\forall A\subseteq L)(\forall a\in L)(a\le supA\Rightarrow (\exists b\in A)(a\le b))\hfill \\ \hfill ({\mathcal{L}}_3)& (\forall A\subseteq L)(\forall a\in L)(a<supA\Rightarrow (\exists b\in A)(a<b))\hfill \end{array}$$

We analyzed the connections between these four conditions:

(1)

There is no lattice satisfying $({\mathcal{L}}_1)$.

(2)

If $(L,\le )$ satisfies $({\mathcal{L}}_2)$, then $(L,\le )$ is a chain.

(3)

$(L,\le )$ satisfies $({\mathcal{L}}_3)$ if and only if $(L,\le )$ is a chain.

In particular, for finite lattices satisfying condition $(\mathcal{L})$ the following characterization has been established: $(L,\le )$ satisfies condition $(\mathcal{L})$ if and only if $(L,\le )$ is a kite-tail lattice, where a kite-tail lattice is defined as a finite vertical sum of the lattice 2 and the diamond $M_2$ defined as

$$\begin{array}{cc}& 2=(\{0,1\},\le )\text{with}\le =\{(0,0),(1,1),(0,1)\}\hfill \\ & M_2=(\{0,1,\alpha ,\beta \},\le )\text{with}\hfill \\ & \le =\{(0,0),(1,1),(\alpha ,\alpha ),(\beta ,\beta ),(0,1),(0,\alpha ),(0,\beta ),(\alpha ,1),(\beta ,1)\}\hfill \end{array}$$

If the kite-tail lattice $(L,\le )$ is not finite, then it satisfies condition $(\mathcal{L})$, but the converse is not true. For more details we refer to [26].

7. Axioms for the Ordering of Fuzzy Quantities

The problem of ordering fuzzy quantities (i.e., fuzzy sets on the real line) has been tackled by many researchers. Till now none of the ordering methods has been widely accepted. In [27] a set of axioms for an ordering procedure has been introduced.

Let M be an ordering method, $\mathcal{S}$ the set of fuzzy quantities for which M can be applied and $\mathcal{A}$ a finite subset of $\mathcal{S}$. The statement “two elements A and B in $\mathcal{A}$ satisfy that A has a higher ranking than B when the ordering method M is applied to the fuzzy quantities in $\mathcal{A}$” will be denoted as “$A\succ B$ by M on $\mathcal{A}$”. Similarly, “$A\sim B$ by M in $\mathcal{A}$” means that A has the same ranking as B and $A\succsim B$ is equivalent to $A\succ B$ or $A\sim B$. The following facts were assumed:

(i)

The fuzzy quantities satisfy the conditions for the application of the ranking method considered.

(ii)

When a ranking method is applied on a set $\mathcal{S}$ of fuzzy quantities, exactly one of the following relations hold: $A\succ B$, $B\succ A$, $A\sim B$.

In [27] the following axiom system for a ranking method M on a set $\mathcal{S}$ of fuzzy quantities has been proposed:

(A1)

For an arbitrary finite subset $\mathcal{A}$ of $\mathcal{S}$ and $A\in \mathcal{A}$, $A\succsim A$ by M on $\mathcal{A}$, i.e., the relation ≿ is reflexive.

(A2)

For an arbitrary finite subset $\mathcal{A}$ of $\mathcal{S}$ and $(A,B)\in {\mathcal{A}}^2$, $A\succsim B$ and $B\succsim A$ by M on $\mathcal{A}$ implies $A\sim B$ by M on $\mathcal{A}$, i.e., ≿ is anti-symmetric.

(A3)

For an arbitrary finite subset $\mathcal{A}$ of $\mathcal{S}$ and $(A,B,C)\in {\mathcal{A}}^3$, $A\succsim B$ and $B\succsim C$ by M on $\mathcal{A}$ implies $A\succsim C$ by M on $\mathcal{A}$, i.e., ≿ is transitive.

(A4)

For an arbitrary finite subset $\mathcal{A}$ of $\mathcal{S}$ and $(A,B)\in {\mathcal{A}}^2$, $infsuppA>supsuppB$ should imply $A\succsim B$ by M on $\mathcal{A}$. This means that if two fuzzy quantities have separate (non-intersecting) supports, then the fuzzy quantity with the support on the right is at least as good as the one with the support on the left.

(A5)

Let $\mathcal{S}$ and ${\mathcal{S}}^{\prime }$ be two arbitrary finite sets of fuzzy quantities for which the ranking method M can be applied and $(A,B)\in {(\mathcal{S}\cap {\mathcal{S}}^{\prime })}^2$. Then $A\succ B$ by M on ${\mathcal{S}}^{\prime }$ if and only if $A\succ B$ by M on $\mathcal{S}$. This means that the ranking order of A and B is independent of any other fuzzy quantity.

(A6)

Let A, B, $A+C$ and $B+C$ be elements of $\mathcal{S}$. If $A\succsim B$ by M on $\{A,B\}$, then $A+C\succsim B+C$ by M on $\{A+C,B+C\}$. This means that the fuzzy addition of fuzzy quantities is compatible with the ordering ≿.

(A7)

Let A, B, $AC$ and $BC$ be elements of $\mathcal{S}$ and $C\ge 0$ (i.e., $suppC\subseteq [0,+\infty ]$). If $A\succsim B$ by M on $\{A,B\}$, then $AC\succsim BC$ by M on $\{AC,BC\}$. This means that the fuzzy multiplication with non-negative fuzzy quantities is compatible with the ordering ≿.

For an extensive study of more than 35 ranking methods for fuzzy quantities with respect to the axioms mentioned above, we refer to [27], [28] and [29]. The concluding table from [27] is presented in Table 1; ‘Y’ denotes the fulfillment of an axiom, ‘N’ is used when the method does not satisfy the given axiom.

Table 1. Fulfilment of axioms for ordening methods discussed in [27].

Ordering Method	(A1)	(A2)	(A3)	(A4)	(A5)	(A6)	(A7)
$Y_1$	Y	Y	Y	Y	Y	N	N
$Y_2$	Y	Y	Y	Y	Y	Y	N
$Y_3$	Y	Y	Y	N	Y	N	N
$Y_4$	Y	Y	Y	Y	Y	N	N
C	Y	Y	Y	N	Y	N	N
$FR$	Y	Y	Y	Y	Y	Y	N
$CL$	Y	Y	Y	Y	Y	Y	N
$L{W}^{\lambda }$	Y	Y	Y	Y	Y	Y	N
$C{M}_1^{\lambda }$	Y	Y	Y	Y	Y	Y	N
$C{M}_2^{\lambda }$	Y	Y	Y	Y	Y	Y	N
$A{D}^{\alpha }$	Y	Y	Y	Y	Y	Y	Y
K	Y	Y	Y	N	N	N	N
W	Y	Y	Y	Y	N	N	N
$J^k$	Y	Y	Y	Y	N	N	N
$C{H}^k$	Y	Y	Y	Y	N	N	N
$K{P}^k$	Y	Y	Y	Y	N	N	N

8. Axioms for Defuzzification

In fuzzy systems such as knowledge-based systems and control systems the last step is defuzzification, i.e., a technique to transform the obtained fuzzy set, in particular fuzzy number, into a single value or member. There exist many defuzzification techniques such as: random choice of maxima, first of maxima, last of maxima, middle of maxima, center of gravity, mean of maxima, basic defuzzification distribution, generalized level set defuzzification, induced center of gravity, semi-linear defuzzification, fuzzy mean, weighted fuzzy mean, quality method, extended quality method, center of area, extended center of area, constraint decision defuzzification and fuzzy clustering defuzzification. For a compact introduction to these techniques we refer to [30]. In order to get some insight into these very diverse techniques, Van Leekwijck and Kerre [30] proposed a set of criteria a defuzzification technique should preferably satisfy, of course depending also on the specific application. For example a continuity condition is very important for fuzzy controllers but less important for decision support systems. The criteria were divided into several groups, according the mathematical structure that is needed in the underlying universe: arbitrary universes, ordered universes and universes endured with an algebraic structure such as the real line $\mathbb{R}$ were considered.

(i)

Defuzzification axioms in arbitrary universes.

Since there is no structure in the underlying universe of the fuzzy set to be defuzzified, the criteria depend only on the operations on the unit interval $[0,1]$.

(D1)

Core selection axiom:

$$(\forall A\in \mathcal{F}(X))(D(A)\in coreA)$$

where $\mathcal{F}(X)$ denotes the class of all fuzzy sets on the universe X, $D(A)$ is the defuzzification value of A in X and $coreA$ is defined by:

$$coreA=\{x\mid x\in X\text{and}(\forall y\in X)(A(y)\le A(x))\}.$$

Axiom (D1) expresses that the defuzzification operator chooses an element with the highest degree of membership.

(D2)

Scale invariance axiom

According to Norwich and Turksen [31] a necessary condition for any application on one or more membership functions can only be meaningful if it is scale invariant. Since the membership degrees can be interpreted on different scales, the scale invariance axiom depends on the scale chosen. For example if the only information conveyed in the fuzzy set being an ordering of the elements of X based on the degree of membership $A(x)$, the defuzzification operator should be invariant under any order preserving mapping f, i.e., $D(f(A))=D(A)$, where

$$f(A):X\to [0,1]:x\mapsto f(A(x)).$$

For other scales than an ordinal one, such as interval scale, ratio scale, relative scale and absolute scale, we refer to [30].

(ii)

Defuzzification in universes with an ordinal scale

Two more axioms can be considered.

(D3)

Monotonicity axiom

Let A and B be two fuzzy sets on X satisfying

• $B(D(A))=A(D(A))$,
• $(\forall x<D(A))(B(x)<A(x))$,
• $(\forall x>D(A))(B(x)\ge A(x))$,

then $D(B)\ge D(A)$, which means that the defuzzification value can only move to that side where the elements are getting better.

(D4)

Triangular conorm axiom

Let A and B be two fuzzy sets on X for which $D(A)\le D(B)$, then

$$D(A)\le D(A{\cup }_{S}B)\le D(B),$$

which means that the defuzzification value of the union (modelled by a triangular conorm S) of two fuzzy sets should lie between the defuzzification values of both.

(iii)

Defuzzification of fuzzy quantities

(D5)

Domain translation axiom

This criterion states that the relative position of the defuzzification value should remain after a translation of the fuzzy set, i.e., $D(B)=D(A)+b$, with $B(x)=A(x-b)$, $\forall x\in \mathbb{R}$ and $b\in \mathbb{R}$.

(D6)

Domain rescaling axiom

This criterion states that the defuzzification value should be accordingly adopted after a rescaling of the fuzzy set, i.e., $D(B)=\alpha D(A)$, with $B(x)=A\left(\frac{x}{\alpha }\right)$, $\forall x\in \mathbb{R}$ and $\alpha \in \mathbb{R}\backslash \left\{0\right\}$.

(D7)

Continuity axiom

A small change in any of the degrees of membership should not result in a big change in the defuzzification value, i.e.,

$$(\forall a\in \mathbb{R})(\forall ϵ>0)(\exists {\Delta }^{*}>0)(\forall \Delta \in \mathbb{R})(|\Delta |<{\Delta }^{*}\Rightarrow |D({\Delta }_{a}A)-D(A)|<ϵ),$$

with

$${\Delta }_{a}A(x)=\left\{\begin{array}{cc}A(x)+\Delta \hfill & \text{if}x=a\hfill \\ A(x)\hfill & \text{else}\hfill \end{array}\right.$$

An example of a defuzzification method is the first of maxima (FOM). It is defined on universes with an ordinal scale and requires that the core of a fuzzy set has a smallest element. It is defined by $FOM(A)=mincore(A)$, for $A\in \mathcal{F}(X)$. The least of maxima (LOM) is another defuzzification method defined on universes with an ordinal scale. It requires the core of fuzzy sets to have a greatest element and it is defined by $LOM(A)=maxcore(A)$, for $A\in \mathcal{F}(X)$. Both methods fulfil the axioms (D1), (D2), (D3), (D4) for $S=max$ and (D5).

Other examples of defuzzification methods are the middle of maxima (MOM) satisfying (D1), (D2), (D3) and (D5). In addition, both the method of center of gravity (COG) and the method of center of area (COA) satisfy axioms (D3), (D5), (D6) and (D7). For details and an extensive classification of the most widely used defuzzification methods, we refer to [30].

9. Axioms for a Fuzzy Implication

Fuzzy implications play a key role in many domains of fuzzy logic, especially in approximate reasoning for extending inference mechanisms such as modus ponens, modus tollens and method of cases. The most simple definition of a fuzzy implication is a $[0,1]\times [0,1]\to [0,1]$ mapping I that reduces to the binary implication in the corners of the unit scale, i.e., $I(0,0)=I(1,1)=I(0,1)=1$ and $I(1,0)=0$.

In [32] Smets and Magrez introduced a set of axioms a fuzzy implication should satisfy. Many authors have continued this work, in particular our research group has made many contributions to the classification, axiomatization and study of fuzzy implications. In [33] the following broadly accepted definition for a fuzzy implication was used: a fuzzy implication I is a $[0,1]\times [0,1]\to [0,1]$ mapping I satisfying the following basic axioms:

(FI1)

First place antitonicity

$$(\forall (x_1,x_2,y)\in {[0,1]}^3)(x_1<x_2\Rightarrow I(x_1,y)\ge I(x_2,y))$$

(FI2)

Second place isotonicity

$$(\forall (x,y_1,y_2)\in {[0,1]}^3)(y_1<y_2\Rightarrow I(x,y_1)\le I(x,y_2))$$

(FI3)

Dominance of falsity of the antecedent

$$(\forall x\in [0,1])(I(0,x)=1)$$

(FI4)

Dominance of truth of the consequent

$$(\forall x\in [0,1])(I(x,1)=1)$$

(FI5)

Boundary condition

$$I(1,0)=0$$

Many other potential axioms have been proposed in the fuzzy literature, in order to obtain a fuzzy implication that satisfies a given property:

(FI6)

Neutrality of truth

$$(\forall x\in [0,1])(I(1,x)=x)$$

(FI7)

Exchange principle

$$(\forall (x,y,z)\in {[0,1]}^3)(I(x,I(y,z))=I(y,I(x,z)))$$

(FI8)

Ordering principle

$$(\forall (x,y)\in {[0,1]}^2)(I(x,y)=1\iff x\le y)$$

(FI9)

Strong fuzzy negation principle

The mapping $N_I$ defined as

$$(\forall x\in [0,1])(N_I(x)=I(x,0))$$

is a strong fuzzy negation, i.e., a $[0,1]-[0,1]$ mapping that is decreasing, $N_I(0)=1$, $N_I(1)=0$ and involutive, $N_I(N_I(x))=x$, $\forall x\in [0,1]$.

(FI10)

Consequent boundary

$$(\forall (x,y)\in {[0,1]}^2)(I(x,y)\ge y)$$

(FI11)

Identity

$$(\forall x\in [0,1])(I(x,x)=1)$$

(FI12)

Contrapositivity principle

$$(\forall (x,y)\in {[0,1]}^2)(I(x,y)=I(N(y),N(x)))$$

where N is a strong fuzzy negation.

(FI13)

Continuity

I is a continuous mapping

For a complete overview of the interrelationships between these additional axioms we refer to [33] and [34]. Table 2 can be found in [33] and lists all dependencies between the eight additional axioms. For example: FI7 ∧ FI8 ⇒ FI6 means that for any fuzzy implication I satisfying the exchange and ordering principle, also neutrality of truth holds. And FI6∧FI7∧FI8∧FI9∧FI10∧FI11∧FI12 $\nRightarrow$ FI13 means that a specific fuzzy implication was found that satisfied FI6 – FI12, but that was not a continuous mapping.

Table 2. Summary of the interrelationships among the eight axioms.

FI7∧FI10∧FI11∧FI12 $\nRightarrow$ FI6

FI8∧FI9∧FI10∧FI11∧FI12∧FI13 $\nRightarrow$ FI6

FI7∧FI8 ⇒ FI6

FI7∧FI9 ⇒ FI6

FI7∧FI13 $\nRightarrow$ FI6

FI6∧FI8∧FI9∧FI10∧FI11∧FI12∧FI13 $\nRightarrow$ FI7

FI6∧FI7∧FI9∧FI10∧FI11∧FI12∧FI13 $\nRightarrow$ FI8

FI6∧FI7∧FI8∧FI10∧FI11 $\nRightarrow$ FI9

FI6∧FI12 ⇒ FI9

FI7∧FI8∧FI12 ⇒ FI9

FI7∧FI12∧FI13 ⇒ FI9

FI7∧FI10∧FI11∧FI12 $\nRightarrow$ FI9

FI7∧FI8∧FI13 ⇒ FI9

FI6∧FI7∧FI10∧FI11∧FI13 $\nRightarrow$ FI9

FI6∧FI8∧FI10∧FI11∧FI13 $\nRightarrow$ FI9

FI8∧FI10∧FI11∧FI12∧FI13 $\nRightarrow$ FI9

FI6 ⇒ FI10

FI7∧FI9 ⇒ FI10

FI7∧FI13 ⇒ FI10

FI7∧FI8 ⇒ FI10

FI7∧FI11∧FI12 ⇒ FI10

FI8∧FI9∧FI11∧FI12∧FI13 $\nRightarrow$ FI10

FI8 ⇒ FI11

FI6∧FI7∧FI9∧FI10∧FI12∧FI13 $\nRightarrow$ FI11

FI6∧FI7∧FI8∧FI10∧FI11 $\nRightarrow$ FI12

FI7∧FI9 ⇒ FI12

FI7∧FI8∧FI13 ⇒ FI12

FI6∧FI7∧FI10∧FI11∧FI13 $\nRightarrow$ FI12

FI6∧FI8∧FI9∧FI10∧FI11∧FI13 $\nRightarrow$ FI12

FI6∧FI7∧FI8∧FI9∧FI10∧FI11∧FI12 $\nRightarrow$ FI13

In [35] the Smets-Magrez axioms were extended to interval-valued and Atanassov’s intuitionistic fuzzy set theory.

10. Triangle Algebras: A Characterization of Interval-valued Residuated Lattices

Residuated lattices (more precisely, bounded integral commutative residuated lattices) are bounded lattices with two extra operators * (which is commutative, associative and has the largest element 1 as neutral element) and ⇒, which satisfy the residuation property:

$$x*y\le z\mathrm{iff}x\le y\Rightarrow z.$$

Residuated lattices are important algebraic structures because, amongst others, BL-algebras, MV-algebras, Heyting algebras and Boolean algebras can all be seen as special cases of it. Each of them naturally forms the semantics of the corresponding logic. Considering a lattice $(L,\le )$, the intervals (i.e. elements of the form $[a,b]$, with $a,b\in L$ and $a\le b$) form a lattice too if the product order is used. In such an interval-valued lattice the exact intervals (i.e., elements of the form $[a,a]$) form a copy of the original lattice, called the diagonal. As a means to handle interval-valued lattices that are also residuated lattices, triangle algebras were introduced in [36]. A triangle algebra is an algebra $(A,\sqcap ,\bigsqcup ,*,\Rightarrow ,\nu ,\mu ,0,u,1)$ of type $(2,2,2,2,1,1,0,0,0)$ such that $(A,\sqcap ,\bigsqcup ,*,\Rightarrow ,0,1)$ is a residuated lattice, and satisfying for all x and y in A,

$$\begin{array}{cccc}(T.1)\hfill & \nu x\le x,\hfill & (T.1^{\prime })\hfill & x\le \mu x,\hfill \\ (T.2)\hfill & \nu x\le \nu \nu x,\hfill & (T.2^{\prime })\hfill & \mu \mu x\le \mu x,\hfill \\ (T.3)\hfill & \nu (x\sqcap y)=\nu x\sqcap \nu y,\hfill & (T.3^{\prime })\hfill & \mu (x\sqcap y)=\mu x\sqcap \mu y,\hfill \\ (T.4)\hfill & \nu (x\bigsqcup y)=\nu x\bigsqcup \nu y,\hfill & (T.4^{\prime })\hfill & \mu (x\bigsqcup y)=\mu x\bigsqcup \mu y,\hfill \\ (T.5)\hfill & \nu u=0,\hfill & (T.5^{\prime })\hfill & \mu u=1,\hfill \\ (T.6)\hfill & \nu \mu x=\mu x,\hfill & (T.6^{\prime })\hfill & \mu \nu x=\nu x,\hfill \\ (T.7†)\hfill & \nu x*\nu y\le \nu (\nu x*\nu y),\hfill & & \\ (T.9)\hfill & \nu x\Rightarrow \nu y\le \nu (\nu x\Rightarrow \nu y),\hfill & & \\ (T.10)\hfill & x=\nu x\bigsqcup (\mu x\sqcap u),\hfill & (T.{10}^{\prime })\hfill & x=\mu x\sqcap (\nu x\bigsqcup u).\hfill \end{array}$$

Some of these axioms can still be weakened or even left out [37]. The unary operators ν and μ correspond to the mappings that map an interval $[a,b]$ on $[a,a]$ and on $[b,b]$ respectively. The constant u corresponds to the interval $[0,1]$. Using these structures the authors could prove that each interval-valued residuated lattice in which the diagonal is closed under all operators is fully determined by the subalgebra on the diagonal and the value $[0,1]*[0,1]$. More specifically, in triangle algebras $x\Rightarrow y$ and $x*y$ are determined by:

• $\nu (x\Rightarrow y)=(\nu x\Rightarrow \nu y)\sqcap (\mu x\Rightarrow \mu y)$,
• $\mu (x\Rightarrow y)=(\mu x\Rightarrow (\mu (u*u)\Rightarrow \mu y))\sqcap (\nu x\Rightarrow \mu y)$,
• $\nu (x*y)=\nu x*\nu y$,
• $\mu (x*y)=(\nu x*\mu y)\bigsqcup (\mu x*\nu y)\bigsqcup (\mu x*\mu y*\mu (u*u))$,

where one has to keep in mind that elements of the forms $\nu z$ and $\mu z$ are always on the diagonal.

Using this characterization, it was examined under which conditions a triangle algebra is distributive, weak divisible, ⊔-definable, a Heyting algebra or an MV-algebra, or has an involutive negation or pseudocomplementation. Some of the results are listed in Table 3, which should be read like this: if the diagonal of a triangle algebra satisfies the given property (mentioned in the first column) and the value of $u*u$ is in the given range (mentioned in the first row), then the triangle algebra satisfies the property at that place in the table. If also the converse holds (for the given value of $u*u$), then the property is underlined. For example (on the fourth row of the table): if the diagonal of a triangle algebra is strong ⊔-definable (in other words, an MV-algebra), then this triangle algebra is ⊔-definable (no matter what the value of $u*u$ is). Conversely, if a triangle algebra is ⊔-definable and $u*u=u$, then its diagonal is an MV-algebra.

Table 3. Properties on triangle algebras and their diagonal.

Diagonal	$\mathit{u}\mathbf{*}\mathit{u}\mathbf{=}\mathbf{0}$	$\mathbf{0}\mathbf{<}\mathit{u}\mathbf{*}\mathit{u}\mathbf{<}\mathit{u}$	$\mathit{u}\mathbf{*}\mathit{u}\mathbf{=}\mathbf{u}$
distributive	distributive	distributive	distributive
P + div	PP + weak div	PP + weak div	PP + weak div
involution	inv	no inv	no inv
pseudocomplementation	no PC	depends on $\neg (u*u)$	PC
MV-algebra	⊔-def	⊔-def	⊔-def
Heyting	not Heyting	not Heyting	Heyting
Heyting + α-LEM	MV	div	Heyting
Boolean algebra	MV	P, not MV	G-algebra, not MV

In this table, P stands for prelinearity, PP for pseudo-prelinearity and LEM for law of excluded middle. The property α-LEM means: for all x on the diagonal, $x\bigsqcup \neg x\bigsqcup \alpha =1$, in which $\alpha =\mu (u*u)$. If $u*u=0$, this is the same as LEM; if $0<u*u$, this is weaker than LEM (for $u*u=u$ it is trivially satisfied). Remark that if 1 is ⊔-irreducible (e.g., in linear residuated lattices), then α-LEM is equivalent with LEM if $\alpha <1$. In this case the residuated lattice has only two elements, as $\neg x=1$ iff $x=0$ because of the residuation principle. A residuated lattice with two elements is a Boolean algebra. For more information about the precise meaning of the properties mentioned, we refer to [37].