An Overview of the Pathway Idea and Its Applications in Statistical and Physical Sciences
Abstract
:1. Introduction
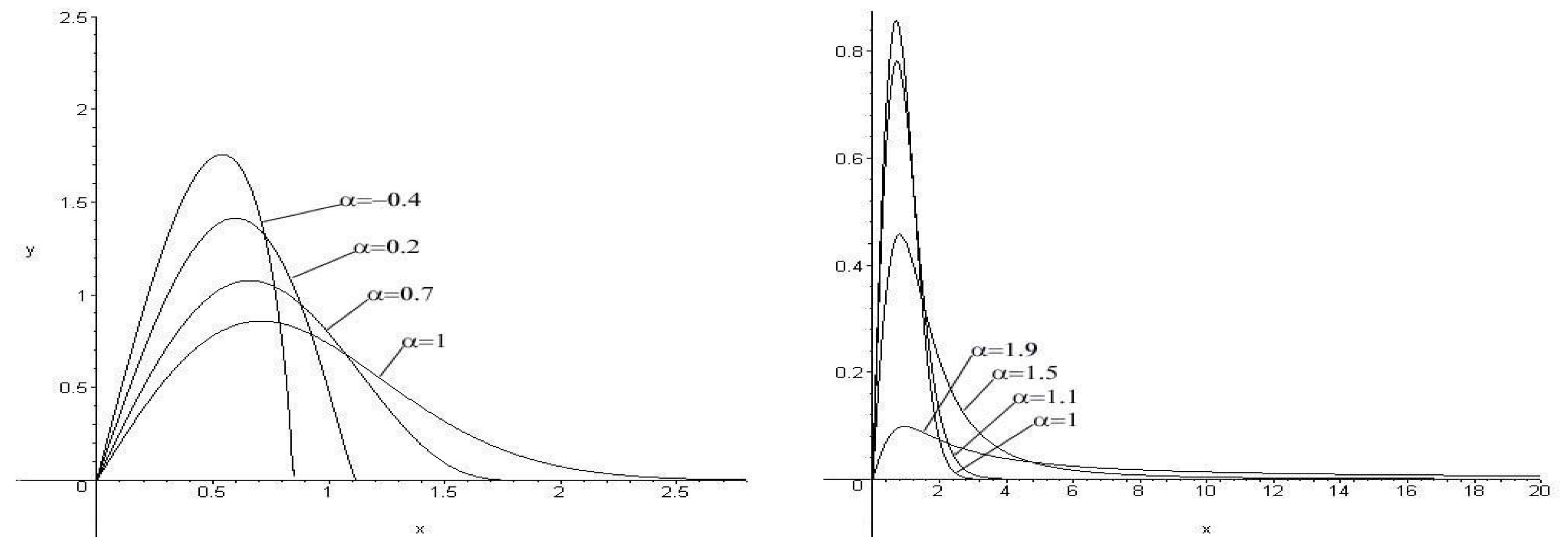
| Gaussian or normal density for | |
| Maxwell-Boltzmann density | |
| Rayleigh density | |
| Hermert density | |
| U-shaped density | |
| Student-t for ν degrees of freedom, | |
| Caushy density for | |
| Standard type-1 beta density | |
| Standard type-2 beta density | |
| Tsallis statistics in Astrophysics, Power law, q-binomial density | |
| Triangular density | |
| F-density | |
| Helley’s density in physics | |
| Gamma density | |
| Chisquare density for ν degrees of freedom | |
| Exponential density (Laplace density with ) | |
| Generalized gamma density | |
| Weibull density | |
| Logistic density for | |
| Fermi-Dirac density, |
1.1. Pathway Model from Mathai’s Entropy Measure
- (i)
- (i)
- (i)
- (i)
1.2. Laplacian Density and Stochastic Processes
1.3. Mittag-Leffler Density and Processes
1.4. Laplace Transform of the Pathway Model
1.5. Multivariate Generalizations
2. Connections to Astrophysics and Statistical Mechanics
2.1. Superstatistics Consideration and Pathway Model
2.2. α-gamma Models Associated with Bessel Function
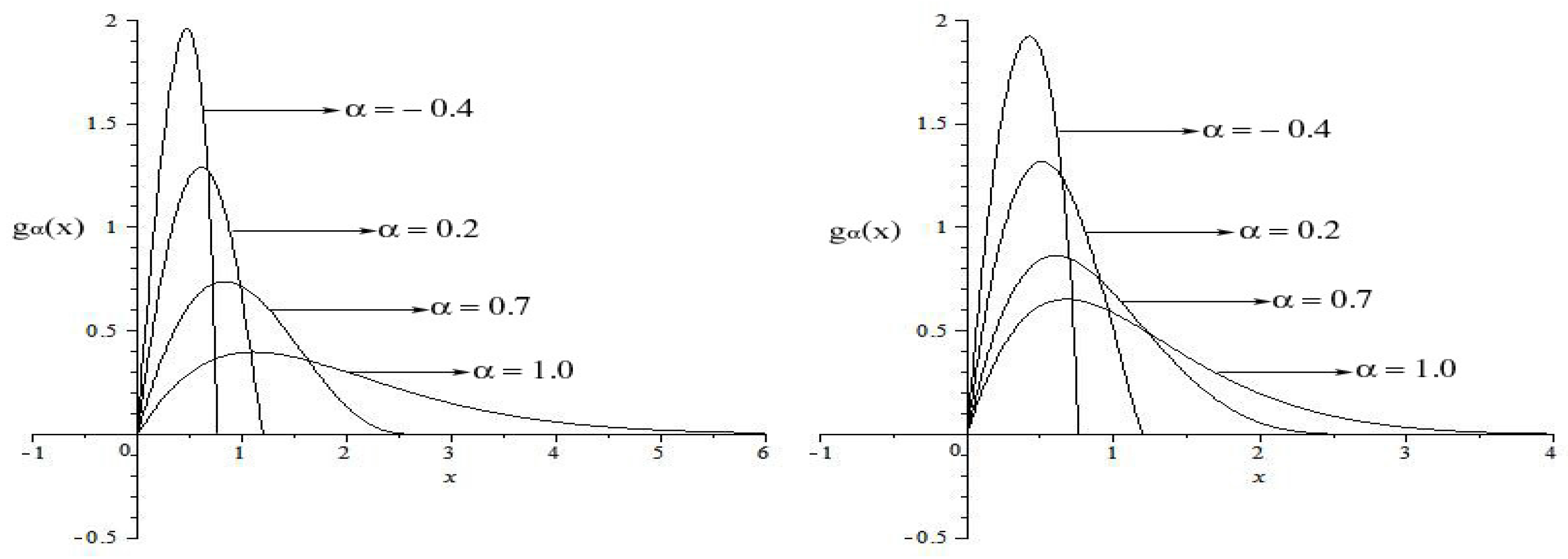
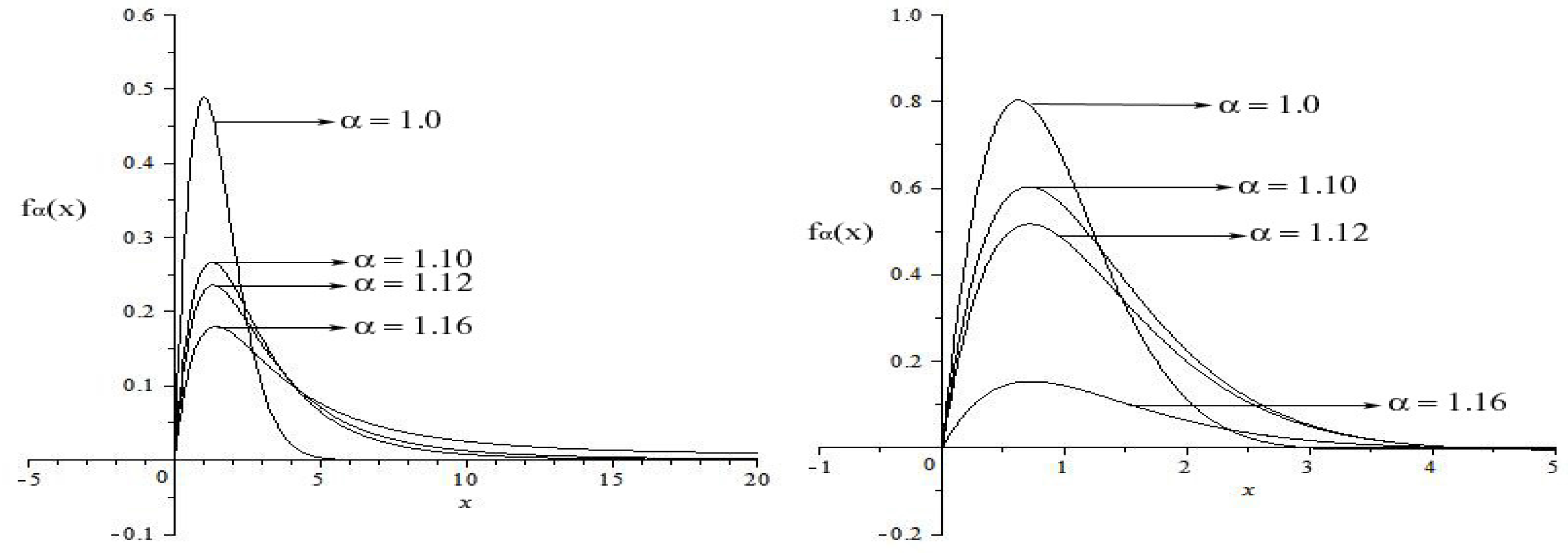
2.3. Tsallis Statistics
2.4. Extension of Thermonuclear Functions through Pathway Model
2.4.1. Inverse Gaussian as a Particular Case of the Pathway Model
2.4.2. An Interpretation of the Pathway Parameter α
3. Pathway Model and Fractional Calculus
3.1. -Transform
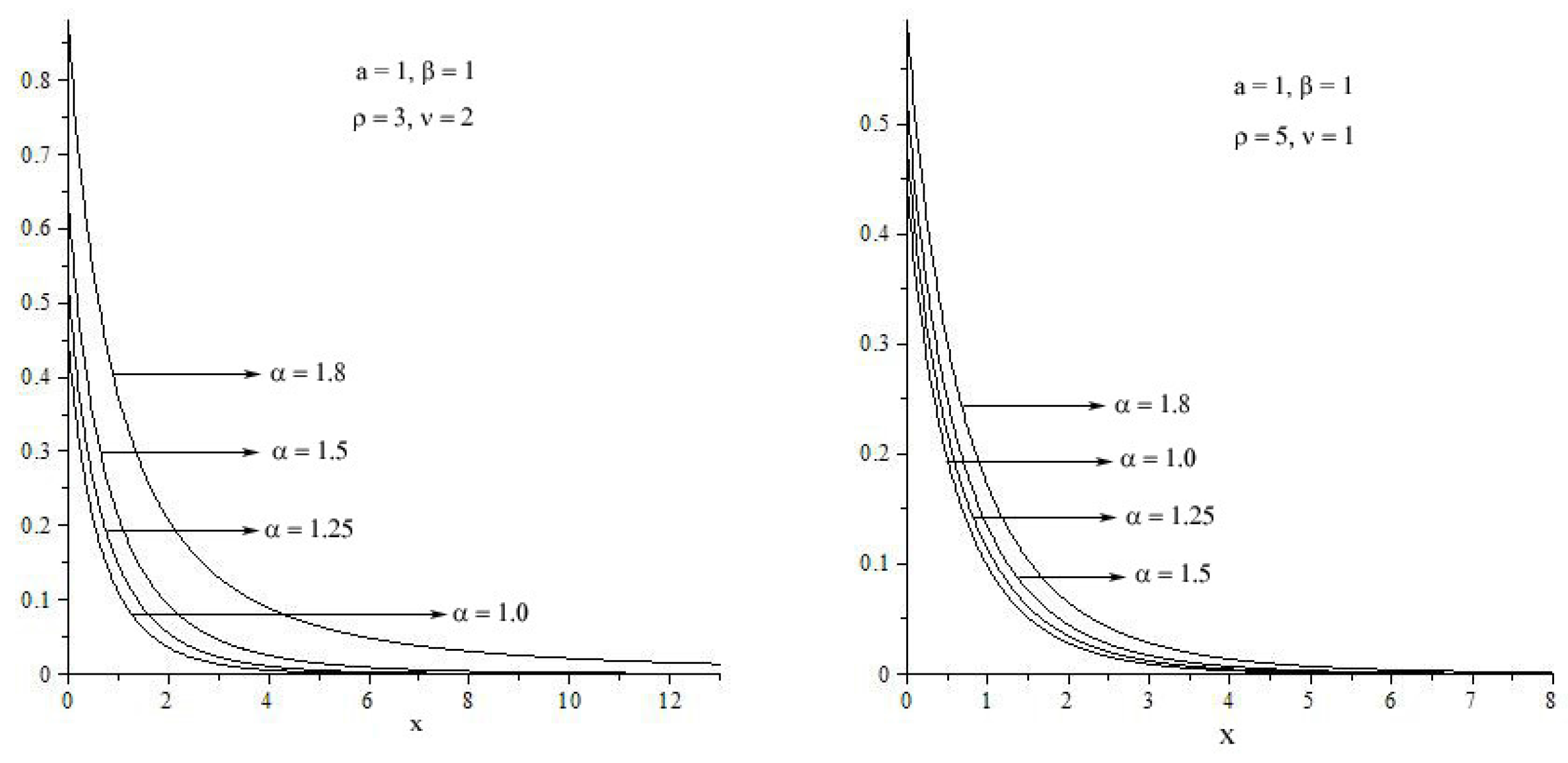
4. A Matrix Variate Pathway Model
4.1. The Normalizing Constants
4.2. Density of the Volume Content
4.3. Connection to Likelihood Ratio Criteria
4.4. Quadratic Forms
4.5. Pathway Fractional Integral
5. Open Problem
Acknowledgments
Conflicts of Interest
References
- Mathai, A.M. A Pathway to matrix-variate gamma and normal densities. Linear Algebra Appl. 2005, 396, 317–328. [Google Scholar] [CrossRef]
- Beck, C. Stretched exponentials from superstatistics. Phys. A 2006, 365, 96–101. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalizations of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. What should a statistical mechanics satisfy to reflect nature? Phys. D 2004, 193, 3–34. [Google Scholar] [CrossRef]
- Honerkamp, J. Stochastic Dynamical Systems: Concepts, Numerical Methods, Data Analysis; VCH Publishers: New York, NY, USA, 1994. [Google Scholar]
- Mathai, A.M. A Handbook of Generalized Special Functions for Statistical and Physical Sciences; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Haubold, H.J.; Kumar, D.; Nair, S.S.; Joseph, D.P. Special functions and pathways for problems in astrophysics: An essay in honor of A.M. Mathai. Fract. Calc. Appl. Anal. 2010, 13, 133–158. [Google Scholar]
- Joseph, D.P. Gamma distribution and extensions by using pathway idea. Stat. Pap. 2009. [Google Scholar] [CrossRef]
- Mathai, A.M.; Rathie, P.N. Basic Concepts in Information Theory and Statistics: Axiomatic Foundations and Applications; Wiley Halsted: New York, NY, USA, 1975. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. On generalized entropy measures and pathways. Phys. A Stat. Mech. Appl. 2007, 3, 493–500. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Pathway model Pathway model, superstatistics Tsallis statistics and a generalized measure of entropy. Phys. A 2007, 375, 110–122. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Pathway parameter and thermonuclear functions. Phys. A Stat. Mech. Appl. 2008, 387, 2462–2470. [Google Scholar] [CrossRef]
- Mathai, A.M. On non-central generalized Laplacianness of quadratic forms in normal variables. J. Multivar. Anal. 1993, 45, 239–246. [Google Scholar] [CrossRef]
- Mathai, A.M.; Provost, S.B.; Hayakawa, T. Bilinear Forms and Zonal Polynomials, Lecture Notes; Springer-Verlag: New York, NY, USA, 1995. [Google Scholar]
- Mathai, A.M. The residual effect of a growth-decay mechanism and the distributions of covariance structures. Can. J. Stat. 1993, 21, 277–283. [Google Scholar] [CrossRef]
- Mathai, A.M. Some properties of Mittag- Leffler functions and matrix variate analogues: A statistical perspective. Fract. Cal. Appl. Anal. 2010, 30, 113–132. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function Theory and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. A pathway from bayesian statistical analysis to superstatistics. 2010; arXiv:1011.5658v1. [Google Scholar]
- Mathai, A.M.; Moschopoulos, P. A Pathway Idea for Model Building. J. Stat. Appl. Proc. 2012, 1, 15–20. [Google Scholar] [CrossRef] [Green Version]
- Pillai, R.N. On Mittag-Leffler functions and related distributions. Ann. Inst. Statist. Math. 1990, 4, 157–161. [Google Scholar] [CrossRef]
- Shanoja Naik, R. Pathway Distributions, Autoregressive Processes and Their Applications . PhD Thesis, Mahatma Gandhi University, Kottayam, Kerala, India, 2008. [Google Scholar]
- Mathai, A.M.; Provost, S.B. Quadratic Forms in Random Variables: Theory and Applications; Marcel Dekker: New York, NY, USA, 2005. [Google Scholar]
- Han, J.H. Gamma function to Beck-Cohen superstatistics. Phys. A 2013, 392, 4288–4298. [Google Scholar] [CrossRef]
- Sebastian, N. Limiting Approach to Generalized Gamma Bessel Model via Fractional Calculus and its Applications in Various Disciplines. 2013; arXiv:1307.7949. [Google Scholar]
- Seema Nair, S.; Kattuveettil, A. Some remarks on the paper “On the q-type Distributions”. Proc. Astrophys. Space Sci. 2010, 11–15. [Google Scholar]
- Sebastian, N. A Generalized Multivariate Gamma Model Associated with Bessel Function. Integral Transforms and Special Functions 2011, 22, 631–645. [Google Scholar] [CrossRef]
- Sebastian, N. A generalized gamma model associated with Bessel function and its applications in statistical mechanics. In Proceedings of AMADE-09, Institute of Mathematics, Belarusian State Mathematics Minsk, Belarus, 2009.
- Anderson, W.J.; Haubold, H.J.; Mathai, A.M. Astrophysical thermonuclear functions. Astrophys. Space Sci. 1994, 214, 49–70. [Google Scholar] [CrossRef]
- Haubold, H.J.; John, R.W. On the evaluation of an integral connected with the thermonuclear reaction rate in the closed form. Astron. Nachr. 1978, 299, 225–232. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. Modern Problems in Nuclear and Neutrino Astrophysics; Akademie-Verlag: Berlin, Germany, 1988. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Review of Mathematical techniques applicable in astrophysical reaction rate theory. Astrophys. Space Sci. 2002, 282, 265–280. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M. The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci. 2000, 273, 53–63. [Google Scholar] [CrossRef]
- Haubold, H.J.; Kumar, D. Extension of thermonuclear functions through the pathway model including Maxwell-Boltzmann and Tsallis distributions. Astropart. Phys. 2008, 29, 70–76. [Google Scholar] [CrossRef]
- Joseph, D.P.; Haubold, H.J. Extended reaction rate integral as solutions of some general differential equations. Proc. Astrophys. Space Sci. 2009, 41–51. [Google Scholar]
- Haubold, H.J.; Mathai, A.M. A heuristic remark on the periodic variation in the number of solar neutrinos detected on Earth. Astrophys. Space Sci. 1995, 228, 113–134. [Google Scholar] [CrossRef]
- Seema Nair, S. Pathway fractional integration operator. Fract. Calc. Appl. Anal. 2009, 12, 237–252. [Google Scholar]
- Kilbas, A.A.; Kumar, D. On generalized Krätzel functions. Integral Transform. Spec. Funct. 2009, 20, 836–845. [Google Scholar] [CrossRef]
- Kumar, D. Type-2 P-transforms. In Proceedings of AMADE-09, Belarusian State University, Minsk, Belarus, 2009.
- Krätzel, E. Integral transformations of Bessel type. Generalized Functions Operational Calculus 1979, 148, 148–155. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume 1. [Google Scholar]
- Kilbas, A.A.; Shlapakov, S.A. On Bessel-type integral transformation and its compositions with integral and differential operators. Dokl. Akad. Nauk Belarusi 1993, 37, 10–14. [Google Scholar]
- Kilbas, A.A.; Saxena, R.K.; Trujillo, J.J. Krätzel function as a function of hypergeometric type. Fract. Calc. Appl. Anal. 2006, 2, 109–130. [Google Scholar]
- Mathai, A.M. Jacobians of Matrix Transformations and Functions of Matrix Argument; World Scientific Publishing: New York, NY, USA, 1997. [Google Scholar]
- Mathai, A.M. Random volumes under a general matrix-variate model. Linear Algebra Appl. 2007, 425, 162–170. [Google Scholar] [CrossRef]
- Jacob, J.; Jose, K.K.; Mathai, A.M. Some properties of real matrix-variate inverted generalized Dirichlet integral. J. Indian Acad. Math. 2004, 26, 175–189. [Google Scholar]
- Jacob, J.; Sebastian George, S.; Mathai, A.M. Some properties of complex matrix-variate generalized Dirichlet integrals. Proc. Indian Acad. Sci. 2005, 15, 1–9. [Google Scholar] [CrossRef]
- Kurian, K.M.; Benny, K.; Mathai, A.M. A matrix-variate extension of inverted Dirichlet integral. Proc. Natl. Acad. Sci. (India) 2004, 74, 1–10. [Google Scholar]
- Thomas, S.; Thannippara, A.; Mathai, A.M. On a matrix-variate generalized type-2 Dirichlet model. Adv. Appl. Stat. 2008, 8, 37–56. [Google Scholar]
- Mathai, A.M. Fractional integrals in the matrix-variate cases and connection to statistical distributions. Integral Transforms Spec. Funct. 2009, 20, 871–882. [Google Scholar] [CrossRef]
- Seema Nair, S. Pathway fractional integral operator and matrix-variate functions. Integr. Transform. Spec. Funct. 2011, 22, 233–244. [Google Scholar] [CrossRef]
- Kober, H. On fractional integrals and derivatives. Q. J. Math. 1940, 11, 193–211. [Google Scholar] [CrossRef]
- Saigo, M. A remark on integral operators involving the Gauss hypergeometric functions. Math. Rep. Kyushu Univ. 1978, 11, 135–143. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebastian, N.; S. Nair, S.; P. Joseph, D. An Overview of the Pathway Idea and Its Applications in Statistical and Physical Sciences. Axioms 2015, 4, 530-553. https://doi.org/10.3390/axioms4040530
Sebastian N, S. Nair S, P. Joseph D. An Overview of the Pathway Idea and Its Applications in Statistical and Physical Sciences. Axioms. 2015; 4(4):530-553. https://doi.org/10.3390/axioms4040530
Chicago/Turabian StyleSebastian, Nicy, Seema S. Nair, and Dhannya P. Joseph. 2015. "An Overview of the Pathway Idea and Its Applications in Statistical and Physical Sciences" Axioms 4, no. 4: 530-553. https://doi.org/10.3390/axioms4040530
APA StyleSebastian, N., S. Nair, S., & P. Joseph, D. (2015). An Overview of the Pathway Idea and Its Applications in Statistical and Physical Sciences. Axioms, 4(4), 530-553. https://doi.org/10.3390/axioms4040530




