Lindelöf Σ-Spaces and R-Factorizable Paratopological Groups

Abstract

We prove that if a paratopological group G is a continuous image of an arbitrary product of regular Lindelöf Σ-spaces, then it is $\mathbb{R}$-factorizable and has countable cellularity. If in addition, G is regular, then it is totally ω-narrow and satisfies $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$, and the Hewitt–Nachbin completion of G is again an $\mathbb{R}$-factorizable paratopological group.

1. Introduction

Our main objective is the study of paratopological groups that can be represented as continuous images of products of Lindelöf Σ-spaces. While the properties of (para)topological groups that are Lindelöf Σ-spaces (referred to as Lindelöf Σ-groups) are well-understood [1,2,3,4], our knowledge about the former class of groups is very modest. The lack of the continuity of the inverse in paratopological groups makes our job more difficult when compared to the case of topological groups. In fact, most of our technique is essentially asymmetric.

Topological groups representable as continuous images of products of Lindelöf Σ-spaces were studied in [5], where it was shown that every uncountable regular cardinal was a weak precaliber for any group G in this class and that G satisfied $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$. According to [2] (Corollary 3.5), a slightly weaker result is valid for Tychonoff paratopological groups representable as continuous images of products of Lindelöf Σ-spaces: these groups G satisfy the inequality $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$. However, the justification of this fact given in [2] contains a gap. In a few words, the problem with the argument in [2] is the existence of a weak σ-lattice of open continuous mappings of a given completely regular paratopological group G onto Hausdorff spaces with a $G_{\mathsf{\delta }}$-diagonal (see Definition 6). As far as we know, all other results in [2] are proven correctly. It is a simple exercise to show that every Hausdorff topological group has the required lattice of open mappings, while the case of paratopological groups is much more elusive.

It follows from our lemmas 9 and 11 that every weakly Lindelöf regular paratopological group has a weak σ-lattice of continuous open mappings onto Hausdorff spaces with a $G_{\mathsf{\delta }}$-diagonal. Since every space representable as a continuous image of a product of Lindelöf Σ-spaces is weakly Lindelöf, these facts fill in the gap in the proof of [2] (Corollary 3.5) (see our Theorem 13).

It turns out that the paratopological groups G, which are continuous images of products of Lindelöf Σ-spaces, have several properties that make them look like Lindelöf Σ-groups. For example, we prove in Theorem 12 that such a group G is $\mathbb{R}$-factorizable and has countable cellularity. If in addition the group G is regular, then it is totally ω-narrow and satisfies $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$, and the Hewitt–Nachbin completion of G is again an $\mathbb{R}$-factorizable paratopological group containing G as a dense subgroup (see Theorem 13). This fact is one of the first results on the preservation of the paratopological group structure under taking the Hewitt–Nachbin completion: almost all known results of this kind refer to topological groups, and their proofs depend essentially on the continuity of the inverse.

Finally, in Section 4, we formulate several open problems regarding paratopological groups representable as continuous images of products of Lindelöf Σ-spaces. We are mainly interested in finding out whether the conclusions “G is totally ω-narrow and satisfies $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$” in Theorem 13 can be extended to Hausdorff paratopological groups G.

The article is organized as follows. In Section 2, we introduce a class $\mathcal{L}\Sigma$ of Hausdorff spaces that contains the Lindelöf Σ-spaces and shares many properties with the latter one. The advantage of working with spaces from the class $\mathcal{L}\Sigma$ resides in the fact that this class is stable with respect to taking Hausdorff continuous images. We collect several results about the permanence properties of the class $\mathcal{L}\Sigma$ and present more facts that will be used in Section 3.

Section 3 contains our main results about paratopological groups representable as continuous images of products of Lindelöf Σ-spaces. A few selected problems related to the material of Section 3 are given with comments in Section 4.

2. Preliminaries

A space X is weakly Lindelöf if every open cover of X contains a countable subfamily whose union is dense in X. Every space with a dense Lindelöf subspace or having countable cellularity is weakly Lindelöf.

According to [6], a Hausdorff space X is called a Lindelöf Σ-space if there exist a countable family $\mathcal{F}$ of closed sets in X and a cover $\mathcal{C}$ of X by compact sets, such that for every $C\in \mathcal{C}$ and every open neighborhood U of C in X, one can find $F\in \mathcal{F}$, such that $C\subseteq F\subseteq U$. In fact, K. Nagami defined in [6] the wider class of Σ-spaces, so the Lindelöf Σ-spaces are simply the Σ-spaces with the Lindelöf property. The reader can find a detailed discussion of distinct ways to define Lindelöf Σ-spaces in [7] (Theorem 1).

It is known that the class of Lindelöf Σ-spaces is countably productive and that an $F_{\mathsf{\sigma }}$-subset of a Lindelöf Σ-space is again a Lindelöf Σ-space [6]. This class of spaces becomes especially stable when one restricts himself to considering Tychonoff spaces only. It turns out that every continuous image, say Y of a Lindelöf Σ-space X, is again a Lindelöf Σ-space, provided that X and Y are Tychonoff [1], (Proposition 5.3.5). In fact, the same conclusion remains valid if X is Hausdorff and Y is regular [4] (Lemma 4.5). However, we do not know whether the latter fact can be extended to the case when both X and Y are Hausdorff. This is why we define here a (possibly) wider class $\mathcal{L}\Sigma$ of Hausdorff spaces that is countably productive and is closed under taking continuous images.

Definition 1. 

A Hausdorff space X is in the class $\mathcal{L}\Sigma$ if there exist a countable family $\mathcal{F}$ of (not necessarily closed) subsets of X and a cover $\mathcal{C}$ of X by compact subsets, such that for every $C\in \mathcal{C}$ and every open neighborhood U of C in X, one can find $F\in \mathcal{F}$, such that $C\subseteq F\subseteq U$. 

It follows from Definition 1 that every Lindelöf Σ-space is in the class $\mathcal{L}\Sigma$. It is also easy to verify that every space $X\in \mathcal{L}\Sigma$ is Lindelöf. Therefore, a regular space in $\mathcal{L}\Sigma$ is normal (hence, Tychonoff), so regular spaces in $\mathcal{L}\Sigma$ are Lindelöf Σ-spaces according to [7] (Theorem 1).

Proposition 2. 

The class $\mathcal{L}\Sigma$ is countably productive and closed under taking continuous images. Further, if Y is an $F_{\sigma }$-subset of a space $X\in \mathcal{L}\Sigma$, then $Y\in \mathcal{L}\Sigma$. 

Proof. 

Let $\{X_k:k\in \mathsf{\omega }\}\subseteq \mathcal{L}\Sigma$ be a family of spaces. For every $k\in \mathsf{\omega }$, let ${\mathcal{F}}_k$ and ${\mathcal{C}}_k$ be families of subsets of $X_k$ witnessing that $X_k\in \mathcal{L}\Sigma$. We can assume that $X_k\in {\mathcal{F}}_k$ for each $k\in \mathsf{\omega }$. To show that $X={\prod }_{k\in \mathsf{\omega }}{X}_k$ is in $\mathcal{L}\Sigma$, we define families $\mathcal{F}$ and $\mathcal{C}$ of subsets of X as follows.

Let $\mathcal{F}$ be the family of sets of the form ${\prod }_{k\in \mathsf{\omega }}{F}_k$, where $F_k\in {\mathcal{F}}_k$ for each $k\in \mathsf{\omega }$ and $F_k\ne X_k$ for at most finitely many indices $k\in \mathsf{\omega }$. Clearly the family $\mathcal{F}$ is countable. Similarly, let $\mathcal{C}$ be the family of sets of the form ${\prod }_{k\in \mathsf{\omega }}{C}_k$, where $C_k\in {\mathcal{C}}_k$ for each $k\in \mathsf{\omega }$. Then, the family $\mathcal{C}$ consists of compact subsets of X. Take an element $C\in \mathcal{C}$ and an open neighborhood U of C in X. Then, $C={\prod }_{k\in \mathsf{\omega }}{C}_k$, where $C_k\in {\mathcal{C}}_k$ for each $k\in \mathsf{\omega }$. By Wallace’s Lemma, there exists a finite set $A\subseteq \mathsf{\omega }$ and open sets $O_k\subseteq X_k$ with $k\in A$, such that $C\subseteq {\prod }_{k\in \mathsf{\omega }}{V}_k\subseteq U$, where $V_k=O_k$ if $k\in A$ and $V_k=X_k$ if $k\in \mathsf{\omega }\setminus A$. For every $k\in A$, there exists $F_k\in {\mathcal{F}}_k$, such that $C_k\subseteq F_k\subseteq O_k$. Let $F={\prod }_{k\in \mathsf{\omega }}{E}_k$, where $E_k=F_k$ if $k\in A$ and $E_k=X_k$ if $k\in \mathsf{\omega }\setminus A$. Then, $F\in \mathcal{F}$ and $C\subseteq F\subseteq {\prod }_{k\in \mathsf{\omega }}{V}_k\subseteq U$. Therefore, the families $\mathcal{F}$ and $\mathcal{C}$ witness that $X\in \mathcal{L}\Sigma$. This proves that the class $\mathcal{L}\Sigma$ is countably productive.

Let $f:X\to Y$ be a continuous onto mapping of Hausdorff spaces, where $X\in \mathcal{L}\Sigma$. Take families $\mathcal{F}$ and $\mathcal{C}$ of subsets of X witnessing that $X\in \mathcal{L}\Sigma$. It is easy to verify that the families ${\mathcal{F}}_Y=\{f\left(F\right):F\in \mathcal{F}\}$ and ${\mathcal{C}}_Y=\{f\left(C\right):C\in \mathcal{C}\}$ of subsets of Y witness that $Y\in \mathcal{L}\Sigma$.

Finally, let $Y={\bigcup }_{k\in \mathsf{\omega }}{B}_k$, where each $B_k$ is a closed subset of a space $X\in \mathcal{L}\Sigma$. Denote by $\mathcal{F}$ and $\mathcal{C}$ families of subsets of X witnessing that $X\in \mathcal{L}\Sigma$, where $\mathcal{F}$ is countable and each $C\in \mathcal{C}$ is compact. Let us verify that the families:

$${\mathcal{F}}_Y=\{F\cap B_k:F\in \mathcal{F},k\in \mathsf{\omega }\}$$

and:

$${\mathcal{C}}_Y=\{C\cap B_k:C\in \mathcal{C},k\in \mathsf{\omega }\}$$

witness that $Y\in \mathcal{L}\Sigma$. It is clear that $|{\mathcal{F}}_Y|\le \mathsf{\omega }$ and that each element of ${\mathcal{C}}_Y$ is a compact subset of Y. Let $K=C\cap B_k$ be an element of ${\mathcal{C}}_Y$, where $C\in \mathcal{C}$ and $k\in \mathsf{\omega }$. Let also V be an open neighborhood of K in Y. Then, there exists an open set O in X, such that $O\cap Y=V$. Since the compact set $C^{\prime }=C\setminus O$ is disjoint from K and the space X is Hausdorff, we can find disjoint open in X neighborhoods $W_1$ and $W_2$ of K and $C^{\prime }$, respectively. The set $W^{*}=W_2\setminus B_k$ is open in X and contains $C^{\prime }$. Hence, the set $U=O\cup W^{*}$ is an open neighborhood of C in X, so we can find an element $F\in \mathcal{F}$, such that $C\subseteq F\subseteq U$. Then, $F\cap B_k$ is an element of ${\mathcal{F}}_Y$ that satisfies:

$$K\subseteq F\cap B_k\subseteq U\cap B_k=O\cap B_k\subseteq O\cap Y=V$$

This completes the proof of the fact that $Y\in \mathcal{L}\Sigma$. ☐

Another important property of the spaces in $\mathcal{L}\Sigma$ is presented in the following result, which is close to [1] (Proposition 5.3.15). However, our proof of Proposition 3 is quite different from the one given in [1], since we work in the class of Hausdorff spaces, which is much wider than the class of Tychonoff spaces considered in [1] (Section 5.3).

Proposition 3. 

If a space $X\in \mathcal{L}\Sigma$ admits a continuous one-to-one mapping onto a Hausdorff space Y with a countable network, then X itself has a countable network. 

Proof. 

Let $f:X\to Y$ be a continuous bijection. It is well known that every Hausdorff space with a countable network admits a continuous one-to-one mapping onto a second countable Hausdorff space. Let $i:Y\to Z$ be a continuous bijection of Y onto a second countable Hausdorff space Z. Then, $g=i\circ f$ is a continuous bijection of X onto Z. Denote by $\mathcal{B}$ a countable base for Z. We can assume that $\mathcal{B}$ is closed under finite intersections and finite unions.

Let families $\mathcal{F}$ and $\mathcal{C}$ of subsets of X witness that $X\in \mathcal{L}\Sigma$, where $\left|\mathcal{F}\right|\le \omega$ and each $C\in \mathcal{C}$ is compact. We claim that the countable family:

$$\mathcal{N}=\{F\cap g^{-1}\left(W\right):F\in \mathcal{F},W\in \mathcal{B}\}$$

is a network for X. Indeed, take a point $x\in X$ and an open neighborhood U of x in X. There exists $C\in \mathcal{C}$, such that $x\in C$. Then, $K=C\setminus U$ is a compact subset of X and $x\notin K$. Hence, the compact subset $g\left(K\right)$ of Z does not contain the point $g\left(x\right)$, and we can find disjoint elements $W,W^{\prime }\in \mathcal{B}$, such that $g\left(x\right)\in W$ and $g\left(K\right)\subseteq W^{\prime }$. Then, $O=U\cup g^{-1}\left(W^{\prime }\right)$ is an open neighborhood of C in X, so there exists an element $F\in \mathcal{F}$, such that $C\subseteq F\subseteq O$. It is clear that $F\cap g^{-1}\left(W\right)$ is an element of $\mathcal{N}$, and we have that:

$$x\in F\cap g^{-1}\left(W\right)\subseteq O\cap g^{-1}\left(W\right)=U\cap g^{-1}\left(W\right)\subseteq U$$

We have thus proven that $\mathcal{N}$ is a countable network for X. ☐

Replacing the family $\mathcal{N}$ in the proof of Proposition 3 with the family:

$${\mathcal{N}}^{\prime }=\{F\cap \overline{g^{-1}\left(W\right)}:F\in \mathcal{F},W\in \mathcal{B}\}$$

we obtain the following version of the proposition:

Proposition 4. 

If a Lindelöf Σ-space X admits a continuous one-to-one mapping onto a Hausdorff space with a countable network, then X has a countable network of closed sets. 

The following lemma was proven in [2] for regular Lindelöf Σ-spaces. Therefore, we extend the corresponding result from [2] to the wider class of Hausdorff $\mathcal{L}\Sigma$-spaces.

Lemma 5. 

If a space $X\in \mathcal{L}\Sigma$ has a $G_{\delta }$-diagonal, then it has a countable network. 

Proof. 

Suppose that $X\in \mathcal{L}\Sigma$. Then, Proposition 2 implies that $X^2\in \mathcal{L}\Sigma$, so the space $X^2$ is Lindelöf. Let $\{U_n:n\in \mathsf{\omega }\}$ be a family of open neighborhoods of the diagonal ${\Delta }_X$ in $X^2$ such that ${\Delta }_X={\bigcap }_{n\in \mathsf{\omega }}{U}_n$. It is clear that $F_n=X^2\setminus U_n$ is a closed Lindelöf subspace of $X^2$. Given $n\in \mathsf{\omega }$ and a point $(x,y)\in F_n$, we can find disjoint open neighborhoods $V_n(x,y)$ and $W_n(x,y)$ of the points x and y, respectively, in X. The open cover $\{V_n(x,y)\times W_n(x,y):(x,y)\in F_n\}$ of the Lindelöf space $F_n$ contains a countable subcover, say $\{V_n(x,y)\times W_n(x,y):(x,y)\in C_n\}$, where $C_n$ is a countable subset of $F_n$. Let:

$$\mathsf{\gamma }=\{V_n(x,y):n\in \mathsf{\omega },(x,y)\in C_n\}\cup \{W_n(x,y):n\in \mathsf{\omega },(x,y)\in C_n\}$$

Then, γ is a countable family of open sets in X. We claim that for every pair $a,b$ of distinct points in X, there exist disjoint elements $V,W\in \mathsf{\gamma }$, such that $a\in V$ and $b\in W$. Indeed, since $(a,b)\in X^2\setminus {\Delta }_X$, there exists $n\in \mathsf{\omega }$, such that $(a,b)\notin U_n$, i.e., $(a,b)\in F_n$. Hence, there exists an element $(x,y)\in C_n$, such that $(a,b)\in V_n(x,y)\times W_n(x,y)$. This means that $V=V_n(x,y)\in \mathsf{\gamma }$ and $W=W_n(x,y)\in \mathsf{\gamma }$ are disjoint open neighborhoods of the points a and b, respectively. This proves our claim.

Let $\mathcal{B}$ be the family of finite intersections of elements of γ. It is clear that $\mathcal{B}$ is a base for a Hausdorff topology τ on X. Then, the space $Y=(X,\tau )$ has a countable base, and the identity mapping of X onto Y is a continuous bijection. Applying Proposition 3, we conclude that X has a countable network. ☐

Given continuous mappings $g:X\to Y$ and $h:X\to Z$, we will write $g\prec h$ if there exists a continuous mapping $p:Y\to Z$ satisfying $h=p\circ g$.

We will also need the notion of a weak σ-lattice of mappings mentioned in the Introduction (see also [2], Definition 3.1).

Definition 6. 

Let Y be a space and $\mathcal{L}$ a family of continuous mappings of $Y$ elsewhere. Then, $\mathcal{L}$ is said to be a weak σ-lattice for Y if the following conditions hold:

(1) 

$\mathcal{L}$ generates the original topology of Y; 

(2) 

every finite subfamily of $\mathcal{L}$ has a lower bound in $(\mathcal{L},\prec );$ 

(3) 

for every decreasing sequence $p_0\succ p_1\succ p_2\succ \cdots$ in $\mathcal{L}$, there exists $p\in \mathcal{L}$ and a continuous one-to-one mapping $\varphi :p\left(Y\right)\to q\left(Y\right)$, such that $q=\varphi \circ p$, where q is the diagonal product of the family $\{p_n:n\in \omega \}$. 

A typical example of a weak σ-lattice for a topological group H is the family of all quotient mappings ${\mathsf{\pi }}_N:H\to H/N$ onto left coset spaces, where N is an arbitrary closed subgroup of type $G_{\mathsf{\delta }}$ in H.

Let us recall that a $G_{\mathsf{\delta },\Sigma }$-set in a space X is the union of an arbitrary family of $G_{\mathsf{\delta }}$-sets in X. Further, a space Y is said to be ω-cellular or, in symbols, $ce{l}_{\mathsf{\omega }}\left(Y\right)\le \mathsf{\omega }$ if every family γ of $G_{\mathsf{\delta }}$-sets in Y contains a countable subfamily λ, such that $\bigcup \mathsf{\lambda }$ is dense in $\bigcup \mathsf{\gamma }$. It is clear that every ω-cellular space has countable cellularity. In fact, the class of ω-cellular spaces is considerably narrower than the class of spaces of countable cellularity. For example, a space Y of countable pseudo-character satisfies $ce{l}_{\mathsf{\omega }}\left(Y\right)\le \mathsf{\omega }$ if and only if it is hereditarily separable.

Our next result is a special case of [2] (Theorem 3.4), which is sufficient for our purposes. We supply it with a short proof based on another fact from [2].

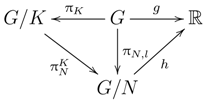
Theorem 7. 

Let $X={\prod }_{i\in I}{X}_i$ be a product of regular Lindelöf Σ-spaces and a Tychonoff space Y be a continuous image of X. If Y has a weak σ-lattice of open mappings onto Hausdorff spaces with a $G_{\delta }$-diagonal, then $ce{l}_{\omega }\left(Y\right)\le \omega$, and the closure of every $G_{\delta ,\Sigma }$-subset of $Y$ is a $G_{\delta }$-set. 

Proof. 

First, we choose a point $a\in X$. For every countable set $J\subseteq I$, denote by $p_J$ the projection of X onto the sub-product $X_J={\prod }_{i\in J}{X}_i$. Then, $X_J$ is a Lindelöf Σ-space, and we identify it with a corresponding closed subspace of X multiplying $X_J$ by the singleton $\left\{p_J\left(a\right)\right\}$. Then, the family:

$$\{p_J:J\subseteq I,|J|\le \mathsf{\omega }\}$$

constitutes a strong σ-lattice of open retractions of X onto Lindelöf Σ-subspaces (see [2], Definition 3.1).

Let $f:X\to Y$ be a continuous onto mapping. Denote by $\mathcal{L}$ a weak σ-lattice of open mappings of Y onto Hausdorff spaces with a $G_{\mathsf{\delta }}$-diagonal. For every $\mathsf{\phi }\in \mathcal{L}$, the composition $g=\mathsf{\phi }\circ f$ is a continuous mapping of X onto the Hausdorff space $\mathsf{\phi }\left(Y\right)$ with a $G_{\mathsf{\delta }}$-diagonal. By [8] (Theorem 1), g depends at most on countably many coordinates, so we can find a countable set $J\subseteq I$ and a mapping $h_J:X_J\to \mathsf{\phi }\left(Y\right)$, such that $g=h_J\circ p_J$. Since $p_J$ is an open continuous mapping, $h_J$ is continuous. Hence, $\mathsf{\phi }\left(Y\right)$ is in the class $\mathcal{L}\Sigma$ as a continuous image of the Lindelöf Σ-space $X_J$. By Lemma 5, $\mathsf{\phi }\left(Y\right)$ has a countable network for each $\mathsf{\phi }\in \mathcal{L}$. It follows that X, f, Y satisfy the conditions of Theorem 3.3 in [2]; hence, $ce{l}_{\mathsf{\omega }}\left(Y\right)\le \mathsf{\omega }$, and the closure of every $G_{\mathsf{\delta },\Sigma }$-subset of Y is a $G_{\mathsf{\delta }}$-set in Y. ☐

We recall that a paratopological group G is called $\mathbb{R}$-factorizable if for every continuous real-valued function f on G, one can find a continuous homomorphism $p:G\to H$ onto a second countable paratopological group H and a continuous real-valued function h on H satisfying $f=h\circ p$. The original definition of $\mathbb{R}$-factorizable paratopological groups in [9] involves separation restrictions on the groups G and H, thus giving rise to the concepts of ${\mathbb{R}}_i$-factorizability for $i=1,2,3$. However, it is shown in [4] that all of these concepts coincide and are equivalent to the one given above.

The following fact is a special case of [10] (Theorem 2.2) formulated in a form convenient for applications in Section 3. More precisely, it will be used in the proof of Theorem 12 to deduce the $\mathbb{R}$-factorizability of paratopological groups representable as continuous images of products of Lindelöf Σ-spaces.

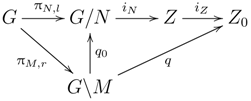
Proposition 8. 

Let $f:H\to M$ be a continuous mapping of a Hausdorff weakly Lindelöf paratopological group H to a metrizable space M. Then, one can find a closed subgroup N of type $G_{\delta }$ in H and a continuous mapping h of the left coset space $H/N$ to M, such that $H/N$ is Hausdorff and the equality $f=h\circ p$ holds, where $p:G\to G/N$ is the quotient mapping. 

3. Continuous Images of Products of Lindelöf Σ-Spaces

In this section we present the proofs of our main results announced in the Introduction. We start with three auxiliary results, Lemmas 9 to 11.

Let us recall that a space X is Urysohn if for every pair $x,y$ of distinct points in X, there exist open neighborhoods $U_x$ and $U_y$ of x and y, respectively, such that $\overline{U_x}\cap \overline{U_y}=\text{∅}$.

Lemma 9. 

Let G be a weakly Lindelöf regular paratopological group, ${\lambda }_0$ a countable family of open neighborhoods of the identity element e in G and $U_0\in {\lambda }_0$. Then, there exists a closed subgroup N of G satisfying the following conditions, where ${\pi }_l:G\to G/N$ and ${\pi }_r:G\to G\setminus N$ are quotient mappings of G onto the left and right coset spaces $G/N$ and $G\setminus N$, respectively:

(a)

$N\subseteq \bigcap {\lambda }_0$; 

(b_l) 

the space $G/N$ is Urysohn and has a $G_{\delta }$-diagonal; 

(b_r) 

the space $G\setminus N$ is Urysohn and has a $G_{\delta }$-diagonal; 

(c)

there exist open neighborhoods $O_l$ and $O_r$ of the elements ${\pi }_l\left(e\right)$ and ${\pi }_r\left(e\right)$ in $G/N$ and $G\setminus N$, respectively, such that ${\pi }_l^{-1}\left(O_l\right)\subseteq U_0$ and ${\pi }_r^{-1}\left(O_r\right)\subseteq U_0$. 

Proof. 

Denote by $\mathcal{N}\left(e\right)$ the family of open neighborhoods of e in G. Since G is weakly Lindelöf, it follows from [11] (Theorem 10) that the index of regularity of G is countable. Hence the Hausdorff number of G is also countable [12] (Proposition 3.5), i.e., for every $U\in \mathcal{N}\left(e\right)$, there exists a countable family $\mathsf{\lambda }\subset \mathcal{N}\left(e\right)$, such that ${\bigcap }_{V\in \mathsf{\lambda }}V{V}^{-1}\subset U$.

We introduce a new group multiplication in G by letting $x*y=y·x$, for all $x,y\in G$. Let $G^{*}$ be the paratopological group $(G,*,\tau )$, where τ is the topology of G. In other words, G and $G^{*}$ differ only in multiplication. Hence, $G^{*}$ is also weakly Lindelöf and has a countable Hausdorff number. Therefore, for every $U\in \mathcal{N}\left(e\right)$, there exists a countable family $\mathsf{\lambda }\subset \mathcal{N}\left(e\right)$, such that ${\bigcap }_{V\in \mathsf{\lambda }}V*V^{-1}\subset U$ or, equivalently, ${\bigcap }_{V\in \mathsf{\lambda }}{V}^{-1}V\subset U$.

Let ${\mathsf{\gamma }}_0={\mathsf{\lambda }}_0$. Making use of the inequalities $Hs\left(G\right)\le \mathsf{\omega }$ and $Hs\left(G^{*}\right)\le \mathsf{\omega }$, one can define a sequence $\{{\mathsf{\gamma }}_n:n\in \mathsf{\omega }\}$ of countable subfamilies of $\mathcal{N}\left(e\right)$ satisfying the following conditions for each $n\in \mathsf{\omega }$:

(i)

For every $V\in {\mathsf{\gamma }}_n$, there exists $W\in {\mathsf{\gamma }}_{n+1}$, such that $W^2\subset V$;

(ii_r) 

${\bigcap }_{W\in {\mathsf{\gamma }}_{n+1}}W{W}^{-1}\subset V$, for each $V\in {\mathsf{\gamma }}_n$;

(ii_l) 

${\bigcap }_{W\in {\mathsf{\gamma }}_{n+1}}{W}^{-1}W\subset V$, for each $V\in {\mathsf{\gamma }}_n$.

Then, $\mathsf{\gamma }={\bigcup }_{n\in \mathsf{\omega }}{\mathsf{\gamma }}_n$ is a countable subfamily of $\mathcal{N}\left(e\right)$. Let us show that $N=\bigcap \mathsf{\gamma }$ is as required.

Since ${\mathsf{\lambda }}_0={\mathsf{\gamma }}_0\subseteq \mathsf{\gamma }$, it follows that $N\subseteq \bigcap {\mathsf{\lambda }}_0$. This implies the validity of (a) of the lemma. Condition (ii${}_r$) implies that $N{N}^{-1}\subseteq V$ for every $V\in {\mathsf{\gamma }}_n$ and every $n\in \mathsf{\omega }$, so $N{N}^{-1}\subseteq N$. Since N contains the identity e of G, we see that N is a subgroup of G. Let ${\mathsf{\pi }}_l:G\to G/N$ and ${\mathsf{\pi }}_r:G\to G\setminus N$ be the quotient mappings. By (i), there exists $V\in {\mathsf{\gamma }}_1\subset \mathsf{\gamma }$, such that $V^2\subset U_0$. Then, $O_l={\mathsf{\pi }}_l\left(V\right)$ is an open neighborhood of ${\mathsf{\pi }}_l\left(e\right)$ in $G/N$ and ${\mathsf{\pi }}_l^{-1}\left(O_l\right)=VN\subset V^2\subset U_0$. Similarly, $O_r={\mathsf{\pi }}_r\left(V\right)$ is an open neighborhood of ${\mathsf{\pi }}_r\left(e\right)$ in $G\setminus N$ and ${\mathsf{\pi }}_r^{-1}\left(O_r\right)=NV\subset V^2\subset U_0$. Hence, (c) of the lemma is valid, as well.

Our next step is to show that condition (b${}_l$) of the lemma is also fulfilled, i.e., the coset space $G/N$ is Urysohn and, hence, Hausdorff. In particular, the subgroup $N={\mathsf{\pi }}_l^{-1}{\mathsf{\pi }}_l\left(e\right)$ is closed in G. A similar verification of item (b${}_r$) is left to the reader, since it only requires the use of (ii${}_r$) in place of (ii${}_l$).

Take an arbitrary element $x\in G$, such that $x\notin N$. Since the space $G/N$ is homogeneous, it suffices to show that the points ${\mathsf{\pi }}_l\left(e\right)$ and ${\mathsf{\pi }}_l\left(x\right)$ have disjoint closed neighborhoods in $G/N$. As $x\notin N$, there exists an element $U\in {\mathsf{\gamma }}_n$, for some $n\in \mathsf{\omega }$, such that $x\notin U$. By (ii${}_l$), there exists $V\in {\mathsf{\gamma }}_{n+1}$, such that $x\notin V^{-1}V$. Applying (i) twice, we can find $W\in {\mathsf{\gamma }}_{n+3}$, such that $W^4\subseteq V$. Then, $W^{-2}{W}^4\subseteq W^{-4}{W}^4\not\ni x$, whence it follows that:

$$W^{-1}{W}^2\cap Wx{W}^{-2}=\text{∅}$$

(1)

Since the mapping ${\mathsf{\pi }}_l$ of G onto $G/N$ is open and $N\subseteq W$ (and, therefore, $N=N^{-1}\subseteq W^{-1}$), we have the following inclusions:

$${\mathsf{\pi }}_l^{-1}\left(\overline{{\mathsf{\pi }}_l\left(W\right)}\right)=\overline{{\mathsf{\pi }}_l^{-1}\left({\mathsf{\pi }}_l\left(W\right)\right)}=\overline{WN}\subseteq W^{-1}WN\subseteq W^{-1}{W}^2$$

(2)

and:

$${\mathsf{\pi }}_l^{-1}\left(\overline{{\mathsf{\pi }}_l\left(Wx\right)}\right)=\overline{{\mathsf{\pi }}_l^{-1}\left({\mathsf{\pi }}_l\left(Wx\right)\right)}=\overline{WxN}\subseteq WxN{W}^{-1}\subseteq Wx{W}^{-2}$$

(3)

Combining Equations (1) to (3), we see that the closed subsets $\overline{{\mathsf{\pi }}_l\left(W\right)}$ and $\overline{{\mathsf{\pi }}_l\left(Wx\right)}$ of $G/N$ are disjoint. Since ${\mathsf{\pi }}_l\left(W\right)$ and ${\mathsf{\pi }}_l\left(Wx\right)$ are open neighborhoods of ${\mathsf{\pi }}_l\left(e\right)$ and ${\mathsf{\pi }}_l\left(x\right)$, respectively, in $G/N$, the latter space is Urysohn.

Finally we verify that $G/N$ has a $G_{\mathsf{\delta }}$-diagonal. For every $U\in \mathcal{N}\left(e\right)$, let:

$$O_U=\bigcup \{{\pi }_l\left(xU\right)\times {\pi }_l\left(xU\right):x\in G\}$$

Then, the countable family $\mathcal{F}=\{O_U:U\in \mathsf{\gamma }\}$ of open entourages of the diagonal Δ in $G/N\times G/N$ satisfies $\Delta =\bigcap \mathcal{F}$. Indeed, take arbitrary elements $a,b\in G$, such that ${\mathsf{\pi }}_l\left(a\right)\ne {\mathsf{\pi }}_l\left(b\right)$. Then, $a^{-1}b\notin N$, so we can find an element $U\in {\mathsf{\gamma }}_n$, for some $n\in \mathsf{\omega }$, such that $a^{-1}b\notin U$. By (ii${}_l$), there exists $V\in {\mathsf{\gamma }}_{n+1}$, such that $a^{-1}b\notin V^{-1}V$. Now, we apply (i) to take $W\in {\mathsf{\gamma }}_{n+2}$ with $W^2\subseteq V$. We claim that $({\mathsf{\pi }}_l\left(a\right),{\mathsf{\pi }}_l\left(b\right))\notin O_W$. Indeed, otherwise, there exists $x\in G$, such that ${\mathsf{\pi }}_l\left(a\right)\in {\mathsf{\pi }}_l\left(xW\right)$ and ${\mathsf{\pi }}_l\left(b\right)\in {\mathsf{\pi }}_l\left(xW\right)$. The latter implies that $a\in xWN$ and $b\in xWN$, whence:

$$a^{-1}b\in N^{-1}{W}^{-1}{x}^{-1}xWN\subset W^{-2}{W}^2\subset V^{-1}V$$

which is a contradiction. Since the family $\mathcal{F}$ is countable, we conclude that the coset space $G/N$ has a $G_{\mathsf{\delta }}$-diagonal. A similar argument shows that the right coset space $G\setminus N$ has a $G_{\mathsf{\delta }}$-diagonal. This completes the proof. ☐

The next result is almost evident, so we omit its proof.

Lemma 10. 

The class of spaces with a $G_{\delta }$-diagonal is countably productive. 

Lemma 11. 

Let G be a weakly Lindelöf regular paratopological group and $\mathcal{A}$ the family of closed subgroups N of G that satisfy conditions $\left(b{}_l\right)$ and $\left(b{}_r\right)$ of Lemma 9. Then, $\mathcal{A}$ is closed under countable intersections. 

Proof. 

Let $\{N_k:k\in \mathsf{\omega }\}\subseteq \mathcal{A}$ be a sequence of subgroups of G. For every $k\in \mathsf{\omega }$, denote by ${\mathsf{\pi }}_k$ the quotient mapping of G onto the left coset space $G/N_k$. Let also $\phi$ be the diagonal product of the family $\{{\mathsf{\pi }}_k:k\in \mathsf{\omega }\}$. Then, $\phi$ is a continuous mapping of G to the product space $Z={\prod }_{k\in \mathsf{\omega }}G/N_k$. Each of the factors $G/N_k$ has a $G_{\mathsf{\delta }}$-diagonal, and so does Z, by Lemma 10. Hence the subspace $\mathsf{\phi }\left(G\right)$ of Z also has a $G_{\mathsf{\delta }}$-diagonal. Similarly, the space Z and its subspace $\mathsf{\phi }\left(G\right)$ are Urysohn since the factors $G/N_k$ are Urysohn.

Put $N={\bigcap }_{k\in \mathsf{\omega }}{N}_k$, and let $\mathsf{\pi }:G\to G/N$ be the quotient mapping. For every $k\in \mathsf{\omega }$, there exists a mapping $p_k:G/N\to G/N_k$, such that ${\mathsf{\pi }}_k=p_k\circ \mathsf{\pi }$. The mapping $p_k$ is continuous and open since so are π and ${\mathsf{\pi }}_k$. The diagonal product of the family $\{p_k:k\in \mathsf{\omega }\}$, say p, is a continuous mapping of $G/N$ to $Z={\prod }_{k\in \mathsf{\omega }}G/N_k$. It is clear that p satisfies the equality $\mathsf{\phi }=p\circ \mathsf{\pi }$. It is also easy to see that the fibers of the mappings $\phi$ and π coincide, i.e., p is a continuous bijection of $G/N$ onto $\mathsf{\phi }\left(G\right)$. Indeed, take arbitrary points $x,y\in G$ with $\mathsf{\phi }\left(x\right)=\mathsf{\phi }\left(y\right)$. We have to show that $\mathsf{\pi }\left(x\right)=\mathsf{\pi }\left(y\right)$. It follows from the definition of $\phi$ that ${\mathsf{\pi }}_k\left(x\right)={\mathsf{\pi }}_k\left(y\right)$, for each $k\in \mathsf{\omega }$. Hence, $x^{-1}y\in {\bigcap }_{k\in \omega }{N}_k=N$ and $\mathsf{\pi }\left(x\right)=\mathsf{\pi }\left(y\right)$. Therefore, the equality $\mathsf{\phi }=p\circ \mathsf{\pi }$ implies that $p:G/N\to \mathsf{\phi }\left(G\right)$ is a continuous bijection.

Finally, since the space $\mathsf{\phi }\left(G\right)$ is Urysohn and has a $G_{\mathsf{\delta }}$-diagonal and p is continuous and one-to-one, we infer that the space $G/N$ is also Urysohn and has a $G_{\mathsf{\delta }}$-diagonal. A similar argument shows that the right coset space $G\setminus N$ has the same property. This proves that $N\in \mathcal{A}$.

In the following theorem, we do not impose any separation restriction on the paratopological group G.

Theorem 12. 

Let $X={\prod }_{i\in I}{X}_i$ be a product of regular Lindelöf Σ-spaces and $f:X\to G$ a continuous mapping of X onto a paratopological group G. Then, the group G is $\mathbb{R}$-factorizable and has countable cellularity. 

Proof. 

Consider a continuous real-valued function g defined on G. We can assume the group G is a regular space. Indeed, let ${\mathsf{\phi }}_r:G\to Reg\left(G\right)$ be the canonical continuous homomorphism, where $Reg\left(G\right)$ is the regularization of G (see [13,14]). Then, $Reg\left(G\right)$ is a regular paratopological group, and by the definition of $Reg\left(G\right)$, there exists a continuous real-valued function $g_r$ on $Reg\left(G\right)$, such that $g=g_r\circ {\mathsf{\phi }}_r$. Hence, G is $\mathbb{R}$-factorizable if so is the group $Reg\left(G\right)$. It also follows from [15] (Proposition 2.2) that the groups G and $Reg\left(G\right)$ have the same cellularity. Notice that ${\mathsf{\phi }}_r\circ f$ is a continuous mapping of X onto $Reg\left(G\right)$. Thus, we can assume that G itself is regular.

By a recent theorem of Banakh and Ravsky in [16], every regular paratopological group is completely regular. Each factor $X_i$, being a regular Lindelöf space, is normal and, hence, Tychonoff. Therefore, the product space X is Tychonoff, as well. Our next step is to show that G has a weak σ-lattice of open mappings onto Hausdorff spaces with a $G_{\mathsf{\delta }}$-diagonal.

Take an arbitrary point $x^{*}$ in X and denote by $\sigma \left(x^{*}\right)$ the subspace of X consisting of the points $x\in X$ that differ from $x^{*}$ at most on finitely many coordinates. Clearly $\sigma \left(x^{*}\right)$ is dense in X. Since the class of Lindelöf Σ-spaces is finitely productive (this follows, e.g., from Proposition 2) [1] (Corollary 1.6.45) implies that the subspace $\sigma \left(x^{*}\right)$ of X is Lindelöf. Hence, $f(\sigma \left(x^{*}\right))$ is a dense Lindelöf subspace of G, so the space G is weakly Lindelöf. Applying Lemma 9, we see that the topology of the group G is initial with respect to the family $\mathcal{L}$ of quotient mappings of G onto Urysohn left coset spaces with a $G_{\mathsf{\delta }}$-diagonal, and the same is valid for the family $\mathcal{R}$ of quotient mappings of G onto Urysohn right coset spaces with a $G_{\mathsf{\delta }}$-diagonal. Making use of Lemma 11, one can easily prove that both $\mathcal{L}$ and $\mathcal{R}$ are weak σ-lattices of continuous open mappings for G. A routine verification of this fact is omitted.

Since G is a continuous image of the product space X, Theorem 7 implies that $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$. As $c\left(G\right)\le ce{l}_{\mathsf{\omega }}\left(G\right)$, we conclude that G has countable cellularity. It remains to show that the group G is $\mathbb{R}$-factorizable. This requires several steps.

Following the notation in Lemma 11, we denote by $\mathcal{A}$ the family of all closed subgroups N of G, such that the coset spaces $G/N$ and $G\setminus N$ are Urysohn and have a $G_{\mathsf{\delta }}$-diagonal.

Claim 1. The coset spaces $G/N$ and $G\setminus N$ have a countable network, for each $N\in \mathcal{A}$.

Let ${\mathsf{\pi }}_{N,l}:G\to G/N$ be the quotient mapping, where $N\in \mathcal{A}$. Then, $f_N={\mathsf{\pi }}_{N,l}\circ f$ is a continuous mapping of X onto the left coset space $G/N$. Notice that $X_J={\prod }_{i\in J}{X}_i$ is a Lindelöf Σ-space for every countable set $J\subset I$; hence, [8] (Theorem 1) implies that $f_N$ depends on at most countably many coordinates, i.e., one can find a countable set $J\subset I$ and a continuous mapping $h:X_J\to G/N$, such that $f_N=h\circ p_J$, where $p_J:X\to X_J$ is the projection. It is clear that h is a surjective mapping. Applying Proposition 2, we conclude that $G/N\in \mathcal{L}\Sigma$. Hence, by Lemma 5, the space $G/N$ has a countable network. The same argument applied to the quotient mapping ${\mathsf{\pi }}_{N,r}:G\to G\setminus N$ enables us to deduce that the right coset space $G\setminus N$ also has a countable network. This proves Claim 1.

Claim 2. For every $N\in \mathcal{A}$, there exists $M\in \mathcal{A}$, such that ${\pi }_{M,r}\prec {\pi }_{N,l}$, and similarly, for every $L\in \mathcal{A}$, there exists $K\in \mathcal{A}$, such that ${\pi }_{K,l}\prec {\pi }_{L,r}$.

By the symmetry argument, it suffices to verify the first part of the claim. Let N be a closed subgroup of G, such that the left coset space $G/N$ is Urysohn and has a $G_{\mathsf{\delta }}$-diagonal. By Claim 1, the space $G/N$ has a countable network. Denote by Z the semi-regularization of the space $G/N$ (see [14], p. 204), and let $i_N:G/N\to Z$ be the identity mapping. Since $G/N$ is Hausdorff, it follows from [17] (Proposition 1) that the space Z is regular. It is clear that the mapping $i_N$ is continuous, so Z has a countable network as a continuous image of the space $G/N$. In particular, Z is Lindelöf and normal. Since Z has a countable network, we can find a continuous bijection $i_Z:Z\to Z_0$ onto a separable metrizable space $Z_0$. Then, $p=i_Z\circ i_N\circ {\mathsf{\pi }}_{N,l}$ is a continuous mapping of G onto $Z_0$. By Proposition 8, there exists a closed subgroup M of type $G_{\mathsf{\delta }}$ in G and a continuous mapping $q:G\setminus M\to Z_0$, such that $p=q\circ {\mathsf{\pi }}_{M,r}$, where ${\mathsf{\pi }}_{M,r}$ is the quotient mapping of G onto $G\setminus M$. According to Lemma 9 we can assume without loss of generality that $M\in \mathcal{A}$. Let $q_0=i_N^{-1}\circ i_Z^{-1}\circ q$. The mapping $q_0$ of $G\setminus M$ to $G/N$ is well defined, since $i_N$ and $i_Z$ are bijections. Thus, the following diagram commutes.

Since ${\mathsf{\pi }}_{N,l}$ and ${\mathsf{\pi }}_{M,r}$ are continuous open mappings, so is $q_0$. This implies that ${\mathsf{\pi }}_{M,r}\prec {\mathsf{\pi }}_{N,l}$. Claim 2 is proven.

Claim 3. For every $N\in \mathcal{A}$, there exists $K\in \mathcal{A}$, such that $K\subseteq N$ and K is invariant in G.

Indeed, take an arbitrary element $N\in \mathcal{A}$, and let $N_0=N$. By Claim 2, there exists $M_0\in \mathcal{A}$, such that ${\mathsf{\pi }}_{M_0,r}\prec {\mathsf{\pi }}_{N_0,l}$. Hence, $M_{0}x\subseteq x{N}_0$ or, equivalently, $M_0\subseteq x{N}_0{x}^{-1}$, for each $x\in G$. Applying Claim 2 once again, we find $N_1\in \mathcal{A}$, such that $N_1\subseteq x^{-1}{M}_{0}x$ for each $x\in G$. Continuing this way, we define sequences $\{N_k:k\in \mathsf{\omega }\}\subseteq \mathcal{A}$ and $\{M_k:k\in \mathsf{\omega }\}\subseteq \mathcal{A}$, such that $M_k\subseteq x{N}_k{x}^{-1}$ and $N_{k+1}\subseteq x{M}_k{x}^{-1}$ for each $x\in G$. Then, the subgroup $K={\bigcap }_{k\in \mathsf{\omega }}{M}_k={\bigcap }_{k\in \mathsf{\omega }}{N}_k$ of G is as required. Indeed, it follows from Lemma 11 that $K\in \mathcal{A}$, so both coset spaces $G/K$ and $G\setminus K$ are Urysohn and have a $G_{\mathsf{\delta }}$-diagonal. It also follows from our definition of K that:

$$x^{-1}Kx\subseteq x^{-1}{M}_{k}x\subseteq N_k$$

for all $x\in G$ and $k\in \mathsf{\omega }$, so $x^{-1}Kx\subseteq {\bigcap }_{k\in \mathsf{\omega }}{N}_k=K$. This inclusion is in fact the equality, so K is a closed invariant subgroup of G. Since $K\subseteq N_0=N$, this completes the proof of Claim 3.

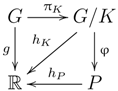
We are now in the position to complete our argument. Let us recall that g is an arbitrary continuous real-valued function on G. Since G is Hausdorff and weakly Lindelöf, we apply Proposition 8 to find a closed subgroup N of type $G_{\mathsf{\delta }}$ in G, such that g is constant on each left coset of N in G. Therefore, there exists a real-valued function h on $G/N$, such that $g=h\circ {\mathsf{\pi }}_{N,l}$, where ${\mathsf{\pi }}_{N,l}:G\to G/N$ is the quotient mapping. Since ${\mathsf{\pi }}_{N,l}$ is continuous and open, the function h is also continuous. By Lemma 9, there exists $N_1\in \mathcal{A}$ with $N_1\subseteq N$. Then, Claim 3 implies the existence of an invariant subgroup K of G, such that $K\in \mathcal{A}$ and $K\subseteq N_1$. The inclusions $K\subseteq N_1\subseteq N$ mean that there exists a mapping ${\mathsf{\pi }}_N^K:G/K\to G_N$, such that ${\mathsf{\pi }}_{N,l}={\mathsf{\pi }}_N^K\circ {\mathsf{\pi }}_K$, where ${\mathsf{\pi }}_K:G\to G/K$ is the quotient homomorphism.

Since the mappings ${\mathsf{\pi }}_{N,l}$ and ${\mathsf{\pi }}_K$ are continuous and open, so is ${\mathsf{\pi }}_N^K$. Hence, $h_K=h\circ {\mathsf{\pi }}_N^K$ is a continuous real-valued function on $G/K$. Notice that $G/K$ is a paratopological group, by the invariance of K in G, and $G/K$ is Hausdorff by our choice of $K\in \mathcal{A}$. The group $G/K$ has a countable network by Claim 1; hence, we can apply [9] (Corollary 3.11) according to which $G/K$ is $\mathbb{R}$-factorizable. Therefore, we can find a continuous homomorphism $\mathsf{\phi }:G/K\to P$ onto a second countable paratopological group P and a continuous real-valued function $h_P$ on P, such that $h_K=h_P\circ \mathsf{\phi }$. Therefore, the following diagram commutes.

It remains to note that the continuous homomorphism $\mathsf{\psi }=\mathsf{\phi }\circ {\mathsf{\pi }}_K$ and the function $h_P$ satisfy the equality $g=h_P\circ \mathsf{\psi }$, which implies the $\mathbb{R}$-factorizability of the group G. ☐

A topological group G is said to be ω-narrow (see [1], Section 3.4) if it can be covered by countably many translations of any neighborhood of the identity. A paratopological group is totally ω-narrow if it is a continuous homomorphic image of an ω-narrow topological group or, equivalently, if the topological group $G^{*}$ associated with G is ω-narrow [12] (Subsection 1.1).

If the paratopological group G in Theorem 12 is regular, we are able to complement the conclusion of the theorem as follows:

Theorem 13. 

Let $X={\prod }_{i\in I}{X}_i$ be a product space, where each $X_i$ is a regular Lindelöf Σ-space and $f:X\to G$ a continuous mapping of X onto a regular paratopological group G. Then, the group G is totally ω-narrow and satisfies $ce{l}_{\omega }\left(G\right)\le \omega$, and the Hewitt–Nachbin completion $\upsilon G$ of the group G is again a paratopological group containing G as a dense subgroup. Furthermore, the group $\upsilon G$ is $\mathbb{R}$-factorizable. 

Proof. 

Every regular paratopological group is Tychonoff according to [16]. Hence, applying Theorem 12, we conclude that G is a Tychonoff $\mathbb{R}$-factorizable paratopological group. By [17] (Proposition 3.10), G is totally ω-narrow.

The inequality $ce{l}_{\mathsf{\omega }}\left(G\right)\le \mathsf{\omega }$ was established in the proof of Theorem 12 under the assumption of the regularity of G.

Finally, according to [18] (Theorem 2.3), the Hewitt–Nachbin completion of a Tychonoff $\mathbb{R}$-factorizable paratopological group is again an $\mathbb{R}$-factorizable paratopological group containing the original group as a dense subgroup. ☐

Since the Sorgenfrey line $\mathbb{S}$ is a regular paratopological group that fails to be totally ω-narrow, Theorem 13 implies the following curious fact:

Corollary 14. 

The Sorgenfrey line $\mathbb{S}$ is not a continuous image of any product of regular Lindelöf Σ-spaces. 

The above corollary also follows from Theorem 12, since the group $\mathbb{S}$ is not $\mathbb{R}$-factorizable according to [1] (Example 8.1.8). We also note that the conclusion of Corollary 14 is valid for every uncountable subgroup of $\mathbb{S}$.

Remark 1. 

We present here a direct proof of the fact that the regular group G in Theorem 13 is totally ω-narrow. We hope that it can help to treat the more general case when G is Hausdorff. 

Let τ be the topology of G. Denote by ${\tau }^{-1}$ the family $\{U^{-1}:U\in \tau \}$. Then, $G^{\prime }=(G,{\tau }^{-1})$ is a paratopological group conjugated to G, and the inversion in G is a homeomorphism of G onto $G^{\prime }$. Hence, $G^{\prime }$ is also a continuous image of X, so the groups G and $G^{\prime }$ have the same properties. Let $\Delta =\left\{\right(x,x):x\in G\}$ be the diagonal in the paratopological group $G\times G^{\prime }$. According to [9] (Lemma 2.2), Δ is a closed subgroup of $G\times G^{\prime }$ topologically isomorphic to the topological group $G^{*}$ associated with G. Therefore, it suffices to show that the group Δ is ω-narrow. Let O be a neighborhood of the identity $e^{*}$ in Δ. There exists an open neighborhood U of the identity e in G, such that $\Delta \cap (U\times U^{-1})\subseteq O$. By Lemma 9 and Claims 1 and 3 in the proof of Theorem 12, we can find a closed invariant subgroup N of G, such that the quotient group $G/N$ has a countable network and ${\mathsf{\pi }}^{-1}\left(V\right)\subseteq U$ for some open neighborhood V of the identity in $G/N$, where $\mathsf{\pi }:G\to G/N$ is the quotient homomorphism. It is clear that $G^{\prime }/N$ is a paratopological group conjugated to $G/N$ and that $G^{\prime }/N$ has a countable network. Let ${\mathsf{\pi }}^{\prime }:G^{\prime }\to G^{\prime }/N$ be the quotient homomorphism. Then, $\mathsf{\phi }=\mathsf{\pi }\times {\mathsf{\pi }}^{\prime }$ is a continuous homomorphism of $G\times G^{\prime }$ onto the paratopological group $G/N\times G^{\prime }/N$ with a countable network. Clearly, the subgroup ${\Delta }_N=\{(\mathsf{\pi }\left(x\right),{\mathsf{\pi }}^{\prime }\left(x\right)):x\in G\}$ of $G/N\times G^{\prime }/N$ also has a countable network and, hence, is Lindelöf. In particular, the group ${\Delta }_N$ is ω-narrow. Therefore, we can find a countable subset D of ${\Delta }_N$, such that $DW={\Delta }_N=WD$, where $W={\Delta }_N\cap (V\times V^{-1})$ (we identify the groups $G/N$ and $G^{\prime }/N$ algebraically). Let C be a countable subset of Δ, such that $\mathsf{\phi }\left(C\right)=D$. It easily follows from our choice of the sets V and W that $\Delta \cap {\mathsf{\phi }}^{-1}\left(W\right)\subseteq \Delta \cap (U\times U^{-1})\subseteq O$, so we have the equality $CO=\Delta =OC$. This proves that the topological group $\Delta \cong G^{*}$ is ω-narrow.

4. Open Problems

A space Y is said to have the Knaster property if every uncountable family γ of open sets in Y contains an uncountable subfamily λ, such that every two elements of λ have a non-empty intersection [1] (Section 5.4). It is clear that every space with the Knaster property has countable cellularity; the converse is valid under $MA$ plus the negation of $CH$ and fails under $CH$.

Problem 15. 

Let a (Hausdorff) paratopological group G be a continuous image of a product of a family of Lindelöf Σ-spaces. Does G have the Knaster property? Is it ω-narrow? 

It is worth mentioning that if G itself is a Lindelöf Σ-space, then it has the Knaster property and is totally ω-narrow, since the topological group $G^{*}$ associated with G is again a Lindelöf Σ-space (see, e.g., [9], Corollary 2.3, and [1], Theorem 5.4.7).

Problem 16. 

Let G be as in Problem 15.

(a)

Does the topological group $G^{*}$ associated with G satisfies $c\left(G^{*}\right)\le \omega$? 

(b)

Is the group $G^{*}$$\mathbb{R}$-factorizable? 

(c)

Is the group $G^{*}$ω-narrow? 

What if, in addition, the group G in (a), (b) or (c) is Hausdorff or regular? 

Let us note that Theorem 13 answers (c) of Problem 16 in the affirmative for a regular paratopological group G. Since every $\mathbb{R}$-factorizable topological group is ω-narrow, the affirmative answer to (b) of Problem 16 would imply the same answer to (c) of the problem.

Let us recall that a space Y is said to be perfectly κ-normal if the closure of every open set in Y is a $G_{\mathsf{\delta }}$-set. Every metrizable space is evidently perfectly κ-normal; it is much less evident that arbitrary products of metrizable spaces are also perfectly κ-normal [19] (Theorem 2).

Problem 17. 

Let a Hausdorff (regular) paratopological group G be a continuous image of a dense subspace of a product of separable metrizable spaces. Is G perfectly κ-normal or $\mathbb{R}$-factorizable? 

Every paratopological group G admits the natural left quasi-uniformity ${\mathcal{L}}_G$ whose base consists of the sets:

$$U_V^l=\{(x,y)\in G^2:x^{-1}y\in V\}$$

where V runs through all open neighborhoods of the identity in G. Since every quasi-uniformity is generated by a family of upper quasi-uniformly continuous quasi-pseudometrics, the following problem arises in an attempt to show that the group G in Theorem 12 is ω-narrow independently of whether it is regular or not.

Problem 18. 

Does every upper quasi-uniformly continuous quasi-pseudometric on an arbitrary product of Lindelöf Σ-spaces depend at most on countably many coordinates?