Generalized Yang–Baxter Operators for Dieudonné Modules

Abstract

An enrichment of a category of Dieudonné modules is made by considering Yang–Baxter conditions, and these are used to obtain ring and coring operations on the corresponding Hopf algebras. Some examples of these induced structures are discussed, including those relating to the Morava K-theory of Eilenberg–MacLane spaces.

1. Introduction

Dieudonné modules appear as representations of Hopf algebras, in different settings. Categories of Hopf algebras are equivalent to those of Dieudonné modules, the equivalence being given by the functor that represents each Hopf algebra by its Dieudonné module. This equivalence suggests the definition of categories of Dieudonné modules, which can be enriched by considering universal bilinear products (or, in another direction, universal cobilinear coproducts), whose equivalent at the level of Hopf algebras give monoidal (or comonoidal) structures.

Here, we start with categories of Dieudonné modules in their own right, not simply as the equivalent of categories of Hopf algebras, and enrich them in a different way: we define Yang–Baxter operators on such Dieudonné modules, exploring some examples, and only then do we look at the effect these operators might have on the equivalent Hopf algebras.

In Section 2, we define Yang–Baxter operators for Dieudonné modules, presenting several examples. These come mostly from the Dieudonné modules for the Hopf algebras one obtains by applying Morava K-theory to Eilenberg–MacLane spaces. In Section 3, we review the equivalence between categories of Hopf algebras and of Dieudonné modules. For a (suitable) Hopf algebra H (over a perfect field of characteristic p), each coalgebra map $H\otimes H\to H$ induces a map on Dieudonné modules. If this map can be viewed as part of a Yang–Baxter operator, we analyze the conditions that the original coalgebra map must necessarily satisfy. Section 4 works in the opposite direction: maps of Dieudonné modules induce maps of Hopf algebras (via the category equivalence), and we apply this fact to construct, for each Yang–Baxter operator on a Dieudonné module $DH$, a pair of ring structures on H. We also obtain a corresponding pair of coring structures on H (and a third one, induced by a diagonal map on $DH$). Both of these constructions can be viewed as a representation of the original Yang–Baxter operator, as can be confirmed by their application to the examples of Section 2.

2. Generalized Yang–Baxter Operators for Dieudonné Modules

Fix a prime p. ${\mathbb{Z}}_p$ will denote the ring of p-adic integers.

Definition 2.1. A Dieudonné module $M_{*}$ is a graded abelian group together with a degree-preserving ${\mathbb{Z}}_p$-action and two homomorphisms $F:M_{*}\to M_{*}$ and $V:M_{*}\to M_{*}$, such that:

$$F\left(M_n\right)\subseteq M_{pn}\mathit{ for all }n$$

$$V\left(M_{pn}\right)\subseteq M_n\mathit{ for all }n$$

$$V\left(x\right)=0\mathit{ if }x\in M_k\mathit{ and }k\ne pn\mathit{ for any }n$$

$$VF=FV=p$$

$$p^{s+1}{M}_{p^{s}k}=0\mathit{ if }(k,p)=1\mathit{ for any }s$$

The p in the fourth condition must be understood as p-times the identity morphism. The grading is usually over the non-negative integers.

In most cases, a Dieudonné module $M_{*}$ will be denoted just by M, and the inner grading will be implicit in our notation, as will be the actions of V and F on the degree of the elements on which they operate.

It is convenient to interpret Dieudonné modules M simply as (graded) left modules over the ring $R={\mathbb{Z}}_p[F,V]/(FV-p)$. We proclaim that $\mathrm{deg}\left(F\right)=1$ and $\mathrm{deg}\left(V\right)=-1$, and put $\mathrm{deg}\left(ax\right)=p^{\mathrm{deg}\left(a\right)}\mathrm{deg}\left(x\right)$ for any $a\in R$ and $x\in M$. $ax$ is defined as zero if this previous calculation of $\mathrm{deg}\left(ax\right)$ does not result in an integer. This alternative view of Dieudonné modules will be preferred throughout this work.

${\mathcal{DM}}_{*}$ (or $\mathcal{DM}$, for short) denotes the category of (graded) Dieudonné modules, with morphisms what one would expect: graded group homomorphisms $f:M\to N$ preserving the action of R; that is, such that $f\left(ax\right)=af\left(x\right)$ for all $a\in R$ and $x\in M$.

Example 2.2. The ring R (with grading as above defined) is a Dieudonné module, with V and F acting by means of the ring operation.

Example 2.3. The polynomial ring ${\mathbb{Z}}_p[F,V]$ is a Dieudonné module, with V and F acting by means of the ring operation (again, the grading is the one defined above).

The next two examples come from the Dieudonné modules associated with the Hopf algebras that are obtained when one applies Morava K-theory (with $v_n=1$) to some Eilenberg–MacLane spaces. These Hopf algebras, and the corresponding Dieudonné modules, are periodically graded. We adapt this situation to our definition, by modifying the periodical grading into a $\mathbb{Z}$-grading in a consistent way. The correspondence between categories of Hopf algebras and of Dieudonné modules will be discussed in Section 3.

Example 2.4. Fix $n\in \mathbb{N}$.

Consider, for each $k\in {\mathbb{N}}_0$ and $i\in \{0,\cdots ,n-1\}$, an element $a_{\left(i\right)}^k$ of degree $p^{kn+i}$; Define N as the free $\mathbb{Z}/\left(p\right)$-module generated by the $a_{\left(i\right)}^k$; V acts on N by:

$$V\left(a_{\left(i\right)}^k\right)=\left\{\begin{array}{cc}{a}_{(i-1)}^k\hfill & \mathrm{if}\mathit{i}\ne \mathit{n}\hfill \\ \\ a_{\left(0\right)}^{k-1}\hfill & \mathrm{if}\mathit{i}=\mathit{n}\mathrm{and}\mathit{k}\ne 0\hfill \\ \\ 0\hfill & \mathrm{if}\mathit{i}=\mathit{n}\mathrm{and}\mathit{k}=0\hfill \end{array}\right.$$

Furthermore,

$$F\left(a_{\left(i\right)}^k\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\mathit{i}\ne 0\hfill \\ \\ a_{(n-1)}^{k+1}\hfill & \mathrm{if}\mathit{i}=0\hfill \end{array}\right.$$

This gives an action of R on N.

The previous elements $a_{\left(i\right)}^k$ generalize the $a_{\left(i\right)}$ one encounters in the Morava K-theory of Eilenberg–MacLane spaces. These were defined in [1]. By changing the notation, we can view them as belonging to a polynomial algebra. Put:

$V_k^m=a_{(n-1-m)}^k$ for $m=0,\cdots ,n-1$ and $k\in \mathbb{Z}$, with degree $p^{kn}{p}^{n-1-m}$.

$$\mathrm{Define }V\left(V_k^m\right)=\left\{\begin{array}{cc}{V}_k^{m+1}\hfill & \mathrm{if}\mathit{m}\ne \mathit{n}\hfill \\ \\ V_{k-1}^0\hfill & \mathrm{if}\mathit{m}=\mathit{n}\hfill \end{array}\right.$$

and

$$F\left(V_k^m\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\mathit{m}\ne 0\hfill \\ \\ V_k^{n-1}\hfill & \mathrm{if}\mathit{m}=0\hfill \end{array}\right.$$

One can check, from the definition of degree for each $V_k^m$, that V divides the degree by p (for terms with degree a power of p) and F multiplies the degree by p.

We can interpret each $V_k^m$ as the m-th power of $V_k^1$ (and this last element has degree $p^{(k+1)n-2}$).

Define $M=\mathbb{Z}/\left(p\right)[V_0,V_1,\cdots ]/(V_0^n=0,V_k^n=V_{k-1}^0\mathrm{for}\mathrm{k}\ne 0)$.

From what was declared above, M is as a Dieudonné module. The relations in the quotient of the polynomial algebra are suggested by what occurs for the Morava K-theory of Eilenberg–MacLane spaces, which inspired the definition of the action of V (and F) on the polynomial algebra. This will be explored below.

Fix an integer j. Let $I=(i_0,\cdots ,i_{n-1})$, where $i_k\in \{0,1\}$. Define $s\left(I\right)$ as the sequence $(i_1,i_2,\cdots ,i_{n-1},0)$, a left translation, and $s^{-1}\left(I\right)$ as the sequence $(0,i_0,i_1,\cdots ,i_{n-2})$, a right translation.

Theorem 2.5. ([2,3]) The periodically graded Dieudonné module $D({\overline{K\left(n\right)}}_{*}\left(K(\mathbb{Z}/\left(p^j\right),q)\right)$ is a free $\mathbb{Z}/\left(p^j\right)$ module on generators $a^I=a_{\left(0\right)}^{i_0}\cdots a_{(n-1)}^{i_{n-1}}$, where $i_k\in \{0,1\}$ and $\sum _{k=0}^{n-1}{i}_k=q$, in degree $\sum _{k=0}^{n-1}{i}_k{p}^k$, with:

$$V\left(a^I\right)=\left\{\begin{array}{cc}{a}^{s\left(I\right)}\hfill & \text{if}{i}_0=0\hfill \\ {(-1)}^{q-1}p{a}^{(i_1,i_2,\cdots ,i_{n-1},1)}\hfill & \text{if}{i}_0=1\hfill \end{array}\right.$$

and

$$F\left(a^I\right)=\left\{\begin{array}{cc}p{a}^{s^{-1}\left(I\right)}\hfill & \text{if}{i}_{n-1}=0\hfill \\ {(-1)}^{q-1}{a}^{(1,i_0,i_1,\cdots ,i_{n-2})}\hfill & \text{if}{i}_{n-1}=1\hfill \end{array}\right.$$

We will not define here Dieudonné modules for periodically-graded Hopf algebras, and so, one must not interpret the object in the previous theorem as an instance of our definition of Dieudonné modules. The Dieudonné theory for periodically-graded Hopf algebras (and periodically-graded Hopf rings) is developed in [4]. We adapt this result to obtain a $\mathbb{Z}$-graded Dieudonné module whose generators are modeled by those described above.

Example 2.6. Fix n and $q<n$ in $\mathbb{N}$.

We consider maps of sets $I:{\mathbb{N}}_0\to \{0,1\}$, such that $I\left(k\right)=0$, except eventually on n consecutive integers, say $(i,\cdots ,i+n-1)$, and, moreover, satisfying ${\sum }_{j=0}^{n-1}I(i+j)=q$. We require also that any such I satisfies $I\left(0\right)=0$. Give each I degree ${\sum }_{j=0}^{n-1}I(i+j)p^{i+j}$.

For each I, define the left translation $s\left(I\right)$ as $s\left(I\right)\left(k\right)=I(k+1)$ for all $k\in {\mathbb{N}}_0$. Define the right translation $s^{-1}\left(I\right)$ as $s^{-1}\left(I\right)\left(k\right)=I(k-1)$ for all $k\in \mathbb{N}$ and $s^{-1}\left(I\right)\left(0\right)=0$. By construction, $deg\left(s\left(I\right)\right)=p^{-1}deg\left(I\right)$ and $deg\left(s^{-1}\left(I\right)\right)=pdeg\left(I\right)$.

Consider the free module M over $\mathbb{Z}/\left(p^j\right)$ on all such maps. This can be given a Dieudonné module structure by putting $V\left(I\right)=s\left(I\right)$ and $F\left(I\right)=p{s}^{-1}\left(I\right)$.

We want to enrich the category $\mathcal{DM}$ with additional structure. This structure, via the equivalence between the category of Dieudonné modules and a corresponding category of Hopf algebras [5,6], will also add structure to those Hopf algebras H, and it will be interesting to see how that reflects on the operations in the definition of each H. One way to enrich $\mathcal{DM}$, giving it a braided group or quantum flavor, is to define generalized Yang–Baxter operators for Dieudonné modules.

Let M be a Dieudonné module in $\mathcal{DM}$ and $A:M{\otimes }_{\mathbb{Z}}M\to M{\otimes }_{\mathbb{Z}}M$ a bilinear morphism. $1:M\to M$ denotes the identity morphism. For this A, define:

$$A^{12}=A{\otimes }_{\mathbb{Z}}1:M{\otimes }_{\mathbb{Z}}M{\otimes }_{\mathbb{Z}}M\to M{\otimes }_{\mathbb{Z}}M{\otimes }_{\mathbb{Z}}M$$

and

$$A^{23}=1{\otimes }_{\mathbb{Z}}A:M{\otimes }_{\mathbb{Z}}M{\otimes }_{\mathbb{Z}}M\to M{\otimes }_{\mathbb{Z}}M{\otimes }_{\mathbb{Z}}M$$

Definition 2.7. If M is a Dieudonné module in $\mathcal{DM}$, a generalized Yang–Baxter operator for M is an invertible bilinear map $A:M{\otimes }_{\mathbb{Z}}M\to M{\otimes }_{\mathbb{Z}}M$, such that:

$$A^{12}{A}^{23}{A}^{12}=A^{23}{A}^{12}{A}^{23}\mathit{(as a composition of maps)}$$

That is, these $A^{ij}$ satisfy braided group relations.

Example 2.8. For any Dieudonné module M, the identity map $A:M{\otimes }_{\mathbb{Z}}M\to M{\otimes }_{\mathbb{Z}}M$ is trivially a generalized Yang–Baxter operator.

Example 2.9. For any Dieudonné module M with a chosen basis, define $A:M{\otimes }_{\mathbb{Z}}M\to M{\otimes }_{\mathbb{Z}}M$ on basis elements by $A(x\otimes y)=y\otimes x$ (and expand by linearity on both arguments).

This is an invertible map, and moreover, the Yang–Baxter condition is in this case satisfied on basis elements, for:

$$A^{12}{A}^{23}{A}^{12}(x\otimes y\otimes z)=A^{12}{A}^{23}(y\otimes x\otimes z)=A^{12}(y\otimes z\otimes x)=z\otimes y\otimes x$$

and

$$A^{23}{A}^{12}{A}^{23}(x\otimes y\otimes z)=A^{23}{A}^{12}(x\otimes z\otimes y)=A^{23}(z\otimes x\otimes y)=z\otimes y\otimes x.$$

Call this the switch Yang–Baxter operator.

Example 2.10. Define $\mathsf{\alpha }:R\to R$ as the identity on all powers of V and F, except on those $F^k$ with $p\nmid k$, where $\mathsf{\alpha }\left(F^k\right)=F^{pk}$, and expand to R by linearity.

Furthermore, define $\mathsf{\beta }:R\to R$ as the identity on all powers of V and F, except on those $V^{pk}$ with $p\nmid k$, where $\mathsf{\beta }\left(V^{pk}\right)=V^k$, and again, expand by linearity.

Both α and β are invertible: the inverse of α is similar to β, but exchange the role of the powers of V with those of F (the same happens for the inverse of β.)

Put $A=\mathsf{\alpha }\otimes \mathsf{\beta }$, which is invertible. Then, if S, T and U are any powers of V or F, we can easily check that $A^{12}{A}^{23}{A}^{12}(S\otimes T\otimes U)=A^{23}{A}^{12}{A}^{23}(S\otimes T\otimes U)$, and so, A is a generalized Yang–Baxter operator.

For example, if $S\otimes T\otimes U=V^n\otimes F^{pm}\otimes V^{pq}$, with $p\nmid m$ and $p\nmid q$, we get:

$$A^{12}{A}^{23}{A}^{12}(V^n\otimes F^{pm}\otimes V^{pq})=A^{12}{A}^{23}(V^n\otimes F^{pm}\otimes V^{pq})=A^{12}(V^n\otimes F^{pm}\otimes V^q)=V^n\otimes F^{pm}\otimes V^q$$

and

$$A^{23}{A}^{12}{A}^{23}(V^n\otimes F^{pm}\otimes V^{pq})=A^{23}{A}^{12}(V^n\otimes F^{pm}\otimes V^q)=A^{23}(V^n\otimes F^{pm}\otimes V^q)=V^n\otimes F^{pm}\otimes V^q$$

Example 2.11. The previous example is a particular case of a more general situation. Suppose we look for $\mathsf{\alpha }:R\to R$ and $\mathsf{\beta }:R\to R$ that map each power of F or V into another power of either (and not into a linear combination of more than one such power).

Then, if again $A=\mathsf{\alpha }\otimes \mathsf{\beta }$ and S, T and U are any powers of V or F, we get:

$$A^{12}{A}^{23}{A}^{12}(S\otimes T\otimes U)={\mathsf{\alpha }}^2\left(S\right)\otimes \mathsf{\beta }\mathsf{\alpha }\mathsf{\beta }\left(T\right)\otimes \mathsf{\beta }\left(U\right)$$

and

$$A^{23}{A}^{12}{A}^{23}(S\otimes T\otimes U)=\mathsf{\alpha }\left(S\right)\otimes \mathsf{\alpha }\mathsf{\beta }\mathsf{\alpha }\left(T\right)\otimes {\mathsf{\beta }}^2\left(U\right)$$

An invertible A of this form will be a generalized Yang–Baxter operator if both α and β are idempotent and satisfy $\mathsf{\beta }\mathsf{\alpha }\mathsf{\beta }=\mathsf{\alpha }\mathsf{\beta }\mathsf{\alpha }$.

This last equation is satisfied if, like in the previous example (where α and β where idempotent), the two operators commute, but that is not necessary.

Take for instance $\alpha \left(F^k\right)=F^{pk}$ if $p\nmid k$ or $p|k$, but $p^2\nmid k$ and the identity elsewhere, and $\beta \left(F^k\right)=F^{p^{2}k}$ if $p\nmid k$ and the identity elsewhere.

Then, these homomorphisms do not commute:

If $p\nmid k$, $\mathsf{\alpha }\mathsf{\beta }\left(F^k\right)=\mathsf{\alpha }\left(F^{p^{2}k}\right)=F^{p^{2}k}$, but $\mathsf{\beta }\mathsf{\alpha }\left(F^k\right)=\mathsf{\beta }\left(F^{pk}\right)=F^{pk}$.

However, if $p\nmid k$, $\mathsf{\alpha }\mathsf{\beta }\mathsf{\alpha }\left(F^k\right)=\mathsf{\alpha }\mathsf{\beta }\left(F^{pk}\right)=\mathsf{\alpha }\left(F^{pk}\right)=F^{p^{2}k}$ and $\mathsf{\beta }\mathsf{\alpha }\mathsf{\beta }\left(F^k\right)=\mathsf{\beta }\mathsf{\alpha }\left(F^{p^{2}k}\right)=\mathsf{\beta }\left(F^{p^{2}k}\right)=F^{p^{2}k}$.

Furthermore, if $p|k$, but $p^2\nmid k$, $\mathsf{\alpha }\mathsf{\beta }\mathsf{\alpha }\left(F^k\right)=\mathsf{\alpha }\mathsf{\beta }\left(F^{pk}\right)=\mathsf{\alpha }\left(F^{pk}\right)=F^{pk}$ and $\mathsf{\beta }\mathsf{\alpha }\mathsf{\beta }\left(F^k\right)=\mathsf{\beta }\mathsf{\alpha }\left(F^k\right)=\mathsf{\beta }\left(F^{pk}\right)=F^{pk}$.

This, together with the fact that on all other powers of F or V, both α and β are the identity, proves that $A=\mathsf{\alpha }\otimes \mathsf{\beta }$ is a generalized Yang–Baxter operator.

Example 2.12. For the Dieudonné module in Example 2.4, define $\mathsf{\beta }:M\to M$ by $\mathsf{\beta }\left(V_k^{pr}\right)=V_k^r$ if $p\nmid r$ and $pr\le n$, and the identity elsewhere.

Furthermore, define $\alpha :M\to M$ by $\mathsf{\alpha }\left(V_k^{r(n-1)}\right)=V_k^{pr(n-1)}$ if $p\nmid r$ and $r\le k$, and the identity elsewhere.

This gives a Yang–Baxter operator $A=\mathsf{\alpha }\otimes \mathsf{\beta }:M\otimes M\to M\otimes M$.

This example is an expansion of Example 2.10. The limitations on the range of values that r may take (both for α and β above) allow for the behaviors of the $V_k^r$ to be mutually independent. The choice of those $V_k^r$ where β does not act as the identity comes from the relation $V_k^{n-1}=F_k$ in the Dieudonné ring for the Morava K-theory of Eilenberg–MacLane spaces, as described in [3,7].

Example 2.13. If, in the setting of the previous example, we allow the behaviors of the $V_k^r$ to affect those for different values of k; we can put:

$\mathsf{\beta }\left(V_k^{pr}\right)=V_k^r$ if $p\nmid r$ and $pr<{(n+1)}^{k}n$, and the identity elsewhere, and

$\mathsf{\alpha }\left(V_k^{r(n-1)}\right)=V_k^{pr(n-1)}$ if $p\nmid r$ and $r(n-1)<{(n+1)}^{k}n$, and the identity elsewhere.

This way, the only restrictions on the values of r are those that come from the order of each element in the polynomial algebra: since $V_k^{n+1}=V_{k-1}$ (and $V_0^n=0$), we have $V_k^{{(n+1)}^{k}n}=0$ (and $V_k^{{(n+1)}^{k}n-1}\ne 0$). This reflects the relations between the various generators in the equivalent Hopf algebra.

Example 2.14. For the Dieudonné module in Example 2.6. and again inspired by the Morava K-theory generators $a_{\left(j\right)}$, put $\mathsf{\beta }\left(I\right)=s\left(I\right)$ if $I(n-1-pr)=1$ (with $p\nmid r$ and $pr\le n$) and $I\left(j\right)=0$ for $j<n-1-pr$, and the identity elsewhere, and $\mathsf{\alpha }\left(I\right)=s^{-1}\left(I\right)$ if $I(n-1-r(n-1\left)\right)=1$ (with $p\nmid r$ and $r<k$) and $I\left(j\right)=0$ for $j<n-1-r(n-1)$, and the identity elsewhere.

This example can be viewed as a generalization of Example 2.12: an element $I:{\mathbb{N}}_0\to \{0,1\}$ where $I\left(j\right)=0$ for all j, except for a certain index $i\le n-1$ has an interpretation as a $a_{\left(i\right)}=V_1^{n-1-i}$, with degree $p^i$.

These α and β form a Yang–Baxter operator $A=\mathsf{\alpha }\otimes \beta$, since they are both idempotent and $\mathsf{\beta }\mathsf{\alpha }\mathsf{\beta }=\mathsf{\alpha }\mathsf{\beta }\mathsf{\alpha }$ (for this last property, it is useful to notice that α and β cannot be both different from the identity on any given I).

3. The Influence of the Dieudonné Module Yang–Baxter Operators on the Corresponding Hopf  Algebras

Definition 3.1. The Witt polynomials ${\mathsf{\omega }}_n$, for $n\ge 0$, are given by:

$${\omega }_n\left(x\right)=x_0^{p^n}+p{x}_1^{p^{n-1}}+\cdots +p^n{x}_n$$

where $x=(x_0,x_1,\cdots )$.

The Witt polynomials are important for the next result.

Theorem 3.2. ([8]) There exists a unique Hopf algebra structure on the polynomial algebra ${\mathbb{Z}}_p[x_0,x_1,\cdots ]$, such that the Witt polynomials ${\omega }_n$ are primitive.

From now on, whenever we refer to the Hopf algebra ${\mathbb{Z}}_p[x_0,x_1,\cdots ]$, we mean the free commutative algebra over the indeterminates together with the unique coproduct that makes the Witt polynomials primitive.

We can also consider just the algebra ${\mathbb{Z}}_p[x_0,x_1,\cdots ,x_k]$. In this case, the coproduct defined from Theorem 3.2 restricts to a co-product in this finitely-generated algebra, and we will call $CW\left(k\right)$ the Hopf algebra ${\mathbb{Z}}_p[x_0,x_1,\cdots ,x_k]$ together with the restricted coproduct.

If we want to work in the graded case, start by giving each $x_i$ degree $p^{i}m$ for some fixed $m\in \mathbb{N}$, and then, define $C{W}_m\left(k\right)$ to be the graded Hopf algebra corresponding to $CW\left(k\right)$. We will also write $CW\left(\infty \right)$ for the Hopf algebra ${\mathbb{Z}}_p[x_0,x_1,\cdots ]$.

Proposition 3.3. [8] Let $\left[p\right]:{\mathbb{Z}}_p[x_0,x_1,\cdots ]\to {\mathbb{Z}}_p[x_0,x_1,\cdots ]$ be p-times the identity map in the abelian group of Hopf algebra maps ${\mathbb{Z}}_p[x_0,x_1,\cdots ]\to {\mathbb{Z}}_p[x_0,x_1,\cdots ]$. Then, $\left[p\right]\left(x_i\right)\cong x_{i-1}^p(modp)$.

Next, we want to consider Hopf algebras over a perfect field ${\mathbb{F}}_p$ with characteristic p. Define Hopf algebras $H\left(k\right)={\mathbb{F}}_p\otimes CW\left(k\right)={\mathbb{F}}_p[x_0,x_1,\cdots ,x_k]$. In the graded case, write $H\left(n\right)={\mathbb{F}}_p[x_0,x_1,\cdots ,x_k]$, where $n=p^{k}m$ for $(p,m)=1$ and each $x_i$ has degree $p^{i}m$. Write $H\left(\infty \right)$ for ${\mathbb{F}}_p[x_0,x_1,\cdots ]$.

Definition 3.4. For a Hopf algebra H over ${\mathbb{F}}_p$, the Frobenius is the homomorphism $F:H\to H$ taking an element x to the element $x^p$. The Verschiebung $V:H\to H$ is the dual to the Frobenius in the dual algebra.

The Verschiebung can be described as follows: if an element $x\in H$ has p-fold co-product ${\mathsf{\Psi }}^p\left(x\right)=\sum x^{\prime }\otimes x^{\prime }\otimes \cdots \otimes x^{\prime }+{\sum }_{\text{not}\text{all}\text{y}\text{equal}}{y}^{\prime }\otimes y^{\prime \prime }\otimes \cdots \otimes y^{p+1}$, then the Verschiebung on x is $V\left(x\right)=\sum x^{\prime }$.

Since we are dealing with Hopf algebras over a perfect field ${\mathbb{F}}_p$, both the Verschiebung and the Frobenius are homomorphisms of Hopf algebras.

All of our Hopf algebras will be bicommutative. We call such a (graded) Hopf algebra connected if $H_0\cong {\mathbb{F}}_p$.

Define ${\mathcal{H}A}_{*}$ (or just $\mathcal{H}A$, for short) as the category of graded, connected, bicommutative Hopf algebras over ${\mathbb{F}}_p$.

The Hopf algebras $H\left(n\right)={\mathbb{F}}_p[x_0,x_1,\cdots ,x_k]$ described above form a set of projective generators for ${\mathcal{H}A}_{*}$ [9].

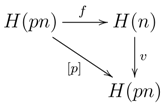
We have a morphism $v:H\left(n\right)={\mathbb{F}}_p[x_0,x_1,\cdots ,x_k]\to {\mathbb{F}}_p[x_0,x_1,\cdots ,x_{k+1}]=H\left(pn\right)$ given by inclusion. Furthermore, by Proposition 3.3, there exists a unique map of Hopf algebras $f:H\left(pn\right)\to H\left(n\right)$ making the following diagram commute.

This map satisfies $vf=\left[p\right]$ and also $fv=\left[p\right]$.

We now define Dieudonné modules for Hopf algebras in ${\mathcal{H}A}_{*}$.

Definition 3.5. The Dieudonné module for a Hopf algebra $H\in {\mathcal{H}A}_{*}$ is the graded abelian group:

$${\left\{D_{n}H\right\}}_{n\ge 1}={\left\{{\mathrm{Hom}}_{{\mathcal{H}A}_{*}}(H\left(n\right),H)\right\}}_{n\ge 1}$$

together with homomorphisms:

$$F:D_{n}H\to D_{pn}H$$

and

$$V:D_{pn}H\to D_{n}H$$

constructed from the previous maps f and v by composition on the left.

These homomorphisms reflect, thus, in Dieudonné modules, the Verschiebung and the Frobenius defined on Hopf algebras.

We have $VF=FV=p$ (here, p stands for p-times the identity map).

Furthermore, if $n=p^{s}k$ with $(p,k)=1$, then the order of the identity map in ${\mathrm{Hom}}_{{\mathcal{H}A}_{*}}(H\left(n\right),H\left(n\right))$ is $p^{s+1}$, and so, $p^{s+1}{D}_{n}H=0$.

We have defined thus a functor $D:{\mathcal{H}A}_{*}\to {\mathcal{D}M}_{*}$. This functor provides the following equivalence of categories.

Theorem 3.6. ([5,6]) The above functor D has a right adjoint $U:{\mathcal{D}M}_{*}\to {\mathcal{H}A}_{*}$, and the pair $(D,U)$ forms an equivalence of categories.

The proof confirms the fact that an abelian category with a set of small projective generators is equivalent to a category of modules over some ring [10,11].

Let H be a connected Hopf algebra. Given a Hopf algebra map $A:H\otimes H\to H\otimes H$, there is a natural way to induce a map $A:DH\otimes DH\to DH\otimes DH$ on the corresponding Dieudonné modules.

Suppose $n<m$. Then, $H\left(n\right)\subset H\left(m\right)$. We have a map $inc:H\left(n\right)\to H\left(m\right)$, given by inclusion, and another $proj:H\left(m\right)\to H\left(n\right)$, which is the identity on $H\left(n\right)$ and is zero outside it.

Define ${\mathsf{\Delta }}_1:H\left(n\right)\to H\left(n\right)\otimes H\left(m\right)$ by ${\mathsf{\Delta }}_1=i\otimes inc$, where i is the identity on $H\left(n\right)$. Furthermore, define ${\mathsf{\Delta }}_2:H\left(m\right)\to H\left(n\right)\otimes H\left(m\right)$ by ${\mathsf{\Delta }}_2=proj\otimes i$, where in this case i is the identity on $H\left(m\right)$.

The following compositions show the construction of two maps, one in $D_{n}H$ and the other in $D_{m}H$, from the maps above, and from $f\in D_{n}H$ and $g\in D_{m}H$.

$$H\left(n\right)\stackrel{{\mathsf{\Delta }}_1}{\to }H\left(n\right)\otimes H\left(m\right)\stackrel{A}{\to }H\left(n\right)\otimes H\left(m\right)\stackrel{p_1}{\to }H\left(n\right)\stackrel{f}{\to }H$$

$$H\left(m\right)\stackrel{{\mathsf{\Delta }}_2}{\to }H\left(n\right)\otimes H\left(m\right)\stackrel{A}{\to }H\left(n\right)\otimes H\left(m\right)\stackrel{p_2}{\to }H\left(m\right)\stackrel{g}{\to }H$$

Here, $p_1$ and $p_2$ are the projections into the first and the second factors, respectively.

$A:H\otimes H\to H\otimes H$ thus gives rise to $A:DH\otimes DH\to DH\otimes DH$ by

$f\otimes g⟼(f\circ p_1\circ A\circ {\mathsf{\Delta }}_1)\otimes (g\circ p_2\circ A\circ {\mathsf{\Delta }}_2)$

whenever $f\in D_{n}H$ and $g\in D_{m}H$.

If one writes $\tilde{f}$ for $f\circ p_1\circ A\circ {\mathsf{\Delta }}_1$ and $\tilde{g}$ for $g\circ p_2\circ A\circ {\mathsf{\Delta }}_2$, the induction above is $f\otimes g⟼\tilde{f}\otimes \tilde{g}$.

This notation is not entirely indicative, since $\tilde{f}$ depends not only on f, but also on g (and the same goes for $\tilde{g}$). We will write down this dependency explicitly, by using ${\tilde{f}}_{{}_g}$ and ${\tilde{g}}_{{}_f}$ instead of $\tilde{f}$ and $\tilde{g}$.

One can check what relations such an induced A must verify in order to be a generalized Yang–Baxter operator on the corresponding Dieudonné module for H and obtain in the process corresponding relations for the original A at the Hopf algebra level. Because of the dependency referred to in the previous paragraph, these relations can be difficult to read.

We take a $f\otimes g\otimes h$ in $D_{n}H\otimes D_{m}H\otimes D_{k}H$. Then,

$$\begin{array}{cc}\hfill A^{12}{A}^{23}{A}^{12}(f\otimes g\otimes h)& =A^{12}{A}^{23}({\tilde{f}}_{{}_g}\otimes {\tilde{g}}_{{}_f}\otimes h)\hfill \\ & =A^{12}({\tilde{f}}_{{}_g}\otimes {\widetilde{\left({\tilde{g}}_{{}_f}\right)}}_h\otimes {\tilde{h}}_{{\tilde{g}}_{{}_f}})\hfill \\ & ={\widetilde{\left({\tilde{f}}_g\right)}}_{{\widetilde{\left({\tilde{g}}_{{}_f}\right)}}_h}\otimes {\tilde{\left({\widetilde{\left({\tilde{g}}_{{}_f}\right)}}_h\right)}}_{{\tilde{f}}_{{}_g}}\otimes {\tilde{h}}_{{\tilde{g}}_{{}_f}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill A^{23}{A}^{12}{A}^{23}(f\otimes g\otimes h)& =A^{23}{A}^{12}(f\otimes {\tilde{g}}_{{}_h}\otimes {\tilde{h}}_{{}_g})\hfill \\ & =A^{23}({\tilde{f}}_{{\tilde{g}}_{{}_h}}\otimes {\widetilde{\left({\tilde{g}}_{{}_h}\right)}}_f\otimes {\tilde{h}}_{{}_g})\hfill \\ & ={\tilde{f}}_{{\tilde{g}}_{{}_h}}\otimes {\tilde{\left({\widetilde{\left({\tilde{g}}_{{}_h}\right)}}_f\right)}}_{{\tilde{h}}_{{}_g}}\otimes {\widetilde{\left({\tilde{h}}_g\right)}}_{{\widetilde{\left({\tilde{g}}_{{}_h}\right)}}_f}\hfill \end{array}$$

The relations are then, for any f, g and h under the above assumptions,

$$\begin{array}{cc}{\widetilde{\left({\tilde{f}}_g\right)}}_{{\widetilde{\left({\tilde{g}}_{{}_f}\right)}}_h}={\tilde{f}}_{{\tilde{g}}_{{}_h}}\hfill & \\ \\ {\tilde{\left({\widetilde{\left({\tilde{g}}_{{}_f}\right)}}_h\right)}}_{{\tilde{f}}_{{}_g}}={\tilde{\left({\widetilde{\left({\tilde{g}}_{{}_h}\right)}}_f\right)}}_{{\tilde{h}}_{{}_g}}\hfill & \\ \\ {\tilde{h}}_{{\tilde{g}}_{{}_f}}={\widetilde{\left({\tilde{h}}_g\right)}}_{{\widetilde{\left({\tilde{g}}_{{}_h}\right)}}_f}\hfill \end{array}$$

4. Yang–Baxter Operators on Dieudonné Modules, Hopf Ring and Hopf Coring Structures

One defines a bilinear map for R-modules M, N and L as a map $g:M\otimes N\to L$ that satisfies:

(1) $Vg(m\otimes n)=g(Vm\otimes Vn)$

(2) $Fg(Vm\otimes n)=g(m\otimes Fn)$

(3) $Fg(m\otimes Vn)=g(Fm\otimes n)$

for every $m\in M$ and $n\in N$.

We reprint here a result from [4], which works for categories of Hopf algebras over a perfect field of either zero or p characteristic. For our purposes here, the second part is what will be used in the deduction of the Yang–Baxter operators’ influence on the original Hopf algebras. In the present work, these will always be connected.

Lemma 4.1. Any bilinear pairing ${\circ }_{ij}:D{H}_i\otimes D{H}_j\to D{H}_{i+j}$ induces a bilinear pairing ${\circ }_{ij}^{\prime }:H_i\otimes H_j\to H_{i+j}$.

Proof. Suppose first that the characteristic of the base field is zero.

To define uniquely the map ${\circ }^{\prime }:H_i\otimes H_j\to H_{i+j}$, it is enough to fix its value on the primitives of $H_i\otimes H_j$ (since this is a connected Hopf algebra), Suppose $x\otimes 1$, with x a primitive of $H_i$, is such an element (the other only possibility, a $1\otimes y$ with y a primitive of $H_j$, can be dealt with similarly). If the degree of x is $n=p^{k}m$, define the homomorphism $\widehat{x}\in D_n{H}_i$ by $\widehat{x}\left(1\right)=1$, $\widehat{x}\left({\omega }_k\right)=x$ and $\widehat{x}\left({\mathsf{\omega }}_i\right)=0$ for $i\ne k$. Define also $\widehat{1}\in D_0{H}_j$ by $\widehat{1}\left(1\right)=1$. Then, $\widehat{x}\circ \widehat{1}$ is in $D_n{H}_{i+j}$, and we define $x{\circ }^{\prime }1$ as $[\widehat{x}\circ \widehat{1}]\left({\omega }_k\right)$. (If the degree of x is not of the form $n=p^{k}m$, define $x{\circ }^{\prime }1=0$.)

If the characteristic of the base field is a prime, we can run into additional problems. In this case, we have to work from the condition of connectedness. If x in $H_i$ has zero Verschiebung, then we can still define $x{\circ }^{\prime }1$ as in the reference above. If $V\left(x\right)$ is non-zero, by connectedness, there exists an $r>0$, such that the repeated Verschiebung $V^r\left(x\right)$ is zero, but $V^{r-1}\left(x\right)=b$ is non-zero. If the degree of b is $n=p^{k}m$, define $\widehat{x}\in D_n{H}_i$ by $\widehat{x}\left(1\right)=1$, $\widehat{x}\left({\omega }_k\right)=b$ and $\widehat{x}\left({\omega }_i\right)=0$ for $i\ne k$. Then, $x{\circ }^{\prime }1$ is defined as $[\widehat{x}\circ \widehat{1}]\left({\omega }_k^r\right)$. (If the degree of b is not of the form $n=p^{k}m$, define $x{\circ }^{\prime }1=0$.) We can similarly define $1{\circ }^{\prime }y$ for $y\in H_j$. If either x or y are primitives, this will coincide with what was done before. Finally, just define $x{\circ }^{\prime }y=\left(x{\circ }^{\prime }1\right)\left(1{\circ }^{\prime }y\right)$.

This definition works for the general case of $p\ge 2$.  ☐

The category of Dieudonné modules that we have defined has universal bilinear products [8]. This is the basis of the equivalence between categories of Hopf rings and of Dieudonné rings (which are Dieudonné modules with additional products) from [4,8].

Suppose you have a Yang–Baxter operator $A:DH\otimes DH\to DH\otimes DH$, and suppose $A_1=p_1\circ A$ and $A_2=p_2\circ A$ are bilinear maps of Dieudonné modules. Then, the induced maps on $H\otimes H$, $A_1^{\prime }:H\otimes H\to H$ and $A_2^{\prime }:H\otimes H\to H$, are maps of coalgebras that give H two structures of the Hopf ring [4]. The Yang–Baxter condition on the Dieudonné modules gives a relation between the two Hopf ring structures. Before we use this in our previous examples, we obtain a description of the equivalent Hopf algebra for each of the Dieudonné modules that were presented in Section 2, following the conclusions of Theorem 3.6.

Example 4.2. R, viewed as a Dieudonné module (as in Example 2.2), is equivalent to $DH\left(\infty \right)$, since clearly $R\simeq {\mathrm{Hom}}_{{\mathcal{H}A}_{*}}(H\left(n\right),H\left(\infty \right))$.

Example 4.3. For Example 2.3, we have ${\mathrm{Hom}}_{{\mathcal{H}A}_{*}}(H\left(n\right),CW\left(\infty \right))\simeq {\mathbb{Z}}_p[F,V]$, and so, $DCW\left(\infty \right)\simeq {\mathbb{Z}}_p[F,V]$.

Example 4.4. The Dieudonné module from Example 2.4 was suggested by the one for the Hopf algebra $K{\left(n\right)}_{*}\left({\mathbf{K}}_1\right)$, where ${\mathbf{K}}_1$ is the first Eilenberg–MacLane space $K(\mathbb{Z}/(p),1)$. This and the Hopf ring for further Eilenberg–MacLane spaces are completely described in [1]. By analogy, in our example, we get that the Hopf algebra corresponding to M is a truncated polynomial algebra generated by the $a_{\left(i\right)}^k$, where the p-th algebra power of each of these generators is zero (for $K{\left(n\right)}_{*}\left({\mathbf{K}}_1\right)$, the algebra relations depend on elements $v_n$ that we are not considering in this example). The coalgebra structure is given by $\psi \left(a_{\left(i\right)}^k\right)={\sum }_{j=0}^i{a}_{\left(j\right)}^k\otimes a_{(i-j)}^k$.

Example 4.5. For the Hopf algebra corresponding to the Dieudonné module in Example 2.6, we again adapt the periodically-graded situation from [1]. Each map $I:{\mathbb{N}}_0\to \{0,1\}$ in the conditions of Example 2.6 (namely, non-zero, except eventually on the n consecutive integers $i,\cdots ,i+n-1$) will correspond to an element of the form $a_{\left(i\right)}^{I\left(i\right)}\circ \cdots \circ a_{(i+n-1)}^{I(i+n-1)}$, where the ∘ notation is inspired by the subjacent Hopf ring structure (which is not dealt with here). The algebra in question will be free on these elements (over ${\mathbb{F}}_p$), with the algebra product of an $a_{\left(i\right)}^{I\left(i\right)}\circ \cdots \circ a_{(i+n-1)}^{I(i+n-1)}$ and an $a_{\left(j\right)}^{I\left(j\right)}\circ \cdots \circ a_{(j+n-1)}^{I(j+n-1)}$ given by an element $a_{\left(k\right)}^{I\left(k\right)}\circ \cdots \circ a_{(k+n-1)}^{I(k+n-1)}$ obtained by rearranging the $a_{\left(i\right)}$ and $a_{\left(j\right)}$ in increasing order of indexes, summing (mod two) the superscripts $I\left(i\right)$ and $I\left(j\right)$ for the same indexes and multiplying the result by the index of the permutation obtained from $(i,\cdots ,i+n-1)$ and $(j,\cdots ,j+n-1)$ by concatenation and by eliminating any repetitions of indexes that may appear in both of these sub-permutations. We determine also that this product should be zero if the resulting element is not of the form of those I in the definition of the original Dieudonné module (this has to do with I being nonzero only for q elements in a range of n consecutive natural numbers.)

As for the coalgebra structure, take a $a_{\left(i\right)}^{I\left(i\right)}\circ \cdots \circ a_{(i+n-1)}^{I(i+n-1)}$, and define formally its coproduct as:

$$(a_{\left(i\right)}^{I\left(i\right)}\otimes a_{\left(i\right)}^{I\left(i\right)})\circ (a_{\left(i\right)}^{I\left(i\right)}\otimes a_{(i+1)}^{I(i+1)}+a_{(i+1)}^{I(i+1)}\otimes a_{\left(i\right)}^{I\left(i\right)})\circ \cdots \circ ({\sum }_{r=0}^k{a}_{(i+r)}^{I(i+r)}\otimes a_{(n+i-r)}^{I(n+i-r)})\circ \cdots \circ ({\sum }_{r=0}^{n-1}{a}_{(i+r)}^{I(i+r)}\otimes a_{(n-1+i-r)}^{I(n-1+i-r)})$$

where we distribute (formally) in order to obtain a sum of elements given by ∘ “products” of the $a_{\left(i\right)}$.

We now turn to the Yang–Baxter operators for the Dieudonné modules from Section 2 and deduce the induced $A_1^{\prime }$ and $A_2^{\prime }$ on the corresponding Hopf algebras.

Example 4.6. Consider first the switch operator from Example 2.9.

Clearly, the induced $A_1$ and $A_2$ are projections onto the opposite factors: $A_1=p_2$ and $A_2=p_1$. If we consider a Dieudonné module $DH$ for a Hopf algebra H in $\mathcal{H}A$, the induced products on H can be deduced as follows.

Suppose $x\in H$ is such that $V^r\left(x\right)=0$, but $V^{r-1}\left(x\right)\ne 0$. Then,

$A_1^{\prime }(x,1)=A_1(\widehat{x},\widehat{1})\left({\omega }_k^r\right)=\widehat{1}\left({\omega }_k^r\right)=0$ and:

$A_1^{\prime }(1,x)=A_1(\widehat{1},\widehat{x})\left({\omega }_k^r\right)=\widehat{x}\left({\omega }_k^r\right)={\left[\widehat{x}\left({\omega }_k\right)\right]}^r={\left[V^{r-1}\left(x\right)\right]}^r$

This is a non-commutative ring structure that exists thus for any H in $\mathcal{H}A$. The other one (also non-commutative) comes from:

$A_2^{\prime }(x,1)=A_2(\widehat{x},\widehat{1})\left({\omega }_k^r\right)=\widehat{x}\left({\omega }_k^r\right)={\left[\widehat{x}\left({\omega }_k\right)\right]}^r={\left[V^{r-1}\left(x\right)\right]}^r$ and:

$A_2^{\prime }(1,x)=A_2(\widehat{1},\widehat{x})\left({\omega }_k^r\right)=\widehat{1}\left({\omega }_k^r\right)=0$

Note that, as defined in the proof of Lemma 4.1, $A_1^{\prime }(x,y)=A_1^{\prime }(x,1)A_1^{\prime }(1,y)$ (and the same happens for $A_2^{\prime }$). This means that $A_1^{\prime }$ is right-sided, that is it can only be nonzero whenever x is one, and $A_2^{\prime }$ is left-sided (can only be nonzero whenever y is one).

Example 4.7. Continuing Example 2.10, identify $V^k$ with ${\widehat{\omega }}_k$, in the notation of Lemma 4.1, and $F^k$ with $1\circ f^k$, where f is the map mentioned just before Definition 3.5.

We have, for $x\in H\left(\infty \right)$, such that $V^r\left(x\right)=0$, but $V^{r-1}\ne 0$, $A_1^{\prime }(x,1)=A_1(\widehat{x},\widehat{1})\left({\omega }_k^r\right)=\alpha \left(\widehat{x}\right)\left({\omega }_k^r\right)$. This last value is equal to ${\left[\widehat{x}\left({\omega }_k\right)\right]}^r={\left(V^{r-1}\left(x\right)\right)}^r$, except if $\widehat{x}=F^k=1\circ f^k$ and $p\nmid k$, where it equals ${[1\circ f^{pk}\left({\omega }_k\right)]}^r={\left[f^{pk}\left({\omega }_k\right)\right]}^r=0$. Furthermore, $A_1^{\prime }(1,x)=A_1(\widehat{1},\widehat{x})\left({\omega }_k^r\right)=\alpha \left(\widehat{1}\right)\left({\omega }_k^r\right)=\left(\widehat{1}\right)\left({\omega }_k^r\right)=0$ by definition of $\widehat{1}$.

This gives the first of our two new ring operations on $H\left(\infty \right)$. It is clearly non-commutative, and moreover, $A_1^{\prime }(x,y)=0$ whenever $y\ne 1$ (since, by definition, $A_1^{\prime }(x,y)=A_1^{\prime }(x,1)A_1^{\prime }(1,y)$).

For $A_2^{\prime }$, we get:

$A_2^{\prime }(x,1)=A_2(\widehat{x},\widehat{1})\left({\omega }_k^r\right)=\beta \left(\widehat{1}\right)\left({\omega }_k^r\right)=\left(\widehat{1}\right)\left({\omega }_k^r\right)=0$, and

$A_2^{\prime }(1,x)=A_2(\widehat{1},\widehat{x})\left({\mathsf{\omega }}_k^r\right)=\beta \left(\widehat{x}\right)\left({\mathsf{\omega }}_k^r\right)$

This equals ${\left[\widehat{x}\left({\mathsf{\omega }}_k\right)\right]}^r={\left(V^{r-1}\left(x\right)\right)}^r$, except if $k=pm$ for some m and $p\nmid m$ (so that $\widehat{x}=V^{pm}={\widehat{\mathsf{\omega }}}_{pm}$), where it equals zero, since ${\widehat{\mathsf{\omega }}}_{pm}\circ v=\widehat{1}$.

This second ring operation is also non-commutative. In this example, the relation between the induced products $A_1^{\prime }$ and $A_2^{\prime }$ comes from the original Yang–Baxter operator: α and β were both idempotent and satisfied the braid condition $\mathsf{\alpha }\mathsf{\beta }\mathsf{\alpha }=\mathsf{\beta }\mathsf{\alpha }\mathsf{\beta }$. This reflects on the elements x in $H\left(\infty \right)$ for which $A_1^{\prime }$ or $A_2^{\prime }$ is nonzero.

The previous example worked from the generators of the corresponding polynomial algebra, and thus, the same deductions can be easily adapted to the situation of Example 4.3.

Example 4.8. In Example 2.12, we again had a Yang–Baxter operator of the form $A=\alpha \otimes \beta$. The Hopf algebra in Example 4.4 will then have two induced coalgebra structures, coming from $A_1(x,y)=\alpha \left(x\right)$ and $A_2(x,y)=\beta \left(y\right)$ (where x and y are in the Dieudonné module).

The polynomial generators of the Hopf algebra are interpreted as elements in the Dieudonné module (as powers of the $V_k$). This means that the induced $A_1^{\prime }$ and $A_2^{\prime }$ have the same behavior: $A_1^{\prime }(x,y)=x$ for x and y in the Hopf algebra, except whenever $x=V_k^{r(n-1)}$ with $p\nmid r$, and $r\le k$, where it is $V_k^{pr(n-1)}$; $A_2^{\prime }(x,y)=y$ for x and y in the Hopf algebra, except whenever $y=V_k^{pr}$ with $p\nmid r$ and $pr\le k$, where it is $V_k^r$

Example 4.9. For the same Hopf algebra and the Yang–Baxter operator from Example 2.13, we get structures similar to those in the previous example, the difference being in the range of indexes where the generators of the algebra exist.

Example 4.10. For Example 2.14 and the Hopf algebra in Example 4.5, we have also $A_1(I,J)=\mathsf{\alpha }\left(I\right)$ and $A_2(I,J)=\mathsf{\beta }\left(J\right)$, and so, the two new ring structures will be projections on the first and second factors, except if $I(n-1-r(n-1\left)\right)=1$ and $I\left(j\right)=0$ for $j<n-1-r(n-1)$ (with $p\nmid r$ and $r<k$), for which $A_1(I,J)=s^{-1}\left(I\right)$, and if $J(n-1-pr)=1$ and $J\left(j\right)=0$ for $j<n-1-pr$ (with $p\nmid r$ and $pr\le n$), for which $A_2(I,J)=s\left(J\right)$.

The notion of bilinear map on Dieudonné modules has a dual, that of the cobilinear map, which is explored in [12].

A cobilinear map for R-modules M, N and L is a map $g:M\to N\otimes L$ satisfying:

(1) $g\left(Fm\right)=(F\otimes F)\left(gm\right)$

(2) $(F\otimes 1)\left(g\right(Vm\left)\right)=(1\otimes V)\left(gm\right)$

(3) $(1\otimes F)\left(g\right(Vm\left)\right)=(V\otimes 1)\left(gm\right)$

for every $m\in M$.

There exists a universal cobilinear map on the category of Dieudonné modules. In the connected case, this allows for the equivalence between the category of Dieudonné corings and a corresponding category of Hopf corings [12].

The following result is symmetric to Lemma 4.1.

Lemma 4.11. [12] Any cobilinear map $g:DH\to D{H}_1\otimes D{H}_2$, where H, $H_1$ and $H_2$ are connected Hopf algebras in $\mathcal{HA}$, induces a cobilinear map $g^{\prime }:H\to H_1\otimes H_2$.

Proof. Since H is connected, it is enough to define $g^{\prime }$ on primitives and induced primitives [12].

Given a primitive $q\in H$, pick a positive m and consider $\tilde{q}\in {\mathrm{Hom}}_{\mathcal{HA}}(H\left(m\right),H)$ given by $\tilde{q}\left(1\right)=1$, $\tilde{q}\left({\omega }_m\right)=q$ and $\tilde{q}\left({\omega }_i\right)=0$ for $i\ne m$ (here, ${\omega }_i$ are the Witt polynomials).

Then, $g\left(\tilde{q}\right)$ is in $D{H}_1\otimes D{H}_2$, and so, the projections on $D{H}_1$ and $D{H}_2$ are such that:

$$g_1\left(\tilde{q}\right)=\mathsf{\alpha }\mathrm{ for some }r\mathrm{ and some }\mathsf{\alpha }\in {\mathrm{Hom}}_{\mathcal{HA}}(H\left(r\right),H_1)$$

and

$$g_2\left(\tilde{q}\right)=\mathsf{\beta }\mathrm{ for some }s\mathrm{ and some }\mathsf{\beta }\in {\mathrm{Hom}}_{\mathcal{HA}}(H\left(s\right),H_2)$$

Define then $g^{\prime }\left(q\right)$ as $\mathsf{\alpha }\left({\mathsf{\omega }}_r\right)\otimes \mathsf{\beta }\left({\mathsf{\omega }}_s\right)$.

If $q^{\left(n\right)}$ is an induced primitive (relative to the primitive q), we can still define $\tilde{q}$ and obtain α and β as before.

Put then $g^{\prime }\left(q^{\left(n\right)}\right)=\mathsf{\alpha }\left({\left({\omega }_r\right)}^{\left(n\right)}\right)\otimes \mathsf{\beta }\left({\left({\mathsf{\omega }}_s\right)}^{\left(n\right)}\right)$.  ☐

Given $H\in \mathcal{H}A$, fix an element in $DH$, for example $\widehat{1}$. We can define two inclusions $i_1:DH\to DH\otimes DH$ and $i_2:DH\to DH\otimes DH$ by $i_1\left(x\right)=x\otimes \widehat{1}$ and $i_2\left(x\right)=\widehat{1}\otimes x$.

For a Yang–Baxter operator $A:DH\otimes DH\to DH\otimes DH$, suppose $A_1=A\circ i_1$ and $A_2=A\circ i_{2}A$ are cobilinear maps of Dieudonné modules. Then, the induced maps $A_1^{\prime }:H\to H\otimes H$ and $A_2^{\prime }:H\to H\otimes H$ are algebra maps that give H two structures of Hopf coring [12]. We write down what these induced structures mean for the previous examples.

Example 4.12. For the switch operator A from Example 2.9 on any $DH$, we get $A_1\left(x\right)=A\circ i_1\left(x\right)=A(x\otimes \widehat{1})=\widehat{1}\otimes x$ and $A_2\left(x\right)=A\circ i_2\left(x\right)=A(\widehat{1}\otimes x)=x\otimes \widehat{1}$ for any $x\in DH$.

Thus, $A_1=i_2$ and $A_2=i_1$ in this case.

For a primitive $q\in H$, we get $A_1\left(\tilde{q}\right)=\widehat{1}\otimes \tilde{q}$, and so, $A_1^{\prime }\left(q\right)=1\otimes q$. For an induced primitive $q^{\left(n\right)}$, we get $A_1^{\prime }\left(q^{\left(n\right)}\right)=1\otimes \tilde{q}\left(q^{\left(n\right)}\right)=0$. This defines the first coring operation on H.

For $A_2$, we get, similarly, $A_2\left(\tilde{q}\right)=\tilde{q}\otimes \widehat{1}$ for a primitive $q\in H$, and so, $A_2^{\prime }\left(q\right)=q\otimes 1$ and $A_2^{\prime }\left(q^{\left(n\right)}\right)=\tilde{q}\left(q^{\left(n\right)}\right)\otimes 1=0$ for an induced primitive. This gives the second coring operation.

Example 4.13. Continuing Example 2.10, we get $A_1\left(x\right)=A\circ i_1\left(x\right)=A(x\otimes \widehat{1})=\mathsf{\alpha }\left(\widehat{1}\right)\otimes \mathsf{\beta }\left(x\right)=\widehat{1}\otimes \mathsf{\beta }\left(x\right)$.

For the induced operation on the Hopf algebra $H\left(\infty \right)$, consider first a Witt polynomial ${\omega }_i$ in $H\left(\infty \right)$ (those form its primitive elements). We get:

$A_1\left({\tilde{\mathsf{\omega }}}_i\right)=\mathsf{\alpha }\left({\tilde{\mathsf{\omega }}}_i\right)\otimes \widehat{1}$, and so, $A_1^{\prime }\left({\mathsf{\omega }}_i\right)=\mathsf{\alpha }\left({\tilde{\mathsf{\omega }}}_i\right)\left({\mathsf{\omega }}_i\right)\otimes 1$. This works for the general case of Example 2.11. For 2.10, we get further that $A_1^{\prime }\left(x\right)$ is the inclusion $x\otimes 1$, except on those ${\mathsf{\omega }}_i$ for which ${\tilde{\mathsf{\omega }}}_i={\widehat{\mathsf{\omega }}}_i$ is of the form $1\circ f^k$ with $p\nmid k$, where it equals $f^k\left({\mathsf{\omega }}_i\right)\otimes 1=0$.

For induced primitives x, we get also the inclusion $x\otimes 1$, except on the elements of the same form, where it is zero.

The second possible operation comes from $A_2\left({\tilde{\mathsf{\omega }}}_i\right)=\widehat{1}\otimes \mathsf{\beta }\left({\tilde{\mathsf{\omega }}}_i\right)$. This gives $A_2^{\prime }\left({\mathsf{\omega }}_i\right)=\beta \left({\tilde{\mathsf{\omega }}}_i\right)\left({\omega }_i\right)\otimes 1$. This will be the identity, except on those ${\mathsf{\omega }}_{pk}$ with $p\nmid k$, where one gets $\mathsf{\beta }\left({\tilde{\mathsf{\omega }}}_{pk}\right))={\tilde{\mathsf{\omega }}}_k$, and so, $A_2^{\prime }\left({\mathsf{\omega }}_{pk}\right)={\tilde{\mathsf{\omega }}}_k\left({\mathsf{\omega }}_{pk}\right)\otimes 1=0$. The same behavior reflects on induced primitives. Thus, the operations $A_1^{\prime }$ and $A_2^{\prime }$ are symmetric.

Example 4.14. The Yang–Baxter operator from Example 2.12 is also of the form $A=\mathsf{\alpha }\otimes \mathsf{\beta }$. This means that the deductions in the previous example are also at hand.

The polynomial generators $a_{\left(i\right)}^k$ of the Hopf algebra are not primitive, since the coalgebra structure has, as a coproduct, $\psi \left(a_{\left(i\right)}^k\right)={\sum }_{j=0}^i{a}_{\left(j\right)}^k\otimes a_{(i-j)}^k$. These generators correspond to elements of the same nature in the Dieudonné module (we used the identification $V_k^m=a_{(n-1-m)}^k$ for $m=0,\cdots ,n-1$). It is enough thus to define the induced operations, which are maps of algebras, on these generators. We get: $A_1\left(a_{\left(i\right)}^k\right)=\alpha \left(a_{\left(i\right)}^k\right)\otimes 1=\alpha \left(V_k^{n-1-i}\right)\otimes 1$. This becomes $V_k^{n-1-i}\otimes 1=a_{\left(i\right)}^k\otimes 1$ except if $p\nmid (n-1-i)$ and $n-i-1\le k$, where one gets $V_k^p(n-1-i)\otimes 1=a_{(n-1-p(n-1-i\left)\right)}^k\otimes 1=a_{\left(\right(n-1\left)\right(1-p)+pi)}^k\otimes 1$.

The second algebra structure comes from $A_2\left(a_{\left(i\right)}^k\right)=1\otimes \mathsf{\beta }\left(a_{\left(i\right)}^k\right)=1\otimes \mathsf{\beta }\left(V_k^{n-1-i}\right)$. This becomes $1\otimes V_k^{n-1-i}=1\otimes a_{\left(i\right)}^k$, except if $n-1-i=pr$ for some r, such that $p\nmid r$ and $pr\le n$, where one gets $1\otimes V_k^r=1\otimes a_{(n-1-r)}^k$.

Example 4.15. Example 2.13 gives the same definitions for the induced products as the previous example. Nonetheless, in this case, the elements $a_{\left(i\right)}^k$ for different values of k are not independent, which means that the restrictions on the range of values that r and k may assume make for structures that differ from those in that example.

Example 4.16. Continuing Example 2.14, for the Hopf algebra in Example 4.5, we again have $A=\mathsf{\alpha }\otimes \mathsf{\beta }$, and so, $A_1\left(x\right)=\widehat{1}\otimes \mathsf{\beta }\left(x\right)$ and $A_2\left(x\right)=\mathsf{\alpha }\left(x\right)\otimes \widehat{1}$. Reading the definitions of α and β, on the generators I, we get then, as structures:

$A_1\left(I\right)=1\otimes s\left(I\right)$ if $I(n-1-pr)=1$, $p\nmid r$, $pr\le n$ and $I\left(j\right)=0$ for $j<n-1-pr$, and $1\otimes I$ elsewhere.

and $A_2\left(I\right)=s^{-1}\left(I\right)\otimes 1$ if $I(n-1-r(n-1\left)\right)=1$, $p\nmid r$, $r<k$ and $I\left(j\right)=0$ for $j<n-1-r(n-1)$, and $I\otimes 1$ elsewhere.

There is a different way of obtaining induced coring structures from Yang–Baxter operators. Consider again an operator $A:DH\otimes DH\to DH\otimes DH$ and compose it with the diagonal map $\mathsf{\Delta }:DH\to DH\otimes DH$. This gives a map $A_3:DH\to DH\otimes DH$, which again induces an algebra map $A_3^{\prime }:H\to H\otimes H$. We look at this map for the different examples we had before.

Example 4.17. The switch operator from Example 2.9 induces the same $A_3$ as the identity operator, which is simply the diagonal: $A_3\left(x\right)=sw\circ \mathsf{\Delta }\left(x\right)=sw(x\otimes x)=x\otimes x$ for $x\in DH$.

For a primitive $q\in H$, $A_3^{\prime }\left(q\right)=q\otimes q$. On induced primitives, $A_3^{\prime }\left(q^{\left(n\right)}\right)=\tilde{q}\left(q^{\left(n\right)}\right)\otimes \tilde{q}\left(q^{\left(n\right)}\right)=0$, and so, the switch operator on Dieudonné modules induces in this way the diagonal operator on the corresponding Hopf algebras (but nonzero only on primitives.)

Example 4.18. For Example 2.10 and the Hopf algebra $H\left(\infty \right)$, $A_3\left(x\right)=\alpha \left(x\right)\otimes \beta \left(x\right)$.

On Witt vectors, the induced $A_3^{\prime }$ becomes $A_3^{\prime }\left({\omega }_i\right)=\alpha \left({\omega }_i\right)\otimes \beta \left({\omega }_i\right)$. From the considerations in Example 4.13, we see that $A_3^{\prime }$ is zero, except if $p\nmid i$, and ${\tilde{\omega }}_i$ is not of the form $1\circ f^k$ with $p\nmid k$, where it becomes the diagonal.

Example 4.19. For Example 2.12, we again have $A_3\left(x\right)=\mathsf{\alpha }\left(x\right)\otimes \mathsf{\beta }\left(x\right)$ for x in the Dieudonné module. The considerations in Example 4.14 imply that the induced $A_3^{\prime }$ on the generators $a_{\left(i\right)}^k$ will be the diagonal, except if either $p\nmid (n-1-i)$ (and $n-1-i\le k$) or $n-1-i=pr$ for some r, such that $p\nmid r$ (and $pr\le n$). Both conditions cannot be satisfied simultaneously. This means that, because of the behavior of these particular α and β, one of the components in the image by $A_3^{\prime }$ of any element in the Hopf algebra will always be the identity.

Example 4.20. The previous example works also for the Yang–Baxter operator in Example 2.13 if we take into account the restrictions discussed in Example 4.15.

Example 4.21. From Example 2.14, we get that $A_3$ of a generator I can be the identity, $1\otimes I$, $I\otimes 1$, $1\otimes s\left(I\right)$, $s^{-1}\left(I\right)\otimes 1$ or $s^{-1}\left(I\right)\otimes s\left(I\right)$. These values will depend, as before, on the range of the indexes at play. In particular, the last value, which corresponds to a $\mathsf{\alpha }\left(I\right)\otimes \mathsf{\beta }\left(I\right)$ where neither α nor β are the identity, occurs whenever $n-1-pr=n-1-r(n-1)$, that is if $n-1$ is the prime p. Since we must also have that $pr\le n$, this implies that $r=1$.