Yang-Baxter Systems, Algebra Factorizations and Braided Categories

Abstract

The Yang-Baxter equation first appeared in a paper by the Nobel laureate, C.N. Yang, and in R.J. Baxter’s work. Later, Vladimir Drinfeld, Vaughan F. R. Jones and Edward Witten were awarded Fields Medals for their work related to the Yang-Baxter equation. After a short review on this equation and the Yang-Baxter systems, we consider the problem of constructing algebra factorizations from Yang-Baxter systems. Our sketch of proof uses braided categories. Other problems are also proposed.

1. Introduction

The Yang-Baxter equation first appeared in a paper by the Nobel laureate, C.N. Yang, and in R.J. Baxter’s work. At the 1990 International Mathematics Congress, Vladimir Drinfeld, Vaughan F. R. Jones and Edward Witten were awarded Fields Medals for their work related to the Yang-Baxter equation.

This equation plays a crucial role in many areas of mathematics, physics and computer science. Many scientists have used the axioms of various algebraic structures or computer calculations in order to produce solutions for it, but the full classification of its solutions remains an open problem.

In our previous special issue on Hopf algebras, quantum groups and Yang-Baxter equations, several papers [1,2,3,4,5,6], as well the feature paper [7], covered many topics related to the Yang-Baxter equation.

The interest in the Yang-Baxter equation is also motivated by its many applications and interpretations. As an example of categorical interpretation, let us consider the following extension for the duality between finite dimensional algebras and coalgebras to the category of finite dimensional Yang–Baxter structures (from [8] and, also, [4]). That duality can be illustrated by the following diagram:

The previous duality extension resembles the duality extension from [9]. Furthermore, the extension of the duality between finite dimensional algebras and coalgebras could lead to further developments of the current paper.

The following list of recent papers could be an introduction and a motivation to study Yang-Baxter systems: [10,11,12,13,14].

The next section provides a mathematical background on Yang-Baxter systems, and Section 3 contains the main problems and results.

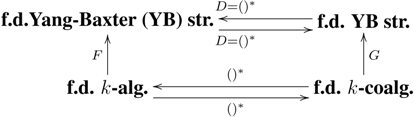
2. Preliminaries

We work over the field k, and all the unadorned tensor products are tensor products over k.

The identity map on a k-vector space V is denoted by $I=I_V$.

All the algebras considered are k-algebras, and they are associative and with a unity; the product in a k-algebra A is denoted by $\mu :A\otimes A\to A$, while the unit map is denoted by $\iota :k\to A$.

For any vector spaces V and W, $\tau ={\tau }_{V,W}:V\otimes W\to W\otimes V$ denotes the natural bijection defined by ${\tau }_{V,W}(v\otimes w)=w\otimes v$.

Let $R:V\otimes V\to V\otimes V$ be a k-linear map. Define $R_{12}=R\otimes I$, $R_{23}=I\otimes R$ and $R_{13}=(I\otimes \tau )\circ (R\otimes I)\circ (I\otimes \tau )$. Each of the $R_{ij}$ is thus a linear endomorphism of $V\otimes V\otimes V$.

Definition 2.1 An invertible k-linear map, $R:V\otimes V\to V\otimes V$, is called a Yang-Baxter operator (or, simply, a YB operator) if it satisfies the equation:

$$R_{12}\circ R_{23}\circ R_{12}=R_{23}\circ R_{12}\circ R_{23}$$

(1)

Equation (1) is usually called the braid equation. It is a well-known fact that the operator R satisfies (1) if and only if $R\circ {\tau }_{V,V}$ satisfies the quantum Yang-Baxter equation:

$$R_{12}\circ R_{13}\circ R_{23}=R_{23}\circ R_{13}\circ R_{12}$$

(2)

Example 2.2 ([15]) If A is a k-algebra, then for all non-zero $r,s\in k$, the linear map:

$$R_{r,s}^A:A\otimes A\to A\otimes A,a\otimes b\mapsto sab\otimes 1+r1\otimes ab-sa\otimes b$$

(3)

is a Yang-Baxter operator.

This construction played an important role in the construction of Yang-Baxter systems from algebra factorizations (see [16]).

Yang-Baxter systems were introduced in [17], as a spectral-parameter independent generalization of quantum Yang-Baxter equations related to non-ultralocal integrable systems, previously studied in [18].

Yang-Baxter systems are conveniently defined in terms of Yang-Baxter commutators. Consider three vector spaces, $V,V^{\prime },V^{″}$, and three linear maps, $R:V\otimes V^{\prime }\to V\otimes V^{\prime }$, $S:V\otimes V^{″}\to V\otimes V^{″}$ and $T:V^{\prime }\otimes V^{″}\to V^{\prime }\otimes V^{″}$. Then, a Yang-Baxter commutator is a map $[R,S,T]:V\otimes V^{\prime }\otimes V^{″}\to V\otimes V^{\prime }\otimes V^{″}$ defined by:

$$[R,S,T]=R_{12}\circ S_{13}\circ T_{23}-T_{23}\circ S_{13}\circ R_{12}$$

(4)

In terms of a Yang-Baxter commutator, the quantum Yang-Baxter Equation (2) is expressed simply as $[R,R,R]=0$.

Definition 2.3 Let V and $V^{\prime }$ be vector spaces. A system of linear maps,

$$W:V\otimes V\to V\otimes V,Z:V^{\prime }\otimes V^{\prime }\to V^{\prime }\otimes V^{\prime },X:V\otimes V^{\prime }\to V\otimes V^{\prime },$$

is called a WXZ-system, or a Yang-Baxter system, provided the following equations are satisfied:

$$[W,W,W]=0$$

(5)

$$[Z,Z,Z]=0$$

(6)

$$[W,X,X]=0$$

(7)

$$[X,X,Z]=0$$

(8)

The next remark plays an important role in this paper.

Remark 2.4 Given a WXZ-system as in Definition 2.3, one can construct a Yang-Baxter operator on $V^{″}=V\oplus V^{\prime }$, provided the maps $W,X,Z$ are invertible. This is a special case of a gluing procedure described in ([19], (Theorem 2.7)) (cf. [19], (Example 2.11)). Let $R=W\circ {\tau }_{V,V}$, $R^{\prime }=Z\circ {\tau }_{V^{\prime },V^{\prime }}$, $U=X\circ {\tau }_{V^{\prime },V}$. Then, the linear map:

$$R^{″}=R{\oplus }_U{R}^{\prime }:V^{″}\otimes V^{″}\to V^{″}\otimes V^{″}$$

given by: $R{\oplus }_U{R}^{\prime }{|}_{V\otimes V}=R$, $R{\oplus }_U{R}^{\prime }{|}_{V^{\prime }\otimes V^{\prime }}=R^{\prime }$ and for all $x\in V$, $y\in V^{\prime }$,

$$\left(R{\oplus }_U{R}^{\prime }\right)(y\otimes x)=U(y\otimes x),\left(R{\oplus }_U{R}^{\prime }\right)(x\otimes y)=U^{-1}(x\otimes y)$$

is a Yang-Baxter operator.

Definition 2.5 An algebra A is said to be entwined with an algebra B if there exists a linear map $\varphi :B\otimes A\to A\otimes B$ satisfying the following four conditions:

(1) 

$\varphi \circ (I_B\otimes {\mu }_A)=({\mu }_A\otimes I_B)\circ (I_A\otimes \varphi )\circ (\varphi \otimes I_A)$,

(2) 

$\varphi \circ ({\mu }_B\otimes I_A)=(I_A\otimes {\mu }_B)\circ (\varphi \otimes I_B)\circ (I_B\otimes \varphi )$,

(3) 

$\varphi \circ (I_B\otimes {\iota }_A)={\iota }_A\otimes I_B$,

(4) 

$\varphi \circ ({\iota }_B\otimes I_A)=I_A\otimes {\iota }_B$,

The map ϕ is known as an algebra factorization map, and the triple ${(A,B)}_{\varphi }$ is called an algebra factorization.

3. Algebra Factorizations, Yang-Baxter Systems and Braided Categories

Let $R:V\otimes V\to V\otimes V$ be a Yang-Baxter operator on V.

For an integer $n\ge 2$, let $R_i=R_{i,i+1}=R_{i,i+1}^n=I^{\otimes (i-1)}\otimes R\otimes I^{\otimes (n-i-1)}$, $i=1,\cdots ,n-1$.

On the tensor algebra, $T\left(V\right)$, we consider the following product:

for: $x=x_1\otimes \cdots \otimes x_n\in T^n\left(V\right)$, $n\ge 1$, and $y=y_1\otimes \cdots \otimes y_p\in T^p\left(V\right)$, $p\ge 1$,

$$\mu (x\otimes y)=xy=(R_p\cdots R_{n+p-1})\cdots (R_1\cdots R_n)(x\otimes y)$$

$$1x=x=x1\forall x\in T\left(V\right)$$

Although the invertibility of R is not essential for the following theorem, we assume that R is invertible in order to give a proof for it using braided categories.

Theorem 3.1 Starting with a WXZ-system as in Definition 2.3 and Remark 2.4, using the above notations and denoting by $R=W\circ {\tau }_{V,V}$, $R^{\prime }=Z\circ {\tau }_{V^{\prime },V^{\prime }}$, $U=X\circ {\tau }_{V^{\prime },V}$, we have the following properties.

(i) 

$(T\left(V\right),\mu ,1_k)$ and $(T\left(V^{\prime }\right),{\mu }^{\prime },1_k)$ are k-algebra structures.

(ii) 

There exists an algebra factorization, $\varphi :T\left(V^{\prime }\right)\otimes T\left(V\right)\to T\left(V\right)\otimes T\left(V^{\prime }\right)$, defined by ${\varphi }_{n,m}:T^n\left(V^{\prime }\right)\otimes T^m\left(V\right)\to T^m\left(V\right)\otimes T^n\left(V^{\prime }\right),$

$$\begin{array}{l}x\otimes y\mapsto (U_{m,m+1}\cdots U_{n+m-1,n+m})\cdots (U_{12}\cdots U_{n,n+1})(x\otimes y)\\ x\otimes 1_k\mapsto 1_k\otimes x,1_k\otimes y\mapsto y\otimes 1_k.\end{array}$$

Proof. A direct proof was presented in [20].

Another approach to this problem could be via braided algebras, and this was done in the revision of [20].

Now, we would like to prove it using the properties of a braided category. We start by proving (ii).

We use Remark 2.4 in order to obtain a new Yang-Baxter operator defined over $V^{″}=V\oplus V^{\prime }$, which will generate the braiding of a monoidal category.

The objects of this category are: $\{k,V^{″},V^{″}\otimes V^{″},V^{″}\otimes V^{″}\otimes V^{″},\cdots \}$.

The morphisms of this category are endomorphisms of $V^{″}$ and their tensor products.

Now: $R^{″}=R{\oplus }_U{R}^{\prime }:V^{″}\otimes V^{″}\to V^{″}\otimes V^{″}$ can be extended to a braiding.

The restrictions of the braiding generated by $R^{″}$ to subspaces of the form:

$V^{\otimes m}\otimes V^{\otimes n}\otimes V^{\otimes p},V^{\otimes m}\otimes V^{\otimes n}\otimes {\left(V^{\prime }\right)}^{\otimes p},{\left(V^{\prime }\right)}^{\otimes m}\otimes V^{\otimes n}\otimes V^{\otimes p},{\left(V^{\prime }\right)}^{\otimes m}\otimes {\left(V^{\prime }\right)}^{\otimes n}\otimes {\left(V^{\prime }\right)}^{\otimes p}\subset {\left(V^{″}\right)}^{\otimes m}\otimes {\left(V^{″}\right)}^{\otimes n}\otimes {\left(V^{″}\right)}^{\otimes p}$

imply that ϕ is an algebra factorization.

The proof of part (ii) includes the proof for part (i). □

Remark 3.2 From the previous theorem, $T_R\left(V\right)\otimes T_{R^{\prime }}\left(V^{\prime }\right)$ has an algebra structure associated with that algebra factorization. It is an open problem to study the relation between that structure and $T_{R{\oplus }_U{R}^{\prime }}(V\oplus V^{\prime })$ (see Remark 2.4).

Remark 3.3 In a natural way, $(T\left(V\right),\mu ,1_k)$ gets a bialgebra structure (if R is invertible).

The map, $\Delta \left(v\right)=v\otimes 1_k+1_k\otimes v\forall v\in V$, extends naturally to T(V). This can be done using the fact that any $x\in V^{\otimes n}$ can be thought of as a sum of products of n elements from V and requesting that $\Delta (v_1...v_n)=\Delta \left(v_1\right)...\Delta \left(v_n\right)$. The fact that R is invertible is essential here. The associativity of μ implies $\Delta \left(xy\right)=\Delta \left(x\right)\Delta \left(y\right)\forall x,y\in T\left(V\right)$.

The coassociativity of Δ follows from the fact that $(\Delta \otimes I)\circ \Delta \left(v\right)=(I\otimes \Delta )\circ \Delta \left(v\right)\forall v\in V$. For $x\in V^{\otimes n}$, $(\Delta \otimes I)\circ \Delta \left(x\right)=(I\otimes \Delta )\circ \Delta \left(x\right)$ follows from the definition of Δ.

We define $\epsilon \left(1_k\right)=1_k,\epsilon \left(v\right)=0\forall v\in V$, and by a similar argument we have $\epsilon \left(x\right)=0\forall x\in V^{\otimes n},n\ge 1$ (because ε is an algebra morphism).

The compatibility between Δ and ε follows, because $\epsilon \left(1_k\right)=1_k$ and $\epsilon \left(x\right)=0\forall x\in V^{\otimes n},n\ge 1$.

Remark 3.4 From the previous theorem, Remarks 3.2 and 3.3 and the assumption that U is invertible, it follows that $T_R\left(V\right)\otimes T_{R^{\prime }}\left(V^{\prime }\right)$ inherits a bialgebra structure. This can be done in the same spirit as Remark 3.3. (The invertibility of U is a key ingredient.)

This new bialgebra structure is different from any kind of bicrossed product of bialgebras presented in Section IX.2 of [21].